Real-Time Emergency Collision Avoidance for Unmanned Surface Vehicles with COLREGS Flexibly Obeyed
Abstract
:1. Introduction
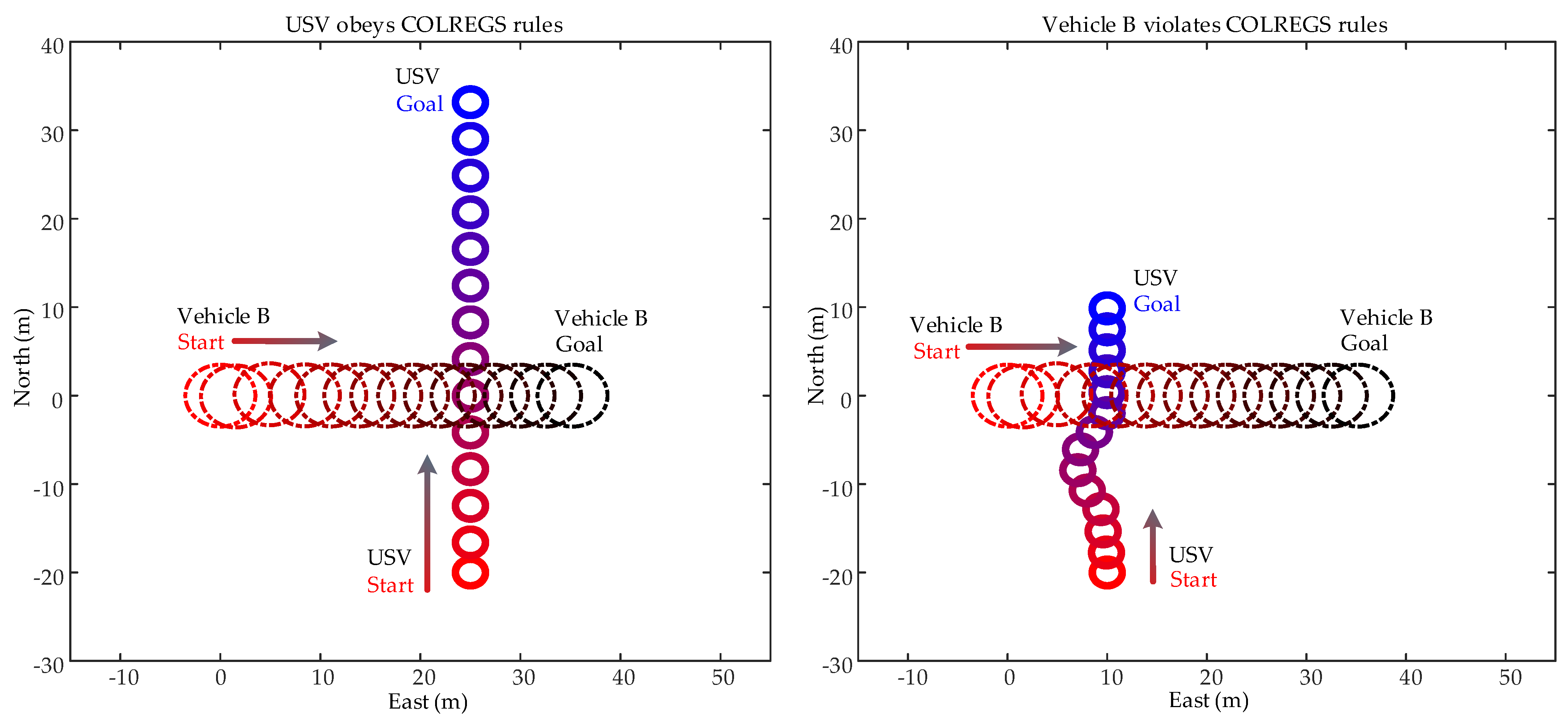
- A real-time collision-avoidance method is proposed for USVs to efficiently handle multiple obstacles and flexibly consider the COLREGS rules in the determination of TVO. For safety purposes, the motion uncertainty of the target ship is considered in an expandable set. Instead of blindly obeying the COLREGS rules, the USV can take an action that violates the rules in the context of a high collision risk.
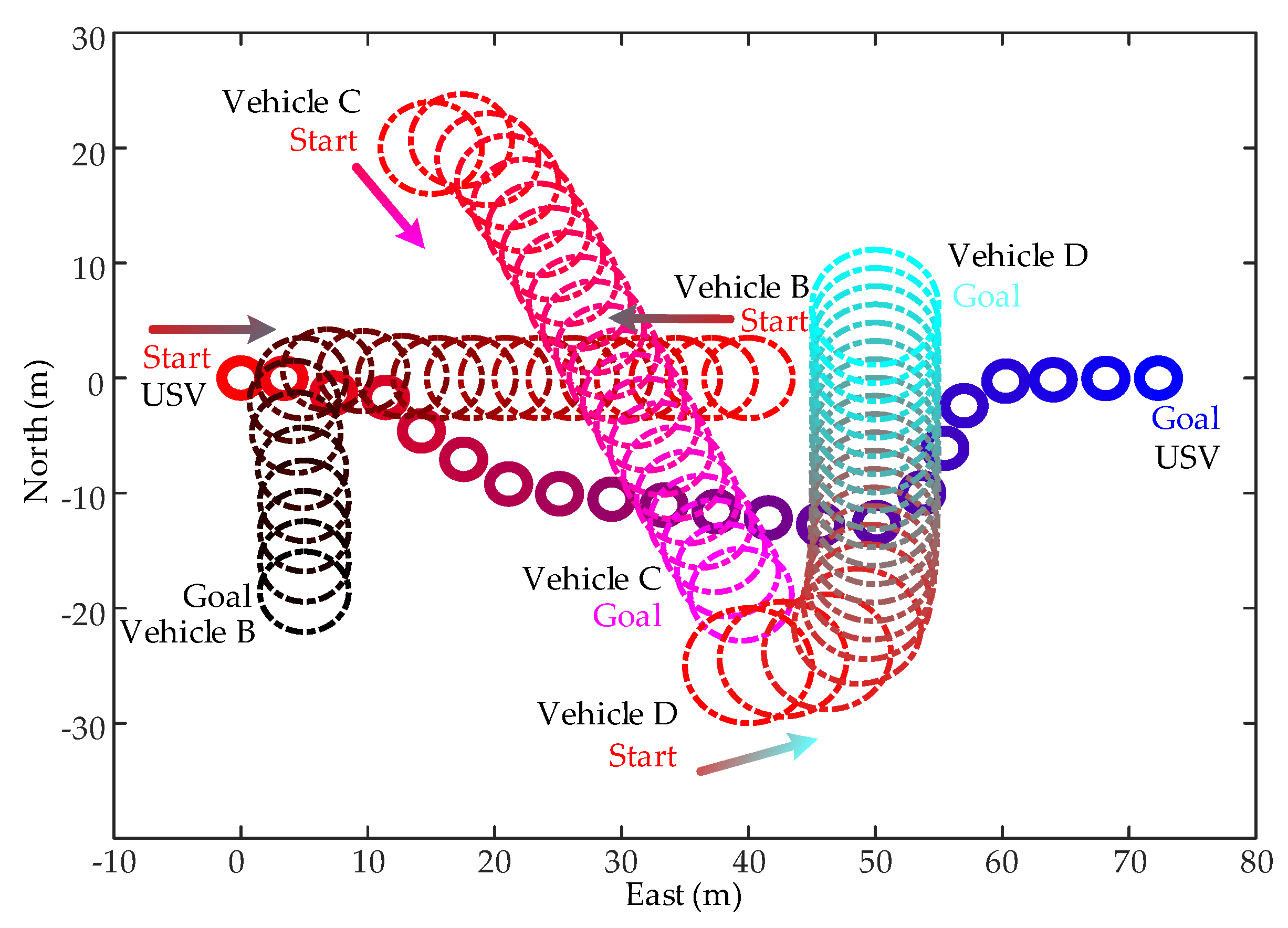
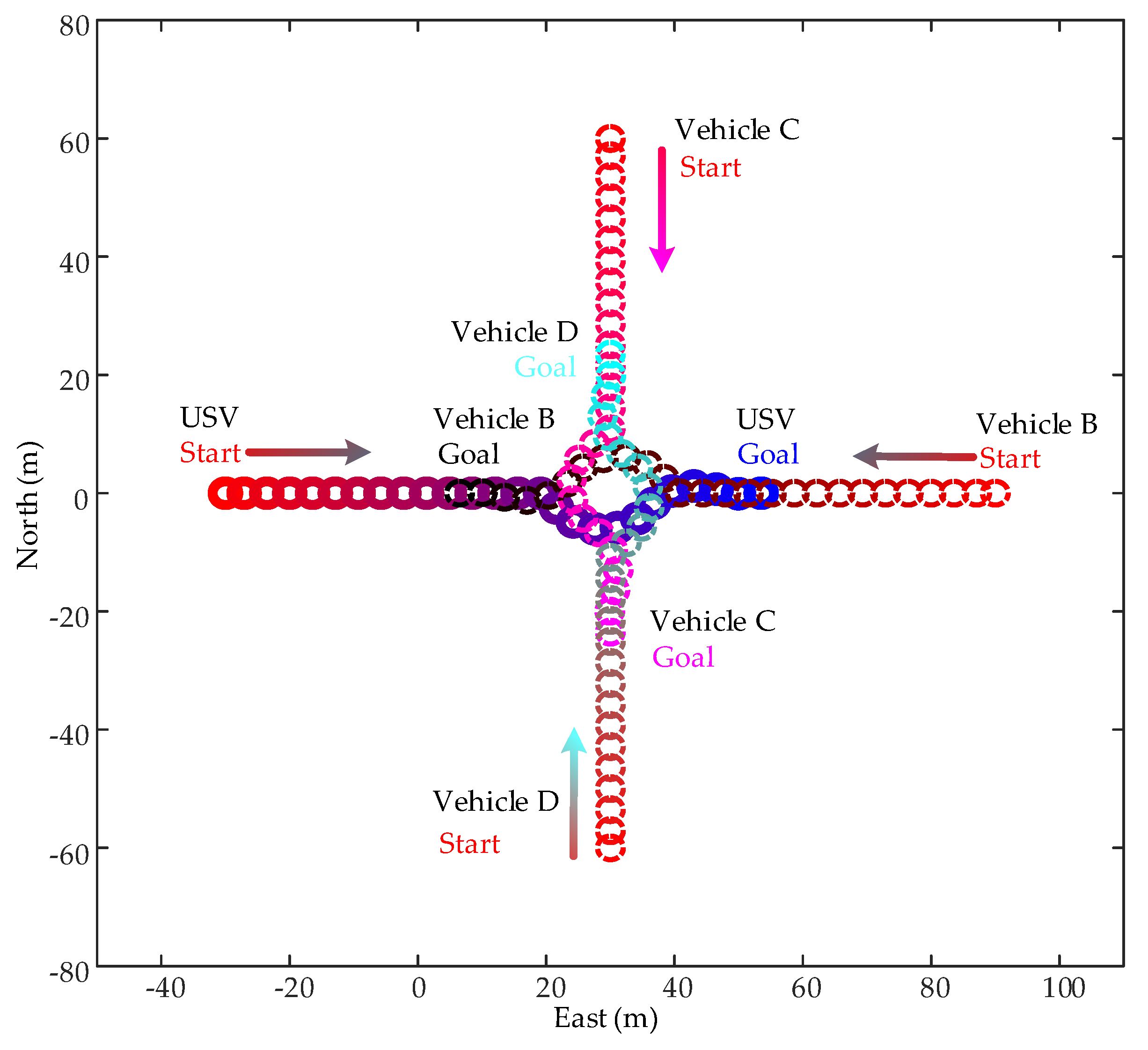
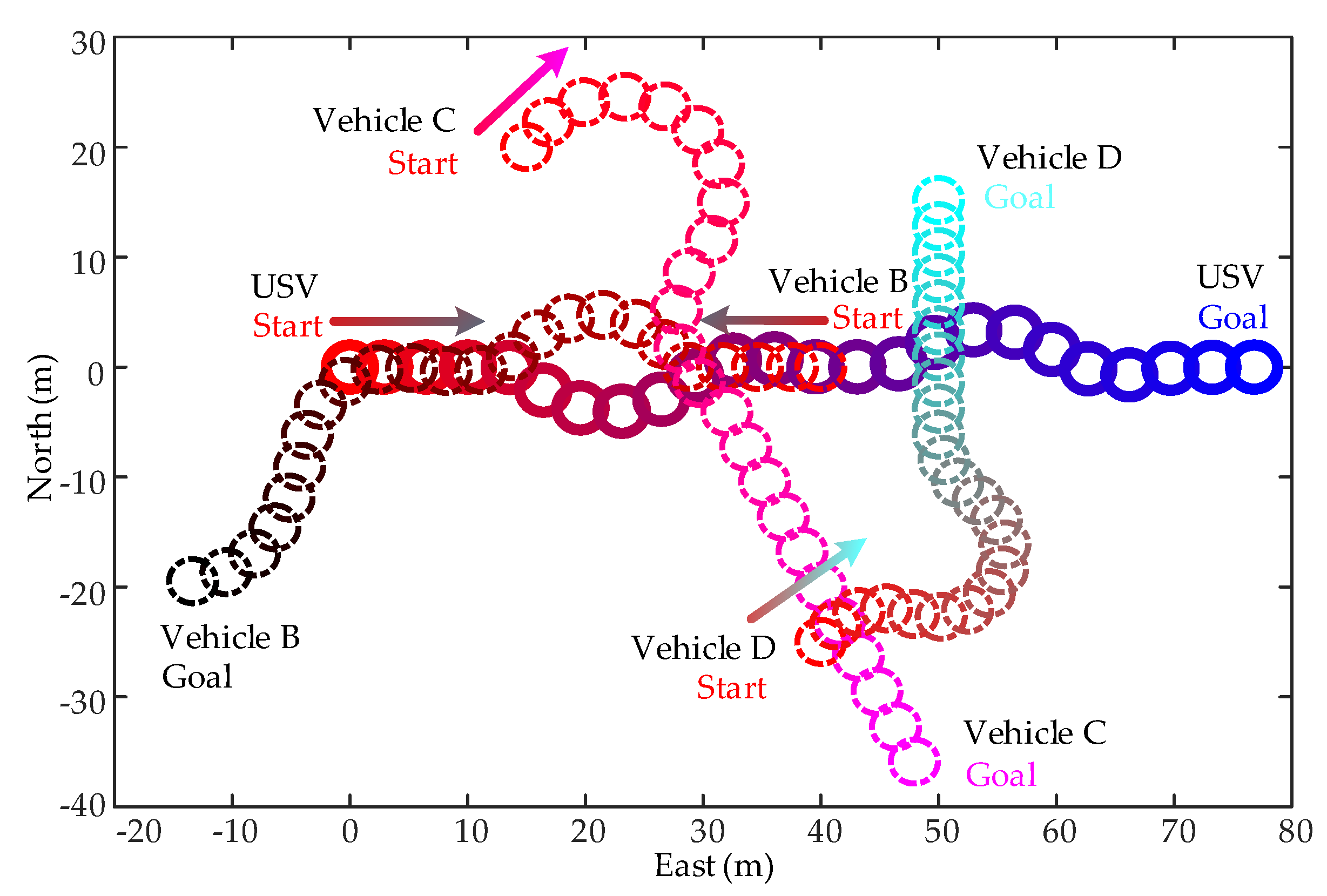
- Other than most existing methods that only take passive actions to avoid the moving target, the proposed method has no conflicts to take synchronous active actions for multiple vehicles.
- A discrete simultaneous planning and executing (SPAE) controller design is developed to promptly realize the assigned collision-free velocity. Compared to most conventional controllers, there is no need to fine-tune control gains and it is easy for non-control readers to understand and implement.
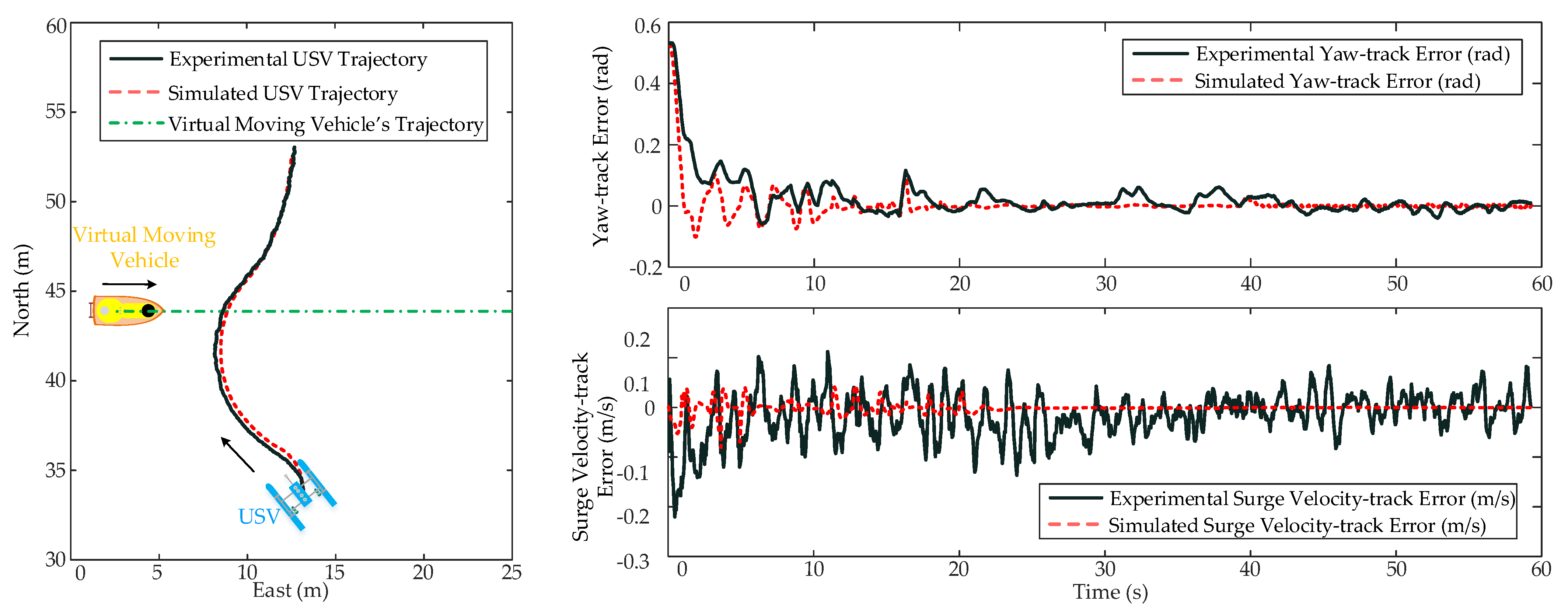
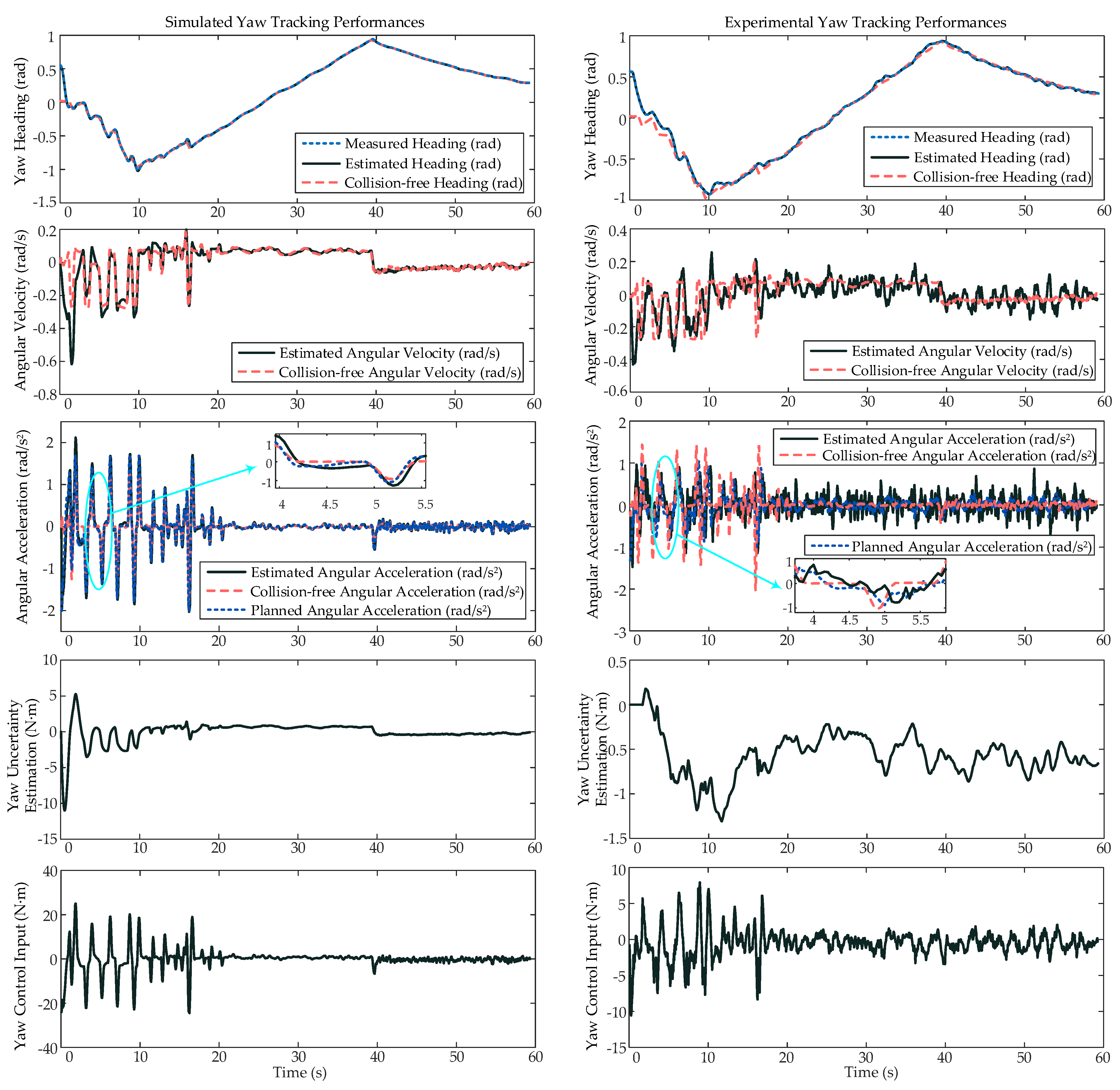
- To validate the proposed SPAE controller design, both simulations and experiments are conducted to realize a selected crossing scenario between two vehicles.
2. Collision Risk Assessment
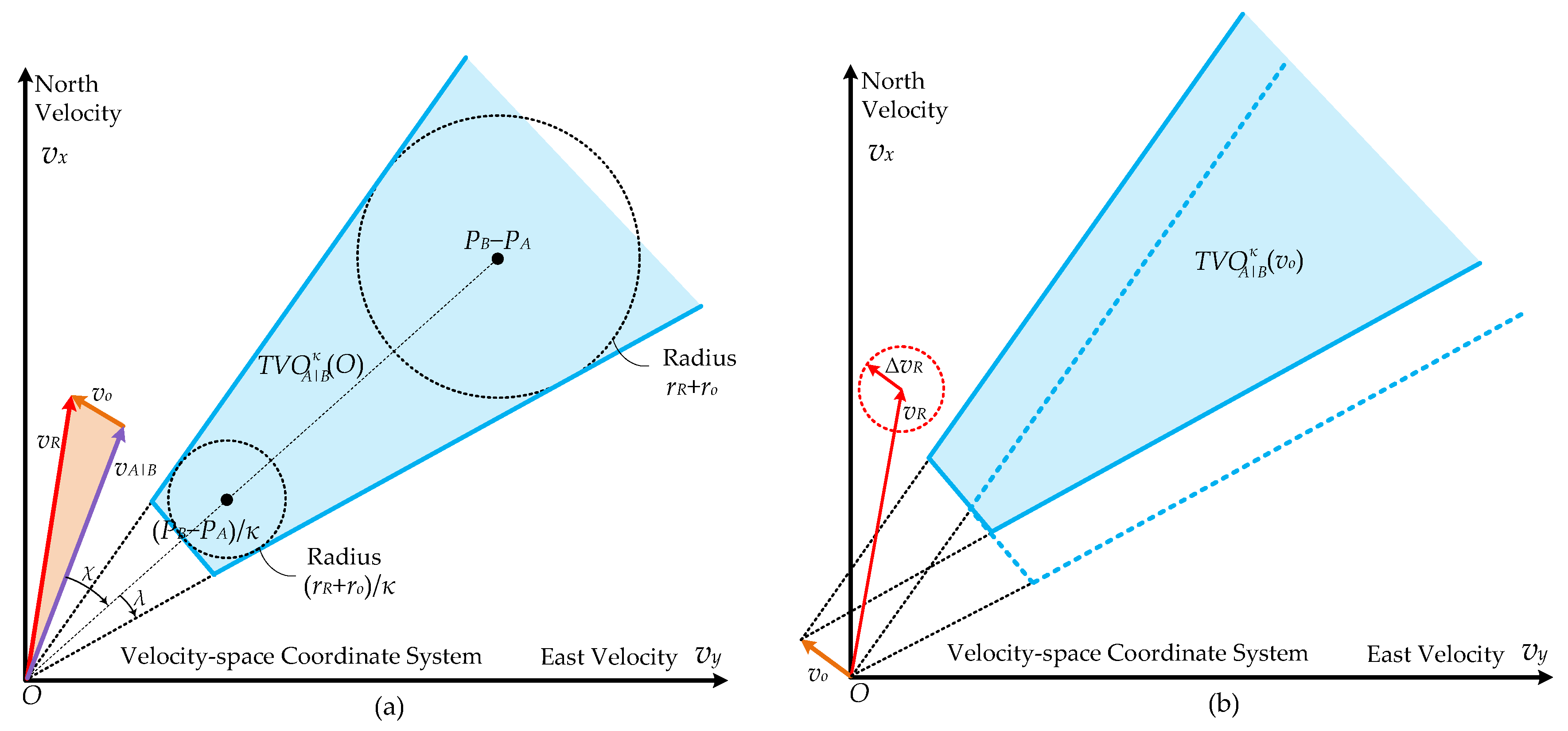
3. TVO-Based Collision Avoidance
4. Obstacle Expansion Induced by Motion Uncertainties and COLREGS Rules
4.1. COLREGS Rules
- Overtaking: The own ship should be taken as an overtaking ship when it comes up with another ship from a direction more than 22.5 degrees abaft its beam. The own ship can pass the moving ship on its port side or the starboard side.
- Head-on: When two head-on ships encounter each other on the reciprocal or nearly reciprocal courses, they should alter their courses to starboard such that each should pass on the port side of the other.
- Crossing: When two ships are crossing and have a collision risk, the ship with the other on its own starboard side should keep out of the way and shall, if the circumstances of the case admit, avoid crossing ahead of the other ship.
4.2. Obstacle Expansion Encouraged by COLREGS
5. USV Control System Design
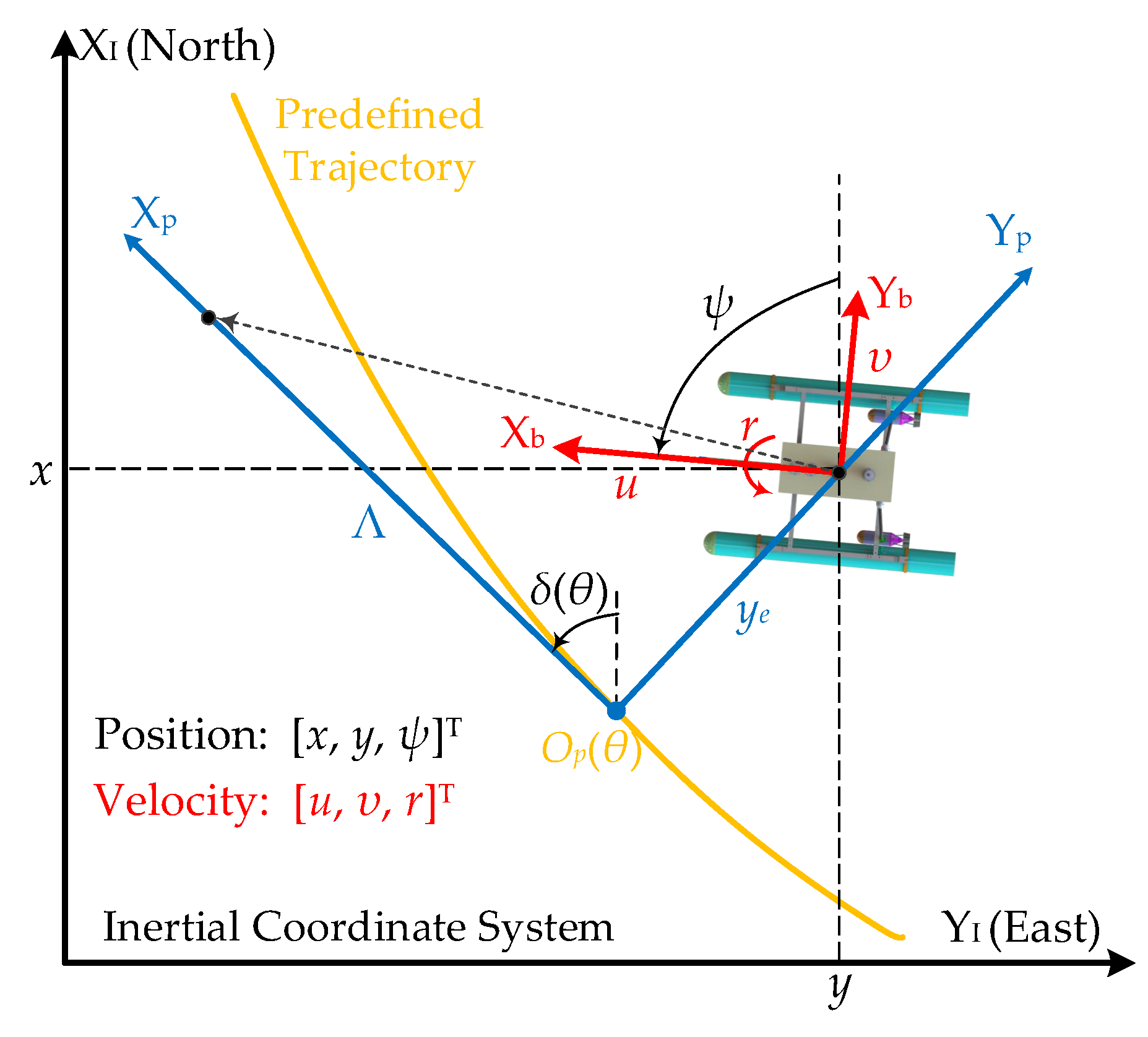
5.1. Mathematical Model for Marine Surface Vessels
5.2. Desired Surge Speed and Yaw Heading Assignment
5.3. State Estimation by Using a Three-Order Differentiator
5.4. SPAE Controller Design
- First-order polynomial planning for surge velocity-track motion: for a given time period , a first-order polynomial can be uniquely determined by satisfying the speed-track constraints of the present velocity-track error at time and a zero velocity-track error at time . To execute the acceleration-track error by using the planned acceleration as a reference, i.e., , the surge acceleration can be planned aswhere is the planned surge acceleration for the surge control execution. The collision-free acceleration can be obtained by using the above differentiator with as the input.
- Third-order polynomial planning for yaw heading-track motion: for a given time period , a third-order polynomial planning can be uniquely determined by satisfying the yaw-track constraints of the present states at time and zero states at time . Here, can be assigned as the planned angular acceleration. To execute the angular acceleration-track error by using the planned angular acceleration as a reference, i.e., , the angular acceleration can be planned aswhere is the planned angular acceleration for the yaw control execution. Similarly, the collision-free angular acceleration can be obtained by using the above differentiator with as the input.
5.5. System Convergence Analysis
5.5.1. Surge Velocity-Track Convergence
5.5.2. Yaw Heading-Track Convergence
6. Main Results and Discussions
6.1. System Setup
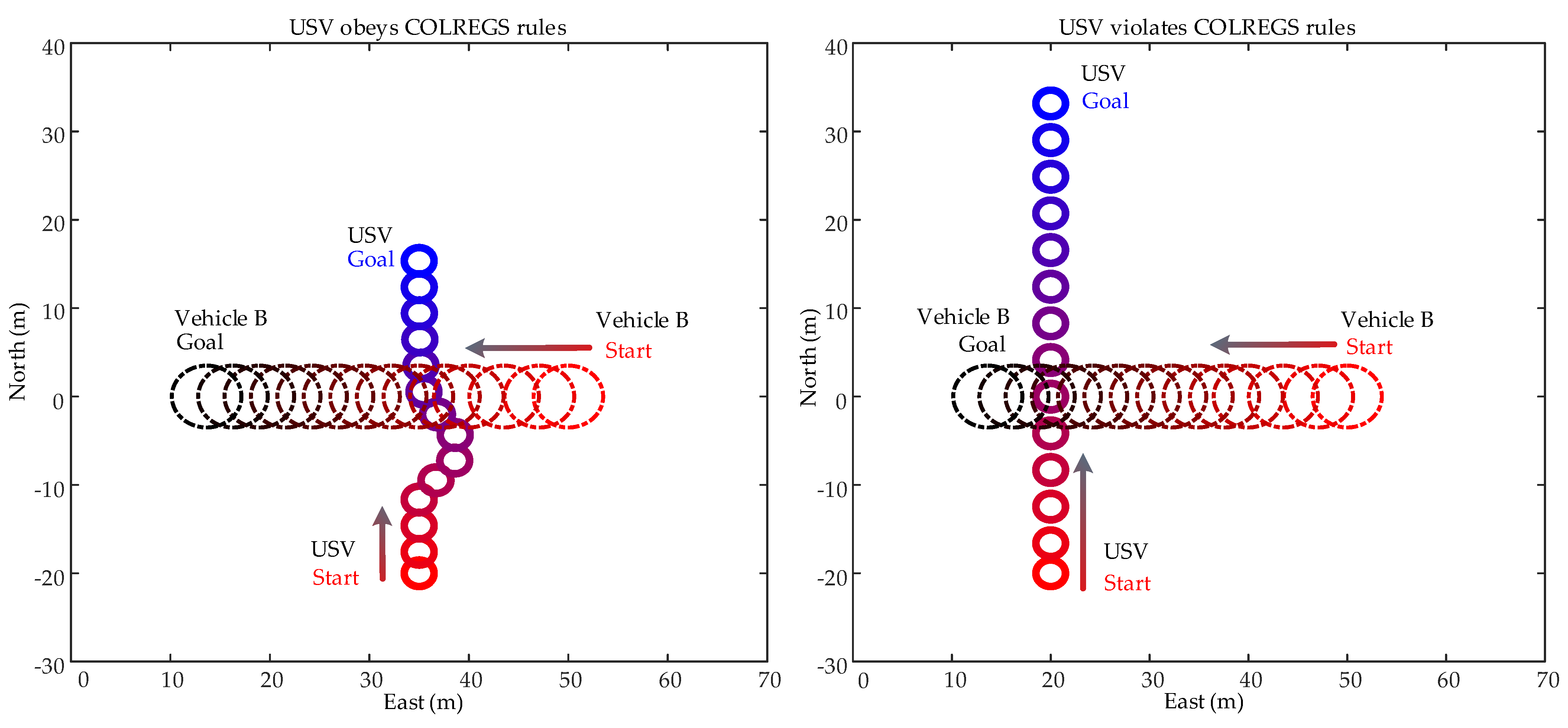
6.2. USV Passive Collision Avoidance
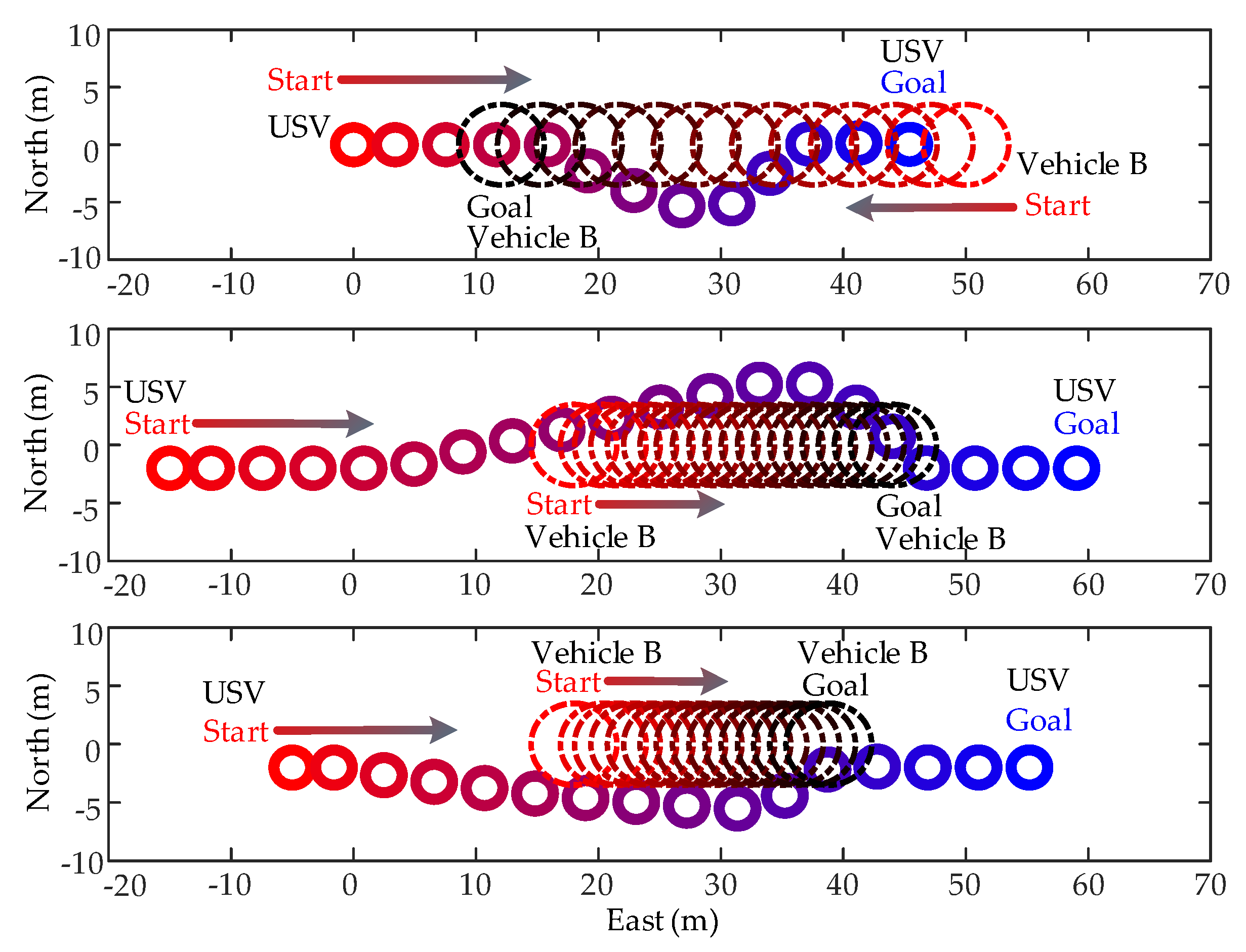
6.3. Active Collision Avoidance among Multiple Vehicles
6.4. Simulated and Experimental Validations of the Proposed SPAE Controller
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Campbell, S.; Naeem, W.; Irwin, G.W. A review on improving the autonomy of unmanned surface vehicles through intelligent collision avoidance manoeuvres. Annu. Rev. Control 2012, 36, 267–283. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Zhang, Y.; Yu, X.; Yuan, C. Unmanned surface vehicles: An overview of developments and challenges. Annu. Rev. Control 2016, 41, 71–93. [Google Scholar] [CrossRef]
- Qu, Y.; Xu, H.; Yu, W.; Feng, H.; Han, X. Inverse optimal control for speed-varying path following of marine vessels with actuator dynamics. J. Mar. Sci. Appl. 2017, 16, 225–236. [Google Scholar] [CrossRef]
- Vu, M.T.; Choi, H.S.; Kim, J.Y.; Tran, N.H. A study on an underwater tracked vehicle with a ladder trencher. Ocean Eng. 2016, 127, 90–102. [Google Scholar] [CrossRef]
- Vu, M.T.; Choi, H.S.; Nguyen, N.D.; Kim, S.K. Analytical design of an underwater construction robot on the slope with an up-cutting mode operation of a cutter bar. Appl. Ocean Res. 2019, 86, 289–309. [Google Scholar] [CrossRef]
- Zhang, W.; Shen, P.; Qi, H.; Zhang, Q.; Ma, T.; Li, Y. AUV path planning algorithm for terrain aided navigation. J. Mar. Sci. Eng. 2022, 10, 1393. [Google Scholar] [CrossRef]
- Zeng, X.; Xia, M.; Luo, Z.; Shang, J.; Xu, Y.; Yin, Q. Design and control of an Underwater Robot Based on Hybrid Propulsion of Quadrotor and Bionic Undulating Fin. J. Mar. Sci. Eng. 2022, 10, 1327. [Google Scholar] [CrossRef]
- Zhu, M.; Sun, W.; Wen, Y.; Huang, L. Extended state observer-based parameter identification of response model for autonomous vessels. J. Mar. Sci. Eng. 2022, 10, 1291. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, D.; Chen, Z.; Hu, X.; Lan, W. Adaptive dynamic surface control for formations of autonomous surface vehicles with uncertain dynamics. IEEE Trans. Control Syst. Technol. 2012, 21, 513–520. [Google Scholar] [CrossRef]
- Qu, Y.; Cai, L. Nonlinear positioning control for underactuated unmanned surface vehicles in the presence of environmental disturbances. IEEE/ASME Trans. Mechatronics 2022, 27, 1–11. [Google Scholar] [CrossRef]
- Sarda, E.I.; Qu, H.; Bertaska, I.R.; von Ellenrieder, K.D. Station-keeping control of an unmanned surface vehicle exposed to current and wind disturbances. Ocean Eng. 2016, 127, 305–324. [Google Scholar] [CrossRef] [Green Version]
- Caceres-Cruz, J.; Arias, P.; Guimarans, D.; Riera, D.; Juan, A.A. Rich vehicle routing problem: Survey. ACM Comput. Surv. 2014, 47, 32. [Google Scholar] [CrossRef]
- Ayawli, B.B.K.; Chellali, R.; Appiah, A.Y.; Kyeremeh, F. An overview of nature-inspired, conventional, and hybrid methods of autonomous vehicle path planning. J. Adv. Transp. 2018, 2018, 8269698. [Google Scholar] [CrossRef]
- Huang, S.; Teo, R.S.H.; Tan, K.K. Collision avoidance of multi unmanned aerial vehicles: A review. Annu. Rev. Control 2019, 48, 147–164. [Google Scholar] [CrossRef]
- Yasin, J.N.; Mohamed, S.A.; Haghbayan, M.H.; Heikkonen, J.; Tenhunen, H.; Plosila, J. Unmanned aerial vehicles (uavs): Collision avoidance systems and approaches. IEEE Access 2020, 8, 105139–105155. [Google Scholar] [CrossRef]
- Ozturk, U.; Cicek, K. Individual collision risk assessment in ship navigation: A systematic literature review. Ocean Eng. 2019, 180, 130–143. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, L.; Chen, P.; Negenborn, R.R.; van Gelder, P.H.A.J.M. Ship collision avoidance methods: State-of-the-art. Saf. Sci. 2020, 121, 451–473. [Google Scholar] [CrossRef]
- Akdağ, M.; Solnør, P.; Johansen, T.A. Collaborative collision avoidance for Maritime Autonomous Surface Ships: A review. Ocean Eng. 2022, 250, 110920. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Y.; Wang, B.; Ding, S.; Jiang, P. A lightweight sea surface object detection network for unmanned surface vehicles. J. Mar. Sci. Eng. 2022, 10, 965. [Google Scholar] [CrossRef]
- Shi, J.; Liu, Z. Track pairs collision detection with applications to ship collision risk assessment. J. Mar. Sci. Eng. 2022, 10, 216. [Google Scholar] [CrossRef]
- Song, L.; Chen, H.; Xiong, W.; Zaopeng, D.; Mao, P.; Xiang, Z.; Hu, K. Method of emergency collision avoidance for unmanned surface vehicle (USV) based on motion ability database. Pol. Marit. Res. 2019, 26, 55–67. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Zhang, G.; Liu, C.; Zhang, W. COLREGs-constrained adaptive fuzzy event-triggered control for underactuated surface vessels with the actuator failures. IEEE Trans. Fuzzy Syst. 2020, 29, 3822–3832. [Google Scholar] [CrossRef]
- Bakdi, A.; Vanem, E. Fullest COLREGs evaluation using fuzzy logic for collaborative decision-making analysis of autonomous ships in complex situations. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18433–18445. [Google Scholar] [CrossRef]
- Lyu, H.; Yin, Y. COLREGS-constrained real-time path planning for autonomous ships using modified artificial potential fields. J. Navig. 2019, 72, 588–608. [Google Scholar] [CrossRef]
- Zhu, Z.; Lyu, H.; Zhang, J.; Yin, Y. An efficient ship automatic collision avoidance method based on modified artificial potential field. J. Mar. Sci. Eng. 2021, 10, 3. [Google Scholar] [CrossRef]
- Tan, G.; Zhuang, J.; Zou, J.; Wan, L.; Sun, Z. Artificial potential field-based swarm finding of the unmanned surface vehicles in the dynamic ocean environment. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420925309. [Google Scholar] [CrossRef]
- Colito, J. Autonomous mission planning and execution for unmanned surface vehicles in compliance with the marine rules of the road. Master’s Thesis, University of Washington, Seattle, WA, USA, 2007. [Google Scholar]
- Zhao, L.; Roh, M.I. COLREGs-compliant multiship collision avoidance based on deep reinforcement learning. Ocean Eng. 2019, 191, 106436. [Google Scholar] [CrossRef]
- Xu, X.; Cai, P.; Ahmed, Z.; Yellapu, V.S.; Zhang, W. Path planning and dynamic collision avoidance algorithm under COLREGs via deep reinforcement learning. Neurocomputing 2022, 468, 181–197. [Google Scholar] [CrossRef]
- Xu, X.; Lu, Y.; Liu, X.; Zhang, W. Intelligent collision avoidance algorithms for USVs via deep reinforcement learning under COLREGs. Ocean Eng. 2020, 217, 107704. [Google Scholar] [CrossRef]
- Li, L.; Wu, D.; Huang, Y.; Yuan, Z.M. A path planning strategy unified with a COLREGS collision avoidance function based on deep reinforcement learning and artificial potential field. Appl. Ocean Res. 2021, 113, 102759. [Google Scholar] [CrossRef]
- Xu, Q.; Yang, Y.; Zhang, C.; Zhang, L. Deep convolutional neural network-based autonomous marine vehicle maneuver. Int. J. Fuzzy Syst. 2018, 20, 687–699. [Google Scholar] [CrossRef]
- Xie, S.; Garofano, V.; Chu, X.; Negenborn, R.R. Model predictive ship collision avoidance based on Q-learning beetle swarm antenna search and neural networks. Ocean Eng. 2019, 193, 106609. [Google Scholar] [CrossRef]
- Song, A.L.; Su, B.Y.; Dong, C.Z.; Shen, D.W.; Xiang, E.Z.; Mao, F.P. A two-level dynamic obstacle avoidance algorithm for unmanned surface vehicles. Ocean Eng. 2018, 170, 351–360. [Google Scholar] [CrossRef]
- Song, L.; Chen, Z.; Zaopeng, D.; Xiang, Z.; Mao, Y.; Su, Y.; Hu, K. Collision avoidance planning for unmanned surface vehicle based on eccentric expansion. Int. J. Adv. Robot. Syst. 2019, 16, 172988141985194. [Google Scholar] [CrossRef]
- Fiorini, P.; Shiller, Z. Motion planning in dynamic environments using velocity obstacles. Int. J. Robot. Res. 1998, 17, 760–772. [Google Scholar] [CrossRef]
- Snape, J.; Guy, S.J.; Vembar, D.; Lake, A.; Lin, M.C.; Manocha, D. Reciprocal collision avoidance and navigation for video games. In Proceedings of the Game Developers Conference, San Francisco, CA, USA, 5–9 March 2012; Volume 1. [Google Scholar]
- Berg, J.v.d.; Guy, S.J.; Lin, M.; Manocha, D. Reciprocal n-body collision avoidance. In Robotics Research; Springer: Berlin/Heidelberg, Germany, 2011; pp. 3–19. [Google Scholar]
- Kuwata, Y.; Wolf, M.T.; Zarzhitsky, D.; Huntsberger, T.L. Safe maritime autonomous navigation with OLREGS, using velocity obstacles. IEEE J. Ocean. Eng. 2014, 39, 110–119. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, W.; Shi, P. A real-time collision avoidance learning system for unmanned surface vessels. Neurocomputing 2016, 182, 255–266. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, L.; van Gelder, P.H.A.J.M. Generalized velocity obstacle algorithm for preventing ship collisions at sea. Ocean Eng. 2019, 173, 142–156. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Skjetne, R.; Smogeli, ØN.; Fossen, T.I. A nonlinear ship manoeuvering model: Identification and adaptive control with experiments for a model ship. Model. Identif. Control 2004, 25, 3–27. [Google Scholar] [CrossRef] [Green Version]
- Qu, Y.; Cai, L. Nonlinear station keeping control for underactuated unmanned surface vehicles to resist environmental disturbances. Ocean Eng. 2022, 246, 110603. [Google Scholar] [CrossRef]
- Skjetne, R. The maneuvering problem. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2005. [Google Scholar]
- Fossen, T.I.; Pettersen, K.Y. On uniform semiglobal exponential stability (USGES) of proportional line-of-sight guidance laws. Automatica 2014, 50, 2912–2917. [Google Scholar] [CrossRef] [Green Version]
- Fossen, T.I.; Pettersen, K.Y.; Galeazzi, R. Line-of-sight path following for Dubins paths with adaptive sideslip compensation of drift forces. IEEE Trans. Control Syst. Technol. 2015, 23, 820–827. [Google Scholar] [CrossRef] [Green Version]
- Caharija, W.; Pettersen, K.Y.; Bibuli, M.; Calado, P.; Zereik, E.; Braga, J.; Gravdahl, J.T.; Sørensen, A.J.; Milovanović, M.; Bruzzone, G. Integral line-of-sight guidance and control of underactuated marine vehicles: Theory, simulations, and experiments. IEEE Trans. Control Syst. Technol. 2016, 24, 1623–1642. [Google Scholar] [CrossRef] [Green Version]
- Qu, Y.; Cai, L.; Xu, H. Curved path following for unmanned surface vehicles with heading amendment. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 51, 4183–4192. [Google Scholar] [CrossRef]
- Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D.; Khan, A. A constrained A* approach towards optimal path planning for an unmanned surface vehicle in a maritime environment containing dynamic obstacles and ocean currents. Ocean Eng. 2018, 169, 187–201. [Google Scholar] [CrossRef] [Green Version]
- Singh, Y.; Bibuli, M.; Zereik, E.; Sharma, S.; Khan, A.; Sutton, R. A novel double layered hybrid multi-robot framework for guidance and navigation of unmanned surface vehicles in a practical maritime environment. J. Mar. Sci. Eng. 2020, 8, 624. [Google Scholar] [CrossRef]
- Lekkas, A.M.; Fossen, T.I. Integral LOS path following for curved paths based on a monotone cubic hermite spline parametrization. IEEE Trans. Control Syst. Technol. 2014, 22, 2287–2301. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Peng, Z. ESO-based line-of-sight guidance law for path following of underactuated marine surface vehicles with exact sideslip compensation. IEEE J. Ocean. Eng. 2017, 42, 477–487. [Google Scholar] [CrossRef]
- Qu, Y.; Cai, L. An adaptive delay-compensated filtering system and the application to path following control for unmanned surface vehicles. ISA Trans. 2022; 1–13, in press. [Google Scholar] [CrossRef]
- Levant, A.; Livne, M.; Yu, X. Sliding-mode-based differentiation and its application. IFAC-PapersOnLine 2017, 50, 1699–1704. [Google Scholar] [CrossRef]
- Levant, A.; Yu, X. Sliding-mode-based differentiation and filtering. IEEE Trans. Autom. Control 2018, 63, 3061–3067. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Z.; Yang, G. Finite-time-convergent differentiator based on singular perturbation technique. IEEE Trans. Autom. Control 2007, 52, 1731–1737. [Google Scholar] [CrossRef]
- Wang, X.; Lin, H. Design and frequency analysis of continuous finite-time-convergent differentiator. Aerosp. Sci. Technol. 2012, 18, 69–78. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Shirinzadeh, B. High-order nonlinear differentiator and application to aircraft control. Mech. Syst. Signal Process. 2014, 46, 227–252. [Google Scholar] [CrossRef]
- Wang, X.; Cai, L. Aircraft navigation based on differentiation-integration observer. Aerosp. Sci. Technol. 2017, 68, 109–122. [Google Scholar] [CrossRef]
- Chai, Y.; Cai, L. Realization of reachability for the control of a class of nonlinear systems. IEEE Trans. Autom. Control 2019, 65, 1073–1088. [Google Scholar] [CrossRef]
- Yang, Q.; Cai, L. State-dependent finite-time controller design and its application to positioning control task for underactuated unmanned surface vehicles. Ocean Eng. 2023, 267, 113311. [Google Scholar] [CrossRef]









| Items | Specifications | Values |
|---|---|---|
| Truncated value | 20 | |
| USV configuration radius | 2 (m) | |
| Configuration radius of moving vehicles | 2, 3.5, 4.5, and 5.5 (m) | |
| Secure encounter distance | (m) | |
| The reaction distance to avoid obstacle | (m) | |
| Maximum expansion of velocity magnitude | ||
| Gain of velocity measurement uncertainty | ||
| Expansion rate of magnitude | ||
| b | Maximum bearing angle | |
| c | Minimum relative speed | |
| Maximum expansion of orientation | ||
| Scaling gain of orientation | ||
| Differentiator parameter | ||
| Differentiator parameter | ||
| Differentiator parameter | ||
| Differentiator parameter | ||
| Differentiator parameter | ||
| Surge planning time period | s | |
| Surge uncertainty estimation gain | ||
| Yaw planning time period | s | |
| Yaw uncertainty estimation gain |
| Comparative | Indexes | |||
|---|---|---|---|---|
| Methods | Number of | Number of | Number of | Successful |
| Encounter | Collision | Violated Rules | Percentage | |
| Velocity Obstacle (VO) | 100 | 4 | 18 | 96% |
| VO with COLREGS Blindly Obeyed | 100 | 2 | 0 | 98% |
| Proposed Method | 100 | 0 | 5 | 100% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, Y.; Cai, L. Real-Time Emergency Collision Avoidance for Unmanned Surface Vehicles with COLREGS Flexibly Obeyed. J. Mar. Sci. Eng. 2022, 10, 2025. https://doi.org/10.3390/jmse10122025
Qu Y, Cai L. Real-Time Emergency Collision Avoidance for Unmanned Surface Vehicles with COLREGS Flexibly Obeyed. Journal of Marine Science and Engineering. 2022; 10(12):2025. https://doi.org/10.3390/jmse10122025
Chicago/Turabian StyleQu, Yang, and Lilong Cai. 2022. "Real-Time Emergency Collision Avoidance for Unmanned Surface Vehicles with COLREGS Flexibly Obeyed" Journal of Marine Science and Engineering 10, no. 12: 2025. https://doi.org/10.3390/jmse10122025
APA StyleQu, Y., & Cai, L. (2022). Real-Time Emergency Collision Avoidance for Unmanned Surface Vehicles with COLREGS Flexibly Obeyed. Journal of Marine Science and Engineering, 10(12), 2025. https://doi.org/10.3390/jmse10122025







