Properties of the Acoustic Vector Field near the Underwater Planar Cavity Baffle and Its Application
Abstract
:1. Introduction
2. The Method of Calculating the Acoustic Vector Field near the Planar Cavity Baffle
3. The Properties of the Acoustic Vector Field near the Planar Cavity Baffle
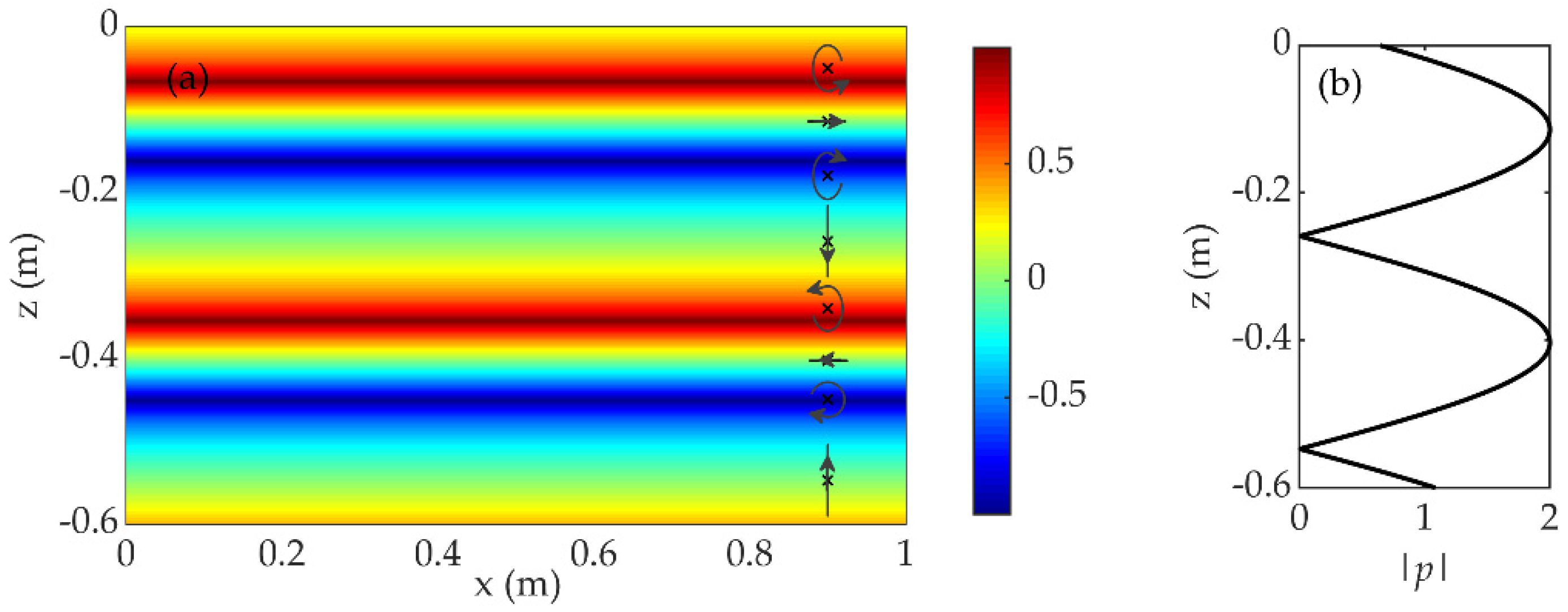
3.1. The Properties of Pressure, Particle Velocity, and Complex Intensity near the Baffle Based on the Euler Description
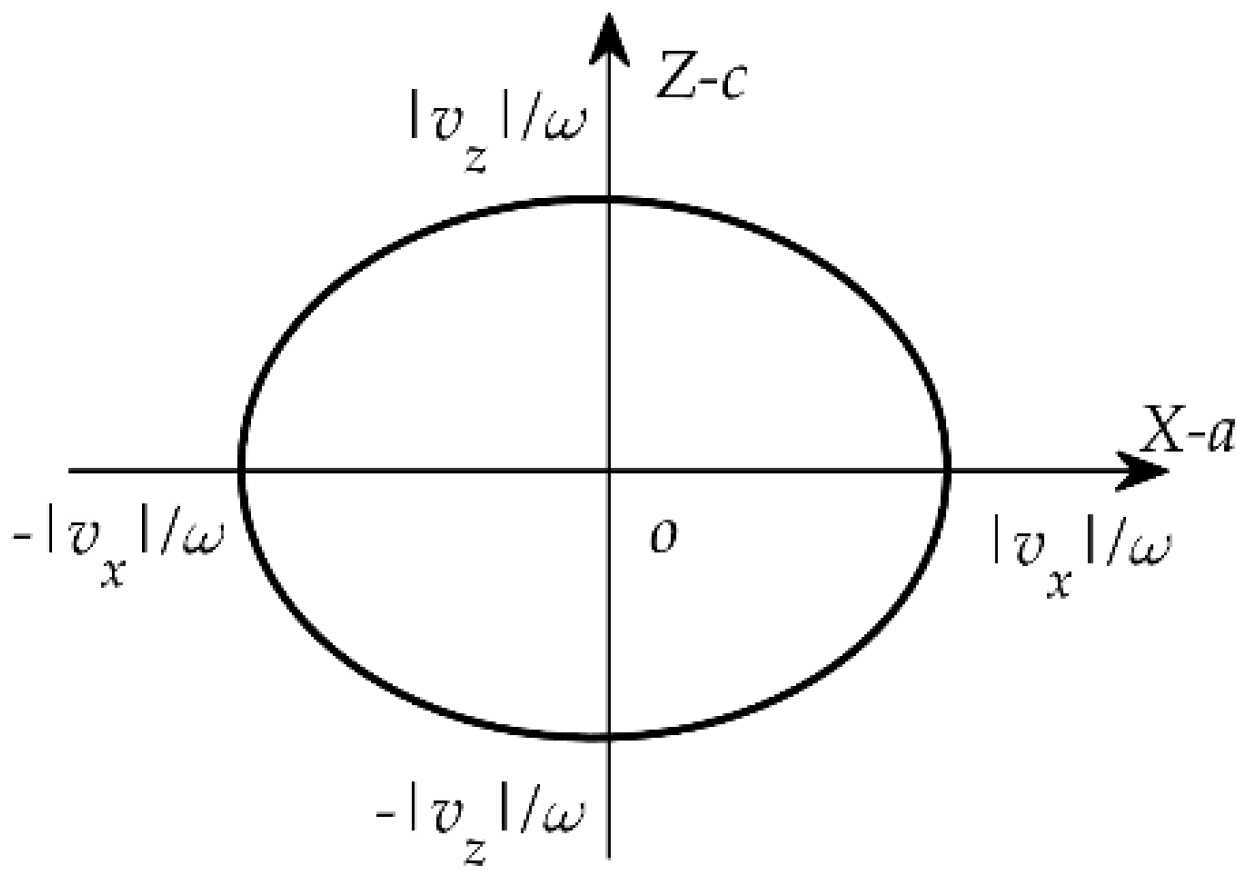
3.2. The Properties of the Acoustic Particle Motion near the Baffle Based on the Lagrange Description
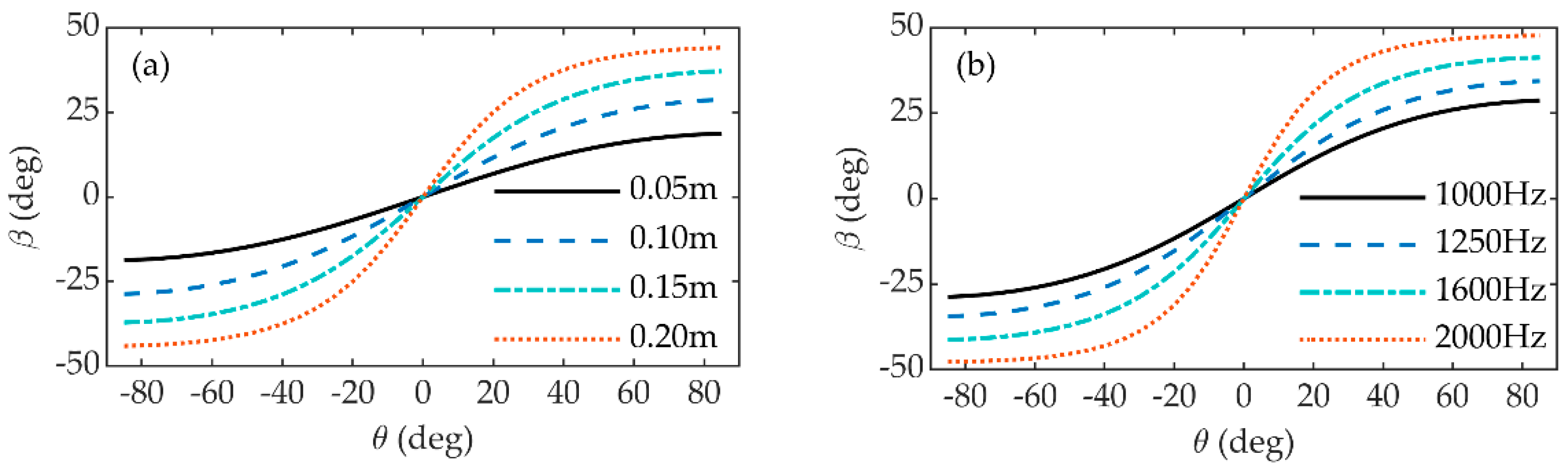
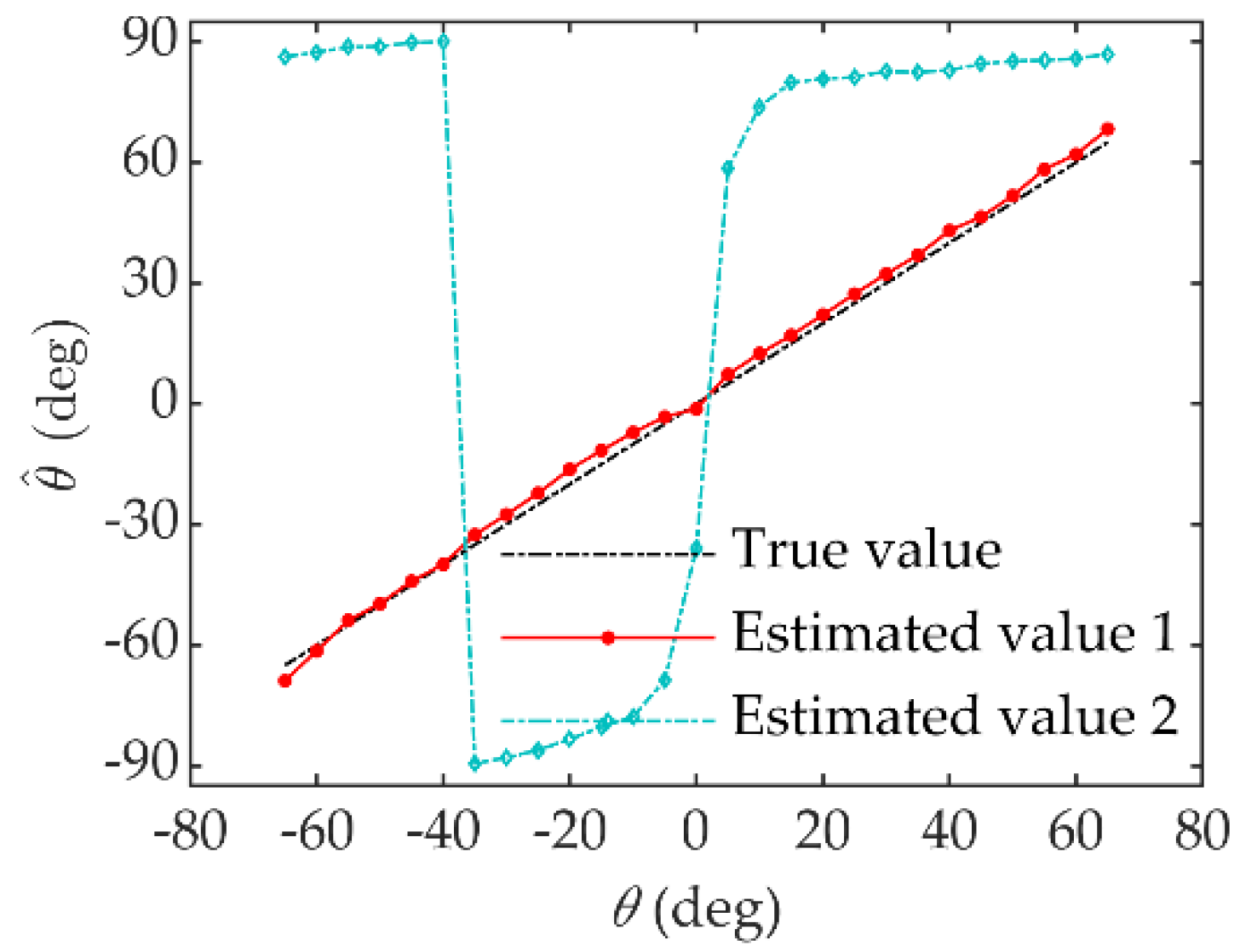
4. The Application of the Properties of the Acoustic Vector Field near the Baffle
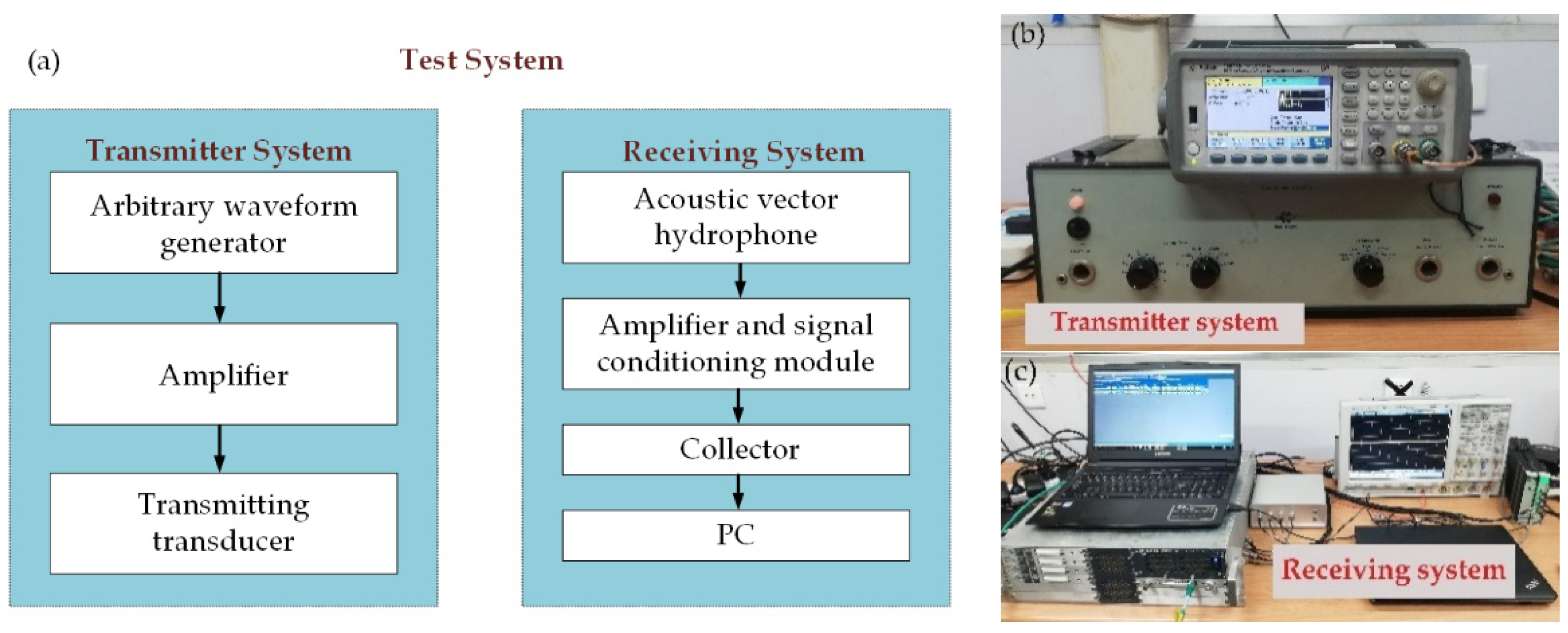
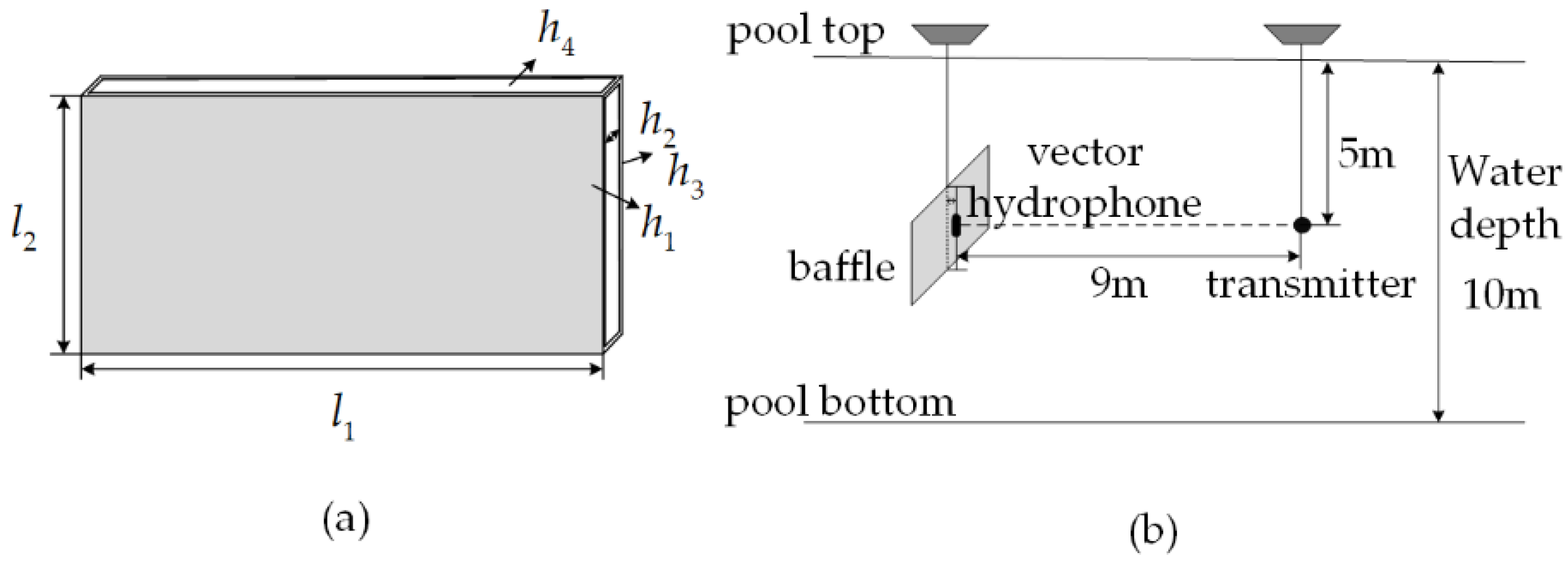
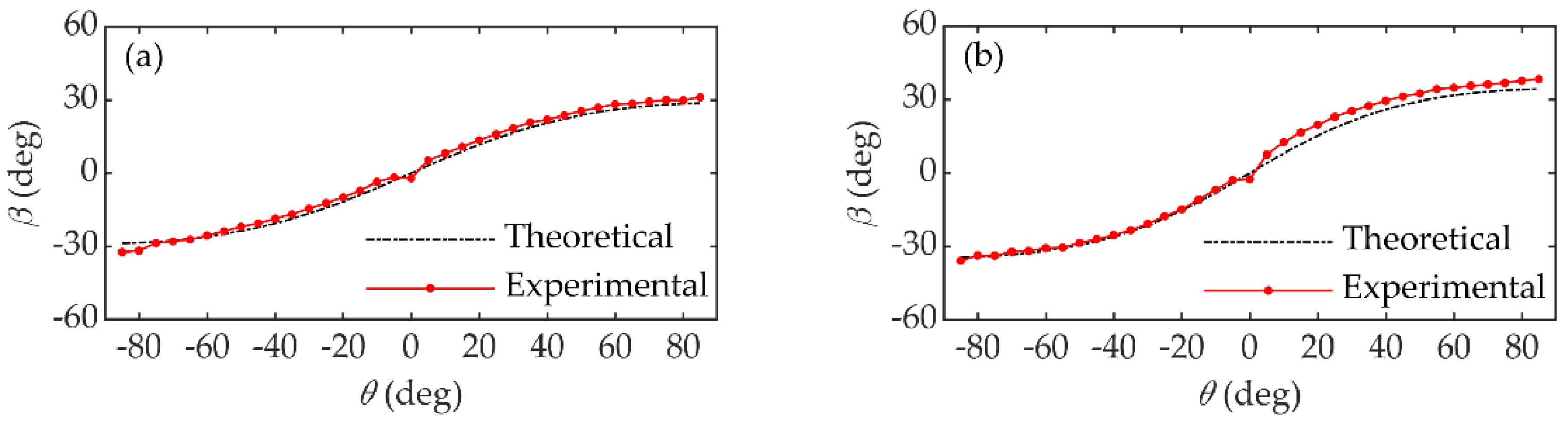
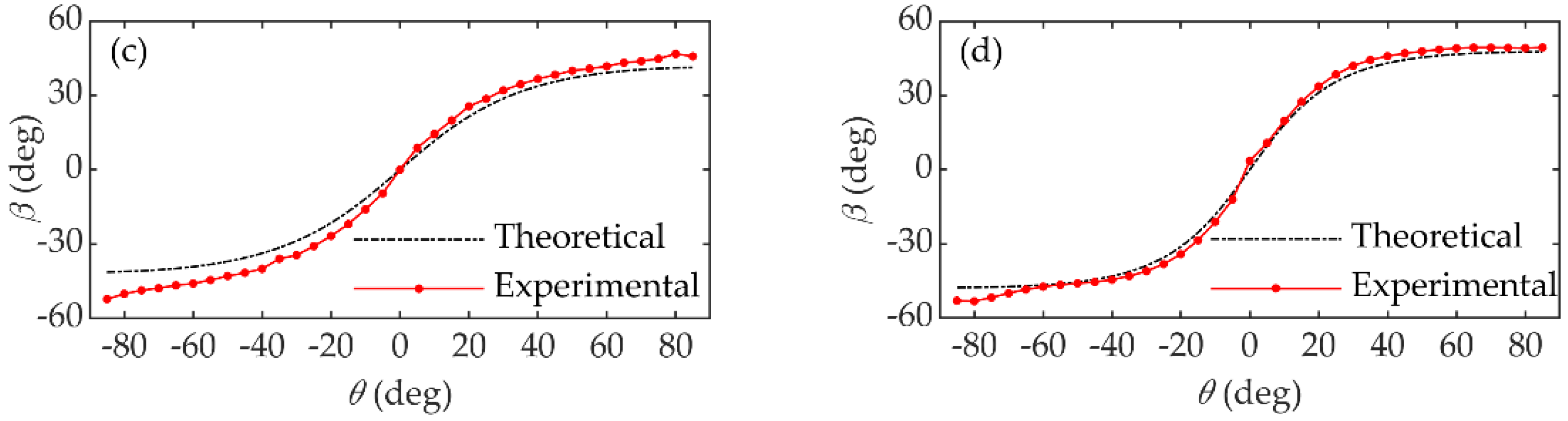
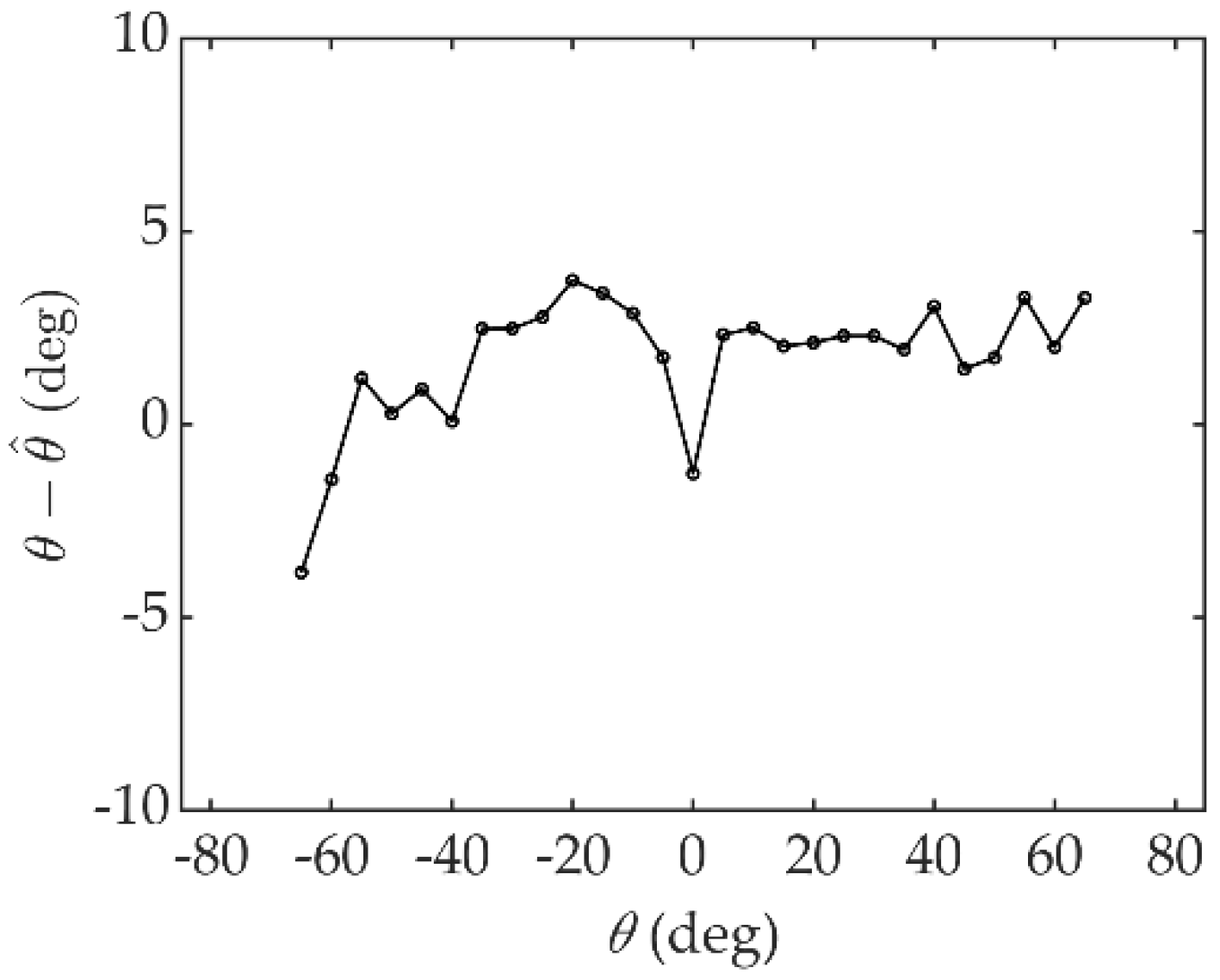
5. Experiment Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Santos, P.; Rodríguez, O.C.; Felisberto, P.; Jesus, S.M. Seabed geoacoustic characterization with a vector sensor array. J. Acoust. Soc. Am. 2010, 128, 2652–2663. [Google Scholar] [CrossRef] [Green Version]
- Han, X.; Yin, J.; Yu, G.; Du, P. Experimental demonstration of single carrier underwater acoustic communication using a vector sensor. Appl Acoust. 2015, 98, 1–5. [Google Scholar] [CrossRef]
- Song, X.; Jian, Z.; Zhang, G.; Liu, M.; Guo, N.; Zhang, W. New Research on MEMS Acoustic Vector Sensors Used in Pipeline Ground Markers. Sensors 2015, 15, 274–284. [Google Scholar] [CrossRef] [Green Version]
- Stinco, P.; Tesei, A.; Dreo, R.; Micheli, M. Detection of envelope modulation and direction of arrival estimation of multiple noise sources with an acoustic vector sensor. J. Acoust. Soc. Am. 2021, 149, 1596–1608. [Google Scholar] [CrossRef]
- Nehorai, A.; Paldi, E. Acoustic vector-sensor array processing. IEEE Trans. Signal Process. 1994, 42, 2481–2491. [Google Scholar] [CrossRef]
- Wu, Y.; Li, G.; Hu, Z.; Hu, Y. Unambiguous directions of arrival estimation of coherent sources using acoustic vector sensor linear arrays. IET Radar. Sonar. Navig. 2015, 9, 318–323. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, J. Coherent signal-subspace processing of acoustic vector sensor array for doa estimation of wideband sources. Signal Process. 2005, 85, 837–847. [Google Scholar] [CrossRef]
- Kosobrodov, R.A.; Nekrasov, V.N. Effect of the diffraction of sound by the carrier of hydroacoustic equipment on the results of measurements. Acoust. Phys. 2001, 47, 323–328. [Google Scholar] [CrossRef]
- Barton, J.P.; Wolff, N.L.; Zhang, H.; Tarawneh, C. Near-field calculations for a rigid spheroid with an arbitrary incident acoustic field. J. Acoust. Soc. Am. 2003, 113, 1216–1222. [Google Scholar] [CrossRef]
- Ji, J.; Liang, G.; Wang, Y.; Lin, W. Influences of prolate spheroidal baffle of sound diffraction on spatial directivity of acoustic vector sensor. Sci. Technol. Sci. 2010, 53, 2846–2852. [Google Scholar] [CrossRef]
- Roumeliotis, J.A.; Kotsis, A.D.; Kolezas, G. Acoustic scattering by an impenetrable spheroid. Acoust. Phys. 2007, 53, 436–447. [Google Scholar] [CrossRef]
- Rapids, B.R.; Lauchle, G.C. Vector intensity field scattered by a rigid prolate spheroid. J. Acoust. Soc. Am. 2006, 120, 38–48. [Google Scholar] [CrossRef]
- Barton, R.J.; Smith, K.B.; Vincent, H.T. A characterization of the scattered acoustic intensity field in the resonance region for simple spheres. J. Acoust. Soc. Am. 2011, 129, 2772–2784. [Google Scholar] [CrossRef]
- Mann, J.A.; Tichy, J. Acoustic intensity analysis: Distinguishing energy propagation and wave-front propagation. J. Acoust. Soc. Am. 1991, 90, 20–25. [Google Scholar] [CrossRef]
- Hawkes, M.; Nehorai, A. Acoustic Vector-Sensor Processing in the Presence of a Reflecting Boundary. IEEE Trans. Signal Process. 2000, 48, 2981–2993. [Google Scholar] [CrossRef]
- Javad, A.S.; Hengameh, K. A Vector-Hydrophone’s Minimal Composition for Finite Estimation-Variance in Direction-Finding Near/Without a Reflecting Boundary. IEEE Trans. Signal Process. 2007, 55, 2785–2794. [Google Scholar] [CrossRef]
- Dall’Osto, D.R.; Choi, J.W.; Dahl, P.H. Measurement of acoustic particle motion in shallow water and its application to geoacoustic inversion. J. Acoust. Soc. Am. 2016, 139, 311–319. [Google Scholar] [CrossRef]
- Campbell, J.; Sabet, S.S.; Slabbekoorn, H. Particle motion and sound pressure in fish tanks: A behavioural exploration of acoustic sensitivity in the zebrafish. Behav. Process. 2019, 164, 38–47. [Google Scholar] [CrossRef]
- Dall’Osto, D.R.; Dahl, P.H. Elliptical acoustic particle motion in underwater waveguides. J. Acoust. Soc. Am. 2013, 134, 109–118. [Google Scholar] [CrossRef]
- Bonnel, J.; Flamant, J.; Dall’Osto, D.R.; Bihan, N.L.; Dahl, P.H. Polarization of ocean acoustic normal modes. J. Acoust. Soc. Am. 2021, 150, 1897–1911. [Google Scholar] [CrossRef]
- Osler, J.C.; Chapman, D.M.; Hines, P.C.; Dooley, G.P.; Lyons, A.P. Measurement and Modeling of Seabed Particle Motion Using Buried Vector Sensors. IEEE J. Ocean. Eng. 2010, 35, 516–536. [Google Scholar] [CrossRef]
- Ebenezer, D.D.; Abraham, P. Effect of multilayer baffles and domes on hydrophone response. J. Acoust. Soc. Am. 1996, 99, 1883–1893. [Google Scholar] [CrossRef]
- Chen, W.; Hu, S.; Wang, Y.; Yin, J.; Korochensev, V.I.; Zhang, Y. Study on acoustic reflection characteristics of layered sea ice based on boundary condition method. Waves Random Complex Media 2020, 31, 2177–2196. [Google Scholar] [CrossRef]
- Ye, C.; Liu, X.; Xin, F.; Lu, T. Influence of hole shape on sound absorption of underwater anechoic layers. J. Sound Vib. 2018, 426, 54–74. [Google Scholar] [CrossRef]
- Gao, N.; Lu, K. An underwater metamaterial for broadband acoustic absorption at low frequency. Appl. Acoust. 2020, 169, 107500. [Google Scholar] [CrossRef]
- Dall’Osto, D.R.; Dahl, P.H.; Choi, J.W. Properties of the acoustic intensity vector field in a shallow water waveguide. J. Acoust. Soc. Am. 2012, 131, 2023–2035. [Google Scholar] [CrossRef]
- Gordienko, V.A.; Krasnopistsev, N.V.; Nasedkin, A.V.; Nekrasov, V.N. Estimation of the Detection Range of a Hydroacoustic System Based on the Acoustic Power Flux Receiver. Acoust. Phys. 2007, 53, 721–729. [Google Scholar] [CrossRef]
- Felisberto, P.; Rodriguez, O.; Santos, P.; Ey, E.; Jesus, S. Experimental results of underwater cooperative source localization using a single acoustic vector sensor. Sensors 2013, 13, 8856–8878. [Google Scholar] [CrossRef] [Green Version]
- Karman, T.V.; Biot, M.A. Mathematical Methods in Engineering, 1st ed.; McGraw-Hill Book Company: New York, NY, USA; London, UK, 1940; pp. 150–158. [Google Scholar]
- Morse, P.M.; Ingard, K.U. Theoretical Acoustics, 2nd ed.; McGraw-Hill Book Company: New York, NY, USA, 1968; pp. 234–239. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Zhu, Z.; Yang, D. Properties of the Acoustic Vector Field near the Underwater Planar Cavity Baffle and Its Application. J. Mar. Sci. Eng. 2022, 10, 138. https://doi.org/10.3390/jmse10020138
Chen H, Zhu Z, Yang D. Properties of the Acoustic Vector Field near the Underwater Planar Cavity Baffle and Its Application. Journal of Marine Science and Engineering. 2022; 10(2):138. https://doi.org/10.3390/jmse10020138
Chicago/Turabian StyleChen, Hongyue, Zhongrui Zhu, and Desen Yang. 2022. "Properties of the Acoustic Vector Field near the Underwater Planar Cavity Baffle and Its Application" Journal of Marine Science and Engineering 10, no. 2: 138. https://doi.org/10.3390/jmse10020138




