Beach Drainage System: A Comprehensive Review of a Controversial Soft-Engineering Method

Abstract

The beach drainage can be included among the soft engineering methods aimed to counteract the shoreline retreat related to the sediment redistribution along the beach profile. The idea that the groundwater table plays a role in the mobilization of the sediment grains underlies the application of the beach drainage system (BDS) as a tool able to modify the natural dynamics of groundwater table at sandy beaches. Indeed, BDS consists of a series of alongshore buried drains aimed to lower the groundwater table. Due to the drainage, the thickening of the layer of dry sand makes the solid grains less prone to be mobilized by the action of the waves at the swash zone, where interaction phenomena between the percolating and the incoming water lens take place. This tool had a troubled history. Its first applications were encouraging. Since then, controversial performances of both experimental and prototype scale experiences have been observed around the world. This paper aims to present an up-to-date full review of the studies and experiments carried out so far, in order to provide the reader with a complete perspective on its strength and weakness as well as open challenges to be faced in the near future.

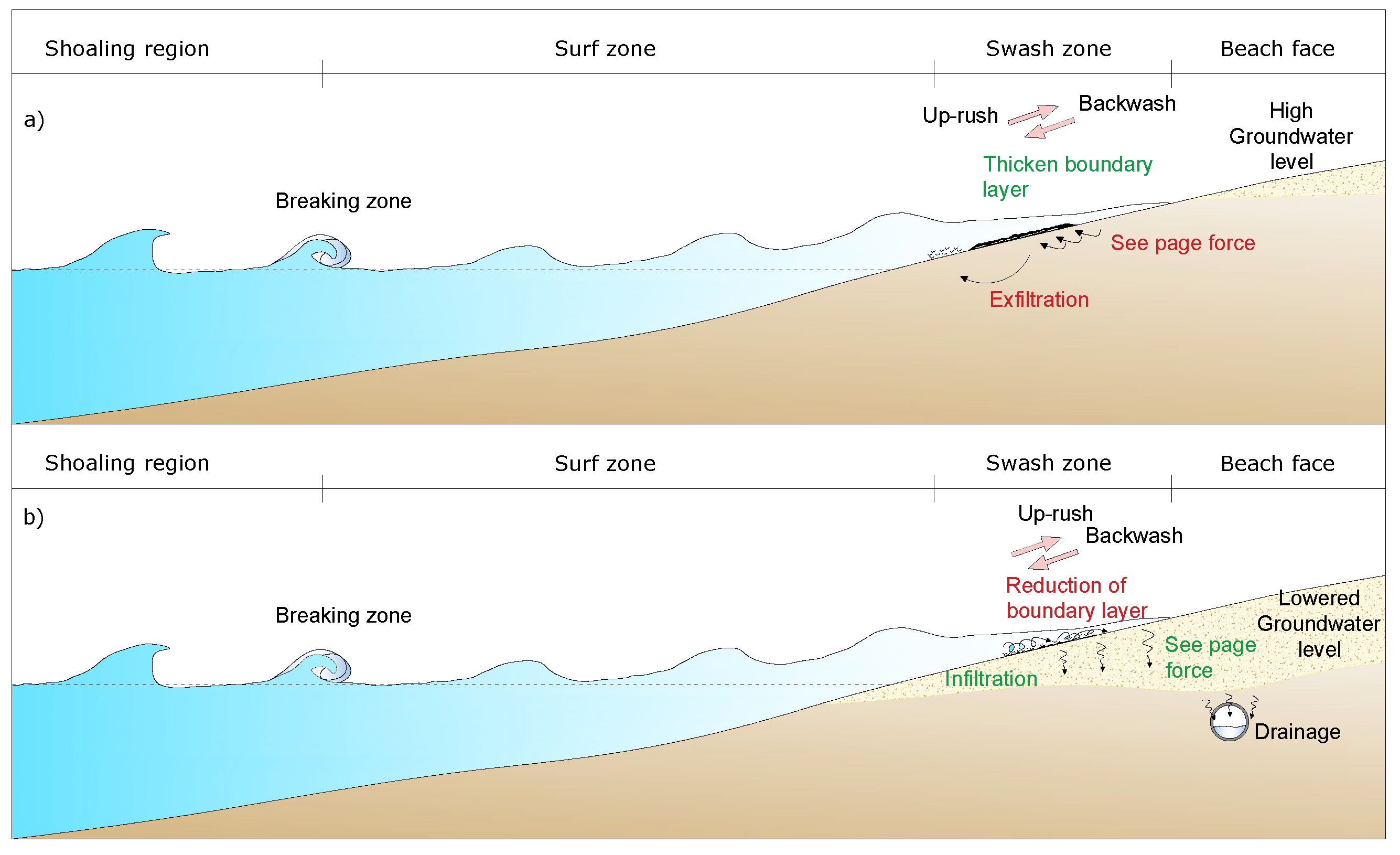
1. Introduction

Whatever the reason, economical, environmental, or social, the erosion process represents a big issue for coastal areas. It can be defined as the permanent tendency of shoreline regression landward, as a result of a disequilibrium of the natural beach dynamics leading to sediment losses. The reasons behind that disequilibrium comprise several factors, both natural and anthropogenic, direct or not, as a result of men-driven environmental changes. Bird [1] gave a list of 21 possible causes. They basically can be grouped into a bunch of general ones:

• reduction of sediment supply;
• changing in the natural forcing (i.e., changing waves climate, sea level rise, comminution, subsidence, etc.);
• interference with human constructions.

The latter, together with a deficiency in sand supply, may cause a deficit in the sediment budget balance over a period of time in the order of years: in a given area it may cause a long-term regression of the shoreline if the incoming sediment transport rate is lower than the leaving one. The shoreline dynamics must be considered also in view of the current beach erosion that could be exacerbated by future possible climate change scenarios (i.e., sea level rise). Therefore, without interventions aimed to stabilize the shoreline position, an increase of coastal vulnerability (hence coastal risk) may happen [2,3]. Even if it is sometimes defined as “acute erosion” [4], the shoreline retreat is often temporary. It is related to cross-shore transport in the surf zone driven by waves and undertow currents, in a storm-related temporal scale (i.e., the same temporal scale as storm surge occurrence [5,6]). To counteract coastal erosion, though, the strategies are not as conspicuous as one can think [7]. One option is abandoning eroded coastal areas and moving landward, letting the natural equilibrium re-build itself. This solution in some cases could be the only option left, even though it is not easily achievable considering the social-economic stresses that affect directly the people [8] and their risk perception [9].

Another alternative is to stabilize the beach by influencing nearshore phenomena. If the protections are artificially built, they are referred to as “hard structures”, such as groins, seawall [10,11,12] or breakwaters [13,14,15,16]. They alter the hydrodynamic regime which in turn modifies the morphodynamics response of the beach or directly interfere with sediment transport rate.

On the other hand, it is possible to gain shore protection by emulating the dune system as much as possible, and by nourishing the beach system, adding it back into the littoral system. In general, these methods are referred to as “soft-engineering”, “non-structural” or “quasi-natural” [17] methods. Hard structures may promote migration of the eroding process to adjacent areas, whilst soft solutions often are long-term unsustainable [18] due to maintenance issues: the choice and the design of one or another have to be adopted having a deep understanding of the causes of the erosion itself [7]. Indeed, in the soft-methods group, it has to be distinguished also the “nature-based solutions” (NBS), properly defined as those that mimic the characteristics of the natural habitat. They are created by human design, engineering, and construction to provide specific services such as coastal risk reduction [19]. NBS, which include for instance salt marsh, oyster reefs, mussel beds, vegetated foreshores, are increasingly being studied and implemented due to their capacity for coastal adaptation and protection and for their capacity to maintain the ecosystem healthy and resilient [20,21,22]. Many NBS designs require a holistic consideration of different fields, ranging from biology, chemistry, and engineering then their implementation is still predominantly case-specific [23,24]. On the other hand, beach nourishments as a well-established non-structural method are often viewed as a valid option. Indeed, they provide a series of benefits, ranging from the restoration buffer to extreme storms, to the increase of recreational attractiveness [25], to the avoided lack of sand on the adjacent beaches. Their temporary nature (i.e., they do not solve the cause of erosion itself [26], rather supply for a local sand deficiency) can be enhanced by the “hybrid” or “mixed” deployment of solutions [2], whose main goal is to retain the added sand by increasing the lifetime of nourishment projects. The environmental sustainability of beach nourishment can be maintained by the adoption of low-impact solutions, both structural (i.e., low-crested submerged breakwaters) and non-structural. Among the “soft” ones, it is possible to name the artificial manipulation of beach groundwater [27]. It has assumed several names, such as “beach dewatering”, “beach management system” (patented by [28]), “Pressure Equalizing Modules” (PEM, patented by [29]) or generally “beach dewatering system”. Hereinafter it is referred to as “Beach Drainage System” (BDS). It relies on the idea that groundwater level in the non-cohesive sandy porous medium, influenced by the seaward oscillations due to the waves (short or long), can, in turn, influence the sediment particle mobilization in the swash zone, according to the difference of the free surface elevation inside and outside the sand. Hence, the system consists of a series of drains placed in the beach, vertically (PEM) or horizontally (BDS) in the inter-tidal zone, that are expected to lower the groundwater table in order to achieve a “drier” beach, that in turn discourages the fluidization of the particles.

So far, the efficiency of BDS is not fully recognized, even though its history dates back for decades and it has been tested in several places in the world, both in the laboratory and in the field (Figure 1).

At the end of the nineties of the last century, Turner and Leatherman [27] provided a very comprehensive up-to-date review of the installed and experimental dewatering systems. At the end of the review, they highlighted that some open questions remained and regarded BDS as an experimental rather than a proven solution to erosion management. Negative feedback to stop erosion was given by Bruun for the drained beach [30], since the drainage does have only a temporary effect and works eventually in mild wave conditions. He concluded the paper admonishing not to use it as a substitute for nourishment, also due to its decreasing performance in time. On the other hand, other studies claim the very effective performance on accreting beaches and quickly recovering after a storm (e.g., [31,32]). Another example of a review paper about the soft-coastal methods was given in 2013 by Mariani et al. [33]. The authors concentrate on both dewatering systems and artificial reefs and updated the state of the art of the BDS.

Among the pros of BDS can be mentioned the lack of visual impact, the simplicity of deployment and removability [34] and the relatively low-cost [35,36]. Nonetheless, the feedback on its performance is sometimes conflicting and dependent on the site-installation conditions. As other “alternative” shoreline retreatment control devices, the claims of the positive benefits of these tools are often characterized by a controversial assessment on their performances [37].

This paper aims to recall all the previous studies, grouped according to the used approach. The paper is structured as follows: in Section 2 a theoretical background and some concepts about the BDS functioning are given. Section 3 refers to the experimental tests carried out in order to gain insight into the functioning of the BDS when controlled conditions are performed. Section 4 reports the experiences and the surveying of field campaigns carried out all around the world to date. Section 5 aims to summarize the studies on BDS carried out by a mathematical approach. Section 6 discusses about the up-to-date findings and results. Section 7 draws some concluding remarks.

2. Theoretical Background

Coastal groundwater dynamics, driven by local gradients due to the tide oscillations as well as the swash-backwash cycle, has been proven to play a crucial role in the sediment mobility in the swash zone [38,39]. The first studies of the correlation among the groundwater table levels at the foreshore, incident waves, and sediment mobility, go back to the forties of the last century [40,41,42]. Bagnold in [40] laid the foundations to the next studies about the morphological response of the beach to the swash motion due to the incident waves on the beach. Grant, in 1948 [41,42], for the first time focused on the possible contribution to beach aggradation and degradation given by groundwater table height relative to incident waves. He argued that when the sand is dry (i.e., when the water table is lower than the upper limit of the up-rush) the water percolates into the porous medium, lowering its velocities. It implies that there is a transition between the turbulent flow regime, caused by the collapsing bores further seaward, and the laminar regime, where flow velocity and water depth are lower, resulting in a sub-critical Reynolds number. In these conditions, not only is the sediment deposited, but laminar conditions persist. On the other hand, for the wet case (i.e., when the water table is higher than the upper limit of the up-rush), Grant demonstrated that for a given configuration of the beach, the higher the water level on the beach face (i.e., the thickness of the swash flow), the larger the velocity. Indeed, the increased depths produce higher velocities, since part of the volume of the water flows out the sand. In this regard, a coeval work of Emery and Foster [43] did state that the escaping flow in wet conditions has velocities sufficient to elutriate sediment particles. It happens during ebb tides when the lagged response of the water table to tidal oscillations induces the groundwater to filter out the porous medium. Nevertheless, hydraulic gradients are relatively small, so tidal-induced groundwater outflow, even for large waves, is unlikely to be able to induce fluidization of the bed [44]. Then it was argued that fluidization is possible only if the swash on the seepage face is considered [45]. Then, even though the tide-induced groundwater oscillation causes excursion that propagates landward, especially in macro-tidal beaches, the contribution to beach face erosion or accretion is given by the combined action of waves, tides, and groundwater dynamics.

Based on this rationale, a series of studies and research works aiming to enhance the deposition by artificially lowering the groundwater surface were performed. To achieve such a goal, the mechanisms that relate the swash-zone hydrodynamics to the sediment transport phenomena that take place have to be well understood. Indeed, in parallel with the investigation of the groundwater dynamics driven by tides (e.g., [46,47]), a series of studies about the role of infiltration on sediment mobility had been tackled [39,48,49,50,51].

The swash zone can be identified as the area that alternatively remains wet and dry in an oscillatory motion. The dynamics of the swash zone spans then over a variety of frequencies ranging from short waves (f > 0.05 Hz) up to infragravity waves (0.003 < f < 0.05 Hz) [52]. Indeed, the interaction between short waves with different frequencies and between short and long waves at the surf-swash zone boundary can lead to the generation and reflection of further low-frequency waves [53]. Whether the swash zone is dominated by the short or infragravity waves, depends on the relative magnitude of the twos in the inner surf zone [49] (Figure 2). While in the surf zone friction is not a dominant process for the cross-shore transport [52], it is in the swash zone. Indeed, turbulent phenomena and sediment transport mechanisms are generated in the swash zone and they present large cross-shore gradients.

The link between enhanced stability of sediment for “dry” beach was addressed to the quantity of water that infiltrates in the highest elevation reached by run-up, reducing the velocity during backwash phase [40,42,43], as depicted in Figure 2. The effect of swash infiltration is to reduce the duration and velocity of the backwash [54]. At least, other two factors have been addressed to be responsible for either mobilizing or stabilizing the sediment grains: the modification of the effective weight of sediment particles due to the seepage force and the thinning or thickening of the boundary layer at the bed [55]. The seepage force acts as a vertical drag force whose effects contribute to the reduction of the swash volume, i.e., it enhances stabilization for infiltration and vice-versa. Nonetheless, the reduction in volume for sand, whose permeability is not as high as for gravel, has fewer importance [56]. The other effect is opposite to these ones: infiltration reduces the thickness of the boundary layer, enhancing the near-bed velocity. During ex-filtration, the boundary layer is thicker and the potential for sediment transport is lowered [48]. The opposite contribution given by the modification of boundary layer and the drag force has been studied by Turner and Masselink [55] and by Turner and Nielsen [57] by means of a modified Shield parameter. In this regard, Nielsen et al. [56] stated that infiltration enhances grains mobility for dense coarse sediment and prevents the mobilization for finer and lighter sediment. Figure 2 shows a scheme of the phenomenon.

This paper aims at giving the reader an overview of past experiences on BDS application. The focus here is not directly posed on the groundwater dynamics driven by waves and tides. Rather, attention is paid to the artificial modification of the natural groundwater level by means of gravitationally or pumped system of drainage.

3. Laboratory Experience

The first study ever on the effects of a drained beach is represented by the laboratory campaign carried out in 1975 by Machemehl [58]. He conducted a laboratory experiment on a draining system deployed perpendicularly to the shoreline and artificially pumped. A first good response of the dewatering for depositing sand at the beach face, with stabilizing behavior at the offshore zone, but with negligible effect in the breaking zone was obtained.

Kawata et al. [59], in 1987, tested a system of horizontal pipes and pumps under controlled conditions in the laboratory (solitary and monochromatic incident waves). Different sand and foreshore initial profile have been adopted: 0.35 mm mean diameter sand and 1:10 slope for solitary tests; a coarser porous medium (0.94 mm), and milder slope (1:30) for regular waves. For solitary waves tests a steeper foreshore, a deeper breaker scour, a higher foreshore berm, and a higher step inshore were observed for the drained configuration if compared to the undrained one. For monochromatic waves tests, the drainage of the beach was observed to accelerate accretion of the foreshore through the development of a berm under mild wave conditions. Stormy conditions were also reproduced; the variation of the beach profile was less accentuated when the system was activated with respect to the case with no draining system, indicating the stabilizing action.

In 1991, the studies carried out by Ogden, Sidel and Weisman [60,61] basically differed in considering the presence of tidal oscillations. The former [60] focused on the influence of the position of the drain, the latter [61] on the influence of tides. The experiments were carried out in a wave flume where irregular waves were generated. The gravity drainage consisted of a 2.54 cm diameter pipe, buried in the sand with a mean diameter of 0.35 mm, scaled according to the fall parameter [7]. They did not find significant effects on the rate of erosion or accretion when the beach drain is used for the condition of negligible tides. On the contrary, they found some accretion on the upper part of the shoreface when tides were considered. In the end, they did not recommend the use of this tool where the tide is negligible, and at least to use a pumping system to enhance the infiltration rate.

In the meanwhile, Sato et al. [62] in 1995 performed three-dimensional and two-dimensional laboratory tests on beach dewatering by pumps on fine sand (d${}_{50}$ = 0.29 mm) to investigate the function, performance, and optimum location for installing a coastal drain system. They confirmed that a coastal drain system enhances the accretion of sediments on the beach face for accretive wave conditions and retards beach erosion for erosive wave conditions. Moreover, the greater the discharge drained by the system, the greater the efficiency. It is due to the larger amount of suspended sediments that migrate shoreward. Their new finding highlights the efficiency of the BDS also in stormy conditions. The breaking bar tends to migrate shoreward if the flow induced by the artificial drainage overcomes the wave-induced offshore component. Furthermore, they found that the best position for the drain is seaward the shoreline.

Other supportive feedback on the reliability of the drainage system was given by Oh and Dean [63,64]. They performed laboratory experiments on two different scales. The influence of drainage was investigated for three different groundwater levels: the mean seawater level (m.s.l.), a level higher than the seawater level (i.e., saturated condition), and a level lower than the seawater level (i.e., drained condition). The tests showed the saturated groundwater condition has a stabilizing influence on the dynamics of sand along the cross-shore direction. This finding was not consistent with previous studies for which higher water table level was observed to enhance erosion. The sand bar swiped up the shore-face, with deposition of sand landward with respect to the equilibrium position. The lowered water table showed less effect on the mobilization of the particles. The small scale experiments have been performed to check the repeatability of the tests carried out at a larger scale, having scaled down the sand characteristics by the fall velocity parameter and the waves by the Froude criterion. Though, the small-scale experiments did not match with the larger scale ones, likely due to poorly-sorted sand. In the end, they stressed the need for additional controlled laboratory experiments.

The laboratory studies of [65,66,67,68,69] at the end of 1990s’ followed indeed. In detail, Weisman et al. [66] performed tests with and without both drainage and tidal cycle for accretive and mildly erosive conditions. They highlighted the scale effects that laboratory models dramatically suffered from, recognizing the greater efficiency of the system at prototype scale rather than laboratory tests one. Moreover, they found that the drain is effective for both the tested waves conditions. Hence, they suggested prototype installations working continuously during a year, at least except under highly erosive sea states and during flood tides when the water table is below the mean water level. At the International Conference of Coastal Engineering in 1996, some works on drainage systems were presented, hinting at the great interest that the community had been showing at that time about the relatively new perspectives that BDS would have opened up. Kanazawa et al. [67], conversely to the classical configuration of the BDS, used a permeable layer buried in a fine sand (median diameter of 0.135 mm) in the same way as [32]. In this study, the used sand was characterized in the laboratory and a permeability coefficient of 6.28 × 10${}^{-5}$ m/s was estimated. Both two-dimensional and three-dimensional experiments were conducted, with different aims. The 2D tests have been carried out to compare the performances on sand stability of three different types of drain layers. The three-dimensional investigation aimed to confirm the 2D results and to furnish qualitatively the extent of the stabilizing effect of the draining layers. In 2D tests, a gravel layer 10 cm wide, a gravel layer coupled with the presence of a draining pipe connecting the gravel layer to the seaward shoreline, and a spring coil mattress connected to the sea by a draining pipe were deployed as three different configurations of the drainage layer. The latter configuration was the one tested also in the wave basin (i.e., in the 3D investigation), but with more permeable sand. For this reason, it was not possible to evaluate the three-dimensional effects that a 2D experiment neglects, which are indeed fully tested in 3D case. From these studies, by three-dimensional modeling, it was possible to estimate, besides the lower set-up and groundwater table rising with respect to the 2D domain, that the shoreline changes experienced with the spring coil mattress permeable layer correspond to a reduction of wave height of about 40%.

Lemckert [68] investigated the efficiency of the drain in a particular condition but still very common: swash zone, worth remind mainly influenced by infragravity waves, is interested in a three-dimensional wave field, resulting from the interaction of regular and edge waves. The porosity of the beach was observed to be more effective than the drainage on modifying the energy of edge waves, so it is realized that high porosity beaches are more effective in reducing the reflected wave field with respect to drained beaches.

Law et al. [69] studied the evolution of transient beach profiles with and without artificial drainage. The results showed that the drain pipe placed beneath the center of the swash zone promotes initial accretion of the beach. The presence of the drain, as expected, induced a steeper upper beach slope. As the tests go on, the influence of the drain reduced. They even concluded that its effect can be in any case positive since it retards the erosion for the first hours. In prototype-scale terms, it may correspond, in some field conditions to one or two days, i.e., the period that the beach needs the most protection in storm conditions.

Gampathi and Chan [70], adopting a similar asset as [32] by using a draining layer, tested the influence of groundwater table on beach profile changes considering accretive and erosive wave climates, different levels of the water table, with and without different assets of the draining layer. It resulted that for increasing water table elevation the deposition of sand at the foreshore decreased when accretive waves were reproduced. On the other hand, it increased for erosive conditions. From the drained test, it has been deducted that the faster the drainage the better the performance. The drainage rate depends, among others, on the position of the drain.

Date back to 2011 the largest laboratory investigations ever carried out, undertaken at Gross Wellen Kannal (GWK) in Hannover (Germany) at prototype-scale. They investigated both the hydrodynamic [71,72,73,74] and the morphodynamic aspects [36,75].

The facilities size let investigate the BDS with no scale effects, that others have already stressed, but still under controlled conditions. The flume is about 300 m long, 5 m wide and 7 m deep. The sand consisted of a 0.33 mm mean diameter sand. The draining system was arranged as two corrugated pipes of 0.20 m diameter. Tests included static conditions (i.e., with no wave propagating in the channel) and dynamic ones with 3 different wave conditions. Static tests aimed to study the system efficiency in lowering the water table without the influence of the waves, in order to define the time in which the system reaches the steady-state. Dynamic tests were performed in order to evaluate the response of the system under different wave conditions. In particular, three different wave energy conditions (High, Medium, and Low energy) were tested out employing a JONSWAP spectrum [76].

In terms of beach profile evolution, from [36] they concluded that under high energy wave conditions the drainage system seemed to be inadequate in giving any stabilizing effect. For medium energy and low energy tests, the beach showed global stabilization and an increased accretion, respectively. The scarce performance of the system observed in the laboratory under different energy of incident waves proves to be dependent on the characteristics of the sand and the drains, as well as their position, and it marks a threshold for an asset of beach drainage that would be effective.

In the end, the authors suggested combining BDS with other coastal defenses, for instance, submerged breakwater to partially dissipate high waves. Indeed, Saponieri et al. [18] tested three configurations: unprotected beach, only BDS protected, and BDS-submerged breakwater coupling protected, the latter with the aim to switch the sea state from high to medium and low energy states. It resulted that drains mainly worked under pressure conditions. The authors suggested enhancing the infiltration capability, for instance, promoting the drainage with a more permeable layer around the pipe. Besides BDS effects on both hydrodynamics and morphodynamics, the joint configuration of BDS and submerged sill highlighted interesting outcomes. The drainage seems to be capable to mitigate also the raising of the mean water level typical of the sheltered region shoreward the structure.

An overview of the discussed research works is presented in

Table 1. Overview of the laboratory experiences. In the table, d${}_{50}$ is the mean diameter of the sand, T${}_m$ is the mean period; T is the wave period; H${}_s$ is the significative wave height; H is the waves height; h is the water depth; K is the sand permeability; H/L is the wave height-length ratio.

Year	Authors	Technology	Site	Facilities	Wave Climates			Sand	Tool Configuration	Tides and Levels
1975	Machemehl et al.	Transversal BDS	-	-	-			-	-	-
1987	Kawata et al.	Filter layer	Kyoto, JPN	Wave tank 21.6 m × 0.75 m × 1.2 m; Wave tank 78 m × 1 m × 1.5 m	T = 0.5–5 s; H = 20.1–29.3 cm; h = 90–100 cm			slope = 1:30; d${}_{50}$ = 0.94 mm	16 pipes of 5 cm × 80 cm at 1.5 cm of spacing
1991;1992	Seidel, Odgen and Weisman	Gravity BDS	Lehigh University, USA	Wave flume 33.66 × 0.91 m × 0.91 m	length Scale = 6.97:1; H${}_s$ = 12 cm; T = 3.03 s			d${}_{50}$ = 0.145 mm	Length = 0.91 m (Distance = 0.91 m; depth = 0.37 m) (Distance = 0.3; depth = 0.37) Diameter = 254 mm	Tide cycle in lab scale 4.7 scale, simple triangular shape
1992–1994	Oh and Dean	BSD	University of Florida, USA	Large wave tank 36 m × 1.8 m × 1.8 m; Small wave tank 15 m × 0.9 m × 0.6 m	H${}_s$ = 0.11, 0.16 m; Ts = 1.5, 2 s; mwl 47 cm			d${}_{50}$ = 0.24, 0.21 mm; slope = 1:18, 1.7	-	3 different levels: −0.11 m, 0 m, +0.11 m mwl
1994; 1997	Sato et al.	Pumped BDS	Kagoshima University	wave basin 26.7 m × 14 m × 1.2 m deep	T = 1 s, 2 s; H = 5 cm, 10 cm			d${}_{50}$ = 0.29 mm; slope = 1:20	Length = 7 m Diameter = 50 mm; discharge max = 0.33 l/s/m; depth = 5 cm; filter layer around the pipe = 1 cm	3 different levels
1995	Ogden; Weisman, Seidel, Ogden	BSD	Lehigh University, USA	33.66 m × 0.91 × 0.91	Froude Scale = 2.64:1 H${}_s$ = 0.12 m, Ts = 3.03 s			d${}_{50}$ = 0.145 mm	Length = 0.91 m (Distance = 0.91 m; depth = 0.37 m) (Distance = 0.3, depth = 0.37 m); Diameter = 254 mm	-
1997	Kanazawa et al.	Differently coupled BDS	Yokohama, JPN	wave flume 38 m × 0.5 m × 1.5 m	H = 8.4, 10, 15 cm; T = 1.34, 1.79 s; H/L = 0.03			d${}_{50}$ = 0.135, 0.16 mm; K = 1.14 × ${10}^{-4}$, 6.28 × ${10}^{-5}$ m/s	Different draining system: gravel layer of 10 cm thick (d${}_{50}$ = 13–20 mm); transversal draining pipe diameter = 4.4 cm; spring coil diameter = 1.5 cm	-
2000	Lemckert	BDS	Griffith University, AUS	Tank 1.8 × 3.6 × 1 m	wave frequency = 0.94 Hz; Stroke lengths = 3.2, 5.7, 8.2, 13.2 cm			slope = 15°, porosities = 0.47, 0.42, 0.38, 0.36, 0.35	Vertical permeable layer	water level kept constant
2002	Law et al.	Pumped BDS	Singapore, SG	Wave flume 45 × 1.6 m × 1.5 high	H = 19.5 cm T = 1.5 s, duration = 36 h			slope = 1:15, d${}_{50}$ = 0.31 mm; fall velocity = 4.2 cm/s	depth = 5–13 cm, average flow rate = 0.15–0.48 l/s/m	h = 71 cm
2004	Gampathi and Chan	Pumped BDS	Singapore, SG	Wave tank 40 m × 0.9 m × 0.9 m	H = 4, 6, 8 cm; T = 0.8, 1, 1.25, 1.60 s			slope = 1:6, d${}_{50}$ = 0.5 mm	flow rate = 4.5 l/min, 7.5 l/min and 8.0 1/min	initial water level = 40 cm, rising level h +5 cm, +10 cm and +13 cm
2011; 2012	Damiani  et al.; Contestabile et al.	BSD	Grosser Wellen Kanal, DE	Wave flume 300 m × 5 m × 7 m	H${}_s$ = 0.76–0.83 m; T${}_m$ = 5.15–5.44 s (50 configurations)	H${}_s$ = 0.57–0.61 m; T${}_m$ = 6.16–6.27 s (50 configurations)	H${}_s$ = 0.39–0.42 m T${}_m$ = 6.24–6.46 s (50 configurations)	d${}_{50}$ = 0.33 mm K = 3.2 × ${10}^{-4}$ m/s	4 pipes; Diameter = 200 mm	h${}_1$ = 4 m, h${}_2$ = 4.2 m
2011; 2013	Aristodemo et al.; Ciavola et al.	BSD	Grosser Wellen Kanal, DE	Wave flume 300 m × 5 m × 7 m	H${}_s$ = 0.76–0.83 m; T${}_m$ = 5.15–5.44 s (50 configurations)	H${}_s$ = 0.57–0.61 m; T${}_m$ = 6.16–6.27 s (50 configurations)	H${}_s$ = 0.39–0.42 m T${}_m$ = 6.24–6.46 s (50 configurations)	d${}_{50}$ = 0.33 mm K = 3.2 × ${10}^{-4}$ m/s	4 pipes; Diameter = 200 mm	-

.

4. Field Campaigns

The pioneering work of Chappel et al. [77] posed the base for groundwater manipulation in the field. In their two pilot studies along the Australian coast, they used a series of wells and pumps to regulate the water table, showing very positive results in beach aggradation after the survey campaign. Furthermore, for the first time, they suggested the installation of horizontal drains.

During the first 1980s, Danish Geotechnical Institute (DGI) installed a water filtration system at Hirtshals, pumping water from buried drain tubes along (and close to) the shoreline. Curtis and Davis [78] reported that during the 8 months of the survey campaign the shoreline propagated seaward, even in the winter season. Though, in this period, the system did not manage to prevent erosion for severe storms. Nonetheless, the positive results boosted further studies and field campaigns. Later, since the positive results of the first experience, a seven years (1985–1991) campaign was led in Danmark by DGI at Thorsminde [31,79,80] resulting in a total accretion of the beach of 30 m${}^3$/m (i.e., per unit meter along the beach) over 7 years, while the neighborhood beaches experienced 25 m${}^3$/m of erosion in the same period. The system was patented in 1987 [28] with the name of Beach Management System^® (BMS). Under that license, another installation was done at Sailfish Port (Florida) by CSI (Coastal Stabilization Inc.) with the American name of STABEACH^®. The system worked for at least 7 years, with some alternating performances. After about 2 years the installation, Dean [81] independently reported that the beach resulted to be in local moderate accretion with a generalized more stable shoreline with respect to the control transects. Instead, different behaviors were exhibited by the northern and southern control sections during the following years. The system however was stopped during the years 1991–1992–1993 in the summer months due to the sea turtles’ nesting period, so it was not possible to study its capabilities on recovering, other than on preventing erosion. Moreover, an accretionary event was recorded even when the system was off. Turner and Leatherman [27] concluded that it was difficult to discern any net positive effect, above all because the system was installed in the transition zone among two sections that experienced different trends of erosion and accretion. In the 1990s this method was investigated through both field and laboratory campaigns. During that period further investigations about the interaction between seepage and swash motion were performed (e.g., [55,57,82]), enhancing the knowledge about their correlation and their function on the sediment particles mobility within the swash zone. The commercial installation of STEABEACH^® was deployed at Nantucket beach, Florida. The project experienced a series of maintenance problems. The pumps did not work as expected, due to sand buildup within the pipes [83]. Even after an increase in the pump size, the dewatering system achieved little success, and consequently, it has been removed by the local government, never reaching its potentiality due to maintenance issues. However, during the operative period of the system, Curtis et al. [84] reported that it had no bad consequences on the local environment, vegetative communities, and public freshwater aquifer.

A field test was carried out by Davis et al. [85] at Dee Why Beach, Australia. The drainage in this experiment was not pumped: they installed the type of drain commonly used for roads, laid vertically. The whole apparatus was surveyed for 18 months, stressing that it did not stop working, even though, due to some damages, the system reduced its efficiency. They stressed, in addition, that gravity drainage is a highly cost-effective means of beach stabilization, prone to extending the life of beach nourishment programs.

Katoh and Yanagishima [32] used an alternative way to drain the sand, by means of a geotextile layer. The field survey was led, after laboratory tests [67], at Kashima (Japan) in an already stable beach. It resulted that in the drained beach the speed of foreshore erosion in a storm slowed down and, in addition, the eroded foreshore is recovered quickly after a storm.

Another field campaign followed in the next years at Kashiwabaru Beach [86], where a 2 years survey was carried out. The drains were laid parallel to the foreshore. From the comparison between the drained part and undrained part of the beach, it appeared that profile changes did not show any definite differences, although a small difference was found in the seaward area of the pipes. Analyzing that small difference, the amount of sand gained by the drain system was estimated as being roughly 5 m${}^3$ for 20 m of beach width.

The commercial installations of BMS or ECOPLAGE had been installed in the following years in different sites, i.e., France [87,88,89], Italy [35,90,91,92], Spain [93]. French ECOPLAGE received good feedback from the site-installation local surveys. Unfortunately, international publications that confirmed the results did not follow, except for some documents (also in the French language) that are redacted by the constructors. The Spanish experience confirmed that beach drainage stops shoreline retreat and enhances quick recovery from storm erosion events. Regarding the systems installed in Italy, inconclusive results had been gained. In Alassio, both Ciavola et al. [35] and Bowman et al. [90] recognized the main role of the system in stabilizing the beach under normal to medium energy conditions, while under high energy conditions positive shoreline accretion trends faded. Again, Ciavola et al. [35] reported the case of Procida (the beach did not benefit from the system and it was early abandoned) and of Bibione (where the survey campaign was interrupted). At Metaponto, as well, the monitoring did not continue as long as it should have to gain certain results. The same issue was for the Ostia site. Vicinanza et al. [92], reporting in detail the case of Procida Island, expressed their not particularly positive opinion about such a system.

A commercial alternative version to the generic BDS is represented by PEM (Pressure Equalizing Modules), patented by [29] and commercialized by EcoShore Inc. In this case, the essence of the tool does not change, except for the position whereby they are installed: they consist of 2 m long permeable tubes deployed vertically into the beach. They, as the name suggested, are placed in rows forming a matrix along the shoreline. They are vented at the top in order to make the pressure to be equalized. Jakobsen and Brøgger [94,95] reported the three-years survey of the installation at Skodbjerge (Denmark), funded by the Danish Ministry of Transport. The functioning period ranged between January 2005 and 2008. At the end of that period, the analysis showed favorable performances. Actually, the report lacks deep analysis and information, above all about the average climate as well as recorded extreme events. The coast of Skodbjerge, historically in erosion, seemed to show a rising level of the beach in the area in front of the PEM, with an accumulation rate greater than 50% with respect to the reference areas (the neighbor check areas where the system was not installed), coming from long-shore sediment transport current. The same system has been deployed also in Malaysia [96], and in Florida [97]. In Malaysia, PEM combined with beach nourishment was installed in a pocket beach, most of it exposed to the main direction of the northeast monsoon. After three years it resulted to be stabilized, even with no natural sediment input: the losses are estimated as 25% of the total amount nourished at the beginning of the survey campaign. The critically eroding Hillsboro Beach (Florida), even with a delay with respect to the expectations, probably due to a reduced depth of the sand than usual, showed an undoubtedly accretive behavior (8.2 m in three years of the campaign; from 2008 to 2011). The survey dealt also with the influence of the system on the local fauna: no negative impacts were recorded.

The latest two field campaigns, independently documented, are [98,99], with two opposite interpretations of the results. The first one describes 4 years of survey in the Netherlands of a passive vertical drainage system. It resulted that no measurable influence on the beach and dune volumes variations were recorded. In [99], on the other end, after five years of “classical” BDS survey on a macro-tidal beach in France, it seemed that the beach drainage allows faster recovery of the upper part of the shoreface after a storm.

Table 2. Overview of the field experiences. In the table, d${}_{50}$ is the mean diameter of the sand, T${}_m$ is the mean period; T${}_p$ is the peak period; H${}_s$ is the significative wave height; H${}_{swell}$ is the average swell waves height; H${}_{wind}$ is the average waves height; H${}_{rms}$ is the root-mean-square wave height.

Year	Authors	Technology	Site	Period	Waves Climate	Sand	Tool Configuration	Tides and Levels
1946–1948	Grant		Santa Monica-South California, USA	-	-	-	-	-
1948	Emery and Foster		El segundo beach; la Jolla, USA	samples every half-hour through a 12 h tidal cycle	76 cm; 107 cm; 70 cm	samples at each beach, 0.18–0.36 mm	-	91 cm; 224 cm; 102 cm; 122 cm
1964	Duncan		Santa Monica-South California, USA	2 campaigns: 27 April and 23 October 1963 of semi-diurnal tide duration (from ebb to ebb tide)	-	-	-	-
1979	Chappel, Eliot et al.	pumped vertical BDS	Durras Beach-South Australia, AUS	3 days	H${}_s$ = 1.5 m, T${}_p$ = 9 s, Swash = 15 m 6 cycle/min	-	150 m; 4 vertical well	-
1992	Davis, Hanslow, Hibbert, Nielsen	Perpendicular BDS	Dee Why Beach, New South Wales, Australia, AUS	February 1991–November 1992	Large swell waves from South East	d${}_{50}$ Swash zone about of 0.5 mm	18 drains; Lenght = 160 m; Depth = 0.4–0.7 m	Microtidal semi-diurnal with a diurnal inequality, range up to 2 m.
1997	Turner and Leatherman; Curtis and Davis; others	pumped BDS (BMS)	Hirtshals, DNK	1981 (6 months)–1983 (8 months)	-	-	Length = 200 m + 220 m; discharge = 400 m${}^3$/h; Diameter = 0.2–0.3 m; depth = 2.5 m below mwl; distance from the shoreline = 5 m	-
1997	Katoh and Yanagishma	Draining layer	Kashiwabaru beach, JPN	Installed in August 1994	-	slope = 1:50, d${}_{50}$ = 0.18 mm	Permeable draining layer: Area = 88 m × 7.8 m; Depth = 2.1 m mwl.	Tide range = 1.5 m
1997; 1998	Turner and Leatherman; Curtis and Davis; others	pumped BDS (BMS)	Thorsminde, DNK	1985	-	Mixed gravel and medium grained sand	Length = 500 m; Diameter = 0.2 m; depth = 2–2.5 m	-
1990; 1997	Dean; Turner and Leatherman	STABEACH	Sailfish Port, Florida, USA	1988	-	medium-grained sand	Diameter = 0.3–0.5 m; Depth = 2.5 m, 1.5 m long horizontal well points attached at approximately 3.0 m intervals along the drain	Tide range = 0.9 m
1998	Curtis et al.	STABEACH	Nantucket, USA (3 sites)	November 1994–February 1997	Shoal = 5 to 16 km off-shore	uniform, medium to coarse sands	Diameter= 0.3 m; perforated (0.5 mm) corrugated pipe wrapped with a geo-textile filter; pumps =190 l/s and 380 l/s	Bidirectional currents (with the tide) reaching 0.82 m/s and 0.98 m/s at maximum ebb and flood conditions
1998	Serra et al.	pumped BDS (BMS)	Ebro Delta, ESP	1996–1998	-	-	-	-
2004; 2008	Damiani and Rossetti; Ciavola et al.	pumped BDS (BMS)	Ostia, IT	February 2001—at least till 2002	-	d${}_{50}$ = 0.15–0.2 mm	-	-
2006	Lambert et al.	ECOPLAGE	Baie d’Agay, Var, FR	from February 2004	T${}_p$ = 55.84–6.2 s; averaged H${}_0$ = 0.48–0.49 m,	fine sand mean (d${}_{50}$ = 0.18 mm) and of ballast (d${}_{50}$ = 0.4 to 2 cm).	Length = 600 m; depth = 2 m	-
2008	Bowman et al.; Ciavola et al.	pumped BDS (BMS)	Alassio, IT	March 2004–March 2005	99% of the waves are of H${}_s$ < 2.5 m	Well-sorted fine sand (0.0125–0.0250 mm)	Lentgth = 198 m; depth = 1.5 m (45 cm below MSL); Diameter = 16 cm, max discharge= 0.5 l/s/m beach front.	Tide range = 0.32 m
2008	Ciavola et al.	pumped BDS (BMS)	Bibione, IT	October 2005–July 2006	-	d${}_{50}$ = 0.16–0.24 mm	Length = 200 m; two parallel pipelines Diameter = 20 cm	-
2008	Ciavola et al.	pumped BDS (BMS)	Metaponto, IT	April 2006–August 2006	-	d${}_{50}$ = 0.34 mm	Length = 200 m; Diameter = 20 cm	-
2008	Ciavola et al.	pumped BDS (BMS)	Lido Adriano, IT	March 2005—at least 2008	Bimodal wave climate	d${}_{50}$ = 0.32 mm; high variability of the sediment and d${}_{50}$ = 0.47 mm near the mouth of the river	Length = 100 m; Diameter = 160 mm. Depth = 1.0–1.2 m below MSL	-
2008; 2010	Ciavola et al.; Vicinanza et al.	ECOPLAGE	Chiaiolella Beach, Procida Island, IT	April 2002–December 2004	H${}_s$ = 7 m (Tr =100), T${}_m$ = 4–6 s	d${}_{50}$ = 0.35 mm	3 different drains lengths: 325 m, 390 m, 100 m; 0.5–0.7 m depth under m.s.l. d = 140 mm; pumps = 18 l/s	-
2007–2008	Brøggeer and Jakobsen	PEM	Skodbjerge, DNK	January 2005 up till January 2008	-	-	175 cm long and are submerged 25 cm under the beach	Mean water level range = 0.7–0.8 m
2018	Christensen and Gable	PEM	Hillsboro beach, Florida, USA	2008–2011	wave directions are from the northeast and east, with 79% of occurrences, which results in a net sediment transport toward the south.	-	90 PEMs in 33 rows	Tidal period = 12.4 h; Mean tide range = 0.77 m; spring tide range = 0.86 m
2008	Brøggeer and Jakobsen	PEM	Malaysia	2008	Yearly average wave height is approximately 0.20 m, but during the NE monsoon the average wave height is 0.75 m	slope = 1:45; d${}_{50}$ 0.3–0.5 mm	100 m × 10 m matrix (9 columns and 5 rows = 100 PEMs)	Highest tide range = 0.4 m
2014; 2015	Walstra et al.; Reedijk et al.	PEM	Egmond, NL	2007–2011	H${}_{rms}$ max exceeding 5 m	d${}_{50}$ about 0.3 mm	l = 2 m, depth = 0.25 m, Diameter= 0.06 m	-
2016	Bain, Toulec et al.	BDS	Quend-Plage, FR	5 years (Jun 2008–September 2013)	H${}_{wind}$ < 0.5 m, T${}_m$ = 4–6 s, H${}_{swell}$ < 0.5 m	d${}_{50}$ = 0.1–0.14 mm	5 m × 900 m 1.5 m depth; 5 parallel drains; Diameter = 160 mm	Semi-diurnal macro-tidal (mean spring range = 5.5 m)

summarizes the reviewed field campaign experiences.

5. Mathematical Modeling

The water table is defined as the surface where the pore pressure is atmospheric. Above the free surface, a layer of unsaturated medium is present: the pores between the solid grains are not full of water, but it results to be a three-phase area: liquid (water), solid (grains), and gas (air). The mathematical modeling of the groundwater motion in an unconfined aquifer (i.e., a flow whose upper boundary is represented by a water table) follows the classical approach of the continuum medium for irrotational flow. The simplest approach for the unconfined unsteady flow (since the presence of the time-dependent forcing) is the one-dimensional linearized Boussinesq equation [100]:

$$K\overline{h}{\displaystyle \frac{{\partial }^{2}h}{\partial x^2}}=n{\displaystyle \frac{\partial h}{\partial t}}$$

(1)

where $\overline{h}$ is the average depth of the aquifer, n is the porosity, h is the instantaneous height of the groundwater table with respect to the impervious bottom layer, K is the permeability, x the spatial coordinate, and t the time. Equation (1) is the combination of Darcy’s law and the mass conservation equation, considering the Dupuit’s assumption [101], which assumes equipotential lines as vertical and streamlines as horizontal and hence a hydrostatic pressure distribution.

Even if the first approach on modeling the groundwater dynamics at the coast is analytical [102,103,104,105,106,107], only Fischione et al. [108], according to the best authors knowledge, engaged to analytically model a beach drained by BDS. They solved the classical Boussinesq equation [109] in an idealized finite-length rectangular domain with a simplified boundary condition to take into account the presence of the drain: a constant groundwater level has been imposed at the shoreward boundary, at a certain distance L from the shoreline, where the effect of the waves has been modeled as a periodic function of the water table.

On the other hand, numerical modeling of groundwater dynamics has been widely investigated. Dominick et al. [110] were among the first ones that tried to numerically predict water table fluctuation due to waves by an implicit finite-difference solution. The groundwater response to tide-induced oscillations has been taken into account in their studies by [47,111,112]. The “BeachWin” model of [113] links beach groundwater and swash, simulating interacting wave motion, beach groundwater flow, and sediment transport in the swash zone. The model uses simplified descriptions of the various processes and does not consider either the effect of vertical flow in porous media on the sediment immersed weight or the increase and decrease of the boundary layer. The model has been validated by Ang et al. [114] for controlled boundary conditions against the experimental results, with no satisfactory results. The numerical work of Li et al. [115] is worth to be mentioned when the numerical modeling of dewatering systems is concerned. They included the drainage effects for the macro-tidal beach, modifying the model presented in [116]. Two different types of dewatering systems were investigated: artificial and gravity drained beaches. In the first place, the original model by [116] included a modified kinematic boundary condition for the water table, which takes into account the capillarity effects as well. The new kinematic boundary condition was incorporated into a boundary element method model. Karambas and Ioannidis [117] modified a numerical model [118] in order to take into account the effect of the draining system. They coupled the Boussinesq type model for the propagation of the waves in the near field with a porous flow model capable to account for sediment transport. Vesterby et al. [87] coupled the commercial model powered by Danish Hydraulic Institute MIKE SHE (for groundwater dynamics) and MIKE 11 (for sea-level fluctuations and wave run-ups) and applied them to the real case of Les Sables d’Olonne [89]. Saponieri and Damiani [119,120] solved Richard’s equation by means of HYDRUS-2D code [121] to simulate the GWK prototype-scale experiments [72]. They tested the model for the static case (i.e., with no waves) in order to check the capability of the model to catch the draining capabilities of the BDS, and eventually use it to optimize the position of the drain according to its best performances. Against the groundwater-coastal hydrodynamic coupling, the approach used by [122,123] resorts to the power of the Computational Fluid Dynamics to model a fine porous medium in presence of wave-forced groundwater table, in presence of a drained beach. The OpenFOAM ^® library has been used to solve the Volume-Averaged Reynolds Averaged Navier–Stokes equation [124]. In [122], different drain diameters have been compared in terms of groundwater table and discharge, while [123] modeled three-dimensional small scale numerical tests for different draining patterns and sand permeability. The dynamic inside the pipe has been studied and analyzed, to gain insight on its hydraulic regime and eventually to define appropriate configurations to prevent the pipe from pressurizing.

6. Discussion

Based on past research studies, it is rather clear that BDS performance is controversial. In part, this is due to both the complex interaction between wave run-up and groundwater dynamics and the influence of infiltration/ex-filtration on sediment transport [51].

For this reason, the initial enthusiasm for this soft engineering method has been extinguished through the years. In Figure 3 the trend of published works about BDS (as extracted from Google Scholar database by using “coastal dewatering” and “beach drainage”, last accessed 20 October 2021) through the years is depicted. It is possible to notice how BDS, in the mid-1990s, had an appeal on the coastal engineers’ community, renewed at the beginning of the 2010s. From that time, only a few attempts to further deepen the knowledge and the use of this system have been made during the last years.

About economic considerations, differently from hard structures whose costs are mostly initial, the costs of the soft solution are spread over a longer period. In general, the maintenance cost of a traditional solution is negligible with respect to the whole cost of deployment. The same does not happen with soft solutions. Contestabile et al. [36] furnished a quick comparison between the BDS and breakwaters: according to that estimation, it takes more than 30 years of BDS activity to cushion the costs of the breakwaters. Of course, the cost of hard engineering structures depends on the geographical area [125] while the cost of maintenance is strictly related to the weather conditions.

With regard to the laboratory experiences, almost all of them were positive and encouraging. From the test results, it is possible to gather the capabilities of BDS on fast recovering but also on accreting the beach. On the other hand, the results are variable and depend on local situations in the field campaigns. Some authors firmly declared the system malfunctioning and its low reliability as a coastal defense method [30,92,98,126]. Others drew opposite conclusions even for the same site, deployed and monitored at different periods (it is the case of Walstra et al. [98] and Reedijk et al. [127]). This outcome can be addressed to the scale effects of the laboratory and to the lack of clear design guidelines for prototype installations. In fact, all these factors contribute simultaneously to BDS shore protection outcomes.

In laboratory studies, there is no net increase of sand on the profile (due to the conservation of sand) [7] and the response of the beach is the increase of the beach face steepness. There is not any interference with the long-shore sediment transport or local bathymetry inhomogeneity. On the other hand, the boundary conditions are controlled. These factors make the systematic study of the drainage system easier and specific, but they do not furnish a holistic approach that seems to contribute to the performance assessment of BDS.

In the field, site-dependent factors played an important role. The field waves conditions for their stochastic nature can be linked to particular chronological order only afterward, at the survey stage, when other factors can play a role on the system (i.e., tidal phase, storm surge and flooding, temporal failure or malfunctioning, etc.). The process of performance evaluation is more difficult if compared to laboratory investigation. The results are also influenced by the survey campaign duration and frequency since the beach can experience a periodical modification of the shoreline and the outcome can be misinterpreted.

It is worth pointing out that some aspects of the system seem to be neglected ever since, e.g., the hydraulic behavior of the pipes, their hydraulic efficiency, and some technical aspects (e.g., the slope of the pipes, their length, their installation, their aeration). Of course, the lack of guidelines as a side effect does not allow the optimum design of the BDS which in turn can lead to an uncontrollable influence on the performances.

The field campaigns can be useful only afterward, once the precise parameters of the design are assured. In this regard, numerical modeling can be essential. In fact, it allows testing varying field conditions, and still focusing only on the aspects that one is interested in. This aspect has to be taken into account in order to obtain clear guidelines, that eventually can make the field experience more controllable and replicable. The detailed simulation of the hydraulic behavior of the BDS can be achieved by means of Computational Fluid Dynamics, which reproduces the physics of the drain and the effect of the tool on the groundwater dynamics, at least from a hydrodynamic point of view. Though, CFD is not feasible for being applied to large time and spatial scales. In this case, the effects of the BDS on groundwater must be included in morphodynamics models.

7. Concluding Remarks

BDS is a tool able to modify the natural dynamics of sandy beaches groundwater table in order to gain shoreline stabilization. Controversial performances that BDS showed in both experimental and prototype scale experiences have been observed so far. This review aims to report all the valuable works that contribute to the assessment of BDS performance. It aims to give a big picture of how unclear the results were, along with the non-uniform undertaken approach. The ineffective and controversial results discouraged tests and application. Nonetheless, its environmental potential (in both ecological and view impact points of view), relatively low costs and the site-dependent positive results might be an encouraging signal for keep studying it and investigating what brought to misleading results or, on the contrary, what favored their goodness. Based on the review, it has been stressed that some open challenges still remain due to the lacking of clear (and shared) guidelines that are needed to design BDS and to perform reliable observations in real scale applications.