Abstract
The stability and tracking controls of a dynamic ship system are studied in this paper, in order to stabilize and track the desired path of a catamaran ship system. The ship sails on a river that is prone to currents, wind, and unknown disturbances from the surrounding environment. Hence, the ship system potentially has stability problems. This paper presents a method for controlling the trajectory of a nonlinear ship system and controlling the ship stabilization. Three steps of the fundamental equations of constrained motion (FECM) with an uncertainty control are used to examine a control force to stabilize and track the ship system. The ship system is considered with six degrees of freedom to describe the stabilization of the ship’s rigid-body motion. The results show the efficiency of the control forces from the FECM, with an uncertainty controller applied to the ship system. They guarantee that the conditions of the ship system are satisfactory, and that the ship follows the desired path.
1. Introduction
A dynamic ship system requires position and orientation controls when the ship system is transported into a river. Environmental disturbances in the river cause unstable movements and stability problems. Several techniques are presented to address these problems. For instance, dynamic position control for a marine surface vessel is required, in order to ensure that the system follows a desired path. A control design was developed using feedback linearization applied to a dynamic model of an underactuated marine vessel [1]. The development of the control law for trajectory tracking control was analyzed using several theorems. A sliding-mode control was proposed to control position tracking for the planar surface vessel in the method used [2], and to guarantee position tracking for unmanned surface vessels (USV) [3]. Other methods for improving ship dynamic positions can be found in the literature [4,5].
In a dynamic position control where it was proposed that a ship’s heading motion is directly controlled, the heading of the ship’s physical body was chosen in the ship heading control by a novel disturbance compensating model predictive control (DC-MPC) [6]. In another case, a ship’s heading motion was represented by yaw-angle tracking [7]. A dynamic surface control (DSC) method was designed to control the position and yaw-angle tracking for underactuated ships [7]. The yaw angle was used as a direct parameter in controller problem design. In a controller design for the dynamic position, network-based Takagi–Sugeno (T–S) fuzzy models for a dynamic positioning system were provided by the yaw angle using a variation method [8]. The model of an underactuated surface ship was considered with three degrees of freedom, including x–y position coordinates and a ship heading. The method is derived from the idea of standard dynamic inversion. The control design was presented as a good choice for underactuated systems control [9]. Another interesting approach for tracking control was presented in [10]. The paper investigates the dynamics of an autonomous underwater vehicle (AUV), which is important for developing the performance of AUV tracking control systems. A model of the AUV is clearly described by Fossen’s equations [11], for a method of tracking control that is also used in many recent research studies. There are also many other interesting studies on new expressions for the nonlinear equations of motion, considered using different coordinates, to describe 3D dynamic motion [12,13,14].
A ship, when sailing, is affected by external forces. In order to compensate for these external forces, a mathematical model of a controller was provided, with components of several scheme designs including a sliding mode controller, adaptive controller, and nonlinear observer [15]. Another control design, considering the motion of a ship–submarine collision, was also presented. The procedure was developed using a new version of the rigid-body dynamic program MCOL (Modesto, CA, USA) coupled with the explicit simulation software LS-DYNA (Los Angeles, CA, USA). A governing equation was designed using two reference frames based on large-amplitude rotational and hydrodynamic forces that affect the ship systems [16]. A bubble drag force influenced the ship’s elastic deformation. The elastic behavior of the ship’s hull was described by a simple non-uniform beam model. The mathematical model was integrated numerically via the fourth-order Runge–Kutta method, to reduce the disturbance of the bending moments of a hull girder [17]. Moreover, a ship system should approach an asymptotic global stability [18]. The stability of the control law was validated using Lyapunov theory [19]. The tracking control design is necessary for controlling a ship’s dynamic position. The problem of how to reduce the energy loss of the system is also an important topic to investigate. A control design consisting of an optimal control theory and Kalman filters was proposed in [20]. Another control design for an adaptive ship steering system through a preset track was presented in [21]. An optimal linear quadratic regulator (LQR) with a symmetric indicator of control quality is a robust approach to use for the ship control problem. The methodology was implemented using the least squares method. The mentioned algorithm successfully stabilized the ship’s trajectory along the desired track.
For a nonlinear tracking control path, many theorems have the problem of providing controllers that consider a ship’s dynamic position. A marine surface vessel has multiple elements which must be taken into account. A mathematical model has been proposed considering related factors of dynamic system identification that are not dependent on the identified problem.
The method of constrained motion has been used to study many control problems for a ship’s dynamic position. A marine surface vessel is subject to environmental disturbances and difficult conditions. Although controller designs are presented in many studies [22,23,24,25,26,27,28,29,30,31], the ship tracking control problem remains an interesting topic to examine. Many researchers are still attempting to solve the problem of designing a controller for maintaining the system. In this paper, we present an alternative process for controlling the ship system when tracking a desired constrained-trajectory motion.
In this work, we used the three steps of the fundamental equation of constrained motion (FECM), that is, the closed-form equation of constrained motion presented by Udwadia and Kalaba [32]. This process helps to describe the ship’s dynamic motion in the case of unconstrained motion and for constrained motion using the constraint equation. Subsequently, the ship tracking control was designed to follow the real-world motion via uncertainty control, in order to compensate for external forces from environmental disturbances and unknown errors from the ship system. In this research, we used the fundamental equation with an uncertainty control [32,33,34] to design a ship tracking and stabilizing control system that can follow a desired path when subjected to environmental disturbances. The simulation results were produced via the MATLAB program (The Mathworks, Inc., Las Vegas, NV, USA), to verify the proposed approach.
The main contribution of our paper is that the methodology proposed in the paper considers simultaneous tracking and stabilizing of a nonlinear six-degrees-of-freedom ship system by conceptualizing the tracking and stabilizing conditions as constraints imposed on the system. The control approach can guarantee the constraint-following behavior in both tracking and stabilizing the ship system, even when there is no exact knowledge of the uncertainties arising from the environment, disturbances, or modelling errors. The approach is presented in a closed form and can be used with multiple constraints. The constraints can be linear or nonlinear and can be holonomic or nonholonomic. In addition, the resulting constraint-following errors of the system can be controlled to meet requirements and ensure that the controlled ship system is able to track a desired path with stability.
2. Fundamental Equations of Constrained Motion
The approach of the closed-form expression for the constrained motion was developed by Udwadia and Kalaba [32] and is called the fundamental equation. The explicit closed form is investigated via classical dynamics. The conceptualization consisted of three steps. First, an unconstrained equation provided the general mass matrix and general force vector of the dynamic system, which were derived from Lagrangian mechanics. Lagrangian mechanics is most useful for modelling the equations of motion for the kinetic energy and potential energy descriptions. The Lagrangian is given by the difference between kinetic energy and potential energy in a system that obeys the Euler–Lagrange equations of motion, as follows:
where is a generalized coordinate of the ship system, the Lagrangian , is the kinetic energy, and is the potential energy. Then, we can use the calculation in Equation (1) to obtain the general mass matrix and general force vector . These results in the expressions of the unconstrained system’s motion are presented as
where is the acceleration of the unconstrained system.
Secondly, the system tracking path requires a constraint equation in order to describe the trajectory constraint. The constraint equations can be holonomic and/or nonholonomic. The products of this step are the constraint matrix and the constraint vector , which are obtained by calculating and formatting the constraint equation according to Newton’s second law of motion, to represent the delineation of the constrained motion. Therefore, we can present the constraint relation in the form
Lastly, this step has brought all the variables from previous steps together to model the motion of the constrained system. To explain the control of the ship system, the constrained system is modeled via the FECM process, which enables the control of the constrained motion while satisfying the constraint equation.
This equation can be used to describe any physical real-world motion, and especially to force a dynamic system through nonlinear motions in constrained systems. Therefore, we apply the fundamental equation in this work for studying the ship’s motion description.
3. Unconstrained Ship’s Motions
In the first step of the procedure, an unconstrained ship system is derived from the rigid-body dynamic model without a constraint equation.
The dynamic ship system, described in an earth-fixed frame and a moving frame, was proposed by Fossen in 2002 [35]. We used the body’s fixed frame to study the ship system with six degrees of freedom, in order to describe a stabilizer control. The six degrees of freedom included: surge, sway, and heave (which describe translation) and roll, pitch, and yaw (which describe rotation). In this paper, the nonlinear equation of motion [11,36] can be given as follows:
where are surge, sway, and heave for the linear velocities, and roll, pitch, and yaw for the angular velocities, respectively. They are described in a moving frame. The position vector of the ship system is presented as , which indicates the coordinates of the ship system in the Earth-Centered Inertial (ECI) frame. The earth-fixed frame and the body-fixed frame with the six degrees of freedom of the ship motion system are shown in Figure 1.
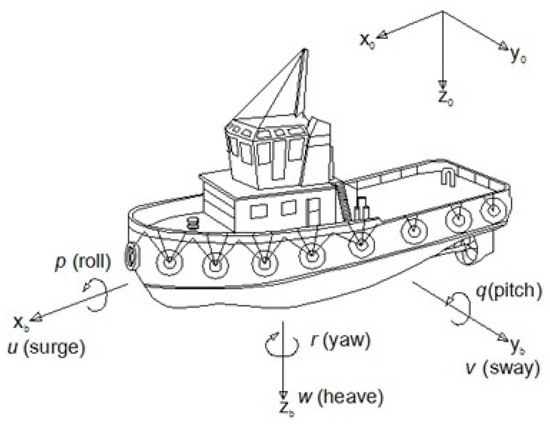
Figure 1.
The ship system with six degrees of freedom.
Subsequently, the position and velocity vectors can be transformed using the following formula:
where the matrix represents a rotation matrix as shown in the following:
where:
and
Using Equation (5), the kinematic coordinates in the ECI frame of the ship system in terms of velocities are given by
The inertia matrix is represented by M, and D is a hydrodynamic damping matrix which combines linear drag forces and nonlinear drag forces . Both matrices are assumed to be diagonal, i.e.,
and , where is given by
where
and,
where:
where ρ is the density of freshwater in , is the drag coefficient, the drag contact area in is represented by , and x, y, and z are the axes. The Coriolis and centripetal matrices can be given by
where , , and are the moments of inertia about the body-fixed frame
and , , and are the products of inertia:
The roll angle is defined to be zero in the first constraint equation. When describing a ship’s stability, this means that the ship’s roll motion is at a stable equilibrium position. Thus, there is no need to consider the restoring forces . However, in Equation (4), we still need to consider the wind force and the wave force. The vector of wind loads is represented by . We can calculate the wind force using the following equation:
where is the density of the liquid, is the wind velocity, is the effective area of jumping net, and is a protection factor. Similarly, is the vector of wave loads, which can be calculated using Morrison’s equation in the following form:
The variable is the area of the object, is the mass coefficient, is the water particle acceleration in the direction , is the water particle velocity in direction , and is the volume of the object.
In this step, we discussed the conceptualization step to describe the mass matrix and the general force vector of the unconstrained ship system (see Equation (2)). In the next section, we consider that the unconstrained motion is subject to an imposed constraint equation, in order to obtain the other main variables (A and b) for computing the dynamic ship system using the FECM (see Equation (3)).
4. Ship’s Constraint Equations
In this paper, two constraint equations are presented, including the roll angle for describing the ship’s stability and the trajectory constraint for the ship tracking path. The first constraint equation is assumed to require zero roll angles, in order to stabilize the ship’s motion when affected by the current waves in the river. Then, the constraint equation is changed from the configuration vector in the body-fixed frame into the ECI frame, and can be given by
The second constraint equation is for the ship to follow the desired trajectory. We assume that the trajectory constraint is governed by
If the system does not initially satisfy the constraint Equations (20) and (21), we can adjust the system by using the trajectory stabilization relation [34]:
where are positive constants.
Having appropriately differentiated Equation (20), we obtain:
and
Similarly, having appropriately differentiated Equation (21), we obtain
and
Next, the constraint equation is described by the constraint matrix (A) and the constraint vector (b), where we obtain the constraint relation proposed in Equation (3). Having rearranged the constraint relation into the form of Equation (22), we obtain
and
where, in the case of Equation (21)
and
The variables and are the positions in the ECI frame, in the following form:
and
We note that , , and are the terms for positions in the moving frame, and , , and are the terms for the Euler angles in the moving frame. Therefore, we obtain the other two parameters and for both constraint equations. All parameters of the unconstrained motion and the constraint equations are implemented to model the ship system for the constrained motion.
5. Constrained Ship’s Motions
The ship system requires a control force in order to control the ship to follow the desired trajectory. The above-mentioned steps give all the required variables for the fundamental equations [32,33,34] that lead to modeling the control force for the ship’s dynamic motion.
5.1. Control of Ship’s Constrained Motion
For the constrained ship system, we model the control force using all the variables from the above steps, to demonstrate the ship’s motion system for constrained motion:
The unconstrained system is extended to follow the desired path in the above-mentioned equation (Equation (21)). From the fundamental equation [34], the control force is proposed as a robust tool for the ship tracking control system. The parameters , , , and can be substituted into the numerical solver. The control force is shown as follows:
where . Using Equation (34) with Equation (33), and calculating these equations by pre-multiplying the equation with the constrained ship system is obtained in terms of the acceleration:
5.2. Control of Ship System’s Uncertainties
In real-world applications, an uncertainty in the system influences the ship’s dynamic motion. The ship moves along the desired path in the real-world motion under uncertain conditions caused by disturbances and other parameters that should be taken into consideration. In this methodology, this system is called the controlled actual system. Unknown errors and disturbances are considered in this methodology, in order to compensate for the uncertain conditions. The uncertainties in the systems are explained in the next section.
In this conceptualization, the following equation of motion [34], which is called the nominal system, is given to describe the ship tracking control system under no uncertainties.
As previously mentioned, uncertainties arise in the system in real-world motion due to several factors such as inexact knowledge of the system. Thus, we need to consider the uncertainties in the system in terms of (delta). Since uncertainties arise in the system both in masses and forces, as described in the methodology, the actual mass is given by where is the mass matrix that represents the nominal mass matrix and is the uncertainty added to the mass matrix in order to describe the actual system. The actual force is given by where represents the nominal generalized force vector and is the uncertainty added to the force vector in order to describe the actual system. Therefore, we obtain the explicit equation of motion of the controlled actual system as follows [34]:
In this conceptualization, the control force is an additional control force added to the system in order to compensate for the uncertainties in the actual system, and , where the acceleration for compensating uncertainties is shown as . The term can be shown in explicit form as [34]:
where s is the sliding surface, given by
where , , , and are discretionary small positive numbers, is the state estimator error, is the differential of , and, is a positive function of time, which is the bound on and . We note that , where the bound implies the uncertainties arising in the actual system. We can estimate the bound on using the formula [34]:
The parameter is a small positive number that is given in the following form
where is obtained by the approximation of
In the following formula, is the number of generalized coordinates of the system. The function is investigated in the following form:
where
We note that represents the infinity norm.
Subsequently, Equation (36) is calculated by pre-multiplying both sides and using Equation (37). The closed form of the equation of motion of the controlled actual system can be obtained as follows:
The explicit steps of the method proposed in the paper illustrate the advancement in improving the results by minimizing the tracking error while simultaneously stabilizing the ship’s motion. We have presented a control design for an uncertain nonlinear constrained ship motion with the three steps of the fundamental equation, which has robust tools including both the constraint-following and uncertainty-compensating controls. To show the improvement of the proposed approach we compared the results of our explicit method with the method proposed in [37]. The results were obtained by controlling a ship’s motion with three degrees of freedom, using both the conceptualization proposed in [37] and our proposed method with the same constraint analysis, that is, an orientation yaw of zero degrees. The simulation result was obtained using MATLAB programming with the same initial conditions and the same integral option. The comparisons are shown in Figure 2.
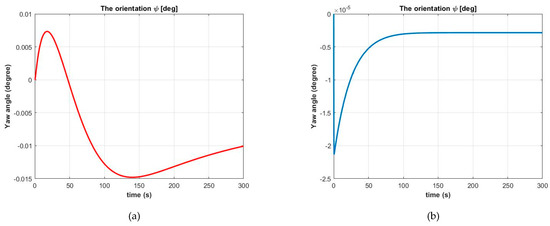
Figure 2.
The comparative results of the two methods between (a) [37] and (b) our proposed method.
In Figure 2a, a time-varying feedback control law and a disturbance adaptation law from [37] have been applied to the 3D ship model. Figure 2b represents the results for the yaw angle from our conceptualization. We can see that our method yields a smaller error compared to the one from [37]. When we consider a situation where the system can be subjected to uncertainties, by adding 20% masses and 30% forces, the results for the yaw angle still satisfy the constraint for our conceptualization. Moreover, the explicit steps in our proposed method can be followed with multiple constraints and any physical motion constraint that is useful, to describe the dynamic motion in real-world applications. Furthermore, all the steps in our conceptualization can be shown in the explicit flowchart, as shown in Figure 3.
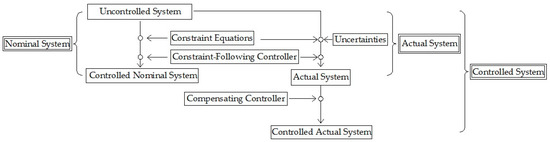
Figure 3.
The flowchart for the proposed method.
6. Numerical Results and Simulations
6.1. The Simulation Results for the Constrained Motion in the Nominal System
The simulation of the system was undertaken using MATLAB programming with the ode15s solver. The main parameters for a catamaran ship are shown in Table 1. In this paper, we used the port stern corner of the ship to reference the origin point of the ECI frame, as shown in Figure 4. Hence, the ship simulation begins with the initial conditions , , z = −1.33,, , and .

Table 1.
The main parameters of catamaran ship model.
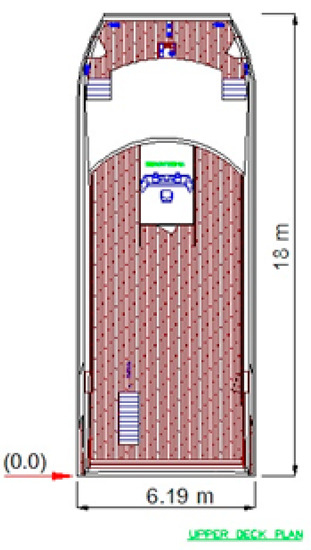
Figure 4.
The reference point of the ship system in the top view.
The ship system can follow the constraints given by Equations (20) and (21) using the control force described in Equation (34). The results of this process are shown in Figure 5, Figure 6, Figure 7 and Figure 8. Figure 5 shows the plot of the positions x and y in the ECI frame of the ship system in the X–Y plane. The ship system can be sailed according to the trajectory constraint proposed in Equation (21).
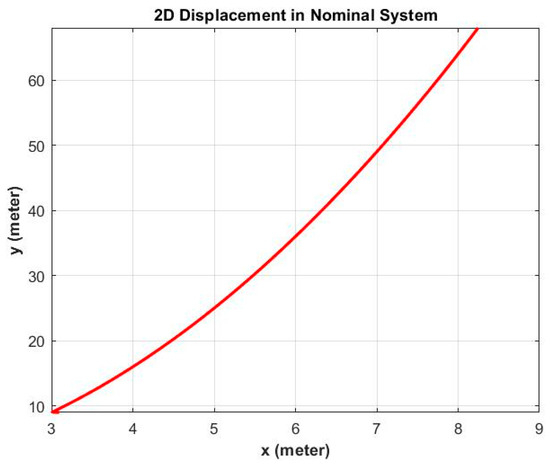
Figure 5.
The constrained route of the ship system for the constraint equation ϕ2s = x2 − y = 0.
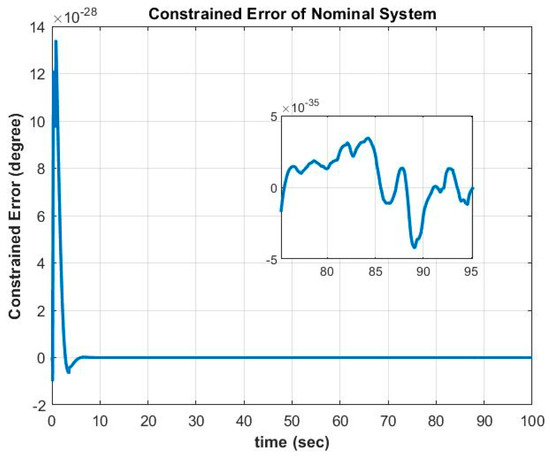
Figure 6.
The error in satisfaction of the constraint equation ϕ1s = pd + qdsinϕtanθ + rdcosϕtanθ = 0.
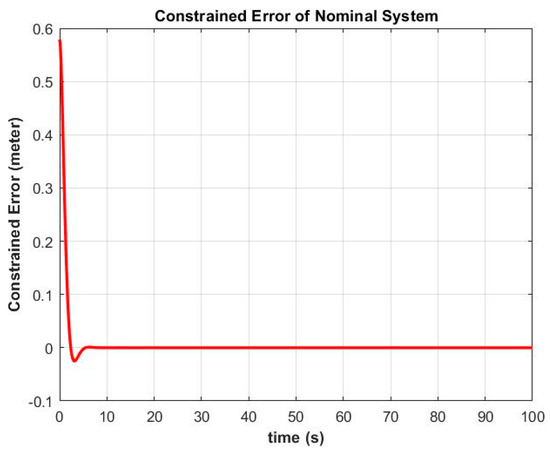
Figure 7.
The error in satisfaction of the constraint equation ϕ2s = x2 − y = 0.
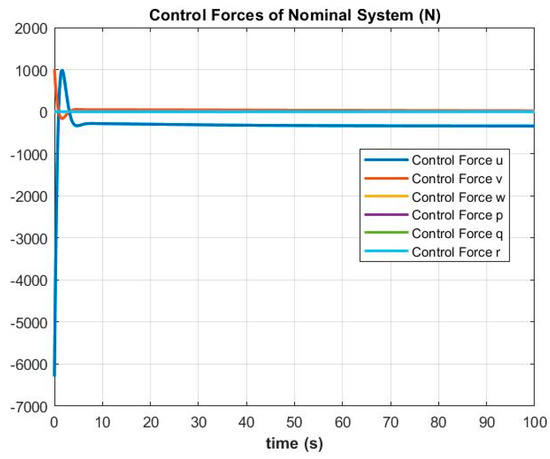
Figure 8.
The nominal control forces applied to the ship for the constraint equations (ϕ1s = pd + qdsinϕtanθ + rdcosϕtanθ = 0) and (ϕ2s = x2 − y = 0).
Figure 6 and Figure 7 show the plots of the constraint errors for the ship control for the constraint Equations (20) and (21).
The plot in Figure 6 shows the error in the satisfaction of constraint Equation (20). We can see that the error is very small, due to the capability of the control force from Equation (34). In Figure 7, the error in the satisfaction of constraint Equation (21) shows a small value, similar to that in Figure 6. Even though the initial conditions start with an error, the trajectory stabilization (Equation (22)) can still make the system converge into the constraint trajectory, with minimal error.
In Figure 8, the control forces are implemented for each of the generalized coordinates of the ship’s dynamic motion. The ship system is subjected to control forces, to guarantee that the system can follow the constraint Equations (20) and (21), respectively.
6.2. The Simulation Results for the Constrained Motion in the Controlled System
When we used the control force in the nominal system in order to control the ship system, we observed that the ship could follow the constraint Equations (20) and (21). The results of the nominal system are perfect in case of the system without uncertainties. Next, we considered the ship system subjected to uncertainties that have arisen in the system. Therefore, we considered uncertainties in the system by adding them to the mass matrix and the force vector, in order to describe the actual system. The uncertainty in the mass was assumed to be 20% of the nominal mass, and the uncertainty in the given force vector was assumed to be 30% of the nominal force. These uncertain forces can arise from wind, currents, and other environmental disturbances that affect the actual ship system. Under uncertain circumstances, the actual ship system is unable to follow the constraint Equation (21) without uncertainty control, as seen in Figure 9.
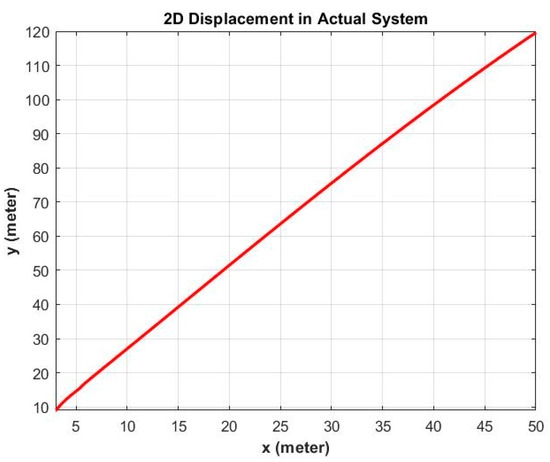
Figure 9.
The ship tracking path for the constraint equation in the actual system without any additional control force.
Thus, we must take the additional control from Equation (36) into account, to compensate for these uncertainties. The results are given as follows.
The ship system begins with the initial conditions and all numerical sets, like the nominal system. The simulation results of the controlled system have input parameter values in the closed form of the equation of motion (Equation (44)) as follows: , , , , , , , and, The results for this controlled system are shown in Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14. The tracking result is the same as that given by the nominal system.
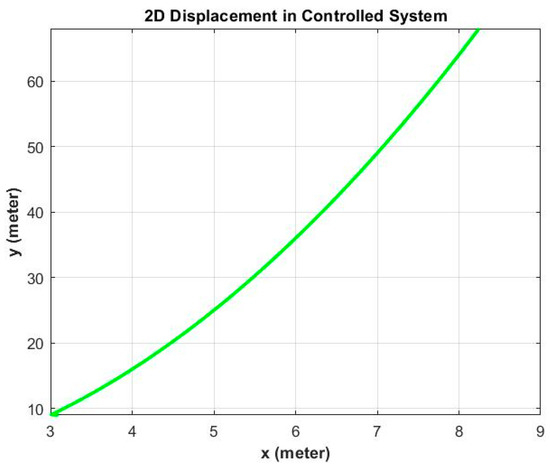
Figure 10.
The ship tracking path in the controlled system.
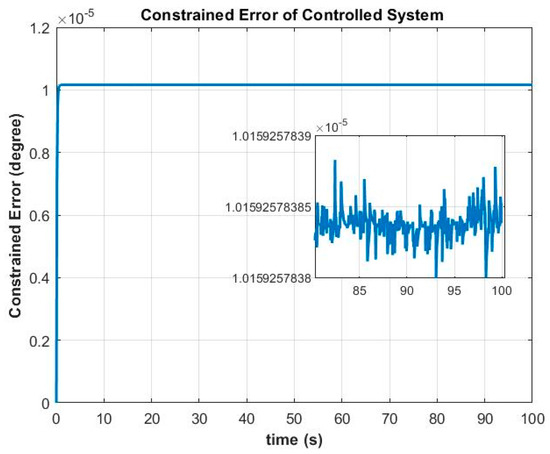
Figure 11.
The error in the controlled system for the constraint equation ϕ1s = pd + qdsinϕtanθ + rdcosϕtanθ = 0.
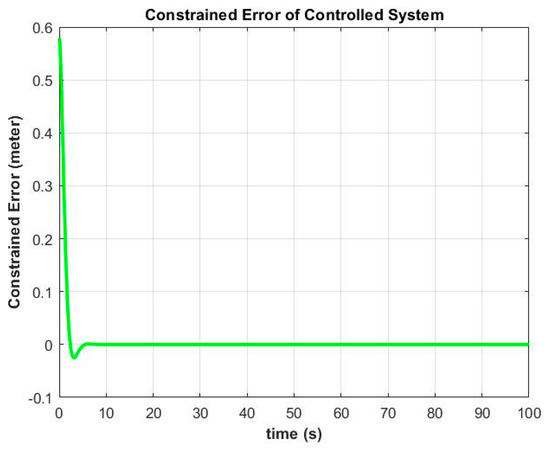
Figure 12.
The error in the controlled system for the constraint equation ϕ2s = x2 – y = 0.
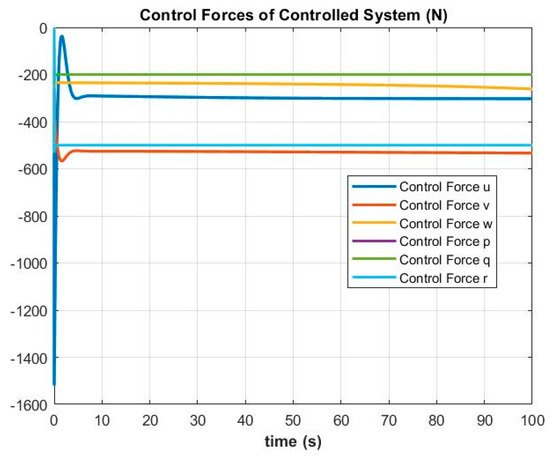
Figure 13.
The additional control forces for the controlled system.
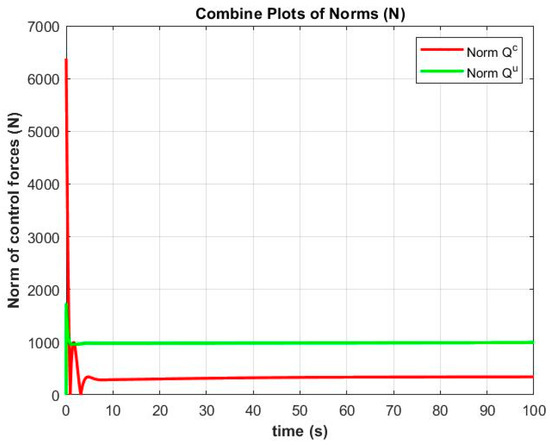
Figure 14.
The comparison between the norms of the nominal control force and the additional control force.
Figure 10 shows the plot of the positions x and y in the ECI frame of the ship control system. We can see that the ship system is able to return to the trajectory constraint proposed in Equation (21), which is the same as the one shown in Figure 5, due to the efficiency of the control force from Equation (36).
Figure 11 and Figure 12 show the plots for the constraint errors that satisfy constraint Equations (20) and (21), respectively.
We can see in Figure 11 that in the controlled system, the constraint error for constraint Equation (20) attempts to reach zero, which is due to the use of the additional control force . For constraint Equation (21), the error in the controlled system also attempts to reach zero, as shown in Figure 12. Although the initial conditions may start with an error, the trajectory stabilization (Equation (22)) allows the system to minimize the constraint errors of the constraint trajectory, in a similar way to that shown in Figure 7.
In Figure 13, the proposed control forces are applied to all generalized coordinates of the ship’s dynamic motion in the controlled system to ensure the ship system is able to follow our desired constraint equations.
Figure 14 shows the norms of the comparison of the nominal control force and the additional control force . The norm of the nominal system is shown with a red line that describes the force generated from the use of the controller for the ship system to follow the constraint equations. Similarly, the norm of the controlled system is shown with a green line, demonstrating the force generated from the power of the controller to compensate for the uncertainties in the actual system. All of these forces guarantee that the ship system is able to follow the constraint equations with the proposed control forces.
7. Conclusions
This paper presents a technique for controlling a dynamic ship system with rigid-body motions. The technique was to apply the controller for the nominal constrained motion and the controller for uncertainties arising in the ship system, in order to force the ship system to obey the constraint equations and to compensate for uncertainties. In this work, the constraint equations were the stabilizer with zero roll angles and the trajectory constraint for the ship tracking path. The ship system could follow the constraint equations by using the control force from the three steps of the fundamental equation in the nominal system. Then, the additional control force was used to control the ship system based on the uncertainties in the actual system. All of the methods were effective in satisfying the conditions.
Author Contributions
Conceptualization, T.W.; methodology, T.W.; software, C.A.; validation, C.A.; formal analysis, C.A.; investigation, T.W.; resources, C.A.; data curation, C.A.; writing—original draft preparation, C.A.; writing—review and editing, T.W.; visualization, C.A.; supervision, T.W.; project administration, T.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pedone, P.; Zizzari, A.A.; Indiveri, G. Path-Following for the Dynamic Model of a Marine Surface Vessel without Closed-Loop Control of the Surge Speed. IFAC Proc. Vol. 2010, 43, 243–248. [Google Scholar] [CrossRef]
- Ashrafiuon, H.; Muske, K.R.; McNinch, L.C.; Soltan, R.A. Sliding-mode tracking control of surface vessels. IEEE Trans. Ind. Electron. 2008, 55, 4004–4012. [Google Scholar] [CrossRef]
- Soltan, R.A.; Ashrafiuon, H.; Muske, K.R. State-dependent trajectory planning and tracking control of unmanned surface vessels. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 3597–3602. [Google Scholar]
- Du, J.; Guo, C. Nonlinear adaptive ship course tracking control based on backstepping and Nussbaum gain. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; Volume 4, pp. 3845–3850. [Google Scholar]
- Sørensen, A.J. A survey of dynamic positioning control systems. Annu. Rev. Control 2011, 35, 123–136. [Google Scholar] [CrossRef]
- Li, Z.; Sun, J. Disturbance compensating model predictive control with application to ship heading control. IEEE Trans. Control Syst. Technol. 2011, 20, 257–265. [Google Scholar] [CrossRef]
- Chwa, D. Global tracking control of underactuated ships with input and velocity constraints using dynamic surface control method. IEEE Trans. Control Syst. Technol. 2010, 19, 1357–1370. [Google Scholar] [CrossRef]
- Wang, Y.L.; Han, Q.L.; Fei, M.R.; Peng, C. Network-based T–S fuzzy dynamic positioning controller design for unmanned marine vehicles. IEEE Trans. Cybern. 2018, 48, 2750–2763. [Google Scholar] [CrossRef]
- Ye, L.; Zong, Q. Tracking control of an underactuated ship by modified dynamic inversion. ISA Trans. 2018, 83, 100–106. [Google Scholar] [CrossRef]
- Li, D.; Du, L. AUV Trajectory Tracking Models and Control Strategies: A Review. Journal of Marine Science and Engineering. J. Mar. Sci. Eng. 2021, 9, 1020. [Google Scholar] [CrossRef]
- Fossen, T.I. Guidance and Control of Ocean Vehicles. Ph.D. Thesis, University of Trondheim, Trondheim, Norway, 1999. [Google Scholar]
- Chu, P.C.; Fan, C. Prediction of falling cylinder through air-water-sediment columns. ASME J. Appl. Mech. Rev. 2006, 73, 300–314. [Google Scholar] [CrossRef][Green Version]
- Alsos, H.S.; Faltinsen, O.M. 3D motion dynamics of axisymmetric bodies falling through water. Ocean Eng. 2018, 169, 442–456. [Google Scholar] [CrossRef]
- Xiang, G.; Xiang, X. 3D trajectory optimization of the slender body freely falling through water using cuckoo search algorithm. Ocean Eng. 2021, 235, 109354. [Google Scholar] [CrossRef]
- Liu, Z. Ship adaptive course keeping control with nonlinear disturbance observer. IEEE Access. 2017, 5, 17567–17575. [Google Scholar] [CrossRef]
- Le Sourne, H.; Donner, R.; Besnier, F.; Ferry, M. External dynamics of ship-submarine collision. In Proceedings of the Preprints of 2nd International Conference on Collision and Grounding of Ships, Copenhagen, Denmark, 1–3 July 2001; pp. 137–144. [Google Scholar]
- Zhang, N.; Zong, Z. The effect of rigid-body motions on the whipping response of a ship hull subjected to an underwater bubble. J. Fluids Struct. 2011, 27, 1326–1336. [Google Scholar] [CrossRef]
- Chen, X.; Tan, W.W. Tracking control of surface vessels via fault-tolerant adaptive backstepping interval type-2 fuzzy control. Ocean Eng. 2013, 70, 97–109. [Google Scholar] [CrossRef]
- Bui, V.P.; Kim, Y.B. Design of sliding mode controller for ship position control. J. Inst. Control Robot. Syst. 2011, 17, 869–874. [Google Scholar] [CrossRef]
- Fotakis, J.O.H.N.; Grimble, M.; Kouvaritakis, B. A comparison of characteristic locus and optimal designs for dynamic ship positioning systems. IEEE Trans. Automat. Contr. 1982, 27, 1143–1157. [Google Scholar] [CrossRef]
- Borkowski, P. Adaptive system for steering a ship along the desired route. Mathematics. J. Mar. Sci. Eng. 2018, 6, 196. [Google Scholar]
- Udwadia, F.E.; Wanichanon, T. Hamel’s paradox and the foundations of analytical dynamics. Appl. Math. Comput. 2010, 217, 1253–1265. [Google Scholar] [CrossRef]
- Udwadia, F.E.; Wanichanon, T. A New Approach to the Tracking Control of Uncertain Nonlinear Multi-Body Mechanical Systems. In Nonlinear Approaches in Engineering Applications 2; Springer: New York, NY, USA, 2014; pp. 101–136. [Google Scholar]
- Cho, H.; Wanichanon, T.; Udwadia, F.E. New continuous control methodology for nonlinear dynamical systems with uncertain parameters. In Proceedings of the 1st ECCOMAS Thematic Conference on International Conference on Uncertainty Quantification in Computational Sciences and Engineering, Crete, Greece, 25–27 May 2015. [Google Scholar]
- Wanichanon, T.; Udwadia, F.E. Nonlinear damping control for uncertain nonlinear multi-body mechanical systems. J. Res. Appl. 2014, 2, 7–19. [Google Scholar]
- Udwadia, F.E.; Wanichanon, T. Comparison of Methods for Tracking Control of Nonlinear Uncertain Multi-Body Mechanical Systems. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 9–15 November 2012; American Society of Mechanical Engineers: New York, NY, USA; pp. 921–940. [Google Scholar]
- Wanichanon, T.; Cho, H.; Udwadia, F.E. An effective approach for the control of uncertain systems. In Proceedings of the 23rd ABCM International Congress of Mechanical Engineering, Rio de Janeiro, Brazil, 6–11 December 2015. [Google Scholar]
- Cho, H.; Wanichanon, T.; Udwadia, F.E. Continuous sliding mode controllers for multi-input multi-output systems. Nonlinear Dyn. 2018, 94, 2727–2747. [Google Scholar] [CrossRef]
- Udwadia, F.E.; Wanichanon, T. A closed-form approach to tracking control of nonlinear uncertain systems using the fundamental equation. In Proceedings of the Earth and Space 2012: Engineering, Science, Construction, and Operations in Challenging Environments, Pasadena, CA, USA, 15–18 April 2012; pp. 1339–1348. [Google Scholar]
- Wanichanon, T.; Cho, H.; Udwadia, F.E. An approach to the dynamics and control of uncertain multi-body systems. Procedia IUTAM 2015, 13, 43–52. [Google Scholar] [CrossRef][Green Version]
- Wanichanon, T.; Udwadia, F.E.; Cho, H. Formation-keeping of uncertain satellites using nonlinear damping control. J. Res. Appl. 2014, 2, 20–33. [Google Scholar]
- Udwadia, F.E.; Kalaba, R.E. Equations of motion for mechanical systems. J. Aerosp. Eng. 1996, 9, 64–69. [Google Scholar] [CrossRef]
- Udwadia, F.E.; Wanichanon, T. Explicit equation of motion of constrained systems. In Nonlinear Approaches in Engineering Applications; Springer: New York, NY, USA, 2012; pp. 315–347. [Google Scholar]
- Udwadia, F.E.; Wanichanon, T. Control of uncertain nonlinear multibody mechanical systems. J. Appl. Mech. 2014, 81, 1–39. [Google Scholar] [CrossRef]
- Fossen, T.I. Marine Control Systems–Guidance. Navigation, and Control of Ships, Rigs and Underwater Vehicles; Marine Cybernetics: Trondheim, Norway, 2002. [Google Scholar]
- Hammad, M.M.; Elshenawy, A.K.; El Singaby, M.I. Trajectory following and stabilization control of fully actuated AUV using inverse kinematics and self-tuning fuzzy PID. PLoS ONE 2017, 12, e0179611. [Google Scholar] [CrossRef]
- Pettersen, K.Y.; Nijmeijer, H. Semi-global practical stabilization and disturbance adaptation for an underactuated ship. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, Australia, 12–15 December 2000; pp. 2144–2149. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).