Abstract
A thorough numerical introspection for assessing the particular issues of large flow separations around a submersible hull by using various turbulence models is described. The generic Defense Advanced Research Projects Agency (DARPA hereafter) Suboff hull is considered in the present study. Detailed descriptions of the mathematics behind the hybrid Shear Stress Transport (SST), Detached Eddy Simulation (DES) and the Improved Delayed Detached Eddy Simulation (IDDES) are given. The ISIS solver of the FineTM/Marine package is used to solve the flow problems. An adaptive mesh refinement is employed for resolving the flow inside the areas hosting significant flow gradients. Two sets of computations are analyzed: one refers to the straight-ahead course, whereas the other is focused on the static drift motions. Four angles of incident flow and three different incoming flow velocities are proposed for clarifying the details of the flow separation. Extensive grid convergence tests are performed for both working regimes and for all the meshes used in the present investigation. Extended verification and validation (V&V hereafter) of the numerical approach is performed through extensive comparisons with the experimental data. Global hydrodynamic performance of the hull as well as the local flow features are discussed in detail. The study is concluded by a series of final remarks aimed at providing useful information for further similar investigations.
1. Introduction
The accurate estimation of forces and moments is crucially important in predicting the response of a hull that moves in a direction which does not coincide with the flow direction. Dynamic forces acting on a vehicle can be broken down into inertial (pressure) and viscous components. At low angles of attack (drift), the flow does not usually separate, and inertial forces dominate. For such cases, good agreement with experimental data can be achieved by using either potential flow or Euler codes. However, for the higher angles of drift, the flow is turbulent and is characterized by large-scale boundary layer separation. Consequently, the viscous effects are important, and it becomes essential to use a Navier–Stokes code to correctly model the physics and thus obtain good agreement with experimental data [1]. The state-of-the-art in the prediction of full-scale maneuvering performance utilizes a combination of experience, heuristics, and empiricism. A complete understanding of Reynolds number effects is essential for extrapolating the model-based solutions to full scale. A reliable prediction of the overall hydrodynamic performances should therefore comprise a good understanding of the scale effects at full-scale Reynolds numbers, as previously proved for propellers by the author [2]. Nonetheless, the preponderance of experimental data available for undersea vehicles is limited to model-scale. The unavailability of full-scale data prevents a thorough validation of the high-Reynolds number capabilities, so the basic validation can only be achieved using the flat-plate-based boundary layer solutions and Reynolds number scaling.
Drag due to separation of the boundary layer from a hull surface, and to eddying and backwash in the separation zone, is a form of pressure resistance, which varies as a power of the ship speed [3]. Hydrodynamic knowledge of separation phenomena and the physical laws which govern them have not progressed to the point where the onset of separation can be predicted in advance with certainty and where the magnitude of separation resistance can be calculated. It is known that the pressure in such a zone is less than atmospheric pressure, so that the water literally sucks backward on the hull. For a surface-piercing hull, if air can be led to the zone to displace the eddying water, the suction is removed, and the separation resistance disappears. On the contrary, for fully submerged hulls running sufficiently below the free surface of the water, this is not possible.
Moore et al. [4] discussed the problems which affect the submerged bodies produced by large vortices washed away from the hull. The authors mentioned the vortices produced by the hull whenever it moves with its axis at an angle to the direction of flow as in a turn in the horizontal plane or in any other direction. The cross flow generates separation which, added to the forward motion, ends up as a conical vortex. It has been found that two opposing vortices are formed, one below and one above the hull in a classic horizontal turn of a hull with double symmetry. The authors have shown how the upper rudder may interfere with the upper vortex, how the vortices get asymmetrical thus causing pitching moments.
Tip vortices originate from all lifting surfaces, such as the sail and control surfaces that are inclined at an angle relative to the flow. Aside from them, the so-called turtle-back vortices produced at the trailing edge of an improperly shaped casing may ultimately lead to large changes in the axial components of the flow into the propeller plane. This in turn can produce significant unsteady forces. Moore et al. [4] have shown how the necklace vortex released by the junction of the sail with the fuselage may become unstable and interfere with the otherwise smooth flow-field around the hull, then being eventually washed in the stream. It has been found that the intensity of the resulting vortices directly depends on the submarine speed and the value of the drift angle. Owing to the fluctuating side forces resulting from the asymmetrical flow patterns, large vibrations can result in an individual vortex before it is shed from the rear of the fuselage to be replaced by a vortex growing from the opposite side. The physical description of flows at higher Reynolds numbers backed by separation associated with a turbulent boundary layer has failed so far, therefore more detailed studies are needed. It has been found that the size of the separated wake is less, and the drag coefficient is about half that with laminar separation. Vortices contained in cavities are extremely loud and far-reaching and may lead to resonance. Experiments have proven that the sound levels may be 20 dB above the normal ambient ocean noise, a fact that must be avoided by any means. Summing up, since these vortices represent lost energy and often loud sounds, they need to be understood and minimized whenever possible by designing a proper configuration of surfaces and appendages.
Obviously, flow unsteadiness represents a major practical problem for all maritime hulls, regardless of their type. This is due to the vibrations induced by their propellers, which originate in the sudden changes in the effective angle of incidence of the propeller blades, as they rotate through the unsteady flow. Besides, released vortices in themselves create excessive hydro-acoustic noise. In the specific case of a submarine, the acoustic signature is crucially important, therefore, it is of great importance to minimize and preferably eliminate any flow separation to diminish the hydro-acoustic noise from the overall acoustic signature.
Historically, analytical and semi-empirical methods were used at first to predict the maneuvering performances of various submerged or free-surface piercing hulls. Most of them were directly concerned with the accurate estimation of parameters such as added mass and inertia coefficients as well as with the linear and nonlinear damping coefficients. Looking back in time, the pioneering work of Peterson [5] may be considered as one of the most comprehensive in providing a description and a multi-criteria comparison of seven widely semi-empirical methods used for predicting relevant linear hydrodynamic coefficients for conventional marine vehicles. The analyzed methods were compared for torpedoes and submersibles for which experimental data were available at that time.
More than a decade later, Chellabi et al. [6] proposed a procedure for determining the underwater vehicle hydrodynamic derivatives using the USAF Datcom method. Then, Holmes [7] illustrated the application of the Datcom method to predict the hydrodynamics coefficients utilizing geometric considerations. The hull shape considered was a body of revolution having a basic submarine shape. A parametric study of a body of revolution was conducted by using semi-empirical methods for the calculation of hydrodynamic coefficients. The geometry of the body was analyzed in non-dimensional length and volume parameters. The effects of varying the nose, mid-body, and base fractions of the body on the hydrodynamic coefficients were investigated. Equations for the hydrodynamic coefficients were determined from the non-dimensional parameters as well. More than another decade later, de Barros et al. [8] reviewed the use of analytical and semi-empirical methods (ASE) to predict the hydrodynamic derivatives of autonomous underwater vehicles and later compared, in de Barros et al. [9], the results with those of numerical methods. The authors concluded that despite of the fast estimate the analytic semi-empirical methods may provide in sizing hydrodynamic coefficients, they were not accurate enough since the non-linear and viscous effects were simply disregarded. Based on that final remark, one may consider the two works of Barros as marking the end of the ASE methods.
Based on the rapid development of hardware resources, mostly computational fluid dynamics (CFD hereafter) techniques have been applied in the past two decades to describe the flow field and calculate the hydrodynamic loads acting upon marine vehicles under several working scenario assumptions. The emergence of parallel computation together with the increase in the computer speed have not reduced typical runtimes for complex or advanced simulations, primarily because decreases in computer memory costs have increased the memory available, which in turn has made it possible to obtain numerical solutions to larger and far more complicated problems.
In terms of the techniques proposed for solving the problem, the unsteady three-dimensional computations employing sliding or/and overset grids are now being performed somewhat routinely. In most cases these computations are being carried out for either isolated components of complicated configurations or for steady state flows, and usually for both. Parallelization is now making it possible to obtain reasonable measure of turnaround time for complete configurations in which all components are accounted for in their true interaction mode. The complexity of flow configurations that are feasible will continue to increase, and along with this will come the need to address widely varying time and length scales in the same physical problem. This in turn, will eventually determine further advances in solution methodology and computational software [10,11].
The Reynolds averaged Navier–Stokes (RANS hereafter) method has been commonly used for predicting the resistance [12,13], self-propulsion [14,15,16,17], maneuvering [18], and near-surface performance [19,20,21]. Aside from that, DES, DDES, large eddy simulation (LES), and direct numerical simulation (DNS) methods have also been used in the studies of hydrodynamic performances [14,22,23], boundary layer [24], and vortex structures [25,26], respectively. As far as the stated scope of the investigations is concerned, the accurate determination of forces and moments [27], the influence exerted by the different turbulence closure models [28,29], and the verification and validation of the results [30,31] should be mentioned. Both model-scale [32] and full-scale computations [33] have been performed and some significant progress has been reported so far. Aside of all those mentioned above, the maneuvering performance and signatures of a submarine were of a major interest since they have been found to be significantly influenced by the flow unsteadiness, thus requiring a better numerical treatment.
Most of the studies on the DARPA Suboff model are only based on the axisymmetric hulls appended with pairs of rudders and stabilizer fins that are small compared to the length of the hull, [14,34,35,36]. Captive model tests provide information on flow physics but have certain limitations imposed by the equipment that constrain its usefulness. The model supports the influence of the measurements and needs to account for the spatial resolution of instrumentation that limits access to the regions around the model where access is not usually possible. Under these circumstances, in spite of the proven importance of experiments, only a few numeric-based studies have described the flow details about conventional submarine hulls so far. As an example, Fureby et al. [37] reported a thorough investigation based on both RANS and LES methods on the flow around the fully appended Defence Science and Technology Organisation (DSTO) generic hull model at straight ahead and during 10° side-slip conditions. It was found that despite the fact that the mechanisms of flow separation were thought for years to be completely understood, they are still subject to deeper investigation. With all these at hand, this is the main reason that motivates the present study.
The main purpose of the present paper is the prediction of the local flow features around a submerged body when massively separated flows occur. The performance of several models for modeling the turbulence is assessed and compared. The choice of the Suboff model is motivated by the large amount of experimental data needed for validations of the theoretical approach. The paper therefore proposes a comparative study of the classical averaging SST model, the hybrid DES-SST, and the innovative improved IDDES approaches, for which the complete mathematical models are provided and described in detail. Extensive V&V computations are performed to emphasize the accuracy of each method proposed to fit the purpose. Three streamwise velocities between 3 and 6 knots and four different drift angles between 10° and 22° are considered.
2. Hull Geometry
The DARPA Suboff hull form converted to a Cartesian coordinate system, whose origin is located at the aft most point of the stern is considered further in the present study. The longitudinal x-coordinate, which coincides with the symmetry axis is oriented towards the bow, whereas the positive lateral y-coordinate is pointing to the starboard side. The vertical z-axis is oriented upwards. The geometry of the hull and appendages shown in Figure 1 was provided by Groves et al. [38] through equations which gave either the axial and radial coordinates for the axisymmetric fuselage, or by Cartesian coordinates for the five non-axisymmetric appendages. The length of the hull model is m, while the maximum diameter is m.

Figure 1.
Suboff geometry.
The cylindrical part of the fuselage extends from m to m. The bridge fairwater (sail) is placed at top dead center of the hull with the leading edge positioned at m behind the bow, and measures 0.368 m in length and 0.46 m in height. The stern appendages consist of four identical foils, i.e., two rudders and two stabilizers, equally spaced on the circumference. They all have the trailing edges positioned at m measured from the bow. The span length at the trailing edge is 0.161 m, whereas the chord length at the tip is 0.154 m. The wetted area of the appended hull measures 6.339 m2, as tabulated in Table 1, which contains the main particulars and mechanic characteristics of the considered hull.

Table 1.
Main particulars of the DARPA Suboff hull.
3. Mathematical Model: Turbulence Modeling
3.1. RANS Formulation
The simulations reported here were performed with the two-equation SST RANS model and two hybrid LES-SST models, namely the DES and IDDES. The governing equations are the continuity equation and the incompressible Navier–Stokes equations, which read in a tensor form as follows:
Here and are the water density and molecular viscosity, respectively. Turbulence simulation typically assumes decomposition of the instantaneous velocity into the resolved component and model component using a suitable strategy. In the Reynolds-averaged Navier–Stokes (RANS) turbulence models the decomposition is defined by:
Here is the mean part of velocity, whereas is the fluctuating velocity component. The mean velocity is defined as:
Introducing (2) in (1) yields to:
Equation set (4) is basically identical to (1), except for the additional turbulence stress tensor in the momentum transport equation, which is defined as:
Closure of the above equation set is achieved through one or two more additional equations which are needed to model the turbulence stress tensor. In the RANS formulation, the turbulence stress tensor is modeled using the Boussinesq approximation according to which:
The SST RANS model solves the transport equations for the turbulent kinetic energy and the specific dissipation rate. Since the mathematical formulation is widely known, it will be skipped in the following and only some discussion on its capabilities and performance will be provided.
The classic model has proven to be successful for flows with moderate adverse pressure gradients but fails for flows with pressure-induced separation. The hyper-sensitivity of the equation to its values in the freestream outside the boundary layer prevented the equation from being the standard scale equation in turbulence modelling, despite its superior performance in the near wall region. As a consequence, the zonal SST model has been proposed to surmount this drawback in which the zonal formulation is based on blending functions, which ensure an automatic selection of the or zones without any need for the user to interact. The additional complexity in the model formulation compared to standard models resides in the necessity to compute the distance from the wall, which is required in the blending functions calculation. This is achieved by the solution of a Poisson equation, a procedure which is performed within the solver.
The two major features of the SST model of Menter [39,40] are therefore the zonal blending of model coefficients as well as the limitation on the growth of the eddy viscosity in rapidly strained flows. The zonal modeling employs the model of Wilcox in the proximity of solid walls and the classic model in the vicinity of boundary layer edges and in free-shear layers. This switching is achieved with a blending function of the model coefficients. The shear stress transport model modifies the eddy viscosity by requiring the turbulent shear stress to be bounded by a constant times the turbulent kinetic energy inside boundary layers.
Blending the and models implies for the latter to be transformed into an equivalent formulation. Practically, the original model is multiplied by a function , whereas the model is transformed by the function , and the corresponding equations of each model are therefore considered together. is enforced as a value of one in the half inner part of the boundary layer (where the model behaves like the original model) and decreases to vanish far from the wall.
Concluding, the SST model used herein modifies the turbulent eddy viscosity function to improve the prediction of separated flows and to avoid the overestimated Reynolds stresses with the and models in adverse pressure gradients. Two-equation models generally underpredict the retardation and separation of the boundary layer due to adverse pressure gradients. This is a serious deficiency leading to an underestimation of the effects of viscous–inviscid interaction. The model uses a modification in the formulation of the eddy viscosity through a blending function in boundary layer flows, which regards the transport of the shear stress as being proportional to that of the turbulent kinetic energy.
3.2. DES Formulation
In contrast to the RANS equations, the equations that are solved for LES are obtained by spatial filtering rather than an averaging process. The instantaneous velocity is decomposed now into a filtered value and a sub-filtered value
where
Here is the filter function based on the filter width defined as: . The spatial filtering removes the smaller eddies associated with higher frequencies, therefore it reduces the range of scales that must be resolved. Inserting the decomposed solution variables into the Navier–Stokes equations results in equations for the filtered quantities. The filtered mass and momentum transport equations can now be written as:
The turbulent stress tensor represents the subgrid-scale stresses. The interaction between the larger, resolved eddies and the smaller, unresolved eddies is modeled using the Boussinesq approximation [41,42,43]. The subgrid-scale turbulent viscosity is defined by a subgrid-scale model that accounts for the effects of small eddies on the resolved flow [44,45]. A detailed mathematical description of the DES model is provided in Appendix A.
3.3. IDDES Formulation
The Delayed Detached Eddy Simulation (DDES) approach proposed by Gritskevich et al. [46] used here is a formulation based on the DES model described above. The DES function is modified to prevent a premature switch of DES to LES mode within boundary layers. The Improved Delayed Detached Eddy Simulation (IDDES) approach, which is employed in the present research is an improvement of the classic DDES model, which is innovatively combined with another hybrid model, namely the Wall-Modeled LES [45]. The mathematical formulation of the IDDES model is given in Appendix B.
4. Numerical Milestones
Finite volume was employed to integrate the equations that describe the flow reported here. The ISIS-CFD unsteady viscous flow solver available in the FineTM/Marine package was used in the present study to fit the purpose. The spatial discretization of the transport equations on unstructured grids is based on a classic finite-volume formulation in which fluxes were built using the modified AVLSMART version of the SMART (Sharp and Monotonic Algorithm for Realistic Transport) bounded difference scheme [47]. The scheme is based on the third order Quadratic Upstream Interpolation for Convective Kinematics (QUICK hereafter) scheme [48]. Velocity field is obtained from the momentum conservation equation and the pressure field is extracted from the mass conservation constraint transformed into a pressure equation. Picard’s procedure is used for the linearization of the equations. The whole discretization is fully implicit in space and time and is formally second order accurate.
Generally, RANS models perform well when the boundary layers are attached. Conversely, they have proven difficulties when separated flows are encountered, as shown by Wilcox [49]. A possible alternative to address this issue is the use of the LES approach, which consists of resolving the largest scales of the turbulence spectrum and of modeling only the scales smaller than a threshold related to the local grid size, as described by Pope [50]. While grid refinement does not always extend the resolved part of the energy cascade in the case of unsteady RANS simulations [51] in the case of LES-based hybrid simulations it results in a wider range of turbulent scales being resolved, thus weakening the role of modeling, as shown by Spalart [52]. Based on all those mentioned above, in the present paper, closure of the turbulence was achieved by using either the SST or the hybrid DES SST and IDDES models. An adaptive mesh refinement based on the flux-component was used wherever the flow gradients are significant.
All the computations were performed in double-precision on 120 cores; therefore, the computational domain was split into multiple-connected sub-domains having approximately the same number of unknowns. This was carried out by the METIS multilevel partitioning algorithm. Communication of faces data between sub-domains was performed according to the Message Passing Interface (MPI) standard. In any unsteady simulation the time step is often determined by the flow properties, rather than by the Courant number, to gain a suitable level of accuracy within a reasonable running time. The time step size was therefore chosen an order lower to the level recommended by the authors of the solver, which suggested in [53] that, a value which can be regarded only as a maximal threshold suitable when using wall functions, which is not the case here.
Several sets of numerical unsteady simulations were performed for the DARPA Suboff hull fully appended with sail, rudders and stabilizing fins, without a propeller, and towed at a speed range between 3 and 6 knots for V&V purposes. The speed interval corresponded to a range of Reynolds numbers between 5.9·106 and 1.8·107, where Re is based on the hull length, the oncoming flow velocity and the dynamic viscosity of the fresh water at 15 °C. The numerical solutions computed by using the SST and hybrid DES SST were previously compared by the author in [12] with the experimental data reported by Crook [54] and Liu et al. [55] who measured the resistance in a deep water towing tank for running speeds between 4.5 and 18 knots.
The first set of computations regarded the resistance in a straight run, intended as validation of the numerical methods used in the present study. Computations were performed in two successive stages. The first stage was based on the RANS solutions. After a period of five seconds of flow acceleration from the rest to the nominal velocity on a half-sinusoidal ramp, the hull was numerically towed at a constant nominal speed, on a straight course with no yaw or trim angles at a neutral rudder position for 20 more seconds. The turbulence model was in this case the standard SST of Menter [41].
For testing the performance of the turbulence hybrid models, computations were restarted for five more seconds, and the turbulence models were switched either to DES SST or to IDDES. Special attention was paid to the time step size such that the resulting Courant number was around 0.3, a value that is commonly viewed as appropriate for such unsteady flow simulations. All the RANS computations for the resistance estimation were performed for a time steps.
On the contrary, when the DES or IDDES computations were carried out, the time step was decreased to a value of s. For purposes related to the investigation of the time step convergence of the numerical solutions, three additional time steps were also considered, i.e.,, , and. The maximum number of non-linear iterations per time step was limited for all the simulations at a value of 10 for the RANS computations. The convergence criterion, which corresponds to the maximum number of orders of magnitude the infinite norm of the residuals had to decrease during each time step was two orders. The maximum number of non-linear iterations per time step was increased by a value of 20 for the LES and IDDES computations, whereas the infinite norm of the residuals was set at three orders.
The second set of computations was devoted to the static drift simulations and was performed over a period of 30 s. Drift angles varying from to increasing in equal steps of were considered as computational cases that will be discussed in the following sections. The flow was again accelerated from rest to the nominal speed on a half-sinusoidal ramp over five seconds and all the other numerical settings were similar to those for the straight-run simulations described above. During the first stage of 25 s that corresponded to the RANS simulations, the turbulence model was the SST. Then the computation was restarted, and the turbulence model was switched either to the DES or to the IDDES for five more seconds, sufficient for the flow to stabilize. Three income velocities corresponding to the same Reynolds numbers as above were again considered. The time step size was kept at the same value as for the straight-course computations as were all the other settings.
4.1. Boundary Conditions
The boundary conditions imposed on the solid walls and used in all the simulations reported herein were of a no-slip type for the hull and appendages, regardless of the chosen turbulence model. The incoming velocity was imposed at the inlet, zero normal second derivative for the exit, and far field conditions for the tank. On the top and bottom boundaries, a Dirichlet-type boundary condition was imposed as a frozen pressure, which kept the pressure constant and equal to zero during the computation. The boundary conditions for the SST turbulence model were:, where, and are the proportionality factor, the Suboff maximum length, the oncoming flow velocity, and the water density, respectively. The proportionality factor of Menter was set as which is recommended for boundary layer flows, [40] On the solid surfaces, the boundary conditions read as follows:. Here is a constant of the model, whereas is the distance of the first point away from the wall, chosen so that . Exactly the same conditions were imposed for the DES/IDDES-based computations, unless otherwise indicated.
4.2. Computational Domain and Meshes
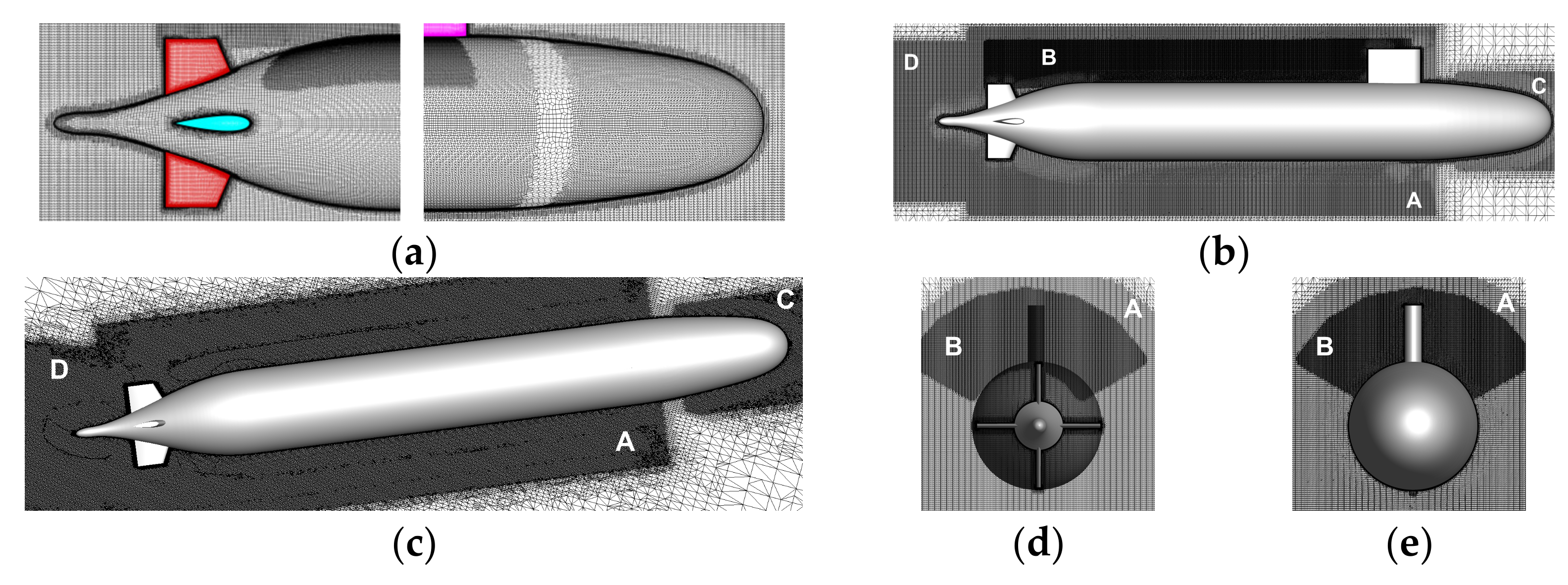
Several trial computations proved that the level of velocity fluctuations in the near wake is greatly sensitive to the aspect ratio of the domain size reported to the hull length (L). The computational domain extended from behind the hull to in front of it, on each side in the lateral direction, and below and above the hull in the vertical direction. Unstructured computational meshes used in the present report were all generated by making use of the HEXPRESS, a component of the NUMECA FineTM/Marine suite. For the five flow cases reported in here, including the associated verification and validation computations, more than fifteen different meshes were successively generated. General requirements such as no zero/negative, nor twisted, neither concave cells were imposed during the iterative generation, following the principles described previously by the author [55,56,57]. Clustering inside the boundary layer of the hull, orthogonality close to the solid surfaces, cells aspect ratio, expansion ratio, and equiangular skewness were closely monitored during each of the five steps in which the generation of each mesh was carried out. Four different grids were initially generated for the straight run computations, not only for the grid independence test, but also for the verification and validation study that will be presented in the followings. Let these grids be denoted by G1 … G4, where G1, consisting of 6.51·106 cells, corresponds to the roughest mesh, whereas the finest grid, G4, contains 5.322·107 cells. Intermediate grids G2 and G3 contained 2.01·107 and 3.75·107 cells, respectively. Twenty-eight layers of cells with a minimum thickness of 10−6 were used inside the boundary layer in all the computations reported in here. The stretching factor was 1.2 everywhere. Four more grids were then generated for the static drift computations set, one for each incidence angle. All the basic quality requirements were imposed in this case as in the straight course computations. Given the particularities of this second set of simulations, additional volumes of mesh clustering were a priori considered inside the areas where the flow gradients were expected to manifest. For the straight run such volumes were created around the hull, where the pressure was expected to vary significantly, as shown in Figure 2a,b (the zone marked by “A” and “C” in the picture). Additionally, another clustering volume denoted by “B” was paced in the wake of the sail, as shown in Figure 2b, for a better capturing of the vortices released by both the sail tip and the juncture with the fuselage, as described previously by the author in [56,57]. Owing to the overwhelming role played in the static drift computations by the oncoming flow direction, volumes of higher density of cells shifted at various angles were placed inside of the wake of main hull and appendages, as shown in Figure 2c,d. They are denoted by “A” and “D” in Figure 2b,d, which correspond to the largest incidence angle considered in the present work,. Since the flow parameters are expected to have significant variations in time, an additional grid refinement based on a flux-component criterion that will be described below has been used for the computations reported in here. The procedure developed for ISIS-CFD is integrated completely in the flow solver. The method is entirely parallelized, including automatic redistribution of the grid over the processors. During a computation, the refinement procedure is called repeatedly. In such a call, first the refinement criterion is calculated, then in a separate step of the procedure the grid is refined based on this criterion. For steady flow, the refinement procedure converges if: once the grid is correctly refined according to the criterion, further calls to the procedure no longer cause any changes [53,54,55,56,57,58,59].
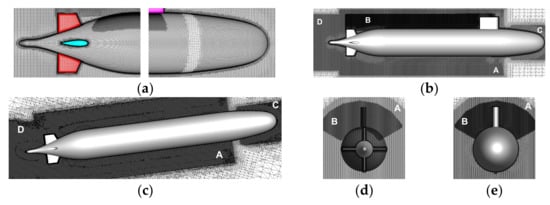
Figure 2.
Computational mesh. (a)-around the hull extremities; (b)-side view of the mesh clustering; (c)-top view of the mesh clustering; (d)-cross view from the aft region; (e)-cross view in the midsection.
The flux-component criterion may be regarded as a truncation error estimator. In a finite-volume discretization, a part of the truncation error always comes from the error in the fluxes, which is related to the interpolations of the different state variables from the cell centers to the faces. With Hessians as approximations of the interpolation errors, a criterion could be built from the Hessians of all the flow variables, weighted the way they appear in the fluxes. However, for practical reasons only the convective and pressure part of the flux were considered, while the turbulence modeling is ignored. Here, instead of considering all the different products of velocity terms that occur in the fluxes, a weight expressed as, is assigned to all the velocity Hessians, where the velocity vector is. Thus, the flux component criterion becomes:
Solutions computed when the adaption based on this criterion proved to simulate accurately the flow in which wakes could be well resolved and conserved over a long distance.
5. Results and Discussions
5.1. Verification & Validation of the Straight Run Case
A series of trial computations were performed to verify and validate the numerical models used in the research reported herein. Given the complexity of the subject of the study, a very detailed V&V is proposed in the following. Since the main subject of the present research is related to the DARPA Suboff hull hydrodynamic performances in a static drift motion, an initial validation might be appropriately required for the straight run working condition. Under such assumption, the overall performance of the hull moving in straight course is evaluated at first. A grid independency test is performed for the four meshes considered in the present study, followed by a V&V analysis of the computational solutions against the existing experimental data. Because the static drift computations require different meshes adapted to the different angular positions of the hull in respect to the stream, several additional investigations are required for each particular computational case to prove the accuracy of the numerical treatment. Because of the huge amount of data computed for all the considered cases, i.e., four incidence angles and four grids for each angle, the discussions related to the V&V will be, without restraining the generality of the problem, focused on the most critical cases only.
5.1.1. Grid Sensitivity and Time Convergence Tests
The grid convergence study was carried out first to demonstrate grid independence on the parallel computation solver. Four meshes denoted below by G1…G4 were generated to host the computations for the straight run case. The initial number of cells for the G1…G4 meshes varied from 8.01·106 cells, corresponding to the coarsest grid, to 6.4·107 cells, corresponding to the finest. The intermediate values are tabulated in Table 2. The time step size for the four simulation runs was kept unchanged at a value of s except for the time step convergence study when it was successively modified, as will be discussed later in the following sub-sections. The Reynolds numbers varied form 5.9·106 to 1.8·107. The average increase ratio of the initial cell number between the two consecutive refinements was around 2, as Table 2 shows. The consecutive computed grid ratio between two consecutive meshes, i.e., varied from 1.93 to 2.06 as also shown in Table 2. Overall, the average grid ratio for the four grids,, may be considered in the followings as being equal to 2.

Table 2.
Computational grids generated for the grid convergence study—hull in straight run.
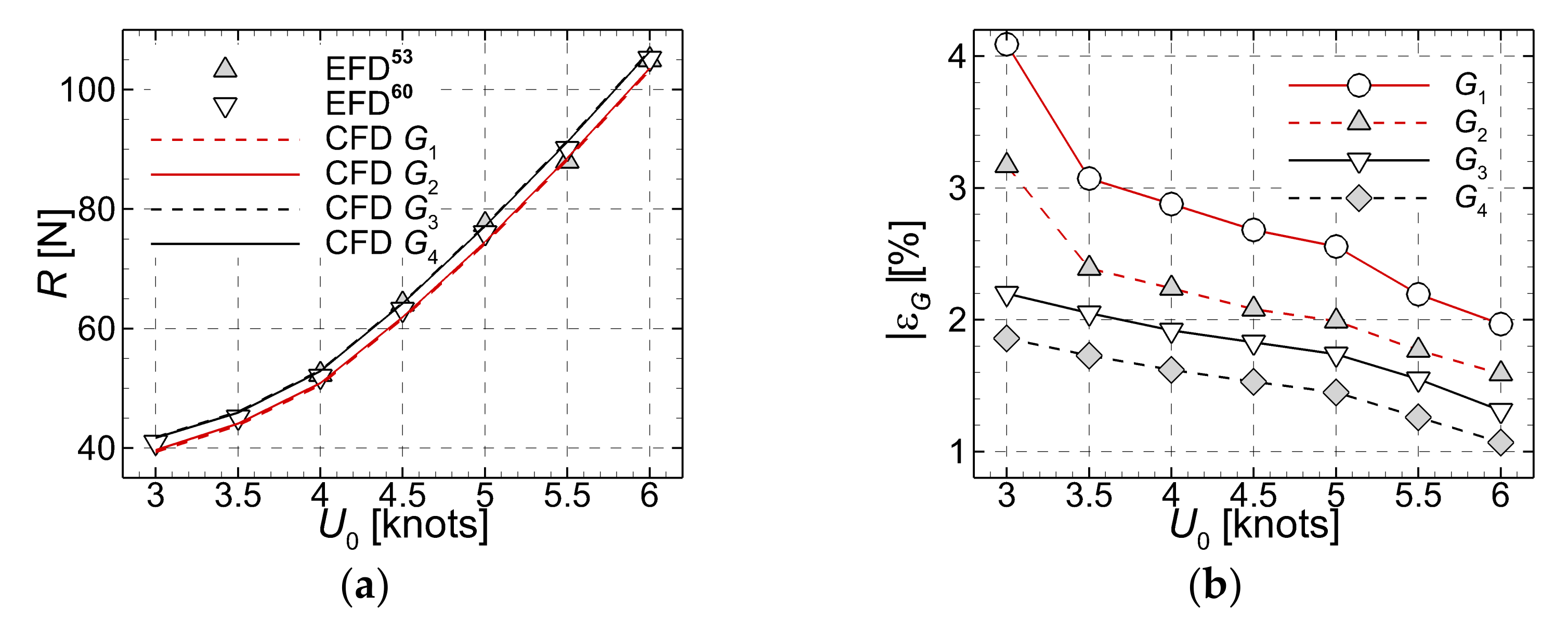
Solutions based on the hybrid SST-IDDES model computed on the four grids were compared to the experimental data (EFD hereafter) provided by Johnson et al. [60] to prove the grid independency of the solution, as shown in Table 3 and Figure 3.

Table 3.
Grid convergence test for the DARPA Suboff hull. Computations in straight run.
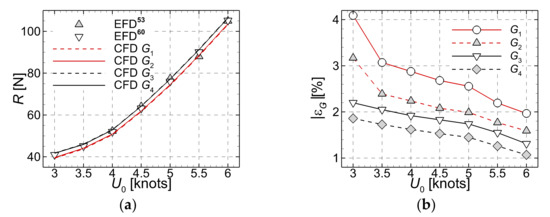
Figure 3.
Grid convergence test performed for the (G1–G4) meshes. (a)-total resistance measured (EFD) [53,60] and computed (CFD); (b)-absolute computational errors.
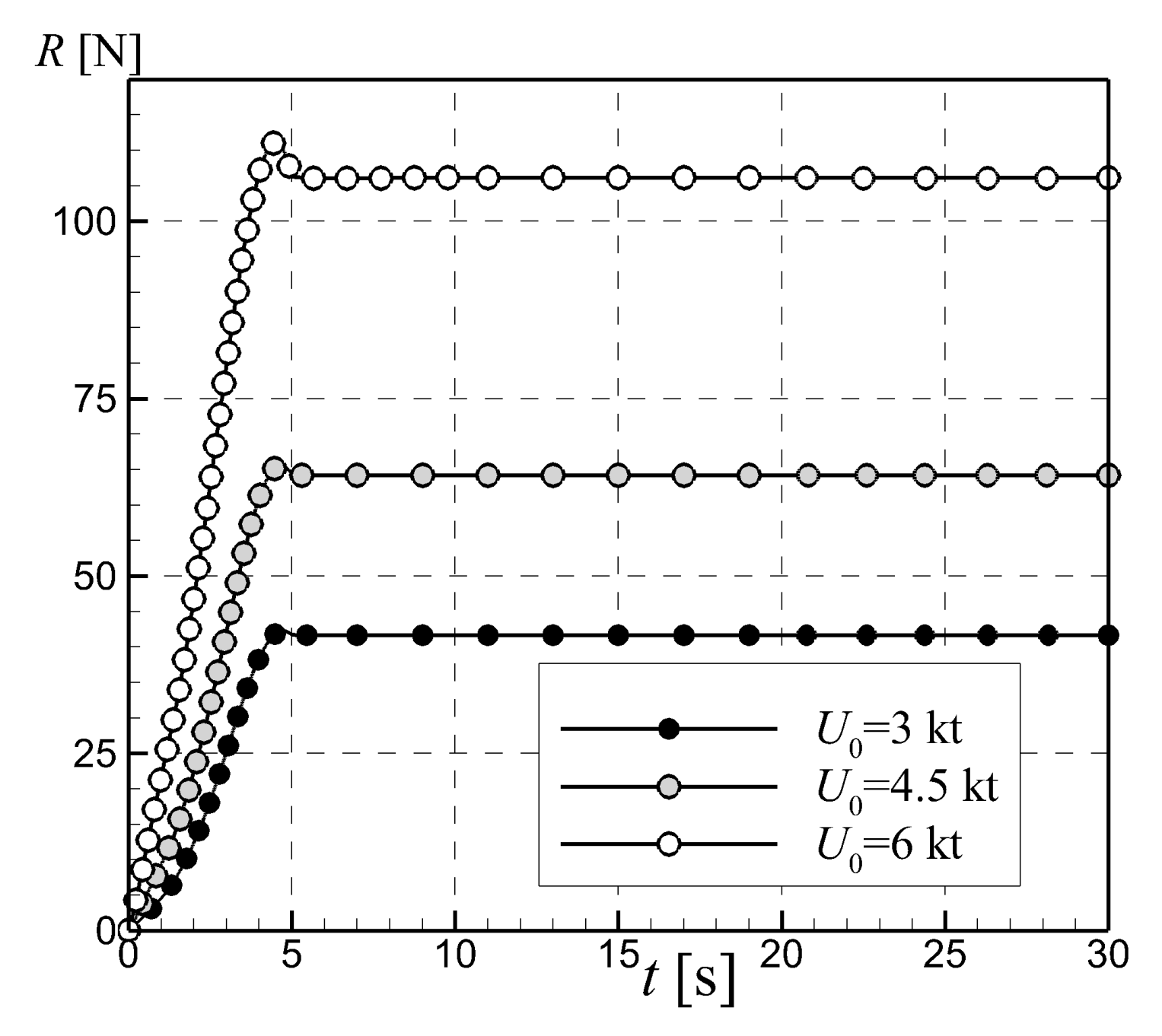
Data tabulated in Table 3 show that solutions computed on the two coarser meshes slightly overestimate the experimental data, whereas the finer meshes slightly underestimate the measured data, as depicted in Figure 3a. The largest errors correspond to the smaller velocities, as Figure 3b, which depicts the solutions tabulated in Table 3. This apparently peculiar fact is attributable to the initial mesh generation process. That is, the settings used when the grid was built up were exclusively based on the parameters associated to the largest Reynolds number. Obviously that choice seemed to be inappropriate for the smaller velocity associated quality requirements since the boundary layer is thicker in those cases. The reasons behind this choice were mainly related to the desire to maintaining the associated computational effort for the grid generation at the lowest possible level. As mentioned above, the flow starts from rest and is accelerated for 5 s on a half-sinusoidal ramp for numerical stability. Solutions converge rather fast after the acceleration period, regardless of the incoming flow velocity, as shown in Figure 4. The hull resistances shown in Figure 4 are all computed on the finest mesh, based on the hybrid IDDES turbulence model. The simulation is performed for time steps, up to a
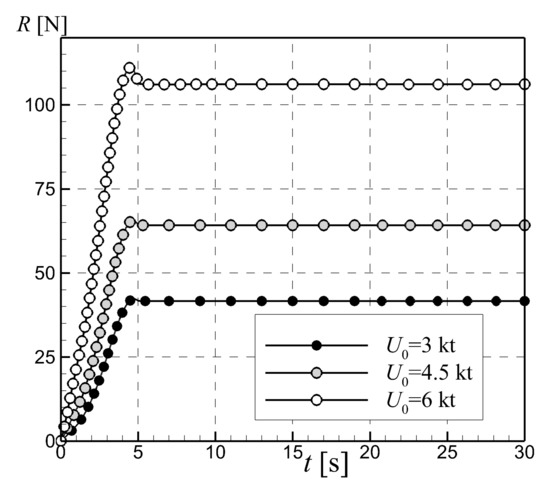
Figure 4.
Time histories of the resistance computed on the finest mesh for three advancing speeds.
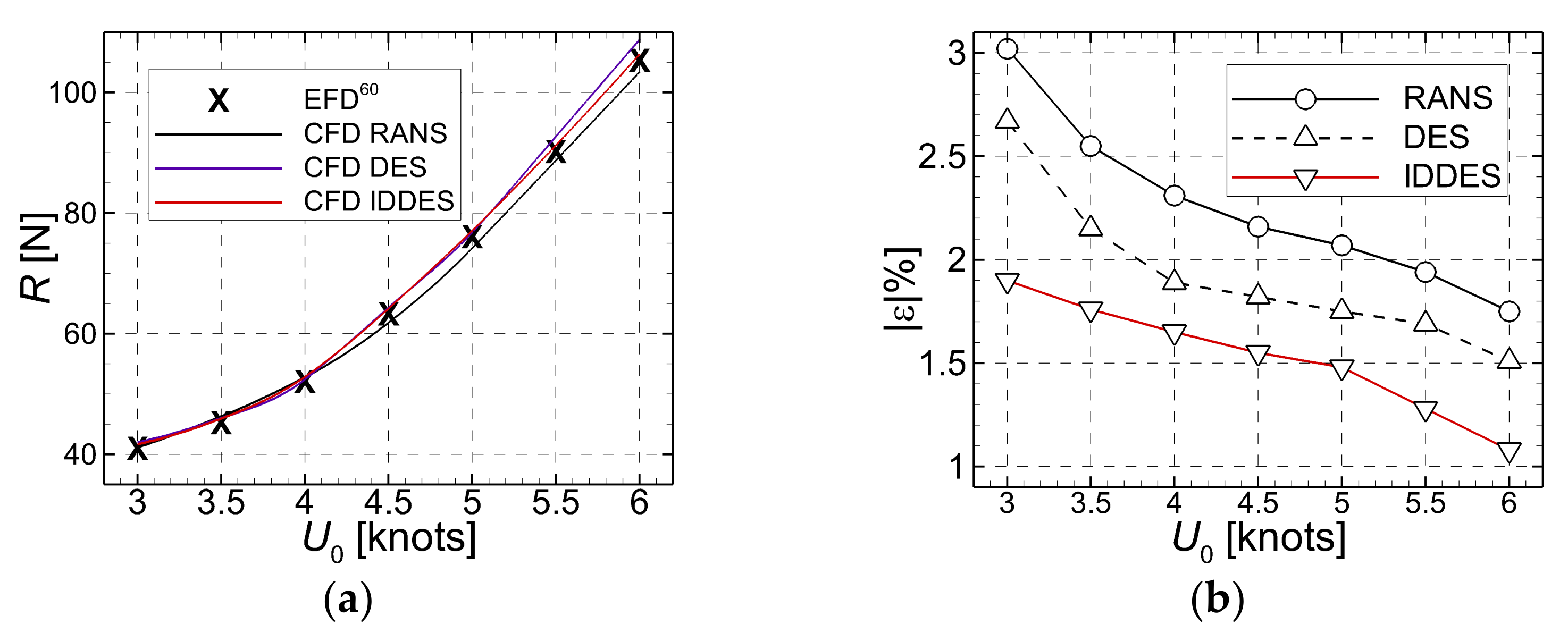
A former study carried out by the author [12] for the same hull moving in a straight course was entirely based on the hybrid SST-DES model of the turbulence closure, which revealed its advantages over the classic RANS approach. The IDDES model is proposed herein as an alternative aimed at describing better the local flow features. Since it might be useful for the reader to have the differences brought by the different turbulence closure approaches, a comparison with the experimental data of Johnson et al. [60] is proposed in the following. Table 4 contains the computed total resistance of the Suboff hull, with the three turbulence models for six oncoming flow velocities, against the corresponding measured values.

Table 4.
Verification for the turbulence models used to simulate the flow on the finest mesh.
All the computations reported here were performed on the finest mesh. Based on the data tabulated in Table 4, one may notice that the level of errors decreases with the increase in the incoming speed.
As discussed above, this trend may be attributable to the computational grid, whose minimum cell thickness was set based on the largest Reynolds number. Even though the highest errors of the RANS simulations may be considered satisfactory from a practical engineering point of view, they may be unacceptable when the instantaneous local flow details are of interest. Despite their higher CPU costs compared to the RANS-based solution, the hybrid DES SST and IDDES solutions, whose absolute errors vary from 2.67% to 1.07% can be considered satisfactory. From this point of view, they may be a good choice compared to the more expensive LES approach. Data tabulated in Table 4 are drawn in Figure 5. Figure 5a depicts the comparison between the total resistance measured (EFD) [60] and computed (CFD), whereas Figure 5b bears out the corresponding absolute computational errors. It is worth mentioning that all the absolute errors are below 3.02%, a fact that may confirm the accuracy of the solver. Apart from that, it may be pointed out that the hybrid turbulence models lead to smaller errors than the classical RANS ( SST.
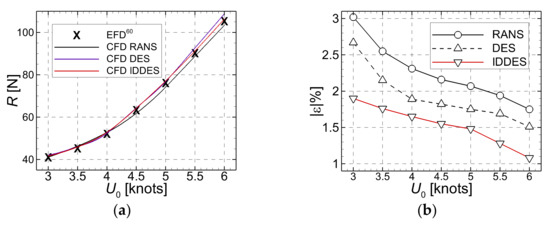
Figure 5.
Comparison between the experimental data [60] and the numerical solutions computed by using different turbulence models on the finest mesh (a)-total resistance measured (EFD) and computed (CFD); (b)-absolute computational errors.
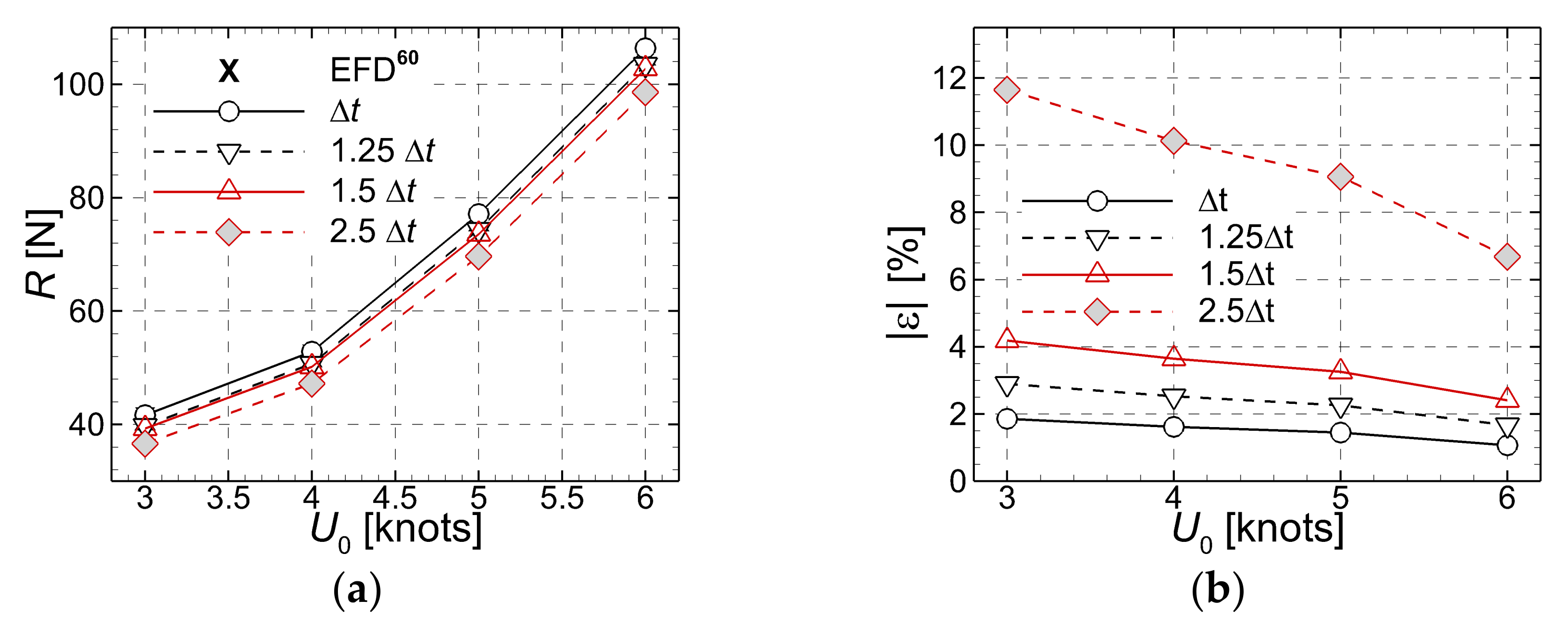
Apart from the mesh fineness, the second key parameter of any numerical simulation is the time step size. To quantify its influence on the accuracy of the solution, a time convergence test was performed for the simpler flow around the hull moving in the straight run case. Closure to turbulence is achieved through the hybrid SST-IDDES model only. Velocities the test was performed at varied from 3 to 6 knots, being distributed in four equally distributed steps. Three additional time steps were considered for this computation, i.e., 1.25, 1.5 and 2.5 times the time step used for the grid convergence tests performed above, which was taken as a basis for further discussions. Comparisons of the computed solutions with the experimental [60] tabulated in Table 5 and depicted in Figure 6 revealed that the increase in the time step size determines a significant loss in accuracy. This was somehow expected since the augmentation of the time step leads to an increase in the Courant number, with negative consequences on the overall accuracy.

Table 5.
Time step convergence test for the DARPA Suboff hull. Computations in the straight run case, IDDES turbulence model.
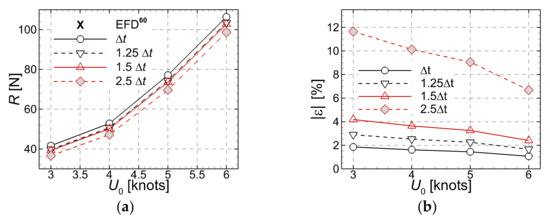
Figure 6.
Time step convergence test. (a)-total resistance measured (EFD) [60] and computed (CFD); (b)-absolute computational errors.
The numerical scheme used in the research reported herein is of a second order of accuracy in time, which means that the computational errors are proportional to the time step at a power of two. The nominal errors tabulated in Table 5 confirm the theoretic issues behind the numerics, therefore it may be considered that the numerical scheme proposed in the present computational test should be considered as being accurate in time.
5.1.2. Verification and Validation
Furthermore, the grid uncertainty was evaluated by using the methodology for monotonic convergence proposed in [61]. V&V of the computed total resistance was performed for all the Suboff speeds considered in the mesh sensitivity study only for the smallest time step. Data used for the V&V estimation for the total resistance are tabulated in Table 3; Table 6. The calculated grid ratio tabulated in Table 2, the associated relative error between the total resistance computed on the finest mesh G4 and the second finest mesh G3,, the ratio between the estimated order of convergence and the theoretical order of convergence, the grid uncertainty, the experimental uncertainty , and the validation uncertainty are tabulated in Table 6.

Table 6.
Verification and validation for the total resistance in the straight run case.
The in Table 6 represents the theoretical order of accuracy, which is given by the order of convection scheme, whereas the validation uncertainty is expressed as a function of grid uncertainty and experimental uncertainty:. The relative error between the finest mesh and the experimental data for the coefficient of total resistance on the finest grid G4 is smaller than the Richardson-based validation numerical uncertainty, see Table 3 and Table 6, therefore the resistance prediction can be considered as being validated. For more details on the V&V procedures, see also the ASME and ITTC provisions [62,63].
5.2. Verification & Validation of the Static Drift Cases
Grid Sensitivity Tests
Several sets of computations were carried out at this stage for checking the solution accuracy based on the discretization resolution. All these additional computations were necessary since different grids were drawn for each incidence angle of the flow (which will be denoted by hereafter) in respect to the Suboff hull. For the sake of similarity with the straight run cases, only the IDDES-based computations will be considered in the followings. For CPU costs reasons, verification and validation was carried out only for the incoming velocities of 3, 4.5, and 6 knots. The analysis was performed for the total resistance force, defined as and yaw moment. are the streamwise and the lateral components of the hydrodynamic resistance.
- case
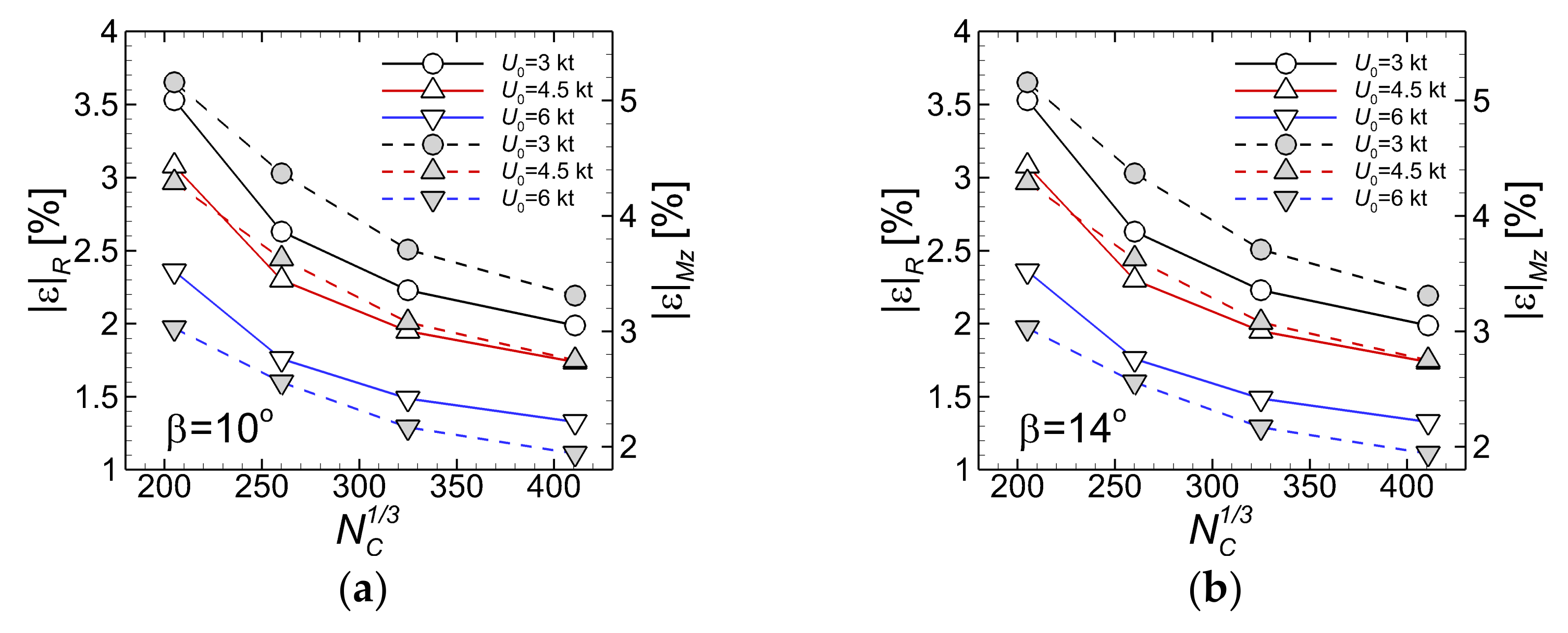
Four additional computational meshes were generated to carry out the grid sensitivity test in the smallest drift angle. The mesh sizes varying from 8.248·106 to 6.58·107 cells are tabulated in Table 7, which also gives the grid ratios between two consecutive meshes, and the whole averaged grid ratio. The associated computational errors of the total resistances and yaw moments on each computational mesh are tabulated in Table 8 which shows that the maximum computational errors range between 1.24% and 3.35% for the total resistance force and between 1.84% and 4.32% for the yaw moment.

Table 7.
Meshes generated for the grid convergence study. Drift angle

Table 8.
Grid convergence study. Run at the drift angle
Since they both correspond to the coarsest grid denoted by G1, one may conclude that the mesh sensitivity test confirms the solver robustness. The largest computational error values correspond to the yaw moment, a fact that may suggest that the grid resolution on each horizontal plane (i.e., in the longitudinal and lateral directions) should be better, despite the higher associated CPU costs.
- case
Four more computational meshes were generated to carry out the grid sensitivity test for the drift angle. The mesh sizes varying from 8.622·106 to 6.931·107 cells are tabulated in Table 9, which also gives the grid ratios between two consecutive meshes, and the averaged grid ratio, as above. The associated computational errors of the total resistances and yaw moments on each computational mesh are tabulated in Table 10, which shows that the maximum computational errors range between 1.33% and 3.53% for the total resistance force and between 1.94% and 5.16% for the yaw moment. The errors are larger than those for the corresponding case, a fact that may again suggest that the finest grid used here should have been even finer.

Table 9.
Meshes generated for the grid convergence study. Drift angle

Table 10.
Grid convergence study. Run at the drift angle
All the numerical errors corresponding to the solutions for the smaller drift angle simulations are shown in Figure 7. Figure 7a contains the errors in the case, whereas Figure 7b contains those computed in the case. Errors computed for the total resistance are drawn with solid lines, while those corresponding to the yaw moments are drawn with broken lines. Obviously, the relative errors decrease monotonically with the increase in the number of cells, as Figure 7 bears out. The monotonic decrease in the absolute errors depicted in Figure 7 proves not only the accuracy of the numerical scheme chosen for the present simulation, but also the robustness of the flow solver. The absolute errors for the yaw moments are slightly larger than those of the total resistance, a fact that may suggest that the mesh resolution in both and directions should be higher in both computation sets. A pilot computation not reported here has shown that an increase by 41% in the number of cells led to a 69% reduction in the relative error, with an increased cost in CPU time of 147% needed for the solution convergence. Having those figures at hand, one may raise the question of the optimal balance between efficiency and accuracy that should be targeted when such a flow problem has to be solved. Owing to the rather low level of the hardware costs nowadays, it seems that a compromise between the two might be the best choice for commonly practical applications, i.e., a solution computed on a sufficiently fine mesh, eventually on more computing cores.
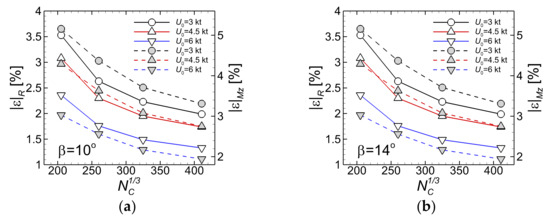
Figure 7.
Absolute errors in the grid convergence test for the static drift computations: (a)-; (b)-.
Next the V&V computations were peformed for the most complex cases considered in the present study since they refer to the larger drift angles of , which are characterized by strong non-linearities induced by the significant flow separations. In this particular case the mesh generation process had to be suited to cover with a better cell density inside the areas where the flow is expected to host large velocity and pressure gradients.
- case
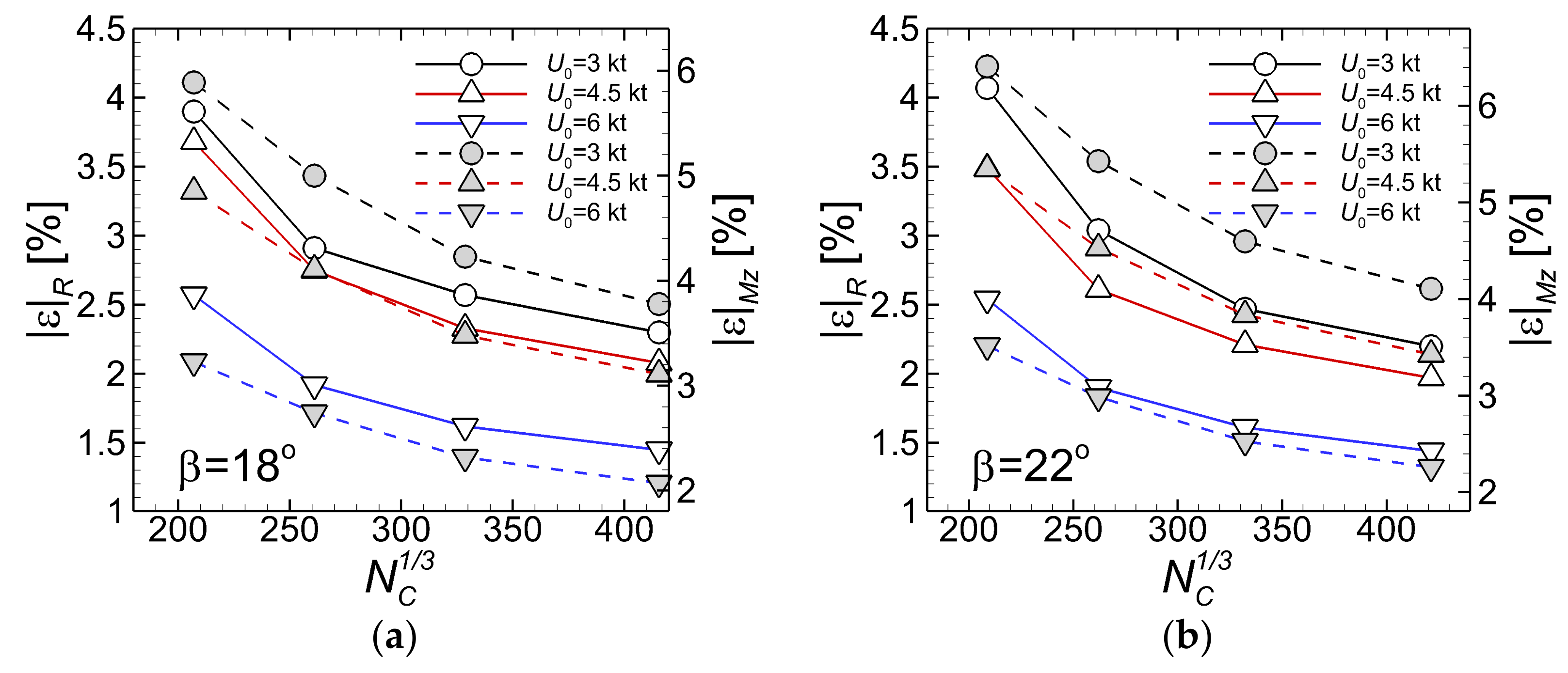
The next set of computations refer to the drift angle of. The mesh sizes varying from 8.872·106 to 7.1731·107 cells are tabulated in Table 11. Grid ratios again vary around 2 and the absolute computational errors are between 3.90% and 1.45% for the total resistance and between 5.89% and 2.07% for the yaw moment, as tabulated in Table 12. Since the largest values of computational errors correspond again to the coarsest grid, as in the smaller drift angles discussed above, the conclusions drawn there remain valid here as well.

Table 11.
Meshes generated for the grid convergence study. Drift angle

Table 12.
Grid convergence study. Run at the drift angle
- case
Mesh convergence computations referring to the drift angle of were again performed on four meshes whose sizes vary from 9.083·106 to 7.483·107 cells as tabulated in Table 13. In this computational case, the grid ratios between every two grids are between 1.98 and 2.04, with an average ratio of 2.02. The absolute computational errors vary from 4.07% to 1.44% for the total resistance and from 6.41% to 2.26% for the yaw moment, as tabulated in Table 14. Again, the largest errors for the computed forces and moments correspond to the coarsest mesh.

Table 13.
Meshes generated for the grid convergence study. Drift angle

Table 14.
Grid convergence study. Run at the drift angle
The numerical errors corresponding to the solutions of the drift angles simulations are shown in Figure 8. Figure 8a depicts the errors of the, while those computed in the case are drawn in Figure 8b. Errors computed for the total resistance are drawn as in Figure 7 with solid lines, while those corresponding to the yaw moments are drawn with broken lines. The relative errors drawn in Figure 8 decrease monotonically with the increase in the number of cells, as in the cases of smaller drift angles. Again, the absolute errors for the yaw moments are slightly larger than those of the total resistance, as expected.
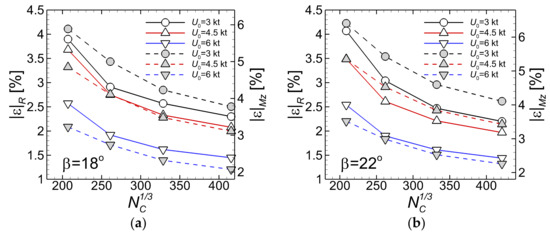
Figure 8.
Absolute errors in the grid convergence test for the static drift computations: (a)-; (b)-.
From the reported solutions one may notice that the largest errors for the total resistance and yaw moment correspond to the static drift angle, as expected. For that reason, the verification and validation will be further performed only in this case in Table 15 and Table 16, by using the same procedure as for the straight run case described at Section 5.1.

Table 15.
Verification and validation of the total resistance computed in the drift angle case.

Table 16.
Verification and validation for the yaw moment computed for drift angle case.
The relative errors between the solution computed on the finest mesh and the corresponding experimental data for the total resistance and the yaw moment values on the finest grid G4 are smaller than the Richardson-based validation of numerical uncertainty. Based on that evidence, the numerical simulation can be therefore considered as being validated for the largest drift angle run as it had been considered in the straight run case discussed above. Wrapping up, based on the extensive V&V computations reported herein, it may be concluded once again that both numerical method accuracy and the robustness of the solver proposed in the present study are proven, regardless of the flow particulars. Doubtlessly, the low level of the computed errors is encouraging the use of the theoretical approaches based on the numerical simulations in determining the hydrodynamic performances instead of the more expensive experimental methods.
5.3. Global Forces and Moments in the Static Drift Motion Case
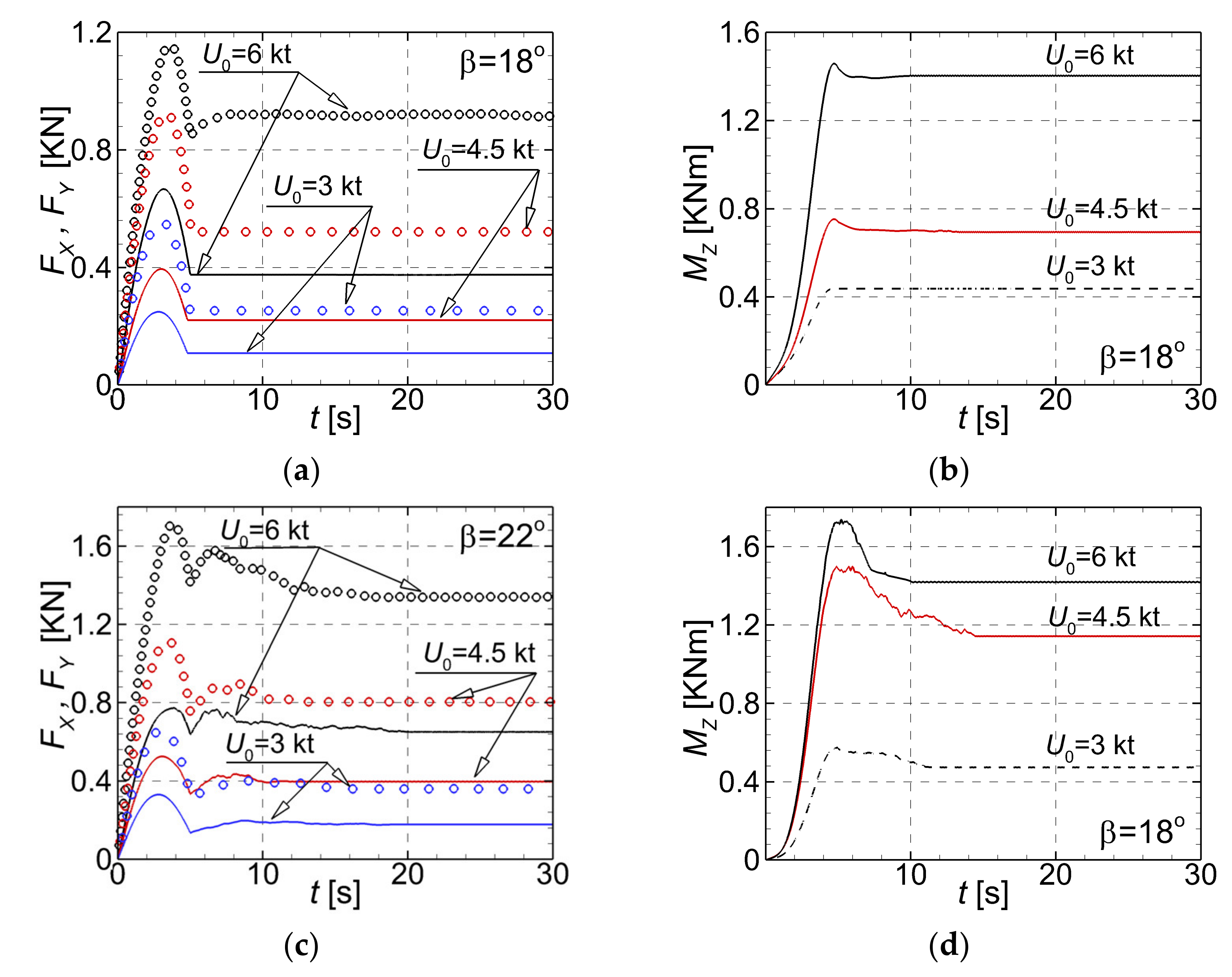
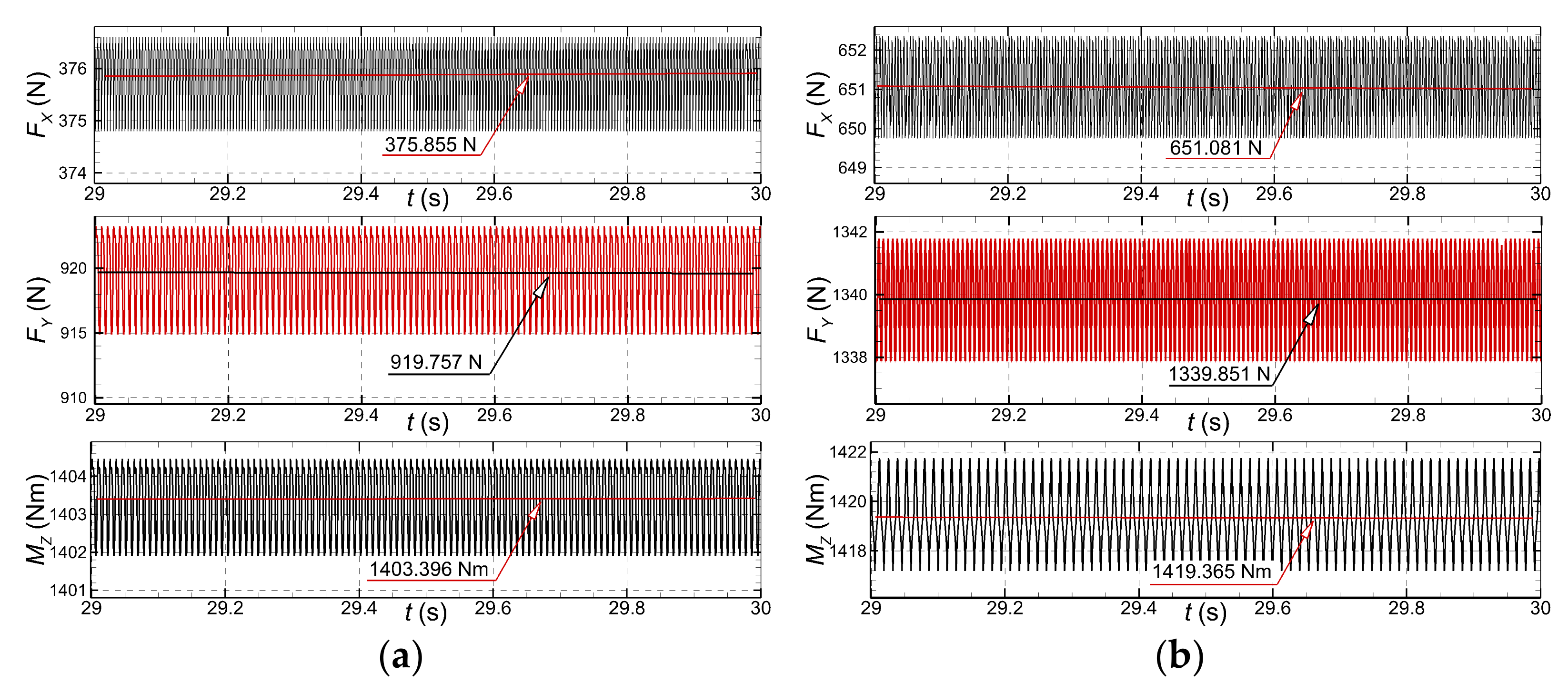
A comparative analysis of the time history of the mean hydrodynamic forces and moments computed for the drift angles cases is proposed in Figure 9. Streamwise forces are drawn with lines, whereas the lateral forces are drawn with symbols in Figure 9a,c respectively. The reported solutions were all computed by using the IDDES turbulence model. All the graphs clearly show that after the five-second period of acceleration of the flow, five more seconds were necessary for the solution to stabilize.
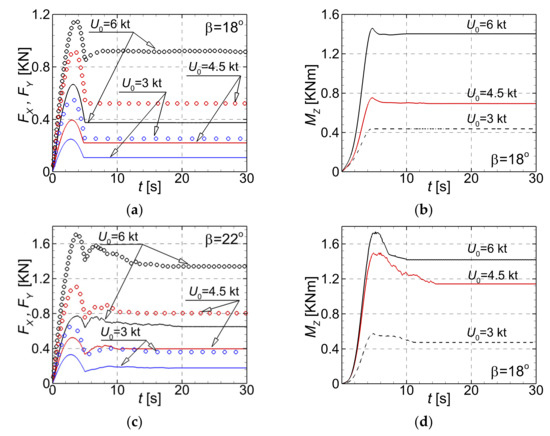
Figure 9.
Time histories of the streamwise and lateral forces and yaw moments computed for three advancing speeds computed for the largest incidence angles: (a)-streamwise and lateral forces in case, (b)-yaw moment in case, (c)-streamwise and lateral forces in case, (d)-yaw moment in case.
When the turbulence model was switched from the RANS-SST to the hybrid IDDES, a slight additional change of the lateral force magnitude could be observed in the highest velocity computational case. Seemingly, that change is attributable to the more appropriate description of the separated flow with the IDDES SST model is. As mentioned above, Figure 9 depicts the mean values of forces and yaw moments. However, the instantaneous time histories show that the solutions manifest an oscillatory pattern around the mean value, as Figure 10 bears out. This conclusion is valid for both IDDES-based solutions computed either in the case shown in Figure 10a or in the case shown in Figure 10b. Several animations not reported here have proven that the period of the oscillations coincides with the period of the separated vortices release.
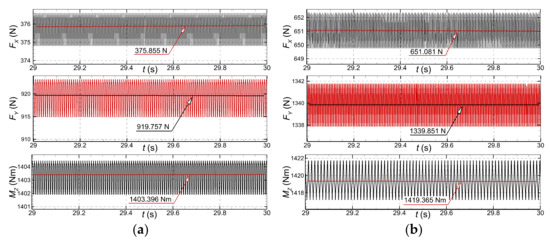
Figure 10.
Detailed time histories of the streamwise and lateral forces and yaw moments computed for: (a)- case, (b)- case.
5.4. Local Flow Features in the Straight Run Case
As stated above, the main purpose of the present paper is the investigation of the local flow around and behind the Suboff hull, knowing how important it is to understand and control the flow for the propulsive performances as well as for the level of the acoustic signal. Since the hydroacustics ensure a long-range highly accurate communication between surface ships and submarines, it requires the use of systems that use very-low-frequency electromagnetic waves that eventually penetrate the ocean subsurface layer. Given its importance, the numerical treatment of noise propagation in the presence of complex separated flows requires not only an understanding of the phenomena, but also an accurate simulation. An inappropriate use of the numerical techniques may easily lead to spurious numerical hydroacustic sources that may contaminate the correctness of the measures needed to take in the initial design stage.
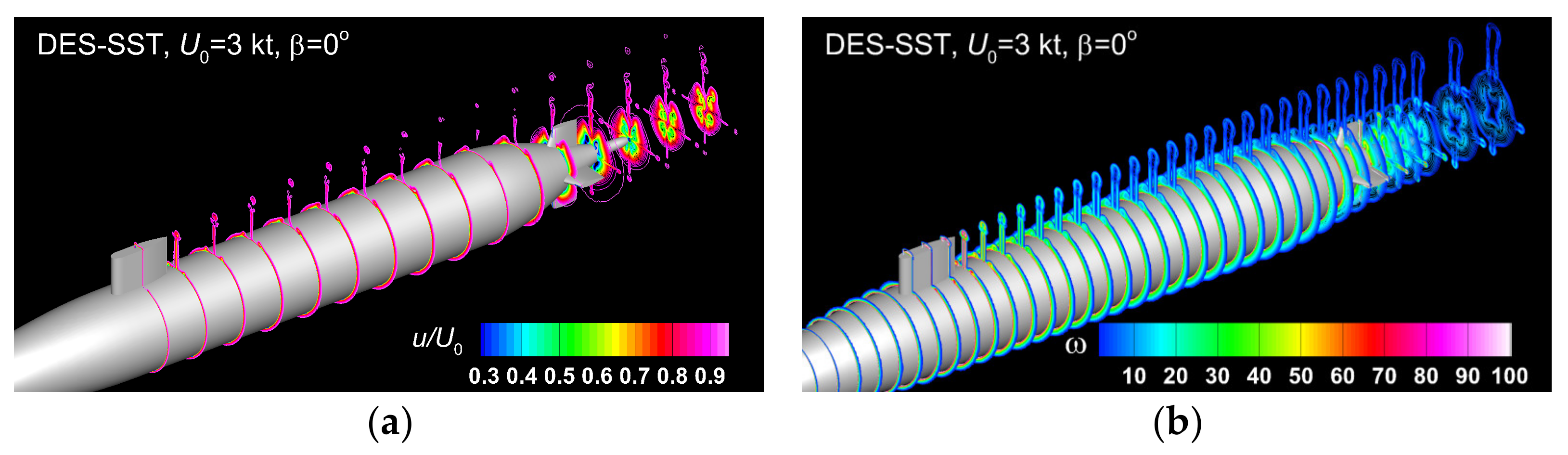
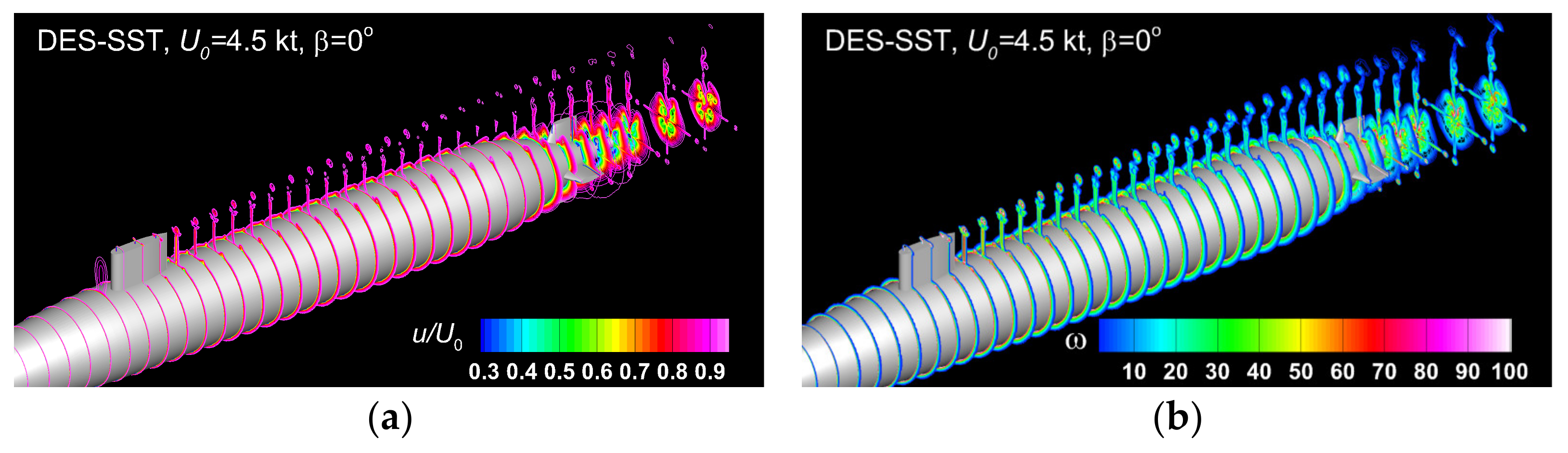
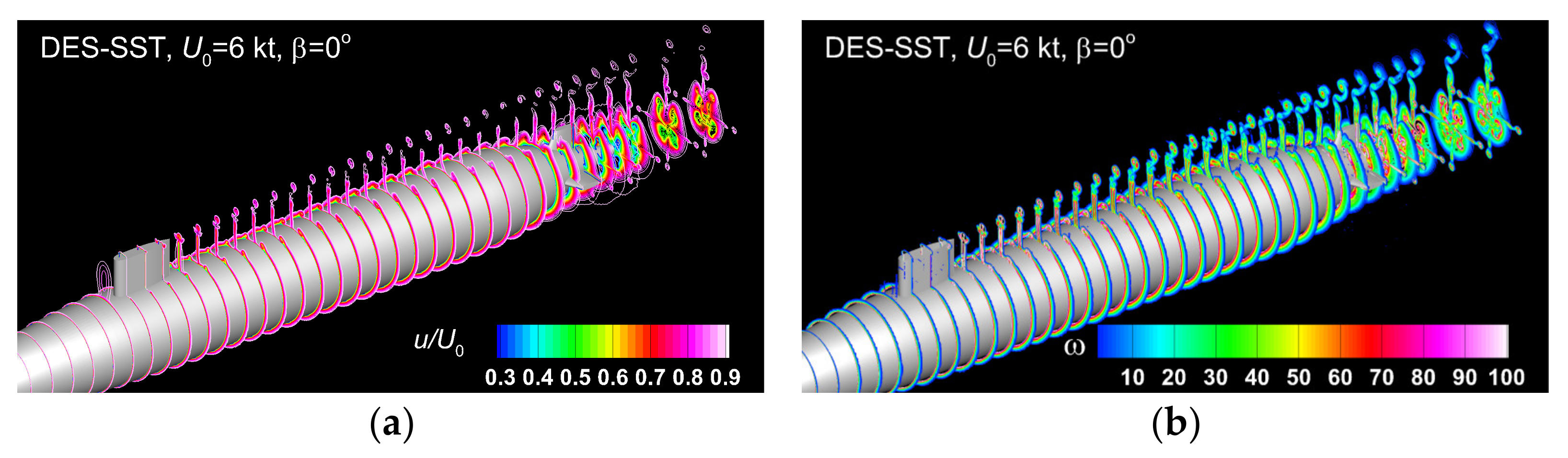
For consistency of the comparisons with the static drift solutions, that will be discussed later, an analysis of the streamwise instant velocity and vorticity contours is firstly proposed. Figure 11, Figure 12 and Figure 13, depict the above-mentioned fields drawn for the three incoming velocities considered. The instantaneous solutions were all computed at using the DES-SST model. The motivation for the author’s choice resides in the fact the corresponding IDDES-based solution, which was predicted to be a better turbulence treatment did not reveal significant differences compared to the DES-SST corresponding one model. The streamwise non-dimensional velocity contours show a perfect symmetry in respect to the center-line plane, as Figure 11a and Figure 13a show. A similar conclusion regards the vorticity distribution except only for the tip bridge released vortices, which show a slight asymmetry at higher velocities, when the finite height of the bridge induces a significant influence on the velocity distribution in the wake [12,64,65].
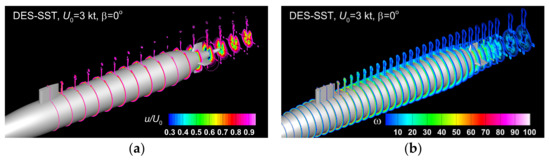
Figure 11.
Instant streamwise non-dimensional velocity (a) and vorticity (b) contours computed at by using the DES-SST turbulence model for.
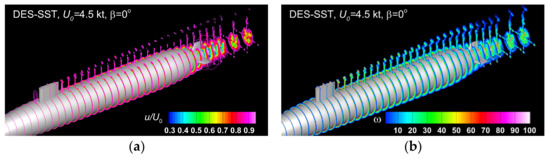
Figure 12.
Instant streamwise non-dimensional velocity (a) and vorticity (b) contours computed at by using the DES-SST turbulence model for.
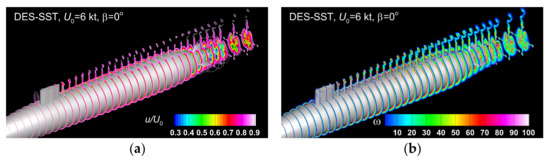
Figure 13.
Instant streamwise non-dimensional velocity (a) and vorticity (b) contours computed at by using the DES-SST turbulence model for.
5.5. Local Flow Features in the Static Drift Motion
Yawed axisymmetric bodies, such as the DARPA Suboff, experience complex, fully three-dimensional flows. Flow regimes at distinct drift angles lead to a continuous modification of the streamwise velocity component. At small incidence angles the flow remains attached, and the axial flow regime dominates, resistance forces are linearly related to the drift angle, therefore the hull loadings should be well predicted by using linear hydrodynamic derivatives. On the contrary, at moderate incidence angles the crossflow boundary layer separates due to an adverse pressure gradient on the leeward side. Vorticity shed from the boundary layer is convected away and coalesces to form a steady symmetric body vortex pair on the leeward side of the hull. Crossflow separation initiates towards the stern, as the incidence angle increases, the separation line moves forwards and leeward. There is a non-linear increase in the lateral force with the incidence angle, due to the low pressure associated with the core of the vortices released by the hull, as shown in Section 5.3. At large drift angles secondary vortices may form in the stern region of the hull. Body vortices become asymmetric, resulting in a significant transverse force, as shown in Section 5.3. Finally, for very large incidence angles the crossflow dominates, the flow pattern tends towards that of the flow around a cylinder, where the boundary layer is shed in the form of a random wake.
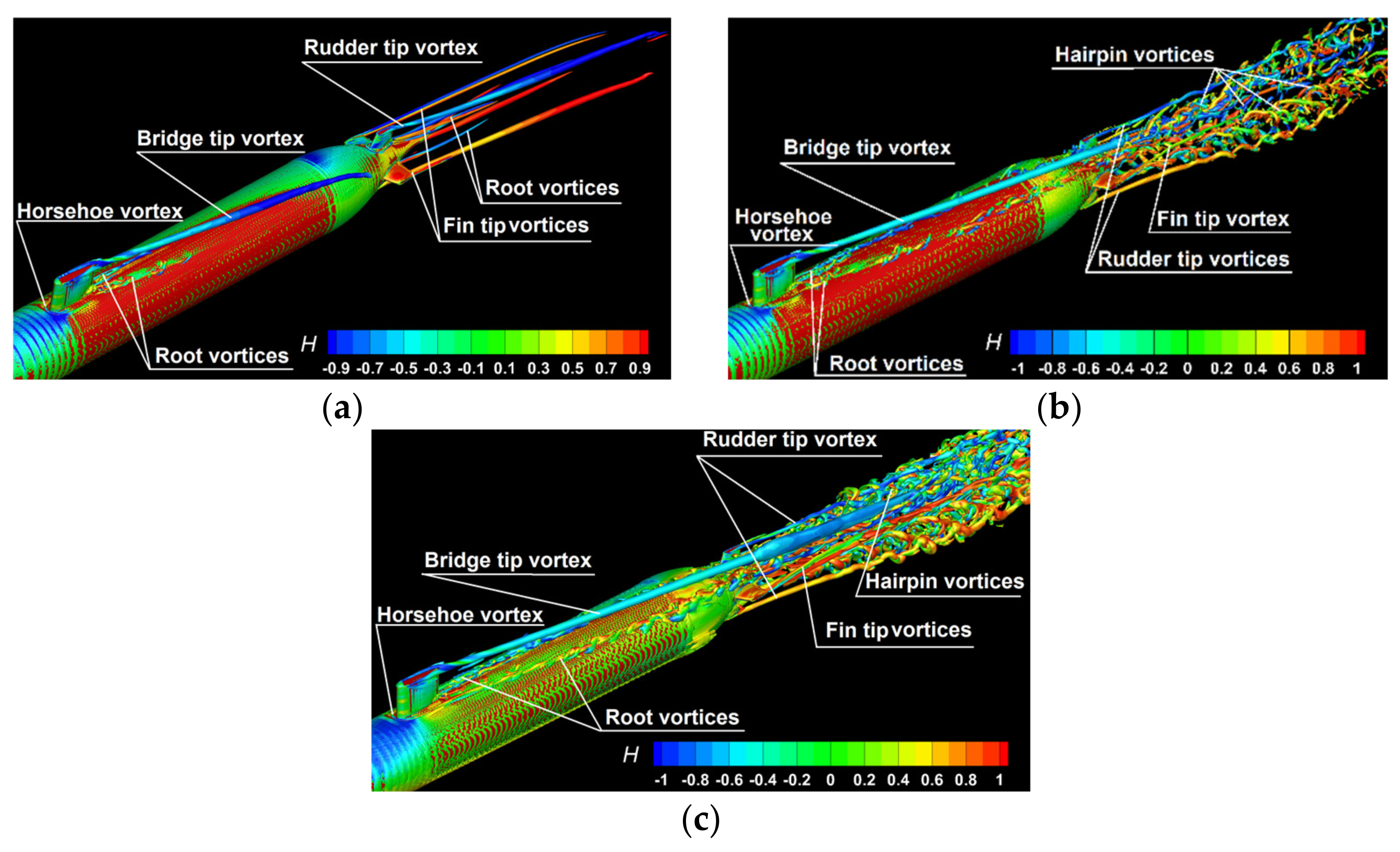
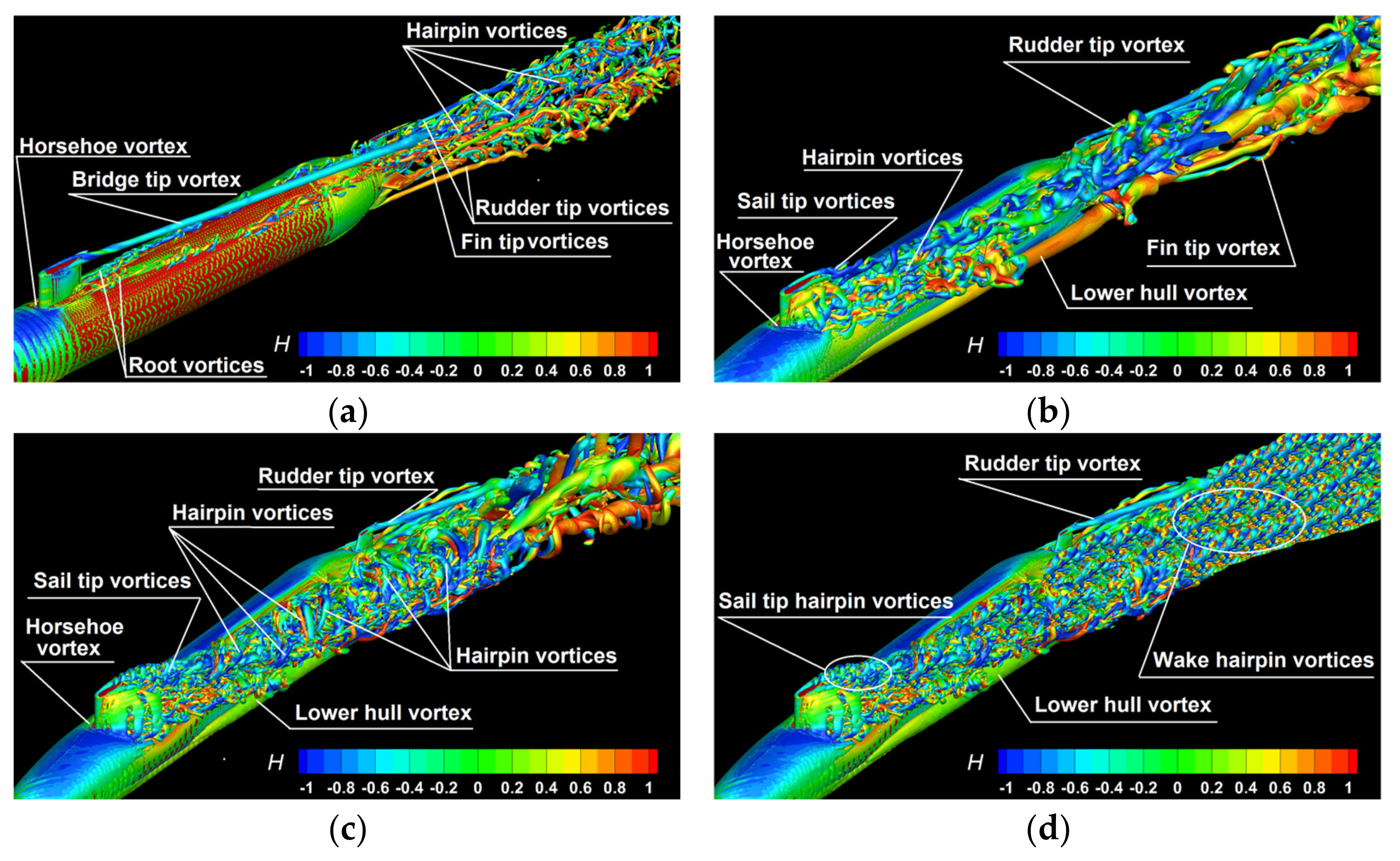
Obviously, a thorough description of the local flow mechanism is of great importance, not only for the accurate forecast of the hydrodynamic loads but also for a correct prediction of the wake structure needed for the propulsive equipment design. Apart from that, the hydrodynamic performances of the rudders and stabilizer fins are significantly affected by the flow non-uniformities. The task is not straightforward at all since six different vortical structures are cohabitant and interact with each other, as will be described in the following. Three of the vortical systems are released by the sail, whereas the others are released by the aft hull and by the tips and roots of the protuberances mounted there, as will be described later. Given its complexity, a detailed comparative study of the flow features is further proposed in terms of the influence of the incoming velocity value, of the drift angle, and of the models used for the turbulence closure, respectively.
5.5.1. Influence of the Oncoming Flow Velocity
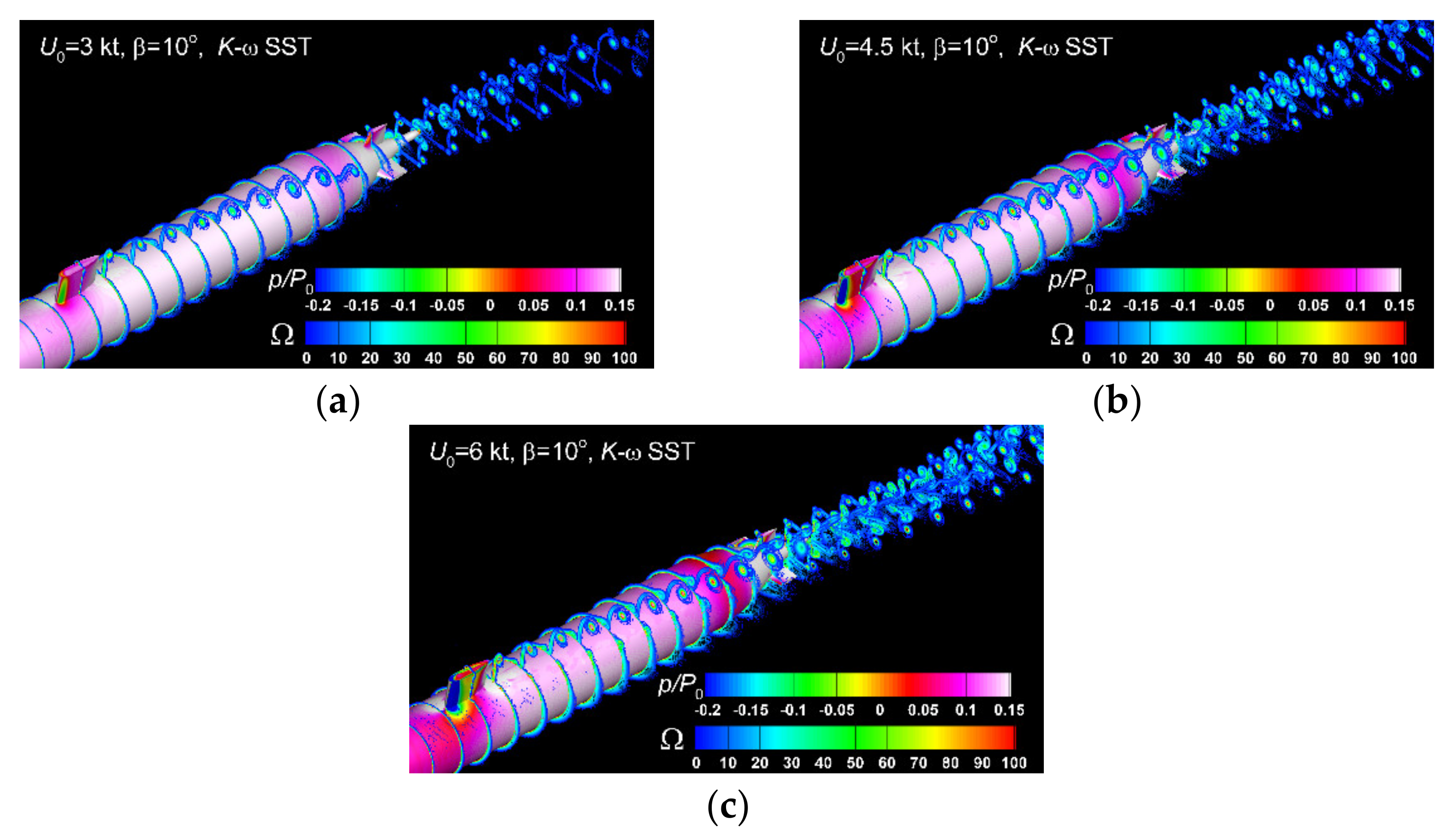
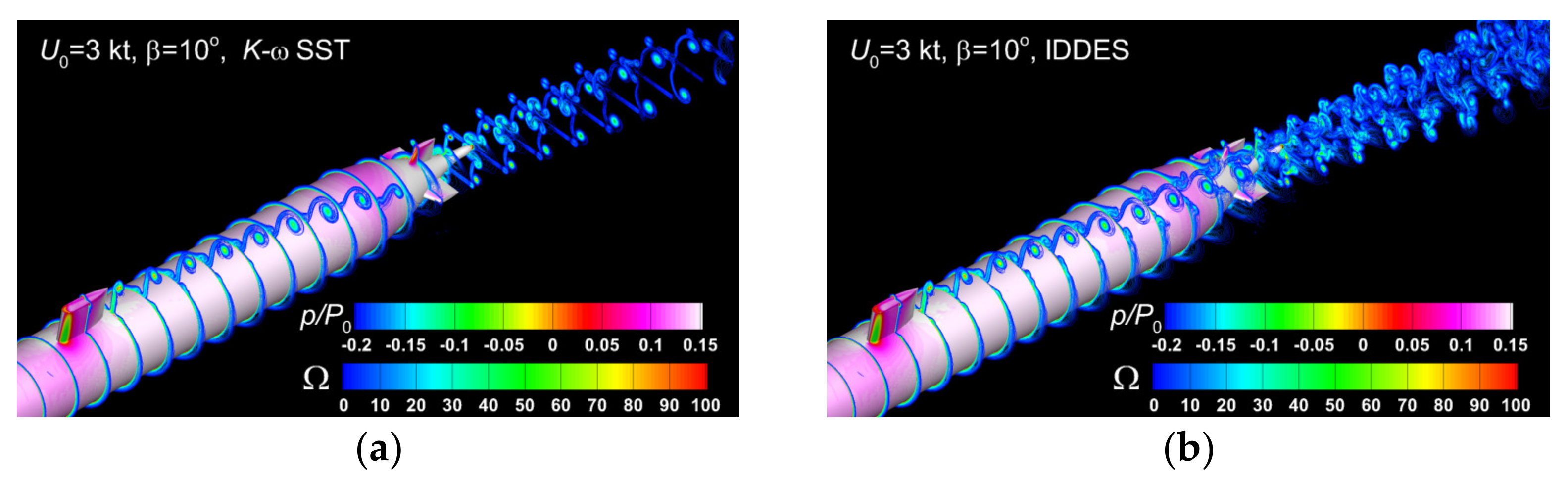
At first, a comparison between the pressure and vorticity fields on the hull and in 22 equidistant cross-sections computed for the three oncoming velocities is proposed in Figure 14, where the relative pressure on the hull surface is drawn by a flood color and the vorticity are drawn with lines. All the solutions are computed in the case by using a RANS-based technique that employs the turbulence model. The three numerical solutions reveal that with the velocity increase, the relative pressure on the leeward of the fairwater bridge decreases to negative values, as expected. The intensity of the bridge-tip vortex increases as the vortices in the wake get stronger as well.
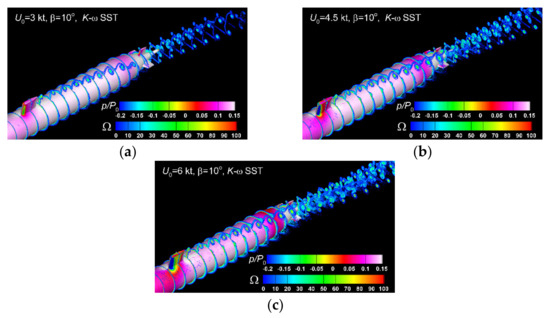
Figure 14.
Wake structure computed for by using the SST turbulence model: (a)—, (b)—, (c)—.
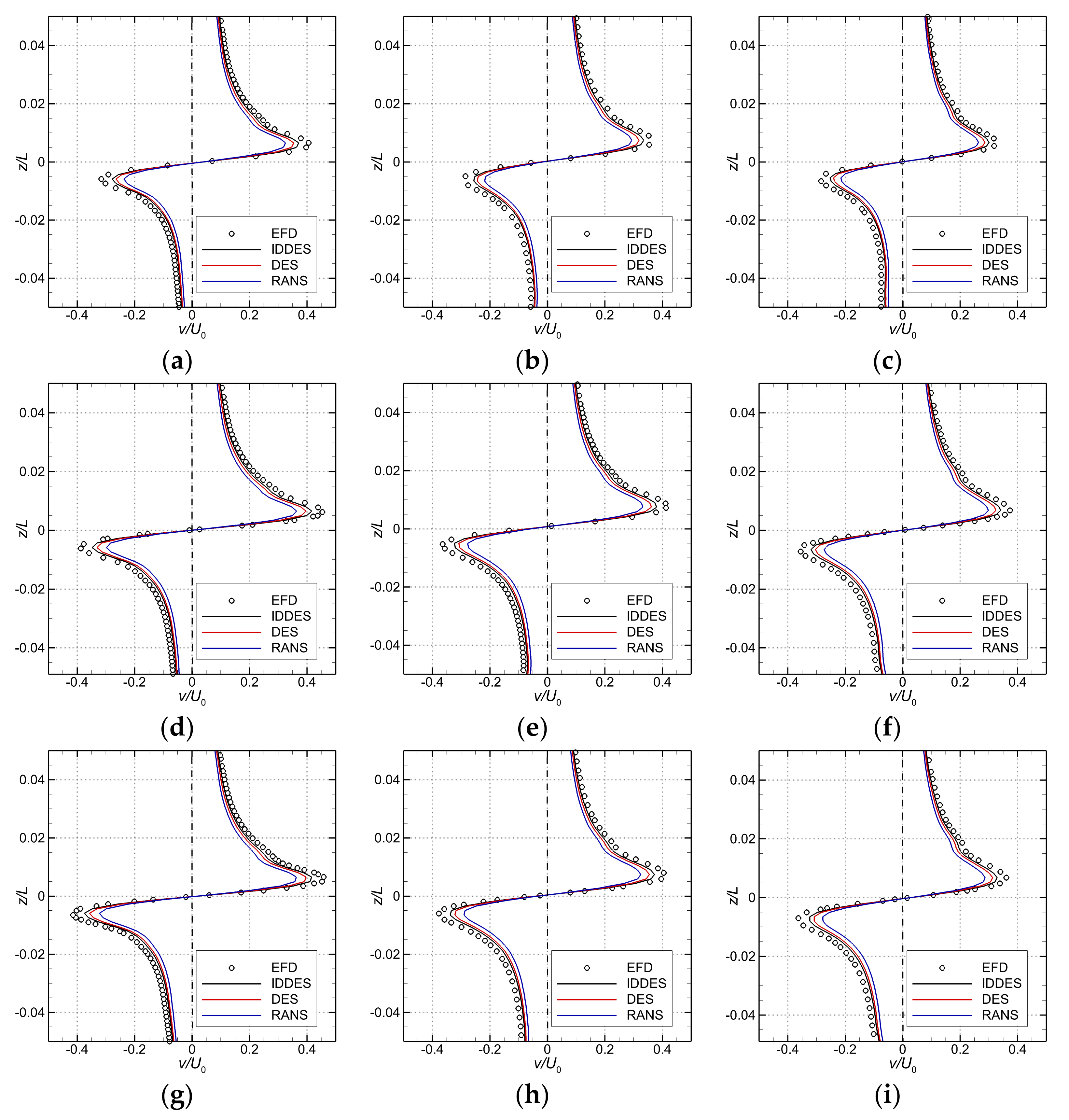
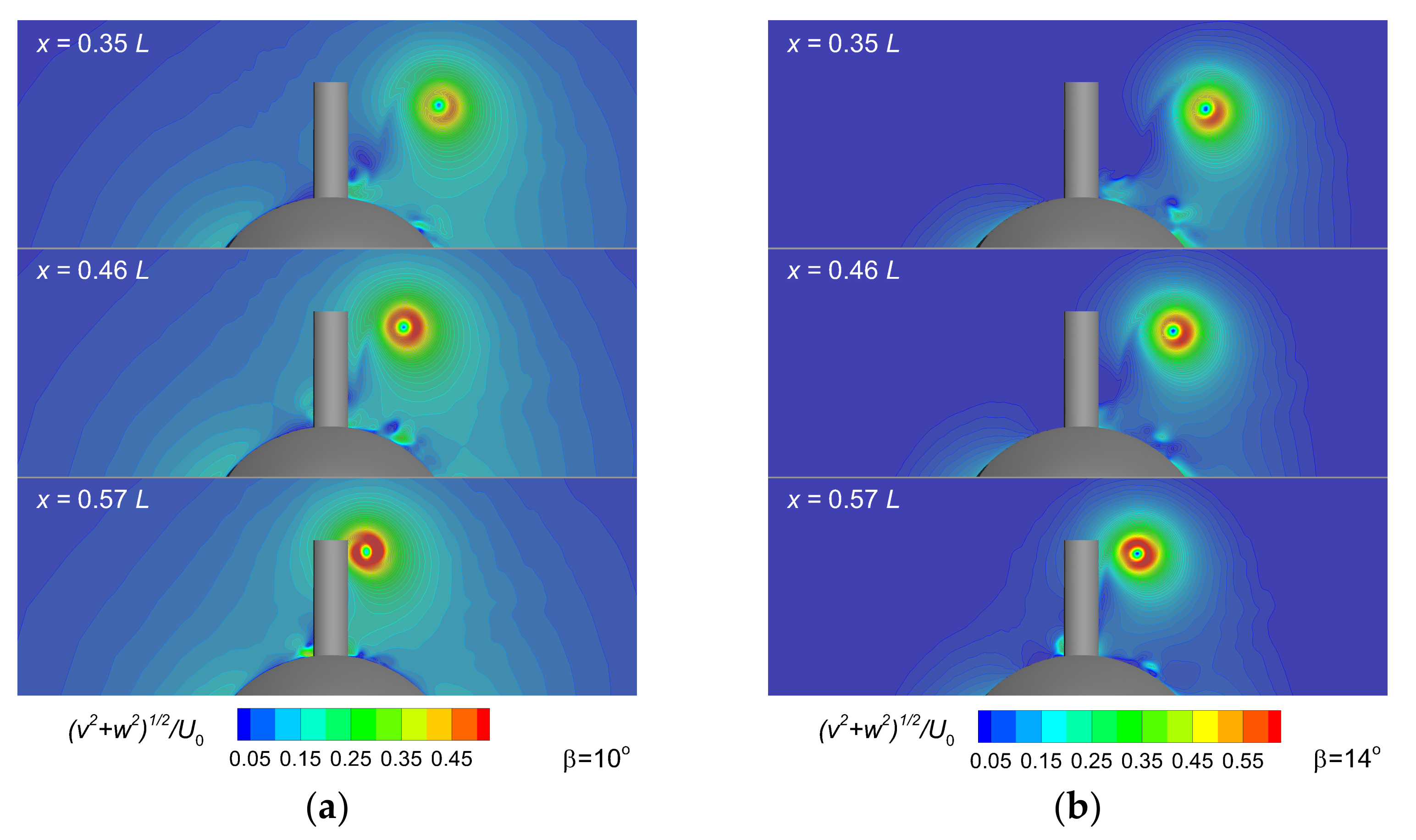
Next, a comparison of the ensemble-averaged and time-averaged in-plane velocity profiles across the center of the bridge-tip vortex core in three cross planes is shown in Figure 15 with the vortex core centers aligned. Obviously, the hybrid DES-SST and IDDES, models under-predict the vortex core in-plane velocity within from the center of the vortex core. On the contrary, the predictions match well with the PIV data for a distance greater than radially, regardless the turbulence model as Figure 15 bears out. Obviously, this is the merit of the turbulence models that use LES for the flow away from the solid boundaries. As the computational grid coarsens with the increasing distance from the trailing edge of the fairwater bridge, in spite of the adaptive mesh refinement, a rather strong dissipation of the coherent vortical structure was observed. This is most likely due to a careless initial grid resolution in the vortex core region. This finding may also suggest that the mesh refinement criteria were insufficiently well chosen for an accurate prediction of the detailed flow development.
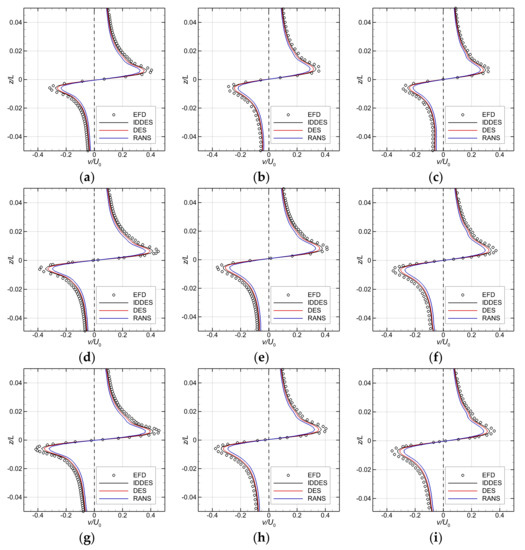
Figure 15.
Time-averaged and instant velocity profiles through the bridge-tip vortex core center computed for at knots (top), knots (middle) and knots (down) in the transverse directions at three different cross planes, where the vortex core centers from IDDES, DES, RANS, and experimental PIV data [60] are aligned. Left column:; middle: ; right column: .
5.5.2. Influence of the Drift Angle
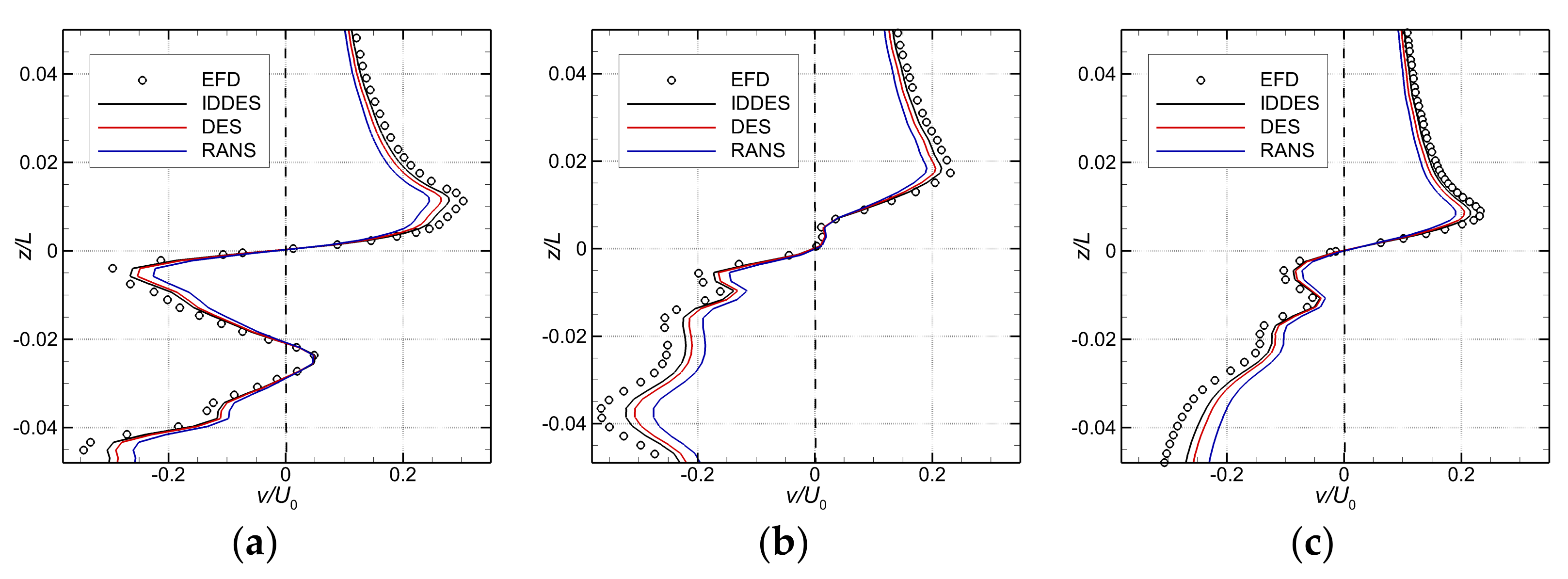
Once the drift angle increases, the anti-symmetric distribution seen in the lowest angle case is affected, as depicted in Figure 16 which is drawn for . Obviously that contamination is determined by the multiple interactions with the other vortical systems formed by the hull, mostly with the hairpin vortices released by the trailing edge of the sail. As a result of that interference, the strength of the tip vortex decreases, provoking a decrease in the relative lateral velocity by 25–30%, regardless of the turbulence model, as shown in Figure 16.
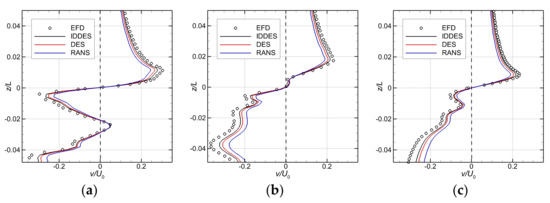
Figure 16.
Time-averaged and instant velocity profiles through the bridge-tip vortex core centre computed for at knots in the transverse directions at three different cross planes, where the vortex core centers from IDDES, DES, RANS and experimental PIV data [60] are aligned: (a)-; (b)-; (c)-.
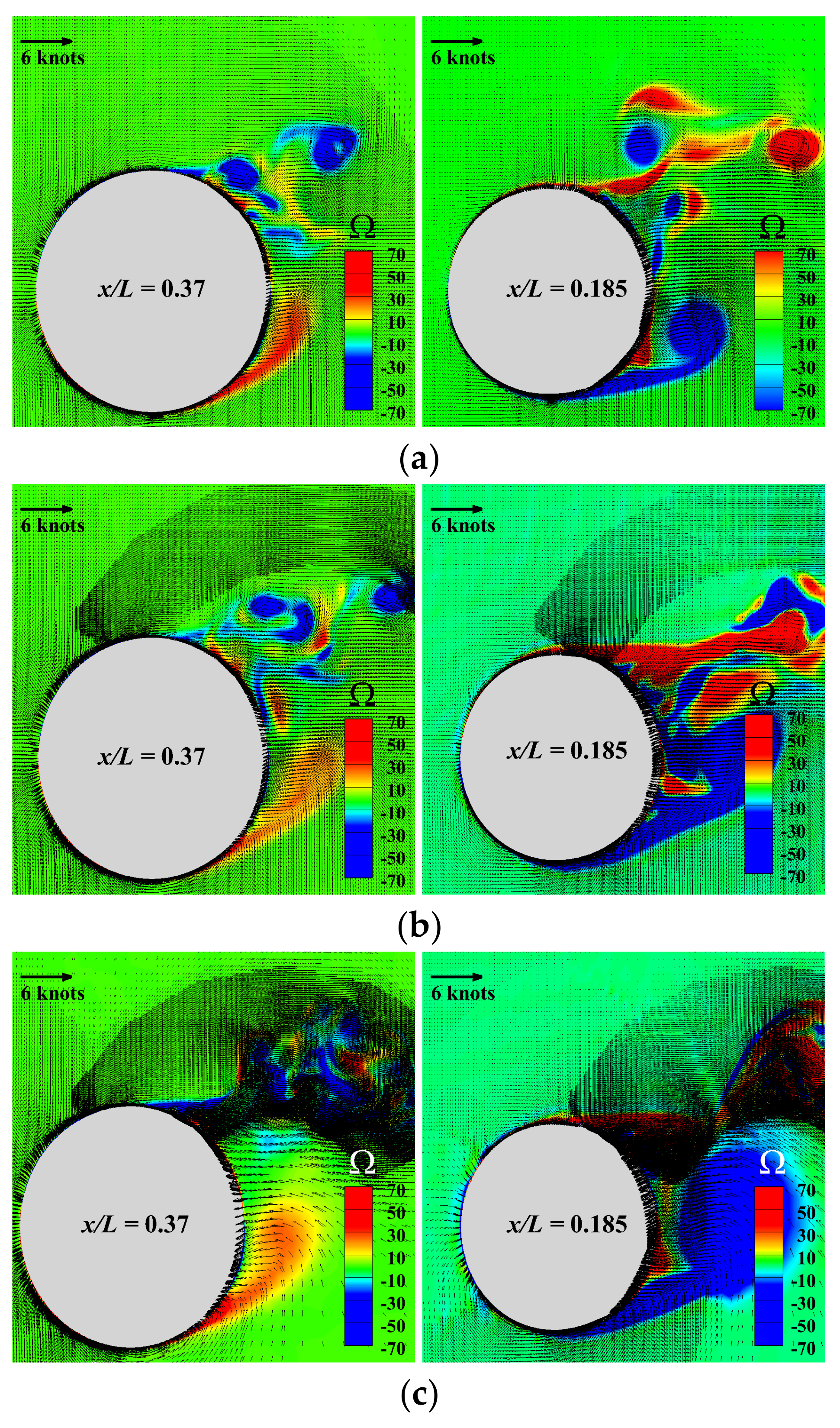
The conclusion above can also be drawn from Figure 17, where the velocity vectors are superposed over the vorticity contour fields drawn comparatively in two different cross-sections placed inside the aft region of the hull. Undoubtedly, the increase in the drift angle makes the flow rather hectic in the aft part of the hull where significant areas of positive and negative vorticity alternate, especially in the plane closer to the aft part of the hull. The boisterous behavior should be related to the periodic variation of forces depicted in Figure 10.
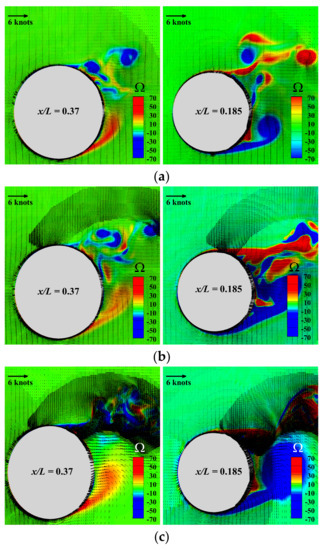
Figure 17.
Cross section distribution of instant vorticity and velocity vectors computed for at by using IDDES turbulence model: (a)- (b)-, (c)-.
Solutions depicted in Figure 17 are all instantaneous, computed at s. Worth mentioning is that the adaptive mesh refinement based on the criterion described in Section 4.2 was applied periodically every different numbers of time steps, a fact that may explain why the mesh refinement for appears to work improperly.
As shown above, probably the most significant vortex of the multiple-released vortical systems is that released by the tip of the fairwater bridge at small and moderate drift angles. Its core longitudinal trajectory, which originates in the tip of the sail and develops downstream with an obvious, but expected, departure from the hull surface, is depicted in Figure 18. A reduction in its strength, which is obviously due to the viscous dissipation, is also observed. The streamwise evolution of the vortex core shows a loss in the relative vertical position to the hull, which is attributable to the interference of the other vortical systems that develop around the hull.
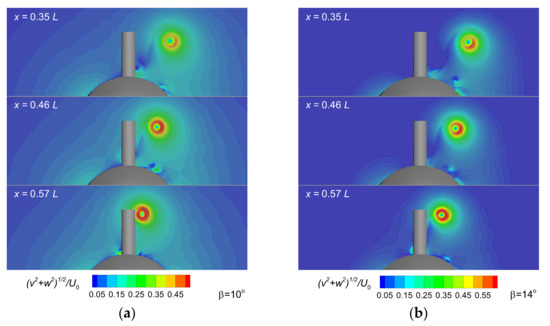
Figure 18.
Instantaneous bridge-tip vortex trajectories computed for at by using IDDES turbulence model: (a)- (b)-.
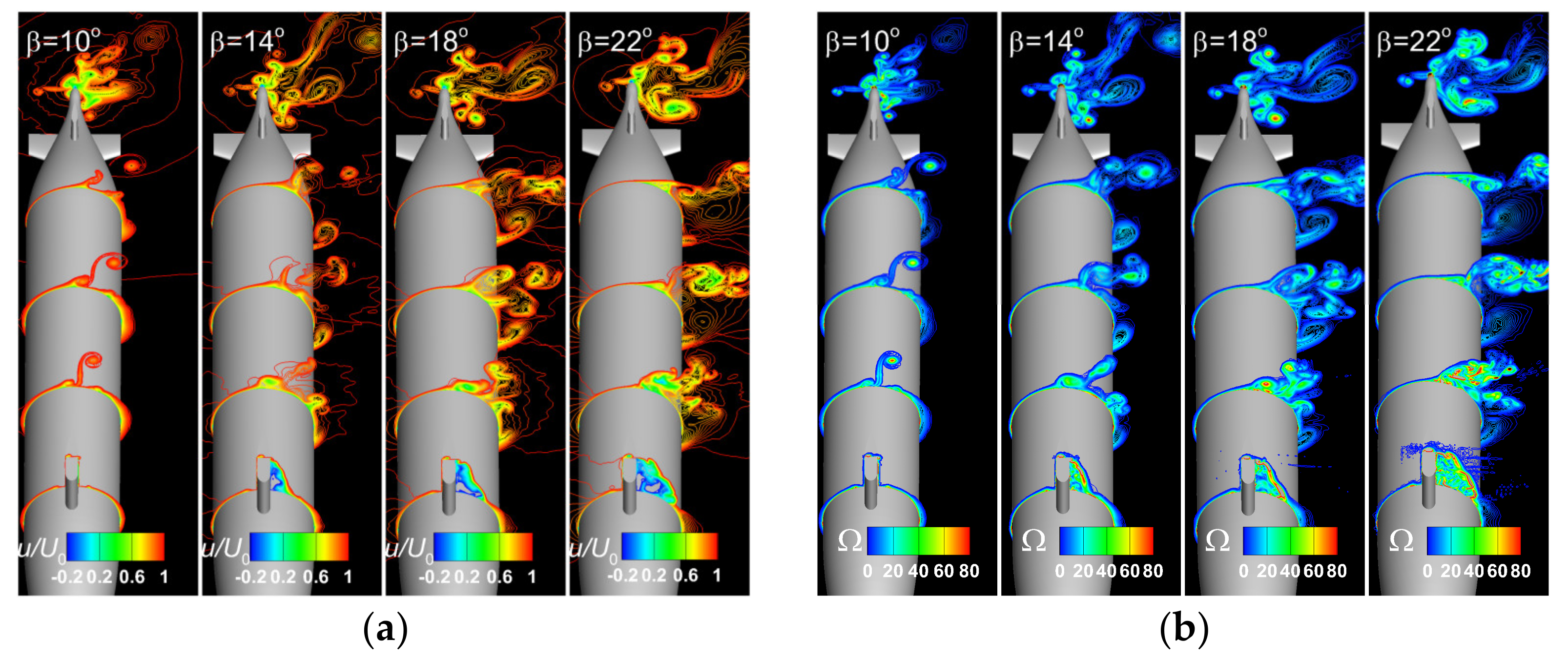
The same behavior is true for the higher drift angles, as proven in Figure 19, which bears out the instantaneous streamwise velocity and vorticity contours drawn for the maximum incoming velocity case at for all the drift angles considered in the present paper. For the sake of the accuracy of the comparison, all the reported solutions were computed by using the IDDES turbulence model, as all the equidistant contour lines are drawn for the same values. From Figure 19a,b one may see that the increase in the drift angle leads to the augmentation of the area of negative relative streamwise velocity in the leeward side of the sail. Then, the interference of the vortices released by the sail with those developed around the main hull results in a contamination of the vortical flow-field not only in terms of the main vortices trajectory, but also of their core intensity.
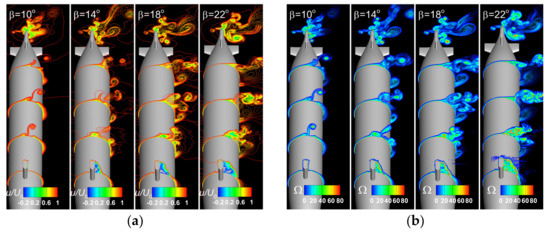
Figure 19.
Non-dimensional instant streamwise velocity and vorticity contours computed for at: (a)-non-dimensional streamwise velocity, (b)-vorticity.
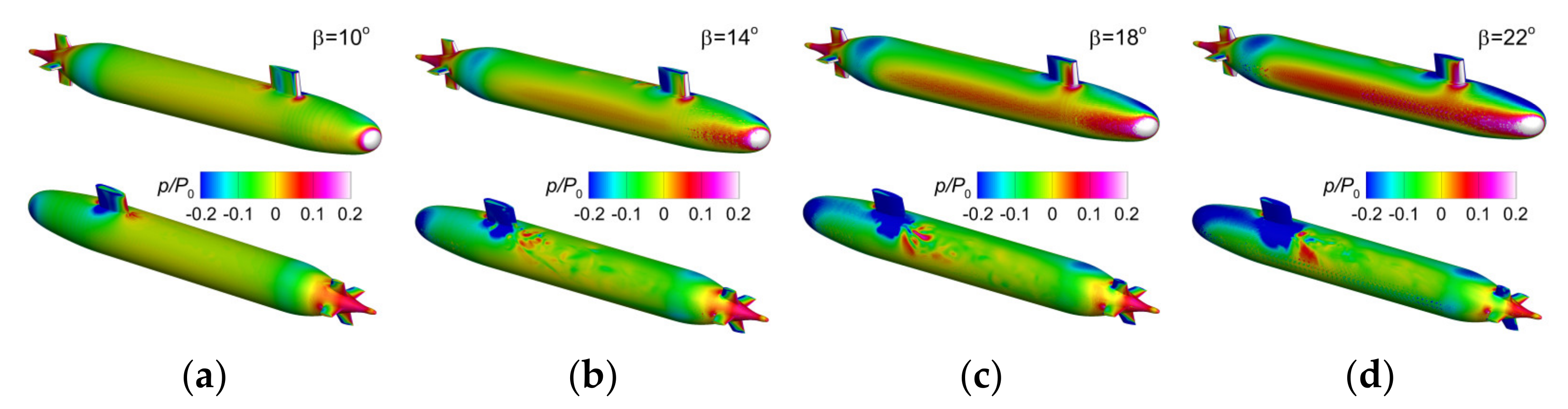
All the discussions related to the velocity- and vorticity fields’ dependence on the drift angle shall be extended to the pressure, the other key parameter of the flow. As expected, the increase in the drift angles influences the pressure distribution of the Suboff hull as well, inasmuch as pressure and velocity are interlinked in the momentum equations. Figure 20 shows the non-dimensional pressure fields on the Suboff hull computed in all the considered drift angle cases at the highest incoming velocity. The increase in the drift angle determines the migration of the stagnation points that are either on the hull or on its vertical protuberances towards the lateral pressure side. On the opposite, areas of low relative pressures can be seen on the leeward side.
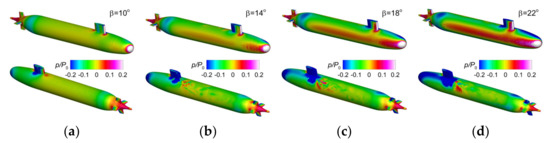
Figure 20.
Comparison between the mean non-dimensional pressure fields on the hull computed for at : (a)-, (b)-, (c)-, (d)-.
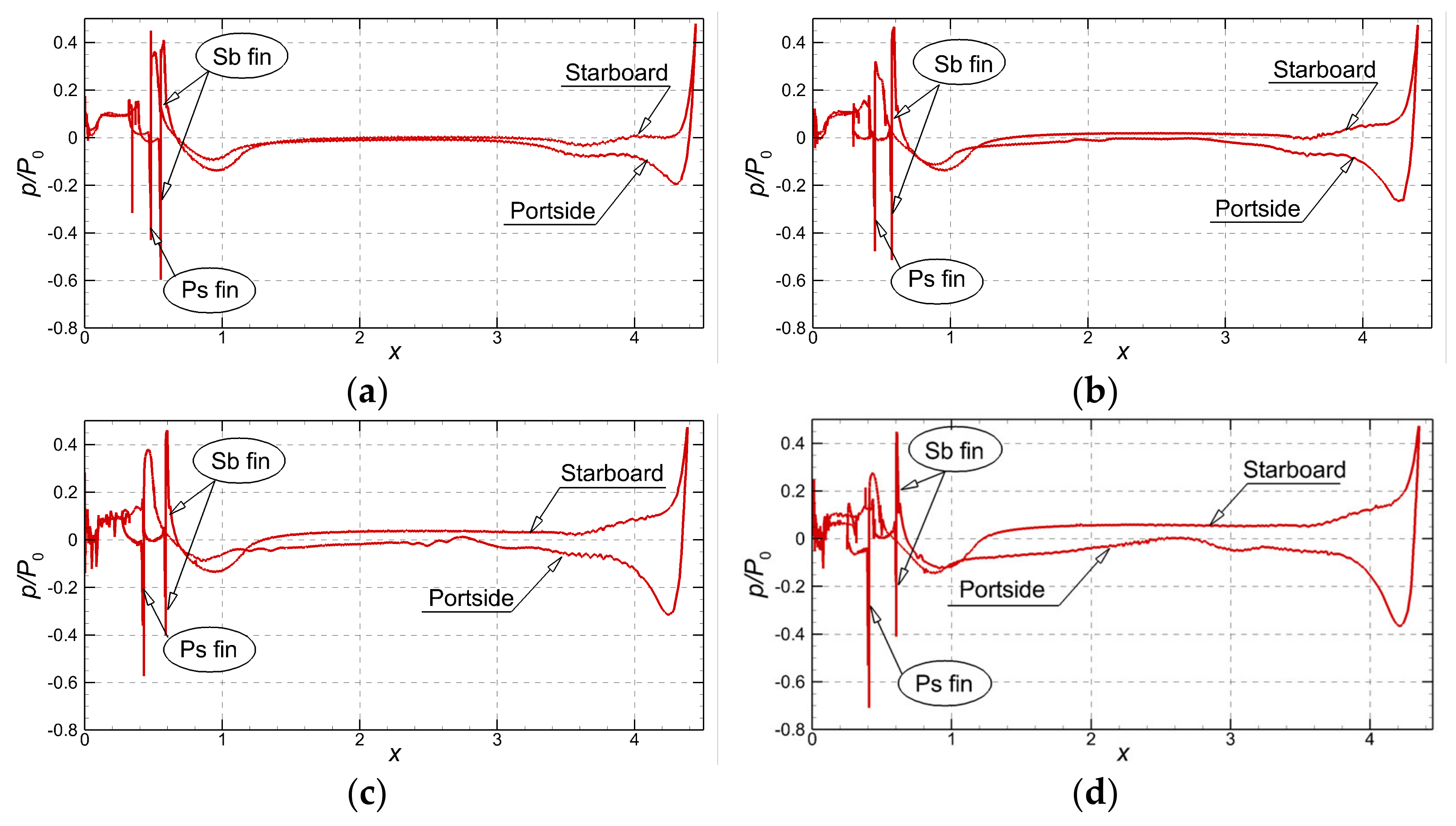
The pressure distributions on a horizontal plane that crosses the hull are shown in Figure 21 for the four drift angles considered in here. In the straight run case portside and starboard curves are coincident. On the contrary, in the static drift regime the non-zero drift angle determines the loss of that distribution symmetry. Figure 21 proves that the gap between the starboard and portside pressures increases with the drift angle increase, which explains the increase in the lateral force. A similar gap increase is seen between the longitudinal positions of the pressure peaks that correspond to the leading edges of the horizontal fins at the aft body.
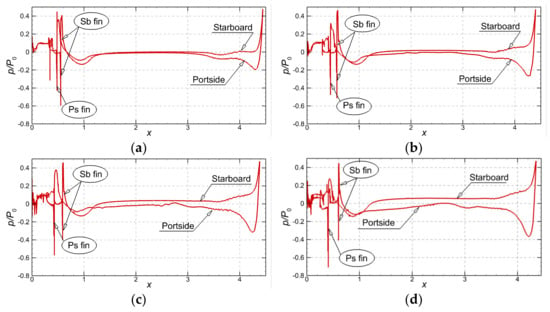
Figure 21.
Comparison between the mean pressures on the Suboff hull computed for at (a)-, (b)-, (c)-, and (d)-.
Unquestionably, the influence of the drift angle on the pressure distribution on the hull manifests on the surrounding fluid domain as well. That is clearly shown in Figure 22, which depicts the instantaneous relative pressure contours in a cross-section plane situated at . The solutions ateconds were all computed for the largest incoming velocity. Closure to turbulence was achieved through the IDDES turbulence model in all the draws. For the clarity of comparison, the pressure fields have the isobars disposed at same level intervals. The figure shows that the increase in the drift angle leads to a significant pressure change inside the fluid domain surrounding the hull, which is correlated with the distributions depicted in Figure 20 and Figure 21.

Figure 22.
Comparison between the non-dimensional mean pressure fields computed at for at (a)-, (b)-, (c)-, (d)-.
5.5.3. Influence of the Turbulence Model
In the followings a comparative analysis of the vortex generation mechanisms is proposed in Figure 23 to clarify the influence exerted by the models used for turbulence [65]. Solutions computed for are compared for the SST, DES and IDDES models, respectivly. The vortex formation mechanisms are described by the isosurfaces of the the second invariant of velocity gradient colored by helicity, which is defined as: where isu (x,t) {\displaystyle \mathbf {u} (x,t)} isi the velocity field and ∇ × u {\displaystyle \nabla \times \mathbf {u} } is the corresponding vorticity field.
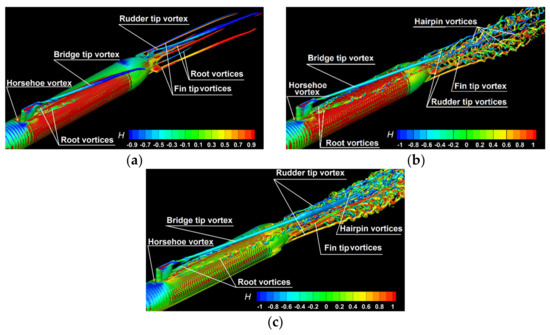
Figure 23.
Vortex formation mechanisms for (a)- SST model, (b)-DES model, (c)-IDDES model.
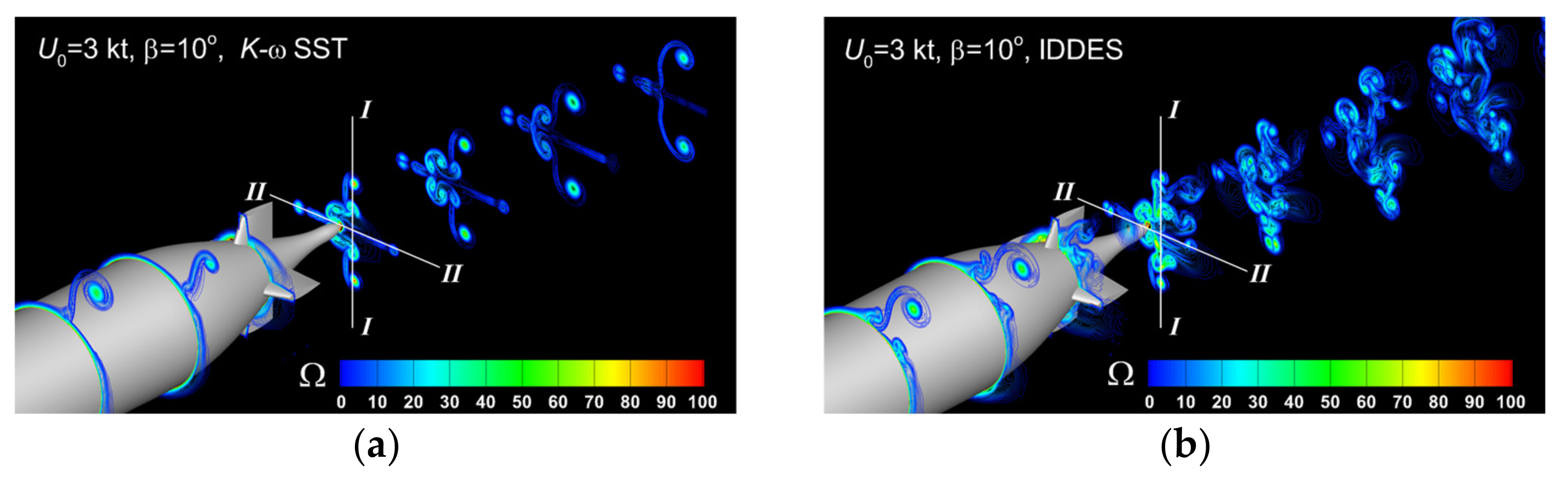
Helicity as a pseudo-scalar quantity can be considered as a measure of the handedness (or chirality) of the flow, being one of the only four integral invariants of the flow equations, the other three being energy, momentum, and angular momentum, whose topological interpretation is a measure of linkage and/or knottedness of vortex lines in the flow. Figure 23 reveals the six vortical systems, which were mentioned above, in the lowest advance velocity flow case. When the hybrid DES SST model is used, the sail root vortices merge with the large-scale hairpin vortices, which become dominant in the wake, as shown in Figure 23b. This fact is even more relevant when the IDDES model is used for the turbulence closure, as the Figure 23c bears out.
The main necklace vortex associated with the horseshoe vortex system formed around the bow base of the bridge is subjected to bimodal large-scale oscillations. The intensity of the bimodal oscillations peaked at vertical sections cutting through the tip of the fairwater bridge. Simulations reported here show the size of the region of high turbulence amplification inside which the horseshoe vortex system extension decreased with the increase in the Reynolds number. Significant patches of vorticity were observed to detach from the leg of the main necklace vortex and to be convected at a small distance from the Suboff hull. Pilot computations proved that before dissipating, these patches could induce relatively large values of the fuselage shear stress beneath. It was observed that their formation is primarily determined by the interaction of the main necklace vortex with the leg of the secondary necklace vortex rather than by the interaction of the main necklace vortex with the tip of the sail. Figure 23 proves the superiority of the IDDES model in terms of ability to resolve the separated flow at large scale. Certainly, this is only due to the ability of the LES model to resolve the turbulence in areas placed away from the hull.
The next analysis regards the pressure and vorticity fields computed when the SST and IDDES models were employed to solve the static drift flow for , as shown comparatively in Figure 24. Similar to Figure 14, the relative pressure on the hull surface is drawn by a flood color and the vorticity are drawn with lines. For the sake of similarity, the vorticity fields are drawn in the same cross-sections and the intervals between consecutive vorticity values are kept unchanged. First of all, one may notice that the non-zero drift angle determines the looseness of the vertical symmetry of the solution shown in Figure 11. Then, the contour lines drawn on the hull reveal the contagion of the vorticity field as a result of the interaction between the horseshoe vortices and the boundary layer developed there. This interference is shed in the downstream, decreases progressively in intensity, and eventually vanishes as a result of the viscous dissipation.
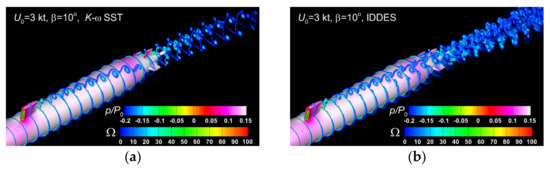
Figure 24.
Vorticity contours computed for at s. by using: (a)- SST turbulence model, (b)-IDDES turbulence model.
To get a better insight on how the flow symmetry is affected by the drift angle, a comparison of the solutions computed using the two turbulence models, a close-up view of the vorticity contours is presented in Figure 25. For clarity of representation purposes, the cross contours are drawn every second cross-plane shown in Figure 24. As shown in the figure, the flow development in respect to the vertical and horizontal directions denoted by I-I and II-II reveal the significant departure from the vertical symmetry, which was expected for the non-zero drift angle. Another important point to mention is the symmetric vorticity distribution in respect to the hull horizontal plane of symmetry when the solution is computed with the SST turbulence model. This feature does not remain valid for the solution computed with the IDDES model, whose better performance in resolving the flow features unveils a significant non-symmetric distribution in the wake. Comparative simulations employing all the turbulence models have proven that the degree of deformation of the tube cores shed at the downstream part of the separated shear layer is much larger in the IDDES model case. Obviously, this is providing additional information on the mechanism for the amplification of the vertical vorticity in the aft near-hull region, with immediate consequences for the velocity field structure needed for an optimal design of a performant propeller, as shown previously by the author in [65,66].
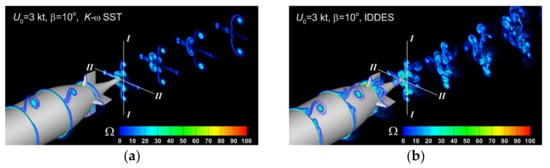
Figure 25.
Details of wake vorticity contours computed for at s. by using: (a)- SST turbulence model, (b)-IDDES turbulence model.
The next discussion is based on a comparison of the vortical topologies computed when the turbulence closure is achieved by the IDDES model. The comparison is presented in Figure 26, which depicts the instant isosurfaces of the second invariant of velocity gradient computed for all the drift angles at and The comparison reveals that with the drift angle augmentation, the presence of the hairpin vortices becomes dominant, suggesting a violent flow separation. Large-scale hairpin-like structures form in the downstream part of the separated shear layer. The legs of these vortices are positioned parallel to the interface between the high-speed outer flow and the recirculating flow past the sail and hull. Several computational tests have mainly proven two particulars:
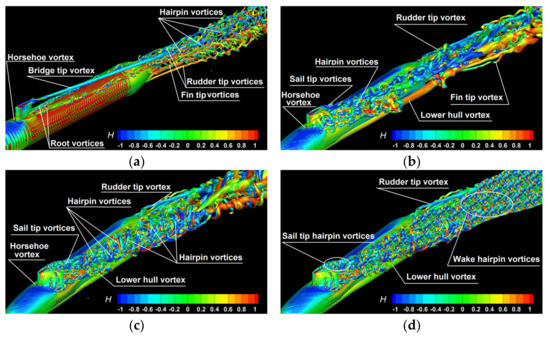
Figure 26.
Instant isosurfaces of the second invariant of velocity gradient () colored by helicity and computed for at by using the IDDES turbulence model: (a)-, (b)-, (c)-, and (d)-.
- –
- The lower legs of some of these hairpin vortices were located randomly in the immediate vicinity of the hull;
- –
- The shear stress distribution on the Suboff hull in the instantaneous flow fields displayed a streaky structure over a part of the separated shear layer region.
Trial computations that employed the IDDES model, not reported here, have proven that due to the richer eddy content of the separated shear layer, the intensity of the non-dimensional pressure root mean square fluctuations beneath the separated shear layer has been found to be more than twice larger in the highest velocity simulations.
6. Concluding Remarks
The paper describes a multiple numerical investigation aimed at clarifying the local flow features around the DARPA Suboff hull running either on a straight course or at various medium and large drift angles. Because of the diversity of the flow cases taken into consideration, an in-depth V&V had to be performed to prove the robustness of the solver as well as the correctness of the chosen numerical approach. Three turbulence closure models were considered to fit the purpose and the solutions were comparatively discussed. Summing up, more than 100 different computations were performed on 20 different meshes generated for all the cases considered and a great deal of data was analyzed to emphasize the main features that made each flow instance unique.
Based on the bird’s-eye view above, the following remarks may conclude the present reported research:
- –
- Flows in which significant separations take place could be properly resolved based on a proper meshing of the computational domain combined with a sufficiently small time step;
- –
- The major contribution of this work is the overall quality of solutions brought by the combined use of adaptive mesh refinement along with the DES or IDDES-based turbulence closure models. Comparing the solutions reported here with the otherwise faster but less accurate RANS methods [15,20], or with the more expensive LES-based methods [23,35,66] one may notice not only the efficiency, but also the accuracy of the method proposed here.
- –
- Taking advantages of the IDDES-SST hybrid model as well as of the adaptive mesh refinement, simulations reported in here could be performed efficiently on a reasonable number of processors by keeping the number of cells at the lowest possible level;
- –
- Extensive comparisons with the experimental data confirmed the overall accuracy of the solutions for both global and local flow features, i.e., forces and moments as well as the velocity and pressure distributions on the hull and in its immediate vicinity;
- –
- High frequency oscillations of the streamwise and lateral forces and yaw moment were observed when the turbulence closure was not based on Reynolds averaging;
- –
- In spite of the slightly higher CPU costs, solutions computed with the hybrid IDDES-SST turbulence model could assure an error about 40% smaller than the one based on the SST model in the highest velocity case;
- –
- The large scale vortical structures could be successfully resolved, regardless of the drift angle the computations were carried out at.
Funding
This research received no external funding.
Acknowledgments
All the computations reported herein were performed on the HPC of the “Dunarea de Jos” University. The author expresses his gratitude to A. Istrate, the system administrator at that time, for his unfailing support.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
The hybrid Detached Eddy Simulation (DES) model is based on an implicit splitting of the computational domain into two regions. In the first one, near solid walls, the conventional RANS equations are solved, whereas in the second one, the governing equations are the filtered Navier–Stokes equations of the Large Eddy Simulation (LES) approach. Hybrid models are not linked to any specific turbulence model, so the model employed in the present study is a variant based on the SST turbulence model of Menter et al. [41,42]. The DES modification of the SST model resides in the way the dissipation term in the transport equation is computed. While the dissipation term of the original model is given by the following equation:
Dissipation in the DES model is expressed as:
In the above equations is the dissipation rate, is a constant of the SST model, whereas the function reads as follows:
Here the turbulent length scale is defined as . is a constant of calibration of the DES model proposed by Menter et al. [42] and is the maximum local grid size defined as . The blending function in Equation (A3) is either 0 or the blending functions or of the SST model of Menter. When, the model of Strelets [43] is recovered. Blending function acts inside the wake of the boundary layer while extends further out into the boundary layer than.
The variable arg1 in the equation above is defined as:
where and is the distance to the nearest wall. is computed with:
On the other hand, arg2 in (A4) is defined as:
were is the kinematic viscosity of water. Transition from RANS to LES of the initial version of DES is substantially dependent on mesh fineness. When the mesh is sufficiently fine near the wall, the LES area tends to be activated too early even though the production term and dissipated term are not yet balanced. This fact usually leads to mesh-induced separation and modeled-stress depletion in the boundary layer, as described by Spalart [44]. The problem can be mitigated by the delayed DES (DDES), which incorporates a delay factor that enhances the ability of the model to distinguish between the LES and RANS regions on the meshes, as described by Spalart [44]. Improved DDES (IDDES) is the latest edition of DES, which supplies selected wall-modeled LES (WMLES) capabilities to the DES formulation, for more details see Shur et al. [45].
Appendix B
The governing equations of the present IDDES model, which complete the equation set (8), written in a tensor form, read as follows:
Here is the production rate, whereas is the turbulent kinetic energy, and is the dissipation rate. The eddy viscosity,, appearing in equation above is defined as:
Here is a constant of the model, S is the magnitude of the strain rate tensor. in (A8) and in (A9) are the SST blending function expressed as in (A13). The variable arg1 in (A6) is now defined as follows:
Here is a constant of the model and is computed now with:
in Equation (A8) is the length scale defined as:
where
Here and are constants of the turbulence model. The LES length scale appearing in Equation (A5) is now computed as:
Here is the maximum edge length of the cell. The empiric blending function in Equation (A12) is defined as:
in which the empirical delay function is given by:
Here is expressed as:
in Equation (A17) is the magnitude of the vorticity tensor. appearing in Equation (A8) is computed as follows:
The elevation function in Equation (A12) is computed with:
in which functions and are respectively defined as:
where
and
Constants used in the IDDES model are taken as:
Additionally, all the other the constants that belong to the classic SST model, are as follows:
References
- Sreenivas, K.; Hyams, D.; Mitchell, B.; Taylor, L.; Briley, W.R.; Whitfield, D.L. Physics Based Simulations of Reynolds Number Effects in Vortex Intensive Incompressible Flows; Report No. OMB No. 0704-0188; NATO Research and Technology Organisation BP 25: Neuilly-Sue-Seine Cedex, France, 2003. [Google Scholar]
- Lungu, A. Scale effects on a tip rake propeller working in open water. J. Mar. Sci. Eng. 2019, 7, 404. [Google Scholar] [CrossRef] [Green Version]
- Gregory, P.A.; Joubert, P.N.; Chong, M.S. Flow over a Body of Revolution in a Steady Turn; Report No. DSTO-TR-1591; Australian Government, Department of Defence; Defence Science and Technology Organisation; Maritime Platforms Division; Platforms Sciences Laboratory: Victoria, Australia, 2004. [Google Scholar]
- Moore, K.J.; Jones, G.; Ndefo, E. Vortex Control in Submarine Design; Paper number 20; Int. Symposium on Naval Submarines; RINA: London, UK, 1991. [Google Scholar]
- Peterson, R.S. Evaluation of Semiempirical Methods for Predicting Linear Static and Rotary Hydrodynamic Coefficients; Report NCSC TM-291-80; Naval Coastal Systems Center: Panama City, FL, USA, 1980. [Google Scholar]
- Chellabi, A.; Nahon, M. Feedback linearization control of undersea vehicles. In Proceedings of the OCEANS ’93, Victoria, BC, Canada, 18–21 October 1993; Volume 1, pp. 410–415. [Google Scholar] [CrossRef]
- Holmes, E.P. Prediction of Hydrodynamic Coefficients Utilizing Geometric Considerations. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 1995. [Google Scholar]
- De Barros, E.A.; Pascoal, A.; de Sa, E. Progress towards a method for predicting AUV derivatives. In Proceedings of the MCMC2006—7th IFAC Conference on Manoeuvring and Control of Marine Craft, Lisbon, Portugal, 20–22 September 2006. [Google Scholar]
- De Barros, E.A.; Dantas, J.L.; Pascoal, A.M. Investigation of normal force and moment coefficients for an AUV at nonlinear angle of attack and sideslip range. IEEE J. Ocean. Eng. 2008, 33, 538–549. [Google Scholar] [CrossRef]
- Stern, F.; Yang, J.; Wang, Z. Computational ship hydrodynamics: Nowadays and way forward. Int. Shipbuild. Prog. 2013, 60, 3–105. [Google Scholar] [CrossRef]
- Stern, F.; Wang, Z.Y.; Yang, J.M. Recent progress in CFD for naval architecture and ocean engineering. In Proceedings of the 11th International Conference on Hydrodynamics (ICHD 2014), Singapore, 19–24 October 2014. [Google Scholar]
- Lungu, A. DES-based computation of the flow around the DARPA suboff. IOP Conf. Ser. Mater. Sci. Eng. 2019, 591, 12053. [Google Scholar] [CrossRef] [Green Version]
- Ӧzden, Y.A.; Ӧzden, M.C.; Demir, E.; Kurdoğlu, S. Experimental and numerical investigation of DARPA Suboff submarine propelled with INSEAN E1619 propeller for self-propulsion. J. Ship Res. 2019, 63, 235–250. [Google Scholar] [CrossRef]
- Chase, N.; Carrica, P.M. Submarine propeller computations and application to self-propulsion of DARPA suboff. Ocean Eng. 2013, 60, 68–80. [Google Scholar] [CrossRef]
- Sezen, S.; Dogrul, A.; Delen, C.; Bal, S. Investigation of self-propulsion of DARPA Suboff by RANS method. Ocean Eng. 2018, 150, 258–271. [Google Scholar] [CrossRef]
- Kinaci, O.K.; Gokce, M.K.; Alkan, A.D.; Kukner, A. On self-propulsion assessment of marine vehicles. Brodogradnja 2018, 69, 29–51. [Google Scholar] [CrossRef]
- Delen, C.; Sezen, S.; Bal, S. Computational investigation of self-propulsion performance of DARPA Suboff vehicle. TAMAP J. Eng. 2017, 1–12. [Google Scholar]
- Dubbioso, G.; Broglia, R.; Zaghi, S. CFD analysis of turning abilities of a submarine model. Ocean Eng. 2017, 129, 459–479. [Google Scholar] [CrossRef]
- Carrica, P.M.; Kim, Y.; Martin, J.E. Near-surface self-propulsion of a generic submarine in calm water and waves. Ocean Eng. 2019, 183, 87–105. [Google Scholar] [CrossRef]
- Amiri, M.M.; Sphaier, S.H.; Vitola, M.A.; Esperança, P.T. URANS investigation of the interaction between the free surface and a shallowly submerged underwater vehicle at steady drift. Appl. Ocean Res. 2019, 84, 192–205. [Google Scholar] [CrossRef]
- Wang, L.; Martin, J.E.; Felli, M.; Carrica, P.M. Experiments and CFD for the propeller wake of a generic submarine operating near the surface. Ocean Eng. 2020, 206, 107304. [Google Scholar] [CrossRef]
- Posa, A.; Balaras, E. A numerical investigation of the wake of an axisymmetric body with appendages. J. Fluid Mech. 2016, 792, 470–498. [Google Scholar] [CrossRef]
- Posa, A.; Balaras, E. Large-eddy simulations of a notional submarine in towed and self-propelled configurations. Comp. Fluids 2018, 165, 116–126. [Google Scholar] [CrossRef]
- Jing, Z.; Ducoin, A. Direct numerical simulation and stability analysis of the transitional boundary layer on a marine propeller blade. Phys. Fluids 2020, 32, 124102. [Google Scholar] [CrossRef]
- Tian, C.; Jiang, F.; Petersen, B.; Andersson, H.I. Antisymmetric vortex interactions in the wake behind a step cylinder. Phys. Fluids 2017, 29, 101704. [Google Scholar] [CrossRef]
- Wang, L.; Guo, C.; Su, Y.; Wu, T. A numerical study on the correlation between the evolution of propeller trailing vortex wake and skew of propellers. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 212–224. [Google Scholar] [CrossRef]
- Vaz, G.; Toxopeus, S.L.; Holmes, S. Calculation of manoeuvring forces on submarines using two viscous-flow solvers. In Proceedings of the ASME 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010; Volume 6, pp. 621–633. [Google Scholar] [CrossRef] [Green Version]
- Phillips, A.B.; Turnock, S.R.; Furlong, M. Influence of turbulence closure models on the vortical flow field around a submarine body undergoing steady drift. J. Mar. Sci. Tech. 2010, 15, 201–217. [Google Scholar] [CrossRef] [Green Version]
- Sakthivel, R.; Vengadesan, S.; Bhattacharyya, S.K. Application of nonlinear k-ε turbulence model in flow simulation over underwater axisymmetric hull at higher angle of attack. J. Nav. Arch. Mar. Eng. 2011, 8, 149–163. [Google Scholar] [CrossRef]
- Simonsen, C.D.; Stern, F. Verification and validation of RANS maneuvering simulation of Esso Osaka: Effects of drift and rudder angle on forces and moments. Comp. Fluids 2003, 32, 1325–1356. [Google Scholar] [CrossRef]
- Zhang, Z.R. Verification and validation for RANS simulation of KCS container ship without/with propeller. J. Hydrodyn. Ser. B 2010, 22, 932–939. [Google Scholar] [CrossRef]
- Lungu, A. Numerical simulation of the resistance and self-propulsion model tests. J. Offshore Mech. Arct. Eng. 2020, 142, 021905. [Google Scholar] [CrossRef]
- Uzun, D.; Sezen, D.; Ozyurt, S.; Atlar, R.; Turan, O. A CFD study: Influence of biofouling on a full-scale submarine. App. Ocean Res. 2021, 109, 102561. [Google Scholar] [CrossRef]
- Toxopeus, S. Viscous-flow calculations for bare hull DARPA SUBOFF submarine at incidence. Int. Shipbuild. Prog. 2008, 55, 227–251. [Google Scholar] [CrossRef]
- Alin, N.; Bensow, R.; Fureby, C.; Huuva, T.; Svennberg, U. Current capabilities of RANS, DES and LES for submarine flow simulations. J. Ship. Res. 2010, 54, 184–196. [Google Scholar] [CrossRef]
- Alin, N.; Chapuis, M.; Fureby, C.; Liefvendahl, M.; Svennberg, U.; Troeng, C. A numerical study of submarine propeller-hull Interactions. In Proceedings of the 28th Symposium on Naval Hydrodynamics, Pasadena, CA, USA, 12–17 September 2010. [Google Scholar]
- Fureby, C.; Anderson, B.; Clarke, D.; Erm, L.; Henbest, S.; Giacobello, M.; Jones, D.; Nguyen, M.; Johansson, M.; Jones, M.; et al. Experimental and numerical study of a generic conventional submarine at 10° yaw. Ocean Eng. 2016, 116, 1–20. [Google Scholar] [CrossRef]
- Groves, N.C.; Huang, T.T.; Chang, M.S. Geometric Characteristics of DARPA (Defense Advanced Research Projects Agency) Suboff Models (DTRC Model Numbers 5470 and 5471); DTRC/SHD-1298-01; David Taylor Research Center: Bethesda, MD, USA, 1989. [Google Scholar]
- Menter, F.R. Zonal two-equation k-omega turbulence models for aerodynamic flows. In Proceedings of the AIAA 24th Fluid Dynamics Conference, Orlando, FL, USA, 6–9 July 1993; pp. 93–2906. [Google Scholar]
- Menter, F.R. Two-equation eddy viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1299–1310. [Google Scholar] [CrossRef] [Green Version]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 19, 339–352. [Google Scholar]
- Menter, F.R.; Kuntz, M. A Zonal SST-DES Formulation; DES Workshop: St Petersburg, FL, USA, 2003. [Google Scholar]
- Strelets, M. Detached eddy simulation of massively separated flows. In Proceedings of the 39th Aerospace sciences meeting and exhibit, Reno, NV, USA, 8–11 January 2001; p. 879. [Google Scholar] [CrossRef]
- Spalart, P.R. Detached-eddy simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modeled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Gritskevich, M.S.; Garbaruk, A.V.; Schütze, J.; Menter, F.R. Development of DDES and IDDES formulations for the K-ω shear stress transport model. Flow Turbul. Combust. 2012, 88, 431–449. [Google Scholar] [CrossRef]
- Przulj, V.; Basara, B. Bounded convection schemes for unstructured grids. In Proceedings of the 15th AIAA Computational Fluid Dynamics Conference, Anaheim, CA, USA, 11–14 June 2001. [Google Scholar]
- Leonard, B.P. A stable and accurate convective modelling procedure based on quadratic up-stream interpolation. Comp. Meth. Appl. Mech. Eng. 1979, 19, 59–98. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD, 2nd ed.; DCW Industries, Inc.: Flintridge, CA, USA, 1998. [Google Scholar]
- Pope, S. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Travin, A.; Shur, M.; Strelets, M.; Spalart, P.R. Detached-Eddy simulations past a circular cylinder. Flow Turbul. Combust. 2000, 63, 293–313. [Google Scholar] [CrossRef]
- Spalart, P.R. Strategies for turbulence modelling and simulations. Int. J. Heat Fluid Flow 2000, 21, 252–263. [Google Scholar] [CrossRef]
- NUMECA International, 2020. Documentation, Theory-guide. Laboratoire de recherche en Hydrodynamique, Energétique et Environnement Atmosphérique, CNRS-UMR 6598, Centrale Nantes, 44321 Nantes Cedex 3, France, 2020. Available online: https://portal.numeca.be/support?fromDate=01-01-2018&tem¬plateUrl=support (accessed on 1 December 2021).
- Crook, T.P. An Initial Assessment of Free Surface Effects on Submerged Bodies. Master’s Thesis, Naval Postgraduate College, Monterey, CA, USA, 1994. [Google Scholar]
- Liu, H.; Huang, T. Summary of DARPA SUBOFF experimental program data, Naval Surface Warfare Center Carderock Division Report No. CRDKNSWC/HD-1298-11, 1998. Available online: https://apps.dtic.mil/sti/pdfs/ADA359226.pdf (accessed on 1 December 2021).
- Lungu, A.; Raad, P.E.; Mori, K. Turbulent early-stage breaking wave simulation. In Proceedings of the 1997 ASME Fluids Engineering Division Summer Meeting, Vancouver, BC, Canada, 22–26 June 1997. FEDSM’97, Part 16, p. FEDSM97-3404. [Google Scholar]
- Lungu, A.; Pacuraru, F. Numerical study of the hull-propeller-rudder interaction. AIP Conf. Proc. 2009, 1168, 693–696. [Google Scholar] [CrossRef]
- Lungu, A. Numerical simulation of the free-surface turbulent flow around a VLCC ship hull. AIP Conf. Proc. 2007, 936, 647–650. [Google Scholar] [CrossRef]
- Visonneau, M.; Deng, G.B.; Guilmineau, E.; Queutey, P.; Wackers, J. Local and global assessment of the flow around the Japan bulk carrier with and without energy saving devices at model and full scale. In Proceedings of the 31st ONR Symposium on Naval Hydrodynamics, Monterey, CA, USA, 11 September 2016. [Google Scholar]
- Johnson, J.M.; Stone, P.; Yang, Z.Y. Experimental study on the DARPA Suboff in straight and yaw motions. Overall performances and LDV-based local flow features analysis. In 5907 ARCS Laboratory Report; ARCS Laboratory: Melbourne, Australia, 2015. [Google Scholar]
- Eça, L.; Hoekstra, M. A Procedure for the Estimation of the Numerical Uncertainty of CFD Calculations Based on Grid Refinement Studies. J. Comp. Phys. 2014, 262, 104–130. [Google Scholar] [CrossRef]
- ASME. Standard for Verification and Validation in Computational Fluid Dynamics and Heat Transfer; V&V 20-2009, New York; The American Society of Mechanical Engineers: New York, NY, USA, 2009. [Google Scholar]
- ITTC 7.5-03-01-01. Uncertainty Analysis in CFD Verification and Validation, Methodology and Procedures, 2021. Available online: https://www.ittc.info/media/9765/75-03-01-01.pdf (accessed on 1 December 2021).
- Ungureanu, C.; Lungu, A. Numerical simulation of the turbulent flow around a strut, mounted on a plate. AIP Conf. Proc. 2009, 1168, 689–692. [Google Scholar] [CrossRef]
- Lungu, A. A DES-based study of the flow around the self-propelled DARPA Suboff working in deep immersion and beneath the free-surface. Ocean Eng. 2022, 244, 110358. [Google Scholar] [CrossRef]
- Lungu, A. A DES-SST based assessment of hydrodynamic performances of the wetted and cavitating PPTC propeller. J. Mar. Sci. Eng. 2020, 8, 297. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).