Investigation on the Lift Force Induced by the Interceptor and Its Affecting Factors: Experimental Study with Captive Model
Abstract
:1. Introduction
2. Test Model
3. Experimental Setup
3.1. Facility
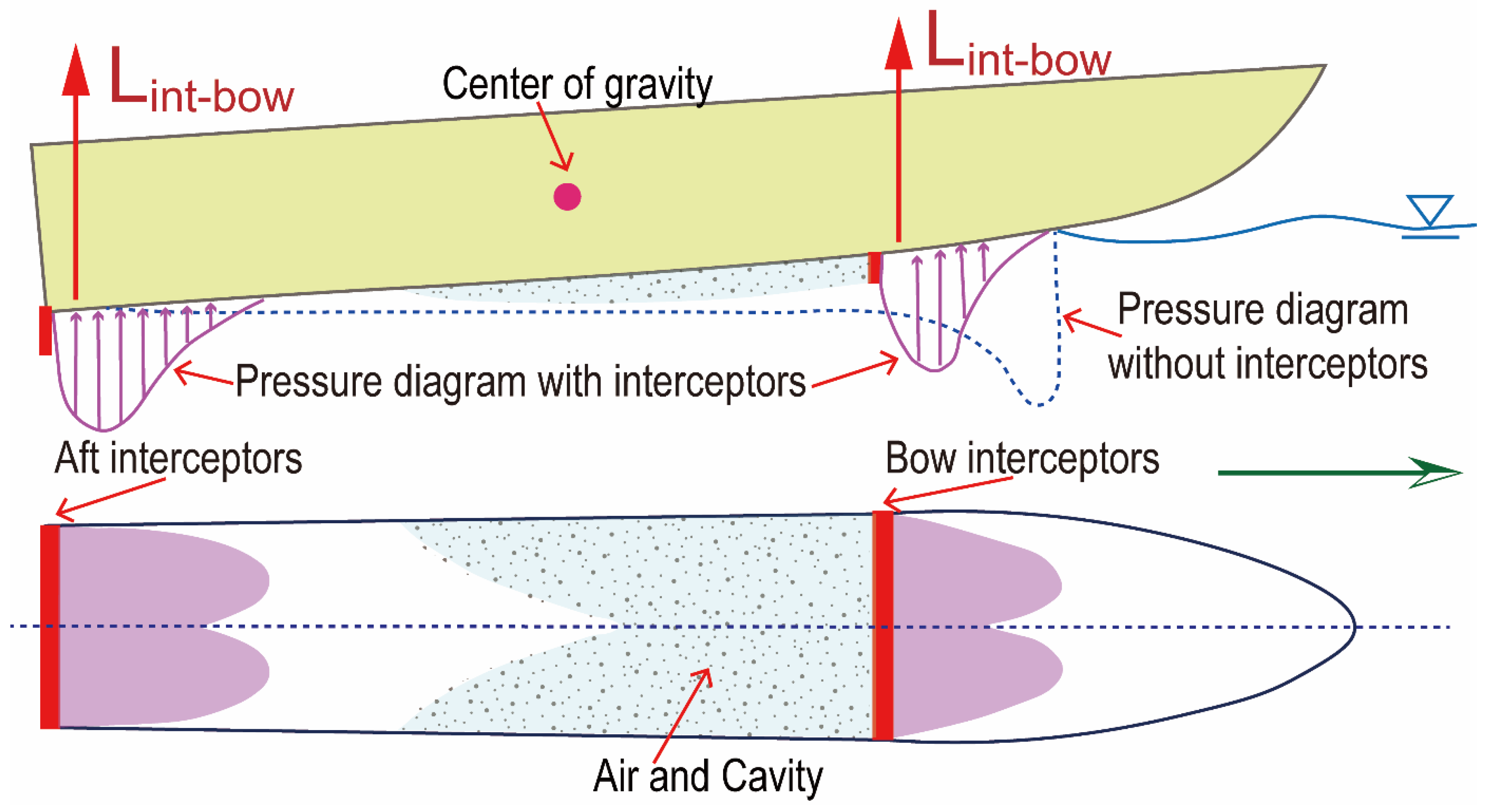
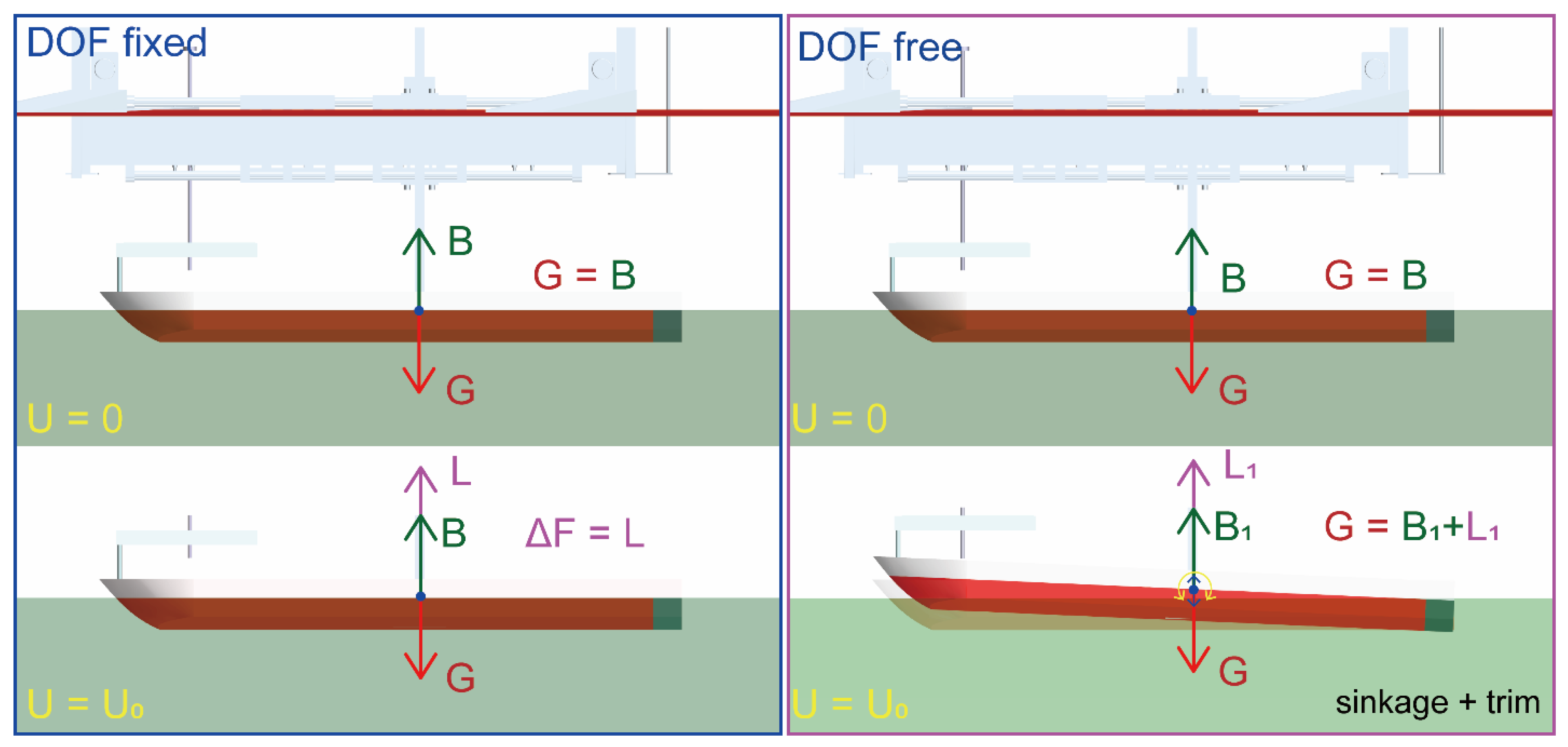
3.2. Lift Force Induced Experimental Measurement Scheme
3.3. Detailed Setup of Towing Tank Test
3.4. The Main Sources of Uncertainty in the Towing Tank Test
- (1)
- The error of the towing tank equipment condition: The stability and accuracy of the speed of the towing carriage in the towing tank is a very important factor. The maximum speed of the towing carriage is 6.5 m/s, and its global speed control tolerance is within 0.3% in this study;
- (2)
- The error of the ship model design and processing: The ship models used in this study are made of glass fiber reinforced plastic, and the surface of the hull is clean and smooth. When the model processing is completed, the processing accuracy of the model is checked using the model inspection platform. The error of the model length is less than 1.0 mm, and the error of half-width below the design waterline is less than 0.5mm, which meets the relevant requirements;
- (3)
- The error of the setup of the towing test of the lift force induced by the interceptor: (a) For model connection and installation: The ship model is connected with the center post of the motion measuring device through a connecting flange. After the model is connected, a line laser will be used for collimation correction, so the longitudinal centerline of the motion measuring device is in the same vertical plane as the centerline of the ship model. The error caused by the connection and installation is very small and can be ignored; (b) For the measurement system: The induced lift measurement system is calibrated before this experiment. Furthermore, the calibration is performed by using a standard weight as the assumed lift force induced by the interceptor and recording the output value of the force sensor. The force transducer used in this test is a three-component sensor, the scales used in the longitudinal, transverse, and vertical ranges of 60 kg, 60 kg, and 120 kg, respectively, the corresponding measurement accuracy is not greater than 0.1% full scale; (c) For the measured external environment: the change of water temperature in the towing tank directly affects the viscous force and Reynolds number of the ship model. Our test is completed in the same time period, and the temperature is collected multiple times during the test every day. The temperature difference of the test under different working conditions is within 0.1 degrees;
- (4)
- The error of the test result analysis and conversion method: The measurement results in this article are comparatively analyzed at the model scale, without real-scale extrapolation based on any assumptions. The data under different working conditions use the same conversion method, so the error in this part can be ignored.
4. Results and Analysis on the Effect of Factors
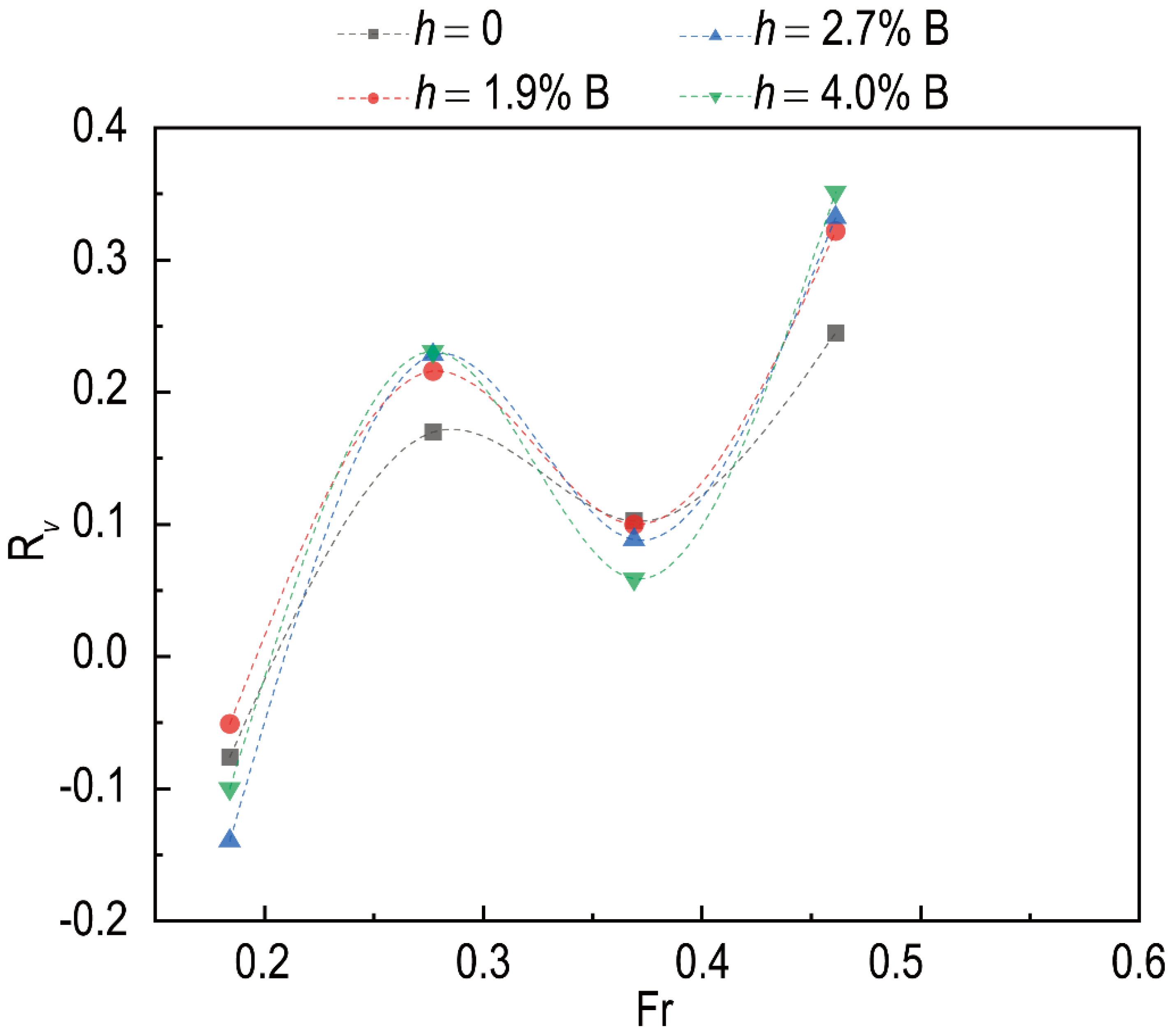
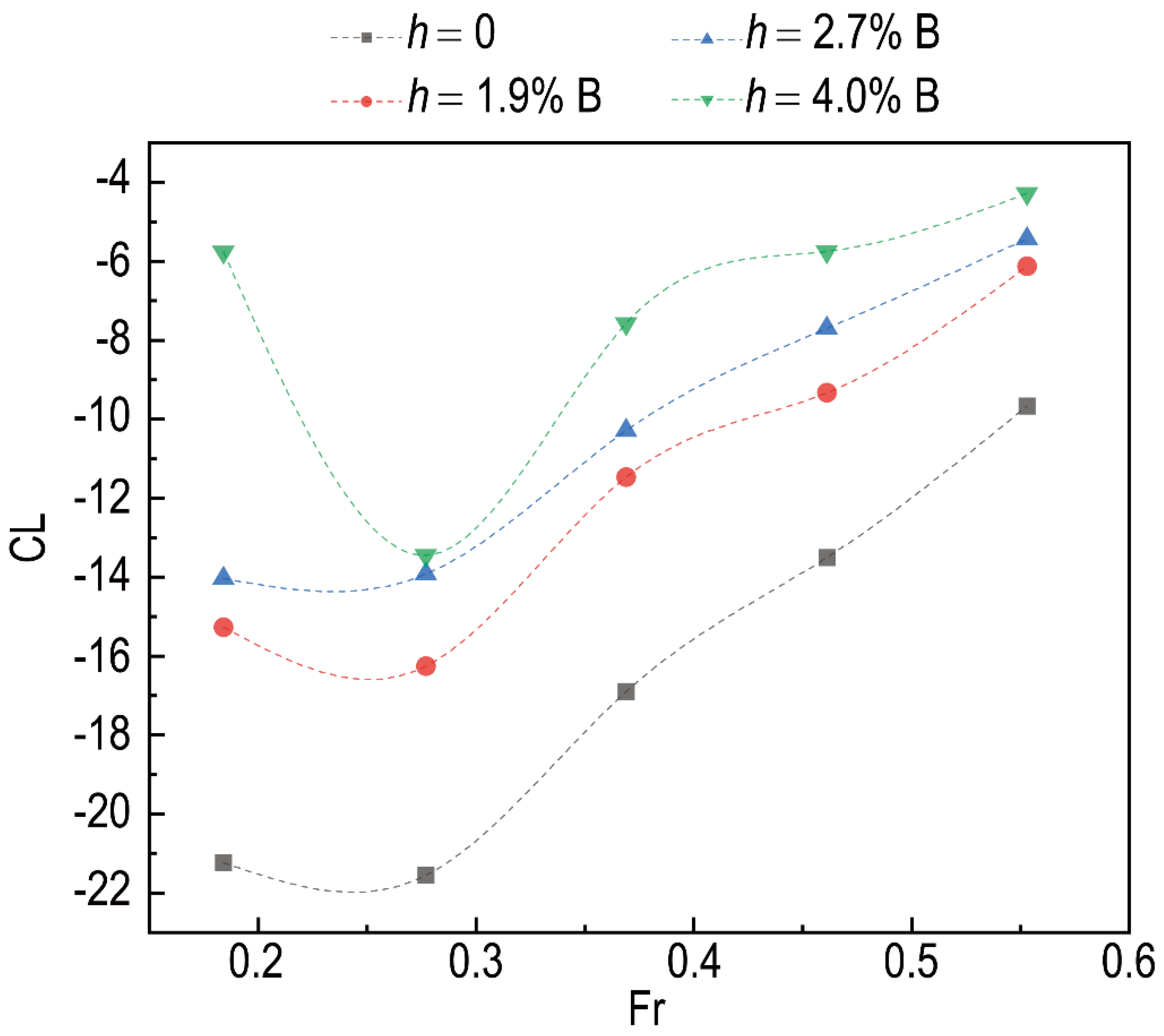
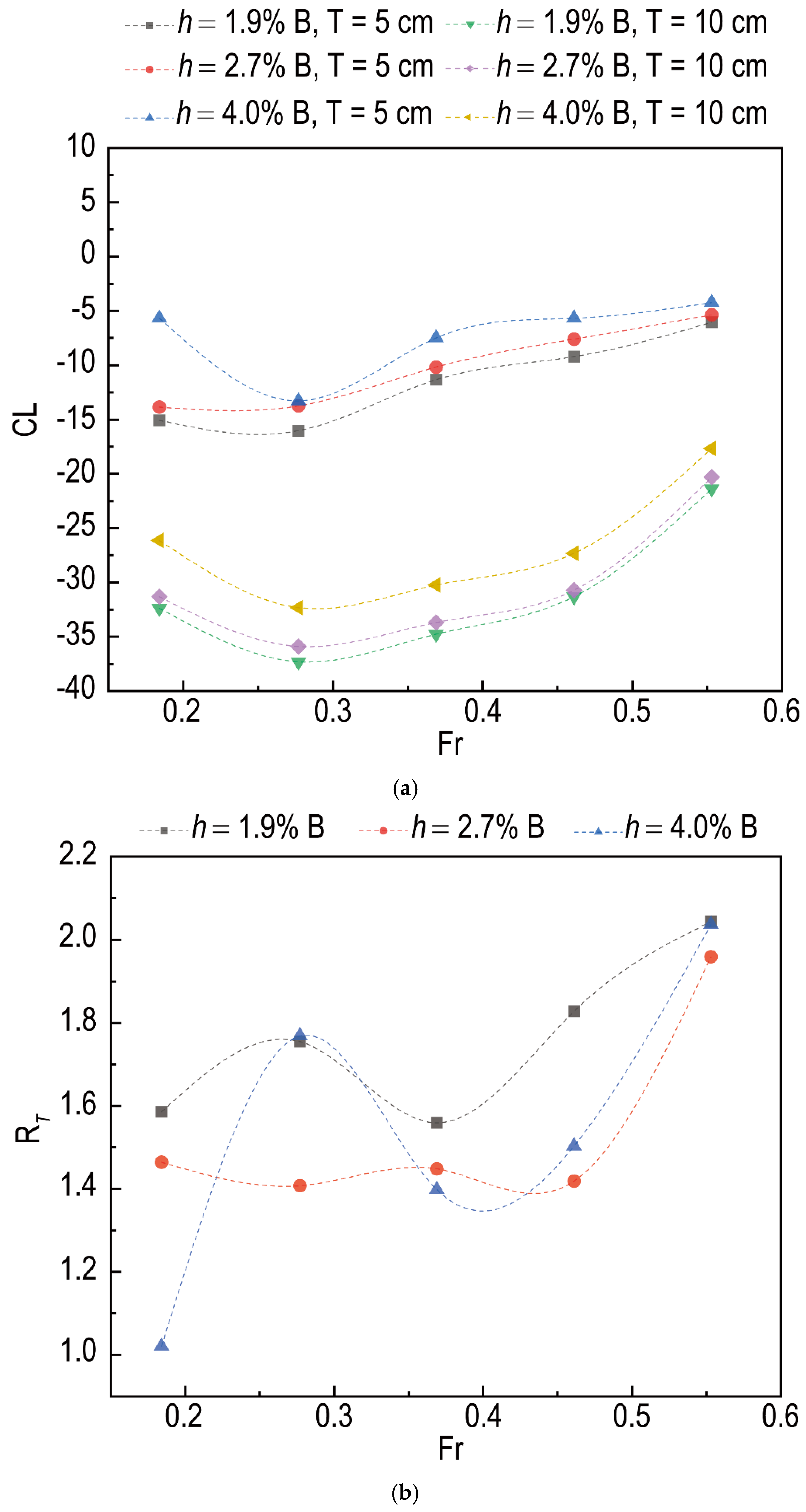
4.1. Effect of Velocity
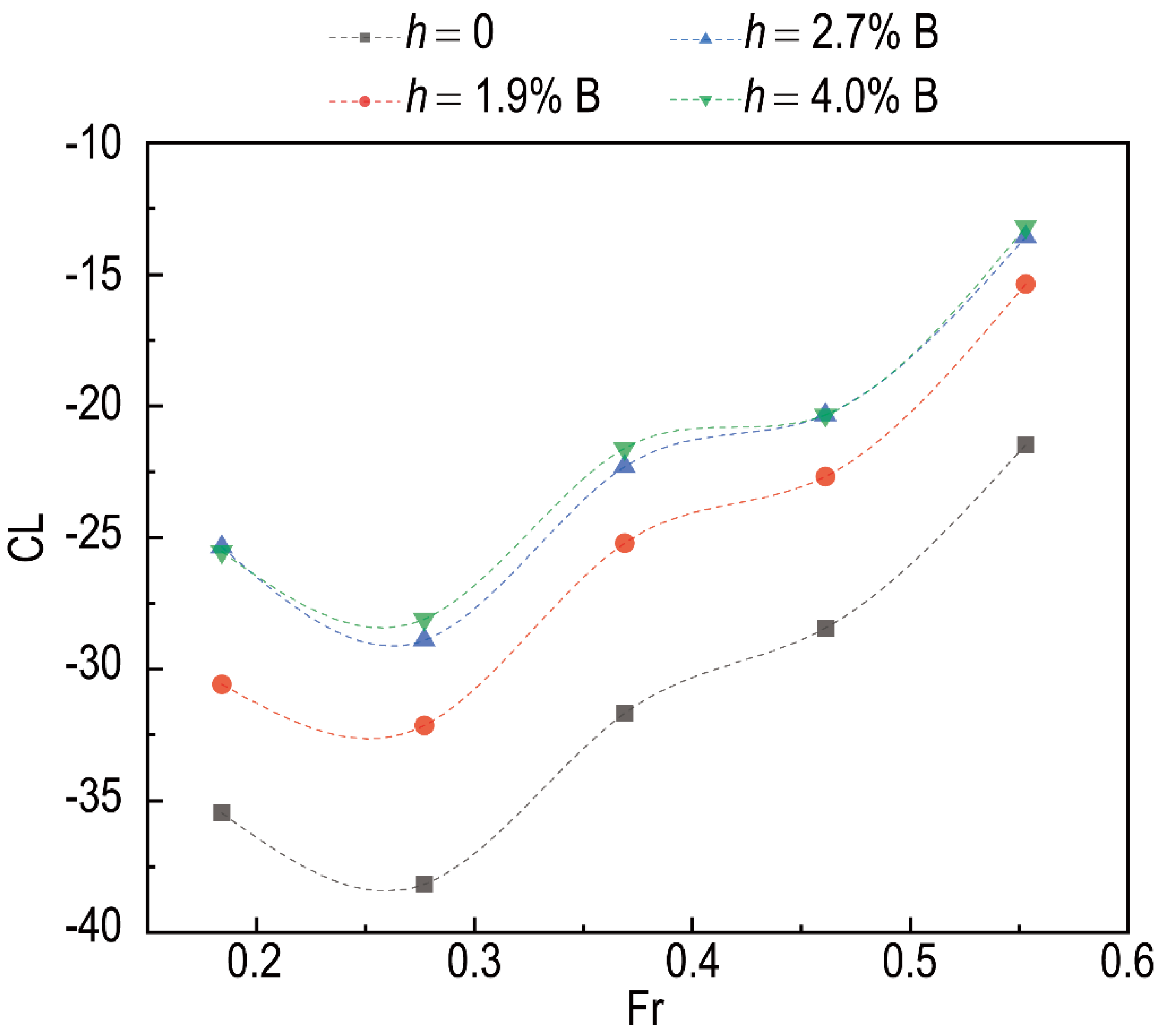
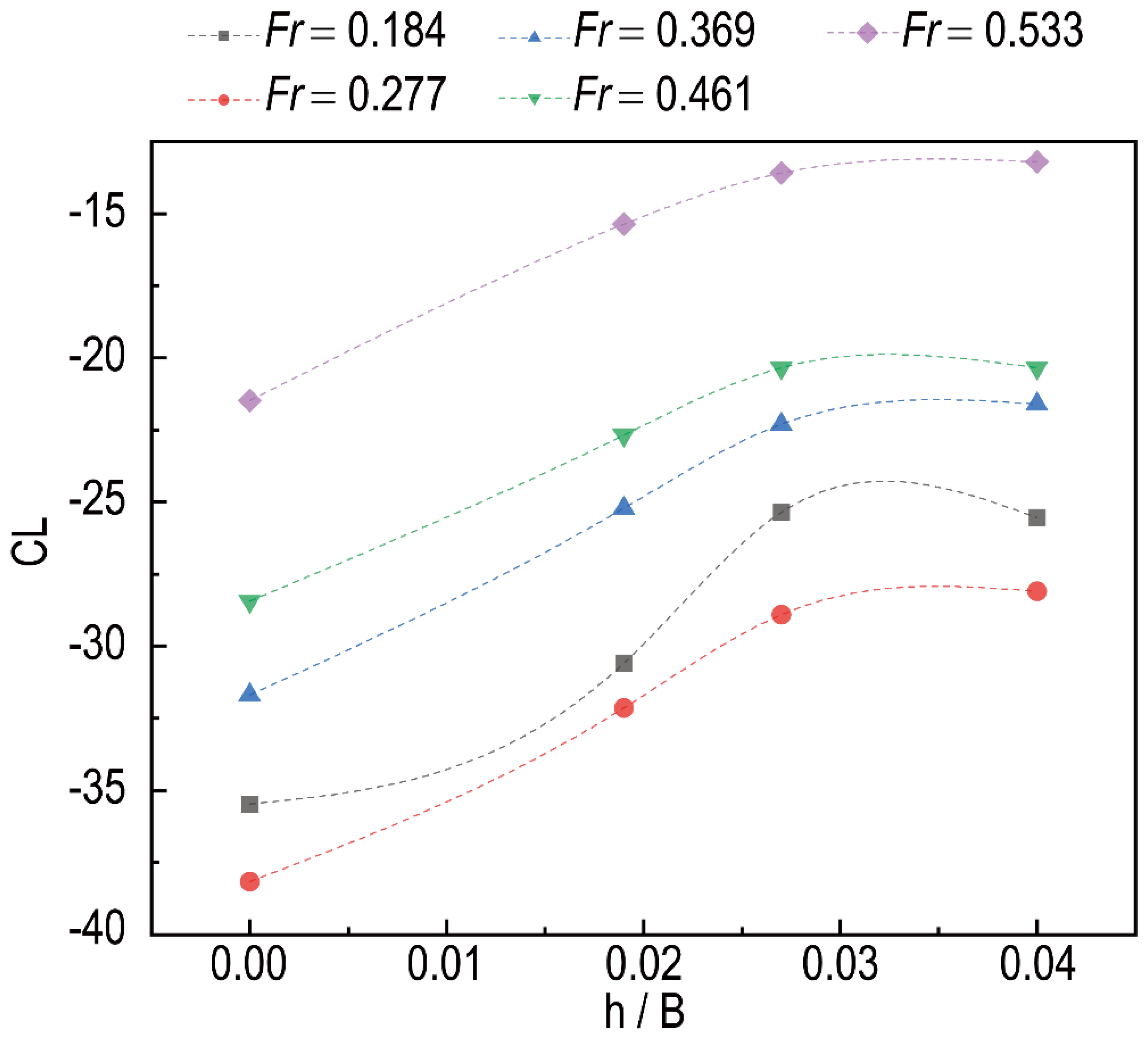
4.2. Effect of Interceptor
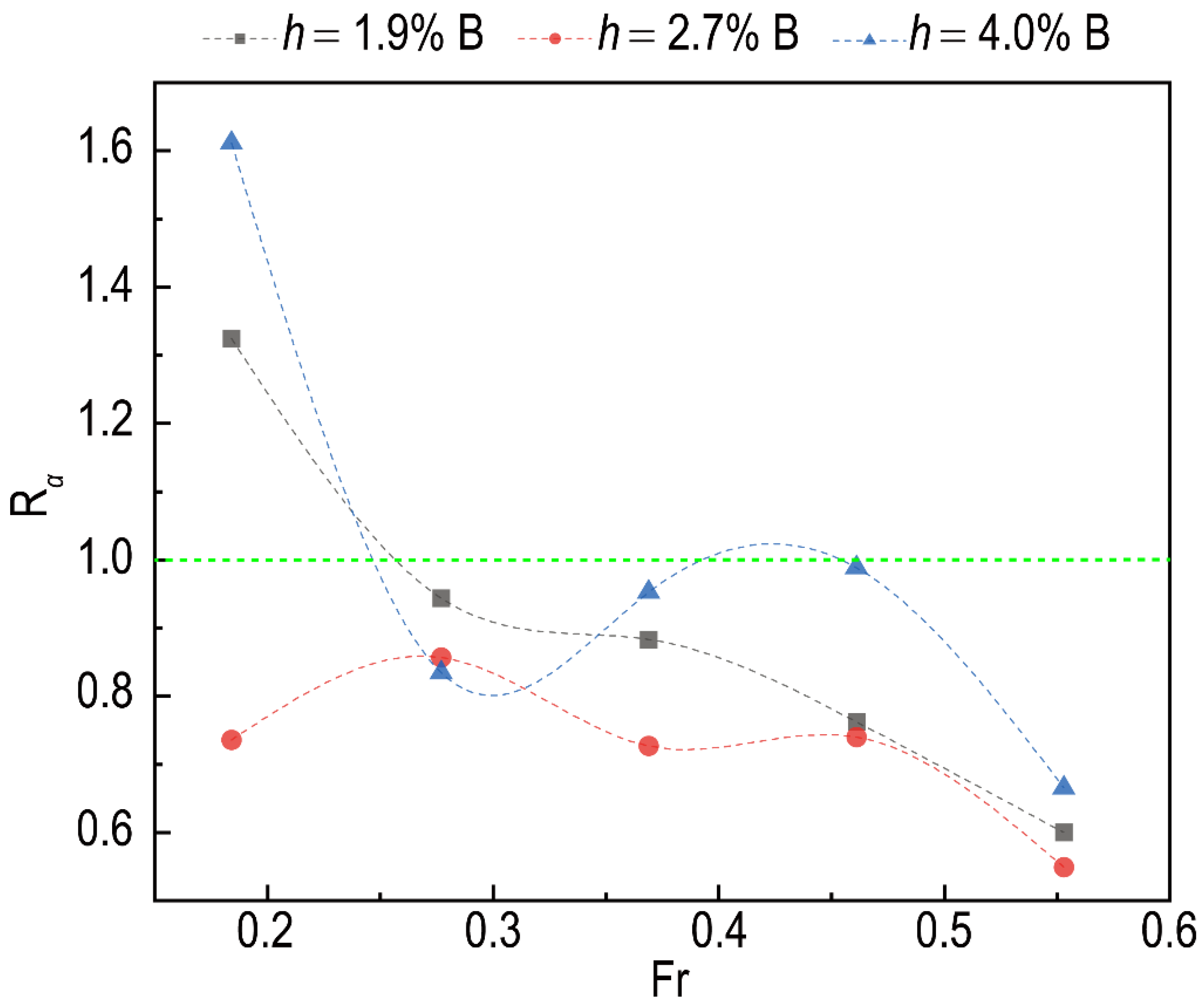
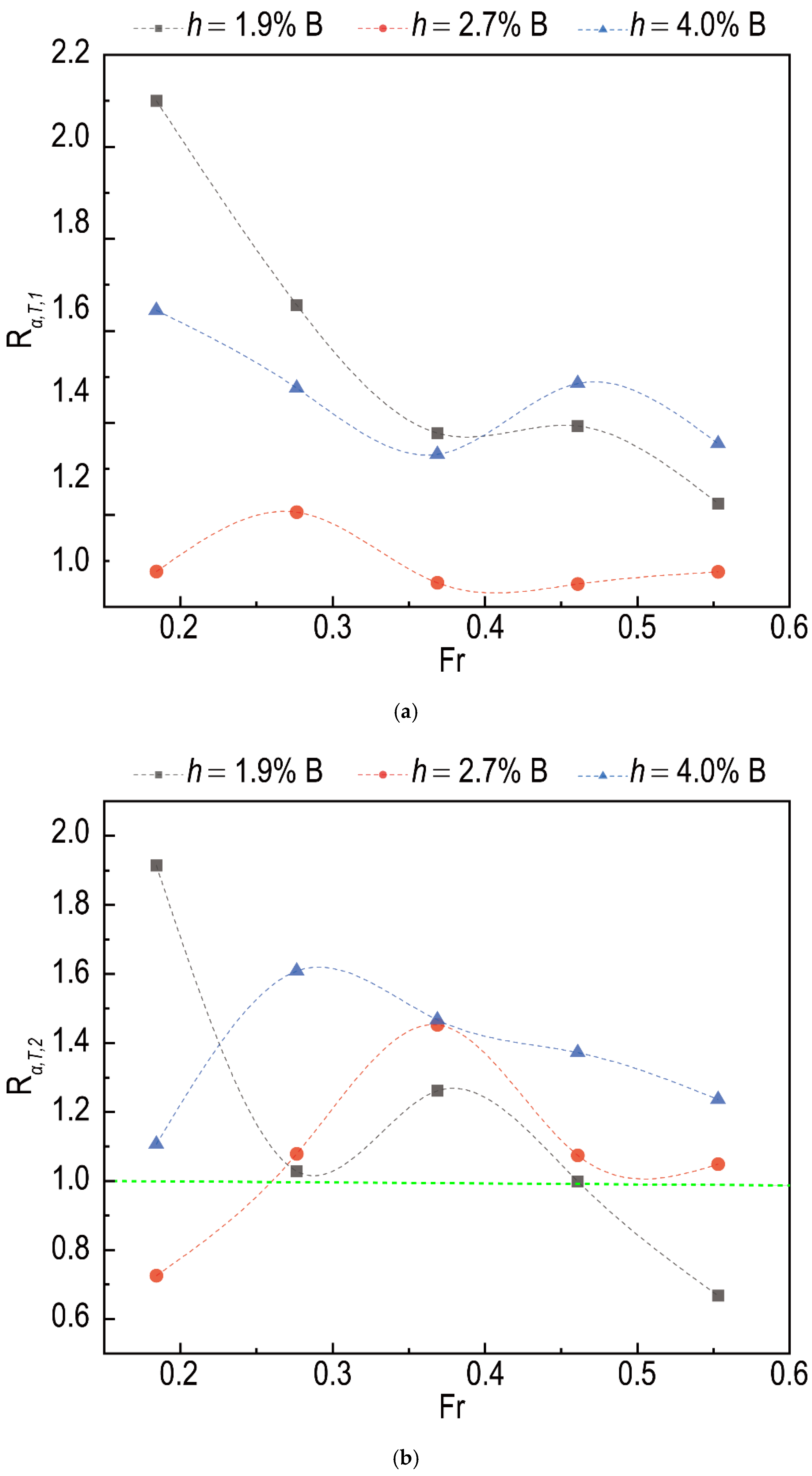
4.3. Effect of Angle
4.4. Effect of Draft
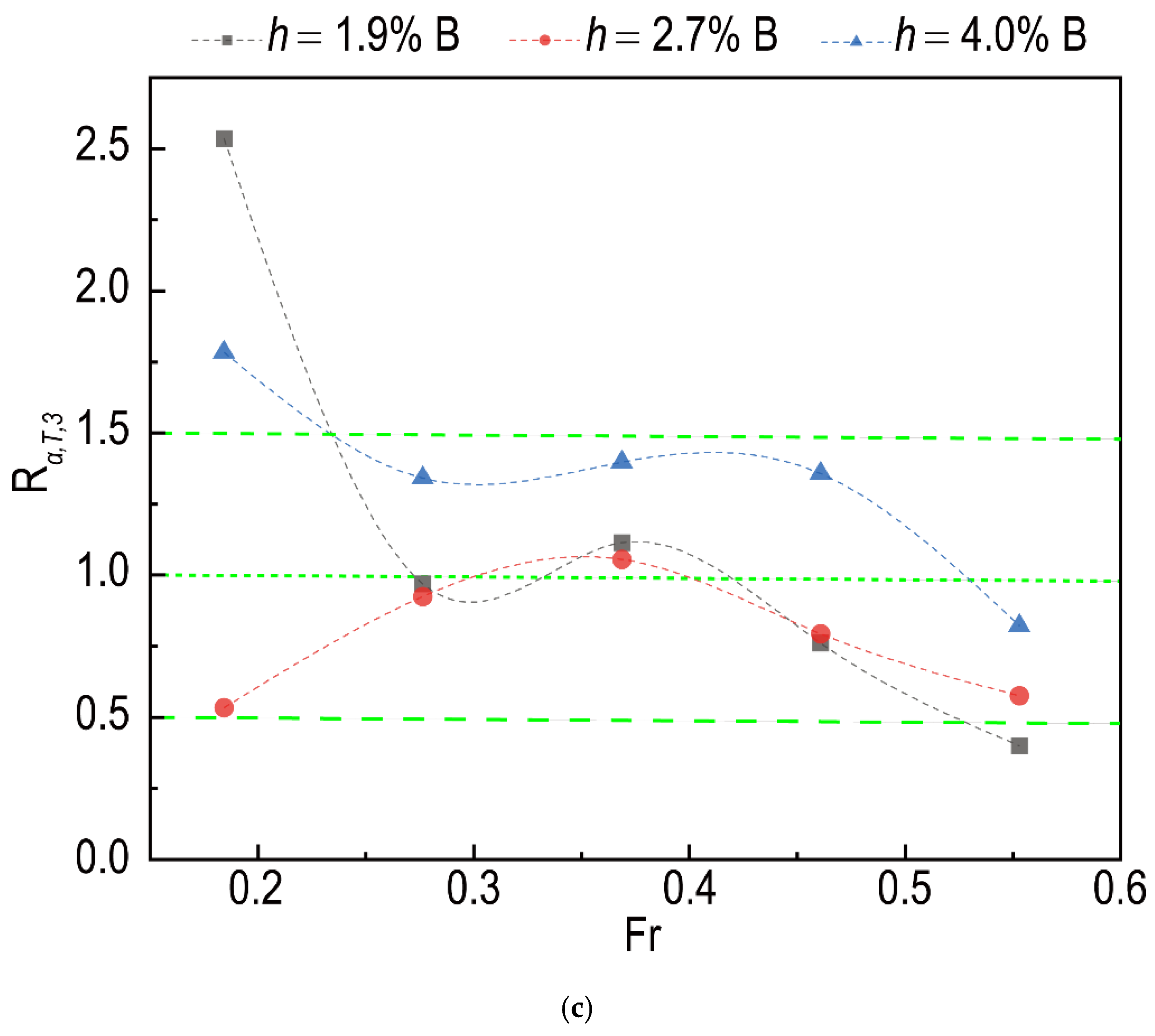
4.5. Coupling Effect of Draft and Angle
5. Conclusions
- (a)
- Velocity is the key factor dominating the effect of the interceptor. The lift coefficient of the test model with the interceptor in the present investigation is proportional to the square of Fr, but the contribution of velocity to the lift coefficient of the plate with the interceptor is changed from speed to speed;
- (b)
- The height of the interceptor is an important factor. The lift coefficient is approximately proportional to the square of h/B at high speeds, but the effect of the interceptor exits in a limited extent of its height, which is about 2.7% B (10 mm) for the present model;
- (c)
- The influence of angle and draft on the effect of the interceptor cannot be neglected for the present study. The effect of the interceptor is weakened when the angle of the plate is reduced and is enhanced when the draft is increased. The influence caused by a 100% increment in the draft for the present model is roughly equivalent to the one caused by a 22.2% reduction in the angle, and compared with the influence of the draft, the effect of angle seems greater.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zseleczky, J.; Hays, J. FFG-7 Model Powing Test With and Without a Stern Wedge; US Naval Academy Report EW-28-84; Hydromechanics Laboratory: Annapolis, MD, USA, 1984. [Google Scholar]
- Zseleczky, J.; Johnson, B. Effects of a Bow Bulb and Various Stern Wedge on the EHP of FFG-7 Class Frigates; US Naval Academy Report EW-6-84; Hydromechanics Laboratory: Annapolis, MD, USA, 1984. [Google Scholar]
- Karimi, M.H.; Seif, M.S.; Abbaspoor, M. An experimental study of interceptor’s effectiveness on hydrodynamic perfor-mance of high-speed planing crafts. Pol. Marit. Res. 2013, 20, 21–29. [Google Scholar] [CrossRef] [Green Version]
- Karimi, M.H.; Seif, M.S.; Abbaspour, M. A study on vertical motions of high-speed planing boats with automatically controlled stern interceptors in calm water and head waves. Ships Offshore Struct. 2015, 10, 335–348. [Google Scholar] [CrossRef]
- Park, J.-Y.; Choi, H.; Lee, J.; Choi, H.; Woo, J.; Kim, S.; Kim, D.J.; Kim, S.Y.; Kim, N. An experimental study on vertical motion control of a high-speed planing vessel using a controllable interceptor in waves. Ocean Eng. 2019, 173, 841–850. [Google Scholar] [CrossRef]
- Mansoori, M.; Fernandes, A.C. The interceptor hydrodynamic analysis for controlling the porpoising instability in high speed crafts. Appl. Ocean Res. 2016, 57, 40–51. [Google Scholar] [CrossRef]
- Talaat, W.M.; Hafez, K.A.; Banawan, A.A. A CFD presentation and visualization for a new model that uses interceptors to harness hydro-energy at the wash of fast boats. Ocean Eng. 2017, 130, 542–556. [Google Scholar] [CrossRef]
- Ghassemi, H.; Mansouri, M.; Zaferanlouei, S. Interceptor hydrodynamic analysis for handling trim control problems in the high-speed crafts. Proc. Inst. Mech. Eng. 2011, 225, 2597–2618. [Google Scholar] [CrossRef]
- Mansoori, M.; Fernandes, A.C. Interceptor and trim tab combination to prevent interceptor’s unfit effects. Ocean Eng. 2017, 134, 140–156. [Google Scholar] [CrossRef]
- Mansoori, M.; Fernandes, A.C. Hydrodynamics of the Interceptor Analysis Via Both Ultrareduced Model Test and Dynamic Computational Fluid Dynamics Simulation. J. Offshore Mech. Arct. Eng. 2017, 139, 021101. [Google Scholar] [CrossRef]
- Mansoori, M.; Fernandes, A.C.; Ghassemi, H. Interceptor design for optimum trim control and minimum resistance of planing boats. Appl. Ocean Res. 2017, 69, 100–115. [Google Scholar] [CrossRef]
- Guo, C.Y.; Song, K.W.; Gong, J.; Jing, T. Influence of interceptor on deep-V ship’s resistance performance. J. Harbin Eng. Univ. 2018, 39, 215–221. [Google Scholar]
- Zhu, F.; Chen, J.W.; He, S.L.; Ni, Q.J. Study on drag reduction mechanism of high speed deep-V boat with interceptor. Wuhan Ligong Daxue Xuebao/J. Wuhan Tec. Univ. 2019, 43, 1007–1011. [Google Scholar]
- Song, K.W.; Guo, C.Y.; Gong, J.; Li, P.; Wang, W. Numerical study on the effect of interceptor on the resistance and wake field of twin-screw ship. J. Shanghai Jiaotong Univ. 2019, 53, 957–964. [Google Scholar] [CrossRef]
- Shen, Y.L.; Gao, X.P.; Huo, C. Influence of interceptor on resistance performance of planning boat. Ship Sci. Technol. 2020, 42, 30–33. [Google Scholar]
- Seok, W.; Park, S.Y.; Rhee, S.H. An experimental study on the stern bottom pressure distribution of a high-speed planing vessel with and without interceptors. Int. J. Nav. Arch. Ocean Eng. 2020, 12, 691–698. [Google Scholar] [CrossRef]
- Pacuraru, F.; Presura, A.; Pacuraru, S. Experimental towing tank tests on high speed displacement ship. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Iasi, Romania, 23–27 June 2020; Volume 916, p. 012080. [Google Scholar]
- Jacobi, G.; Thill, C.H.; Veer, R.V.; Huijsmans, R.H.R. Analysis of the influence of an interceptor on the transom flow of a fast ship by pressure reconstruction from stereoscopic scanning PIV. Ocean Eng. 2019, 181, 281–292. [Google Scholar] [CrossRef]
- Song, K.-W.; Guo, C.-Y.; Wang, C.; Gong, J.; Li, P. Investigation of the influence of an interceptor on the inlet velocity distribution of a waterjet-propelled ship using SPIV technology and RANS simulation. Ships Offshore Struct. 2019, 15, 138–152. [Google Scholar] [CrossRef]
- Suneela, J.; Krishnankutty, P.; Anantha Subramanian, V.A. Numerical investigation on the hydrodynamic performance of high-speed planing hull with transom interceptor. Ships Offshore Struct. 2021, 15, S134–S142. [Google Scholar] [CrossRef]
- Luca, F.; Pensa, C. The prediction of the interceptor performances based on towing tank test data Ship-model correlation and hull form influence. In Proceedings of the IMAM 2013, 15th International Congress of the International Maritime Association of the Mediterranean (IMAM), Coruña, Spain, 14–17 October 2013. [Google Scholar]
- Sverre, S. Experimental investigation of interceptor performance. In Proceedings of the 9th International Conference on Fast Sea Trans-portation FAST2007, Shanghai, China, 23–27 September 2007. [Google Scholar]
- Srikanth, S.; Raju, D. Performance Prediction of High-Speed Planing Craft With Interceptors Using a Variation of the Savitsky Method. In Proceedings of the First Chesapeake Power Boat Symposium, Annapolis, MD, USA, 7–8 March 2008; Society of Naval Architects and Marine Engineers: Alexandria, VA, USA, 2008. [Google Scholar]
- Savitsky, D. Hydrodynamic Design of Planing Hulls. Mar. Technol. SNAME News 1964, 1, 71–95. [Google Scholar] [CrossRef]
- Luca, F.; Pensa, C.; Pranzitelli, A. Experimental and numerical investigation on interceptors’ effectiveness. In Proceedings of the 7th Conference on High Performance Marine Vehicles, Melbourne, FL, USA, 13–15 October 2010. [Google Scholar]
- Mansoori, M.; Fernandes, A.C. Hydrodynamics of the interceptor on a 2-D flat plate by CFD and experiments. J. Hydrodyn. 2015, 27, 919–933. [Google Scholar] [CrossRef]
- Zhou, G.L. Uncertainty Analysis of Ship Model Resistance Test in Towing Tank. Harbin Engineering University. 2002. Available online: http://dx.chinadoi.cn/10.7666/d.Y483205 (accessed on 15 January 2022).
- Deng, R.; Chen, S.Y.; Wu, T.C.; Luo, F.Q.; Jiang, D.P.; Li, Y.L. Investigation on the influence induced by interceptor on the viscous flow field of deep-Vee vessel. Ocean Eng. 2019, 196, 106735. [Google Scholar] [CrossRef]
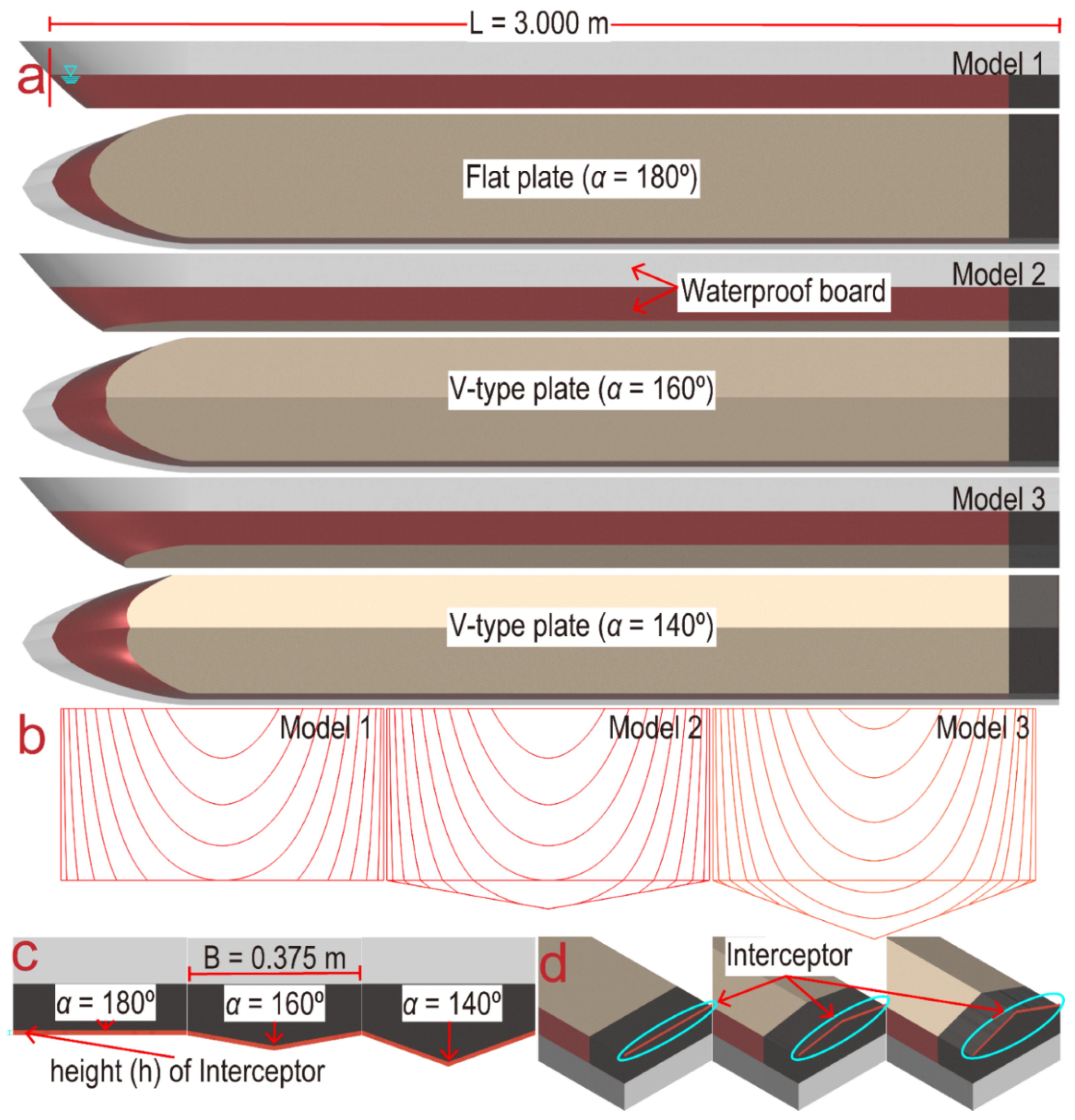




| Model | L (m) | B (m) | α (°) | h (mm) | T (cm) | V (m/s) |
|---|---|---|---|---|---|---|
| 1 | 3.0 | 0.375 | 180 | 0, 7.0, 10.0, 15.0 | 5.0 | 1.0, 1.5, 2.0, 2.5, 3.0 |
| 2 | 3.0 | 0.375 | 160 | 0, 7.0, 10.0, 15.0 | 5.0, 10.0 | 1.0, 1.5, 2.0, 2.5, 3.0 |
| 3 | 3.0 | 0.375 | 140 | 0, 7.0, 10.0, 15.0 | 10.0 | 1.0, 1.5, 2.0, 2.5, 3.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, R.; Zhang, Z.; Luo, F.; Sun, P.; Wu, T. Investigation on the Lift Force Induced by the Interceptor and Its Affecting Factors: Experimental Study with Captive Model. J. Mar. Sci. Eng. 2022, 10, 211. https://doi.org/10.3390/jmse10020211
Deng R, Zhang Z, Luo F, Sun P, Wu T. Investigation on the Lift Force Induced by the Interceptor and Its Affecting Factors: Experimental Study with Captive Model. Journal of Marine Science and Engineering. 2022; 10(2):211. https://doi.org/10.3390/jmse10020211
Chicago/Turabian StyleDeng, Rui, Zezhen Zhang, Fuqiang Luo, Pengnan Sun, and Tiecheng Wu. 2022. "Investigation on the Lift Force Induced by the Interceptor and Its Affecting Factors: Experimental Study with Captive Model" Journal of Marine Science and Engineering 10, no. 2: 211. https://doi.org/10.3390/jmse10020211
APA StyleDeng, R., Zhang, Z., Luo, F., Sun, P., & Wu, T. (2022). Investigation on the Lift Force Induced by the Interceptor and Its Affecting Factors: Experimental Study with Captive Model. Journal of Marine Science and Engineering, 10(2), 211. https://doi.org/10.3390/jmse10020211








