Acoustic Wave Propagation in a Borehole with a Gas Hydrate-Bearing Sediment
Abstract
:1. Introduction
2. Carcione–Leclaire Three-Phase Theory
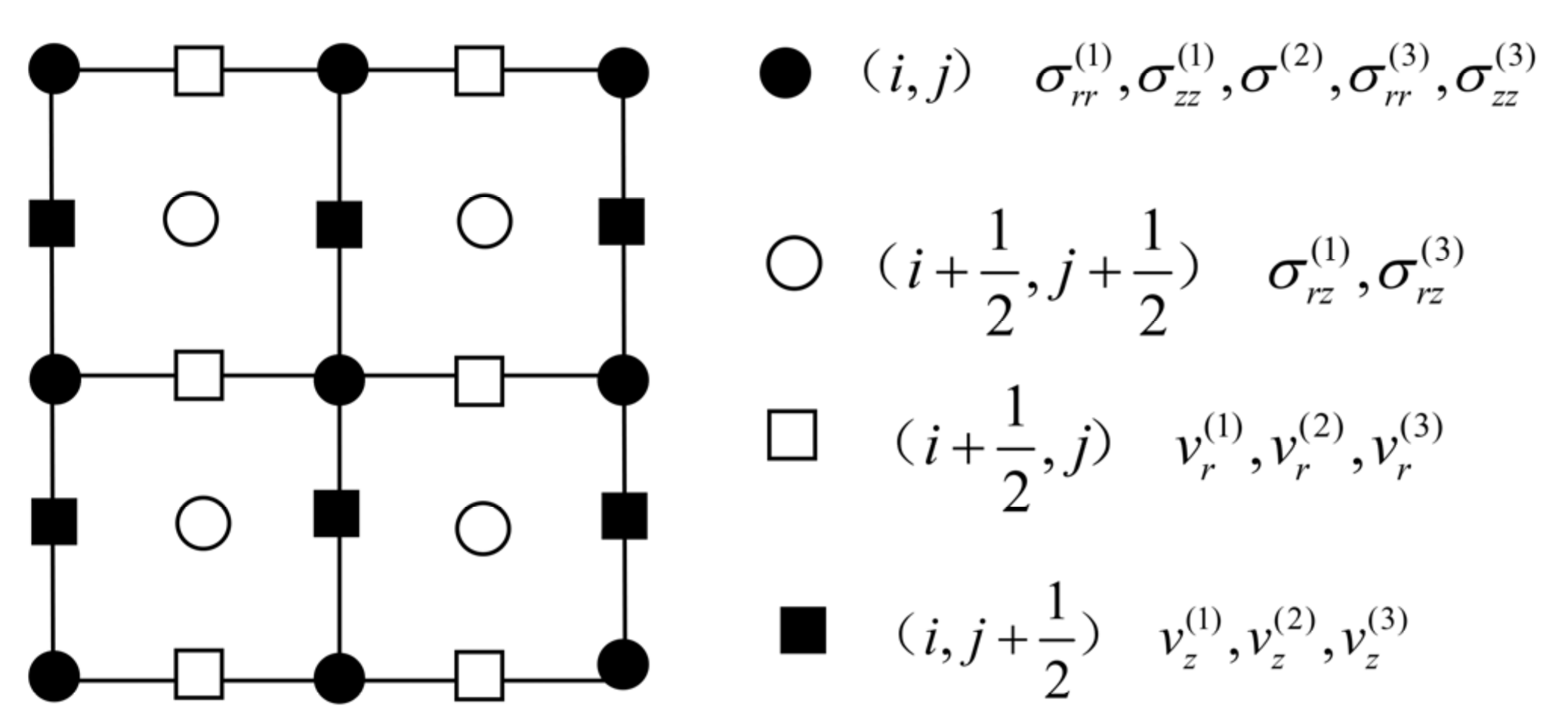
3. Finite Difference Scheme
3.1. Discretization of Equations in the Carcione–Leclaire Three-Phase Theory
3.2. Discretization of the Equations in the Borehole and Borehole Wall
4. RAI Algorithm
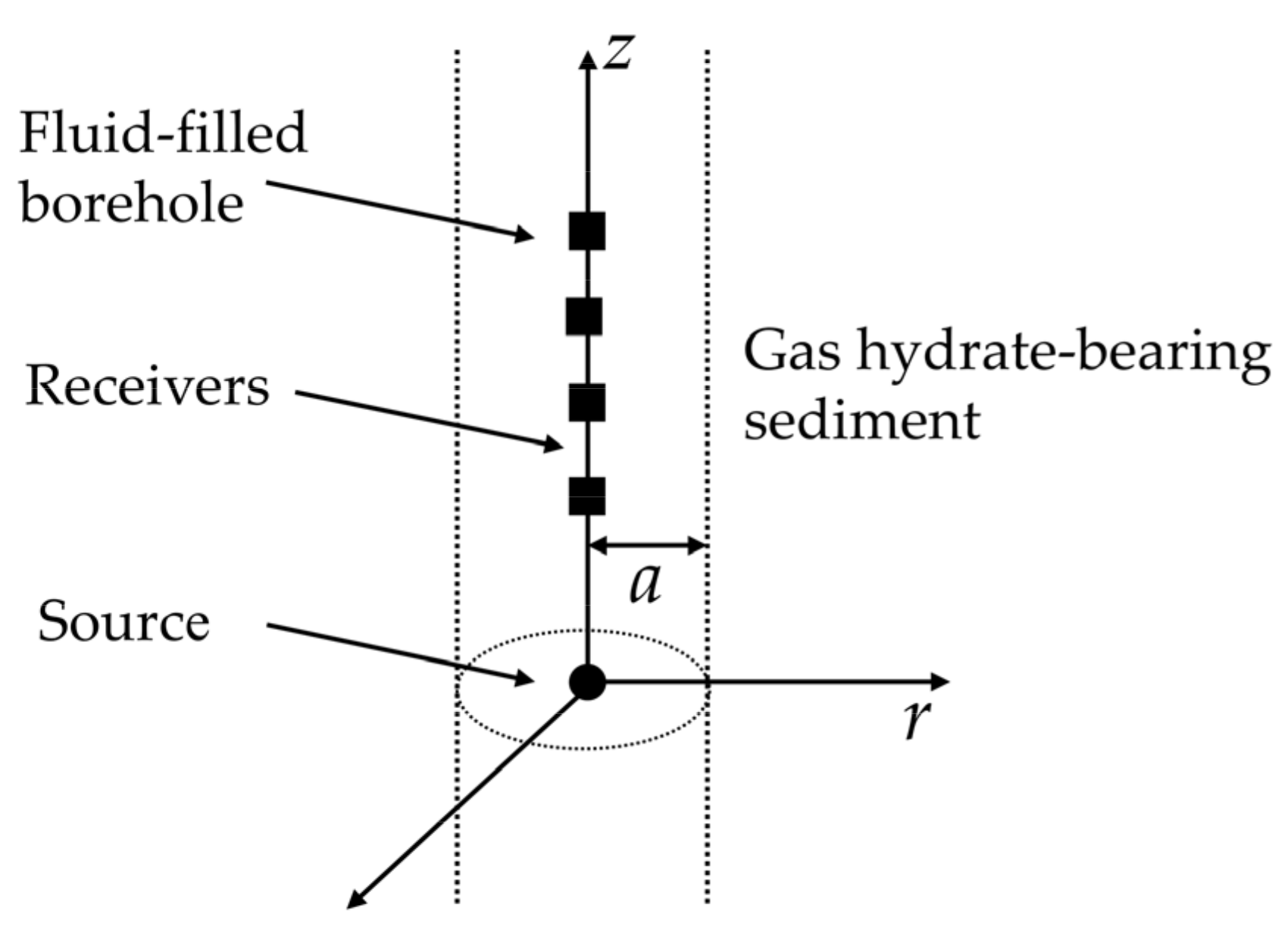
5. Numerical Modeling
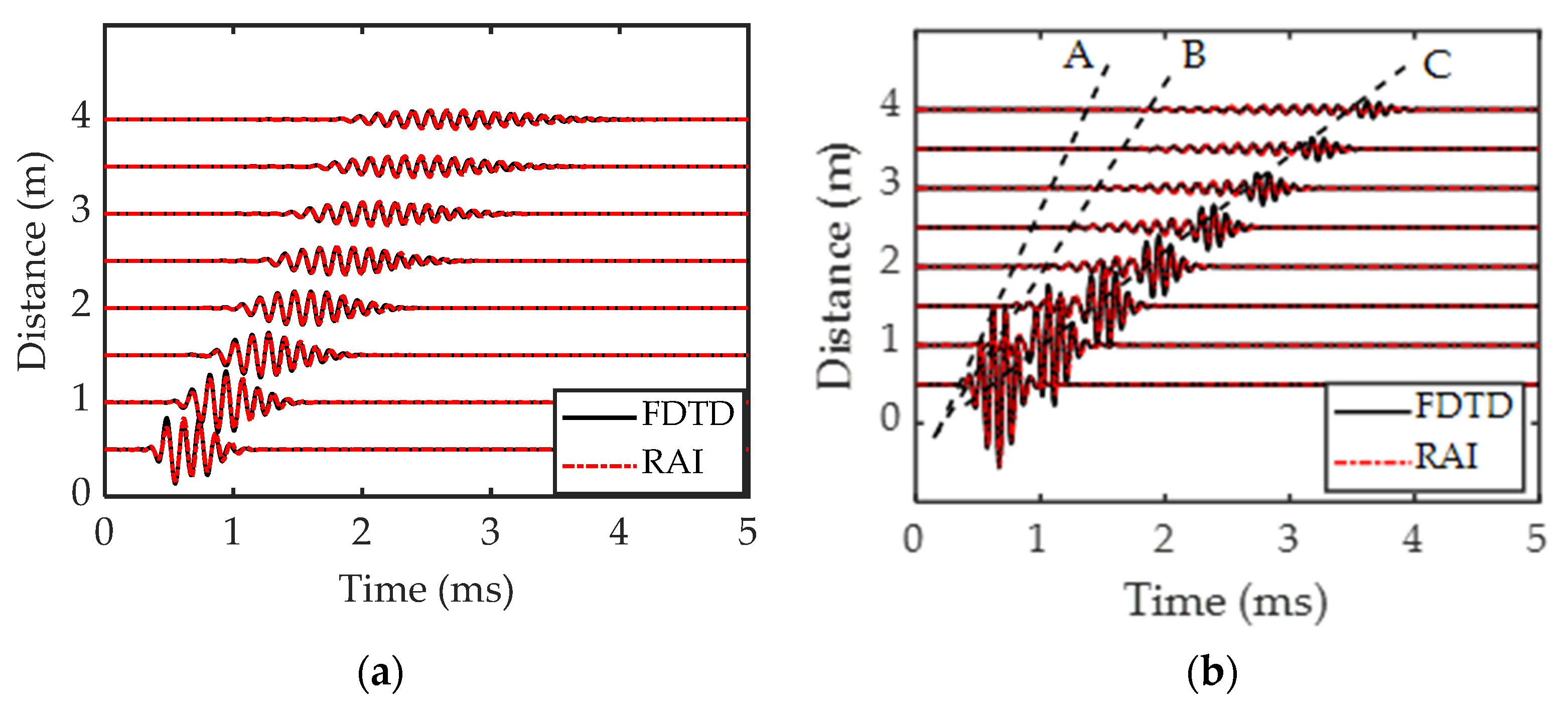
5.1. Homogeneous Three-Phase Porous Media
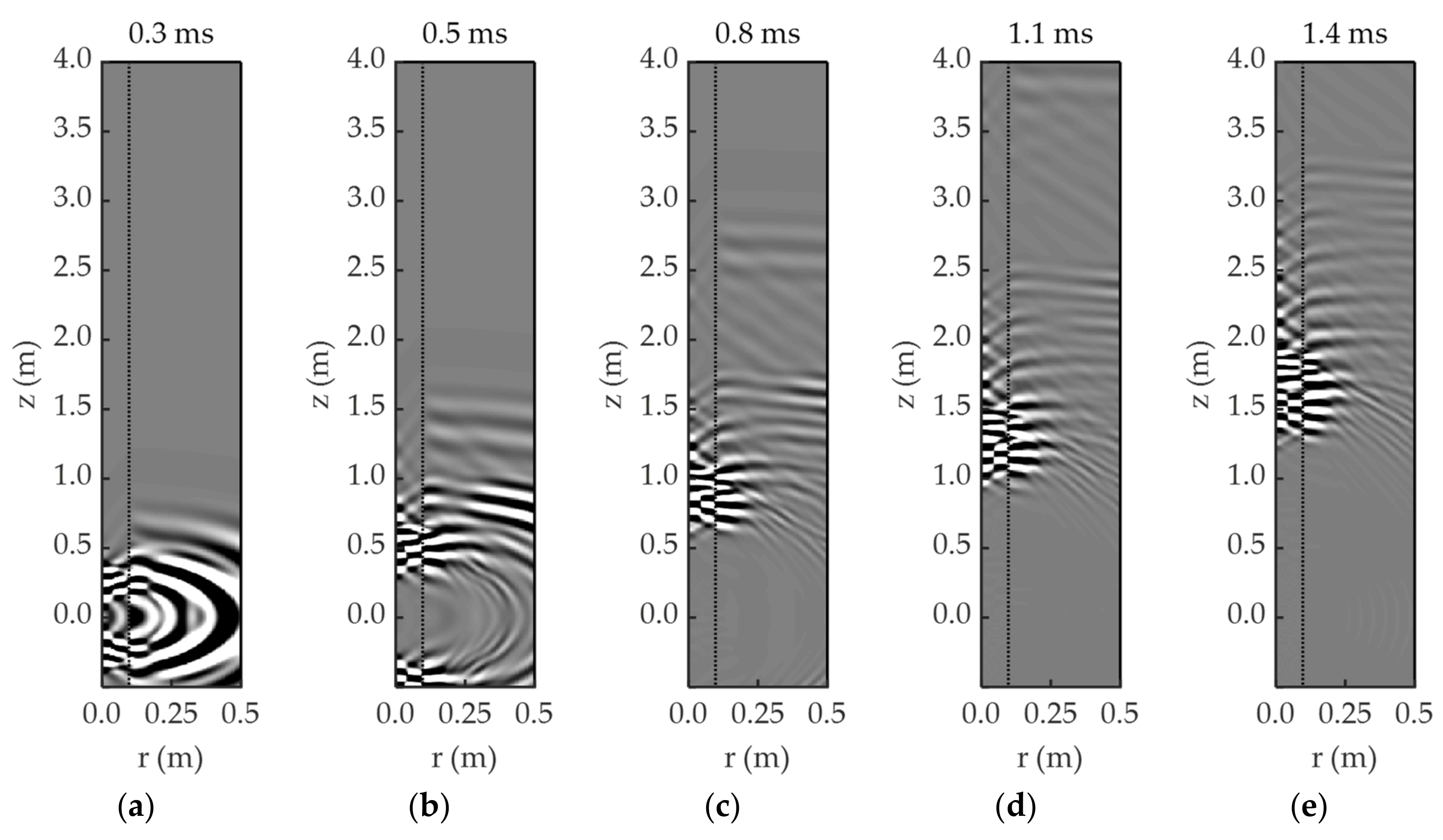
5.2. Horizontally Stratified Three-Phase Porous Medium
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
List of Symbols
| friction coefficient between the solid grain frame and pore fluid | |
| friction coefficient between the solid grain frame and gas hydrate | |
| friction coefficient between the pore fluid and gas hydrate | |
| volume fraction of solid grain | |
| volume fraction of pore fluid | |
| volume fraction of gas hydrate | |
| solid grain density | |
| fluid density | |
| gas hydrate density | |
| permeability of solid-grain frame | |
| permeability of gas–hydrate frame | |
| solid grain bulk modulus | |
| fluid bulk modulus | |
| gas hydrate bulk modulus | |
| solid grain shear modulus | |
| gas hydrate shear modulus | |
| tortuosity for fluid flowing through the solid grain frame | |
| tortuosity for fluid flowing through the gas hydrate | |
| tortuosity for solid grain flowing through the gas hydrate | |
| tortuosity for gas hydrate flowing through the solid grain | |
| average bulk modulus | |
| average shear modulus | |
| and | consolidation coefficient for the solid |
| and | consolidation coefficient for the solid |
Appendix A
References
- Ruppel, C. Tapping methane hydrates for unconventional natural gas. Elements 2007, 3, 193–199. [Google Scholar] [CrossRef]
- Boswell, R. Is gas hydrate energy within reach. Science 2009, 325, 957–958. [Google Scholar] [CrossRef] [PubMed]
- Chong, Z.R.; Yang, S.H.B.; Babu, P.; Linga, P.; Li, X.S. Review of natural gas hydrates as an energy resource: Prospects and challenges. Appl. Energy 2016, 162, 1633–1652. [Google Scholar] [CrossRef]
- Sadeq, D.; Alef, K.; Iglauer, S.; Lebedev, M.; Barifcani, A. Compressional wave velocity of hydrate-bearing Bernheimer sediments with varying pore fillings. Int. J. Hydrogen Energy 2018, 43, 23193–23200. [Google Scholar] [CrossRef]
- Liu, T.; Liu, X.; Zhu, T. Joint analysis of P-wave velocity and resistivity for morphology identification and quantification of gas hydrate. Mar. Pet. Geol. 2019, 112, 104036–104048. [Google Scholar] [CrossRef]
- Yuan, Q.M.; Kong, L.; Xu, R.; Zhao, Y.P. A state-dependent constitutive model for gas hydrate-bearing sediments considering cementing effect. J. Mar. Sci. Eng. 2020, 8, 621. [Google Scholar] [CrossRef]
- Mahabadi, N.; Dai, S.; Seol, Y.; Jang, J. Impact of hydrate saturation on water permeability in hydrate-bearing sediments. J. Pet. Sci. Eng. 2019, 174, 696–703. [Google Scholar] [CrossRef]
- Lee, M.W.; Waite, W.F. Estimating pore-space gas hydrate saturations from well log acoustic data. Geochem. Geophys. Geosyst. 2008, 9, Q07008. [Google Scholar] [CrossRef] [Green Version]
- Ding, J.P.; Cheng, Y.F.; Deng, F.C.; Yang, C.L.; Sun, H.; Li, Q.C.; Song, B.G. Experimental study on dynamic acoustic characteristics of natural gas hydrate sediments at different depths. Int. J. Hydrogen Energy 2020, 45, 26877–26889. [Google Scholar] [CrossRef]
- Leclaire, P.; Cohen-Tenooudji, F.; Puente, J. Extension of Biot’s theory of wave propagation to frozen porous media. J. Acoust. Soc. Am. 1994, 96, 3753–3768. [Google Scholar] [CrossRef] [Green Version]
- Carcione, J.M.; Seriani, G. Wave simulation in frozen porous media. J. Comput. Phys. 2001, 170, 676–695. [Google Scholar] [CrossRef] [Green Version]
- Malinverno, A.; Kastner, M.; Torres, M.E.; Wortmann, U.G. Gas hydrate occurrence from pore fluid chlorinity and downhole logs in a transect across the northern Cascadia margin (Integrated Ocean Drilling Program Expedition 311). J. Geophys. Res. Solid Earth 2008, 113, B08103. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, G.S.; Ning, F.L.; Yu, Y.B.; Zhang, L.; Tu, Y.Z. Well logging in gas hydrate-bearing sediment: A review. Adv. Mater. Res. 2012, 524–527, 1660–1670. [Google Scholar] [CrossRef]
- Carcione, J.M.; Gei, D. Gas-hydrate concentration estimated from P- and S-wave velocities at the Mallik 2L-38 research well, Mackenzie Delta. J. Appl. Geophys. 2014, 56, 73–78. [Google Scholar] [CrossRef]
- Yan, C.L.; Cheng, Y.F.; Li, M.L.; Han, Z.Y.; Zhang, H.W.; Li, Q.C.; Teng, F.; Ding, J.P. Mechanical experiments and constitutive model of natural gas hydrate reservoirs. Int. J. Hydrogen Energy 2017, 42, 19810–19818. [Google Scholar] [CrossRef]
- Bei, K.Q.; Xu, T.F.; Shang, S.H.; Wei, Z.L.; Yuan, Y.L.; Tian, H.L. Numerical modeling of gas migration and hydrate formation in heterogeneousmarine sediments. J. Mar. Sci. Eng. 2019, 7, 348. [Google Scholar] [CrossRef] [Green Version]
- Nair, V.C.; Prasad, S.K.; Sangwai, J.S. Characterization and Rheology of Krishna-Godavari basin Sediments. Mar. Pet. Geol. 2019, 110, 275–286. [Google Scholar] [CrossRef]
- Kumari, A.; Balomajumder, C.; Arora, A.; Dixit, G.; Gomari, S.R. Physio-Chemical and Mineralogical Characteristics of Gas Hydrate-Bearing Sediments of the Kerala-Konkan, Krishna-Godavari, and Mahanadi Basins. J. Mar. Sci. Eng. 2021, 9, 808. [Google Scholar] [CrossRef]
- Rosenbaum, J.H. Synthetic microseismograms: Logging in porous formations. Geophysics 1974, 39, 14–32. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid, I-low frequency range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid, II-higher-frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Biot, M.A.; Willis, D.G. The elastic coefficients of the theory of consolidation. J. Appl. Mech. 1957, 24, 594–601. [Google Scholar] [CrossRef]
- Biot, M.A. Mechanics of deformation and acoustic propagation in porous media. J. Appl. Phys. 1962, 33, 1482–1498. [Google Scholar] [CrossRef]
- Biot, M.A. Generalized theory of acoustic propagation in porous dissipative media. J. Acoust. Soc. Am. 1962, 34, 1254–1264. [Google Scholar] [CrossRef]
- Wang, K.X.; Dong, Q.D. Theoretical analysis and calculation of sound field in an oil well surrounded by a permeable formation. Acta Pet. Sin. 1986, 7, 59–69. [Google Scholar] [CrossRef]
- Wang, K.X.; White, J.E.; Wu, X.Y. P-wave coupling to hole in Biot solid. Acta Geophys. Sin. 1996, 39, 103–113. [Google Scholar]
- Schmitt, D.P. Effects of radial layering when logging in saturated porous formations. J. Acoust. Soc. Am. 1988, 84, 2200–2214. [Google Scholar] [CrossRef]
- He, X. Mode Waves in a Fluid-Filled Borehole Embedded in a Porous Formation. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2006. [Google Scholar]
- Xu, N. Simulation of Acoustic Fields and Inversion of Permeability from Attenuation of Stoneley Waves in Permeable Borehole. Master’s Thesis, Jilin University, Jilin, China, 2011. [Google Scholar]
- Wang, S.L. Study on Permeability Inversion by Using Dipole Acoustic Logging Data. Master’s Thesis, School of Geosciences China University of Petroleum (EastChina), Qingdao, China, 2011. [Google Scholar]
- Xu, X.K.; Chen, X.L.; Fan, Y.R.; Li, X.; Liu, M.J.; Hu, H.C. Influence factors of Stoneley wave and permeability inversion of formation. J. China Univ. Pet. 2012, 36, 97–104. [Google Scholar] [CrossRef]
- Liu, X.E.; Sun, X.F. On inversion method of the flexural wave permeability. Well Logging Technol. 2014, 38, 674–677. [Google Scholar]
- Xu, X.K.; Fan, Y.R.; Zhai, Y.; Wang, S.L.; Liu, M.J. Influence factors analysis of flexural wave permeability inversion in low porosity and low permeability reservior. Well Logging Technol. 2017, 41, 400–404. [Google Scholar]
- Zhang, M.Y. Study on the Influence of Viscous Pore Fluid Stress on Body Waves in Porous Media and Borehole Waves. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2020. [Google Scholar]
- Kristek, J.; Moczo, P.; Chaljub, E.; Kristekova, M. An orthorhombic representation of a heterogeneous medium for the finite-difference modelling of seismic wave propagation. Geophys. J. Int. 2017, 208, 1250–1264. [Google Scholar] [CrossRef]
- Guan, W.; Hu, H.; He, X. Finite-difference modeling of the monopole acoustic logs in a horizontally stratified porous formation. J. Acoust. Soc. Am. 2009, 125, 1942–1950. [Google Scholar] [CrossRef] [PubMed]
- Guan, W.; Hu, H. The parameter averaging technique in finite-difference modeling of elastic waves in combined structures with solid, fluid and porous subregions. Commun. Comput. Phys. 2011, 10, 695–715. [Google Scholar] [CrossRef]
- Wang, T.; Tang, X.M. Finite-difference modeling of elastic wave propagation: A nonsplitting perfectly matched layer approach. Geophysics 2003, 68, 1749–1755. [Google Scholar] [CrossRef]
- Yan, S.G.; Xie, F.L.; Gong, D.; Zhang, C.G.; Zhang, B.X. Borehole acoustic fields in porous formation with tilted thin fracture. Chin. J. Geophys. 2015, 58, 307–313. [Google Scholar] [CrossRef]
- Ou, W.; Wang, Z. Simulation of Stoneley wave reflection from porous formation in borehole using FDTD method. Geophys. J. Int. 2019, 217, 2081–2096. [Google Scholar] [CrossRef]
- Carcione, J.M.; Quiroga-Goode, G. Some aspects of the physics and numerical modeling of Biot compressional waves. J. Comput. Acoust. 1995, 3, 261–272. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, X.; Chen, H. A method of solving the stiffness problem in Biot’s poroelastic equations using a staggered high-order finite-difference. Chin. Phys. 2006, 15, 2819–2827. [Google Scholar] [CrossRef]
- Lin, L.; Zhang, X.; Wang, X. Theoretical analysis and numerical simulation of acoustic waves in gas hydrate-bearing sediments. Chin. Phys. B 2021, 30, 024301. [Google Scholar] [CrossRef]
- Zhang, R.; Li, H.; Wen, P.; Zhang, B. The velocity dispersion and attenuation of marine hydrate-bearing sediments. Chin. J. Geophys. 2016, 59, 539–550. [Google Scholar]
- Lin, L.; Zhang, X.; Wang, X. Wave propagation characteristics in gas hydrate-bearing sediments and estimation of hydrate saturation. Energies 2021, 14, 804. [Google Scholar] [CrossRef]
- Mu, Y.; Zhang, L.; Luo, S.; Wu, Y.; Cui, W.; Miao, X.; Mu, H. Permeability evaluation of carbonate reservoirs through Stoneley wave energies analysis. Well Logging Technol. 2019, 43, 386–390. [Google Scholar]
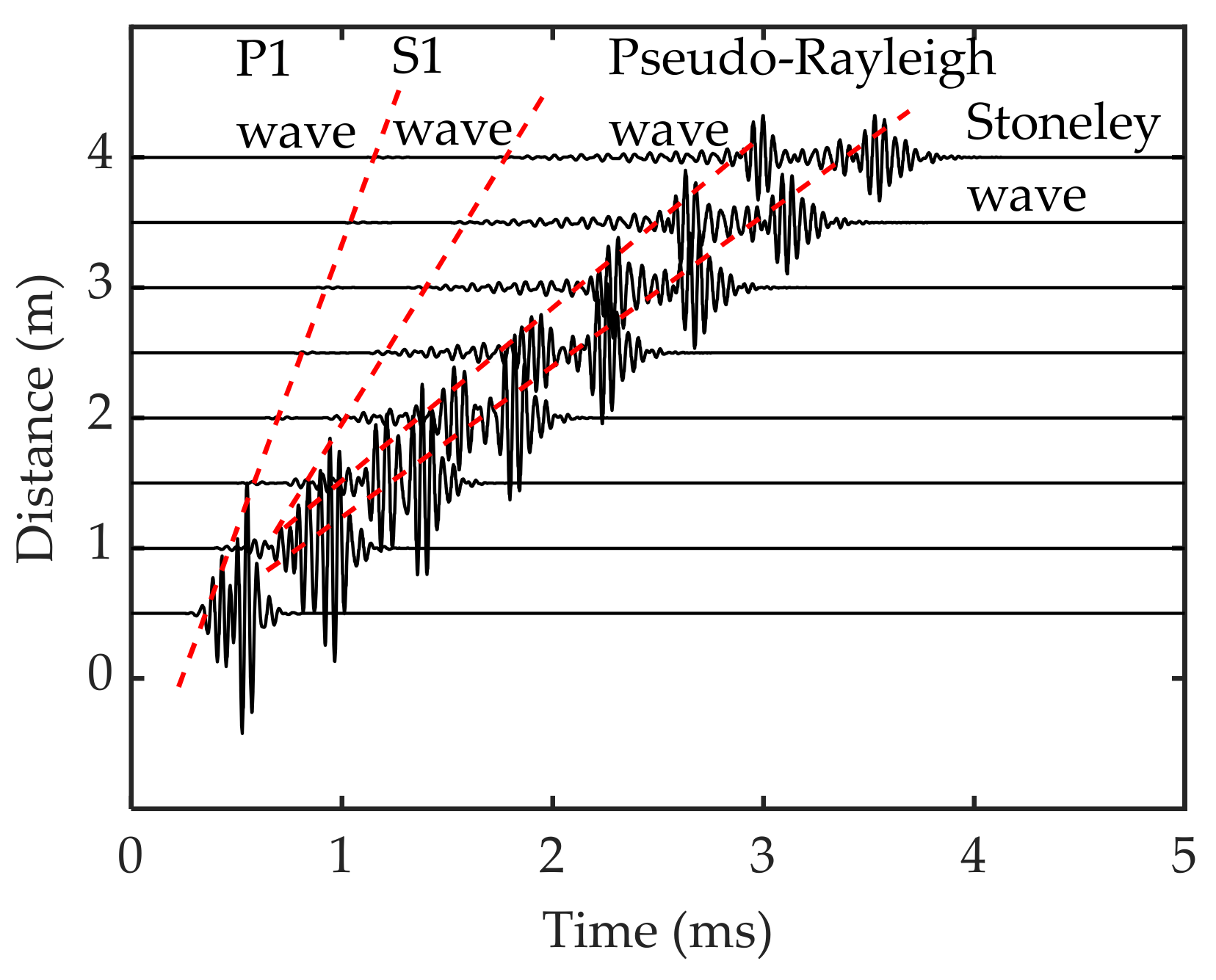


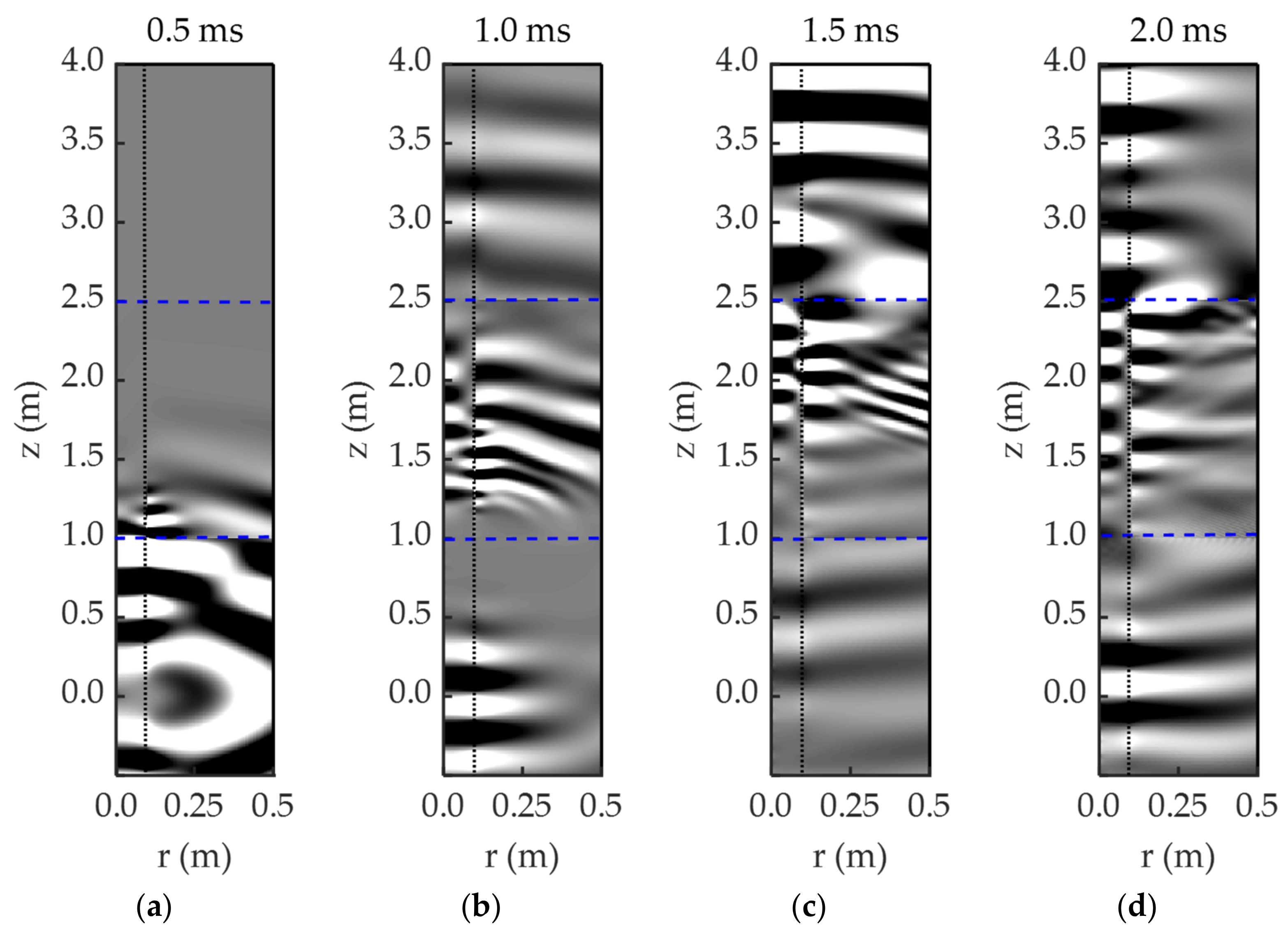
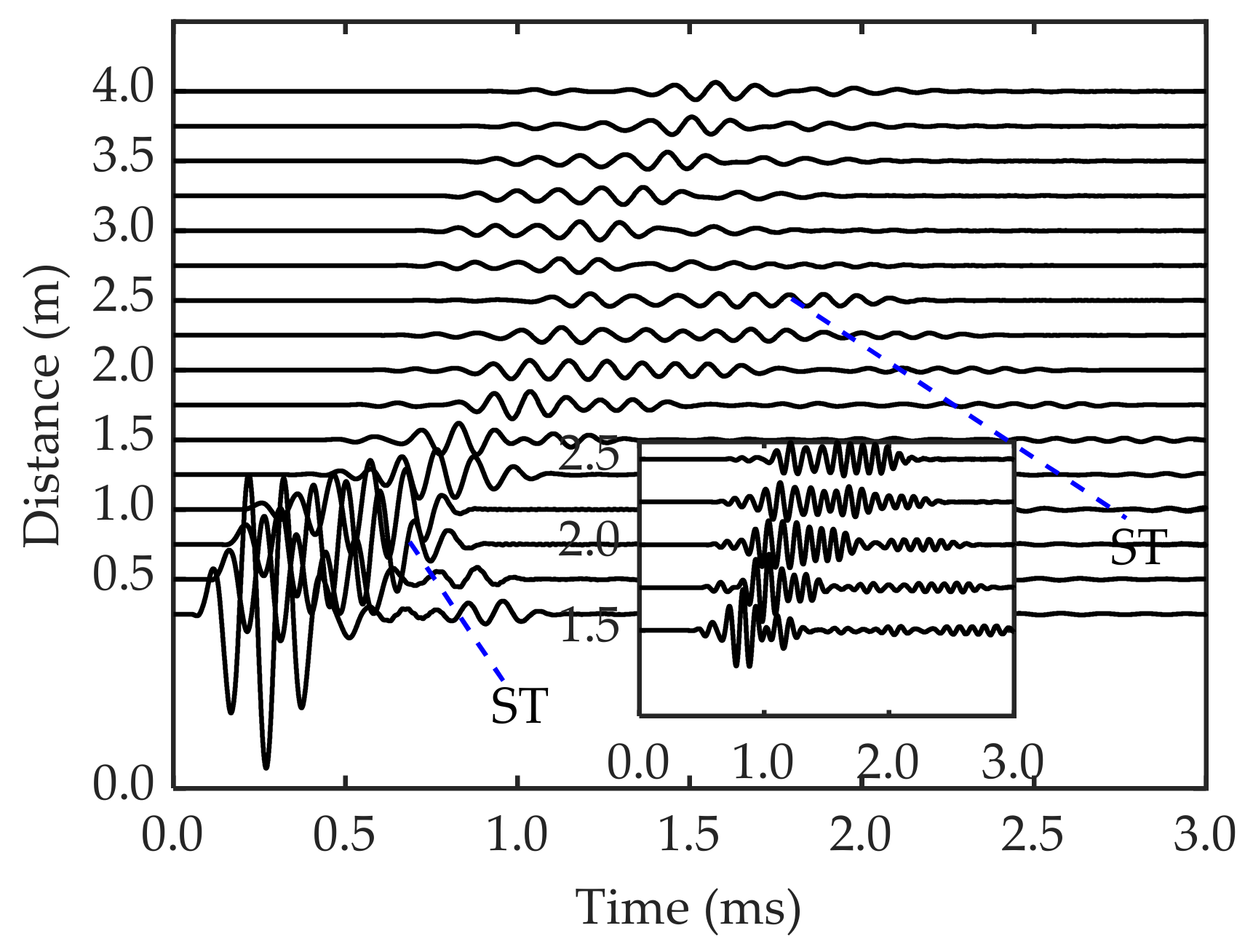
| Parameter | Value |
|---|---|
| Grain density (kg/m3) | 2650 |
| Fluid density (kg/m3) | 1000 |
| Gas hydrate density (kg/m3) | 900 |
| Grain bulk modulus (GPa) | 38.7 |
| Fluid bulk modulus (GPa) | 2.25 |
| Gas hydrate bulk modulus (GPa) | 8.85 |
| Gas hydrate shear modulus (GPa) | 3.32 |
| Grain frame permeability (m2) | 1.07 × 10−13 |
| Gas hydrate frame permeability (m2) | 5 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Zhang, X.; Ji, Y.; Wang, X. Acoustic Wave Propagation in a Borehole with a Gas Hydrate-Bearing Sediment. J. Mar. Sci. Eng. 2022, 10, 235. https://doi.org/10.3390/jmse10020235
Liu L, Zhang X, Ji Y, Wang X. Acoustic Wave Propagation in a Borehole with a Gas Hydrate-Bearing Sediment. Journal of Marine Science and Engineering. 2022; 10(2):235. https://doi.org/10.3390/jmse10020235
Chicago/Turabian StyleLiu, Lin, Xiumei Zhang, Yunjia Ji, and Xiuming Wang. 2022. "Acoustic Wave Propagation in a Borehole with a Gas Hydrate-Bearing Sediment" Journal of Marine Science and Engineering 10, no. 2: 235. https://doi.org/10.3390/jmse10020235






