Tsunami Vulnerability Evaluation for a Small Ancient Village on Eastern Sicily Coast

Abstract

The Ionian sea is prone to tsunamis due to its proximity to the Calabrian subduction zone, which is one of the major tsunamigenic areas of the Mediterranean. The tsunami disaster risk is, nowadays, significantly higher due to the increased exposure of buildings as a result of the economic and touristic growth of the Mediterranean coastal areas. This study focuses on Marzamemi, a small village in the western coast of Sicily, since its morphology and human presence amplify the need to assess its buildings’ vulnerability. The main objective of this research is to quantify the building vulnerability to tsunami hazards using a physical and realistic tsunami scenario. For this purpose, the relative vulnerability index of the buildings in Marzamemi was calculated by means of an improved Papathoma Tsunami Vulnerability Assessment (PTVA) model. The presented approach has three main improvements: (a) a probabilistic tsunami scenario was used; (b) a realistic signal of water surface linked with a specific focal mechanism was adopted; (c) a tsunami wave was propagated from offshore to nearshore using a nonlinear numerical model. The good results of the proposed methodology make it very useful for coastal risk planning conducted by decision makers and stakeholders.

1. Introduction

The study of coastal hazard vulnerability is of great importance for hazard mitigation. Among coastal hazards, there are coastal flooding and tsunamis. The latter are a series of huge waves caused by earthquakes, submarine or coastal landslides and volcanic activity [1]. Rising to several meters, these waves can strike the coast with devastating force. Buildings located in coastal areas or near estuaries and rivers are exposed to danger. A tsunami’s intensity is directly linked to earthquake characteristics, such as the magnitude, the focal depth, the length and the direction of the activated fault. Subduction zones are the main cause of major tsunami events [2,3]. In very deep oceanic waters, tsunamis do not significantly increase in height, but as the waves move fast towards the coastline, they grow in height, becoming potentially destructive.

The main objective of this research is to quantify building vulnerability to tsunami hazards using a physical and realistic tsunami scenario. For this purpose, the relative vulnerability index (RVI) of the buildings was calculated by means of an improved Papathoma Tsunami Vulnerability Assessment (PTVA) model [4,5,6]. The here proposed improvements are in regards to tsunami hydrodynamics and the focal mechanism of the earthquake causing the waves.

The hydrodynamics characteristics of a tsunami wave are related to its risk potential. In the scientific literature, authors often use the run-up and the inundation area to describe the tsunami hydrodynamics [6]. The run-up states the maximum vertical distance between the MWL (mean water level) and the highest point to which the flood zone extends inland. The flooded zone is defined as the maximum horizontal intrusion of the water in the coastal area [7,8]. These properties are related to the magnitude of the earthquake and are a manifestation of the tsunami magnitude [9]. To assess the tsunami buildings vulnerability, an inundation map is needed. Many authors compute vulnerability scores, emphasizing the structure characteristics and computing the flooded area through the run-up (hypothetical, probabilistic or historic data) value, which is linked to an earthquake event [4,5,8,10,11,12,13,14]. Calculating inundated areas using a fixed run-up height is very far from the real hydrodynamics of a tsunami event. Obviously, a numerical hydrodynamic, able to compute the very complex physics of the phenomenon, would provide more realistic results. Generally, authors prefer to quickly resolve the hydrodynamics to obtain qualitative and immediate results. In such a way, the accuracy of hydrodynamics is practically neglected. In the present paper, this issue is removed by using an accurate numerical model for tsunami hydrodynamics. Indeed, the water depth and flow velocity are crucial factors involving the potential building damage [15]. Consequently, the use of hydrodynamic tsunami modelling needs an appropriate boundary condition. This last element is linked to the focal mechanism and to the earthquake’s origin.

In this paper, a real focal mechanism is simulated using a static earthquake scenario (see Section 2.3.1). A great number of Mediterranean areas can be identified with characteristics capable of generating tsunamis. Sicily is one of the Italian regions most exposed to tsunami risk, due to its location within the tectonic plate of the western Mediterranean Sea [16,17].

The western Ionian area, due to the clash between the African and Eurasian tectonic plates, is exposed to tsunamis whose origin is directly related to earthquakes. In particular, the Italian (Calabrian and Sicilian ones) coastal areas are among the most exposed sites to seismogenic tsunami hazards. We state this to point out that the Sicilian coastal areas have a strong anthropization, which makes them more vulnerable [18]. The biggest tsunami in recent time (1908) was registered in Messina; in this case, the maximum observed run-up was about 12 m. The Sicilian coast is densely populated. The population of Sicily is about 5 million, and more than 70% lives in coastal areas [19,20,21,22]. Based on this, the production of flooding and vulnerability maps should be required in order to plan useful strategies for hazard mitigation. In recent decades, due to recent tsunami disasters, researchers have developed numerical models of increasing quality. Several authors simulated the effects of a tsunami striking the Greek and Italian coasts [16,23,24,25,26].

There is a high likelihood for similar events to take place and affect the coasts of Sicily in the future. Furthermore, the disaster risk is now significantly higher due to the increased exposure of the buildings, as a result of the economic and touristic growth of Sicily [27,28,29]. The need to consolidate the safety of coastal human societies against tsunamis requires the assessment of different aspects of vulnerability.

The objective of this study focuses on the assessment of the building vulnerability to tsunamis for the coastal village of Marzamemi, by applying a tsunami vulnerability assessment model [6]. The village was selected together with the Sicilian civil protection. Here, we report the summary of the main motivations: (a) it has great exposure to earthquake tsunamigenic areas; (b) the coastal area is flat and its altitude ranges from 1 m to 6 m above sea level; (c) the continental shelf is tight (about 17 km) and it is engraved by little canyons; (d) despite being a fishing village, it is densely populated during the holiday period; (e) it is a site of archaeological–industrial interest. The Marzamemi population is about 22 thousand and, in the summer, it increases by almost 50%.

Vulnerability expresses the susceptibility of an entity to consequences, such as casualties, damage, destruction or general losses due to the occurrence of a hazard [30]. In this paper, vulnerability refers to the physical type of vulnerability that concerns damage to buildings [4,5]. In order to quantify the building vulnerability, tsunami hydrodynamics and structural characteristics should be considered. In summary, the presented approach has three main improvements: (a) a probabilistic tsunami scenario was used; (b) a realistic signal of water surface linked with a specific focal mechanism was adopted; (c) a tsunami wave was propagated from offshore to nearshore using a nonlinear numerical model.

The major output of our research is addressed to meet the needs of public authorities and stakeholders. The building vulnerability assessment is a fundamental part of the hazard mitigation policies and is useful to decision makers, requiring accurate information about the potential tsunami damages.

2. Materials and Methods

The materials and methods for the case study are described in the following subsections: the description of the studied area, the description of the vulnerability index procedure assessment, the water vulnerability calculus chain and the structural vulnerability index procedure assessment. The hydrodynamic numerical model chain was used to provide the hydraulic parameters needed. This last component was used in particular for the water vulnerability index and the exposure parameters computation. Indeed, such a parameter was used for the structural vulnerability index assessment.

2.1. Studied Area

A Mediterranean case study was adopted to test the presented methodology. The analysed area is in the southern Ionian Sicilian coast (see Figure 1) and consists of low and rocky littorals spaced out by sandy dissipative beaches. In particular, the building vulnerability score was assessed for the ancient village of Marzamemi. The coastal area of the Marzamemi village has great exposure to tsunamigenic earthquakes [16,17]. The coast morphology was defined starting from the upper Pleistocene, when sandstone and sand settled down. At the end of the last European glaciation (Würm), the depressions (upper Pleistocene deposit) were filled by water creating ponds and marshes, which today characterize several coastal areas. The Marzamemi’s marsh is localized beyond the western part of the village (see Figure 2) and was created just after the last European glaciation. The marsh, during the 1700s, was transformed into salt works to supply the low-cost salt to the tuna factory. In 1946, the salt works ceased to operate, and today, this area is a wetland protected area of remarkable faunal interest. The Marzamemi village is located on a calcareous sandstone platform (about 3 m a.s.l.), producing a low rocky coast, most likely an ancient tombolo.

On the northern side of the Marzamemi village, between the sandstone platform and “Bove Marino” cape, there is a sandy, gently sloping beach (“Spinazza”), 20 m wide on average and 800 m long, with a dune system (40 m wide) in almost its totality. South of the Marzamemi village, there is a “Madonnina” bay eclosed on the north by the “pontile Della Balata” dock and on the south by the “La Fossa” harbour (Figure 2). These two coastal structures host both small leisure boats and fishing vessels. In the bay middle, there are two small islands “Isola Grande” (inside the harbour) and “Isola Piccola” where there is a private house. Inside this bay, there is also a gentle slope sandy beach with a maximum width of 20 m. In front of “Isola Piccola”, there is a cusp in the shoreline that probably will become a tombolo. South “La Fossa” harbour, where the shoreline is composed of low calcareous sandstone rocks, interrupted by small sandy beaches (some even 100 m long). The Marzamemi village, born around a little landing that later became a fishery harbour, developed over time in the 17th century (during the Spanish domination), later equipped with a tuna factory. Nowadays, the tuna factory is a beautiful example of historical architecture. The near beach, the evocative old fishery village and the near wild areas (rich in Mediterranean fauna) attract many tourists. In the summer, the number of citizens in the village greatly increases, due to both residential holidays and the “Frontiers film festival” (inaugurated in 2000).

Figure 2 shows the most interesting and characteristics places in Marzamemi. From the South to the Northside, the breakwater, the old tuna factory, the marsh, the low rocky coast and the Spinazza beach can be identified. The village (Figure 2) is located in a plain with a very gentle slope that behind has lands mainly used for greenhouse growing. The civil houses are three stories tall on average, and the structures are rural masonry (the old houses) or reinforced concrete (the new residential houses, built since 1960).

2.2. Relative Vulnerability Index Assessment

In this section, the “classical” PTVA (Papathoma Tsunami Vulnerability Assessment) method was described. The approach consisted of calculating a relative vulnerability index (RVI) score that represented each building’s vulnerability [4,5,31,32]. Moreover, the adopted approach performed very well during a real-life field evaluation [33]. The adopted method defined the RVI by the sum of two elements:

• Structural vulnerability ($SV$). The bearing capacity of a building structure that is the function of the horizontal hydrodynamic force;
• Water vulnerability ($WV$). The vulnerability of building to water intrusion.

The $RVI$ value was calculated by using the following equation:

$$RVI=\frac{2}{3}SV+\frac{1}{3}WV$$

(1)

The second term of Equation (1) was calculated using the following expressions:

$$WV=\frac{Maximumwaterdepth}{Totalbuildingheight}$$

(2)

$$SV=Bv·Surr·Ex$$

(3)

where $Bv$ is the building vulnerability, $Surr$ is the building surroundings and $Ex$ is the exposure to the inundation scenario.

These parameters were calculated by means of on-site surveys. The reader can find the PTVA details in many research papers [4,5,6,13,14]. The detail and the flow chart of the adopted PTVA model are depicted in Figure 3.

For the sake of clarity, it should be noted that the approach here presented had three main improvements: (a) the tsunami scenario was generated using a statistical approach; (b) the tsunami signal was generated using a physics fault mechanism; (c) the $RVI$ was calculated using numerically modelled water depth.

2.3. Water Vulnerabilty Computational Chain

In this section, all the hydrodynamic components of the “computational chain” needed for vulnerability score calculus were defined and described. This chain grouped all the operations needed to assess the $WV$ index that, finally, were combined with $SV$ score for $RVI$ computing (Equation (1) and Figure 3). The water depth obtained from the numerical model was also used for computing the exposure ($Ex$) index (see Section 2.4 and Figure 3). Fortran and MATLAB(r) codes were specifically written for the research purpose. QGIS(r) 3.22.1 was used to create final maps and process the intermediate results. Moreover, MIKE21(r) was used to verify the computational mesh and to simulate earthquakes for calibration purposes. The computational chain consisted of 4 steps, including the definition of the initial condition and maximum water depth and velocity maps. Building a computational chain is a very efficient solution to reach a complex result. Indeed, a sequence of integrated algorithms allows reaching the results controlling errors of each calculus modulus. Well-organized modularity allows “dividing the jobs” among several operators, providing the possibility to rerun either the whole process or a part of it. In the following, a detailed description of the whole computational chain was provided, giving information on the studied area and on the adopted tsunami’s initial condition. Each module of the computational chain was designed and realized by means of specific activities. The list of the developed steps was: (a) subdivision of the urban areas (this subdivision had the main purpose of better arranging surveys and results); (b) producing the topobathymetric map; (c) buildings delimitation; (d) determining the computational domain; (e) creating the computational mesh; (f) verifying the computational mesh; (g) tsunami wave propagation; (h) analysis of the results; (i) producing the maximum water depth and maximum velocity maps.

The first activity was the subdivision of the residential area into 4 zones: A1, A2, A3 and A4 (see Figure 1). The whole domain was about 13.6 km², of which 2.03 km² refers to the residential area, 9.46 km² offshore numerical elaborations and 1.91 km² was not mapped. Zone A1 included the ancient Marzamemi village along with the tuna factory and the old fishermen houses, zone A2 included the newer housing mainly for tourist use. Zone A3 south of the ancient village centre joined the village with the A4 zone, in which there was the harbour and the marina areas.

The second activity was the production of a topobathymetric map. This was built using MIKE21(r) and QGIS(r). The available data were heterogeneous because of their different origins. In particular, gridded data, scattered data and isolines data were used. The topographic and terrain data were taken from the LIDAR DEM (Digital Elevation Model) of the Sicily government. These data were produced by means of a flight campaign (ATA 2007/2008) and were supplied on a regular grid on the GAUS BOAGA national projection (EPSG: 3004). The aerial image (ATA 2007/2008) was used to mark out the zones, whereas the buildings were marked out using satellite imagery from Google Earth. Furthermore, the consistency between the DEM (ATA 2007/2008) and the Google Earth imagery was verified. The shoreline position was extracted from the aerial image (ATA 2007/2008), assuming this as a topographic proxy (red line Figure 1). This avoided the undesired oscillation of the shoreline position due to the heterogeneity among topobathymetric data. The depth contour lines were digitized from Italian nautical charts.

Figure 4 shows the input data needed for the computational mesh construction. The adopted numerical model solved continuity and momentum depth-integrated equations by using an unstructured triangular mesh. The triangles had to follow the Delaunay rule in order to avoid numerical errors. For this reason, a specific module of the calculus chain was designed, capable of generating a Delaunay mesh with the following constraints: (a) the triangles dimension was less in the domain zones with less of a slope; (b) the triangles dimension was less on the buildings border; (c) the triangles dimension was less on the shoreline.

Based on these rules and using the topobathymetric information already described, a triangles density map was created, shown in Figure 5, where the density index was represented by a colour map. The density score ranged between 10 and 50; thus, the smaller the score, the smaller the corresponding triangle dimension. Consequently, the mesh, as shown in Figure 6, was finer near the shoreline and around the buildings’ shapes, and coarser offshore.

The generated numerical grid was validated using MIKE21(r) by propagating random sea states. The validation procedure goal was to determine the computational domain areas where the hydrodynamics were not well described. Furthermore, a few geometric errors highlighted by MIKE21(r) grid viewer were manually corrected. Each boundary mesh node was mapped using 4 integer values representing the type of border. These conditions are shown in Figure 6, where BOUNDS4 is a land boundary line, whereas BOUNDS1, BOUNDS2 and BOUNDS3 are open boundaries. The other node elements were mapped as “inner points”, and could be wet or dry. This mesh (Figure 6) was used to propagate the tsunami scenario from a 20 m depth to the shoreline. The wave propagation was performed using a depth-integrated nonhydrostatic numerical model [34]. The main objective was to calculate the flooded area (water depths) and the current velocities inside the areas themselves.

2.3.1. The Adopted Tsunami Scenario

The hydrodynamic model input was obtained from CAT (Tsunami Alert Center) of the Italian National Institute of Geophysics and Volcanology (INGV). Indeed, in the present paper, the hydrodynamic condition was simulated starting from a probabilistic scenario. To assess the inundation scenarios the PTHA (Probabilistic Tsunami Hazard Assessment), an approach was adopted [35,36]. This method relied on evaluating the probability that a given tsunami event, such as the inundation height, would exceed a fixed threshold. Basili et al. [37] simulated tsunamis produced by different potential seismic sources from several tectonic environments. Here, a probabilistic exceedance curve was obtained from Mediterranean PTHA curves. The tsunami wave height was then extracted for the given probability or return period. The tsunami wave height, with a return period of 2634 years, was calculated from the above-mentioned curves. Finally, the surface elevation signal was generated with a bathymetry movement that replicated a fault shift.

Figure 7 shows the used surface elevation signal representing a tsunami associated with a 2634 years return period. The tsunami surface elevation was resampled with a 30 s time step, because the original time step was 30 min. The signal was assigned to BOUNDS2, corresponding to the bathymetric contour line −20 m a.s.l.

2.3.2. Example of Hydrodynamics Results Treatments

The numerical model results were given in the triangular mesh nodes, in which the current velocity and water depth were known at the time. Furthermore, the model gave back the vectorial velocity map. An example of results is depicted in Figure 8, where a velocity vector corresponding to each node of the triangular mesh is shown. Finally, the maximum water depth and velocity values reached during the time were computed.

Figure 9 shows an example of the maximum velocities and Figure 10 shows an example of the maximum water depth, used as input to build the vulnerability thematic maps.

2.4. Structural Vulnerability

The structural vulnerability ($SV$ as defined in Equation (3)) was used to compute the $RVI$ score (see Equation (1) and Section 2.2). $SV$ is the vulnerability of the bearing capacity of the building structure, linked with the horizontal force related to water currents. It is well known that a building with a poor structure (e.g., poor construction material, with low foundations, etc.) can suffer huge damages, regardless of the presence of low water depth. On the other hand, a building with a very resistant structure that is struck by high water depth might be very damaged, without losing any bearing capacity of the building structure [38]. According to results obtained by Dall’Osso et al. [6], a 2/3 weighting coefficient to $SV$ term was assigned in Equation (1). The $SV$ of a building consists of the attributes of the building’s structure ($Bv$), the water depth (exposure index $Ex$) near the building and the degree of protection ($Prot$), calculated using the equations shown in Figure 3.

The building’s characteristics needed to evaluate $SV$ were collected by means of several surveys (see

Table 1. The table shows the building typologies inside the Marzamemi area. For each zone, the following building characteristics were shown: the type of construction, the use, the stories, the storey height, the percentage of openings and their shape.

Zone	Total Number of Building	Use	Construction Types	Stories	Storey Height (m)	Percentage of Openings (%)	Shape	Number of Buildings
A1	350	Civil	Masonry and wooden floors	1	4–6	<50	Pseudo-rectangular or irregular	36
			Masonry and wooden floors, cement-based brick floors or mixed structures	From 1 to 3	3–4	>50	Pseudo-rectangular or rectangular	161
			Reinforced concrete and rigid frames with brick–cement floors	3	3–4	<50	Pseudo-rectangular	5
				2	3–4	<50	Pseudo-square	65
				1–2	3–4	<50	Irregular	61
				2	3–4	<75	Rectangular	22
A2	365	Civil	Reinforced concrete and rigid frames with brick–cement floors	From 1 to 3	3–4	<50	Pseudo-rectangular	164
				2	3–4	<50	Pseudo-square	14
				1–2	3–4	<50	Irregular	142
				2	3–4	<75	Rectangular	45
A3	85	Civil	Reinforced concrete and rigid frames with brick–cement floors	From 1 to 3	3–4	<50	Pseudo-rectangular	28
				2	3–4	<50	Irregular	12
				2	3–4	<75	Rectangular	26
			Reinforced concrete and rigid frames with brick–cement floors with the possibility of two-dimensional elements (reinforced concrete partitions)	4	3–4	<75	Rectangular	6
		Artisan/Agricultural	Panels and metal frame	1	4–6	<50	Rectangular	1
		Artisanal/Industrial	Mixed masonry and reinforced concrete structures	1	6–8	<75	Rectangular	9
		Residence/Deposits	Masonry and elements in reinforced concrete, with roofing in lightweight deformable materials	1	3–4	<50	Rectangular	1
			Masonry with roofing in lightweight deformable materials	1	3–4	<25	Rectangular	2
A4	184	Civil	Reinforced concrete and rigid frames with brick–cement floors	From 1 to 3	3–4	<50	Pseudo-rectangular	95
				2	3–4	<50	Irregular	9
				2	3–4	<50	Pseudo-square	1
				2	3–4	<75	Rectangular	34
			Reinforced concrete and rigid frames with brick–cement floors with the possibility of two-dimensional elements (reinforced concrete partitions)	4	3–4	<75	Rectangular	9
		Artisan/Agricultural	Mixed masonry and reinforced concrete structures	1	4–6	<75	Pseudo-rectangular	13
			Panels and metal frame	1	4–6	<50	Rectangular	8
		Artisan/Industrial	Nonviable buildings without roofing and stiffening walls	1	6–8	= 25	Rectangular	10
		Residence/Deposits	Masonry with roofing in lightweight deformable materials	1	3–4	<25	Rectangular	2
			Masonry and elements in reinforced concrete, with roofing in lightweight deformable materials	1	3–4	<50	Rectangular	3

). The surveys were arranged by subdividing the whole studied area into four zones (A1, A2, A3 and A4; see Section 2.3 and Figure 1). Starting from the A1 area, the building surveys lasted two weeks. To describe each building, a technical sheet was created with all the characteristics to collect. Most characteristics were surveyed easily through visual observation (e.g., stories, shape, opening percentage, building height and use). However, not all the buildings of area A2 were surveyed because of the pandemic lockdown. In this case, “Google Street View” images were used, and the time taken for the survey was five days. It is worth pointing out that not all the characteristics needed were easy to collect. Indeed, the basement and floor types were not easy to inspect, but could be derived from to the type of structure (e.g., masonry, reinforced concrete, etc.). Moreover, field surveys were certainly useful for a small number of buildings, but could be more difficult and time-demanding for a large number of buildings. Finally, it was not possible to perform a visual inspection of buildings not visible from public areas (i.e., properties gated and hidden by fences or by vegetation.). Nevertheless, it would have been possible to bypass the problem by asking local authorities for data and information, but in the presented case study, there were no survey issues.

3. Results and Discussion

The vulnerability assessment model (PTVA) was field tested in Marzamemi (Sicily). This village was not very densely populated, included residential, commercial and industrial buildings, had a high touristic significance and contained heritage sites based on their historic or natural significance. The selected inundation scenario was a 2634 years return period based on a tsunami, triggered by a submarine earthquake. We selected this tsunami return period because it was also adopted by Italian law in the field of seismic risk.

The numerical Boussinesq-type model [23,34] generated a maximum water depth map (see Figure 10), which was uploaded into a QGIS(r) environment. This allowed the identification of buildings exposed to the selected tsunami scenario, which were digitised as vectorial polygons within the GIS (geographic information system). The selected tsunami scenario would inundate an area of over 0.94 km², containing buildings. The location of the exposed urban areas of Marzamemi is shown in Figure 11. All necessary data to perform the PTVA were collected by visually inspecting each exposed building. The achieved information was inserted into QGIS and assigned to the corresponding polygons (buildings).

The colour-coded scale was obtained by simply classifying RVI scores by equally spacing them out from one to five (Figure 11), as reported by [13]. The overall vulnerability level was medium to low, with 508 buildings having an RVI score lower than the mean RVI (1.98) of the total buildings in Marzamemi village. The buildings identified by the PTVA as the most vulnerable were inside the A1 zone (Figure 12A), and are listed in

Table 2. Number of buildings subdivided by vulnerability classes according to the use category.

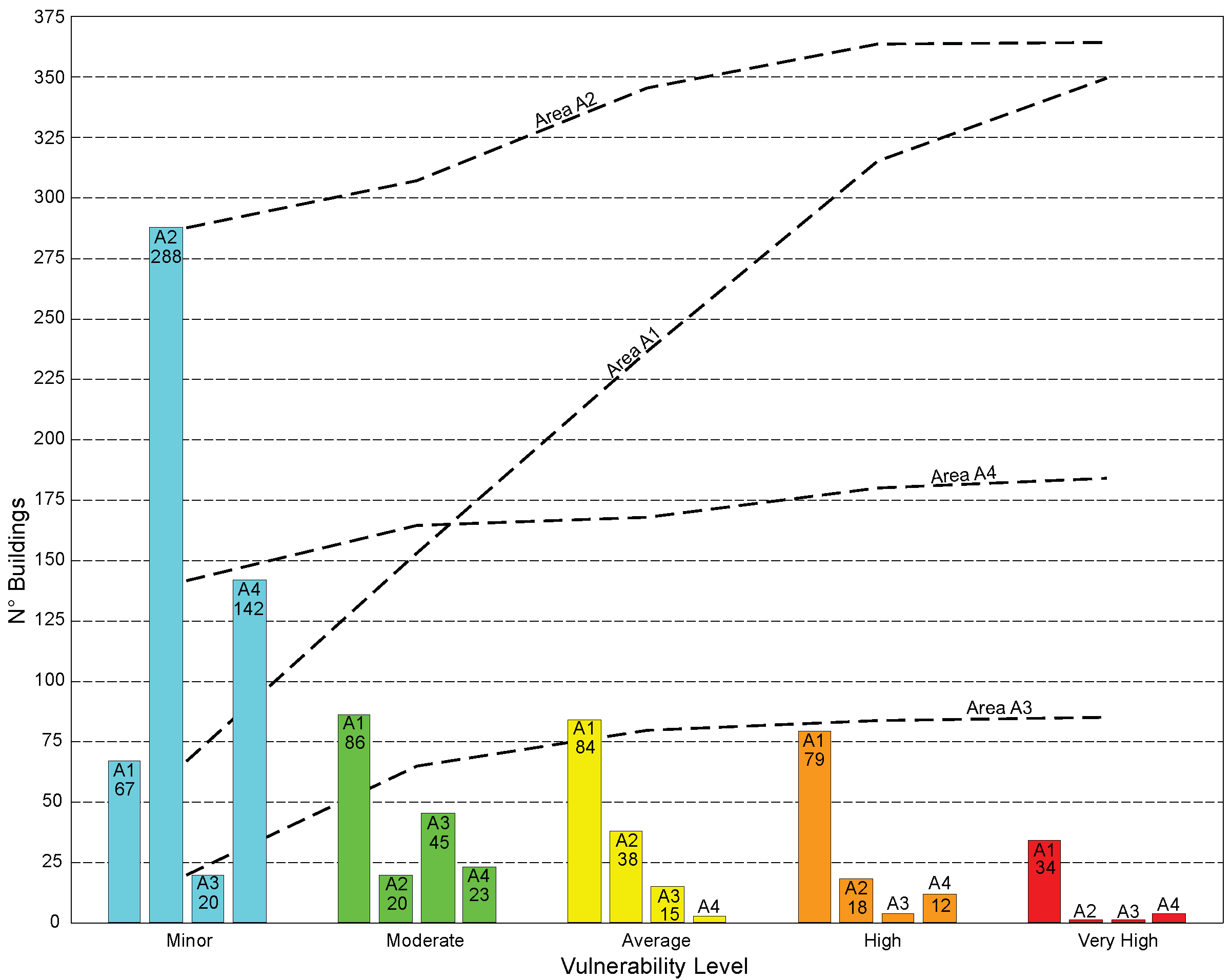
Zone	Total Number of Building	Mean RVI	Building Use Categories	Number of Building	Vulnerability Classes
					Minor	Moderate	Average	High	Very High
A1	350	2.58	E1	17	14	1	0	1	1
			E2	2	2	0	0	0	0
			E3	328	51	85	83	76	33
			E4	3	0	0	1	2	0
A2	365	1.53	E1	6	5	0	0	1	0
			E3	359	283	20	38	17	1
A3	85	2.23	E1	1	1	0	0	0	0
			E3	84	19	45	15	4	1
A4	184	1.64	E1	4	4	0	0	0	0
			E2	1	1	0	0	0	0
			E3	179	137	23	3	12	4

. This table shows the building categories and the corresponding vulnerability classes for each Marzamemi zone. The buildings were classified into four classes in order to better read the present results. Indeed, the risk was also linked to the use of buildings and it was important to compare the vulnerability with the type of building (e.g., schools, churches, factory, etc.) The building use categories were divided into: (E1) rural houses, agricultural greenhouses, sports and recreational facilities, cemeteries, low-tech buildings and livestock buildings; (E2) buildings in high-tech agricultural settlements, buildings in protected natural areas and restricted areas; (E3) civil buildings, cultural, architectural and archaeological heritage under constraint, industrial and craft buildings; (E4) important public buildings (e.g., schools, churches, hospitals, gyms, etc.) and civil protection buildings. A great number of buildings fell within the E3 class, that included high “exposed value” buildings. The E4 class included buildings with a very high “exposed value”, of which there were only three buildings, but with a high/moderate vulnerability. The buildings with very high RVI scores were heritage venues, such as the ancient tuna factory (i.e., building one and two of Figure 12A), and the hlSan Francesco Di Paola church (i.e., building three of Figure 12B). The tsunami flow would completely inundate the ground floor of the small San Francesco Di Paola church (water depth = 0.86 m) and would most likely cause structural damage because of the building’s structural type (masonry and wooden floors).

The first row of ancient buildings in the A1 zone would be hit by a significantly high water depth (>1.20 m), and the poorer construction standards and the fact that the buildings only have a single floor would result in high RVI scores. If a tsunami warning was issued for this area, access to these buildings should be restricted. The ground floor of the buildings of the main square would be inundated by 1 m of water depth, but the lack of protection and the fact that some of these units have only one storey would still result in medium RVI values and a high risk to the resident people (see Table 2). If a complete evacuation of Marzamemi was necessary, the maximum distance to a safe location (i.e., outside of the inundated area) would be less than 700 m.

Area A2 had the first row of buildings with a heterogeneous vulnerability. A very high vulnerability was identified just for one building localized on the north side. The area flooded by the tsunami reached only a width of 300 m onshore.

Buildings located near the coastline often received higher RVI scores, with the exception of the A3 area in the southern part of Marzamemi in front of the small island (Isola Piccola), on which there were buildings composed of reinforced concrete (Figure 12B).

The north side of area A4 was close to the “la Fossa” harbour. Here, the buildings prevalently had moderate vulnerability scores. The high vulnerability was found in structures in front of the coastline. Two of these were masonry and two were wooden structures. In the north side of the A4 area, the inundation tsunami was about 400 m onshore.

The overall results of RVI scores are shown in Figure 13. The maximum number of buildings with a minor vulnerability was achieved by zone A2, with 288 buildings. On the other hand, the A1 zone had a higher number of building with a very high vulnerability (34). The A3 zone had few buildings which, generally, had a moderate–averaged RVI score (Figure 13). Finally, zone A4 only had four buildings with very high RVI scores. Three of these were temporary constructions for vessel recovery and for beach lido accommodation.

4. Conclusions

This paper presented improvements of the “classic” PTVA model, which is a very widespread method for evaluating quantitatively and qualitatively the vulnerability of buildings to seismogenic tsunamis. Three main improvements were introduced: (a) a probabilistic tsunami scenario was used; (b) a realistic signal of water surface linked with a specific focal mechanism was adopted; (c) a tsunami wave was propagated from offshore to nearshore using a nonlinear numerical model.

The classic PTVA model is based on the RVI score, which is the sum of two components. The first, SV, is the structural vulnerability, and the second, WV, is the water vulnerability. Both SV and WV had to be computed using the hydrodynamic conditions (water depths). To assess the hydrodynamic conditions, a numerical model was used, a weakly dispersive Boussinesq model, that was specifically designed and written for the SIMIT-THARSY (Tsunami Hazard Reduction System) project. The numerical model adopted a nonhydrostatic wave flow approach, and it was depth integrated. The model was optimized for rapidly varied shallow water flows, typically found in coastal flooding resulting from tsunamis. Furthermore, the MIKE21(r) software was used for verifying the computational grid and for simulating the earthquakes needed for model calibration. The methodology was applied in a real test case in a coastal village on the eastern side of Sicily. A probabilistic scenario was extracted from PTHA curves, corresponding to a return period of about 2600 years. Using the 2600-year return period, a water surface elevation signal was then generated at −20 m u.s.l offshore the Sicilian coast. The water surface signal was linked to a real seismic source localized in the Ionian sea, compatible with the local conditions. Indeed, here, there were two main crustal structures, the Calabrian arc and the Hellenic arc, which are very active. This approach allowed determining the water depth and water velocity during a tsunami flooding. Finally, the water depths were used to calculate the RVI scores, assessing the response of buildings to a realistic tsunami flooding event, and to create a Marzamemi thematic vulnerability map. This map was essential for demonstrating the relative vulnerability of the area and for providing simple recommendations for emergency managers. The strengths and weaknesses of the PTVA classic method are well-known in the scientific literature, and are linked to the application’s speediness and difficulty in performing surveys. Moreover, the classical model is often applied neglecting the hydrodynamics details and/or neglecting the seismic source’s focal mechanism. The modified PTVA model has new strengths and weakness points. The main weakness was based on the need for accurate numerical modelling that should be developed by a hydraulic expert. This figure is often not available among local authority employees. Detailed bathymetric and seismic data are also needed. The main strengths were a more realistic earthquake scenario and a more physical description of the tsunami flooding event. The earthquake was simulated, reproducing a real fault shift. The earthquake parameters were linked to a return period; thus, the authorities can standardize it for all the future vulnerability studies. The bearing structural capacity was evaluated using a realistic water depth based on local boundary conditions. Future developments of this research should be addressed to determine a new risk mapping methodology. Indeed, the proposed vulnerability assessing method has a great advantage in becoming the next step in the evaluation of tsunami risk. The risk scores depend on the probability of the occurrence of a dangerous event, the vulnerability linked to an event and the number of people/services that might be exposed to the hazard. Indeed, the risk is dependent on the likelihood that a hazard may occur, together with the severity of the harm/consequences suffered. For all these reasons and for all the achieved good results, the proposed methodology will be useful for coastal risk planning purposes.