Buckling and Post-Buckling Behavior of Perfect/Perforated Composite Cylindrical Shells under Hydrostatic Pressure
Abstract
1. Introduction
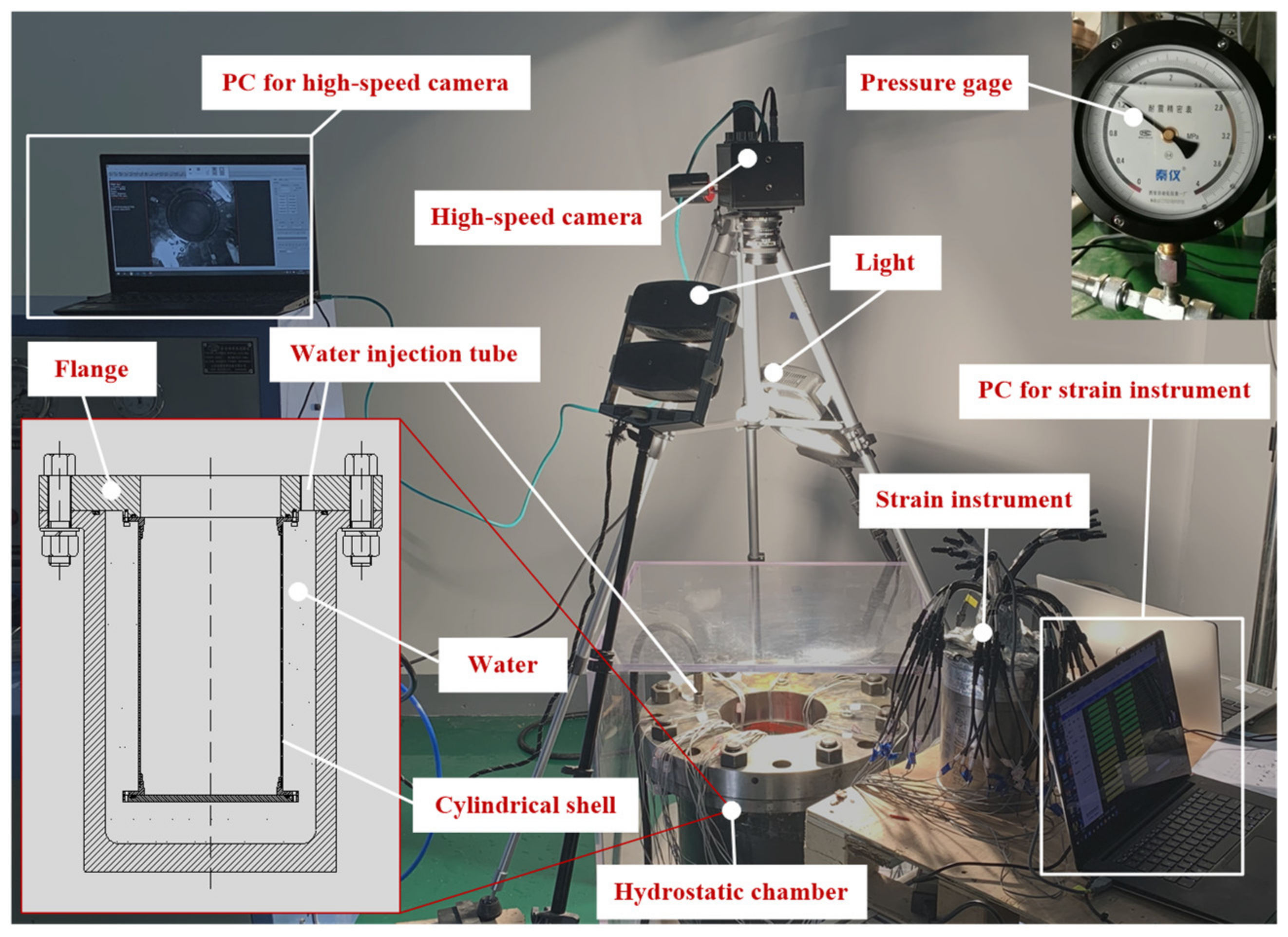
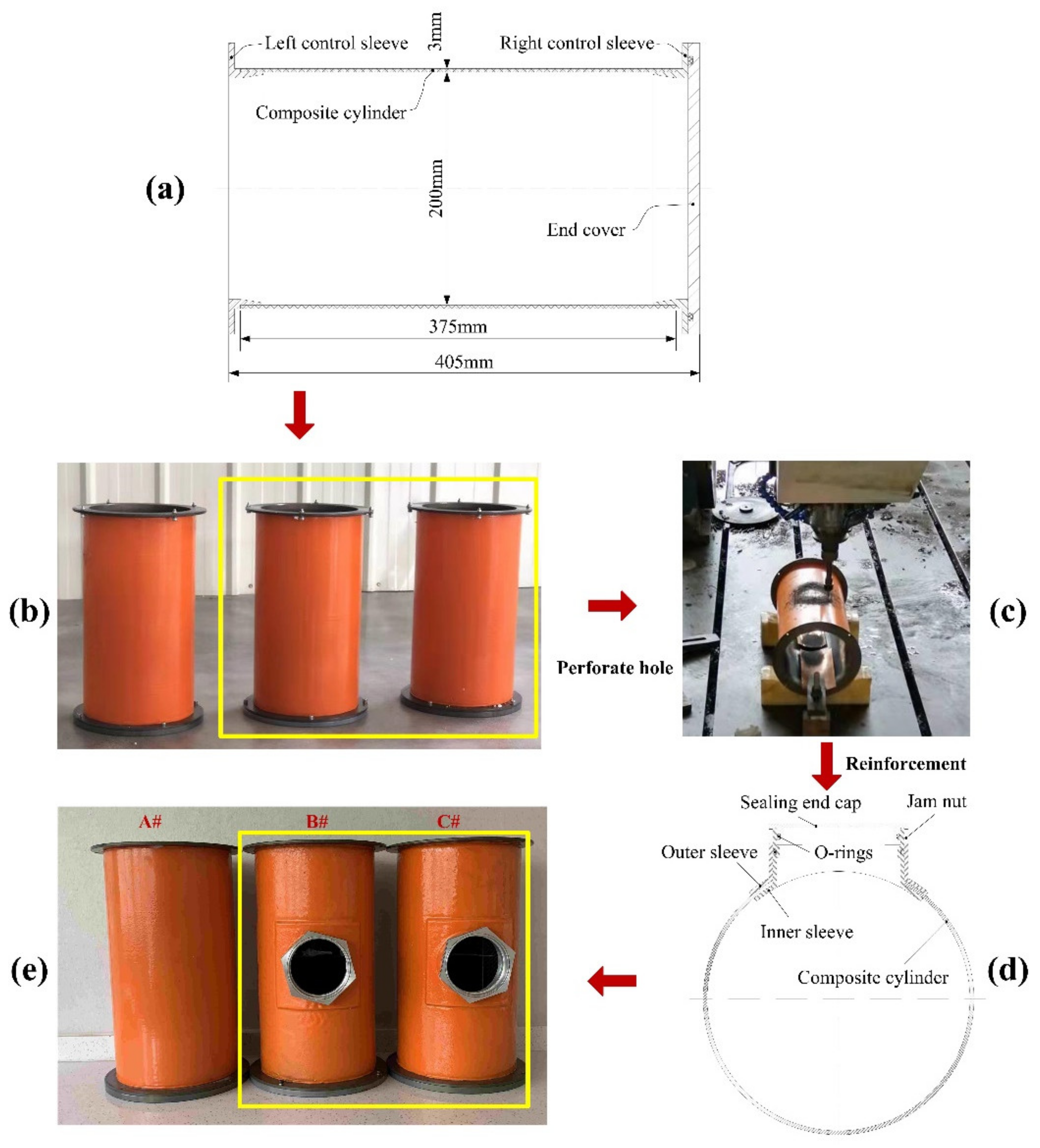
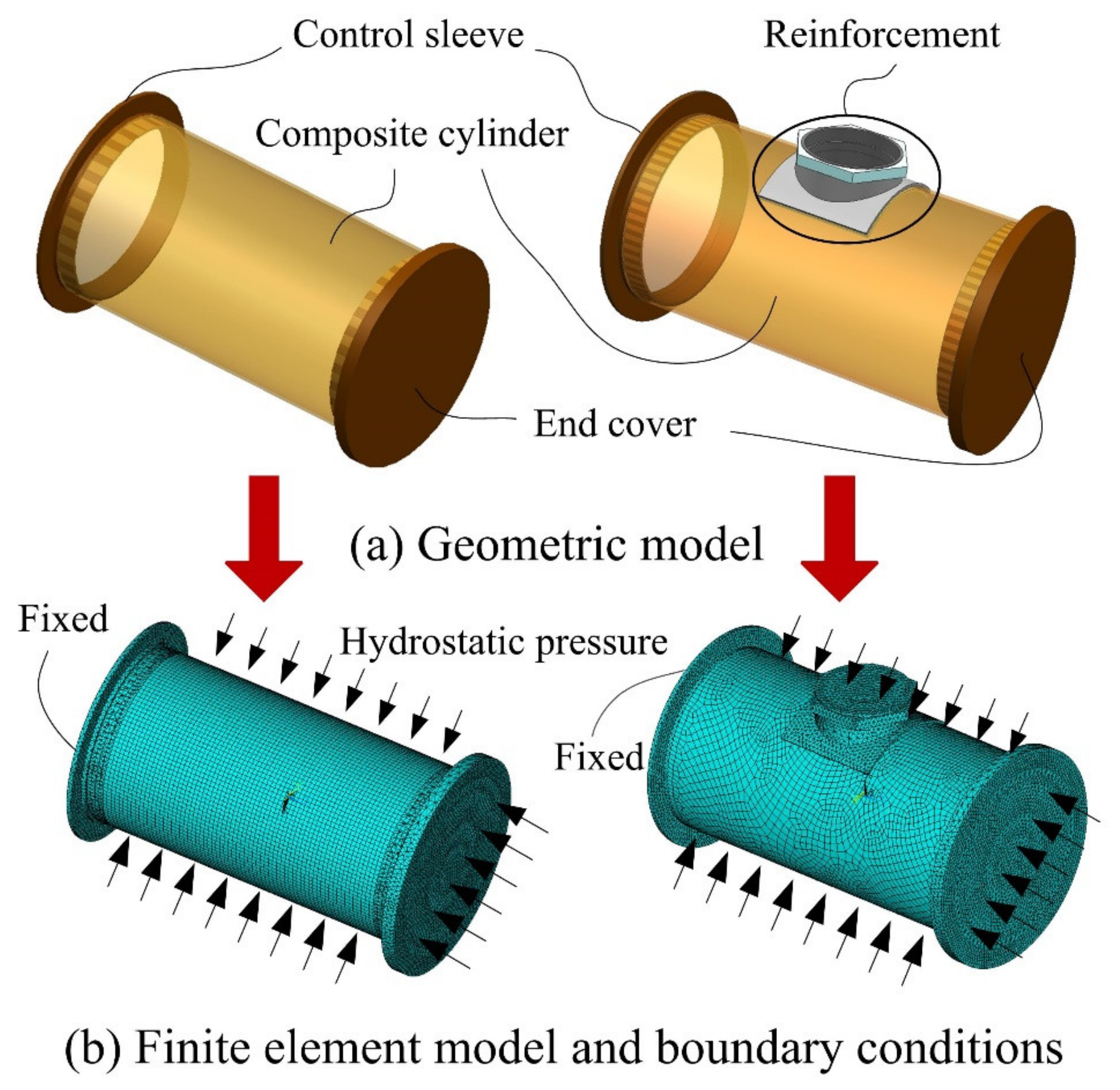
2. Experiment Design
3. Results and Discussion
4. Conclusions
- (1)
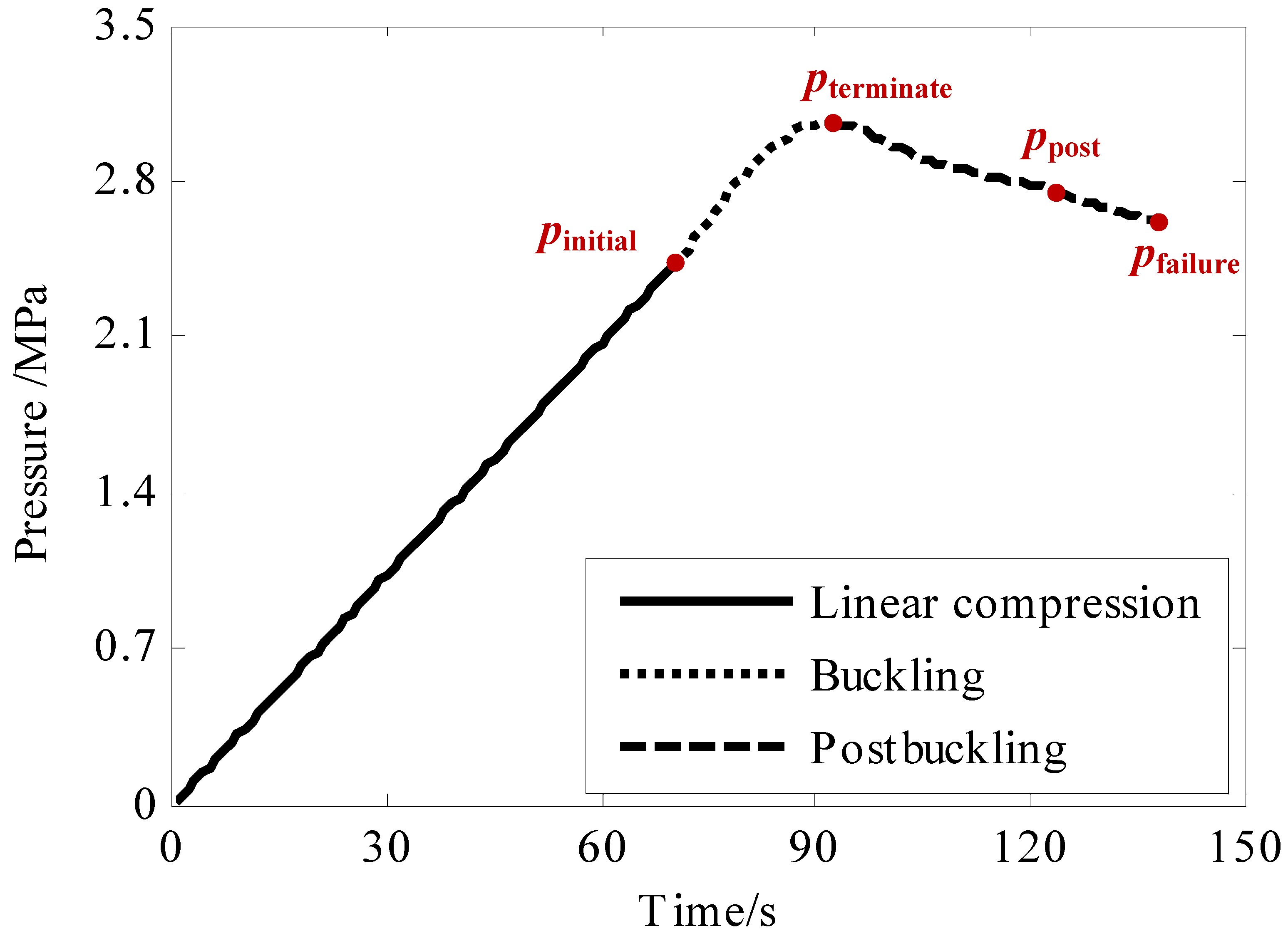
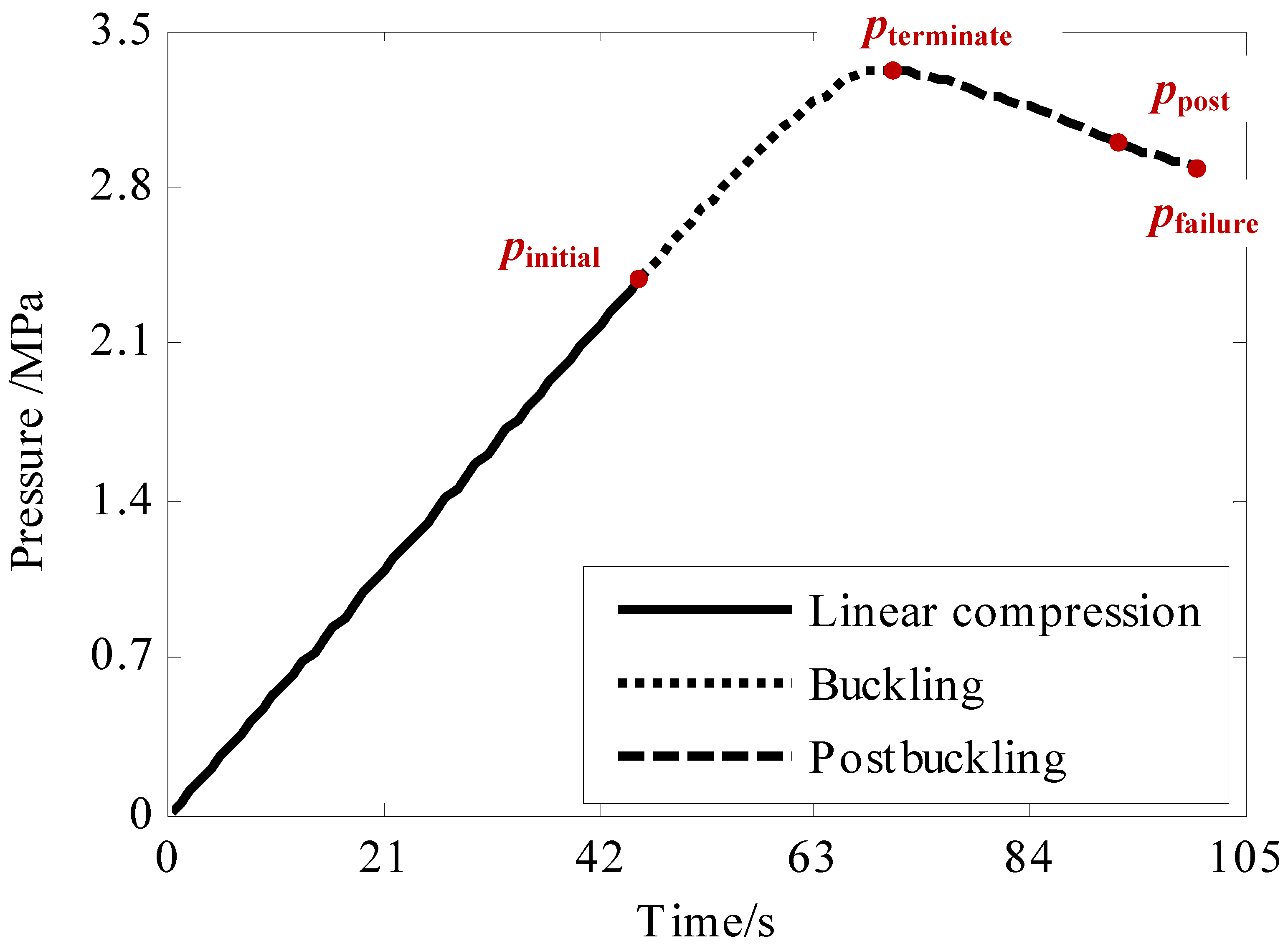
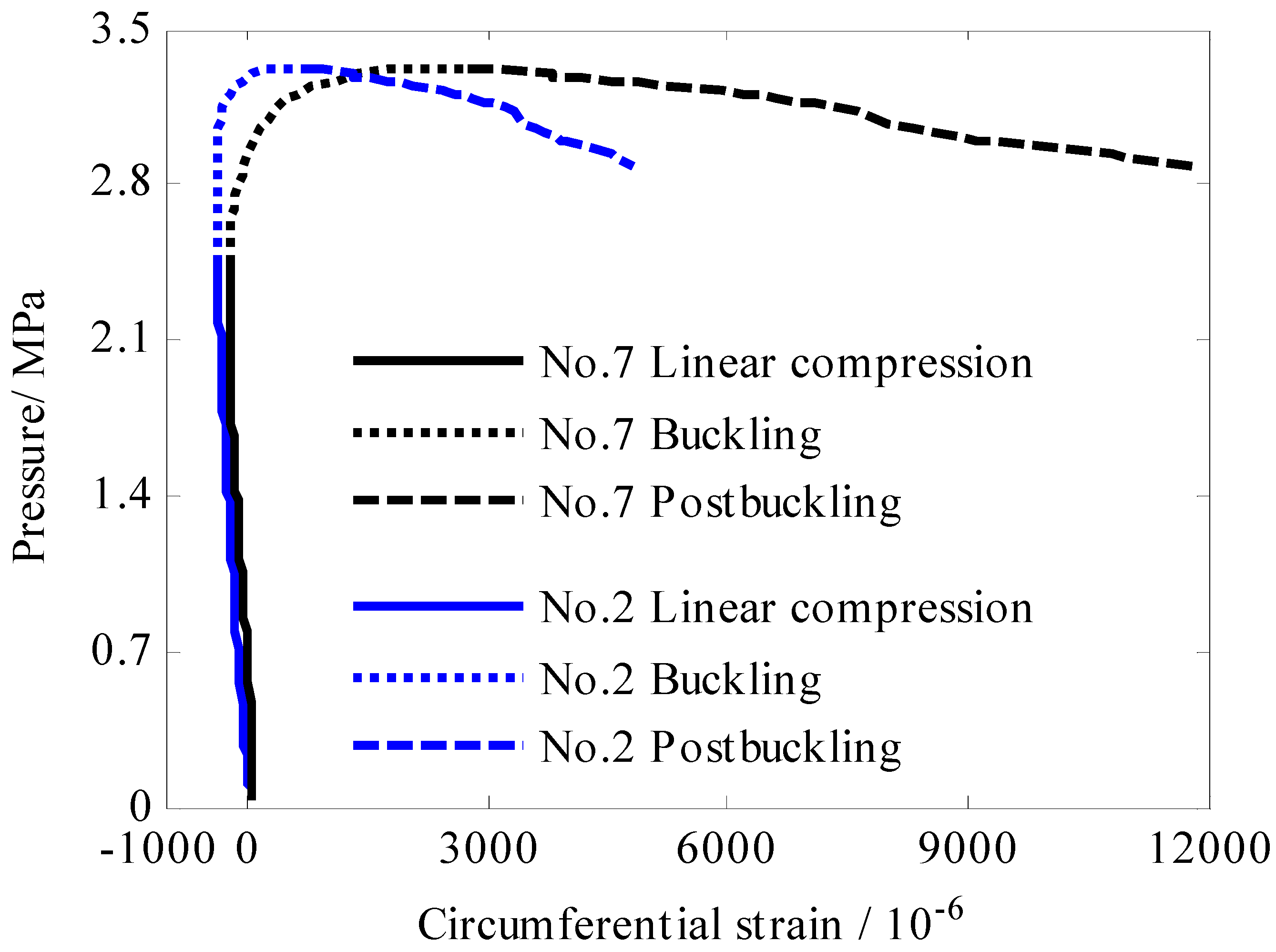
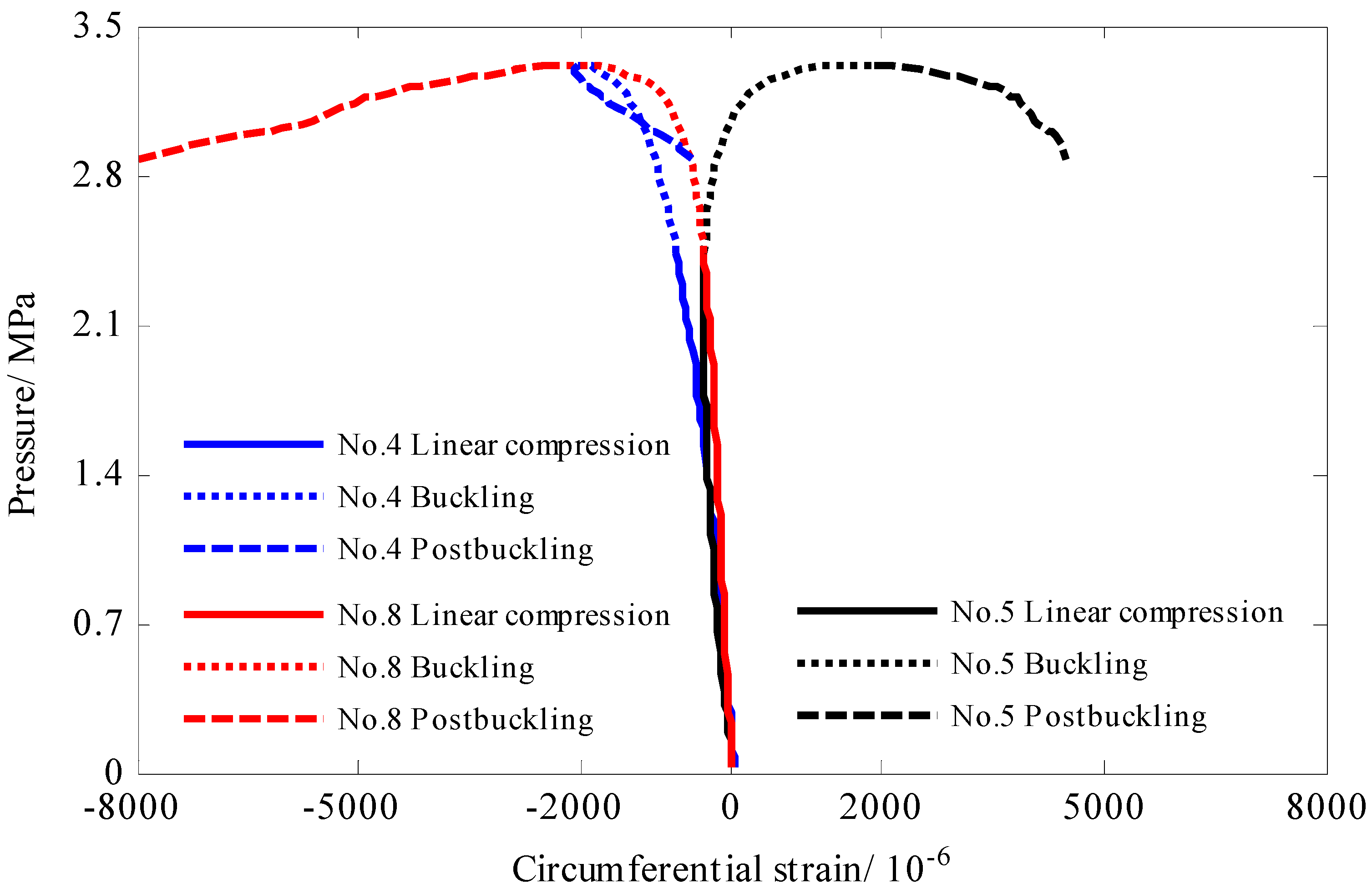
- The buckling behavior of composite cylindrical shell under hydrostatic pressure was a progressive evolution process which accounted for more than 20% of the load history, and the load carrying capacity was still increasing in this stage.
- (2)
- As for the post-buckling behavior, the initial buckling wave was extended while the load carrying capacity of the shell decreases. Both the perfect and perforated composite cylindrical shell collapsed at the trough of the buckling wave.
- (3)
- The buckling shape of the perfect composite cylindrical shell was uniformly symmetrically distributed along the circumference. As for the perforated composite cylindrical shell, the buckling wave presented non-uniform and asymmetrical distribution due to the non-uniform circumferential stiffness.
- (4)
- Regarding the failure mode of thin-walled composite cylindrical shell under hydrostatic pressure, it presented buckling failure initially. As the shell deformation increased, material failure occurred subsequently, and the shell collapsed eventually.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Smith, C.S. Design of submersible pressure hulls in composite materials. Mar. Struct. 1991, 4, 141–182. [Google Scholar] [CrossRef]
- Ross, C.T. A conceptual design of an underwater vehicle. Ocean Eng. 2006, 33, 2087–2104. [Google Scholar] [CrossRef]
- Carvelli, V.; Panzeri, N.; Poggi, C. Buckling strength of GFRP under-water vehicles. Compos. Part B Eng. 2001, 32, 89–101. [Google Scholar] [CrossRef]
- Maali, M.; Bayrak, B.; Kiliç, M.; Sagiroglu, M.; Aydin, A.C. Buckling behavior of double-layered composite cylindrical shells. Int. J. Press. Vessel. Pip. 2021, 191, 104328. [Google Scholar] [CrossRef]
- Ouellette, P.; Hoa, S.V.; Sankar, T.S. Buckling of composite cylinders under external pressure. Polym. Compos. 1986, 7, 363–374. [Google Scholar] [CrossRef]
- Khot, N.S. Buckling and postbuckling behavior of composite cylindrical shells under axial compression. AIAA J. 1970, 8, 229–235. [Google Scholar] [CrossRef]
- Tafreshi, A. Buckling and post-buckling analysis of composite cylindrical shells with cutouts subjected to internal pressure and axial compression loads. Int. J. Press. Vessel. Pip. 2002, 79, 351–359. [Google Scholar] [CrossRef]
- Lopatin, A.V.; Morozov, E.V. Buckling of composite cylindrical shells with rigid end disks under hydrostatic pressure. Compos. Struct. 2017, 173, 136–143. [Google Scholar] [CrossRef]
- Lopatin, A.V.; Morozov, E.V. Buckling of a composite cantilever circular cylindrical shell subjected to uniform external lateral pressure. Compos. Struct. 2012, 94, 553–562. [Google Scholar] [CrossRef]
- Cho, Y.S.; Oh, D.H.; Paik, J.K. An empirical formula for predicting the collapse strength of composite cylindrical-shell structures under external pressure loads. Ocean Eng. 2019, 172, 191–198. [Google Scholar] [CrossRef]
- Imran, M.; Shi, D.; Tong, L.; Elahi, A.; Uddin, M. On the elastic buckling of cross-ply composite closed cylindrical shell under hydrostatic pressure. Ocean Eng. 2011, 227, 108633. [Google Scholar] [CrossRef]
- Ehsani, A.; Rezaeepazhand, J. Stacking sequence optimization of laminated composite grid plates for maximum buckling load using genetic algorithm. Int. J. Mech. Sci. 2016, 119, 97–106. [Google Scholar] [CrossRef]
- Cai, B.; Liu, Y.; Liu, Z.; Tian, X.; Ji, R.; Li, H. Reliability-based load and resistance factor design of composite pressure vessel under external hydrostatic pressure. Compos. Struct. 2011, 93, 2844–2852. [Google Scholar] [CrossRef]
- Amaechi, C.V.; Gillett, N.; Odijie, A.C.; Hou, X.; Ye, J. Composite risers for deep waters using a numerical modelling approach. Compos. Struct. 2019, 210, 486–499. [Google Scholar] [CrossRef]
- Malinowski, M.; Belica, T.; Magnucki, K. Buckling and post-buckling behaviour of elastic seven-layered cylindrical shells—FEM study. Thin-Walled Struct. 2015, 94, 478–484. [Google Scholar] [CrossRef]
- Tsouvalis, N.; Zafeiratou, A.; Papazoglou, V. The effect of geometric imperfections on the buckling behaviour of composite laminated cylinders under external hydrostatic pressure. Compos. Part B Eng. 2003, 34, 217–226. [Google Scholar] [CrossRef]
- Shen, K.C.; Pan, G.; Lu, J. Buckling and layer failure of composite laminated cylinders subjected to hydrostatic pressure. Sci. Eng. Compos. Mater. 2017, 24, 415–422. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Masoodi, A.R. Shell instability analysis by using mixed interpolation. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 419. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Masoodi, A.R. Analyzing FG shells with large deformations and finite rotations. World J. Eng. 2019, 16, 636–647. [Google Scholar] [CrossRef]
- Geier, B.; Meyer-Piening, H.-R.; Zimmermann, R. On the influence of laminate stacking on buckling of composite cylindrical shells subjected to axial compression. Compos. Struct. 2002, 55, 467–474. [Google Scholar] [CrossRef]
- Maalawi, K. Optimal buckling design of anisotropic rings/long cylinders under external pressure. J. Mech. Mater. Struct. 2008, 3, 775–793. [Google Scholar] [CrossRef][Green Version]
- Imran, M.; Shi, D.-Y.; Tong, L.-L.; Elahi, A.; Waqas, H.M.; Uddin, M. Multi-objective design optimization of composite submerged cylindrical pressure hull for minimum buoyancy factor and maximum buckling load capacity. Def. Technol. 2021, 17, 1190–1206. [Google Scholar] [CrossRef]
- Hernández-Moreno, H.; Douchin, B.; Collombet, F.; Choqueuse, D.; Davies, P. Influence of winding pattern on the mechanical behavior of filament wound composite cylinders under external pressure. Compos. Sci. Technol. 2008, 68, 1015–1024. [Google Scholar] [CrossRef]
- Li, Z.-M.; Lin, Z.-Q.; Chen, G.-L. Nonlinear Buckling and Postbuckling Behavior of 3D Braided Composite Cylindrical Shells under External Pressure Loads in Thermal Environments. J. Press. Vessel Technol. 2009, 131, 061206. [Google Scholar] [CrossRef]
- Li, Z.-M.; Zhao, Y.-X.; Chen, X.-D. Non-Linear Buckling and Postbuckling Behavior of 3D Braided Cylindrical Panels under Axial Compression in Thermal Environments. Mech. Adv. Mater. Struct. 2014, 21, 490–504. [Google Scholar] [CrossRef]
- Messager, T.; Pyrz, M.; Gineste, B.; Chauchot, P. Optimal laminations of thin underwater composite cylindrical vessels. Compos. Struct. 2002, 58, 529–537. [Google Scholar] [CrossRef]
- Shen, K.C.; Pan, G. Optimizing the buckling strength of filament winding composite cylinders under hydrostatic pressure. J. Reinf. Plast. Compos. 2018, 37, 892–904. [Google Scholar]
- Lee, G.C.; Kweon, J.H.; Choi, J.H. Optimization of composite sandwich cylinders for underwater vehicle application. Compos. Struct. 2013, 96, 691–697. [Google Scholar] [CrossRef]
- Hur, S.H.; Son, H.J.; Kweon, J.H.; Choi, J.H. Postbuckling of composite cylinders under external hydrostatic pressure. Compos. Struct. 2008, 86, 114–124. [Google Scholar] [CrossRef]
- Ross, C.T.F.; Little, A.P.F.; Haidar, Y.; Waheeb, A.A. Buckling of Carbon/Glass composite tubes under uniform external hydrostatic pressure. Strain 2011, 47, 156–174. [Google Scholar] [CrossRef]
- Moon, C.J.; Kim, I.H.; Choi, B.H.; Kweon, J.H.; Choi, J.H. Buckling of filament-wound composite cylinders subjected to hydrostatic pressure for underwater vehicle applications. Compos. Struct. 2010, 92, 2241–2251. [Google Scholar] [CrossRef]
- Shen, K.-C.; Pan, G. Buckling and strain response of filament winding composite cylindrical shell subjected to hydrostatic pressure: Numerical solution and experiment. Compos. Struct. 2021, 276, 114534. [Google Scholar] [CrossRef]



| Properties | Symbol | Value | Unit |
|---|---|---|---|
| Elastic modulus | E11 | 102 | GPa |
| E22 | 7 | GPa | |
| E33 | 7 | GPa | |
| Poisson’s ratio | v12 | 0.16 | |
| v13 | 0.16 | ||
| v23 | 0.32 | ||
| Shear modulus | G12 | 8 | GPa |
| G13 | 8 | GPa | |
| G23 | 4.5 | GPa |
| Specimens | A# | B# | C# |
|---|---|---|---|
| pinitial/MPa | 2.42 | 2.24 (−7.4%) | 2.44 (0.83%) |
| pterminate/MPa | 3.06 | 3.09 (0.98%) | 3.32 (8.5%) |
| pfailure/MPa | 2.58 | 2.64 (2.3%) | 2.88 (11.6%) |
| Deformation at ppost |  ppost = 2.7 MPa |  ppost = 2.74 MPa |  ppost = 2.96 MPa |
| Failure morphology |  |  |  |
| Specimens | A# | B# | C# |
|---|---|---|---|
| Load history/MPa | 0–3.06 | 0–3.09 | 0–3.32 |
| Buckling Stage/MPa | 2.42–3.06 | 2.24–3.09 | 2.44–3.32 |
| Proportion | 20.9% | 27.5% | 26.5% |
| Specimens | A# | B# | C# |
|---|---|---|---|
| Critical buckling pressure/MPa | 3.02 | 3.07 | 3.07 |
| Buckling mode | 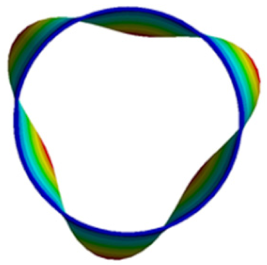 |  |  |
| Specimens | Crest Section | Trough Section | Boundary of Crest and Trough |
|---|---|---|---|
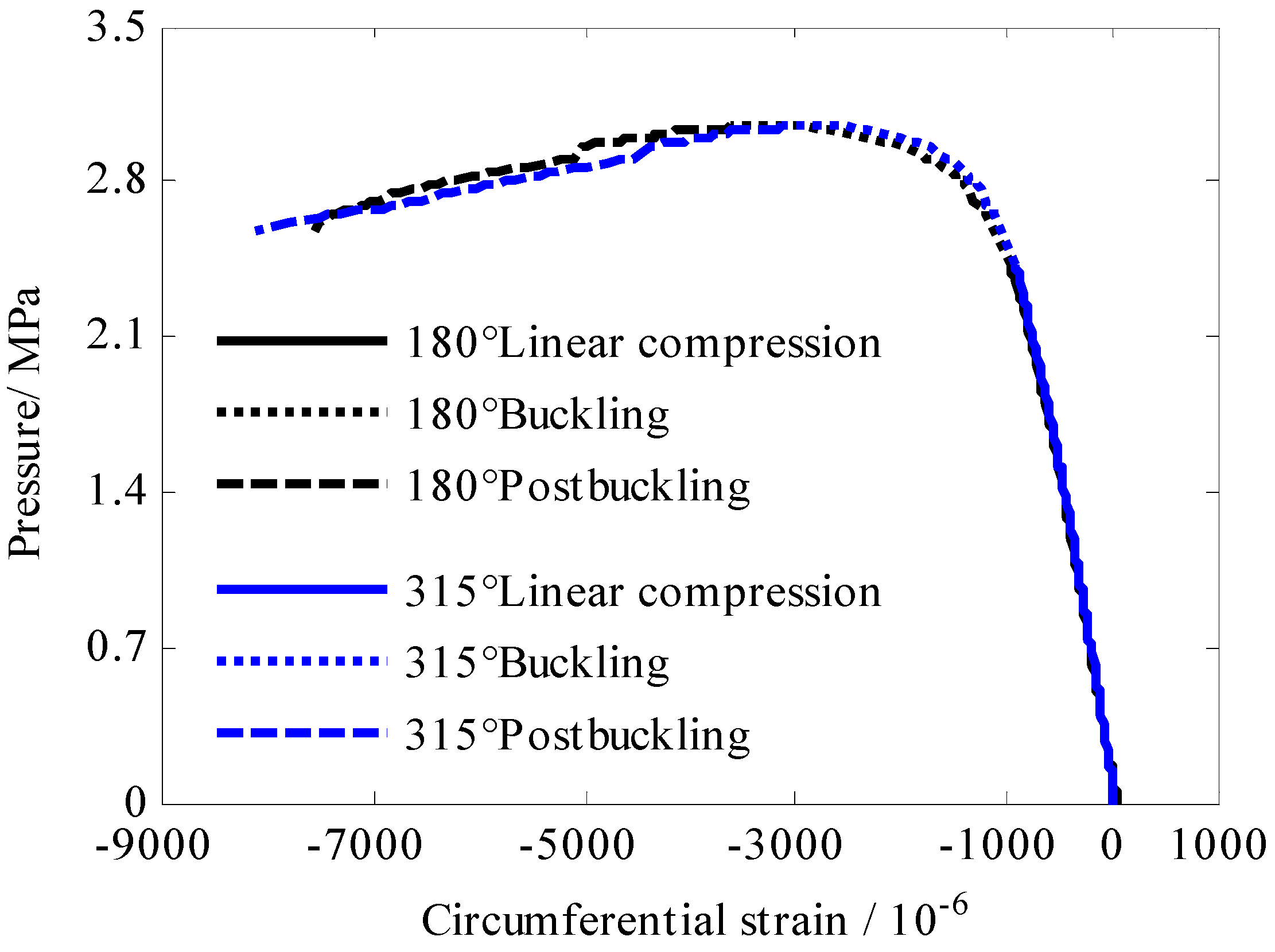
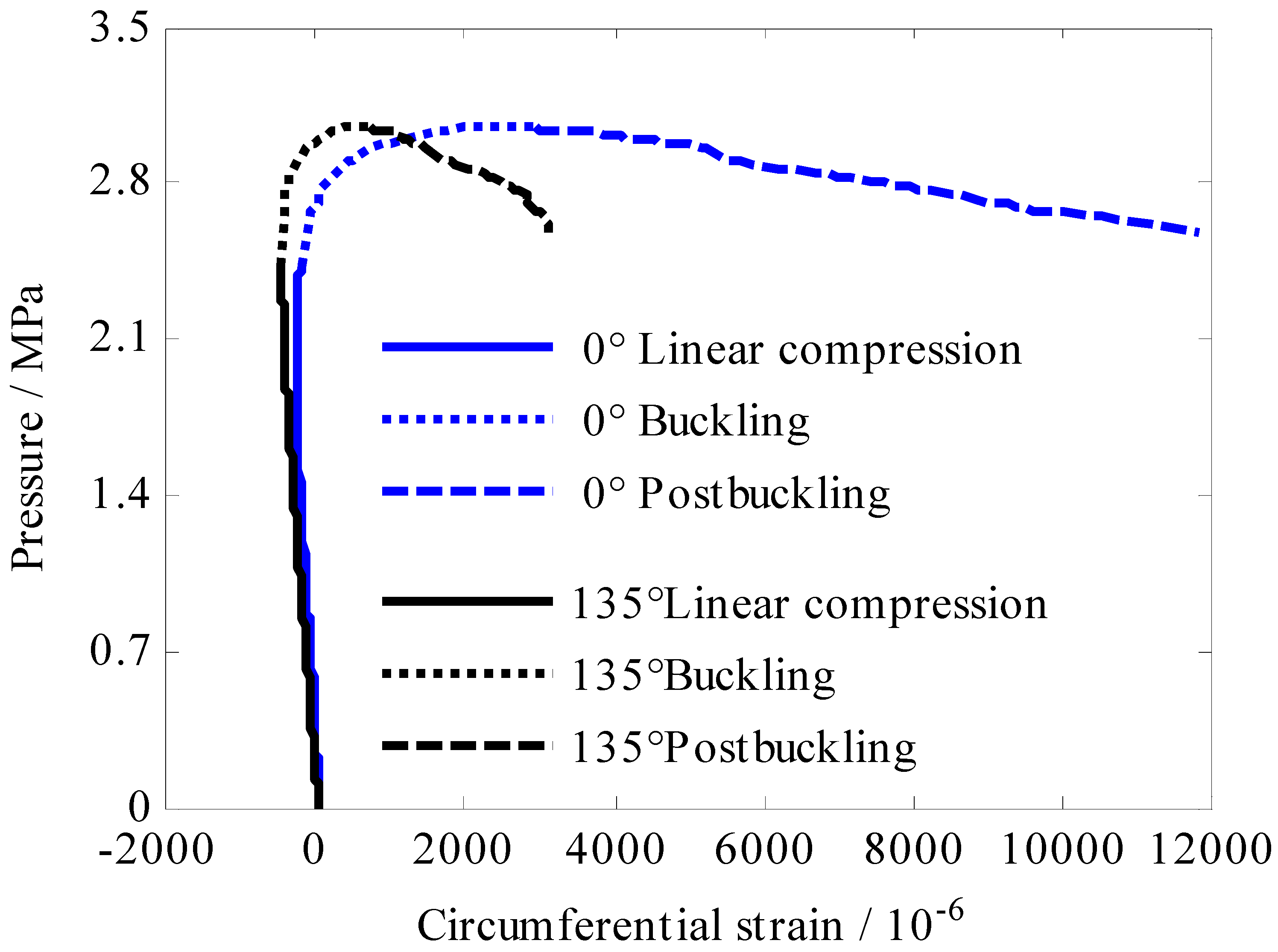
| A# | 180°, 315° | 0°, 135° | 45°, 90°, 270° 225° |
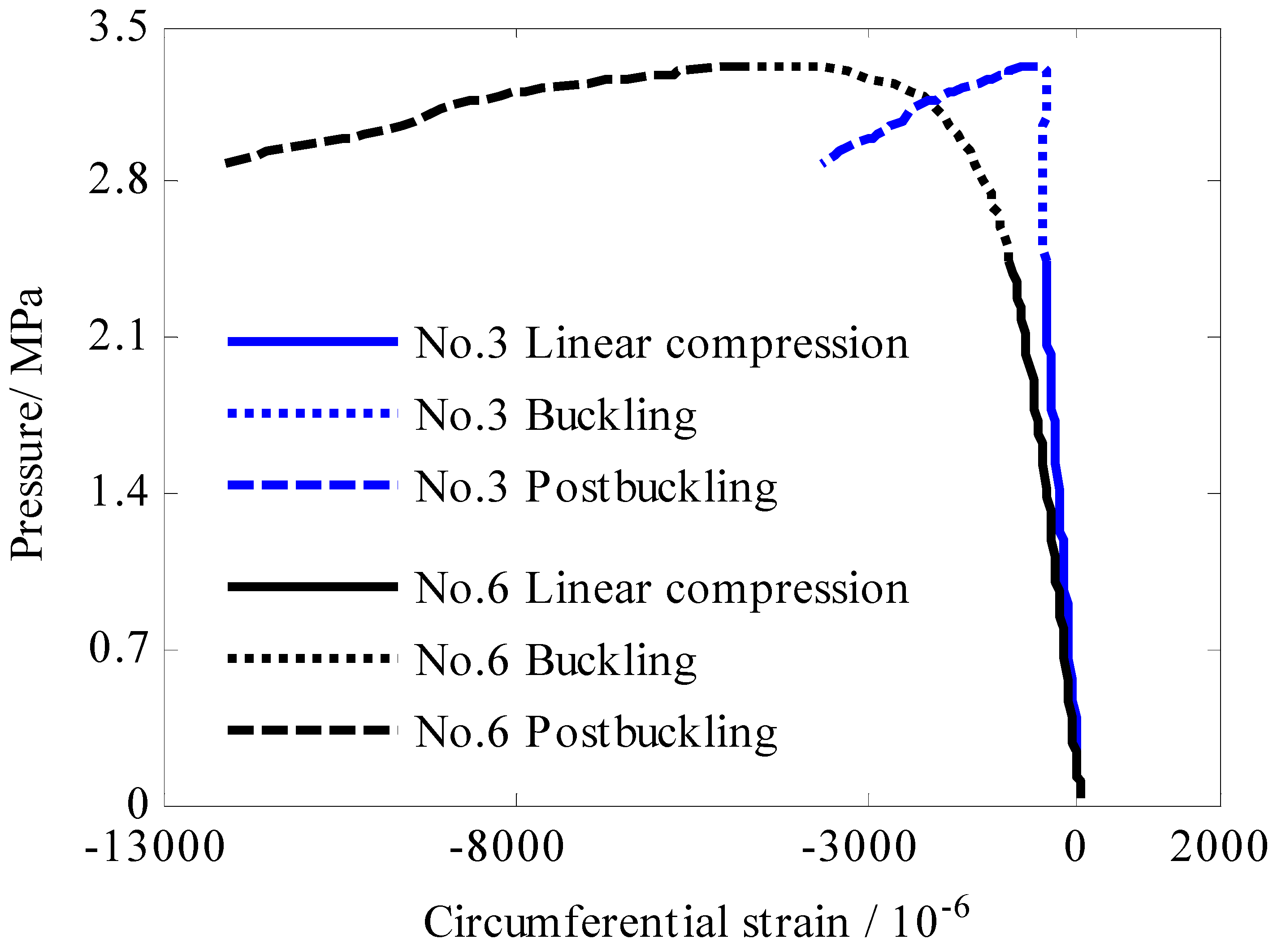
| C# | No.3, No.6 | No.2, No.7 | No.4, No.5, No.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, K.-C.; Yang, Z.-Q.; Jiang, L.-L.; Pan, G. Buckling and Post-Buckling Behavior of Perfect/Perforated Composite Cylindrical Shells under Hydrostatic Pressure. J. Mar. Sci. Eng. 2022, 10, 278. https://doi.org/10.3390/jmse10020278
Shen K-C, Yang Z-Q, Jiang L-L, Pan G. Buckling and Post-Buckling Behavior of Perfect/Perforated Composite Cylindrical Shells under Hydrostatic Pressure. Journal of Marine Science and Engineering. 2022; 10(2):278. https://doi.org/10.3390/jmse10020278
Chicago/Turabian StyleShen, Ke-Chun, Zhao-Qi Yang, Lei-Lei Jiang, and Guang Pan. 2022. "Buckling and Post-Buckling Behavior of Perfect/Perforated Composite Cylindrical Shells under Hydrostatic Pressure" Journal of Marine Science and Engineering 10, no. 2: 278. https://doi.org/10.3390/jmse10020278
APA StyleShen, K.-C., Yang, Z.-Q., Jiang, L.-L., & Pan, G. (2022). Buckling and Post-Buckling Behavior of Perfect/Perforated Composite Cylindrical Shells under Hydrostatic Pressure. Journal of Marine Science and Engineering, 10(2), 278. https://doi.org/10.3390/jmse10020278








