Numerical and Experimental Study of Hydrodynamic Response for a Novel Buoyancy-Distributed Floating Foundation Based on the Potential Theory
Abstract
:1. Introduction
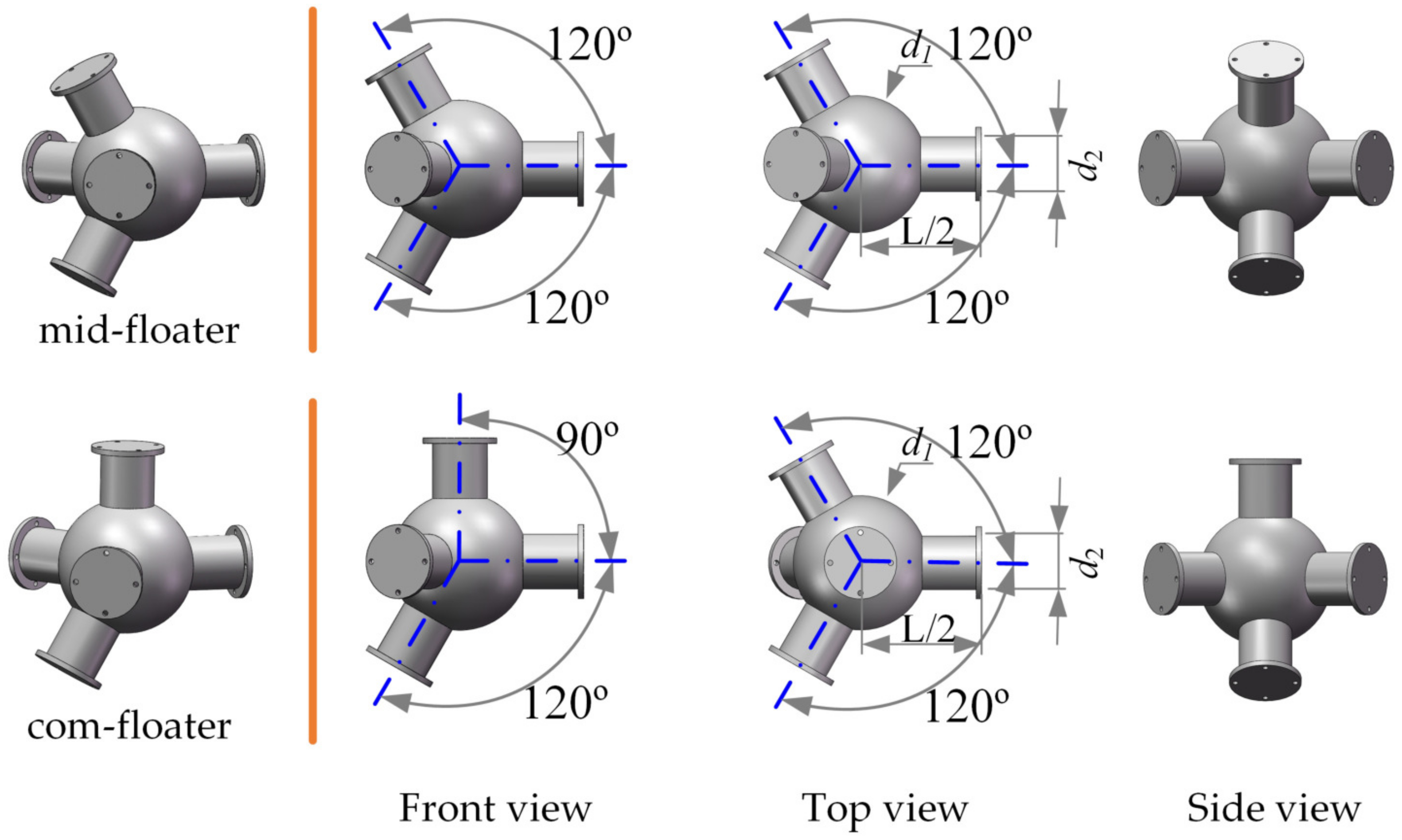
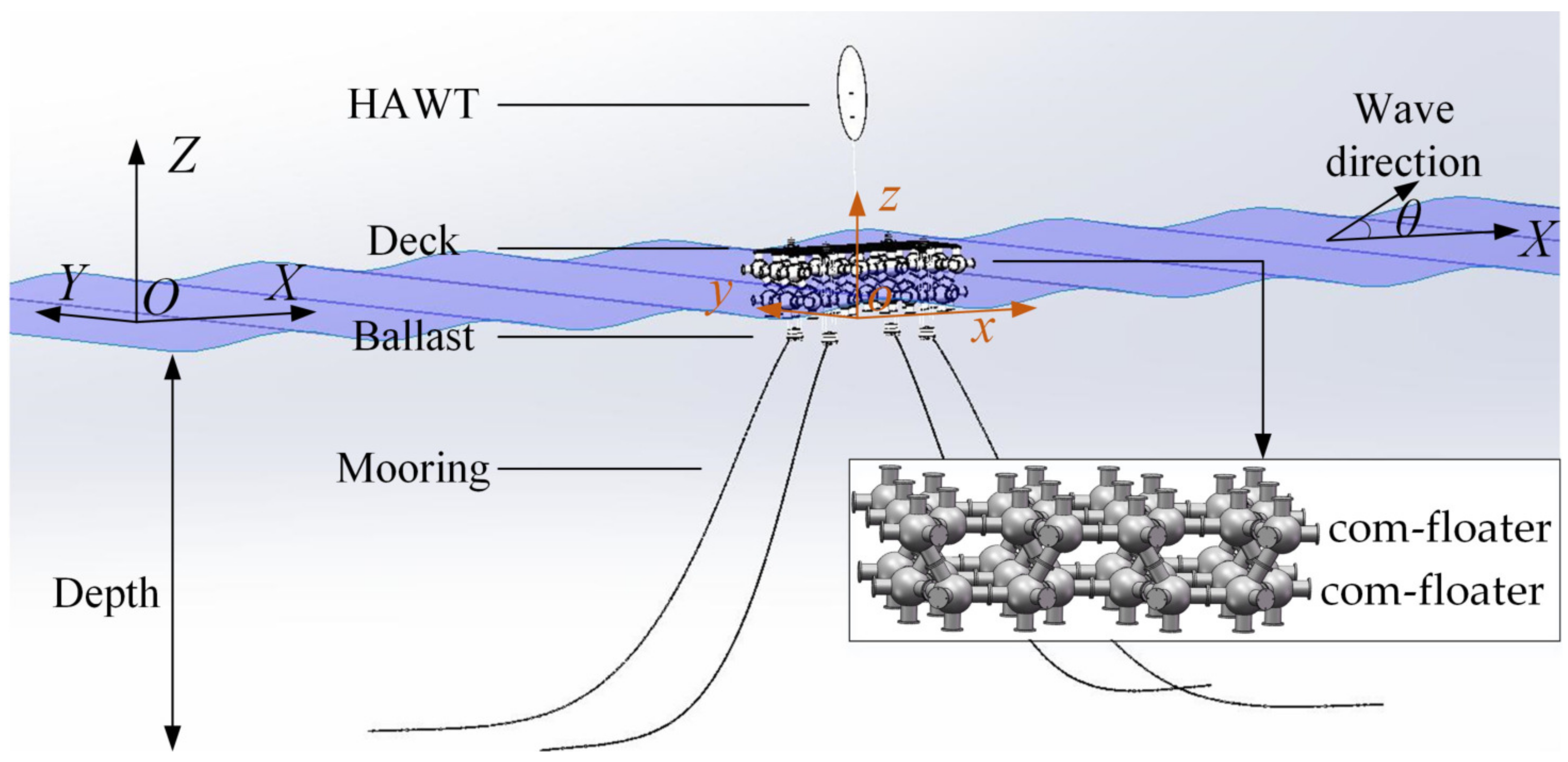
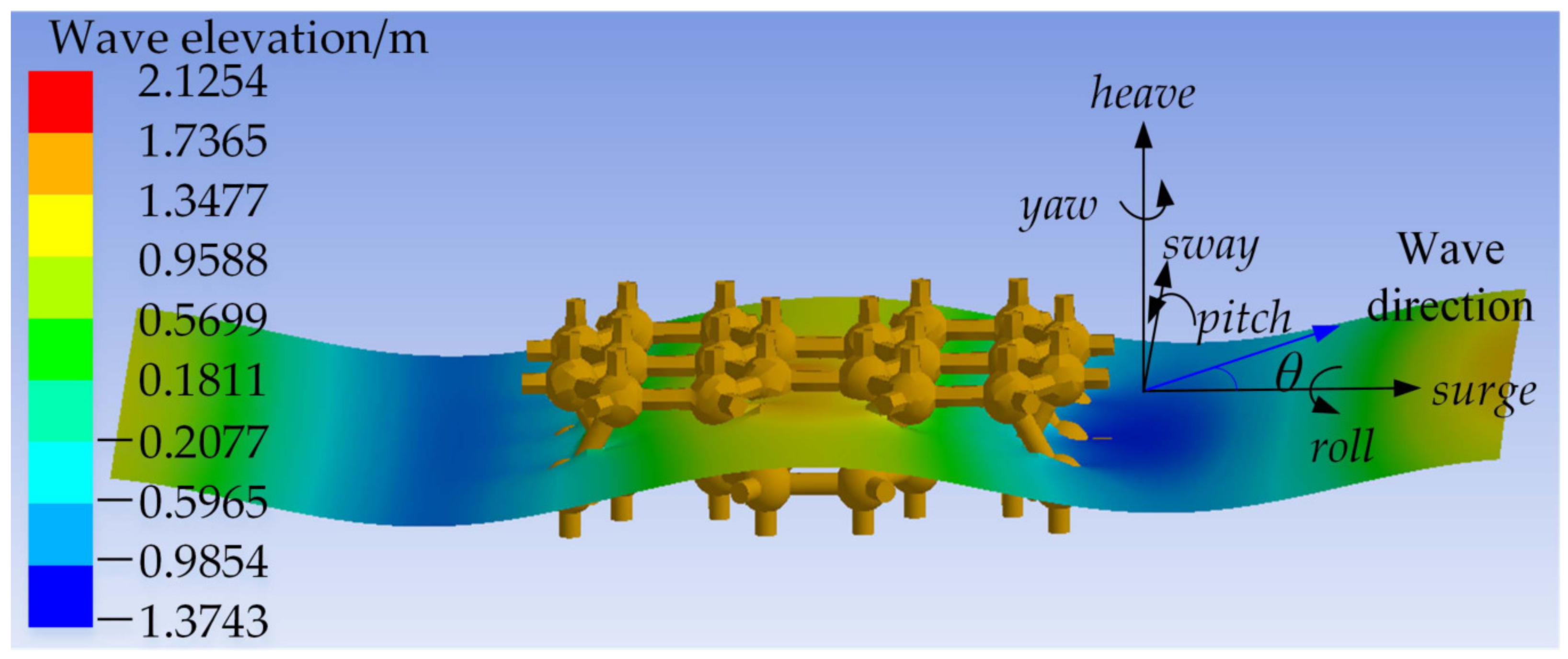
2. Model Description
3. Theory Background
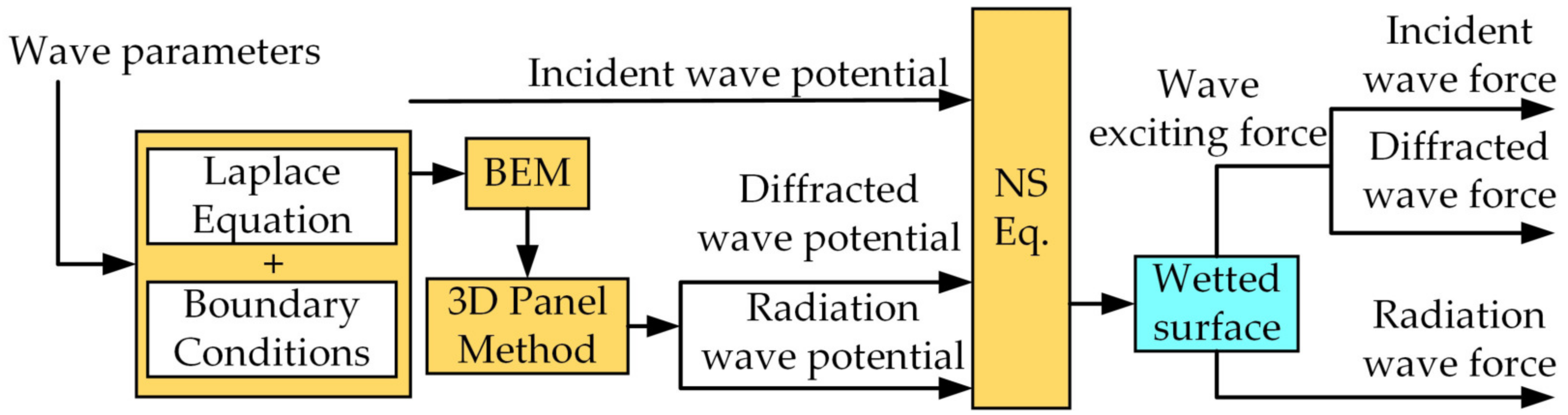
3.1. Potential Theory
3.2. Boundary Element Method
3.3. 3D Panel Method
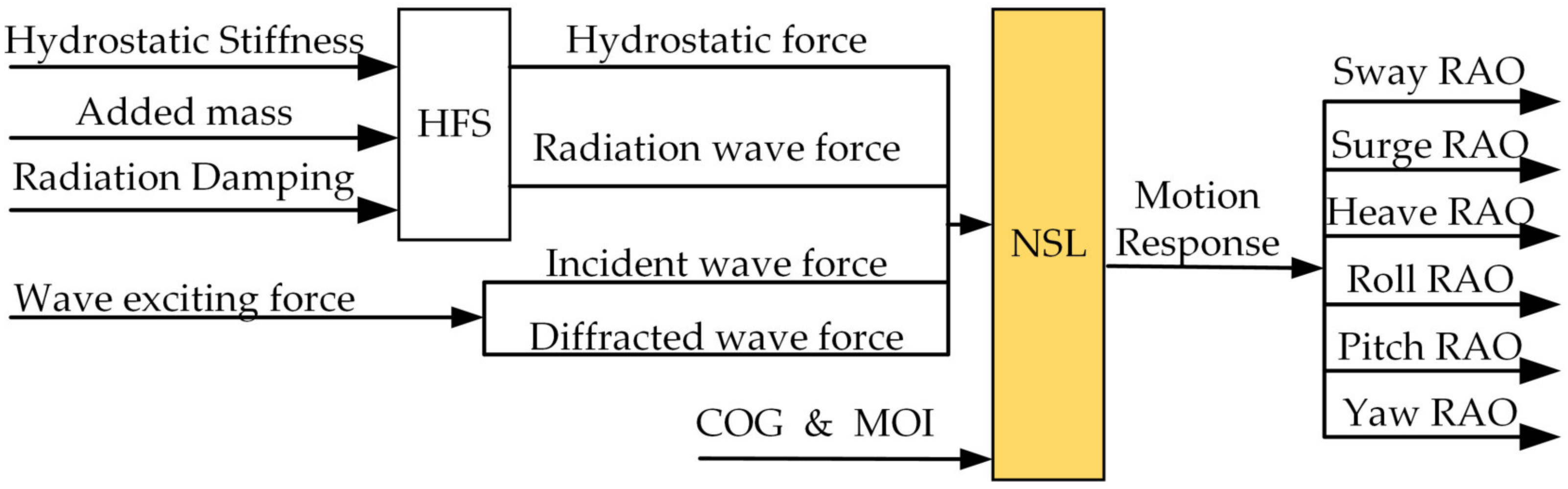
3.4. Wave Force
3.5. The Equation of Motion
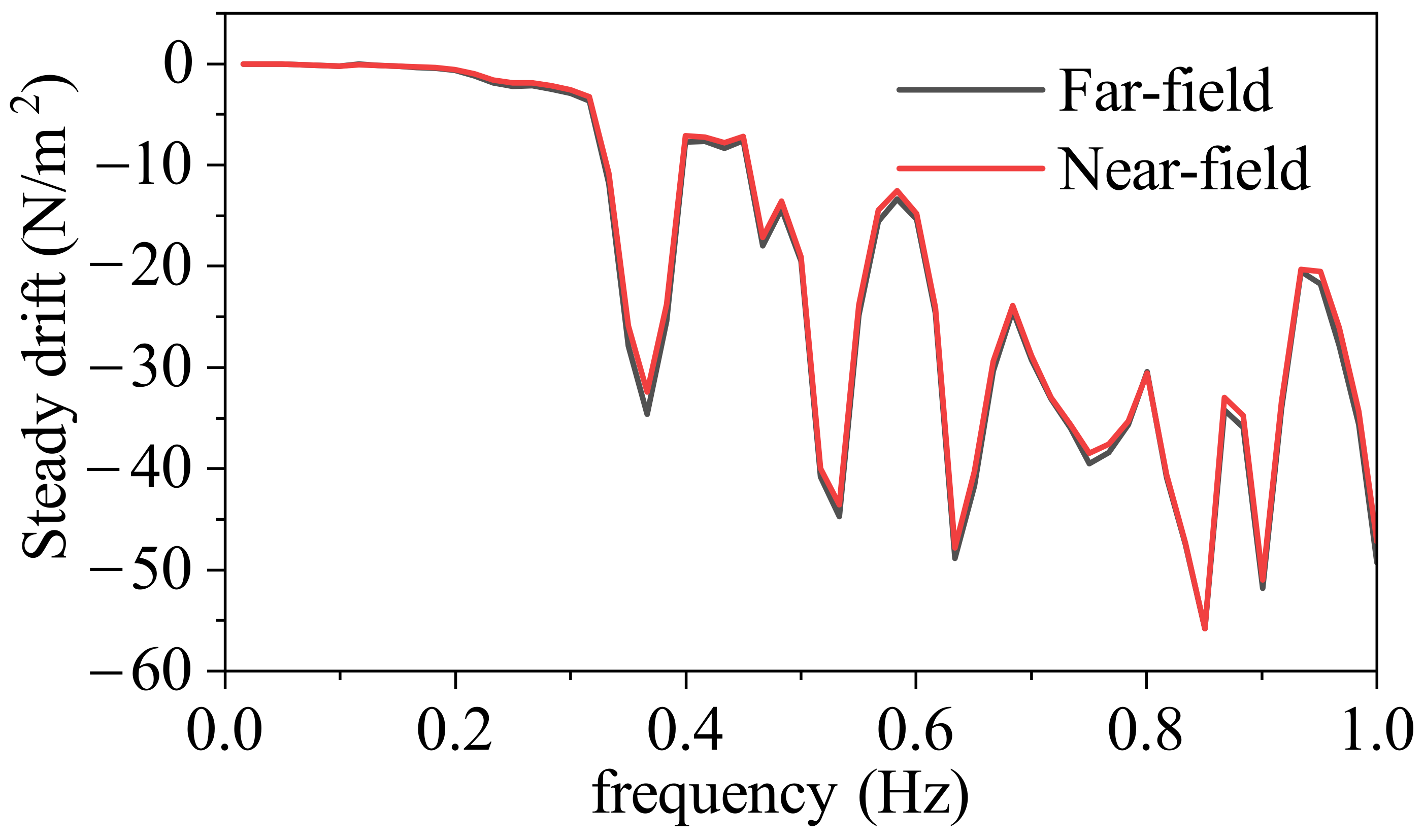
4. Results
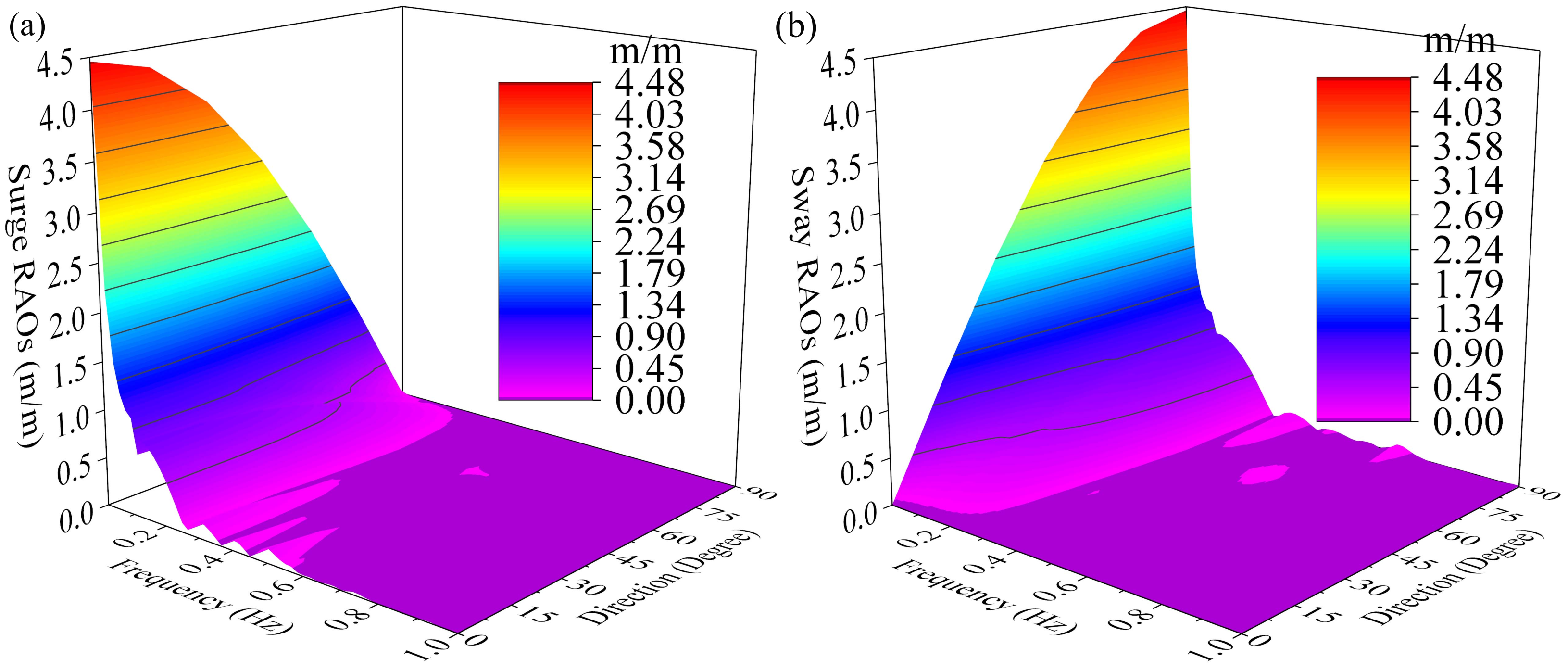
4.1. RAOs under Different Wave Directions
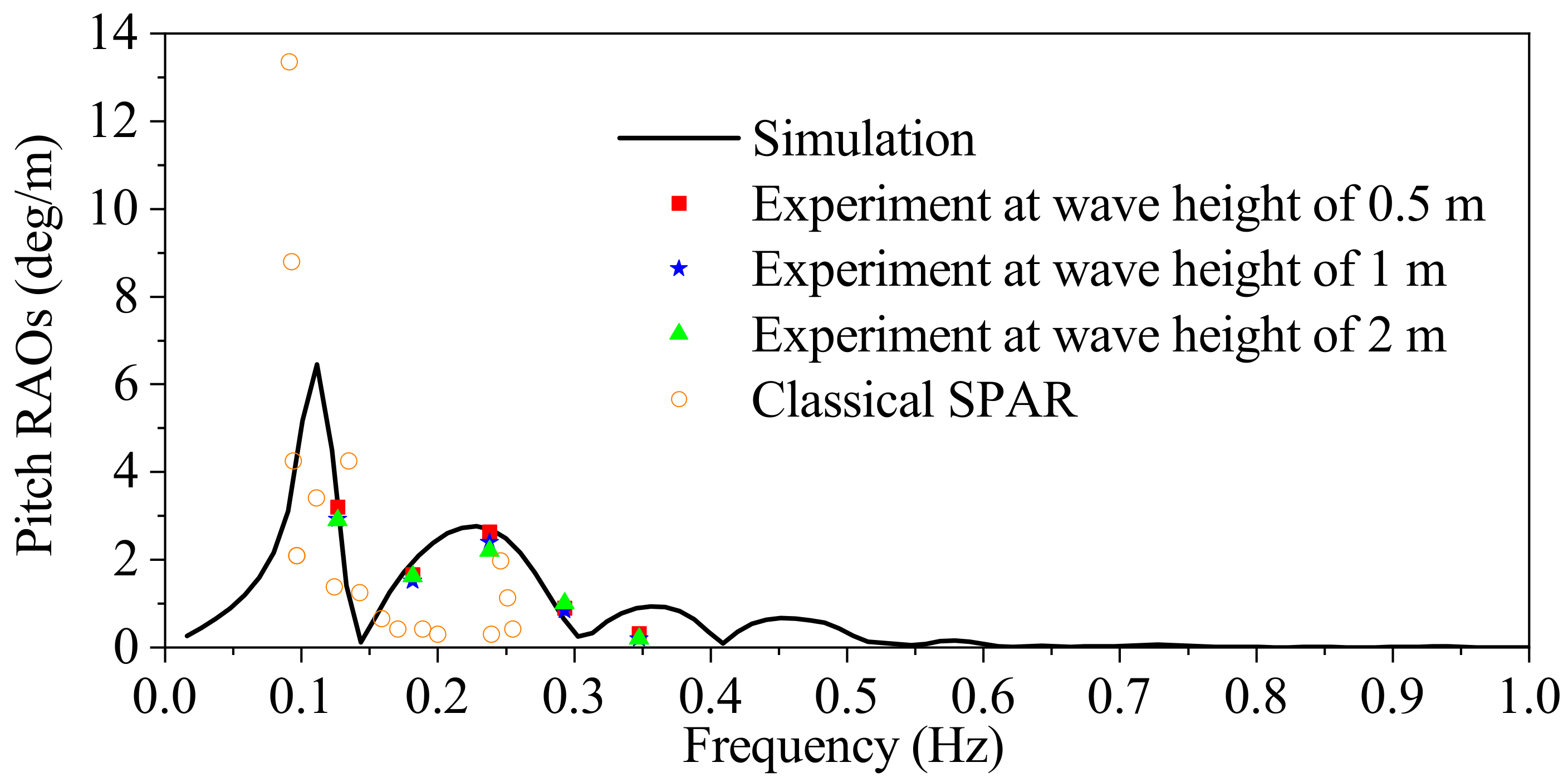
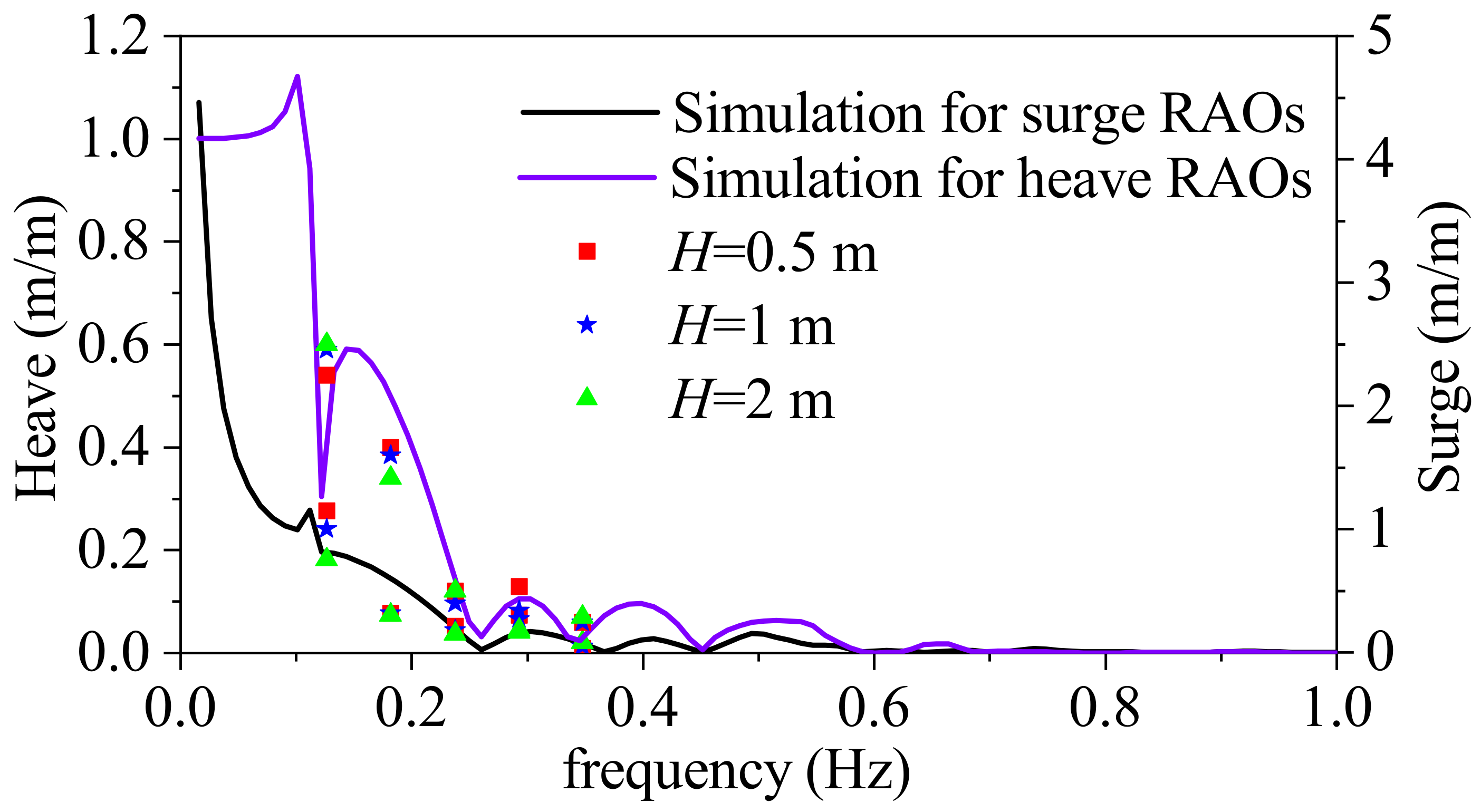
4.2. RAOs Comparison
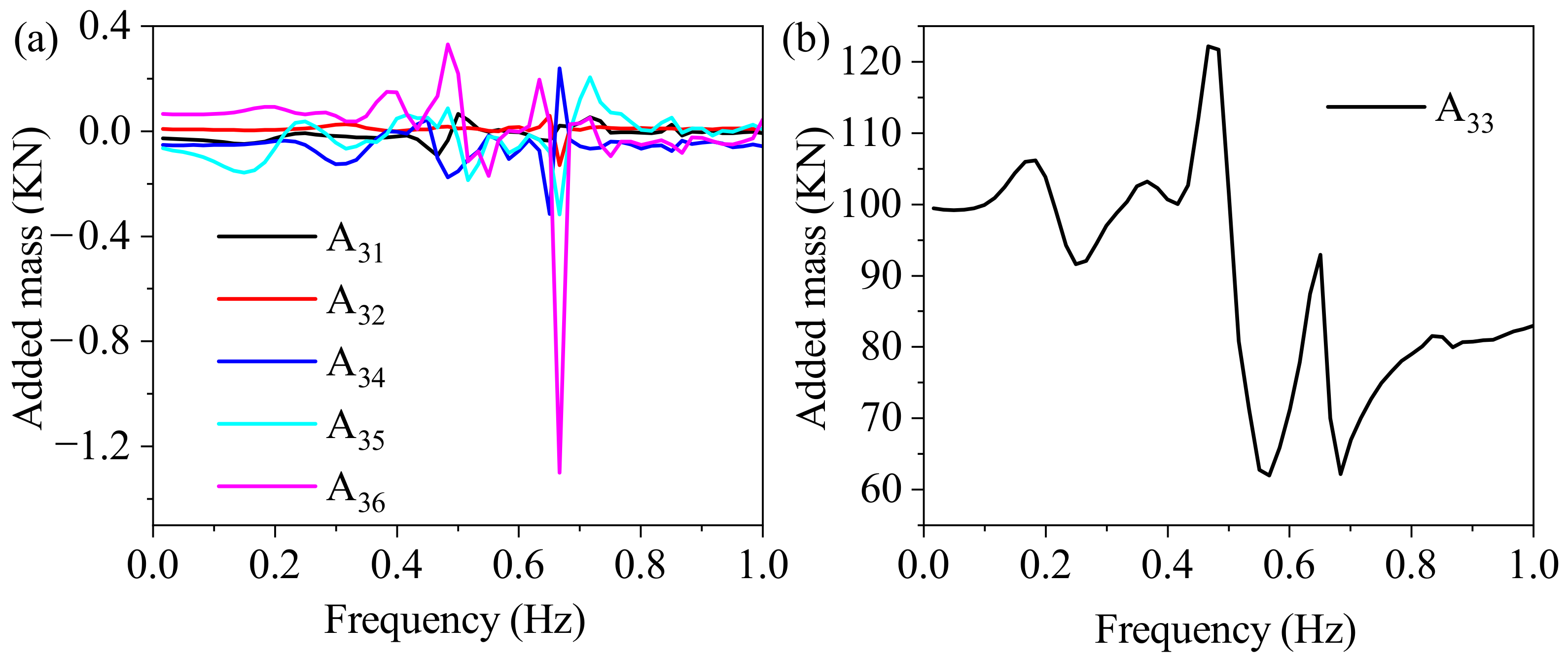
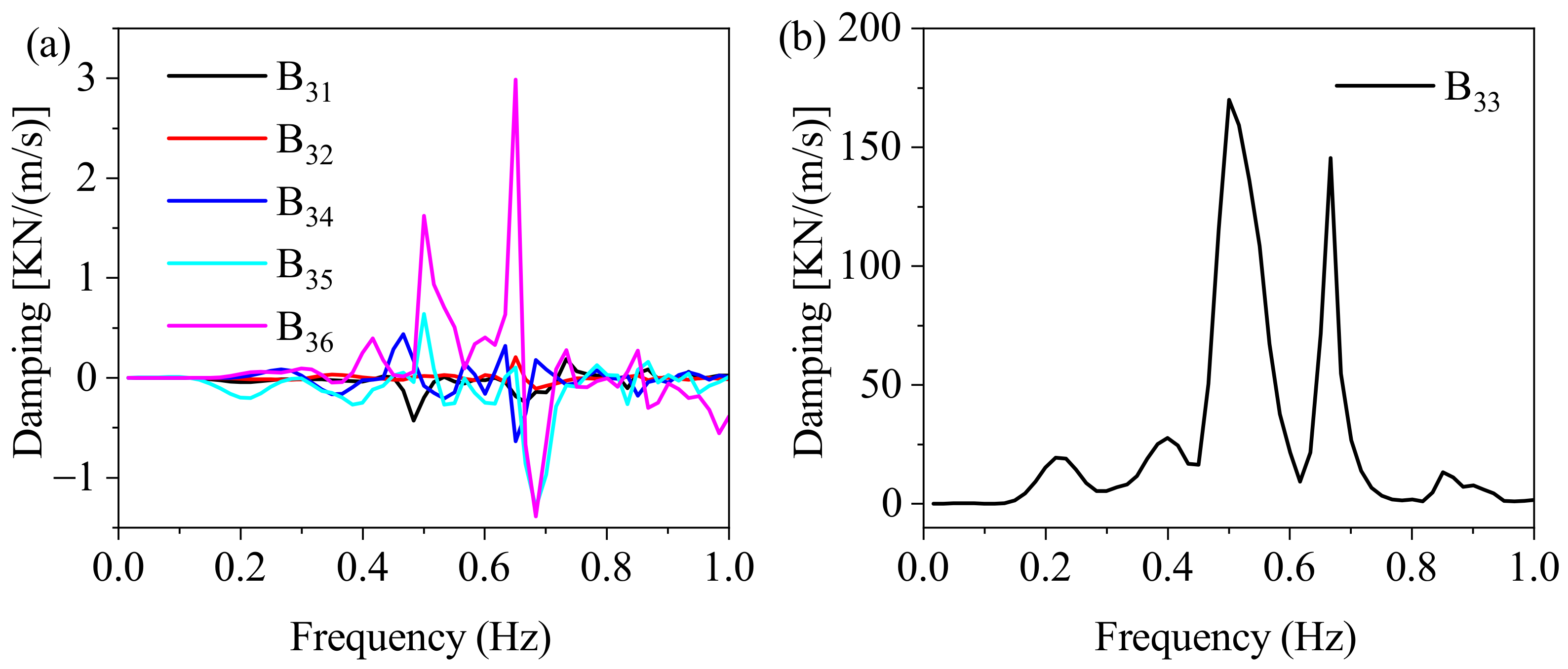
4.3. Symmetry and Coupling
5. Conclusions
- The pitch response on the surge direction is influenced significantly by the wave directions, while the surge response is less impacted. General trends of the pitch and heave responses both decrease with the increase of wave frequencies.
- Regular wave test results show that the pitch RAOs agree well with the numerical results of the potential theory. The proposed floating system behaves well in the low-frequency band, while a classical SPAR has a better performance in the mid-frequency band.
- The coupling relationship between six degrees of freedom shows that the BDFF can be decoupled to make the structure easy to analyze due to the symmetrical design.
- The structural optimization of floaters [34]: Since the overall size and structural properties strongly rely on the floaters, it is important to analyze the influence of the floater spacing, the floater diameter, and the foundation width/length to finally decrease the hydrodynamic response.
- The effect of mooring stiffness on the fluid–structure interaction: Since the nonlinear restoring forces are caused by the excursions of the COG, the wave–body interactions are significantly influenced by the mooring stiffness [56].
- The dependence of the hydrodynamic performance on the wave type: The impact forces caused by unbroken and broken waves are different [45]. In addition, the short crest waves with large wave steep will impact the floating foundation and break.
- The sea-keeping ability under irregular waves: The irregular waves are combinations of regular waves with different wave properties.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BDFF | Buoyancy distributed floating foundation |
| BEM | Boundary element method |
| COG | Center of gravity |
| DOFs | Degrees of freedom |
| Eq. | Equation |
| HDPE | High density polyethylen |
| HVWT | Horizontal vertical wind turbine |
| MOI | Moment of inertia |
| NSL | Newton’s Second Law |
| RAO | Response amplitude operator |
| WEC | Wave energy converter |
References
- Arapogianni, A.; Genachte, A.B.; Ochagavia, R.M.; Vergara, J.P.; Castell, D.; Tsouroukdissian, A.R.; Korbijn, J.; Bolleman, N.; Huera-Huarte, F.J.; Schuon, F.; et al. Deep Water—The Next Step for Offshore Wind Energy; European Wind Energy Association: Brussels, Belgium, 2013; pp. 972–978. [Google Scholar]
- Komatsu, M.; Kumamoto, H.; Ohta, M.; Tanaka, H.; Mori, H.; Miyazaki, S. Development of offshore wind turbine floater that blends into Japanese waters. Mitsubishi Heavy Ind. Tech. Rev. 2016, 53, 30–39. [Google Scholar]
- Bluewater. Floating Wind Systems. Available online: https://www.bluewater.com/products-technology/floating-wind-systems/ (accessed on 20 December 2021).
- Amate, J.; Sánchez, G.D.; González, G. Development of a semi-submersible barge for the installation of a TLP floating substructure. TLPWIND® case study. J. Phys. Conf. Ser. 2016, 749, 012016. [Google Scholar] [CrossRef]
- Vita, L.; Ramachandran, G.; Krieger, A.; Kvittem, M.I.; Merino, D.; Cross-Whiter, J.; Ackers, B.B. Comparison of numerical models and verification against experimental data, using Pelastar TLP concept. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015; Volume 56574, p. V009T09A047. [Google Scholar] [CrossRef]
- Huber, F. The first floating wind turbines. In Proceedings of the 2nd International Conference on Ocean Energy (ICOE 2008), Brest, France, 15–17 October 2008; pp. 15–17. [Google Scholar]
- Adam, F.; Walia, D.; Hartmann, H.; Schünemann, P.; Großmann, J. A novel modular tlp-design for offshore wind turbines using ultra high performance concrete. In Proceedings of the ACMSM25—25th Australasian Conference on Mechanics of Structures and Materials, Brisbane, QLD, Australia, 4–7 December 2018; Wang, C.M., Ho, J.C., Kitipornchai, S., Eds.; Springer: Singapore, 2020; pp. 257–268. [Google Scholar] [CrossRef]
- Iv-Groep. Self-Installing Floating Wind Turbines. Available online: https://iv-groep.nl/en/blog/2020/zelf-installerende-drijvende-windmolens (accessed on 20 December 2021).
- Equinor. Industrialising Floating Offshore Wind. Available online: https://www.equinor.com/en/what-we-do/floating-wind.html (accessed on 20 December 2021).
- Hao, K.J.; Robertson, A.N.; Jonkman, J.; Driscoll, F.; Ng, E.Y.K. Building and calibration of a fast model of the SWAY prototype floating wind turbine. In Proceedings of the 2013 International Conference on Renewable Energy Research and Applications (ICRERA), Madrid, Spain, 20–23 October 2013; pp. 788–793. [Google Scholar] [CrossRef]
- Koh, H.; Lim, Y. Floating performance stage at the Marina Bay, Singapore. In Large Floating Structures; Springer: Singapore, 2015; pp. 37–59. [Google Scholar] [CrossRef]
- Kosasih, K.M.A.; Suzuki, H.; Niizato, H.; Okubo, S. Demonstration experiment and numerical simulation analysis of full-scale barge-type floating offshore wind turbine. J. Mar. Sci. Eng. 2020, 8, 880. [Google Scholar] [CrossRef]
- Henderson, A.R.; Zaaijer, M.; Bulder, B.; Pierik, J.; Huijsmans, R.; van Hees, M.; Snijders, E.; Wijnants, G.H.; Wolf, M.J. Floating windfarms for shallow offshore sites. In Proceedings of the Fourteenth International Offshore and Polar Engineering Conference, Toulon, France, 23–28 May 2004. [Google Scholar]
- Robertson, A.; Jonkman, J.; Masciola, M.; Song, H.; Goupee, A.; Coulling, A.; Luan, C. Definition of the Semisubmersible Floating System for Phase II of OC4; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2014. [CrossRef] [Green Version]
- Galván, J.; Sánchez-Lara, M.; Mendikoa, I.; Pérez-Morán, G.; Nava, V.; Rodríguez-Arias, R. NAUTILUS-DTU10 MW Floating Offshore Wind Turbine at Gulf of Maine: Public numerical models of an actively ballasted semisubmersible. J. Phys. Conf. Ser. 2018, 1102, 012015. [Google Scholar] [CrossRef]
- Roddier, D.; Cermelli, C.; Aubault, A.; Weinstein, A. WindFloat: A floating foundation for offshore wind turbines. J. Renew. Sustain. Energy 2010, 2, 033104. [Google Scholar] [CrossRef]
- Legaz, M.J.; Coronil, D.; Mayorga, P.; Fernández, J. Study of a hybrid renewable energy platform: W2Power. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018; p. V11AT12A040. [Google Scholar] [CrossRef]
- Lefranc, M.; Torud, A. Three wind turbines on one floating unit, feasibility, design and cost. In Proceedings of the OTC Offshore Technology Conference, Houston, TX, USA, 2–5 May 2011; p. OTC-21485-MS. [Google Scholar] [CrossRef]
- Huijs, F.; de Bruijn, R.; Savenije, F. Concept design verification of a semi-submersible floating wind turbine using coupled simulations. Energy Procedia 2014, 53, 2–12. [Google Scholar] [CrossRef] [Green Version]
- Sarlak, H.; Pegalajar-Jurado, A.; Bredmose, H. CFD simulations of a newly developed floating offshore wind turbine platform using OpenFOAM. In Proceedings of the 21st Australasian Fluid Mechanics Conference, Adelaide, Australia, 10–13 December 2018. [Google Scholar]
- Hexicon. TwinWind: Maximising Production, Reducing Cost, Motion Performance. Available online: https://www.hexicon.eu/twinwind/ (accessed on 20 December 2021).
- Le Boulluec, M.; Ohana, J.; Martin, A.; Houmard, A. Tank testing of a new concept of floating offshore wind turbine. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; Volume 55423, p. V008T09A100. [Google Scholar] [CrossRef]
- Baita-Saavedra, E.; Cordal-Iglesias, D.; Filgueira-Vizoso, A.; Morató, À.; Lamas-Galdo, I.; Ȧlvarez-Feal, C.; Carral, L.; Castro-Santos, L. An economic analysis of an innovative floating offshore wind platform built with concrete: The SATH platform. Appl. Sci. 2020, 10, 3678. [Google Scholar] [CrossRef]
- Liu, Z.; Fan, Y.; Wang, W.; Qian, G. Numerical study of a proposed semi-submersible floating platform with different numbers of offset columns based on the deepcwind prototype for improving the wave-resistance ability. Appl. Sci. 2019, 9, 1255. [Google Scholar] [CrossRef] [Green Version]
- Adam, F.; Myland, T.; Schuldt, B.; Großmann, J.; Dahlhaus, F. Evaluation of internal force superposition on a TLP for wind turbines. Renew. Energy 2014, 71, 271–275. [Google Scholar] [CrossRef]
- Sahu, A.; Yadav, N.; Sudhakar, K. Floating photovoltaic power plant: A review. Renew. Sustain. Energy Rev. 2016, 66, 815–824. [Google Scholar] [CrossRef]
- Özgür, K. Modular Floating Buoy System with Multi-Layered Swing Mechanism for Stabilization of Offshore Platform. International Patent Application No. PCT/TR2016/050501, 17 May 2018. [Google Scholar]
- Float Inc. The PSP (Pneumatically Stabilized Platform) Technology. Available online: http://www.floatinc.com/PSPTechnology.aspx (accessed on 20 December 2021).
- Crema, I.; Simonetti, I.; Cappietti, L.; Oumeraci, H. Laboratory experiments on oscillating water column wave energy converters integrated in a very large floating structure. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015; pp. 6–11. [Google Scholar]
- Hao, H.; Guo, Z.; Liao, K.; Xu, G. Studies on the initial stability of an air-cushion supported floating platform for offshore wind turbine. In Proceedings of the Thirteenth ISOPE Pacific/Asia Offshore Mechanics Symposium, Jeju, Korea, 14–17 October 2018. [Google Scholar]
- Diendorfer, C.; Haider, M.; Lauermann, M. Performance analysis of offshore solar power plants. Energy Procedia 2014, 49, 2462–2471. [Google Scholar] [CrossRef] [Green Version]
- Pakozdi, C.; Kendon, T.E.; Stansberg, C.T. Breaking Wave Impact on a Platform Column: An Introductory CFD Study. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; pp. 645–654. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, B.; Vogel, C.; Willden, R.; Zang, J.; Zhang, L. Hydrodynamic performance of a floating breakwater as an oscillating-buoy type wave energy converter. Appl. Energy 2020, 257, 113996. [Google Scholar] [CrossRef]
- Xiang, T.; Istrati, D.; Yim, S.C.; Buckle, I.G.; Lomonaco, P. Tsunami loads on a representative coastal bridge deck: Experimental study and validation of design equations. J. Waterw. Port Coast. Ocean. Eng. 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Vijay, K.; Venkateswarlu, V.; Nishad, C.S. Wave scattering by inverted trapezoidal porous boxes using dual boundary element method. Ocean Eng. 2021, 219, 108149. [Google Scholar] [CrossRef]
- Pan, K.; IJzermans, R.; Jones, B.; Thyagarajan, A.; Van Beest, B.; Williams, J. Application of the SPH method to solitary wave impact on an offshore platform. Comput. Part. Mech. 2016, 3, 155–166. [Google Scholar] [CrossRef] [Green Version]
- Canelas, R.; Ferreira, R.; Crespo, A.; Domínguez, J. A generalized SPH-DEM discretization for the modelling of complex multiphasic free surface flows. In Proceedings of the 8th International SPHERIC Workshop, Trondheim, Norway, 4–6 June 2013; pp. 74–79. [Google Scholar]
- Hasanpour, A.; Istrati, D.; Buckle, I. Coupled SPH–FEM modeling of tsunami-borne large debris flow and impact on coastal structures. J. Mar. Sci. Eng. 2021, 9, 1068. [Google Scholar] [CrossRef]
- Anagnostopoulos, S. Dynamic response of offshore platforms to extreme waves including fluid–structure interaction. Eng. Struct. 1982, 4, 179–185. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.G. Effect of fluid–structure interaction on connection forces in bridges due to tsunami loads. In Proceedings of the 30th US-Japan Bridge Engineering Workshop, Washington, DC, USA, 21–23 October 2014; pp. 21–23. [Google Scholar]
- Istrati, D.; Buckle, I.; Lomonaco, P.; Yim, S. Deciphering the tsunami wave impact and associated connection forces in open-girder coastal bridges. J. Mar. Sci. Eng. 2018, 6, 148. [Google Scholar] [CrossRef] [Green Version]
- Peña, B.; McDougall, A. An investigation into the limitations of the panel method and the gap effect for a fixed and a floating structure subject to waves. In Proceedings of the ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016; p. V007T06A048. [Google Scholar] [CrossRef] [Green Version]
- ANSYS-Inc. AQWA User’s Manual Release 18.0; ANSYS-Inc.: Washington County, PA, USA, 2017. [Google Scholar]
- Chen, M.; Guo, H.; Wang, R.; Tao, R.; Cheng, N. Effects of gap resonance on the hydrodynamics and dynamics of a multi-module floating system with narrow gaps. J. Mar. Sci. Eng. 2021, 9, 1256. [Google Scholar] [CrossRef]
- Istrati, D. Large-Scale Experiments of Tsunami Inundation of Bridges including Fluid-Structure-Interaction. Ph.D. Thesis, University of Nevada, Reno, NV, USA, 2017. [Google Scholar]
- Peregrine, D.; Bredmose, H.; Bullock, G.; Obrhai, C.; Müller, G.; Wolters, G. Water wave impact on walls and the role of air. In Proceedings of the 29th International Conference on Coastal Engineering, Lisbon, Portugal, 19–24 September 2004; pp. 4005–4017. [Google Scholar] [CrossRef]
- Viuff, T.; Leira, B.J.; Xiang, X.; Øiseth, O. Effects of wave directionality on extreme response for a long end-anchored floating bridge. Appl. Ocean Res. 2019, 90, 101843. [Google Scholar] [CrossRef]
- Lyu, G.; Zhang, H.; Li, J. Effects of incident wind/wave directions on dynamic response of a SPAR-type floating offshore wind turbine system. Acta Mech. Sin. 2019, 35, 954–963. [Google Scholar] [CrossRef] [Green Version]
- Rudman, M.; Cleary, P. Oblique impact of rogue waves on a floating platform. In Proceedings of the International Offshore and Polar Engineering Conference, Osaka, Japan, 21–26 July 2009; pp. 572–579. [Google Scholar]
- Istrati, D.; Buckle, I.G. Tsunami Loads on Straight and Skewed Bridges–Part 1: Experimental Investigation and Design Recommendations; Technical Report No. FHWA-OR-RD-21-12; Oregon Department of Transportation Research Section: Washington, DC, USA, 2021. [Google Scholar]
- Istrati, D.; Buckle, I.G. Tsunami Loads on Straight and Skewed Bridges–Part 2: Experimental Investigation and Design Recommendations; Technical Report No. FHWA-OR-RD-21-13; Oregon Department of Transportation Research Section: Washington, DC, USA, 2021. [Google Scholar]
- Van der Meer, J.W.; Briganti, R.; Zanuttigh, B.; Wang, B. Wave transmission and reflection at low-crested structures: Design formulae, oblique wave attack and spectral change. Coast. Eng. 2005, 52, 915–929. [Google Scholar] [CrossRef]
- Xiang, T.; Istrati, D. Assessment of extreme wave impact on coastal decks with different geometries via the arbitrary Lagrangian-Eulerian method. J. Mar. Sci. Eng. 2021, 9, 1342. [Google Scholar] [CrossRef]
- Kurian, V.; Ng, C.; Liew, M. A study on motion responses of classic spar platforms subjected to short crested waves. In Proceedings of the 2013 IEEE Business Engineering and Industrial Applications Colloquium (BEIAC), Langkawi, Malaysia, 7–9 April 2013; pp. 311–315. [Google Scholar]
- Wang, W.H.; Du, Y.Z.; Wang, L.L.; Huang, Y. Wave-free characteristic of heave motion response for new sandglass-type model. Ships Offshore Struct. 2018, 13, 181–193. [Google Scholar] [CrossRef]
- Zhang, J.; Ren, H.; Zhang, L. A nonlinear restoring effect study of mooring system and its application. J. Mar. Sci. Appl. 2012, 11, 74–82. [Google Scholar] [CrossRef]
- Whitney, M.W.; Harik, I.E. Analysis and Design of Bridges Susceptible to Barge Impact; Technical Report No. KTC-97-2; University of Kentucky Transportation Center: Frankfort, KY, USA, 1997. [Google Scholar]
- Jin, W.; Song, J.; Gong, S.; Lu, Y. Evaluation of damage to offshore platform structures due to collision of large barge. Eng. Struct. 2005, 27, 1317–1326. [Google Scholar] [CrossRef]
- Istrati, D.; Hasanpour, A.; Buckle, I. Numerical investigation of tsunami-borne debris damming loads on a coastal bridge. In Proceedings of the 17 World Conference on Earthquake Engineering, Sendai, Japan, 13–18 September 2020; Volume 27. [Google Scholar]
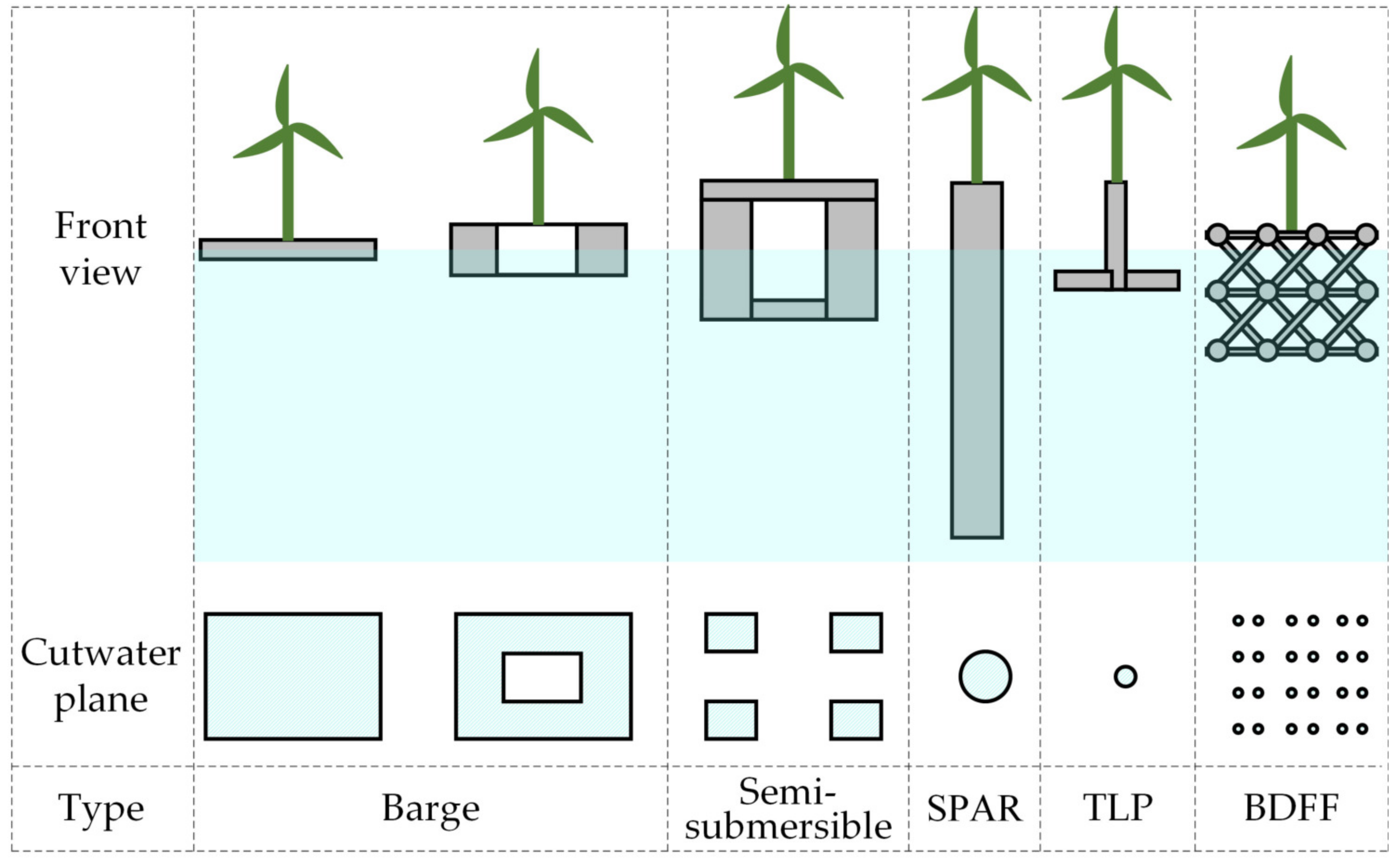
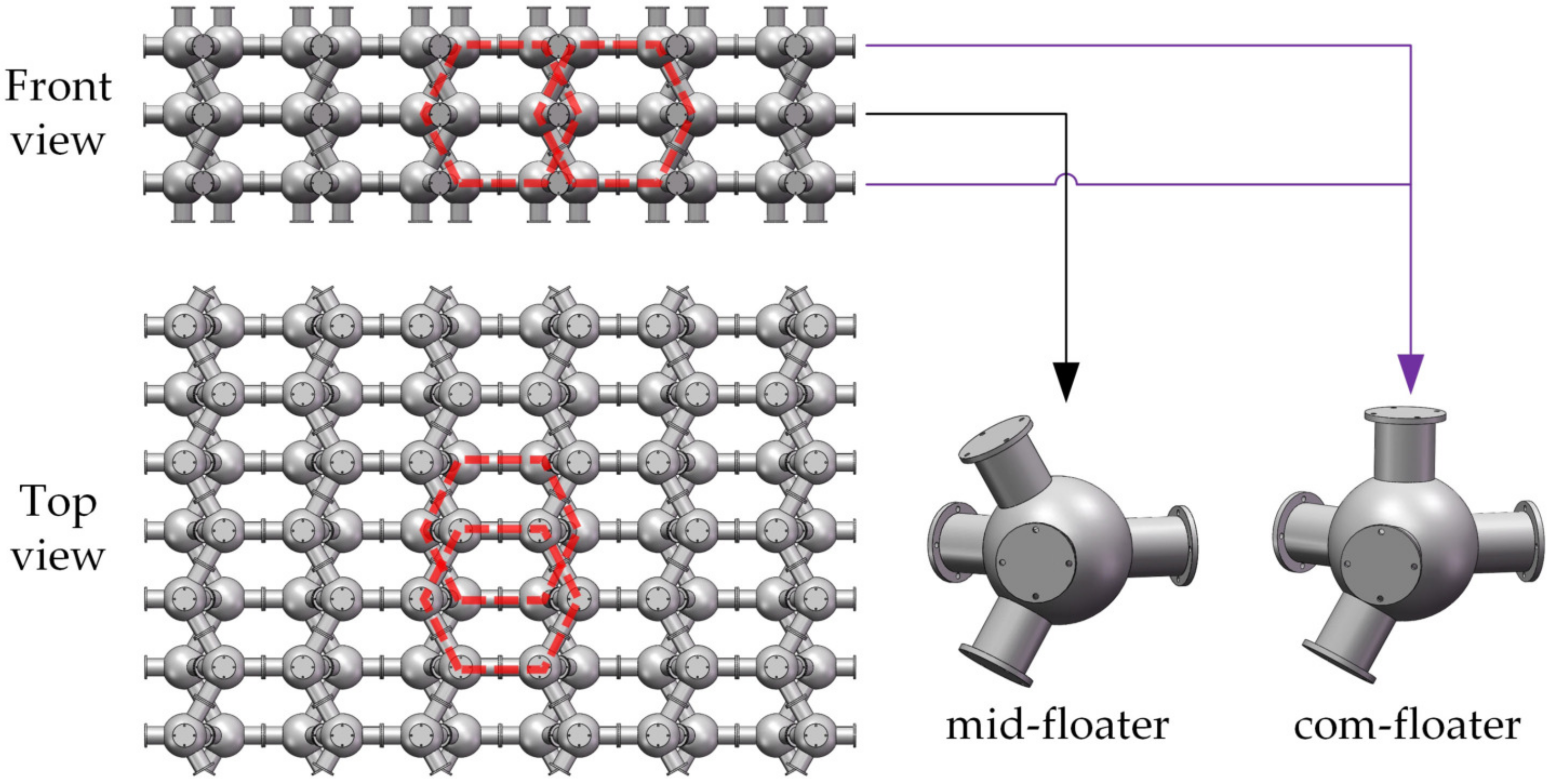


| Stabilized | Conception | Example |
|---|---|---|
| Tension | TLP | BlueWater-TLP, Iberdrola TLPWIND, PelaStar |
| Diwets, GICON®-SOF | ||
| Ballast | SPAR | Hywind, SWAY |
| Buoyancy | Barge | Floatgen, WindBarge |
| Semi-submersible | Tri-floater, OC4-DeepCWind, Nautilus, WindFloat | |
| W2Power, WindSea FLoater, Shimpuu, Tri-Floater | ||
| OO-Star, Sea-Reed, Sea Flower, TwinWind, WindFlo |
| Parameters | Floating System |
|---|---|
| System mass including ballast | 124.5 t |
| Diameter of spherical part of the floater, | 2 m |
| Diameter of cylindrical part of the floater, | 0.8 m |
| Centre-to-centre sphere spacing, L | 3.6 m |
| System draft depth | 3.1 m |
| Position of COG | 0, 0, −3.51 m |
| Moment of inertial, , , | 8425, 9036, 7490 t·m2 |
| Number of mooring cables | 4 |
| Mooring cable length, material | 75 m, anchor steel |
| Chain diameter of mooring cables, type | 0.03 m, studless |
| Cross-section axis stiffness of mooring cables | 7.6 N |
| Pretension of mooring cables | 10.5 N |
| Angle between mooring cables and the surge line | 30 |
| Vertical depth of anchor points | −50 m |
| Mooring anchor radius | 65 m |
| Vertical depth of fairlead points | −11.8 m |
| Fairlead radius | 9 m |
| Case | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Max. mesh size, m | 0.07 | 0.1 | 0.12 | 0.15 | 0.25 | 0.5 |
| No. of diffracted elements | 27,301 | 26,200 | 23,474 | 15,365 | 7850 | 3347 |
| No. of total elements | 35,769 | 34,794 | 32,068 | 23,833 | 10,911 | 5933 |
| Relative error | 0 | 0.008 | 0.02 | 0.05 | 0.09 | 0.26 |
| Computation time, s | 245,232 | 225,180 | 209,988 | 153,504 | 103,392 | 48,816 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, X.; Yao, Y. Numerical and Experimental Study of Hydrodynamic Response for a Novel Buoyancy-Distributed Floating Foundation Based on the Potential Theory. J. Mar. Sci. Eng. 2022, 10, 292. https://doi.org/10.3390/jmse10020292
Qu X, Yao Y. Numerical and Experimental Study of Hydrodynamic Response for a Novel Buoyancy-Distributed Floating Foundation Based on the Potential Theory. Journal of Marine Science and Engineering. 2022; 10(2):292. https://doi.org/10.3390/jmse10020292
Chicago/Turabian StyleQu, Xiaobin, and Yingxue Yao. 2022. "Numerical and Experimental Study of Hydrodynamic Response for a Novel Buoyancy-Distributed Floating Foundation Based on the Potential Theory" Journal of Marine Science and Engineering 10, no. 2: 292. https://doi.org/10.3390/jmse10020292
APA StyleQu, X., & Yao, Y. (2022). Numerical and Experimental Study of Hydrodynamic Response for a Novel Buoyancy-Distributed Floating Foundation Based on the Potential Theory. Journal of Marine Science and Engineering, 10(2), 292. https://doi.org/10.3390/jmse10020292






