Effect of Various Mooring Materials on Hydrodynamic Responses of Turret-Moored FPSO with Emphasis on Intact and Damaged Conditions
Abstract
:1. Introduction
2. Description of FPSO Model, Environmental Data, and Numerical Model Validation
2.1. FPSO Model
2.2. Turret Mooring System
2.3. Environmental Data and Prediction of Wind and Current Forces
2.3.1. Environmental Data
2.3.2. Prediction of Wind and Current Forces
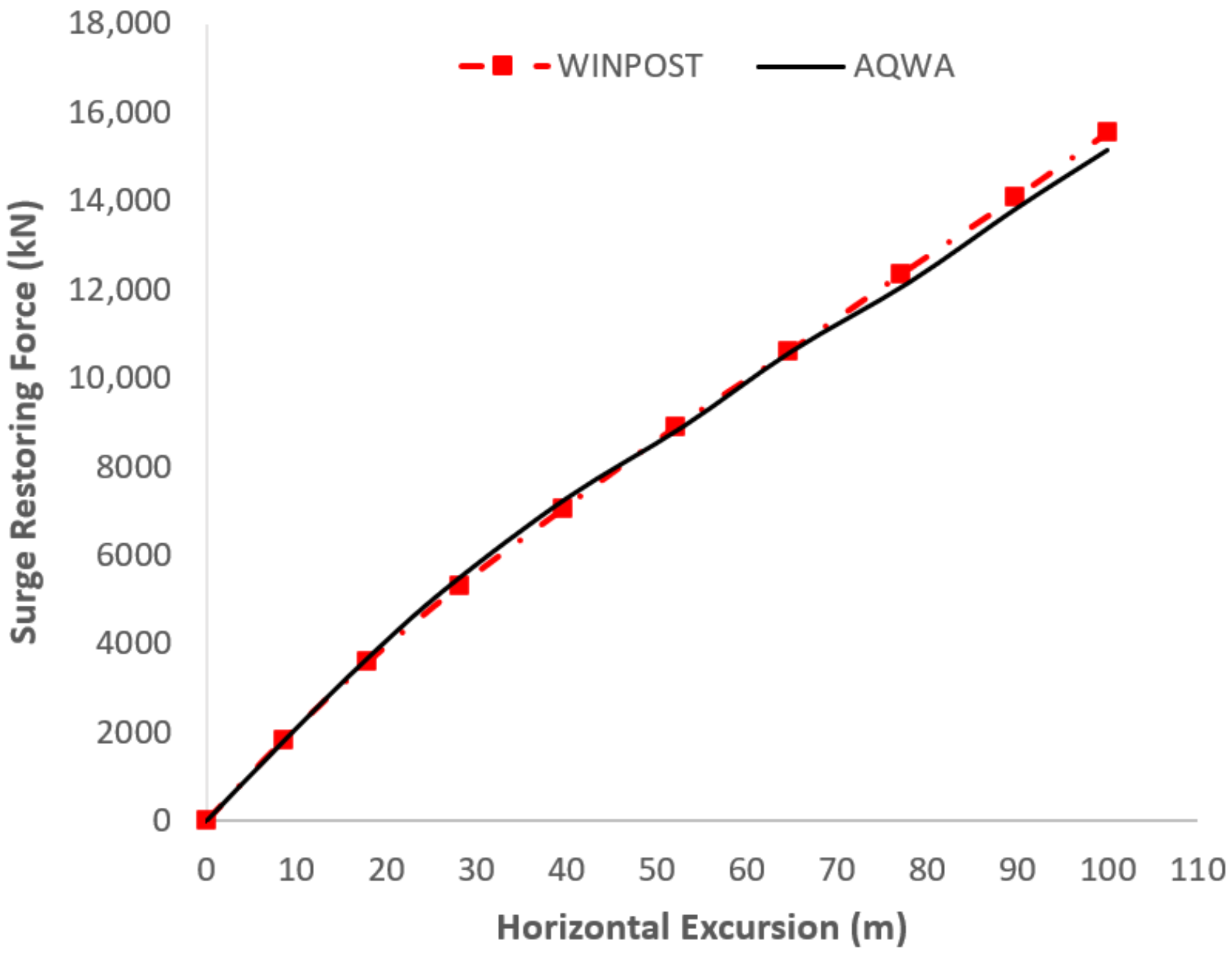
2.4. Validation of Numerical Model
3. Fully Coupled Dynamic Analysis
3.1. Wave Exciting and Radiation Forces
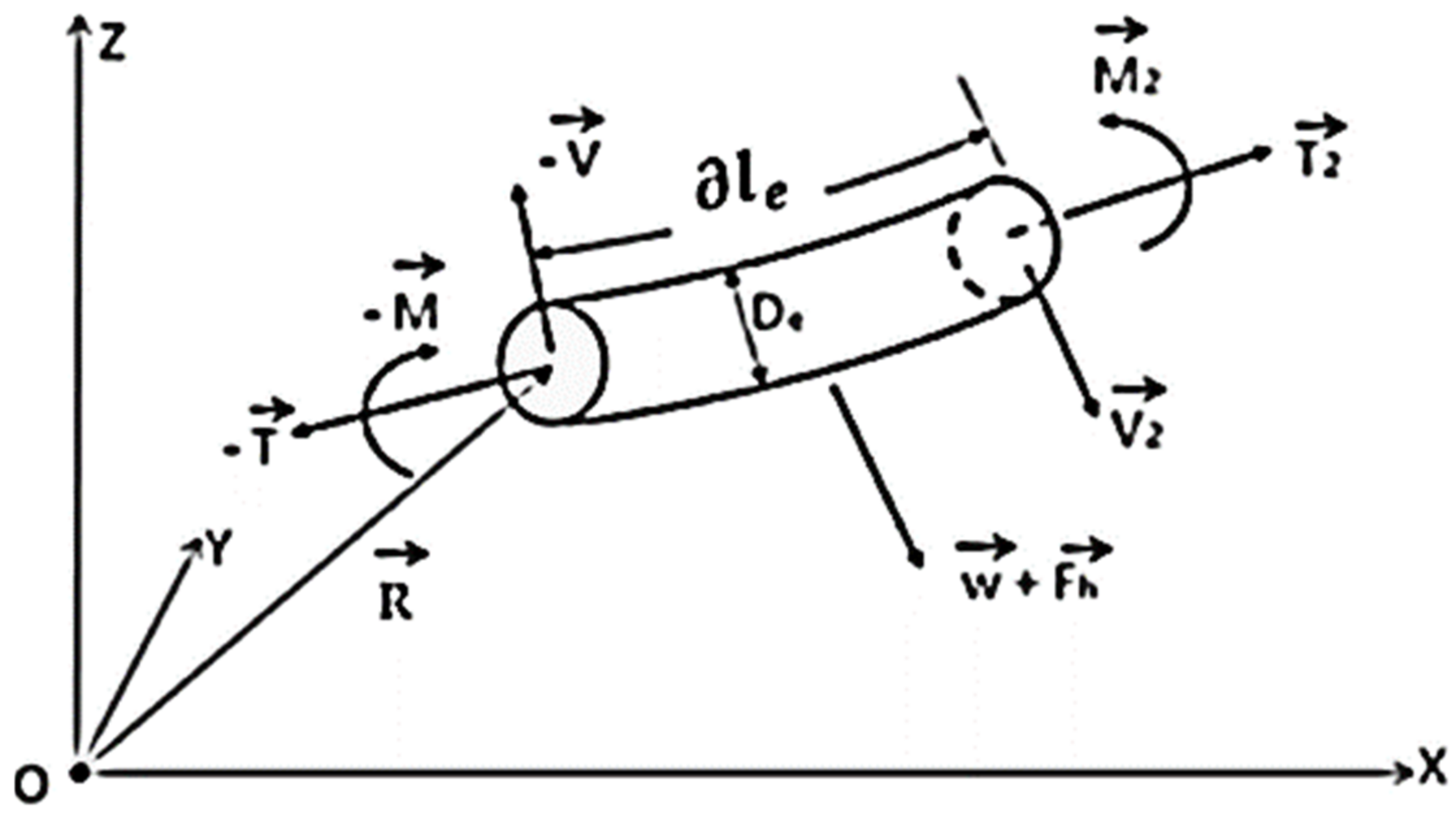
3.2. Mooring Line Dynamics
3.3. Equation of Motion
4. Mooring Material and Line Failure Scenarios
4.1. Mooring Material
4.2. Mooring Line Failure Scenarios
4.3. Selection of Representative Mooring and Risers for Tension Analysis
5. Results and Discussion
5.1. Validation of Numerical Model
5.2. Static Offset Analysis of Different Mooring Line Materials
5.3. Hydrodynamic Responses of FPSO in 6DOF
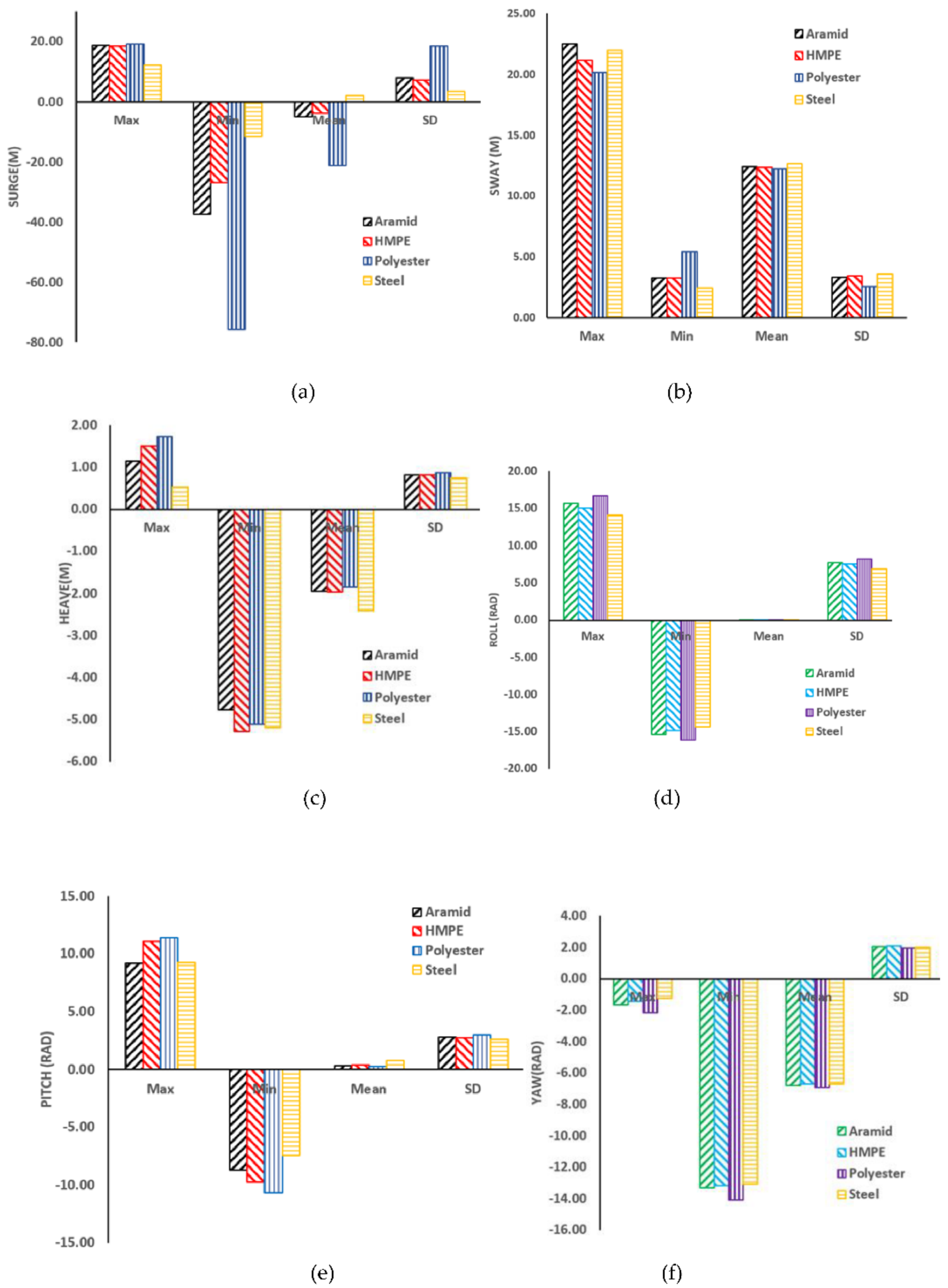
5.3.1. Dynamic Responses in Intact Condition
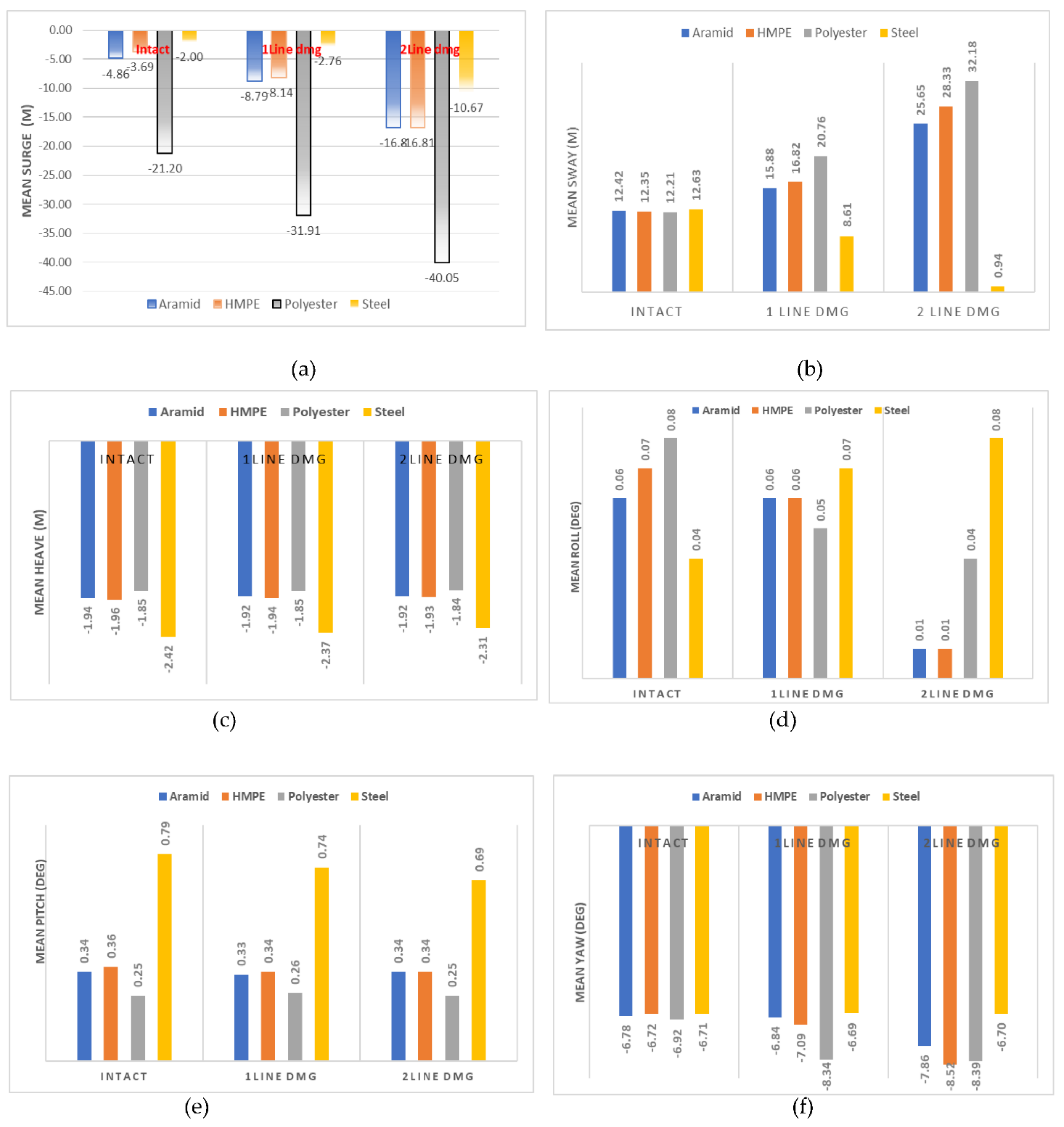
5.3.2. Mean Dynamic Responses in Intact and Damaged Conditions
5.4. Mooring and Riser Tensions in Intact and Damaged Conditions
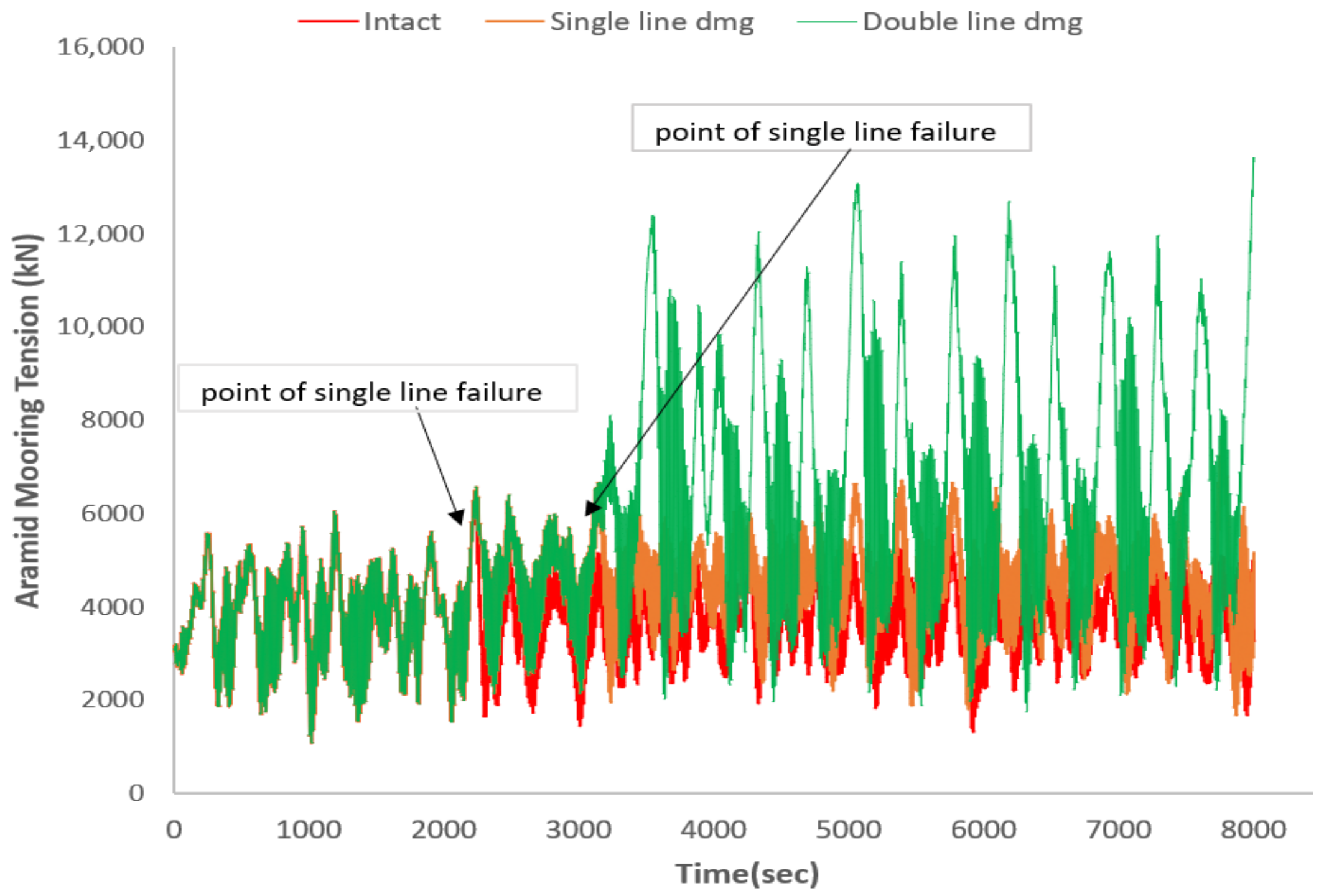
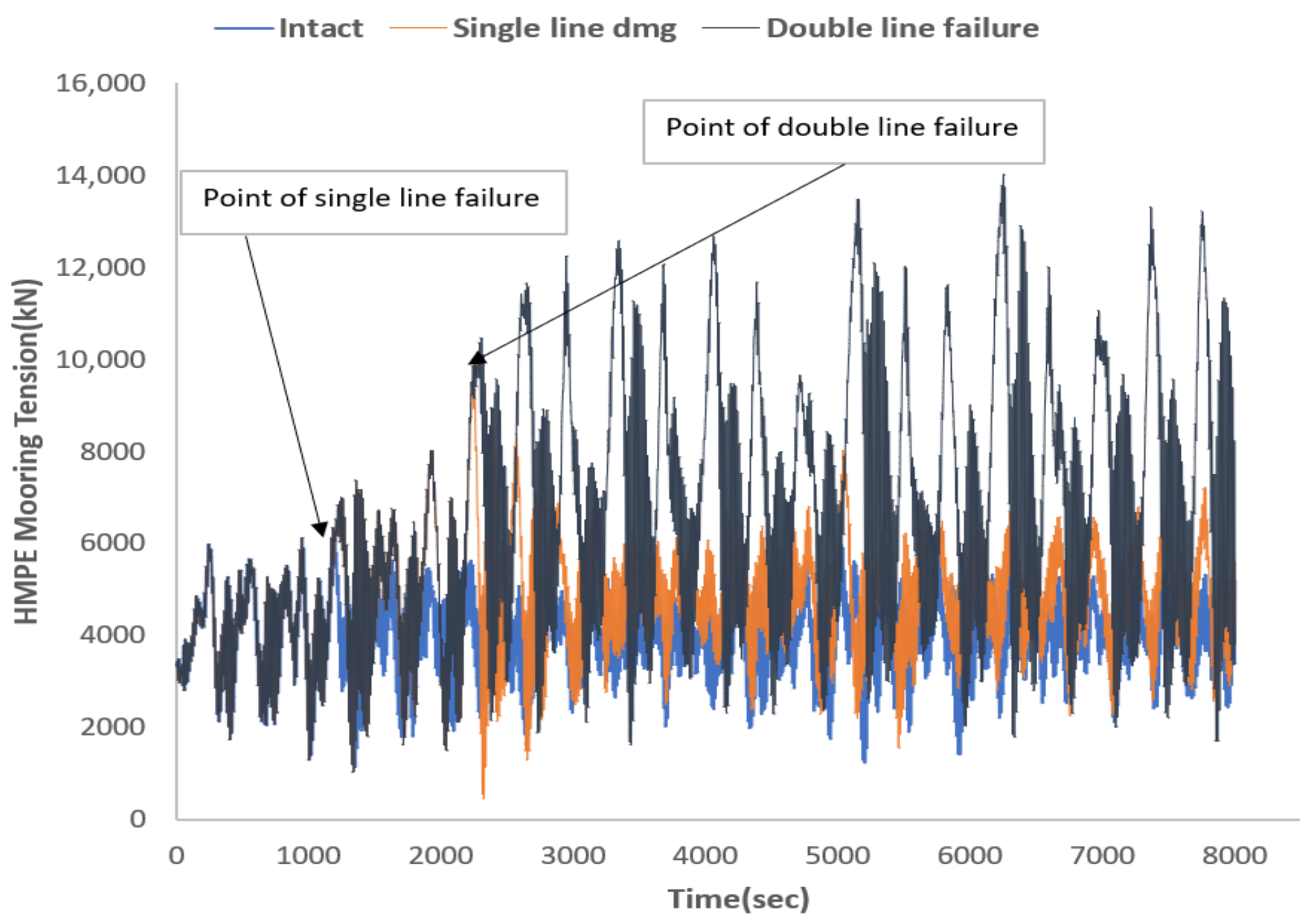
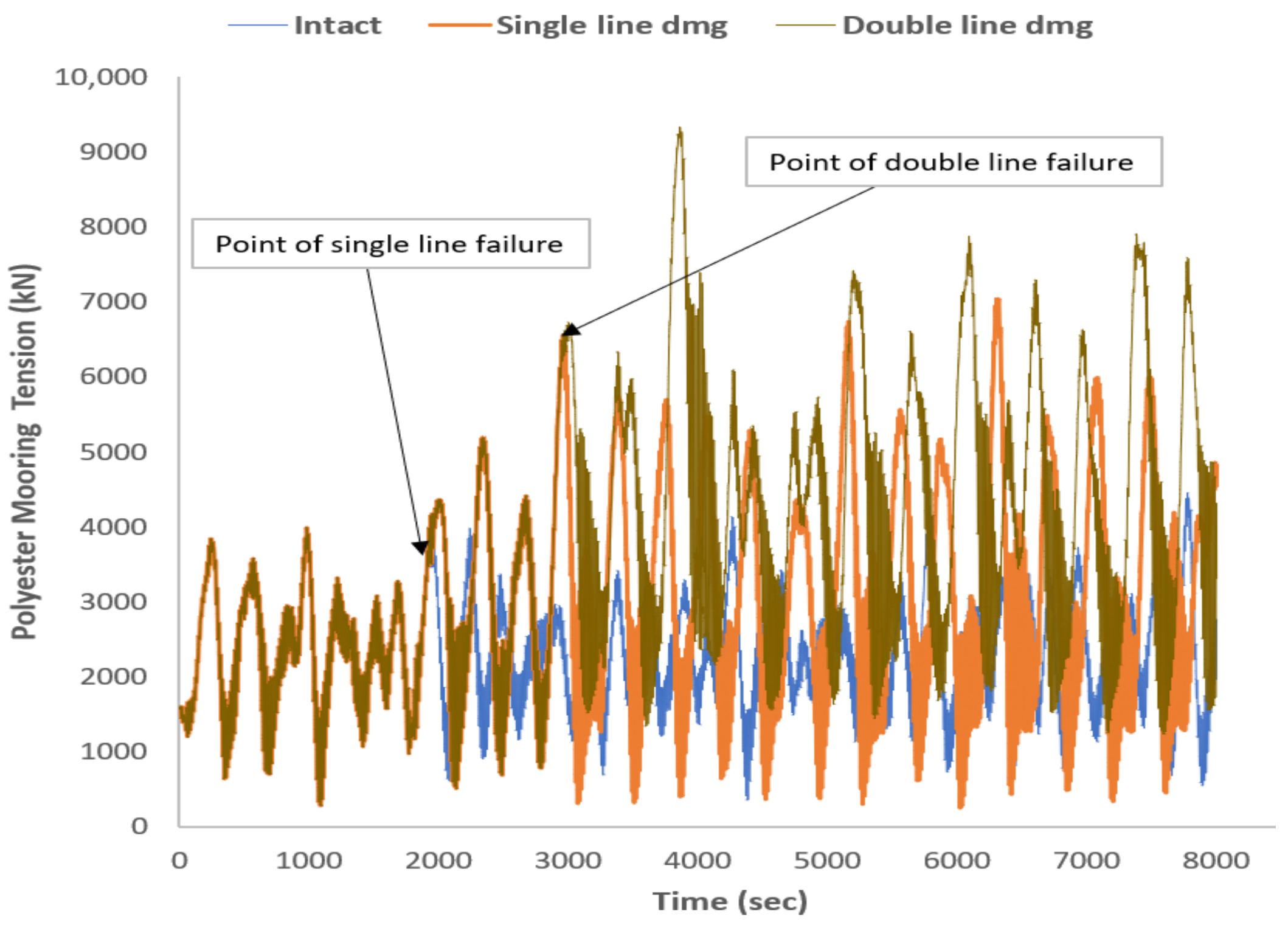
5.4.1. Mooring Line Tension
5.4.2. Riser Tension
6. Conclusions
- The mooring system restoring force increased significantly with increasing mooring material stiffness, and a higher material stiffness led to a higher loss in restoring force in the case of single-line failure. In the case of double-line failure, the percentage reduction in restoring force was within the same range for all materials considered. Thus, in terms of percentage loss in restoring force, the polyester line was the best choice.
- In intact conditions, material stiffness had a significant influence on the surge response for all mooring materials considered. In addition, lines with higher material stiffness had higher heave responses. In this regard, in a case where a reduction is surge and sway is the primary objective, the steel wire would be the best choice.
- The mooring line submerged weight and material stiffness had a significant influence on the ability of the mooring systems to withstand the case of single-line failure, which is a fundamental requirement for a mooring system, as highlighted in Section 2 of DNVGL-S-E301 [6]. On this premise, in terms of surge direction, the steel wire performed best, followed by polyester, Aramid, and HMPE. In the case of double-line failure, lines with lower material stiffness performed better in maintaining the platform in position. Specifically, polyester lines performed best, followed by steel wire, HMPE, and Aramid.
- The highest mean tension was recorded in steel wire, while the HMPE line had the highest tension among the synthetic lines, which is consistent with the restoring behavior of the lines.
- For both failure cases, polyester lines had the highest mean tension increase, followed by HMPE, Aramid, and steel wire, showing that lines with higher material stiffness distributed tension evenly to the other lines in the same group in the event of single- and double-line failure. In this case, steel wire performed best with a minimal increase in line tension in the event of line failure.
- Mooring lines with higher stiffness displayed better capability to withstand platform response in the event of line failure and, consequently, performed better in terms of minimizing the increasing riser tension. In both single- and double-line failure, a minimum increase in riser tension was recorded in the mooring system with steel wire, followed by the Aramid lines.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahmed, M.O.; Yenduri, A.; John, K.V. Evaluation of the Dynamic Responses of Truss Spar Platforms for Different Mooring Materials in Intact and Damaged Line Conditions. In Proceedings of the 29th International Ocean and Polar Engineering Conference, Honolulu, HI, USA, 16–21 June 2019; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2019. [Google Scholar]
- Lian, Y.; Liu, H.; Zheng, J. Numerical investigation on dynamic responses of HMPE mooring system with damaged lines. In Proceedings of the 27th International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2017. OnePetro. [Google Scholar]
- Liu, H.; Huang, W.; Lian, Y.; Li, L. An experimental investigation on nonlinear behaviors of synthetic fiber ropes for deepwater moorings under cyclic loading. Appl. Ocean Res. 2014, 45, 22–32. [Google Scholar] [CrossRef]
- Lian, Y.; Yim, S.C.; Zheng, J.; Liu, H.; Zhang, N. Effects of Damaged Fiber Ropes on the Performance of a Hybrid Taut-Wire Mooring System. J. Offshore Mech. Arct. Eng. 2019, 142, 1–43. [Google Scholar] [CrossRef]
- API RP. API RP 2SM, Recommended Practice for the Design, Manufacturer, Installation, and Maintenance of Synthetic Fiber Ropes for Offshore Moorings; API: Washington, DC, USA, 2014. [Google Scholar]
- ABS. ABS 90-2011; Guidance notes on the application of fiber rope for offshore mooring; American Bureau of Shipping: Houston, TX, USA, 2011. [Google Scholar]
- DVN GL. Design, Testing and Analysis of Offshore Fibre Ropes; Det Norske Veritas: DNV Veritasveien 1; NO-1322 Høvik; DVN GL: Oslo, Norway, 2019. [Google Scholar]
- Lian, Y.; Liu, H.; Hu, L. Feasibility Analysis of a New Hybrid Mooring System Applied for Deep Waters. In Proceedings of the Twenty-fifth International Ocean and Polar Engineering Conference, Kona, HI, USA, 21–26 June 2015; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2015. ISOPE-I-15-297. [Google Scholar]
- Flory, J.F.; Banfield, S.J.; Ridge, I.M.L.; Carr, R. Axial Compression Fatigue in Long-Lay-Length Fiber Mooring Ropes. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1–4 May 2017; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2017. [Google Scholar] [CrossRef]
- Lian, Y.; Liu, H.; Zhang, Y.; Li, L. An experimental investigation on fatigue behaviors of HMPE ropes. Ocean Eng. 2017, 139, 237–249. [Google Scholar] [CrossRef]
- Ćatipović, I.; Alujević, N.; Rudan, S.; Slapničar, V. Numerical Modelling for Synthetic Fibre Mooring Lines Taking Elongation and Contraction into Account. J. Mar. Sci. Eng. 2021, 9, 417. [Google Scholar] [CrossRef]
- Weller, S.; Johanning, L.; Davies, P.; Banfield, S. Synthetic mooring ropes for marine renewable energy applications. Renew. Energy 2015, 83, 1268–1278. [Google Scholar] [CrossRef] [Green Version]
- Utsunomiya, T.; Sato, I.; Tanaka, K. At-Sea Experiment on Durability and Residual Strength of Polyester Rope for Mooring of Floating Wind Turbine. In Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering, Scotland, UK, 9–14 June 2019. [Google Scholar] [CrossRef]
- Pham, H.-D.; Cartraud, P.; Schoefs, F.; Soulard, T.; Berhault, C. Dynamic modeling of nylon mooring lines for a floating wind turbine. Appl. Ocean Res. 2019, 87, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Gordelier, T.; Parish, D.; Thies, P.R.; Johanning, L. A Novel Mooring Tether for Highly-Dynamic Offshore Applications; Mitigating Peak and Fatigue Loads via Selectable Axial Stiffness. J. Mar. Sci. Eng. 2015, 3, 1287–1310. [Google Scholar] [CrossRef] [Green Version]
- Montasir, O.; Yenduri, A.; Kurian, V. Effect of Mooring Line Properties and Fairlead Slopes on the Restoring Behavior of Offshore Mooring System. Res. J. Appl. Sci. Eng. Technol. 2014, 8, 346–353. [Google Scholar] [CrossRef]
- Ja’E, I.A.; Ali, M.O.A.; Yenduri, A.; Nizamani, Z.; Nakayama, A. Optimisation of mooring line parameters for offshore floating structures: A review paper. Ocean Eng. 2022, 247, 110644. [Google Scholar] [CrossRef]
- Rudmana, M.; Cleary, P.W. Oblique impact of rogue waves on a floating platform. In Proceedings of the Nineteenth International Offshore and Polar Engineering Conference, Osaka, Japan, 21–26 June 2009; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2009. OnePetro. [Google Scholar]
- Mai, T.; Greaves, D.; Raby, A.; Taylor, P. Physical modelling of wave scattering around fixed FPSO-shaped bodies. Appl. Ocean Res. 2016, 61, 115–129. [Google Scholar] [CrossRef]
- Lee, I.-H.; Moon, J.-S.; Sim, W.-S.; Lee, W.-S.; Shin, H.-S. Investigation of the Impact Pressure by Breaking Waves on FPSO Appurtenances. In Proceedings of the Twentieth International Offshore and Polar Engineering Conference, Beijing, China, 20–25 June 2010; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2010. OnePetro. [Google Scholar]
- Xu, L.; Barltrop, N.; Okan, B. Bow impact loading on FPSOs 1—Experimental investigation. Ocean Eng. 2008, 35, 1148–1157. [Google Scholar] [CrossRef]
- Maffra, S.A.R.D.S.; Pacheco, M.A.C.; de Menezes, I.F.M.G. Genetic Algorithm Optimization for Mooring Systems. Generations 2003, 1, 3. [Google Scholar]
- DNV GL. DNVGL-OS-E301 Position Mooring; DNV Veritasveien 1; NO-1322 Hovik; DNV GL: Oslo, Norway, 2015. [Google Scholar]
- Ahmed, M.; Nizamani, Z.; Nakayama, A.; Osman, M. Some Recent Fluid-Structure Interaction Approaches for the Wave Current Behaviour with Offshore Structures. CFD Lett. 2020, 12, 15–26. [Google Scholar] [CrossRef]
- Li, Q.; Zhuang, Y.; Wan, D.; Chen, G. Numerical Analysis of the Interaction between a Fixed FPSO Benchmark Model and Focused Waves. In Proceedings of the 28th International Ocean and Polar Engineering Conference, Sapporo, Japan, 10–15 June 2018; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2018. OnePetro. [Google Scholar]
- Anagnostopoulos, S.A. Dynamic response of offshore platforms to extreme waves including fluid-structure interaction. Eng. Struct. 1982, 4, 179–185. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.G. Effect of fluid-structure interaction on connection forces in bridges due to tsunami loads. In Proceedings of the 30th US-Japan Bridge Engineering Workshop, Washington, DC, USA, 21–23 October 2014; pp. 21–23. [Google Scholar]
- Istrati, D. Large-Scale Experiments of Tsunami Inundation of Bridges Including Fluid-Structure-Interaction. Ph.D. Thesis, University of Nevada, Reno, NV, USA, 2017. [Google Scholar]
- Ali, M.O.A.; Ja’E, I.A.; Hwa, M.G.Z. Effects of water depth, mooring line diameter and hydrodynamic coefficients on the behaviour of deepwater FPSOs. Ain. Shams. Eng. J. 2019, 11, 727–739. [Google Scholar] [CrossRef]
- AQWA Inc. AQWA User’s Manual. Release 14.5. ANSYS Inc.: Canonsburg, PA, USA, 2020. Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v201/en/wb2_help/wb2_help.html%23wb2_help (accessed on 30 December 2021).
- Ti, Z.; Li, Y.; Qin, Q. Numerical approach of interaction between wave and flexible bridge pier with arbitrary cross section based on boundary element method. J. Bridge Eng. 2020, 25, 04020095. [Google Scholar] [CrossRef]
- Liu, Z.; Zhuang, Y.; Wan, D.; Chen, G. Numerical Study on Focused Wave Interactions with a Moored Floating Structure. In Proceedings of the 29th International Ocean and Polar Engineering Conference, Honolulu, HI, USA, 16–21 June 2019; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2019. OnePetro. [Google Scholar]
- Xiang, T.; Istrati, D. Assessment of Extreme Wave Impact on Coastal Decks with Different Geometries via the Arbitrary Lagrangian-Eulerian Method. J. Mar. Sci. Eng. 2021, 9, 1342. [Google Scholar] [CrossRef]
- He, G.; Xie, B.; Wang, W.; Liu, S.; Jing, P. Ship Loading Influence on the Slamming Impact of Typical Sections of an S-175 Container Ship. J. Mar. Sci. Eng. 2020, 8, 163. [Google Scholar] [CrossRef] [Green Version]
- Pan, K.; Ijzermans, R.H.A.; Jones, B.D.; Thyagarajan, A.; van Beest, B.W.H.; Williams, J.R. Application of the SPH method to solitary wave impact on an offshore platform. Comput. Part. Mech. 2015, 3, 155–166. [Google Scholar] [CrossRef] [Green Version]
- Lind, S.J.; Rogers, B.D.; Stansby, P.K. Review of smoothed particle hydrodynamics: Towards converged Lagrangian flow modelling. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20190801. [Google Scholar] [CrossRef]
- Canelas, R.; Ferreira, R.; Crespo, A.; Domínguez, J. A generalized SPH-DEM discretization for the modelling of complex multiphasic free surface flows. In Proceedings of the 8th International SPHERIC Workshop, Trondheim, Norway, 4–6 June 2013; Smooth Particle Hydrodynamics Research and Engineering International Community Workshop: Trondheim, Norway, 2013; pp. 74–79. [Google Scholar]
- Hasanpour, A.; Istrati, D.; Buckle, I. Coupled SPH–FEM Modeling of Tsunami-Borne Large Debris Flow and Impact on Coastal Structures. J. Mar. Sci. Eng. 2021, 9, 1068. [Google Scholar] [CrossRef]
- Kim, M.; Koo, B.; Mercier, R.; Ward, E. Vessel/mooring/riser coupled dynamic analysis of a turret-moored FPSO compared with OTRC experiment. Ocean Eng. 2005, 32, 1780–1802. [Google Scholar] [CrossRef]
- Tahar, A.; Kim, M. Hull/mooring/riser coupled dynamic analysis and sensitivity study of a tanker-based FPSO. Appl. Ocean Res. 2003, 25, 367–382. [Google Scholar] [CrossRef]
- Yong, Y.; Baudic, S.; Poranski, P.; Wichers, J.; Stansberg, C.T.; Ormberg, H. Deepstar Study on Predicting FPSO Responses—Model Tests VS Numerical Analysis. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 2004; Offshore Technology Conference: Houston, Texas, USA, 2004. [Google Scholar] [CrossRef] [Green Version]
- MAXSURF Advanced; Bentley Systems Inc.: Exton, Pennsylvania, USA, 2012.
- Ja’e, I.A.; Ali, M.O.A.; Yenduri, A. Numerical Studies on the Effects of Mooring Configuration and line Diameter on the Restoring Behaviour of a Turret- Moored FPSO. In Proceedings of the 5th International Conference on Civil, Structural and Transportation Engineering, Niagara, ON, Canada, 12–14 November 2020. [Google Scholar] [CrossRef]
- Thiagarajan, K.P.; Tian, Z. Heading Instability of Moored Ships in Swell Waves. In Proceedings of the SNAME Maritime Convention 2012; SNAME Maritime Convention: Providence, RI, USA, 2012. [Google Scholar] [CrossRef]
- Zangeneh, R.; Thiagarajan, K.P. Heading Instability Analysis of FPSOs. In Proceedings of the Twenty-fifth International Ocean and Polar Engineering Conference, Kona, HI, USA, 21–26 June 2015; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2015. OnePetro. [Google Scholar]
- OCIMF. Prediction of Wind and Current Loads on VLCCs. In Tech. Rep.; Oil Companies International Marine Forum: London, UK, 1994. [Google Scholar]
- Jae, I.A.; Ali, M.O.A.; Yenduri, A. Numerical Validation of Hydrodynamic Responses and Mooring Top Tension of a Turret Moored FPSO using Simulation and Experimental results. In Proceedings of the 5th International Conference on Architecture and Civil Engineering (ICACE2021), Kualar Lumpur, Malaysia, 18 August 2021. ACE21317. [Google Scholar]
- Montasir, O.A.A. Numerical and Experimental Studies on the Slow Drift Motions and the Mooring line Responses of Truss Spar Platform. Ph.D. Thesis, Universiti Teknologi Petronas, Seri Iskandar, Malaysia, 2012. [Google Scholar]
- ANSYS Inc. AQWA Theory Manual; ANSYS Inc.: Canonsburg, PA, USA, 2015. [Google Scholar]
- Barltrop, N. Floating Structures: A Guide for Design and Analysis; Center for Marine and Petroleum Technology (CMPT): London, UK, 1998. [Google Scholar]
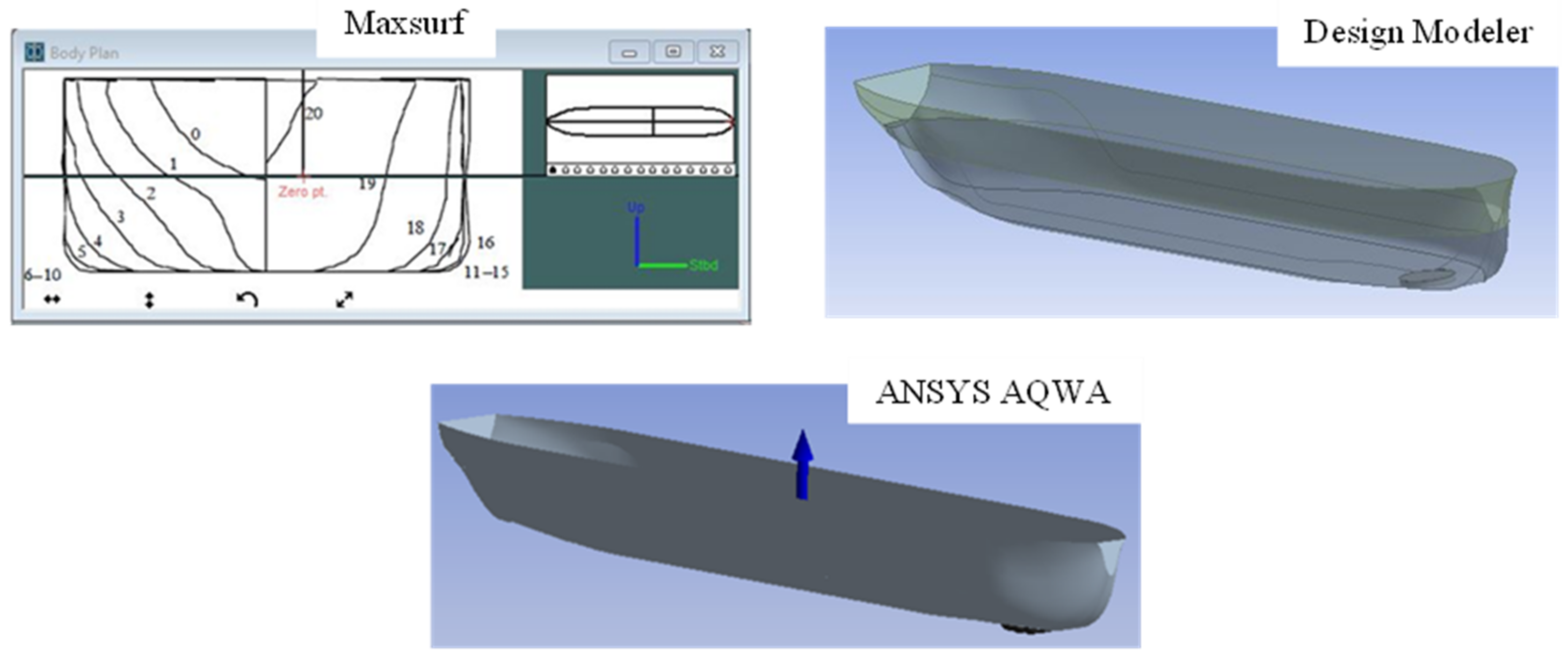
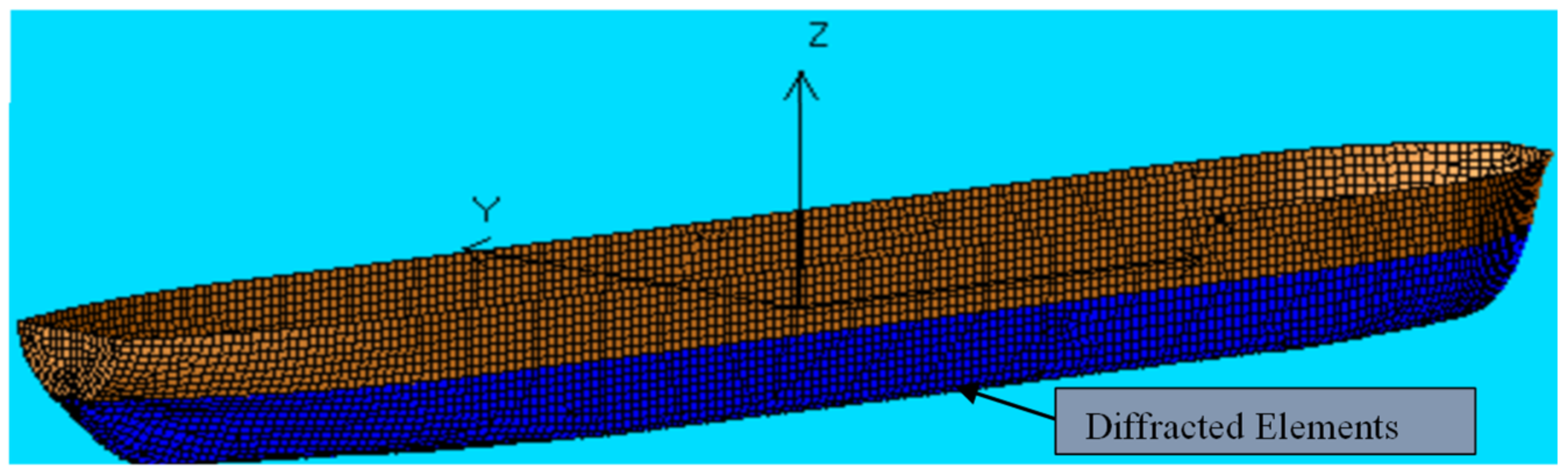
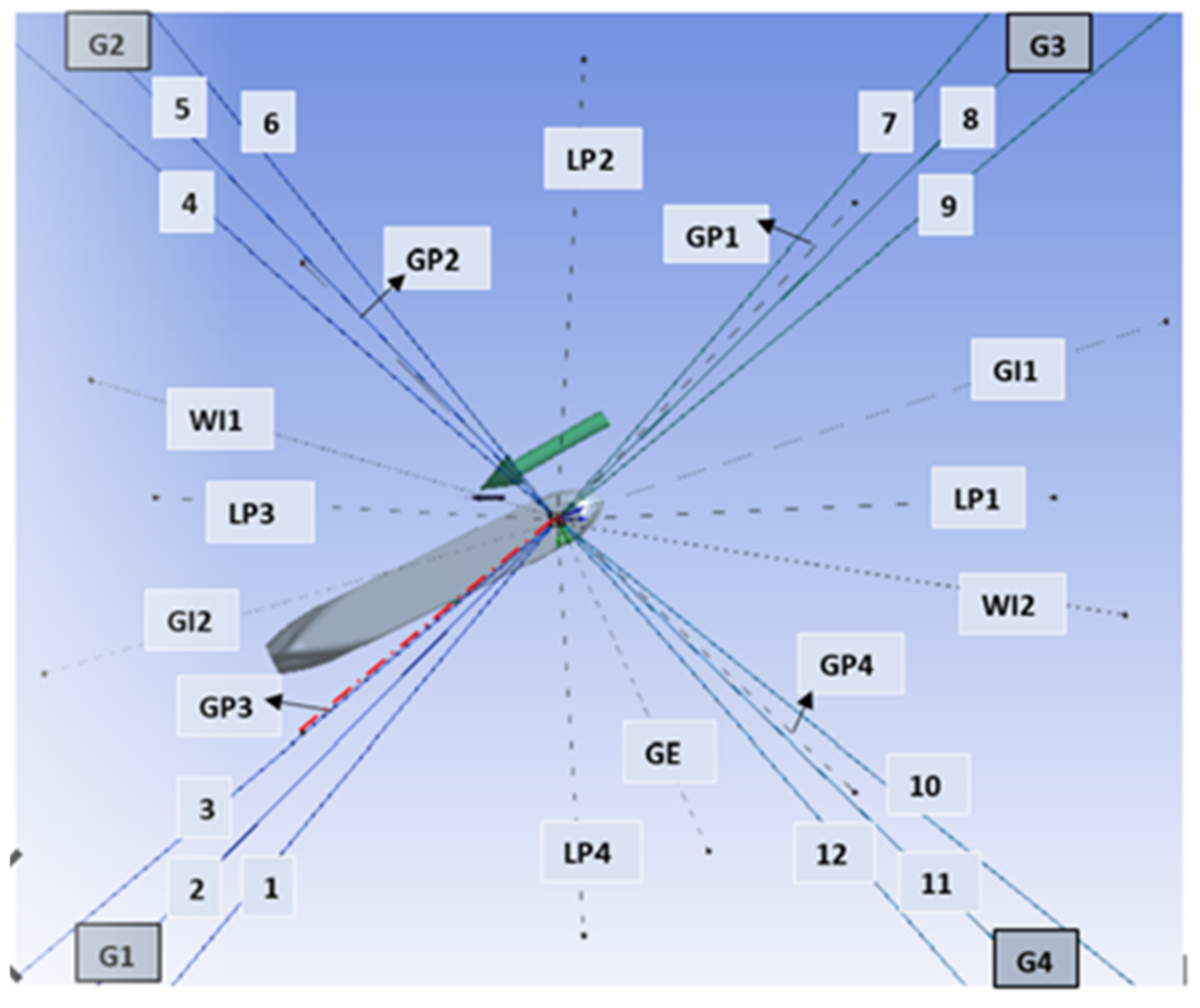
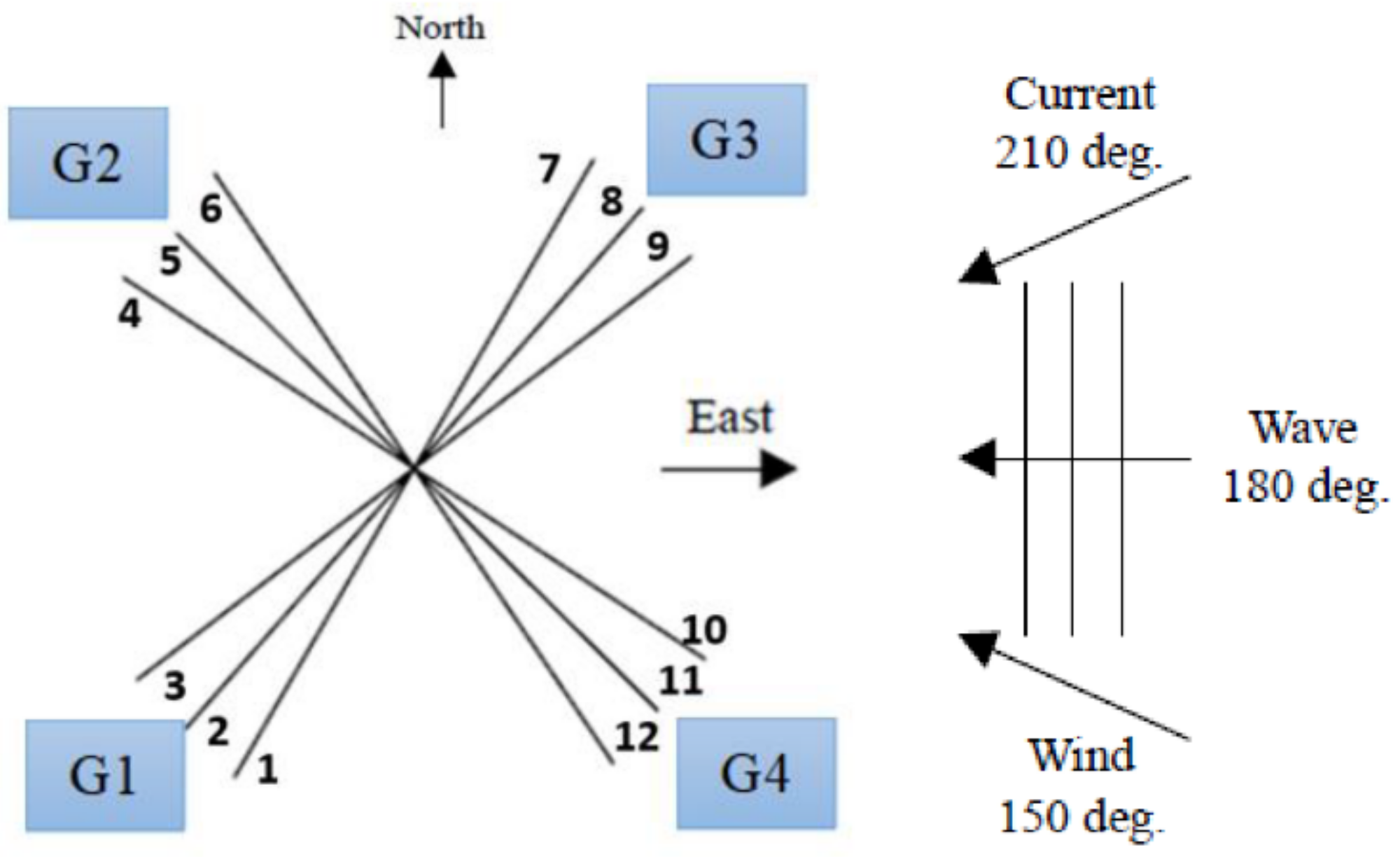



| Parameter | Symbol | Unit | Quantities |
|---|---|---|---|
| Vessel size | kDWT | 200 | |
| Length between perpendicular | Lpp | m | 310 |
| Breadth | B | m | 47.17 |
| Height | H | m | 28.04 |
| Draft (80% loaded) | T | M | 15.121 |
| Displacement | V | MT | 186,051 |
| Block coefficient | Cb | 0.85 | |
| Surge center of gravity from the turret | CGx | m | −109.67 |
| Heave center of gravity from m.w.l. | CGy | m | −1.8 |
| Frontal wind area | AF | m2 | 4209.6 |
| Transverse wind area | AT | m2 | 16,018.6 |
| Roll radius of gyration at CG of the turret | Rxx | m | 14.036 |
| Pitch radius of gyration at CG of the turret | Ryy | m | 77.47 |
| Yaw radius of gyration at CG of the turret | Rzz | m | 79.3 |
| Turret in center line behind Fpp | Xtur | m | 38.75 |
| Turret diameter | Dtur | m | 15.85 |
| Turret elevation below tanker base | m | 1.52 |
| Legend | Top Segment | Middle Segment | Lower Segment |
|---|---|---|---|
| Type | Chain | Polyester | Chain |
| Diameter (mm) | 95.3 | 160 | 95.3 |
| Length (m) | 91.4 | 2438 | 91.4 |
| Wet weight (kg/m) | 164.63 | 4.5 | 164.63 |
| Effective modulus (kN) | 820,900 | 168,120 | 820,900 |
| Breaking load (kN) | 7553 | 7429 | 7553 |
| Normal drag coefficient, CDN | 2.45 | 1.2 | 2.45 |
| Normal added inertia coefficient, CIN | 2.0 | 1.15 | 2.0 |
| Designation | Top Tension (kN) | Outer Diameter (mm) | EA (kN) | Wet Wet (N/m) |
|---|---|---|---|---|
| Liquid production | 1112.5 | 444.5 | 18.3 × 106 | 1037 |
| Gas production | 609.7 | 386.1 | 10.3 × 106 | 526 |
| Water injection | 2020.0 | 530.9 | 18.6 × 106 | 1898 |
| Gas injection | 1352.8 | 287.0 | 31.4 × 106 | 1168 |
| Gas export | 453.9 | 342.9 | 8.6 × 106 | 423 |
| Material | Sw (N/m) | EA (N) | MBL (N) |
|---|---|---|---|
| Polyester | 0.0067 d2 | 6567.19 d2 | 250 d2 |
| HMPE | 0.0062 d2 | 15,000 d2 | 575 d2 |
| Aramid | 0.00565 d2 | 16,567.19 d2 | 450 d2 |
| Steel wire | 0.034 d2 | 45,000 d2 | 600 d2 |
| Property/Mooring Material | Polyester | HMPE | Aramid | Steel Wire |
|---|---|---|---|---|
| Diameter (mm) | 160 | 160 | 160 | 160 |
| Length (m) | 2438 | 2438 | 2438 | 2438 |
| Wet weight (kg/m) | 17.4842 | 16.1794 | 14.7441 | 88.7258 |
| Axial stiffness (kN) | 168,120 | 424,120 | 384,000 | 1,152,000 |
| MBL (kN) | 7429 | 14,720 | 11,520 | 15,360 |
| Mooring Material/Cases | Single Line | Double Lines |
|---|---|---|
| Polyester | Line 9 at 1937 s | Line 8 at 2960 s |
| HMPE | Line 9 at 1186 s | Line 8 at 2241 s |
| Aramid | Line 9 at 2229 s | Line 8 at 3154 s |
| Steel wire | Line 10 at 1794 s | Line 11 at 2464 s |
| Natural Periods (s) | Damping (%) | |||||
|---|---|---|---|---|---|---|
| AQWA | WINPOST | OTRC | AQWA | WINPOST | OTRC | |
| Surge | 205.2 | 204.7 | 206.8 | 3.7 | 4.4 | 3.0 |
| Heave | 10.8 | 10.8 | 10.7 | 4.5 | 11.8 | 6.7 |
| Roll | 12.7 | 12.7 | 12.7 | 3.2 | 0.7 | 3.4 |
| Pitch | 10.7 | 10.8 | 10.5 | 7.5 | 10.5 | 8.0 |
| Source | Surge (m) | Sway (m) | Heave (m) | Roll (°) | Pitch (°) | Yaw (°) | |
|---|---|---|---|---|---|---|---|
| Max | AQWA | 4.44 | 11.2 | 8.33 | 8.2 | 3.37 | −15.21 |
| WINPOST | 2.29 | 13.1 | 10.9 | 3.5 | 4.45 | −3.4 | |
| OTRC | 6.30 | 10.9 | 9.11 | 9.57 | 4.2 | −8.69 | |
| Min | Min | −60.22 | −20.04 | −10.45 | −7.26 | −4.37 | −29.72 |
| Min | −61.30 | −21.4 | −11.3 | −3.6 | −4.99 | −24.6 | |
| Min | −54.10 | −13.6 | −9.52 | −8.77 | −4.07 | −23.3 | |
| Mean | AQWA | −20.77 | −0.48 | 0.11 | 0.06 | 0.17 | −18.37 |
| WINPOST | −22.90 | −0.09 | 0.14 | −0.1 | 0.01 | −16 | |
| OTRC | −21.10 | −0.64 | −0.06 | −0.08 | 0.03 | −16.8 | |
| SD | AQWA | 7.97 | 4.55′ | 2.92 | 1.45 | 1.19 | 5.03 |
| WINPOST | 9.72 | 4.57 | 3.08 | 0.9 | 1.31 | 3.8 | |
| OTRC | 8.78 | 4.05 | 2.81 | 2.18 | 1.26 | 2.46 |
| Line 7 | Line 12 | ||||
|---|---|---|---|---|---|
| Cases | Aramid (kN) | HMPE (kN) | Polyester (kN) | Steel Wire (kN) | |
| Max | 6481.472 | 6334.535 | 4447.136 | 14,606.43 | |
| Min | 1081.697 | 1141.558 | 284.4881 | 5375.512 | |
| Intact | Mean | 3781.335 | 4056.384 | 2309.159 | 10,259.12 |
| Sd | 790.4503 | 813.4267 | 700.696 | 1307.523 | |
| Max | 7592.273 | 9850.349 | 7044.375 | 15,883.23 | |
| Single-line damage | Min | 1081.697 | 460.7601 | 253.2815 | 5380.742 |
| Mean | 4358.207 | 4801.643 | 2979.424 | 11,943.58 | |
| Sd | 1009.639 | 1226 | 1374.189 | 1595.16 | |
| Max | 13,631.85 | 14,007.41 | 9330.236 | 21,607.54 | |
| Double-line damage | Min | 1081.697 | 1032.128 | 284.4881 | 5375.512 |
| Mean | 5771.546 | 6544.601 | 3740.242 | 15,187.81 | |
| Sd | 2507.405 | 2676.009 | 1730.672 | 3299.447 | |
| LP1 | GP4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Aramid (kN) | HMPE (kN) | Polyester (kN) | Steel Wire (kN) | Aramid (kN) | HMPE (kN) | Polyester (kN) | Steel Wire (kN) | ||
| Max | 1655.9 | 1735.81 | 1897.61 | 1567.57 | 2700.60 | 2789.36 | 3053.44 | 2579.80 | |
| Intact | Min | 609.46 | 499.47 | 527.33 | 605.65 | 1450.64 | 1317.80 | 1384.40 | 1435.19 |
| Mean | 1169.09 | 1159.55 | 1289.26 | 1088.17 | 2123.60 | 2110.44 | 2290.40 | 2015.71 | |
| SD | 170.64 | 164.12 | 222.33 | 148.87 | 206.11 | 198.09 | 274.65 | 178.27 | |
| Max | 1798.66 | 2307.53 | 2882.06 | 1567.43 | 2861.72 | 3458.93 | 4158.53 | 2594.06 | |
| Single-line damage | Min | 633.04 | 304.50 | 47.55 | 606.46 | 1479.39 | 1090.26 | 757.13 | 1436.28 |
| Mean | 1198.10 | 1195.55 | 1394.49 | 1123.32 | 2156.96 | 2152.16 | 2417.92 | 2072.43 | |
| SD | 185.88 | 212.04 | 415.48 | 145.58 | 224.17 | 254.61 | 507.08 | 175.86 | |
| Max | 3000.05 | 3058.96 | 4249.34 | 1721.84 | 4275.48 | 4359.87 | 5747.68 | 2820.15 | |
| Double-line damage | Min | 149.55 | 82.18 | 86.85 | 605.65 | 843.48 | 775.47 | 722.99 | 1435.19 |
| Mean | 1277.87 | 1285.23 | 1479.29 | 1182.43 | 2247.09 | 2253.12 | 2505.28 | 2169.08 | |
| SD | 351.33 | 388.27 | 488.70 | 166.50 | 417.73 | 461.85 | 586.97 | 209.34 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ja'e, I.A.; Ali, M.O.A.; Yenduri, A.; Nizamani, Z.; Nakayama, A. Effect of Various Mooring Materials on Hydrodynamic Responses of Turret-Moored FPSO with Emphasis on Intact and Damaged Conditions. J. Mar. Sci. Eng. 2022, 10, 453. https://doi.org/10.3390/jmse10040453
Ja'e IA, Ali MOA, Yenduri A, Nizamani Z, Nakayama A. Effect of Various Mooring Materials on Hydrodynamic Responses of Turret-Moored FPSO with Emphasis on Intact and Damaged Conditions. Journal of Marine Science and Engineering. 2022; 10(4):453. https://doi.org/10.3390/jmse10040453
Chicago/Turabian StyleJa'e, Idris Ahmed, Montasir Osman Ahmed Ali, Anurag Yenduri, Zafarullah Nizamani, and Akihiko Nakayama. 2022. "Effect of Various Mooring Materials on Hydrodynamic Responses of Turret-Moored FPSO with Emphasis on Intact and Damaged Conditions" Journal of Marine Science and Engineering 10, no. 4: 453. https://doi.org/10.3390/jmse10040453
APA StyleJa'e, I. A., Ali, M. O. A., Yenduri, A., Nizamani, Z., & Nakayama, A. (2022). Effect of Various Mooring Materials on Hydrodynamic Responses of Turret-Moored FPSO with Emphasis on Intact and Damaged Conditions. Journal of Marine Science and Engineering, 10(4), 453. https://doi.org/10.3390/jmse10040453







