A Block Sparse-Based Dynamic Compressed Sensing Channel Estimator for Underwater Acoustic Communication
Abstract
:1. Introduction
2. Problem Formulation
2.1. Problem Statement
2.2. UWA Communication Model
2.3. Block Sparse Representation of UWA Channel
3. The Proposed BS-CS Method
| Algorithm 1. |
| 1: (1) Running the BOMP: initialization of |
| 2: |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: |
| 8: (2) Computing the additions: |
| 9: |
| 10: |
| 11: |
| 12: |
| 13: (3) BOMP update: initialization of |
| 14: |
| 15: |
| 16: |
| 17: |
| 18: |
| 19: |
| 20: (4) Deleting some small false detections. |
| 21: |
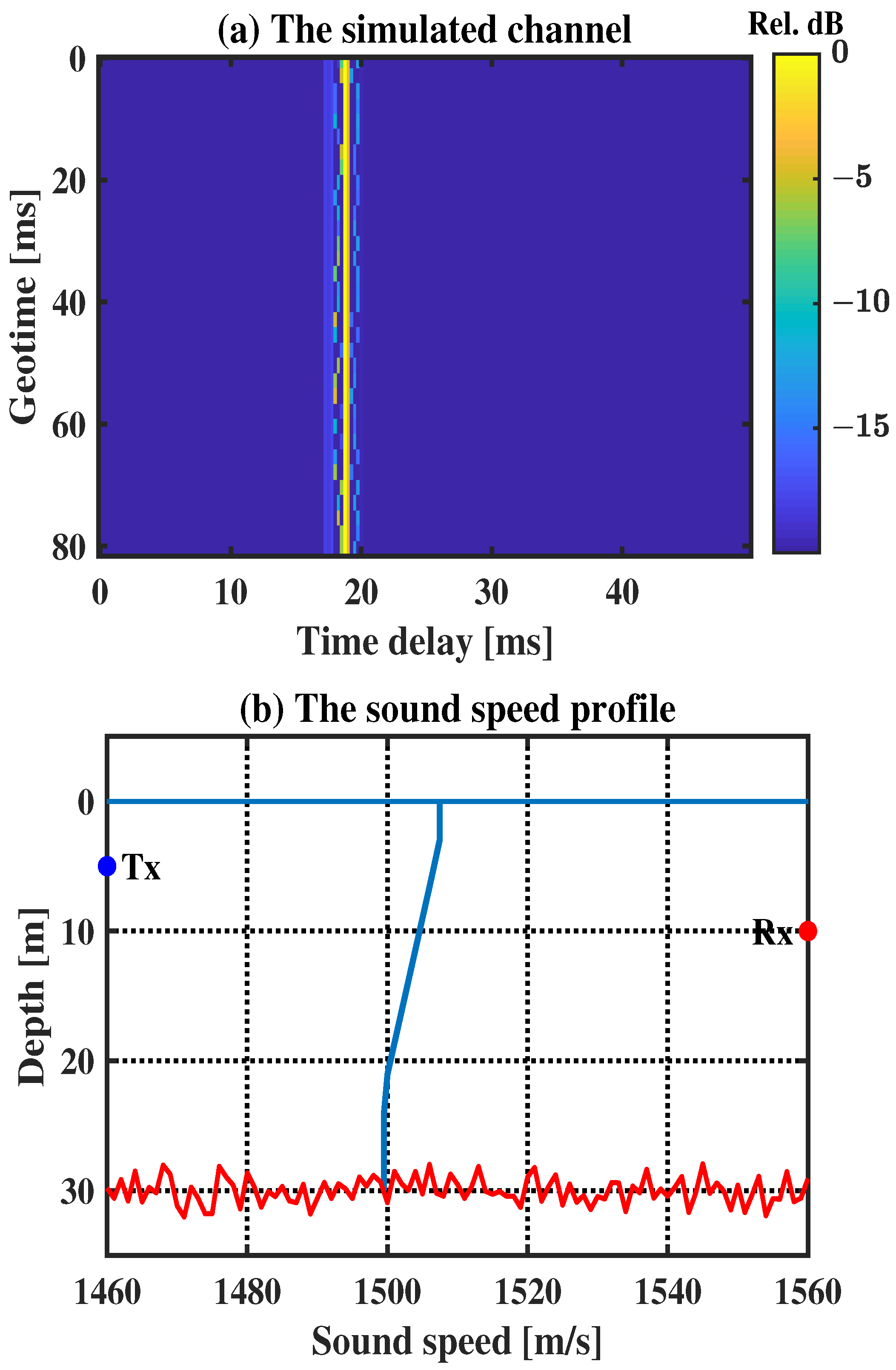
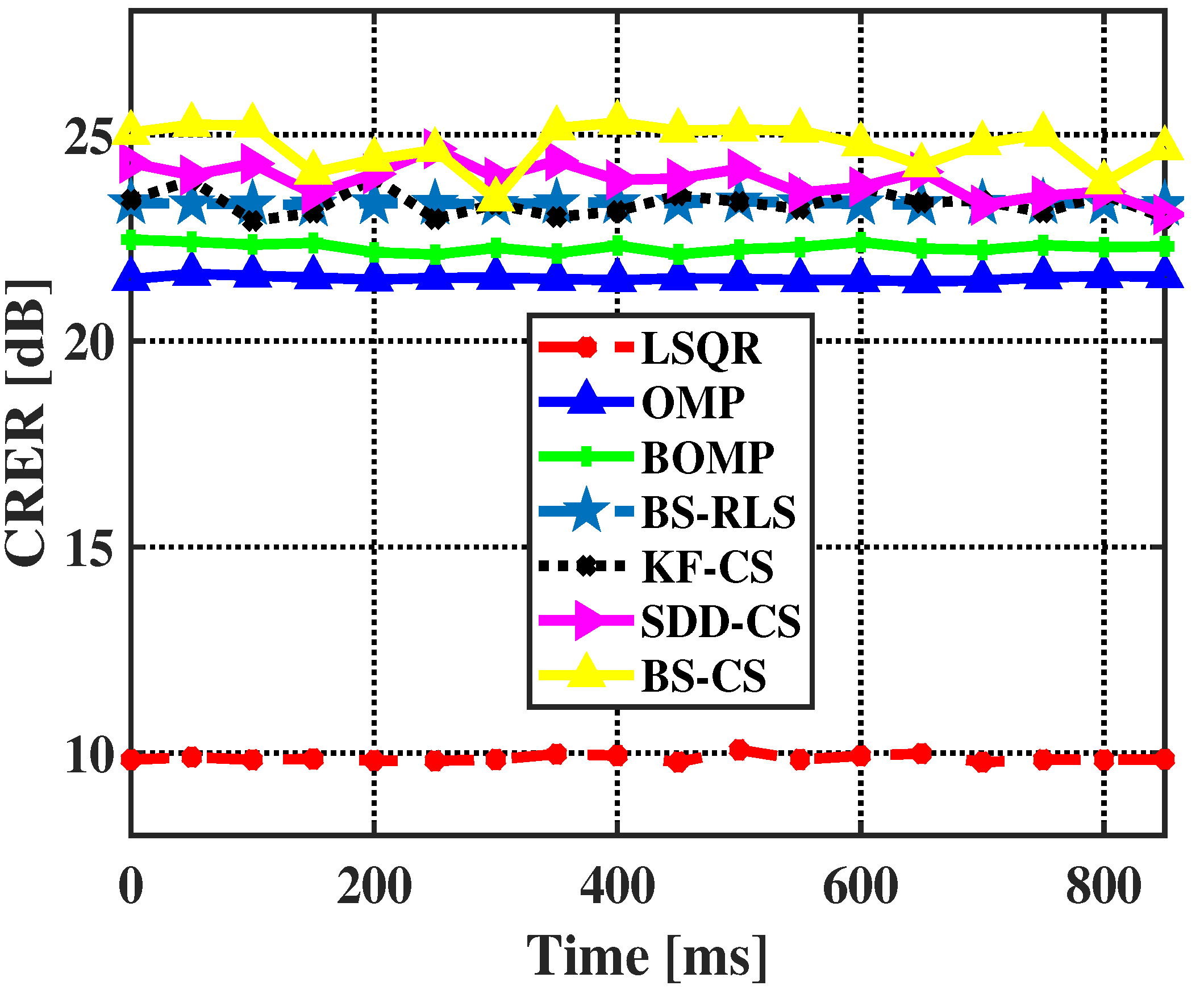
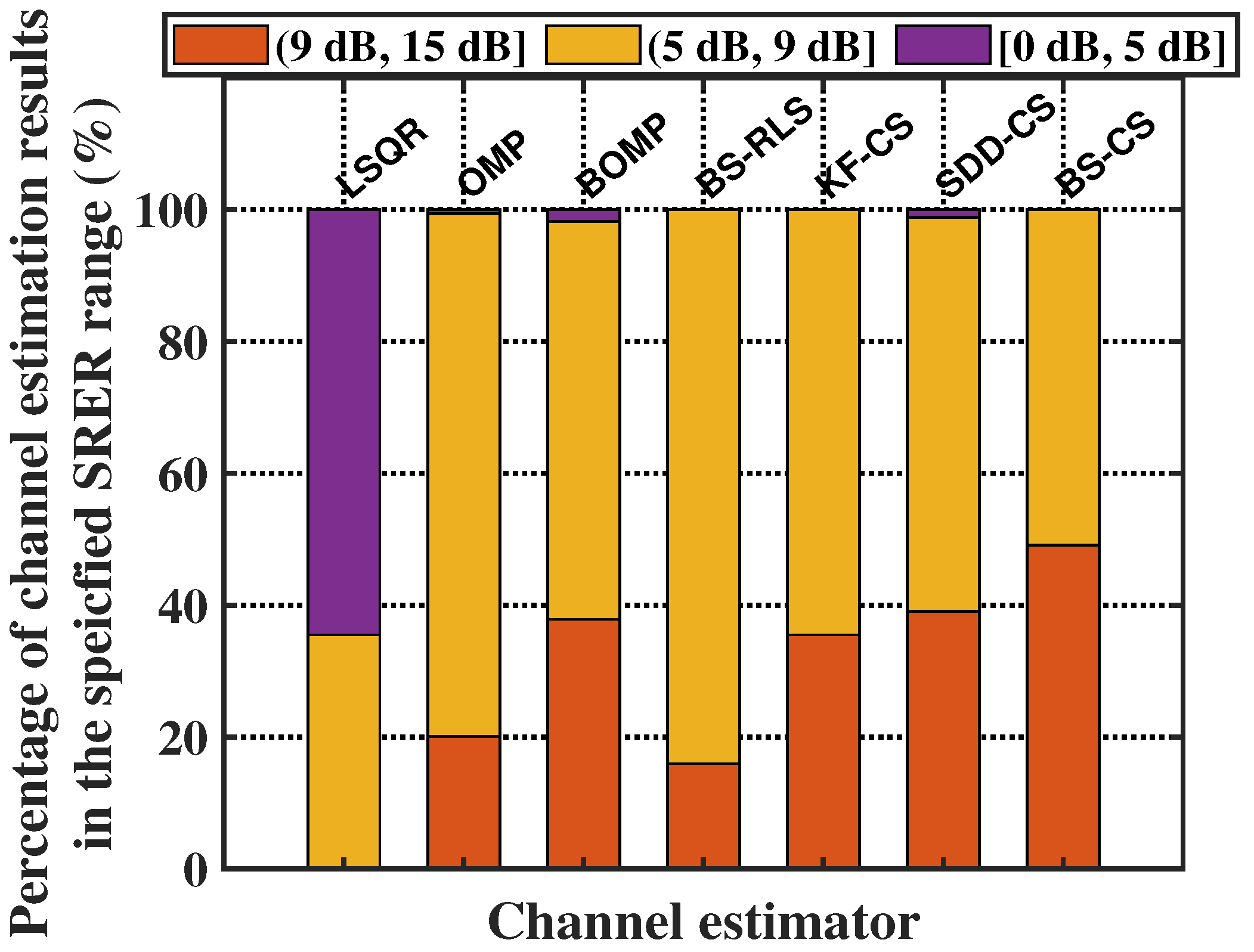
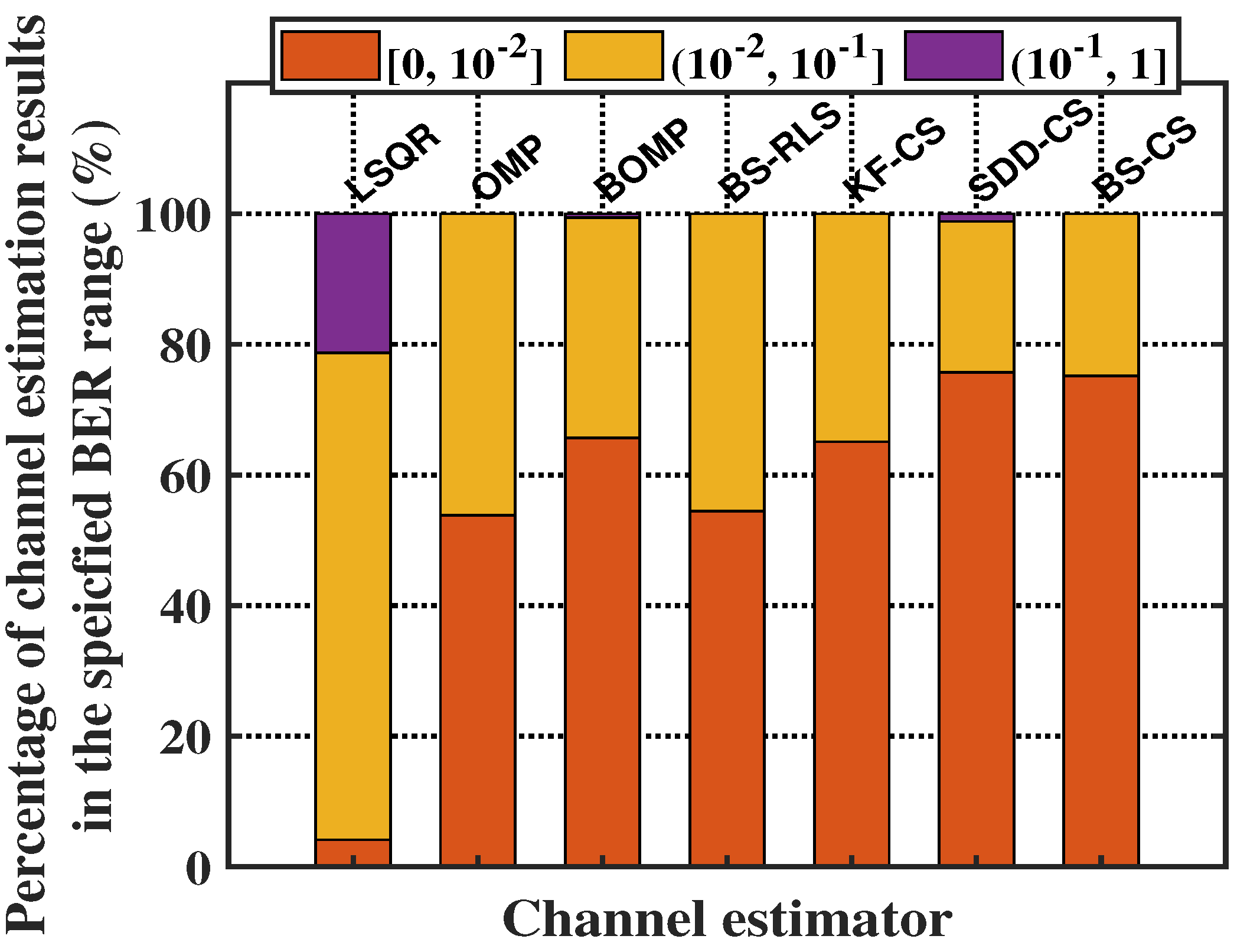
4. Numerical Simulation
- (1).
- LSQR: The classic non-sparse channel estimation algorithm.
- (2).
- OMP: The classic CS channel estimation algorithm.
- (3).
- BOMP: The classic block sparse-based CS channel estimation algorithm.
- (4).
- BS-RLS: The novel block sparse-based channel estimation algorithm, which was proposed to exploit the block sparsity of UWA channels.
- (5).
- KF-CS: The classic DCS channel estimation algorithm.
- (6).
- SDD-CS: The novel DCS-based channel estimation algorithm, which was proposed to explore the hybrid sparsity of UWA channels.
- (7).
- BS-CS: The proposed channel estimation algorithm, which is designed for the block sparse time-varying UWA channels.
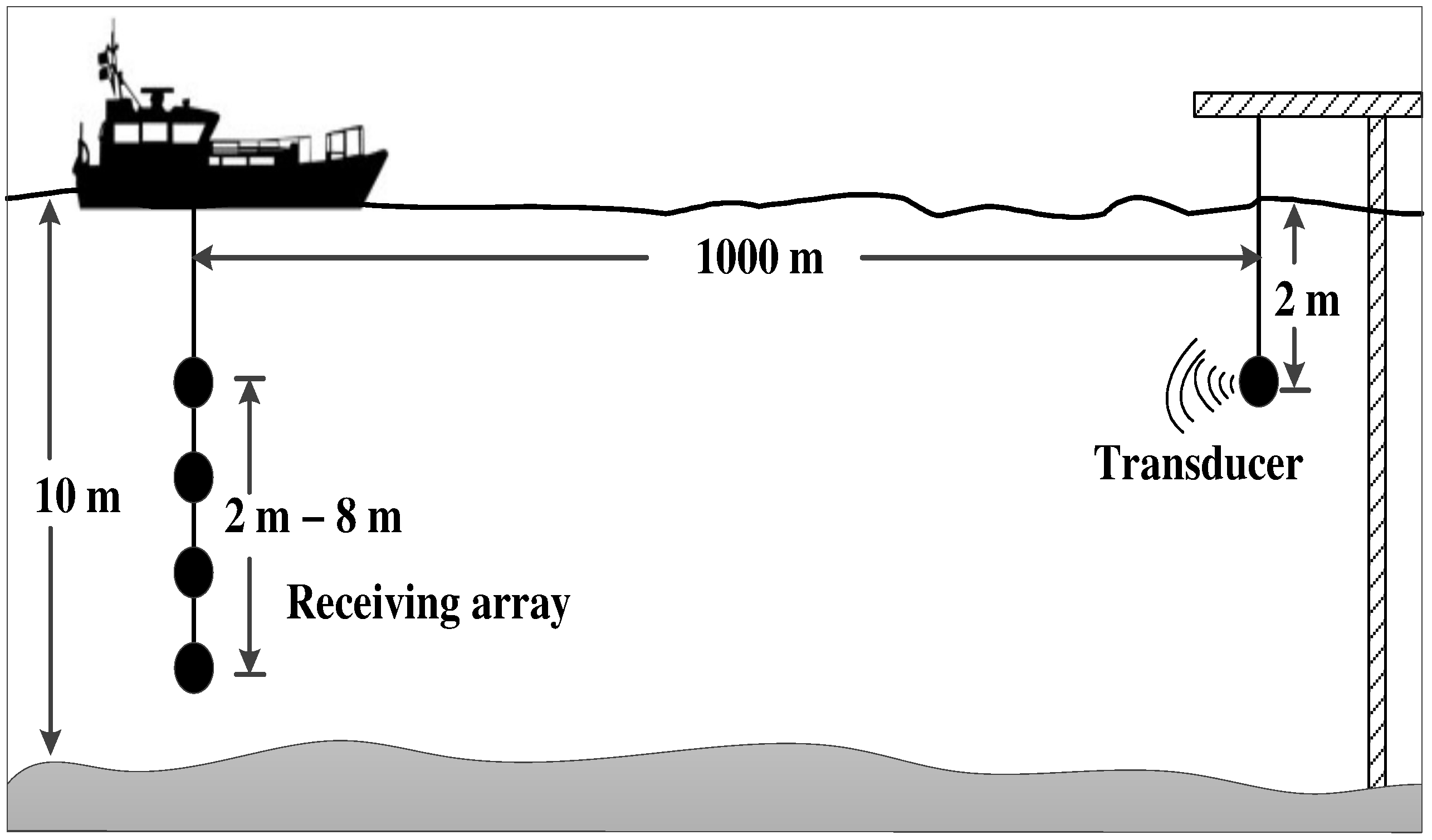
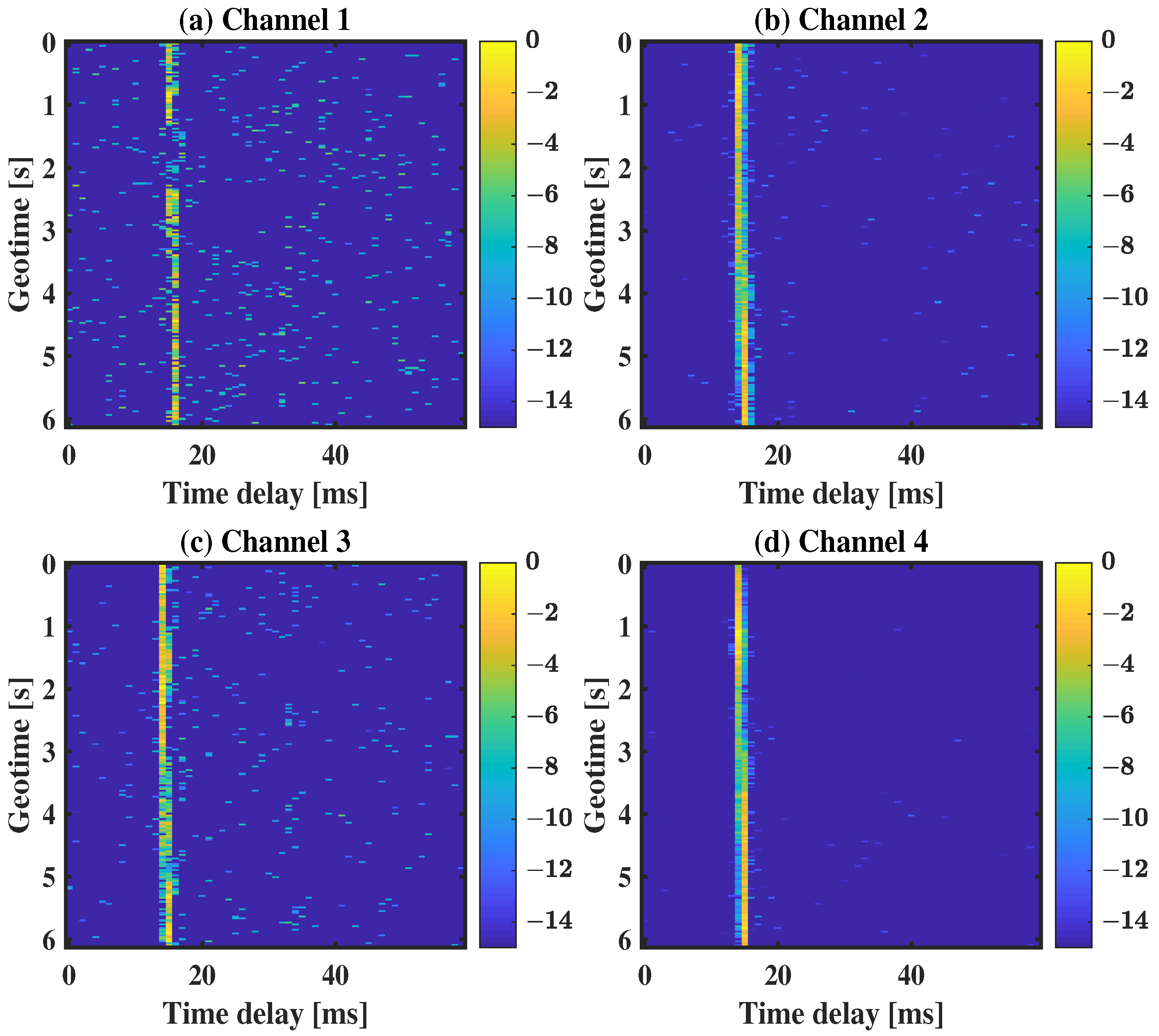
5. Sea Experiment
5.1. Experiment Setup
5.2. Result Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, W.; Gao, X.; Sun, C.; Li, G.Y. Shallow underwater acoustic massive MIMO communications. IEEE Trans. Signal Process. 2021, 69, 1124–1139. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Li, C.; Chen, D.; Meriaudeau, F. Meta-learning-aided orthogonal frequency division multiplexing for underwater acoustic communications. J. Acoust. Soc. Am. 2021, 149, 4596–4606. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Cai, L.; Shen, X.; Zhao, R. Fundamentals and advancements of topology discovery in underwater acoustic sensor networks: A review. IEEE Sens. J. 2021, 21, 21159–21174. [Google Scholar] [CrossRef]
- Khan, M.R.; Das, B.; Pati, B.B. Channel estimation strategies for underwater acoustic (UWA) communication: An overview. J. Frankl. Inst. 2020, 357, 7229–7265. [Google Scholar] [CrossRef]
- Zhou, Y.; Song, A.; Tong, F.; Kastner, R. Distributed compressed sensing based channel estimation for underwater acoustic multiband transmissions. J. Acoust. Soc. Am. 2018, 143, 3985–3996. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gong, G.; Yao, W. Adaptive estimation of sparse channel based on modified RLS for coherent underwater acoustics communications. Appl. Acoust. 2022, 192, 108745–108750. [Google Scholar] [CrossRef]
- Panayirci, E.; Altabbaa, M.T.; Poor, H.V. Channel estimation and equalization for Alamouti SF-coded OFDM-UWA communications. IEEE Trans. Veh. Technol. 2021, 70, 1709–1723. [Google Scholar] [CrossRef]
- Berger, C.R.; Wang, Z.; Huang, J.; Zhou, S. Application of compressive sensing to sparse channel estimation. IEEE Commun. Mag. 2010, 48, 164–174. [Google Scholar] [CrossRef]
- Wu, F.; Yang, K.; Duan, R. Compressed Sensing of Underwater Acoustic Signals via Structured Approximation l0-Norm. IEEE Trans. Veh. Technol. 2018, 67, 8504–8513. [Google Scholar] [CrossRef]
- Cao, X.; Tong, F.; Li, B.; Zheng, S. Experimental evaluation of norm constraint sparsity exploitation for shallow water acoustic communication. Appl. Acoust. 2021, 180, 108111–108116. [Google Scholar] [CrossRef]
- Hu, X.; Wang, Y.; Wu, F.; Huang, A. Using a New Channel Estimation Algorithm to Improve Underwater Acoustic Communication with Multiple Receivers. J. Coast. Res. 2021, 37, 779–783. [Google Scholar] [CrossRef]
- Yan, Z.; Yang, X.; Sun, L.; Wang, J. Inter-carrier interference-aware sparse time-varying underwater acoustic channel estimation based on fast reconstruction algorithm. China Commun. 2021, 18, 216–225. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Wang, C.; Ouyang, D.; Huang, Y. A-OMP: An adaptive OMP algorithm for underwater acoustic OFDM channel estimation. IEEE Wirel. Commun. Lett. 2021, 10, 1761–1765. [Google Scholar] [CrossRef]
- Sundman, D.; Chatterjee, S.; Skoglund, M. A greedy pursuit algorithm for distributed compressed sensing. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 2729–2732. [Google Scholar]
- Vaswani, N. Kalman filtered compressed sensing. In Proceedings of the 2008 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; pp. 893–896. [Google Scholar]
- Jiang, W.; Zheng, S.; Zhou, Y.; Tong, F.; Kastner, R. Exploiting time varying sparsity for underwater acoustic communication via dynamic compressed sensing. J. Acoust. Soc. Am. 2018, 143, 3997–4007. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vaswani, N. LS-CS-residual (LS-CS): Compressive sensing on least squares residual. IEEE Trans. Signal Process. 2010, 58, 4108–4120. [Google Scholar] [CrossRef] [Green Version]
- Vaswani, N.; Lu, W. Modified-CS: Modifying compressive sensing for problems with partially known support. IEEE Trans. Signal Process. 2010, 58, 4595–4607. [Google Scholar] [CrossRef] [Green Version]
- Lu, W.; Vaswani, N. Regularized modified BPDN for noisy sparse reconstruction with partial erroneous support and signal value knowledge. IEEE Trans. Signal Process. 2011, 60, 182–196. [Google Scholar] [CrossRef] [Green Version]
- Munshi, A.; Unnikrishnan, S. Performance Analysis of Compressive Sensing based LS and MMSE Channel Estimation Algorithm. J. Commun. Softw. Syst. 2021, 17, 13–19. [Google Scholar] [CrossRef]
- Jiang, W.; Tong, F.; Zheng, S.; Cao, X. Estimation of Underwater Acoustic Channel With Hybrid Sparsity via Static-Dynamic Discriminative Compressed Sensing. IEEE Sens. J. 2020, 20, 14548–14558. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, S.; Preisig, J.C.; Pattipati, K.R.; Willett, P. Clustered adaptation for estimation of time-varying underwater acoustic channels. IEEE Trans. Signal Process. 2012, 60, 3079–3091. [Google Scholar] [CrossRef]
- Eldar, Y.C.; Kuppinger, P.; Bolcskei, H. Block-sparse signals: Uncertainty relations and efficient recovery. IEEE Trans. Signal Process. 2010, 58, 3042–3054. [Google Scholar] [CrossRef] [Green Version]
- Tian, T.; Wu, F.Y.; Yang, K. Estimation of underwater acoustic channel via block-sparse recursive least-squares algorithm. In Proceedings of the 2019 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Dalian, China, 20–22 September 2019; pp. 1–6. [Google Scholar]
- Wang, Y.; Tu, H.; Liu, W.; Xiao, W.; Lan, Q. Application of a Chebyshev collocation method to solve a parabolic equation model of underwater acoustic propagation. Acoust. Aust. 2021, 49, 281–291. [Google Scholar] [CrossRef]
- El Guide, M.; El Ichi, A.; Jbilou, K. Discrete cosine transform LSQR methods for multidimensional ill-posed problems. J. Math. Model. 2022, 10, 21–37. [Google Scholar]
- Guo, Z.; Song, A.; Towliat, M.; Cimini, L.J.; Xia, X.G. Impacts of channel fluctuations on least-squares channel estimation in underwater acoustic communications. J. Acoust. Soc. Am. 2021, 149, 3929–3942. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.Y.; Yang, K.; Tong, F.; Tian, T. Compressed sensing of delay and doppler spreading in underwater acoustic channels. IEEE Access 2018, 6, 36031–36038. [Google Scholar] [CrossRef]
- Zhang, Y.; Zakharov, Y.V.; Li, J. Soft-decision-driven sparse channel estimation and turbo equalization for MIMO underwater acoustic communications. IEEE Access 2018, 6, 4955–4973. [Google Scholar] [CrossRef]
- Swirszcz, G.; Abe, N.; Lozano, A.C. Grouped orthogonal matching pursuit for variable selection and prediction. Adv. Neural Inf. Process. Syst. 2009, 22, 1–6. [Google Scholar]
- Zhou, Y.; Diamant, R. A Parallel Decoding Approach for Mitigating Near–Far Interference in Internet of Underwater Things. IEEE Internet Things J. 2020, 7, 9747–9759. [Google Scholar] [CrossRef]
- Van Walree, P.A.; Socheleau, F.X.; Otnes, R.; Jenserud, T. The watermark benchmark for underwater acoustic modulation schemes. IEEE J. Ocean. Eng. 2017, 42, 1007–1018. [Google Scholar] [CrossRef] [Green Version]



| Description | Value |
|---|---|
| Carrier frequency | 16,000 Hz |
| Bandwidth | 5000 Hz |
| Channel impulse response duration | 60 ms |
| Length of discrete observation window | 30 |
| Length of feedforward filter | 120 |
| Length of feedback filter | 59 |
| Error tolerance of LS | |
| Length of training sequence for BS-RLS | 400 |
| Channel sparsity for OMP and KF-CS | 6 |
| Block size for BOMP, BS-RLS, and BS-CS | 2 |
| Block sparsity for BOMP, BS-RLS, and BS-CS | 3 |
| Continuous measurement number for SDD-CS | 2 |
| The addition threshold for KF-CS, SDD-CS, and BS-CS | 0.07 |
| Algorithms | SRER (dB) | BER (%) |
|---|---|---|
| LSQR | 4.71 | 7.13 |
| OMP | 8.12 | 1.11 |
| BOMP | 8.40 | 1.04 |
| BS-RLS | 7.82 | 1.17 |
| KF-CS | 8.52 | 0.79 |
| SDD-CS | 8.66 | 0.72 |
| BS-CS | 9.04 | 0.54 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Chen, L.; Li, Y.; Jiang, W. A Block Sparse-Based Dynamic Compressed Sensing Channel Estimator for Underwater Acoustic Communication. J. Mar. Sci. Eng. 2022, 10, 536. https://doi.org/10.3390/jmse10040536
Xu L, Chen L, Li Y, Jiang W. A Block Sparse-Based Dynamic Compressed Sensing Channel Estimator for Underwater Acoustic Communication. Journal of Marine Science and Engineering. 2022; 10(4):536. https://doi.org/10.3390/jmse10040536
Chicago/Turabian StyleXu, Lingji, Lixing Chen, Yaan Li, and Weihua Jiang. 2022. "A Block Sparse-Based Dynamic Compressed Sensing Channel Estimator for Underwater Acoustic Communication" Journal of Marine Science and Engineering 10, no. 4: 536. https://doi.org/10.3390/jmse10040536
APA StyleXu, L., Chen, L., Li, Y., & Jiang, W. (2022). A Block Sparse-Based Dynamic Compressed Sensing Channel Estimator for Underwater Acoustic Communication. Journal of Marine Science and Engineering, 10(4), 536. https://doi.org/10.3390/jmse10040536







