1. Introduction
When the steady incoming flow with a certain Reynolds number bypasses a bluff body, double-row vortices with opposite rotation direction and regular arrangement will shed periodically at the tail of the bluff body, which is called the Karman vortex street. At this time, the fluid produces a periodic alternating force on the structure, causing it to vibrate, which is called vortex-induced vibration (VIV) [
1]. Since it was first reported by Von Kármán in 1911, the Karman vortex has been deeply investigated in many engineering fields. A systematic review of the Karman vortex and VIV can be found in works by Gabbai et al. [
2] and Williamson et al. [
3].
In the early research of the Karman vortex, theoretical analysis and experiment were the main methods [
2]. With the development of computer technology, numerical simulation provides support for the further study of the Karman vortex. Lam et al. [
4] simulated the vortex shedding downstream of an inclined plate by using the finite volume CFD code and the RNG
k-
ω turbulence model, and the results were in good agreement with the experiment. Vagnoli et al. [
5] conducted experiments and numerical simulations on the guide vane of a front-loaded turbine. They believed that the large eddy simulation (LES) is the most appropriate method to obtain reliable results of unstable wake characteristics. However, LES has not been widely used because of the high computational cost. To reduce the simulation time, Zhou et al. [
6] used a dynamic, adaptive, grid-based LES method to solve the evolution of an airplane’s wake vortex. The results showed that the adaptive grid method could generate refined meshes in the vortex core area, and captured the dynamic performance of vortex more effectively. Zeng et al. [
7] used a transition SST model coupled with the SST
k-
ω model and the
γ-
Reθt transition model to simulate the vortex shedding of a hydrofoil, and the results were in good agreement with the experimental data. Compared with the LES model, the transitional SST model greatly saves computing resources on the basis of high accuracy.
In hydraulic machinery, the Karman vortex street mainly exists in the tail of foil-shaped structures such as blades and guide vanes. Many hydropower stations have successively reported the noise, vibration, and structural damage caused by the coincidence of the Karman vortex frequency with the structural natural frequency [
8]. Therefore, a lot of research has been conducted on the performance of the Karman vortex and how to suppress the VIV in hydraulic machinery. For example, Villegas et al. [
9] used the time-resolved particle image velocimetry (TR-PIV) technique to experimentally study the relationship between the fluid force and the wake vortex shedding for a low Reynolds number wing, and then a six-step model describing the vortex–force relation was proposed. Ausoni et al. [
10], through a series of experiments on hydrofoils, found that the Karman vortex may cause cavitation, thus increasing the vortex shedding frequency and the vibration amplitude of the hydrofoil. Besides, the shedding performance of the Karman vortex also changed with the surface roughness of the hydrofoil [
11]. Lee et al. [
12] numerically investigated the wake flow of a modified NACA 0009 hydrofoil, and the results showed that the strength and shedding frequency of the Karman vortex are significantly affected by the cross-sectional shape of the trailing edge.
There are many factors that affect the strength and the shedding frequency of the wake vortex. In addition to the above items, there are also inflow velocity, attacking angle, turbulence intensity, and so on. However, the shape of the trailing edge is the most controllable factor. As early as the 1950s, Donaldson [
13] experimentally studied the influence of different shapes of the trailing edges of the Francis-turbine blades on the excitation force, and successfully eliminated some unpleasant vibrations by trimming the edges. Since then, trailing-edge trimming has gradually become the mainstream method to suppress VIV of blades and guide vanes. Do et al. [
14] numerically researched the wake flow of a blunt-tailed two-dimensional NACA 0015 section with different base cavity shapes and sizes at high Reynolds numbers. The results showed that the base cavity at the trailing edge did not change the intrinsic Strouhal number of this section, but did have a remarkable impact on the local pressure fluctuations, lift fluctuations, and wake structure. Peng et al. [
15] established an intelligent optimization model of the blade trailing-edge profile based on factorial experiments, extreme learning machine (ELM), and particle swarm optimization (PSO), with the goal of reducing the VIV of the stay vane of hydro-turbines. Wang et al. [
16] used the delayed separation vortex technique to simulate the wake of a high Reynolds number turbine blade and found that the characteristics of the wake vortex street changed observably with the suction profile. In addition, the suction boundary layer with an incomplete velocity profile tended to stabilize the wake, suppress the generation of wake vortices, and weaken the unsteady effect of the wake. Zobeiri et al. [
17] compared the wake behind hydrofoils with a sloping tail and an obtuse tail using a laser Doppler velocimetry (LDV). The results showed that the shape of the trailing edge of a guide vane directly affected the distribution of wake vorticity, and the vortices on both sides of the asymmetric trailing edge tended to collide with each other, thereby reducing the vortex excitation energy. Yao et al. [
18] and Zeng et al. [
7] performed a series of experiments and numerical simulations on the hydrodynamic damping of hydrofoils, and found that an asymmetric trimming resulted in a significant increase in hydrodynamic damping under large flow conditions. Lee et al. [
19] and Neidhardt et al. [
20] investigated the effect of the tail thickness of a hydrofoil on the wake performance through numerical simulations. Neidhardt et al. [
20] reported that the elimination of the Karman vortex resonance by trailing-edge modification should be attributed more to a decrease in excitation energy rather than a change in shedding frequency. Xia et al. [
21] respectively performed bevel cuts on the two sides of the trailing edge of an asymmetric guide vane, and compared the effectiveness of the two modifications by numerical methods. For this case, trimming on the side with a larger velocity gradient near the trailing edge could effectively suppress the Karman vortex, while trimming on the other side was less effective. Besides, it was found that the strength of the wake vortex seemed to be directly related to the difference of the velocity gradient on the two sides of the trailing edge.
The purpose of this study is to verify and further explore the influence of the asymmetry of the flow velocity on both sides of the trailing edge on the strength and the shedding frequency of the wake vortex. The results show that as the asymmetry of the flow velocity increases, the vortex shedding frequency first decreases and then increases. The vortex intensity gradually decreases, and then the wake suddenly stabilizes, and the vortex street almost disappears at this time. During this process, two critical states can be observed. As the Reynolds number and the thickness of the trailing edge change, the critical states are slightly advanced or delayed. In addition, the asymmetry of the flow velocity significantly affects the effectiveness of the tail-edge trimming.
3. Results and Discussion
3.1. Influence of Flow Velocity Asymmetry on the Wake Vortex
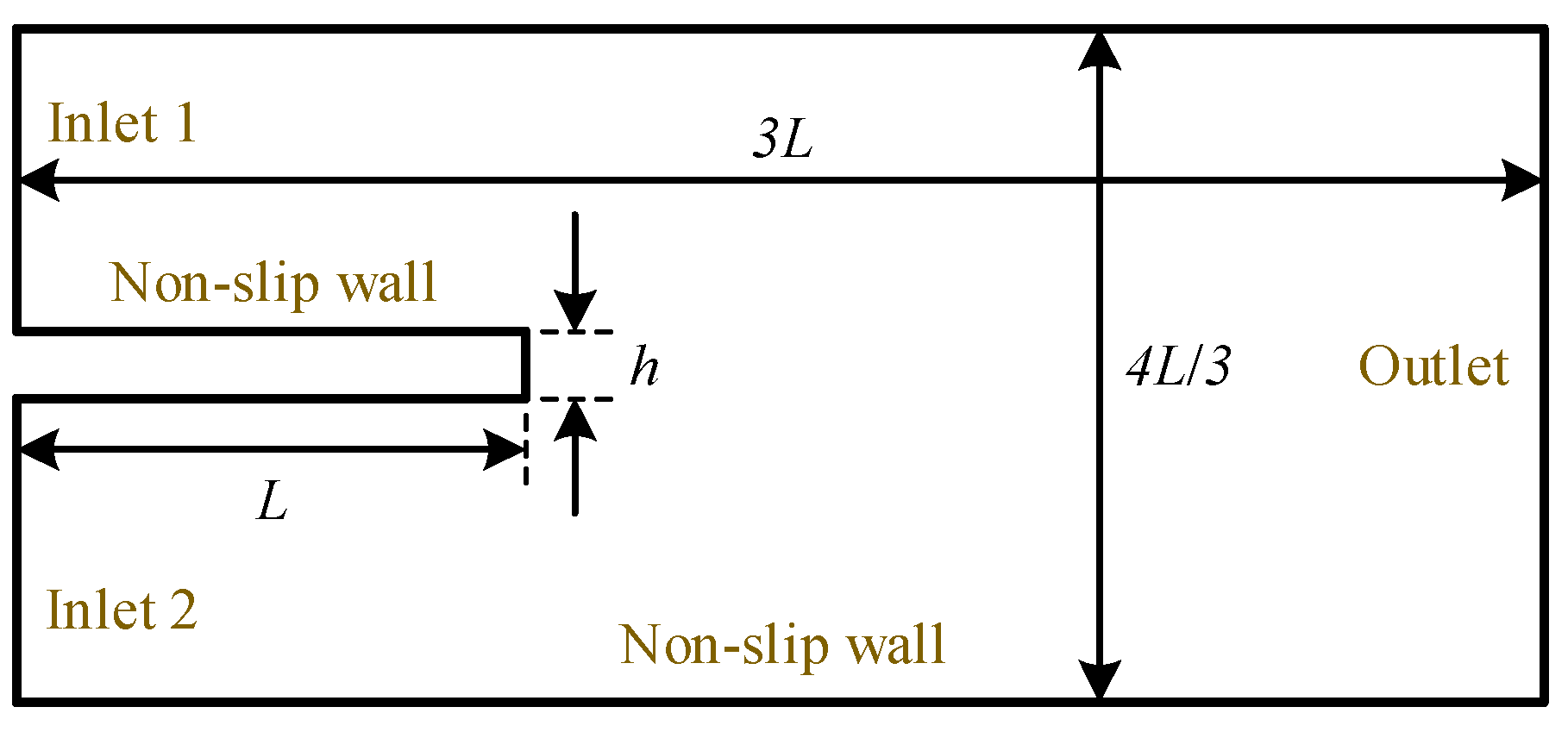
The ratio U1/U2 of the inlet velocities on both sides of the hydrofoil was defined as α (α ≥ 1). The larger α is, the larger the difference of the velocity gradient at the flow separation point on both sides of the trailing edge. Firstly, keeping Uin = (U1 + U2)/2 = 20 L/s (i.e., Re ≈ 1.8 × 106), and α was set as different values for simulation.
Figure 6 shows the contours of the vorticity downstream of the hydrofoil under various conditions. When 1 ≤
α ≤ 2, periodic shedding vortex street was observed. With the increase of
α, the vorticity of the vortex located below the center line of the hydrofoil decreased rapidly, while the vorticity of the upper vortex changed relatively less. When 1 ≤
α ≤ 1.4, the shedding and development of the lower vortex was relatively complete, and the wake vorticity presented the most common form of the Karman vortex street. When 1.53 ≤
α ≤ 2, the upper vortex dominated the wake structure, and the lower vortex gradually disappeared. When
α ≥ 2.2, two stable vortex regions were formed at the tail of the hydrofoil, and no alternate shedding vortex structure was observed.
Figure 7 shows the velocity vectors downstream of the hydrofoil when
α = 1 and
α = 2, which represent the cases in the range of 1 ≤
α ≤ 1.4 and 1.53 ≤
α ≤ 2, respectively. For 1 ≤
α ≤ 1.4, the interaction between the upper and lower vortices was mainly reflected in promoting the formation of each other and pushing each other to develop downstream. When 1.53 ≤
α ≤ 2, the induced velocity of the upper vortex destroyed the further development of the lower vortex to a certain extent, and accelerated the formation of the next lower vortex. At this time, the wake had a higher stability.
In addition to this, the pressure field was also analyzed. The results displayed that the pressure field did not become a key factor affecting the Karman vortex, but showed a certain oscillation under the influence of the vortex. From the pressure contours, the distribution of the pressure field corresponded to the vorticity field, so it was not shown in the paper.
Due to the asymmetry of the flow on the upper and lower sides, it was difficult to accurately judge the magnitude relationship between the vortex intensities under various conditions from the vorticity contours or velocity vectors. The magnitude of the fluid excitation force caused by the pressure field oscillation is a direct factor that determines the strength of VIV. Therefore, the fluctuation amplitude of the lift coefficient was directly used to characterize the vortex intensity. The time domain and frequency domain signals of the lift coefficient,
CL, on the hydrofoil under different
α conditions are shown in
Figure 8a,b. The fluctuation amplitude and dominant frequency of
CL are shown in
Figure 8c, where the dominant frequency of
CL was always equal to the vortex shedding frequency,
fv. When 1 ≤
α ≤ 2, the change of
CL with time was obviously periodic, and the frequency component was relatively single. As
α increased, the pulsation amplitude of
CL gradually decreased, and the variation of the dominant frequency was divided into two stages: (1) when 1 ≤
α ≤ 1.4, the frequency gradually decreased, and (2) when 1.53 ≤
α ≤ 2, the frequency increased with
α. For
α ≥ 2.2,
CL had no obvious fluctuation.
The above results showed that the asymmetry of the flow velocity on both sides of the trailing edge did have a significant impact on the strength and frequency characteristics of the wake vortex. Besides, there were two critical velocity ratios, αc1 and αc2, in the variation of the amplitude and dominant frequency of CL with α. Among them, the frequency of CL reached its minimum value at αc1. According to the current results, it could be roughly judged that αc1 ≈ 1.4. αc2 was the critical velocity for the stability of the wake, and the range was 2 < αc2 ≤ 2.2. When α ≥ αc2, the wake was stable, and the vortex street disappeared. Since these two critical values directly determined the variation of the Karman vortex performance with the velocity ratio, their influencing factors were further explored next.
3.2. Influencing Factors of the Critical Velocity Ratios
Firstly,
Uin = 10
L/s and 30
L/s (i.e.,
Re ≈ 0.9 × 10
6 and 2.7 × 10
6) were set to simulate the effects of the Reynolds number on
αc1 and
αc2.
Figure 9a shows the fluctuation amplitude and dominant frequency of the lift coefficient under different
α, while
Figure 9b shows the range of
αc1 and
αc2 under different
Uin. Overall, the value of
Uin had a negligible effect on
and
St. According to the definitions of
and
St, the amplitude of the lift acting on the hydrofoil was roughly proportional to the quadratic of
Uin, and the vortex shedding frequency,
fv, was approximately proportional to
Uin.
The critical velocity ratio αc1 did not change significantly under different Uin, and the trough of the dominant frequency always remained around α = 1.4 (precisely, 1.29 < αc1 < 1.53). However, the critical value αc2 changed with Uin. From the current results, when the value of Uin was 20 L/s or 30 L/s, 2 < αc2 ≤ 2.2. When Uin was reduced to 10 L/s, αc2 decreased to below 2 (precisely, 1.8 < αc2 ≤ 2). When Uin = 10 L/s and α = 2, no obvious Karman vortex street was observed in the wake of the hydrofoil. This result showed that the smaller the Reynolds number was, the easier it was for the hydrofoil wake to reach a stable state, and the easier it was to suppress the Karman vortex by changing the asymmetry of the flow on both sides.
Experience has shown that in addition to
Uin, the thickness of the trailing edge is also one of the key factors affecting the wake performance. Then, keeping
Uin = 20
L/s, the trailing edge thickness,
h, was changed to
L/20 and 3
L/20, respectively, for simulation, and the results are shown in
Figure 10. In general, with the increase of
h,
showed an increasing trend, while the change of
St was more complicated. When
α <
αc1, the change of
St was small as
h increased. On the contrary, when
α ≥
αc1,
St increased first and then decreased. Among them,
h =
L/10 corresponded to the largest
St,
h =
L/20 was the next, and
h = 3
L/20 corresponded to the smallest. In this case, the trend of
was equivalent to the trend of lift amplitude. That is, the larger
h was, the larger the amplitude of the lift acting on the hydrofoil, indicating a greater intensity of the vortex. The magnitude relationship of
St could not directly reflect the relationship between the vortex shedding frequencies with different
h. After converting
St to
fv, it could be seen that
fv decreased significantly with the increase of
h.
The influence of the thickness, h, on the critical velocity ratios was more significant than that of Uin. When h = L/20, αc1 was around 1.53 (precisely, 1.4 < αc1 < 1.67), 2.2 < αc2 ≤ 2.43; when h = L/10, αc1 was around 1.4, 2 < αc2 ≤ 2.2; when h = 3 L/20, αc1 returned to around 1.53, 1.8 < αc2 ≤ 2. According to the present results, αc1 decreased first and then increased with the increase of trailing-edge thickness, while αc2 decreased monotonically.
According to the above research, in the design of the blades and guide vanes of the hydraulic machinery and other foil-shaped flow components, it can be considered to strengthen the flow asymmetry at the trailing edge to obtain a more stable wake. When the Reynolds number is small and the trailing-edge thickness is large, it is easier to eliminate the Karman vortex street by enhancing the flow asymmetry.
3.3. Influence of Flow Velocity Asymmetry on Trimming Effect
Trailing-edge trimming is the most popular measure to suppress VIV in hydraulic machinery, and one-sided beveling is the most common trimming method. In this paper, a beveled trailing-edge shape (as shown in
Figure 11) was designed to study the influence of the flow asymmetry on the effectiveness of trimming. Bevel cuts were made on both sides of the trailing edge, respectively, and
α = 1.18, 1.4, and 1.67 were set.
The vorticity contours downstream of the modified hydrofoil under different conditions are shown in
Figure 12, where the upper side of the hydrofoil is the high-velocity side. When the low-velocity side was modified, the formation and development process of the vortex on the low-velocity side moved forward, and the damage of the vortex on the high-velocity side on its development was further enhanced. Therefore, the wake of the hydrofoil trimmed on the low-velocity side was more stable. In the case of trimming on the high-velocity side, the vortex on this side was limited to the cutting area, and its shedding strength was weakened. However, the damage of the induced velocity of this vortex to the development of the vortex on the low-velocity side was also weakened. Therefore, a distinct double-row Karman vortex street was observed. In general, the strength of the vortex shedding was reduced regardless of which side was trimmed. However, for the flat foil simulated in this paper, trimming on the low-velocity side suppressed the Karman vortex more effectively. Besides, the trimming enhanced the stability of the wake by affecting the relative position and interaction of the main vortices on the two sides instead of changing the difference between the velocity gradients on the two sides of the trailing edge. It could be inferred that the outflow angle on both sides of the hydrofoil may have a significant impact on the effect of trimming.
To quantify the effect of the trimming, the amplitude-decreased rate,
λA, and the frequency-increased rate,
λf, were introduced, which were defined as follows:
where
A0 and
AM are the amplitudes of the lift coefficient before and after modification, and
f0 and
fM are the vortex shedding frequencies before and after modification, respectively.
The corresponding
λA and
λf of the trimming under different conditions are shown in
Figure 13. From the perspective of the change in amplitude, the trimming on the low-velocity side reduced the amplitude of the lift coefficient by more than 90%, and the larger the
α, the better the effect. The effect of the trimming on the high-velocity side was poor, and the larger the
α, the worse the effect. Judging from the change of the vortex shedding frequency, the
λf corresponding to the low-velocity side trimming was higher. When
α ≈
αc1, the corresponding
λf was the highest, no matter which side was modified.
To verify the above conclusions, two additional beveled trailing-edge shapes were designed, as shown in
Figure 14a,b. The hydrofoil corresponding to
Figure 11 was named foil I. The trimming effects of these three trailing-edge shapes under the condition of
α = 1.4 are shown in
Figure 14c. The results showed that, for this type of flat foil, trimming on the low-velocity side always suppressed the Karman vortex better. It was also found that the effects of trimming in different ways on the vortex strength and shedding frequency significantly differed. However, this was not the focus of this paper, so it was not repeated here.