Ocean Current Prediction Using the Weighted Pure Attention Mechanism
Abstract
:1. Introduction
2. Materials and Methods
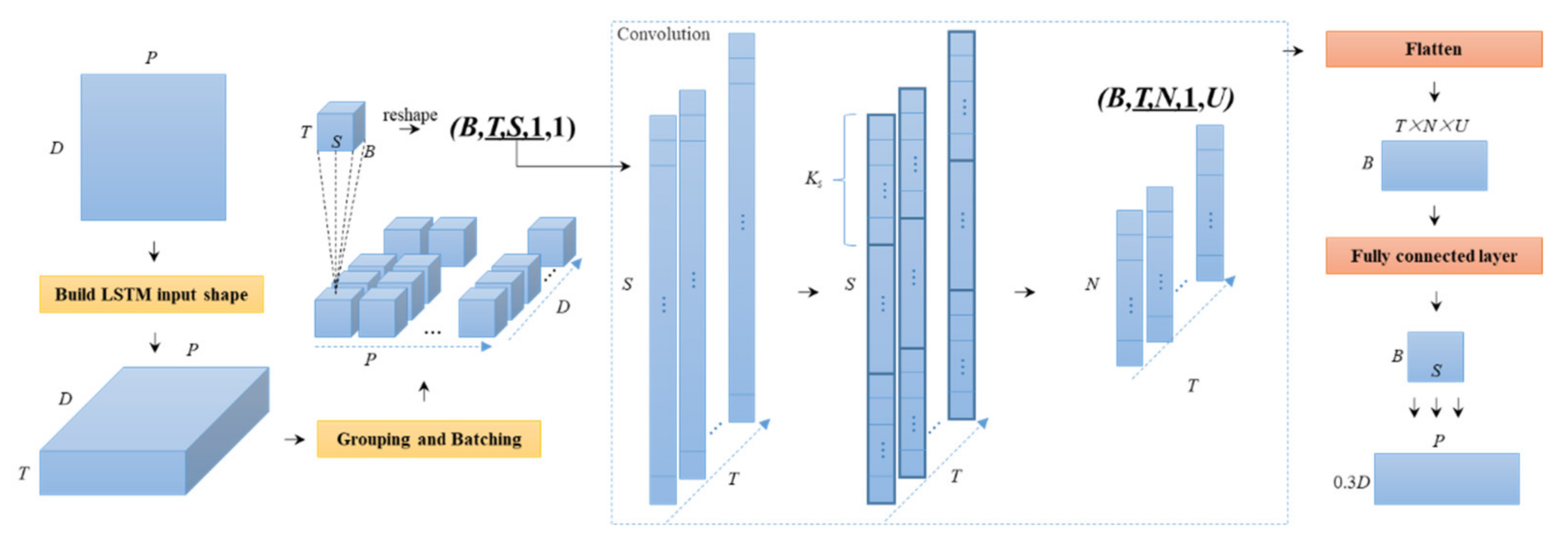
2.1. The ConvLSTM-F Model
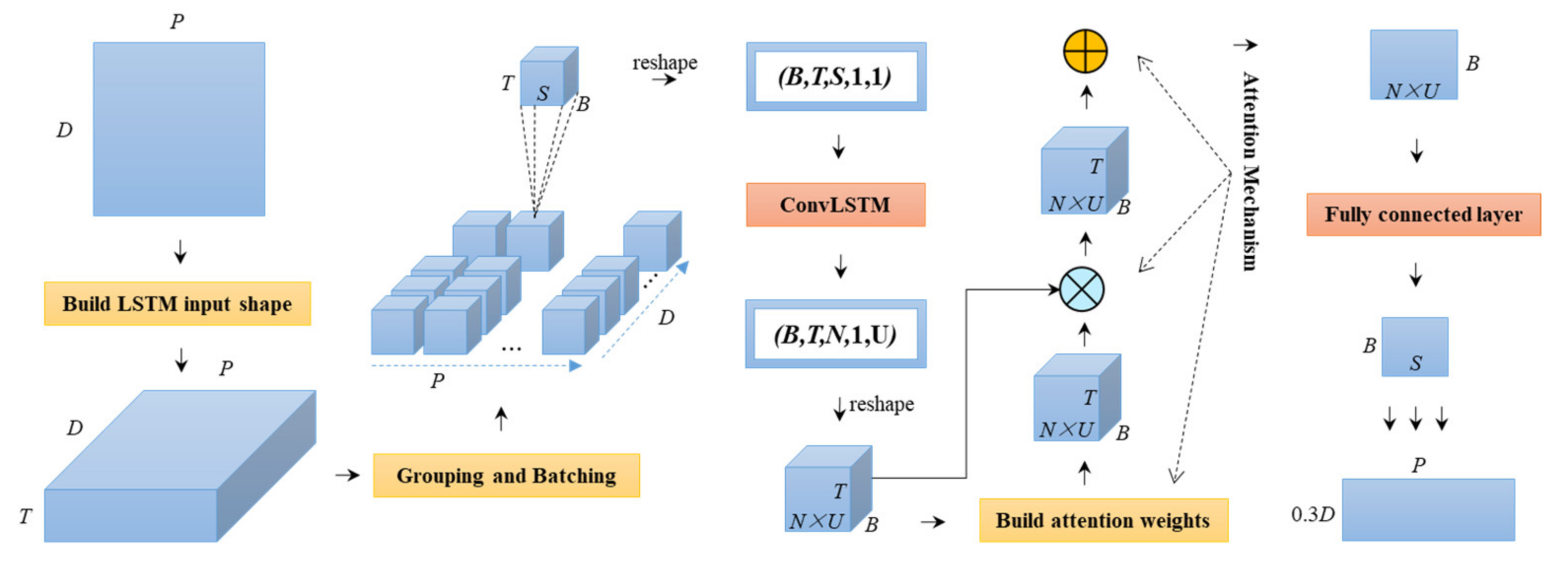
2.2. The A-ConvLSTM Model
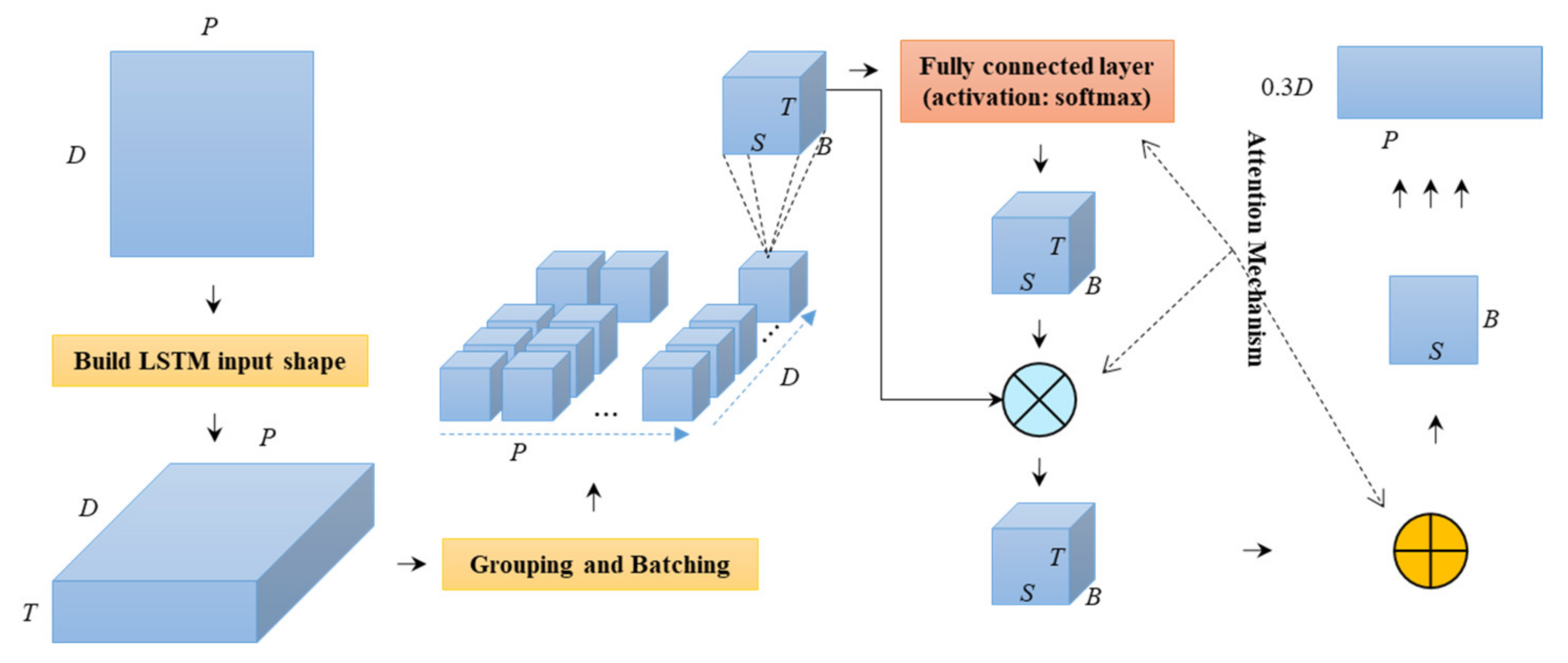
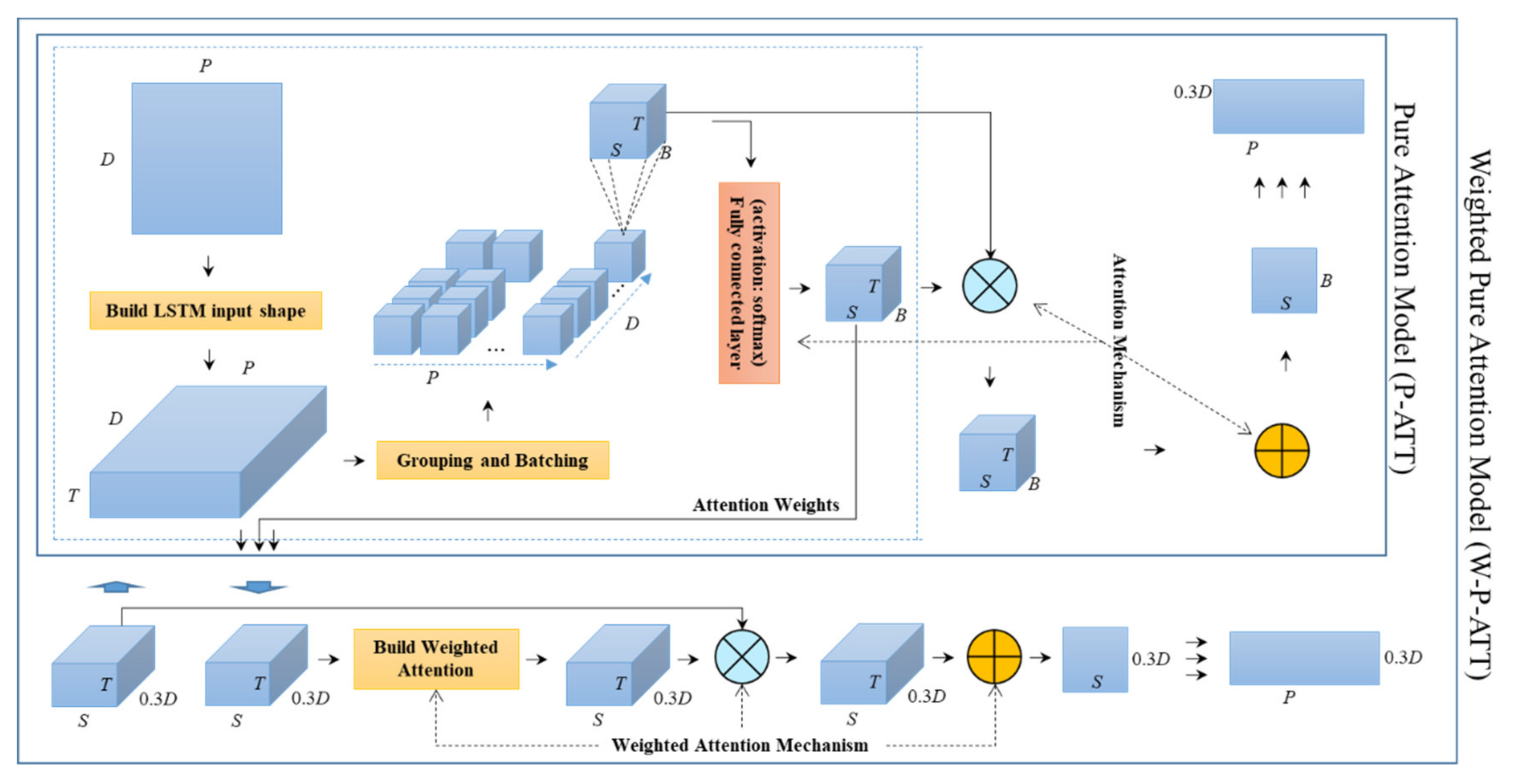
2.3. The P-ATT Model
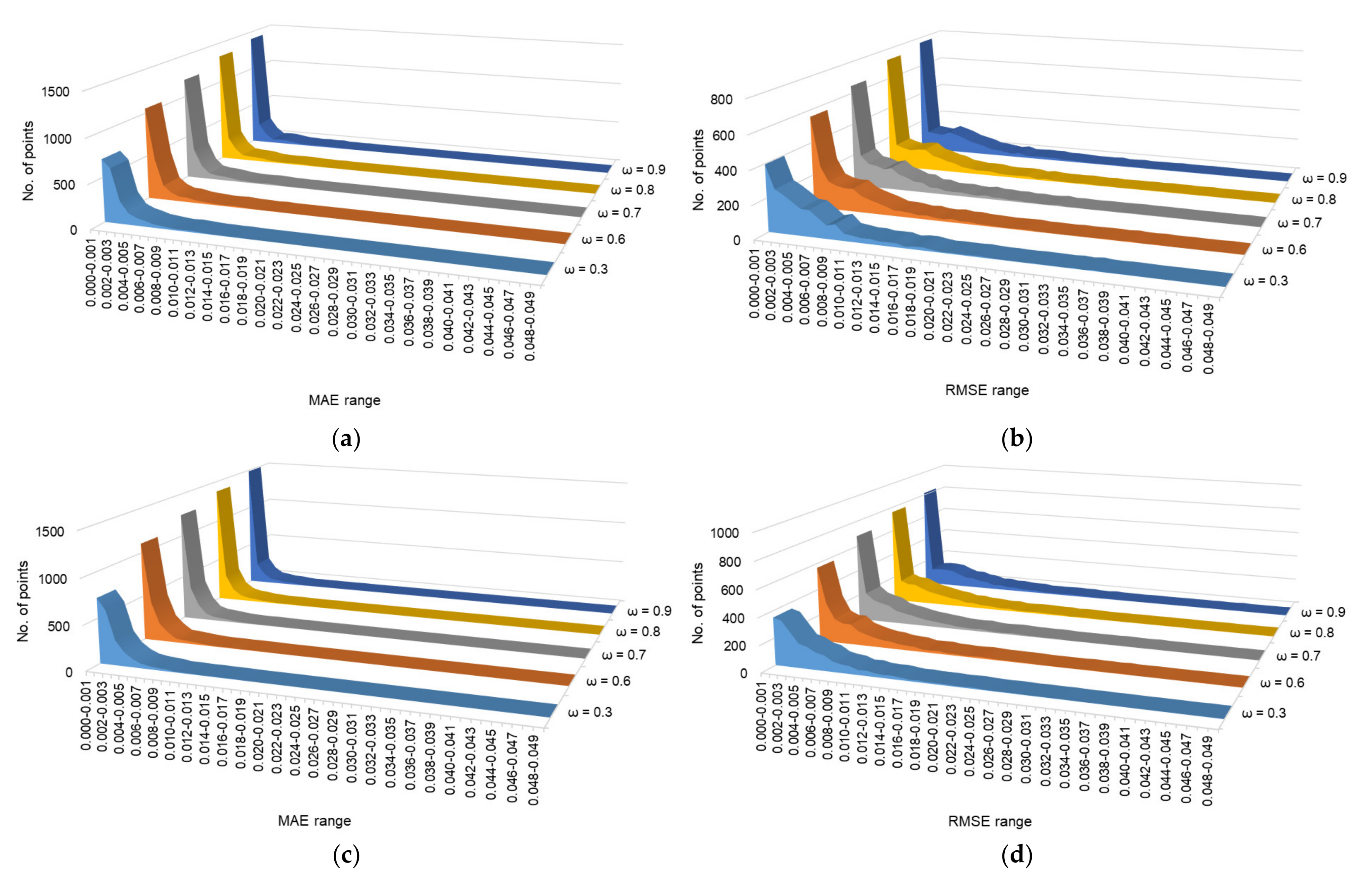
2.4. The W-P-ATT Model
3. Experiment
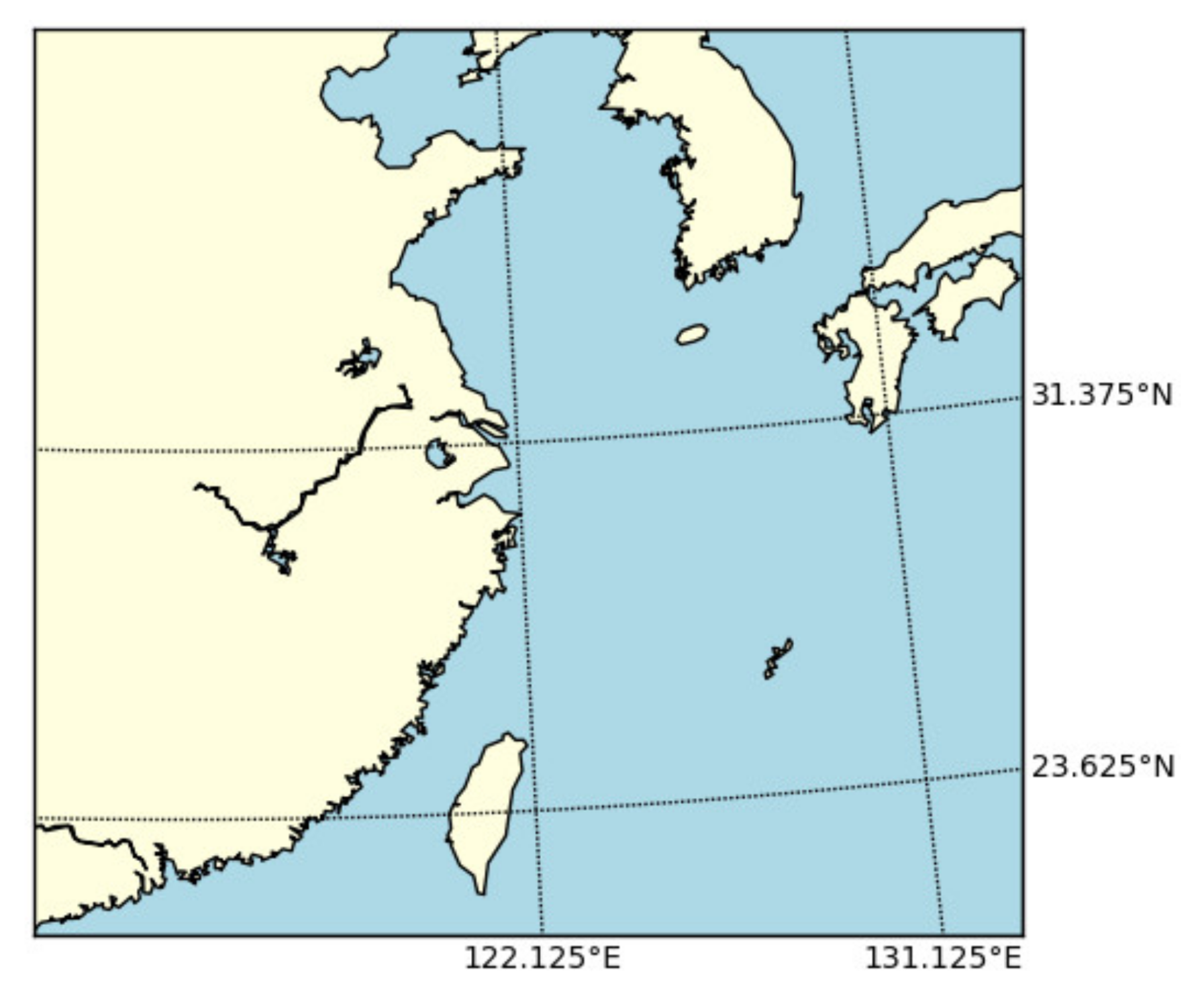
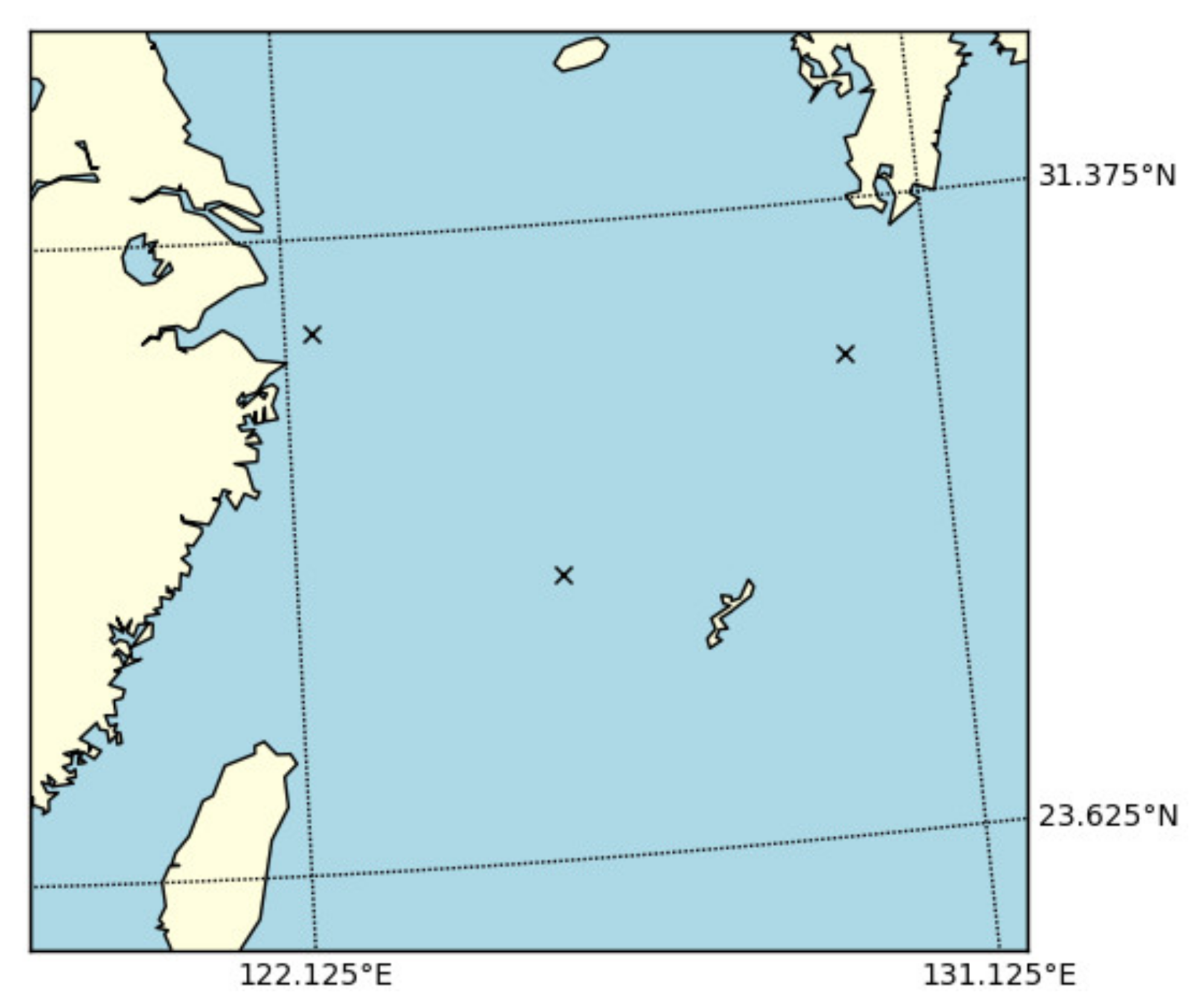
3.1. Data Sets
3.2. Setups
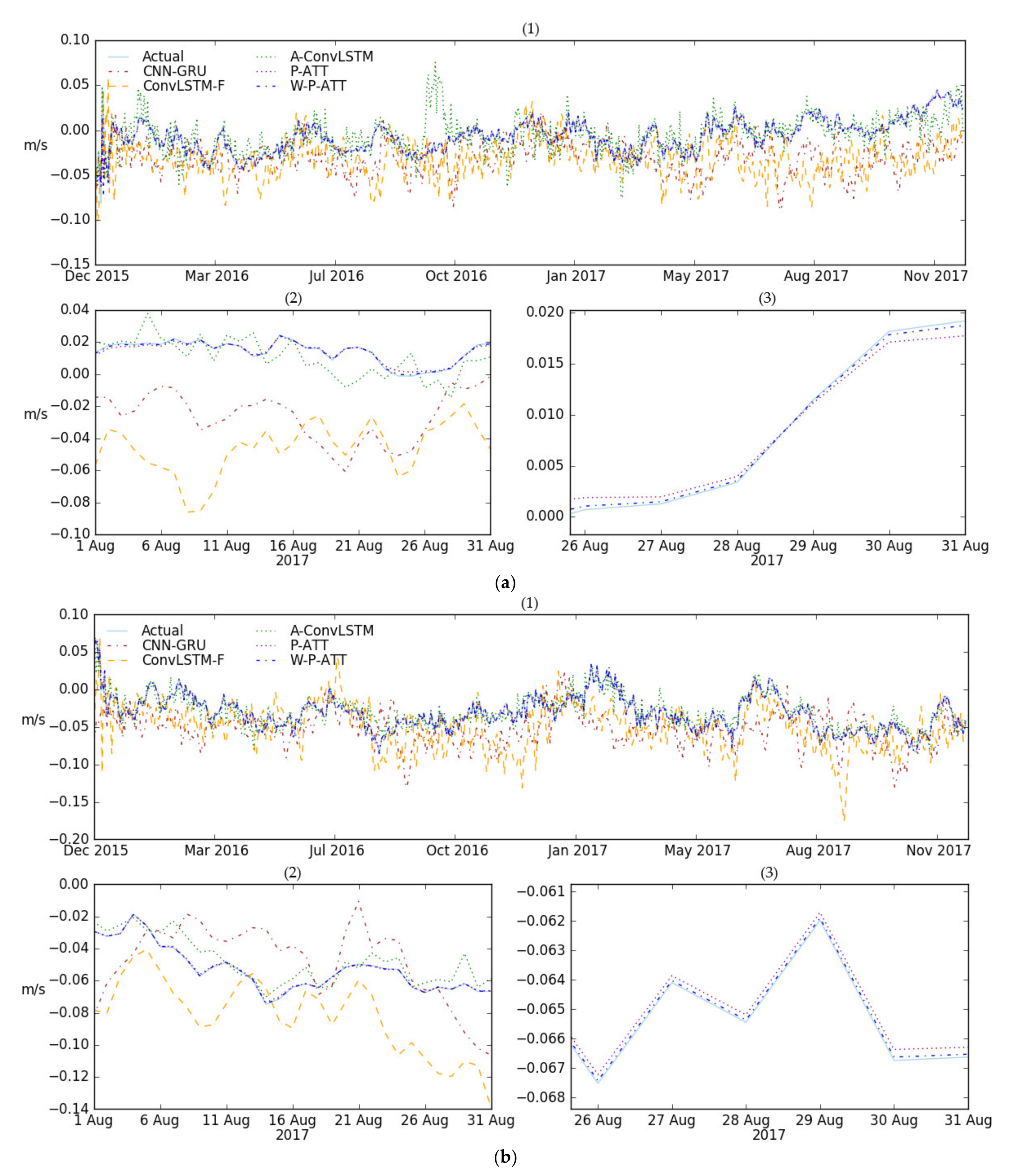
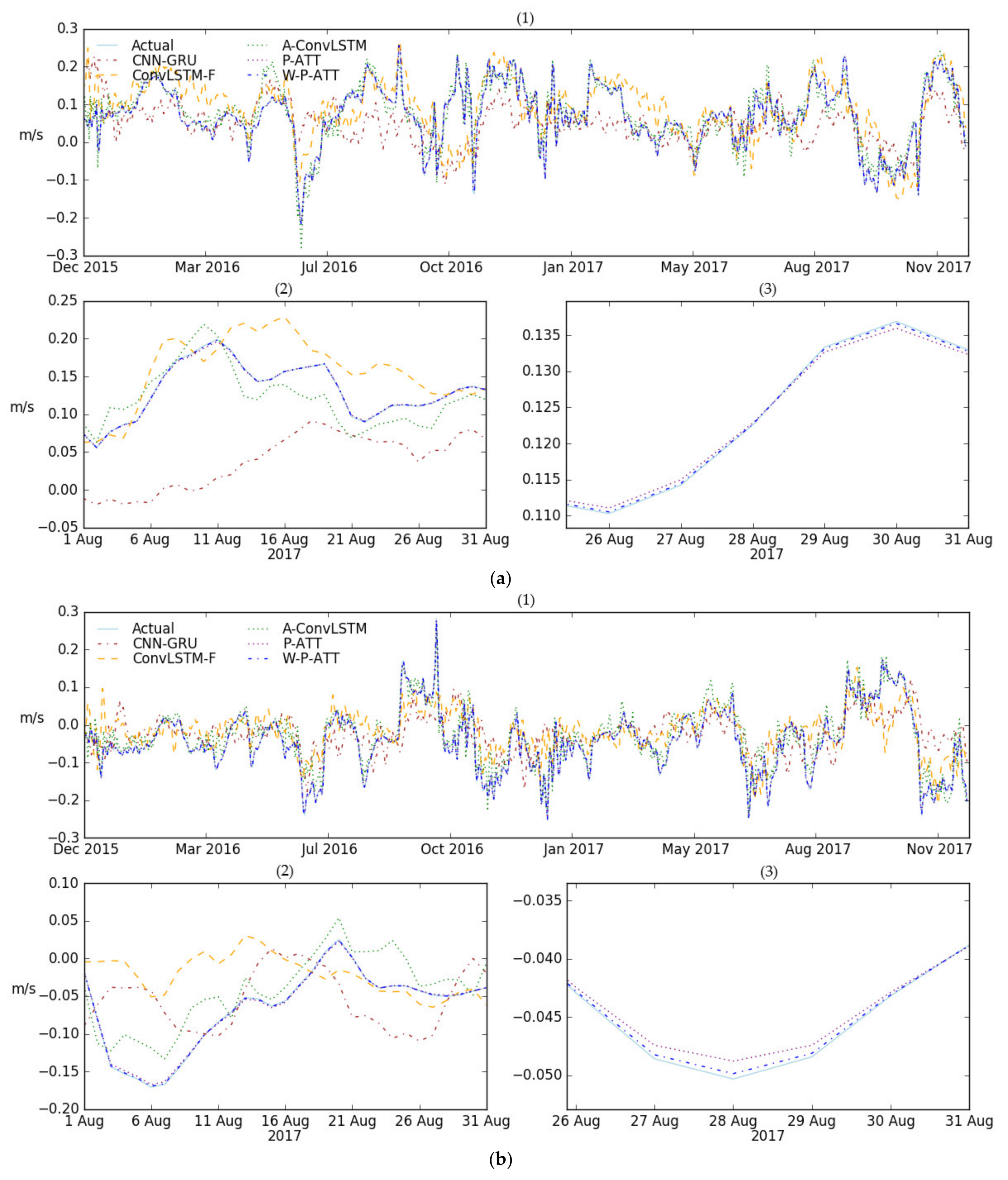
3.3. Results
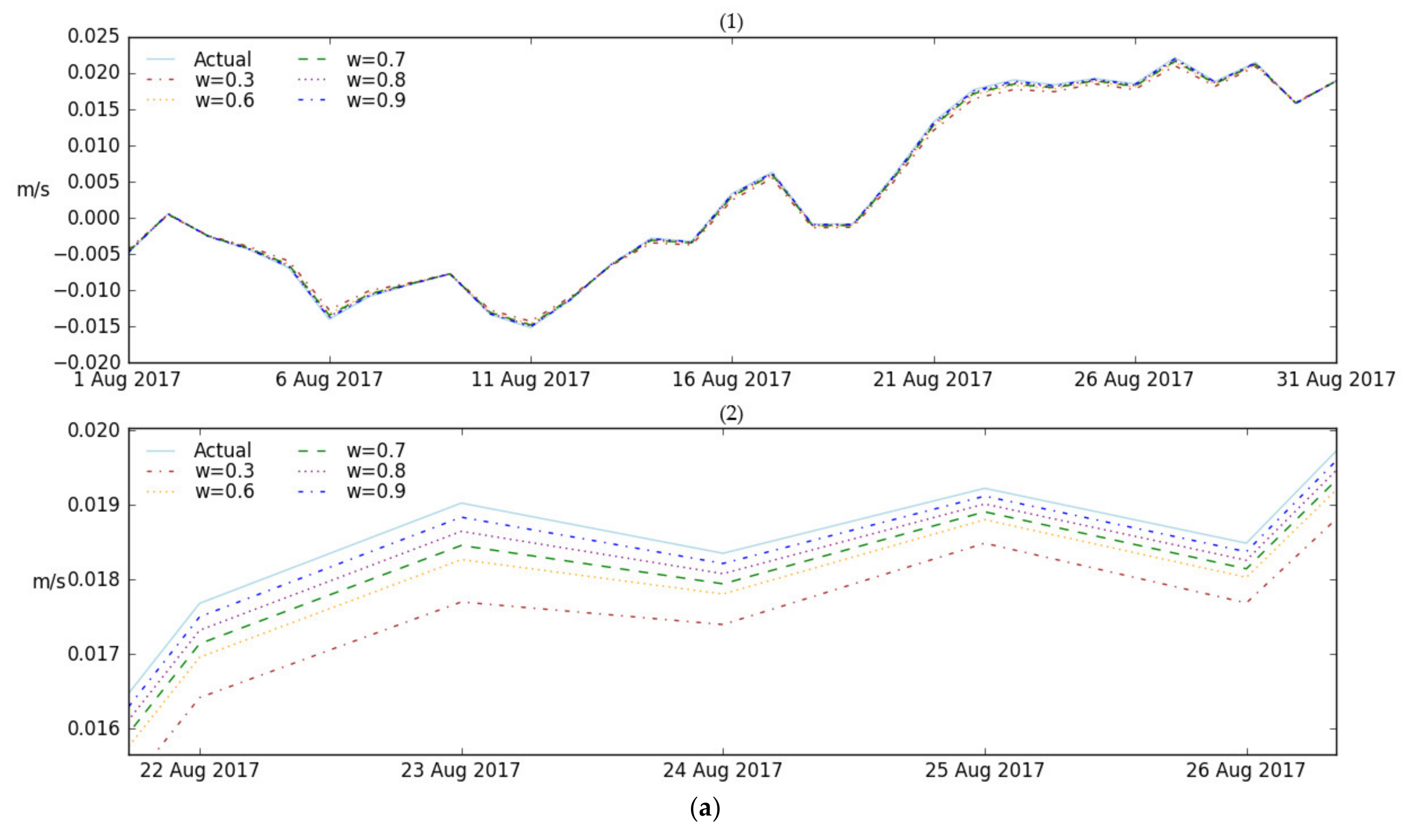
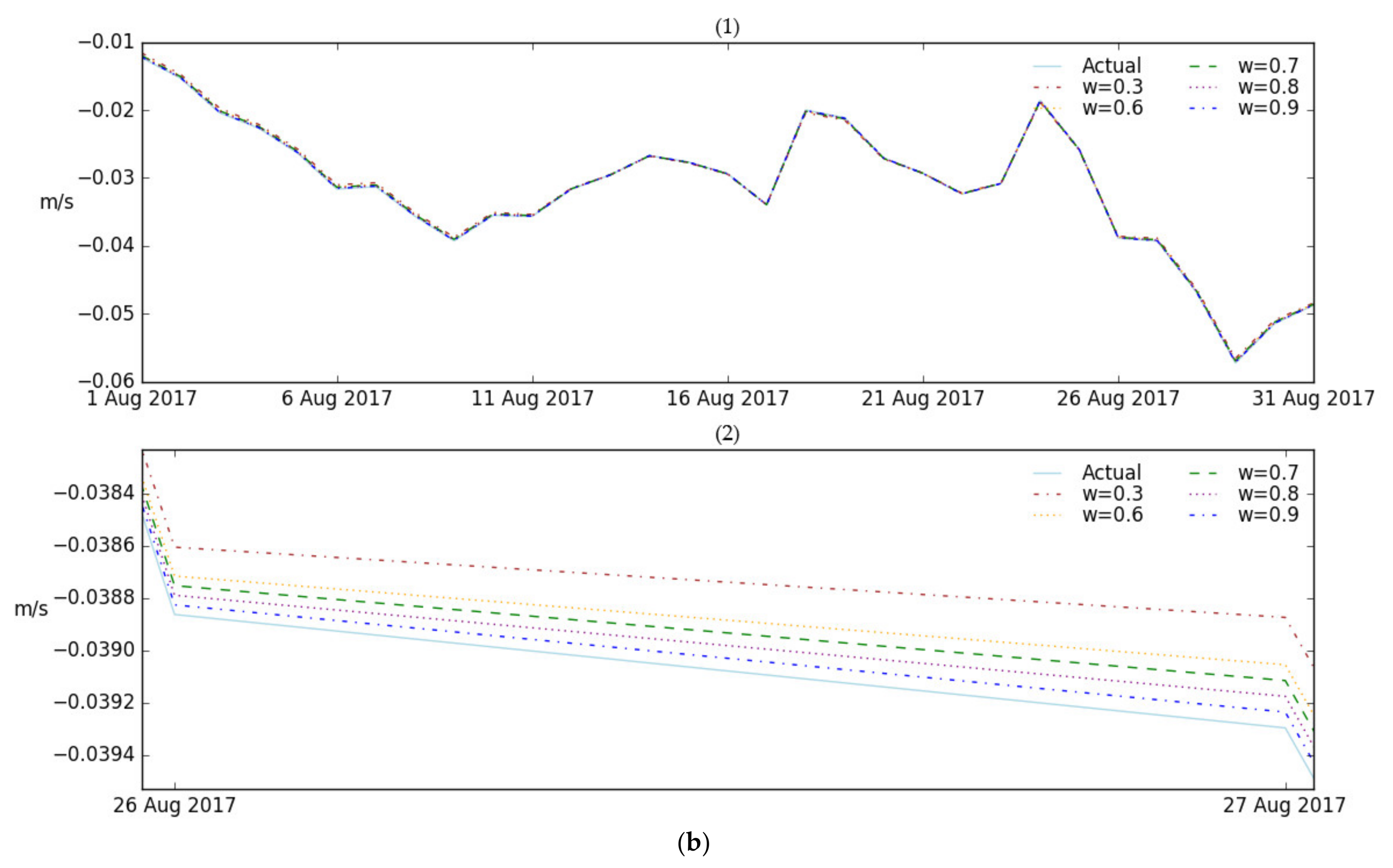
3.3.1. Performance Comparison for Spatial Points
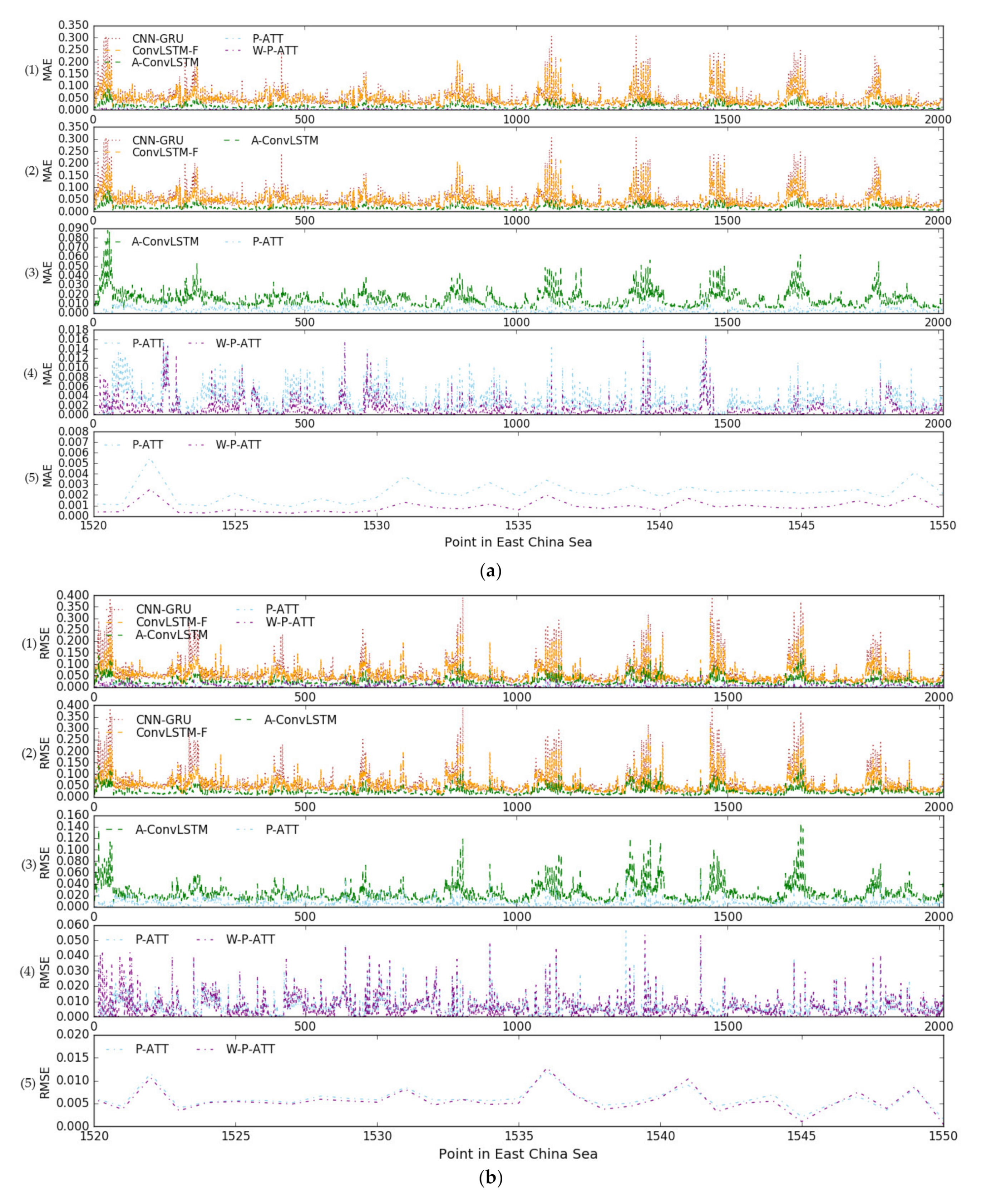
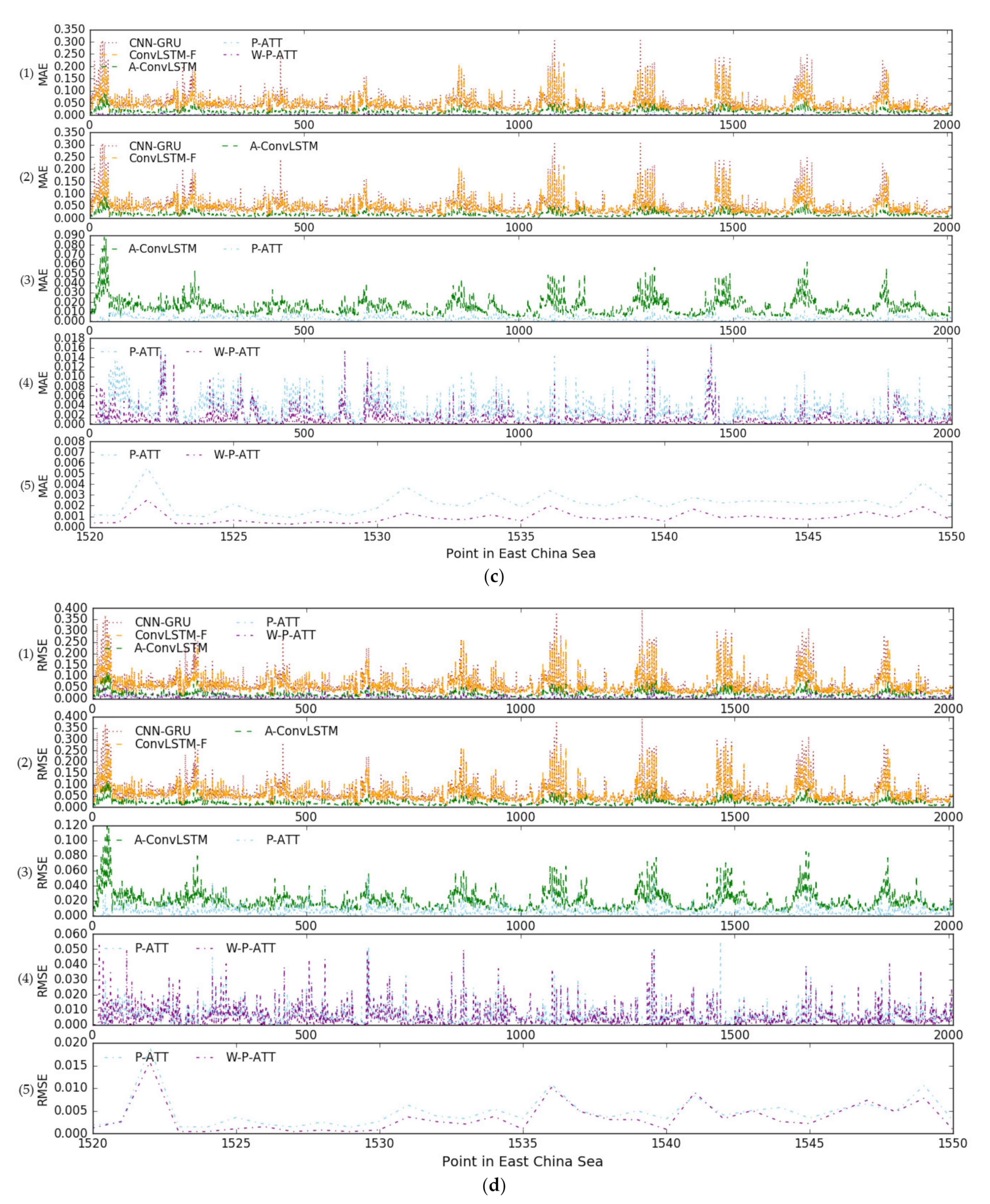
3.3.2. Performance Comparison through MAE and RMSE
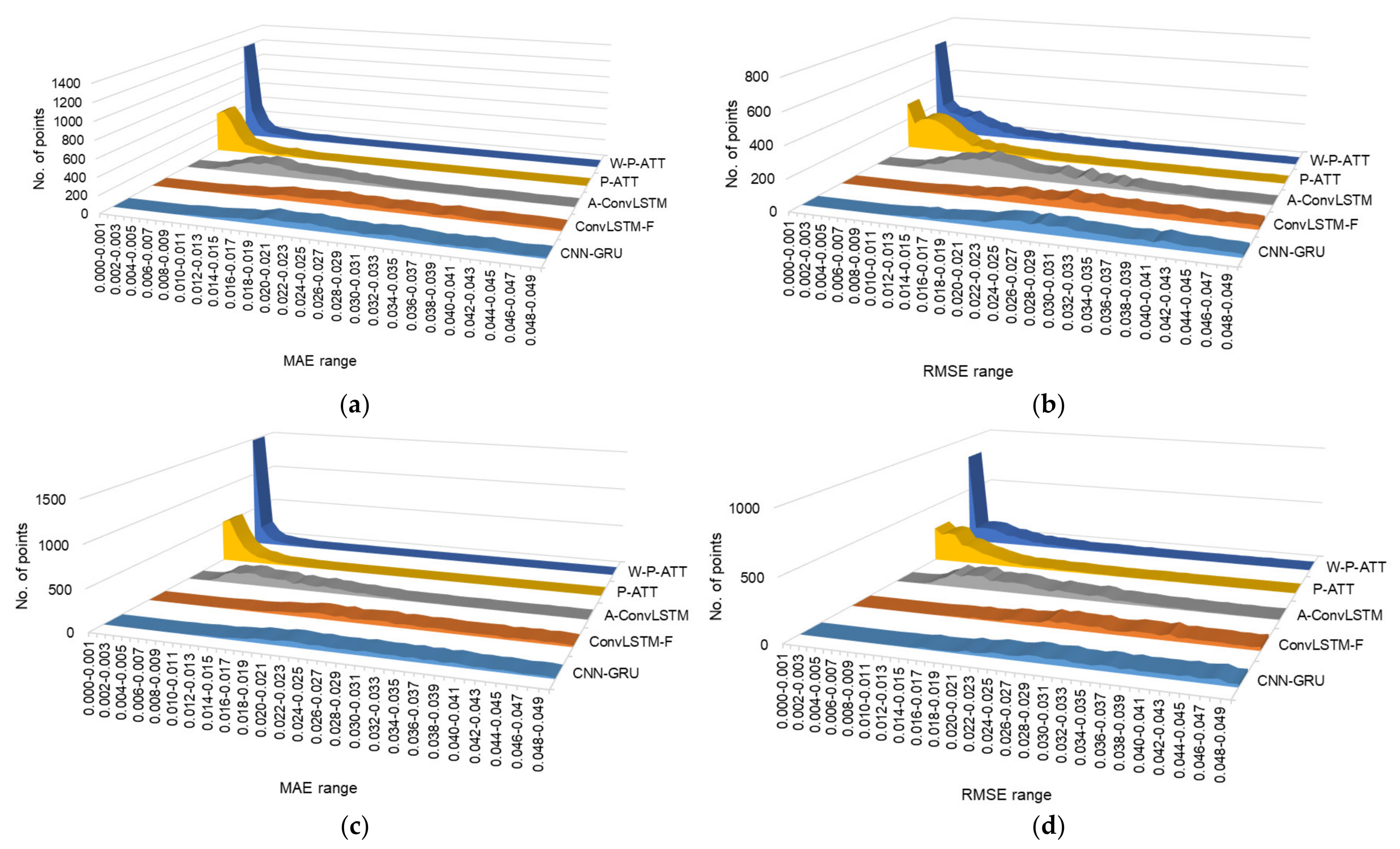
3.3.3. Performance Comparison through Distribution of MAE and RMSE
3.3.4. Performance Comparison through the Average MAE, RMSE, and r
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Klemas, V. Remote sensing of coastal and ocean currents: An overview. J. Coast. Res. 2012, 28, 576–586. [Google Scholar] [CrossRef]
- Armour, K.C.; Marshall, J.; Scott, J.R.; Donohoe, A.; Newsom, E.R. Southern Ocean warming delayed by circumpolar upwelling and equatorward transport. Nat. Geosci. 2016, 9, 549–554. [Google Scholar] [CrossRef]
- Dambach, J.; Raupach, M.J.; Leese, F.; Schwarzer, J.; Engler, J.O. Ocean currents determine functional connectivity in an Antarctic deep-sea shrimp. Mar. Ecol. 2016, 37, 1336–1344. [Google Scholar] [CrossRef]
- Iwasaki, S.; Isobe, A.; Kako, S.I.; Uchida, K.; Tokai, T. Fate of microplastics and mesoplastics carried by surface currents and wind waves: A numerical model approach in the Sea of Japan. Mar. Pollut. Bull. 2017, 121, 85–96. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhang, S.; Wang, J.; Wang, Y.; Mu, J.; Wang, P.; Lin, X.; Ma, D. Microplastic pollution in the surface waters of the Bohai Sea. Environ. Pollut. 2017, 231, 541–548. [Google Scholar] [CrossRef] [PubMed]
- Tamtare, T.; Dumont, D.; Chavanne, C. Extrapolating Eulerian ocean currents for improving surface drift forecasts. J. Oper. Oceanogr. 2021, 14, 71–85. [Google Scholar] [CrossRef]
- Kane, I.A.; Clare, M.A.; Miramontes, E.; Wogelius, R.; Rothwell, J.J.; Garreau, P.; Pohl, F. Seafloor microplastic hotspots controlled by deep-sea circulation. Science 2020, 368, 1140–1145. [Google Scholar] [CrossRef]
- Courtene-Jones, W.; Quinn, B.; Gary, S.F.; Mogg, A.O.; Narayanaswamy, B.E. Microplastic pollution identified in deep-sea water and ingested by benthic invertebrates in the Rockall Trough. North Atlantic Ocean. Environ. Pollut. 2017, 231, 271–280. [Google Scholar] [CrossRef] [Green Version]
- Pohl, F.; Eggenhuisen, J.T.; Kane, I.A.; Clare, M.A. Transport and burial of microplastics in deep-marine sediments by turbidity currents. Environ. Sci. Technol. 2020, 54, 4180–4189. [Google Scholar] [CrossRef]
- Nooteboom, P.D.; Bijl, P.K.; van Sebille, E.; Von Der Heydt, A.S.; Dijkstra, H.A. Transport bias by ocean currents in sedimentary microplankton assemblages: Implications for paleoceanographic reconstructions. Paleoceanogr. Paleocl. 2019, 34, 1178–1194. [Google Scholar] [CrossRef]
- Yamada, M.; Zheng, J. 240Pu/239Pu atom ratios in water columns from the North Pacific Ocean and Bering Sea: Transport of Pacific Proving Grounds-derived Pu by ocean currents. Sci. Total Environ. 2020, 718, 137362. [Google Scholar] [CrossRef] [PubMed]
- Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D.; Khan, A. A constrained A* approach towards optimal path planning for an unmanned surface vehicle in a maritime environment containing dynamic obstacles and ocean currents. Ocean Eng. 2018, 169, 187–201. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.T.; Lai, J.W.; Leu, L.G.; Lu, Y.C.; Chen, J.M.; Shao, H.J.; Chen, H.W.; Chang, K.T.; Terng, C.T.; Chang, Y.C.; et al. Applications of ocean currents data from high-frequency radars and current profilers to search and rescue missions around Taiwan. J. Oper. Oceanogr. 2019, 12, S126–S136. [Google Scholar] [CrossRef] [Green Version]
- Wen, J.; Yang, J.; Wang, T. Path Planning for Autonomous Underwater Vehicles under the Influence of Ocean Currents Based on a Fusion Heuristic Algorithm. IEEE Trans. Veh. Technol. 2021, 70, 8529–8544. [Google Scholar] [CrossRef]
- Immas, A.; Do, N.; Alam, M.R. Real-time in situ prediction of ocean currents. Ocean Eng. 2021, 228, 108922. [Google Scholar] [CrossRef]
- Grossi, M.D.; Kubat, M.; Özgökmen, T.M. Predicting particle trajectories in oceanic flows using artificial neural networks. Ocean Model. 2020, 156, 101707. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, J.; Wang, J. Constrained control of autonomous underwater vehicles based on command optimization and disturbance estimation. IEEE Trans. Ind. Electron. 2018, 66, 3627–3635. [Google Scholar] [CrossRef]
- Elhaki, O.; Shojaei, K. Neural network-based target tracking control of underactuated autonomous underwater vehicles with a prescribed performance. Ocean Eng. 2018, 167, 239–256. [Google Scholar] [CrossRef]
- Fossen, T.I.; Lekkas, A.M. Direct and indirect adaptive integral line-of-sight path-following controllers for marine craft exposed to ocean currents. Int. J. Adapt. Control Signal Process. 2017, 31, 445–463. [Google Scholar] [CrossRef]
- Vu, M.T.; Le Thanh, H.N.N.; Huynh, T.T.; Thang, Q.; Duc, T.; Hoang, Q.D.; Le, T.H. Station-keeping control of a hovering over-actuated autonomous underwater vehicle under ocean current effects and model uncertainties in horizontal plane. IEEE Access 2021, 9, 6855–6867. [Google Scholar] [CrossRef]
- Sarkar, D.; Osborne, M.A.; Adcock, T.A. Spatiotemporal prediction of tidal currents using Gaussian processes. J. Geophys. Res. Ocean. 2019, 124, 2697–2715. [Google Scholar] [CrossRef]
- Yang, G.; Wang, H.; Qian, H.; Fang, J. Tidal current short-term prediction based on support vector regression. In Proceedings of the 2nd Asia Conference on Power and Electrical Engineering (ACPEE), Shanghai, China, 24–26 March 2017. [Google Scholar]
- Kavousi-Fard, A.; Su, W. A combined prognostic model based on machine learning for tidal current prediction. IEEE Geosci. Remote Sens. Lett. 2017, 55, 3108–3114. [Google Scholar] [CrossRef]
- Remya, P.; Kumar, R.; Basu, S. Forecasting tidal currents from tidal levels using genetic algorithm. Ocean Eng. 2012, 40, 62–68. [Google Scholar] [CrossRef]
- Dauji, S.; Deo, M.C.; Bhargava, K. Prediction of ocean currents with artificial neural networks. ISH J. Hydraul. Eng. 2015, 21, 14–27. [Google Scholar] [CrossRef]
- Bayindir, C. Predicting the Ocean Currents Using Deep Learning, version 1.0. arXiv 2019, arXiv:1906.08066. [Google Scholar]
- Dauji, S.; Deo, M.C. Improving numerical current prediction with Model Tree. Indian J. Geo-Mar. Sci. 2020, 49, 1350–1358. Available online: http://nopr.niscair.res.in/handle/123456789/55314 (accessed on 8 December 2021).
- Sarkar, D.; Osborne, M.A.; Adcock, T.A. Prediction of tidal currents using bayesian machine learning. Ocean Eng. 2018, 158, 221–231. [Google Scholar] [CrossRef]
- Saha, D.; Deo, M.C.; Joseph, S.; Bhargava, K. A combined numerical and neural technique for short term prediction of ocean currents in the Indian Ocean. Environ. Syst. Res. 2016, 5, 4. [Google Scholar] [CrossRef] [Green Version]
- Jirakittayakorn, A.; Kormongkolkul, T.; Vateekul, P.; Jitkajornwanich, K.; Lawawirojwong, S. Temporal kNN for short-term ocean current prediction based on HF radar observations. In Proceedings of the 2017 14th International Joint Conference on Computer Science and Software Engineering (JCSSE), Nakhon Si Thammarat, Thailand, 12–14 July 2017. [Google Scholar] [CrossRef]
- Ren, L.; Hu, Z.; Hartnett, M. Short-Term forecasting of coastal surface currents using high frequency radar data and artificial neural networks. Remote Sens. 2018, 10, 850. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Hou, M.; Zhang, F.; Edwards, C.R. An LSTM based Kalman filter for spatio-temporal ocean currents assimilation. In Proceedings of the 14th International Conference on Underwater Networks & Systems, Atlanta, GA, USA, 23–25 October 2019. [Google Scholar] [CrossRef]
- Thongniran, N.; Vateekul, P.; Jitkajornwanich, K.; Lawawirojwong, S.; Srestasathiern, P. Spatio-temporal deep learning for ocean current prediction based on HF radar data. In Proceedings of the 16th International Joint Conference on Computer Science and Software Engineering (JCSSE), Pattaya, Thailand, 10–12 July 2019. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate version 7.0. arXiv 2016, arXiv:1409.0473. [Google Scholar]
- Luong, M.T.; Pham, H.; Manning, C.D. Effective approaches to attention-based neural machine translation version 5.0. arXiv 2015, arXiv:1508.04025. [Google Scholar]
- Chen, P.; Chi, M.Y. STAGRU: Ocean Surface Current Spatio-Temporal Prediction Based on Deep Learning. In Proceedings of the 2021 International Conference on Computer Information Science and Artificial Intelligence (CISAI), Kunming, China, 17–19 September 2021; pp. 495–499. [Google Scholar] [CrossRef]
- Zeng, X.; Qi, L.; Yi, T.; Liu, T. A Sequence-to-Sequence Model Based on Attention Mechanism for Wave Spectrum Prediction. In Proceedings of the 2020 11th International Conference on Awareness Science and Technology (iCAST), Qingdao, China, 7–9 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y.; Yu, J.; Li, Q.; Shi, S. Prediction of sea surface temperature using a multiscale deep combination neural network. Remote Sens. Lett. 2020, 11, 611–619. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, J.; Yu, J.; Xu, L. An Adaptive Scale Sea Surface Temperature Predicting Method Based on Deep Learning with Attention Mechanism. IEEE Geosci. Remote Sens. Lett. 2020, 17, 740–744. [Google Scholar] [CrossRef]
- Liu, J.; Jin, B.; Wang, L.; Xu, L. Sea surface height prediction with deep learning based on attention mechanism. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Liu, J.; Jin, B.; Yang, J.; Xu, L. Sea surface temperature prediction using a cubic b-spline interpolation and spatiotemporal attention mechanism. Remote Sens. Lett. 2021, 12, 478–487. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need version 5.0. aiXiv 2017, arXiv:1706.03762. [Google Scholar]

| Parameter | CNN-GRU | ConvLSTM-F | A-ConvLSTM | P-ATT | W-P-ATT |
|---|---|---|---|---|---|
| Kernel Size | (5, 1) | (5, 1) | (5, 1) | / | / |
| Stride | (5, 1) | (5, 1) | (5, 1) | / | / |
| Time Step | / | 10 | |||
| Input Shape | (10, 2010, 1) | (10, 2010, 1, 1) | (10, 15, 1, 1) | (10, 15) | (10, 15) |
| No. of GRU Units | 256 | / | / | / | / |
| No. of Convolution filters | 256 | 256 | 256 | / | / |
| Batch Size | 32 | ||||
| Spatial Group Size | / | / | 15 | ||
| Spatial Scope | 23.625° N–31.375° N, 122.125° E–131.125° E | ||||
| Training-time range | 1 January 2011 to 19 December 2015 | ||||
| Testing-time range | 20 December 2015 to 14 December 2017 | ||||
| Metrics | CNN-GRU | ConvLSTM-F | A-ConvLSTM | P-ATT | W-P-ATT (ω = 0.7) |
|---|---|---|---|---|---|
| MAE (u_current) | 0.0434 | 0.0387 | 0.0172 | 0.0028 | 0.0017 |
| RMSE (u_ current) | 0.0563 | 0.0508 | 0.0232 | 0.0061 | 0.0051 |
| r (u_ current) | 0.6215 | 0.6499 | 0.9091 | 0.9899 | 0.9901 |
| MAE (v_current) | 0.0468 | 0.0426 | 0.0145 | 0.0026 | 0.0014 |
| RMSE (v_ current) | 0.0607 | 0.0557 | 0.0193 | 0.0059 | 0.0049 |
| r (v_ current) | 0.5881 | 0.6155 | 0.9240 | 0.9908 | 0.9916 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Yang, J.; Liu, K.; Xu, L. Ocean Current Prediction Using the Weighted Pure Attention Mechanism. J. Mar. Sci. Eng. 2022, 10, 592. https://doi.org/10.3390/jmse10050592
Liu J, Yang J, Liu K, Xu L. Ocean Current Prediction Using the Weighted Pure Attention Mechanism. Journal of Marine Science and Engineering. 2022; 10(5):592. https://doi.org/10.3390/jmse10050592
Chicago/Turabian StyleLiu, Jingjing, Jinkun Yang, Kexiu Liu, and Lingyu Xu. 2022. "Ocean Current Prediction Using the Weighted Pure Attention Mechanism" Journal of Marine Science and Engineering 10, no. 5: 592. https://doi.org/10.3390/jmse10050592
APA StyleLiu, J., Yang, J., Liu, K., & Xu, L. (2022). Ocean Current Prediction Using the Weighted Pure Attention Mechanism. Journal of Marine Science and Engineering, 10(5), 592. https://doi.org/10.3390/jmse10050592





