DS-Based 2-DOF PID Controller of a Regasification System for LNG-Fueled Marine Engine
Abstract
:1. Introduction
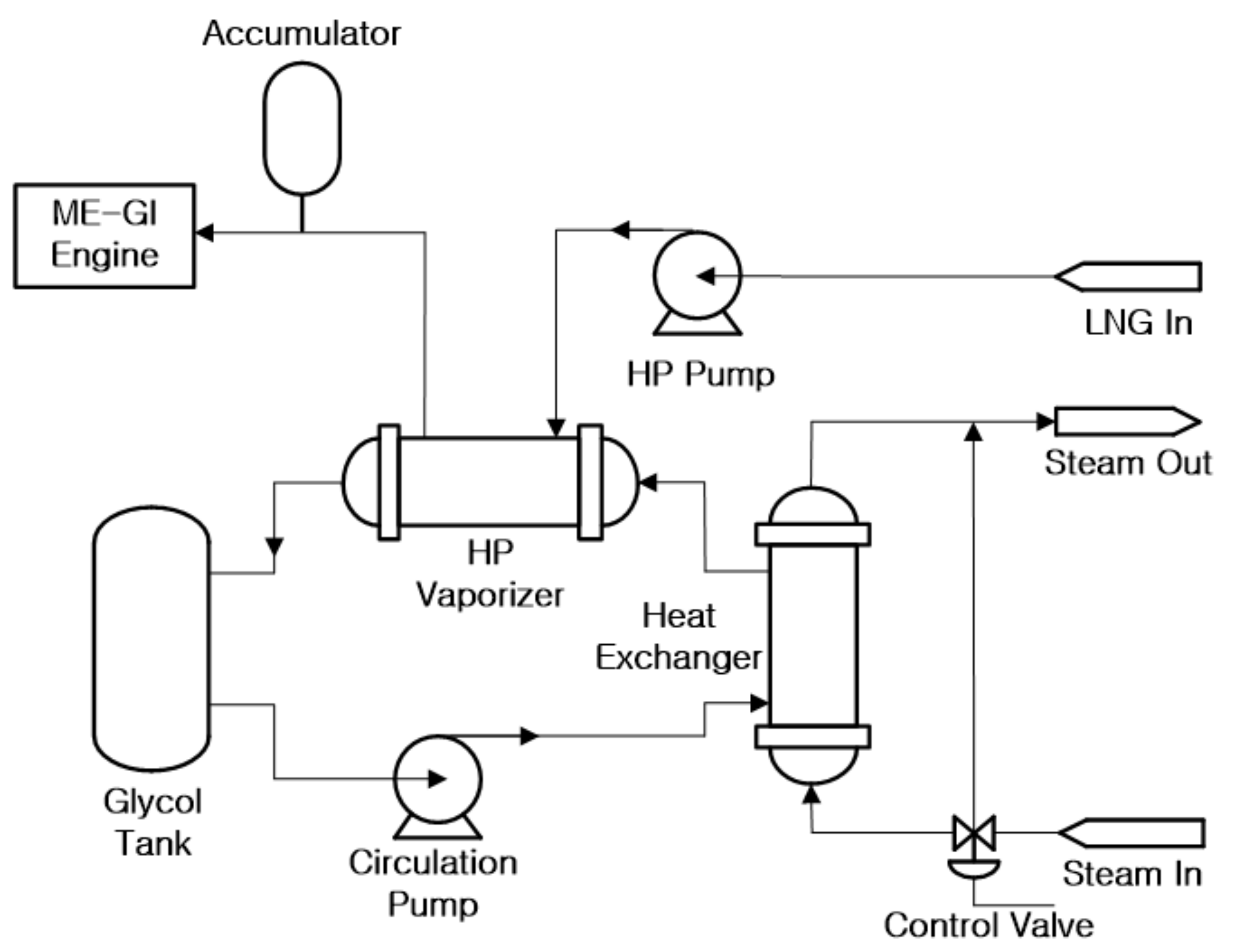
2. Structure of Regasification System and Modelling
3. The Proposed 2-DOF PID Controller
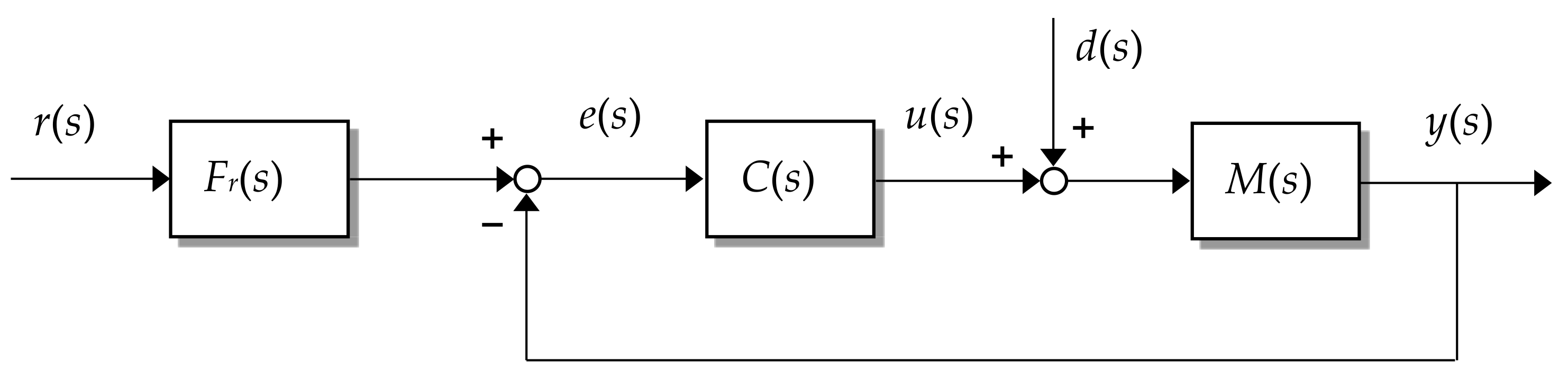
3.1. Structure of Control System
3.2. Set-Point Filter
3.3. Direct Synthesis Method
4. Parameter Tuning
5. Simulation
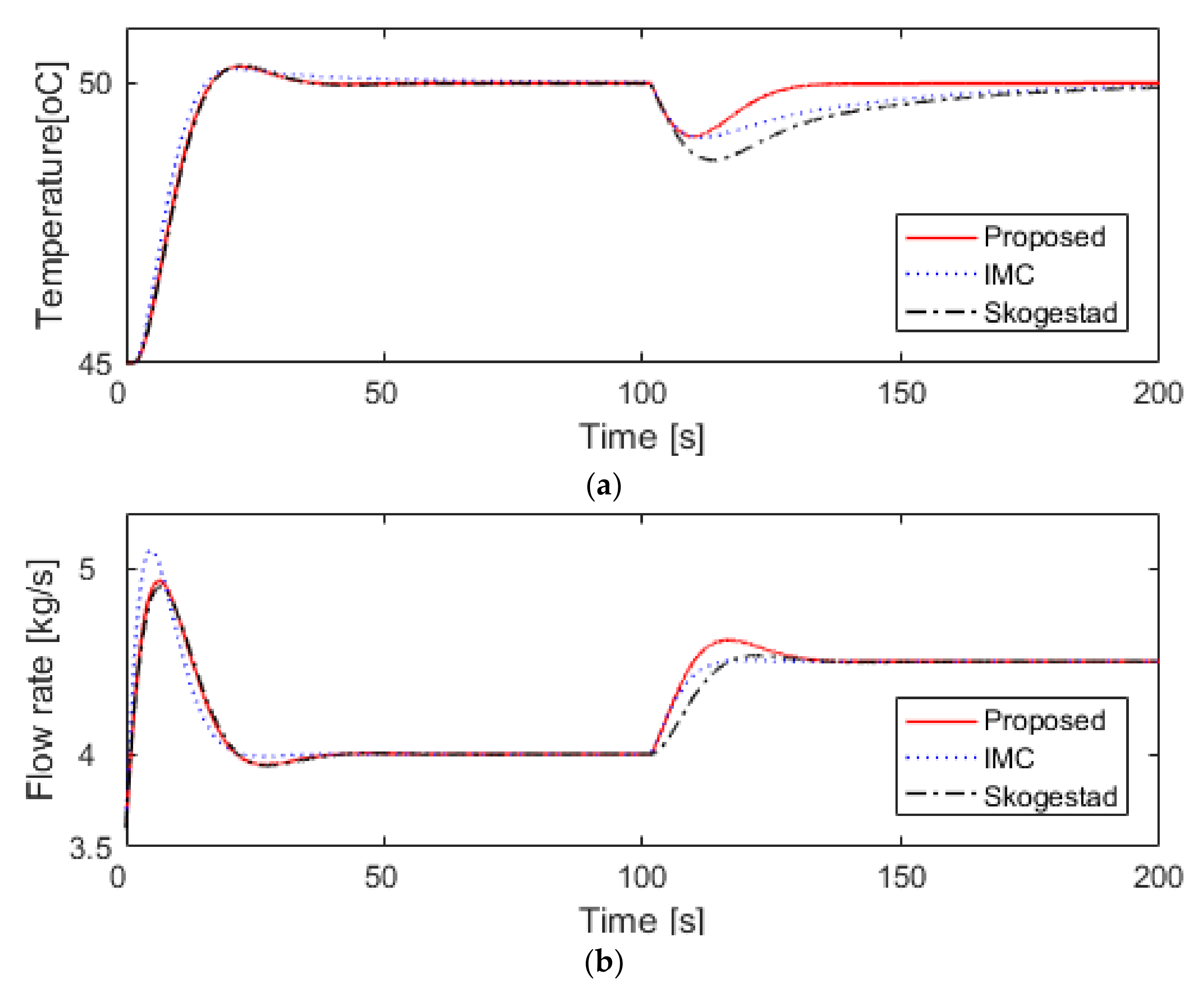
5.1. Nominal Heat Exchanger
5.2. Uncertain Heat Exchanger
5.3. Effect of Set-Point Filter
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- IMO Homepage. Available online: http://www.imo.org/en/OurWork/Environment/PollutionPrevention/Airpollution/Pages/Default.aspx (accessed on 22 March 2022).
- MAN Diesel & Turbo. ME-GI Duel Fuel MAN B&W Engines: A Technical, Operational and Cost-effective Solution for Ships Fuelled by Gas, MAN Diesel & Turbo 2012. Available online: https://www.man-es.com/?utm_medium=sea&utm_source=google&utm_campaign=always_sea_2022_man_brand_energy_solutions_bmm_all&utm_term=crossbrand&gclid=EAIaIQobChMI-P3bu6q29wIVYphmAh0kVwK7EAAYAiAAEgLbMfD_BwE&gclsrc=aw.ds (accessed on 22 March 2022).
- Jafarzadeh, S.; Paltrinieri, N.; Utne, I.B.; Ellingsen, H. LNG-fuelled fishing vessels: A systems engineering approach. Transp. Res. Part D Transp. Environ. 2017, 50, 202–222. [Google Scholar] [CrossRef]
- Åström, K.J.; Hägglund, T. Advanced PID Control; ISA: Pittsburgh, PA, USA, 2006. [Google Scholar]
- Choi, S. Configuration and analysis of a feed-forward control system for jacket cooling water temperature of marine prime diesel engine. J. Korean Soc. Mar. Eng. 2008, 32, 1303–1308. [Google Scholar]
- Ahn, J.K.; So, M.O. Cascade temperature control for jacket cooling water system of two-stroke low speed marine main diesel engine. J. Korean Soc. Mar. Eng. 2018, 42, 457–462. [Google Scholar]
- Vasičkaninová, A.; Bakošová, M. Control of heat exchanger using neural network predictive controller combined with auxiliary fuzzy controller. Appl. Therm. Eng. 2015, 89, 1046–1053. [Google Scholar] [CrossRef]
- Oravec, J.; Bakošová, M.; Mészáros, A.; Míková, N. Experimental investigation of alternative robust model predictive control of a heat exchanger. Appl. Therm. Eng. 2016, 105, 774–782. [Google Scholar] [CrossRef]
- Duka, A.V.; Oltean, S.E. Fuzzy control of a heat exchanger. In Proceedings of the 2012 IEEE International Conference on Automation Quality and Testing Robotics 2012, Cluj-Napoca, Romania, 24–27 May 2012; pp. 135–139. [Google Scholar]
- Beirami, H.; Zerafat, M.M. Self-tuning of an interval type-2 fuzzy PID controller for a heat exchanger system. Iran. J. Sci. Technol. Trans. Mech. Eng. 2015, 39, 113–129. [Google Scholar]
- Kumar, A.; Garg, K.K. Comparison of Ziegler-Nichols, Cohen-Coon and fuzzy logic controllers for heat exchanger model. Int. J. Sci. Eng. Technol. Res. 2015, 4, 1917–1920. [Google Scholar]
- Emhemed, A.A.A.; Alsseid, A.; Hanafi, D. Modelling and controller design for temperature control of power plant heat exchanger. Univers. J. Control Autom. 2017, 5, 49–53. [Google Scholar] [CrossRef]
- Padhee, S.; Khare, Y.B.; Singh, Y. Internal model based PID control of shell and tube heat exchanger system. In Proceedings of the IEEE Technology Students’ Symposium, Kharagpur, India, 14–16 January 2011; pp. 297–302. [Google Scholar]
- Padhee, S. Performance Evaluation of Different Conventional and Intelligent Controllers for Temperature Control of Shell and Tube Heat Exchanger System. Master’s Dissertation, Thapar University, Patiala Punjab, India, 2011. [Google Scholar]
- Padhee, S. Controller design for temperature control of heat exchanger system: Simulation studies. World Sci. Eng. Acad. Soc. (WSEAS) Trans. Syst. Control 2014, 9, 485–491. [Google Scholar]
- Khanvilkar, S.; Jadhav, S.P.; Vyawahare, V.; Kadam, V. Comparative study of fuzzy and IMC based controllers for heat exchanger system. In Proceedings of the 2016 International Conference on Automatic Control and Dynamic Optimization Techniques, Pune, India, 9–10 September 2016; pp. 344–348. [Google Scholar]
- Sarabeevi, G.M.; Beebi, M.L. Temperature control of shell and tube heat exchanger system using internal model controllers. In Proceedings of the 2016 International Conference on Next Generation Intelligent Systems, Kottayam, India, 1–3 September 2016. [Google Scholar]
- Manikandan, R.; Vinodha, R. Multiple model based adaptive control for shell and tube heat exchanger process. Int. J. Appl. Eng. 2016, 11, 3175–3180. [Google Scholar]
- Skorospeshkin, M.V.; Sukhodov, M.S.; Skorospeshkin, V.N.; Rymashevskiy, P.O. An adaptive control system for a shell-and-tube heat exchanger. In Proceedings of the International Conference on Information Technologies in Business and Industry, Journal of Physics: Conference Series, Tomsk, Russia, 21–26 September 2016. [Google Scholar]
- Xiao, Y.; Cui, G.; Chen, J.; Zhao, B. Improved model control strategy with dynamic adaption for heat exchangers in energy system. Int. J. Comput. Methodol. Numer. Heat Transf. Part A Appl. 2017, 72, 458–478. [Google Scholar] [CrossRef]
- Tavakoli, S.; Tavakoli, M. Optimal tuning of PID controller for first order plus time delay models using dimensional analysis. In Proceedings of the 4th International Conference on Control and Automation, Montreal, QC, Canada, 12 June 2003; pp. 942–946. [Google Scholar]
- Jin, G.G.; Son, Y.D. Design of a nonlinear controller and tuning rules for first-order plus time delay models. Stud. Inform. Control 2019, 28, 157–166. [Google Scholar] [CrossRef] [Green Version]
- Skogestad, S. Simple analytic rules for model reduction and PID controller tuning. J. Process Control 2003, 13, 291–309. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.T.; Cho, W.H.; Edgar, T.F. Simple analytic PID controller tuning rules revisited. Ind. Eng. Chem. Res. 2014, 53, 5038–5047. [Google Scholar] [CrossRef]
- Shamsuzzoha, M. A unified approach for proportional-integral-derivative controller design for time delay processes. Korean J. Chem. Eng. 2015, 32, 583–596. [Google Scholar] [CrossRef]
- Chen, D.; Seborg, D.E. PI/PID controller design based on direct synthesis and disturbance rejection. Ind. Eng. Chem. Res. 2002, 41, 4807–4822. [Google Scholar] [CrossRef]
- Anil, C.; Sree, R.P. Tuning of PID controllers for integrating systems using direct synthesis method. ISA Trans. 2015, 57, 211–219. [Google Scholar] [CrossRef] [PubMed]
- So, H.R. Design of 2-DOF PID Controllers for First Order Plus Time Delay Systems Using Direct Synthesis Method. Ph.D. Thesis, Korea Maritime and Ocean University, Busan, Korea, 2022. [Google Scholar]
- Korkmaz, M.; Aydogdu, O.; Dogan, H. Design and performance comparison of variable parameter nonlinear PID controller and genetic algorithm based PID controller. In Proceedings of the 2012 Int. Symp. on Innovation in Intelligent Systems and Applications(INISTA), Trabzon, Turkey, 2–4 July 2012; pp. 1–5. [Google Scholar]
- So, G.B. Design of Nonlinear PID Controllers and Their Application to A Heat Exchanger System for LNG-Fuelled Marine Engines. Ph.D. Thesis, Korea Maritime and Ocean University, Busan, Korea, 2018. [Google Scholar]
- So, G.B. A modified 2-DOF control framework and GA based intelligent tuning of PID controllers. Processes 2021, 9, 1–19. [Google Scholar] [CrossRef]
- System Identification Toolbox, Getting Started Guide; Mathworks: Natick, MA, USA, 2020.
- System Identification Toolbox, User’s Guide; Mathworks: Natick, MA, USA, 2020.
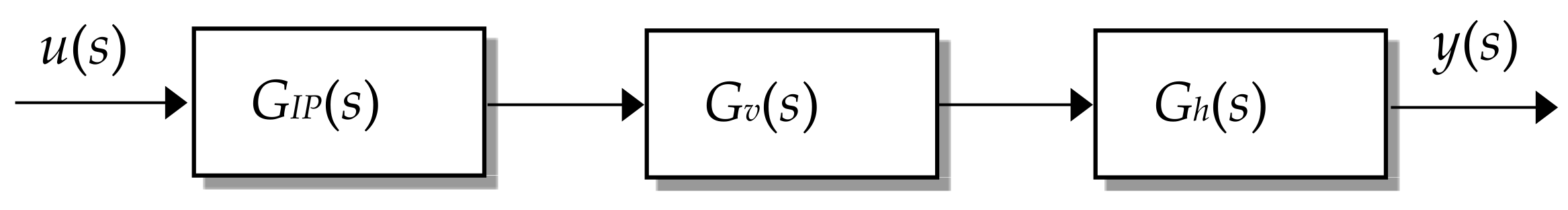





| Parameters | Values |
|---|---|
| 0.05 (bar/mA) | |
| 2 (kg/(s·bar)) | |
| 3 (s) | |
| 12.5 (°C·s/kg) | |
| 30 (s) | |
| Lh | 1.5 (s) |
| Tuning Methods | Parameters | ||||
|---|---|---|---|---|---|
| Kp | Ti | Td | Tc | b | |
| Proposed | 4.6763 | 14.0444 | 1.3902 | 4.7985 | 0.96 |
| IMC | 4.2728 | 32.6280 | 1.9212 | 4.0550 | |
| Skogestad | 2.9813 | 30.5780 | - | 4.100 | - |
| Tuning Methods | Tracking Performance | Disturbance Performance | |||||
|---|---|---|---|---|---|---|---|
| tr | ts | OS (%) | IAE | Mpeak | trcy | IAE | |
| Proposed | 9.814 | 30.694 | 0.602 | 46.682 | 0.949 | 35 | 15.017 |
| IMC | 8.925 | 43.103 | 0.511 | 46.086 | 0.984 | 132 | 38.114 |
| Skogestad | 10.067 | 31.181 | 0.633 | 47.896 | 1.369 | 131 | 51.193 |
| Tuning Methods | Tracking Performance | Disturbance Performance | |||||
|---|---|---|---|---|---|---|---|
| tr | ts | OS (%) | IAE | Mpeak | trcy | IAE | |
| Proposed | 7.644 | 32.655 | 0.143 | 38.510 | 1.532 | 47 | 22.038 |
| IMC | 6.291 | 23.326 | 0.607 | 35.612 | 1.547 | 129 | 38.111 |
| Skogestad | 6.829 | 38.794 | 1.396 | 44.818 | 1.654 | 126 | 51.185 |
| Set-Point Filter | Tracking Performance | Disturbance Performance | |||||
|---|---|---|---|---|---|---|---|
| tr | ts | OS (%) | IAE | Mpeak | trcy | IAE | |
| With filter | 9.814 | 30.694 | 0.602 | 46.682 | 0.949 | 35 | 15.017 |
| Without filter | 6.237 | 35.475 | 2.926 | 53.364 | 0.949 | 35 | 15.017 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
So, G.-B. DS-Based 2-DOF PID Controller of a Regasification System for LNG-Fueled Marine Engine. J. Mar. Sci. Eng. 2022, 10, 606. https://doi.org/10.3390/jmse10050606
So G-B. DS-Based 2-DOF PID Controller of a Regasification System for LNG-Fueled Marine Engine. Journal of Marine Science and Engineering. 2022; 10(5):606. https://doi.org/10.3390/jmse10050606
Chicago/Turabian StyleSo, Gun-Baek. 2022. "DS-Based 2-DOF PID Controller of a Regasification System for LNG-Fueled Marine Engine" Journal of Marine Science and Engineering 10, no. 5: 606. https://doi.org/10.3390/jmse10050606
APA StyleSo, G.-B. (2022). DS-Based 2-DOF PID Controller of a Regasification System for LNG-Fueled Marine Engine. Journal of Marine Science and Engineering, 10(5), 606. https://doi.org/10.3390/jmse10050606






