Numerical Simulation of Unsteady Cavitation Flow in a Low-Specific-Speed Centrifugal Pump with an Inducer
Abstract
:1. Introduction
2. Geometric Model and Experimental System
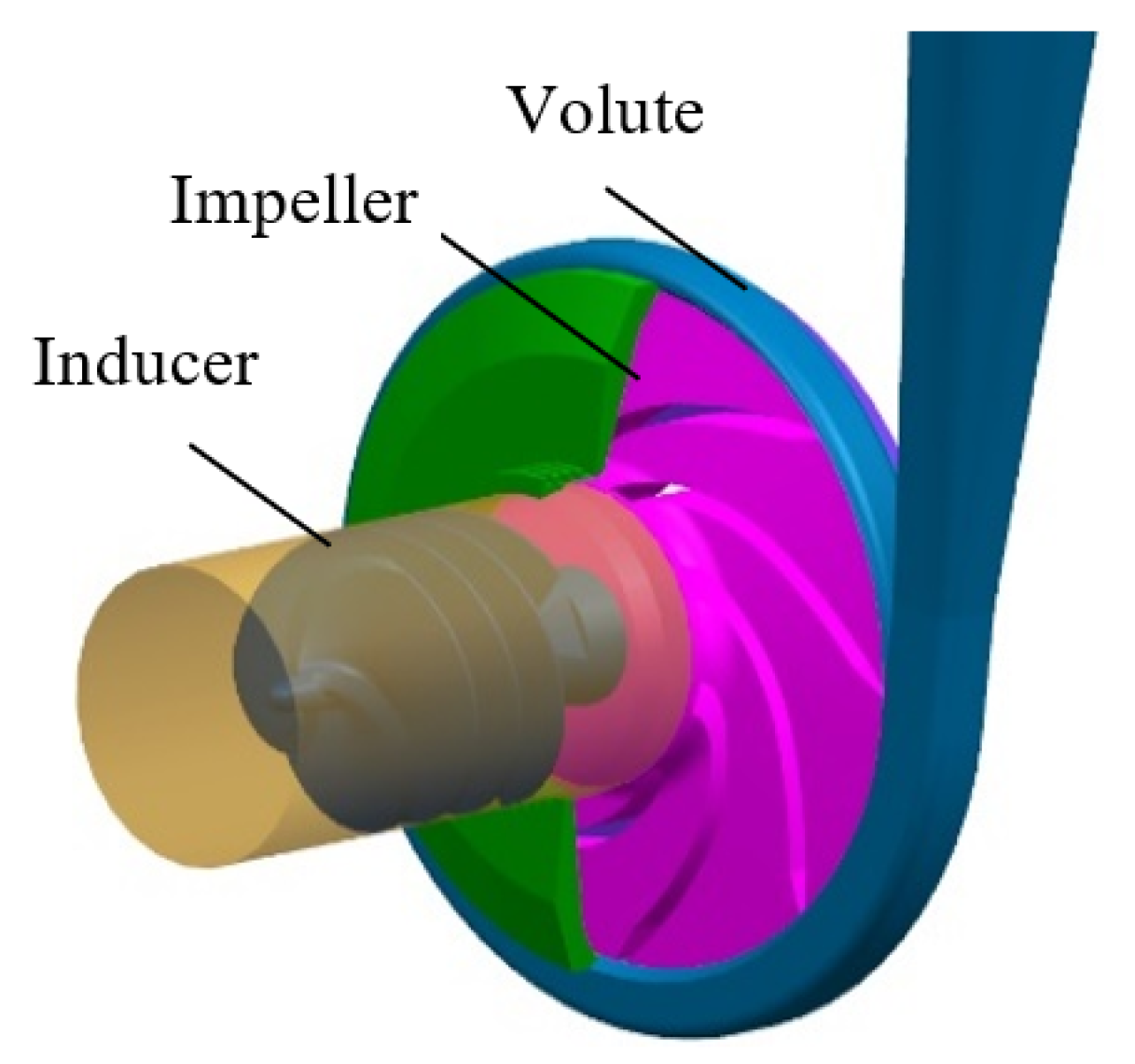
2.1. Geometric Model and Mesh Generation
2.2. Numerical Simulation Method
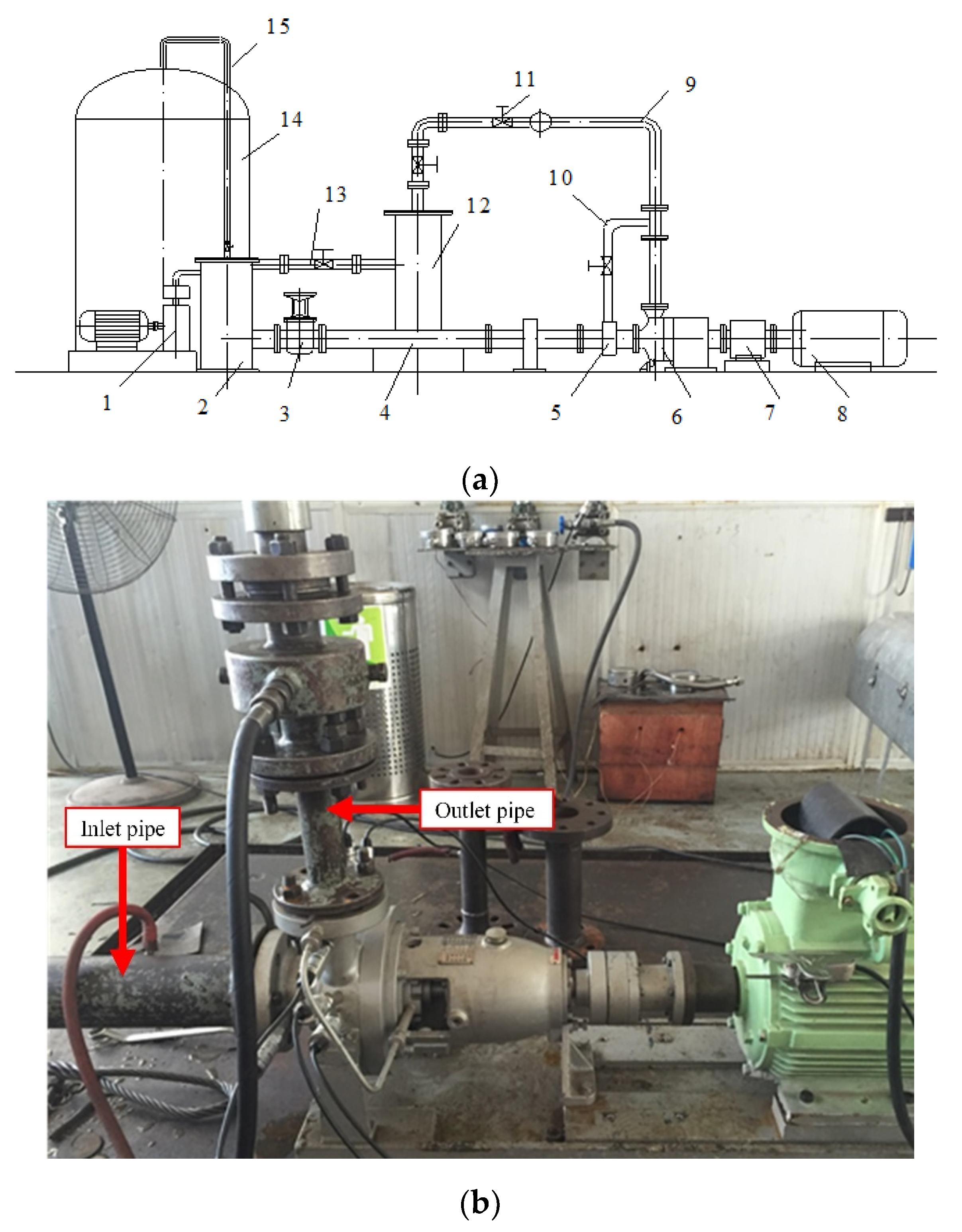
3. Experimental System
4. Results and Discussion
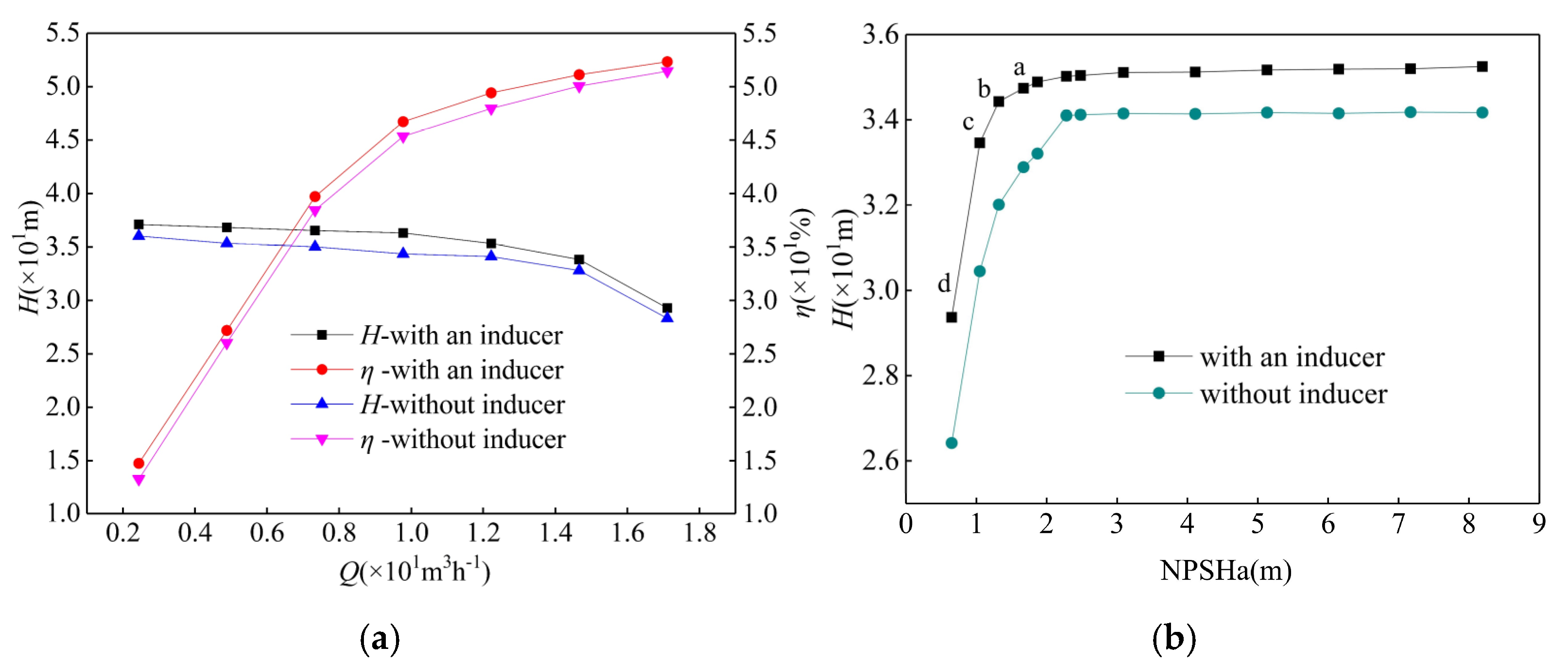
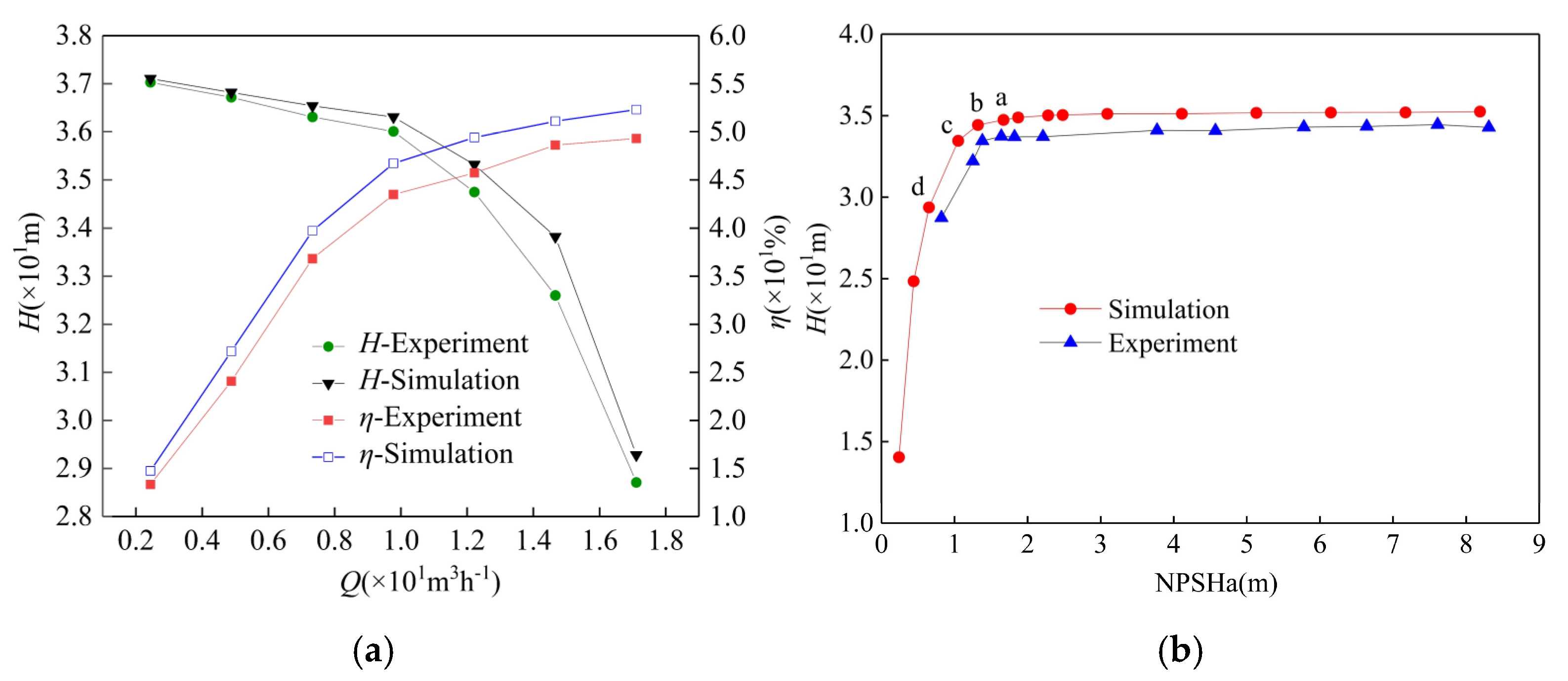
4.1. The Performance Curves of Centrifugal Pump
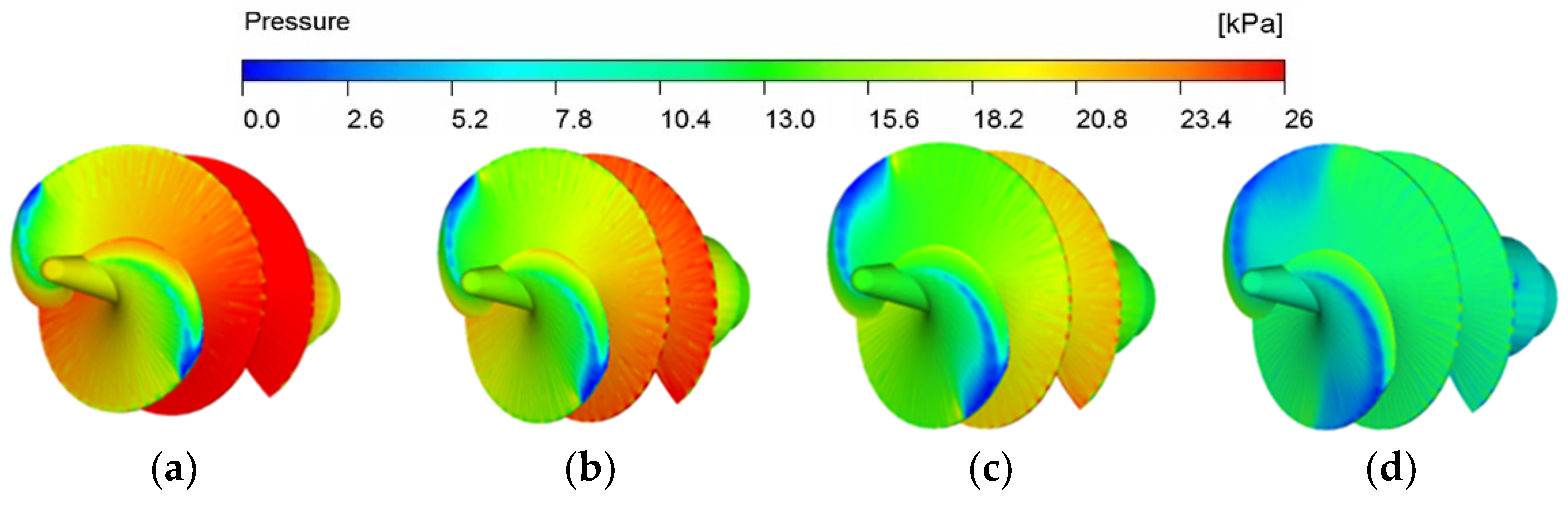
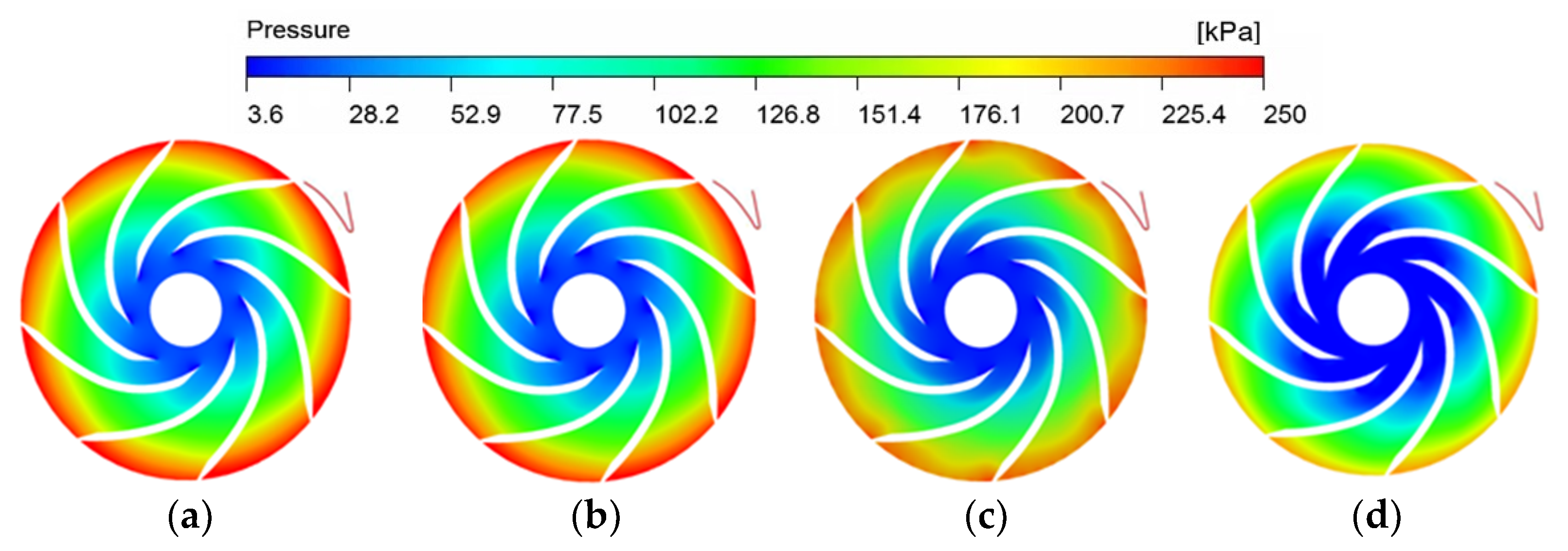
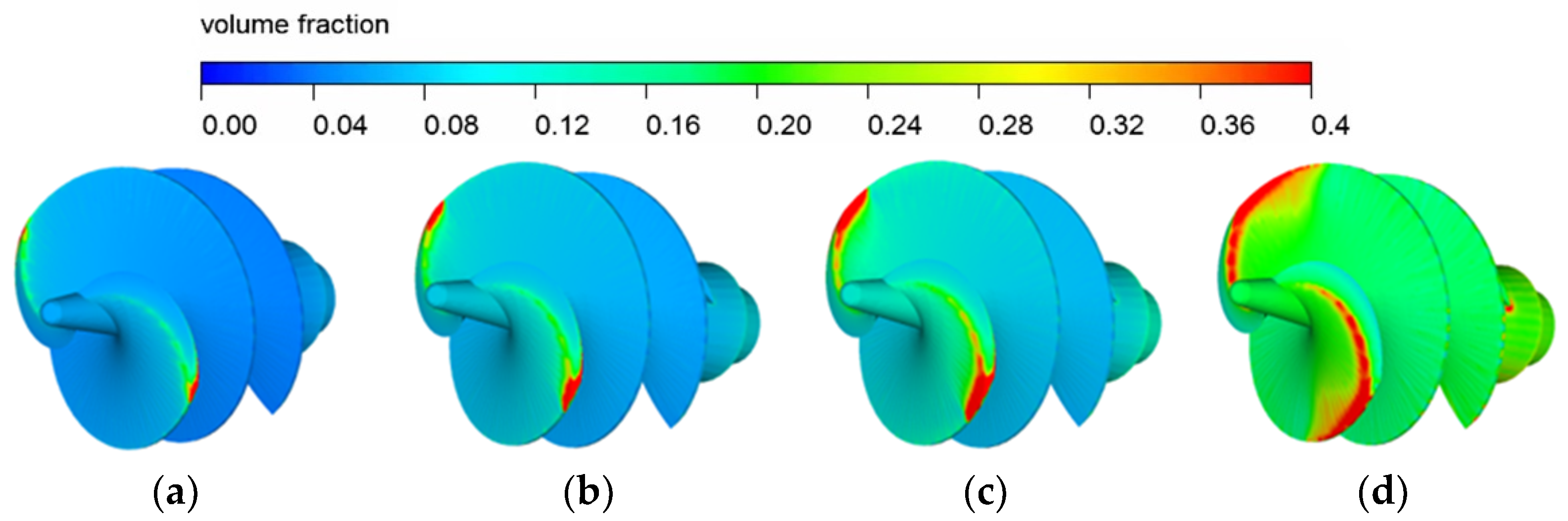
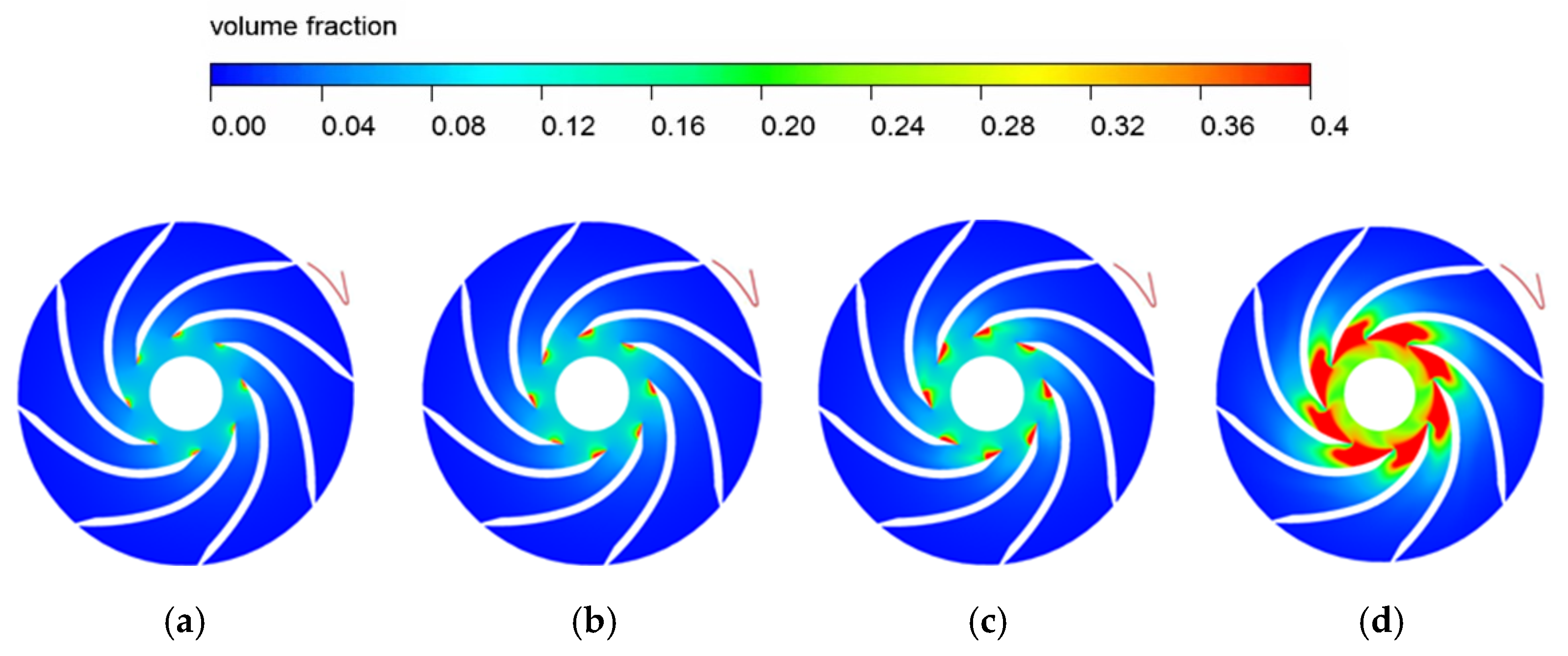
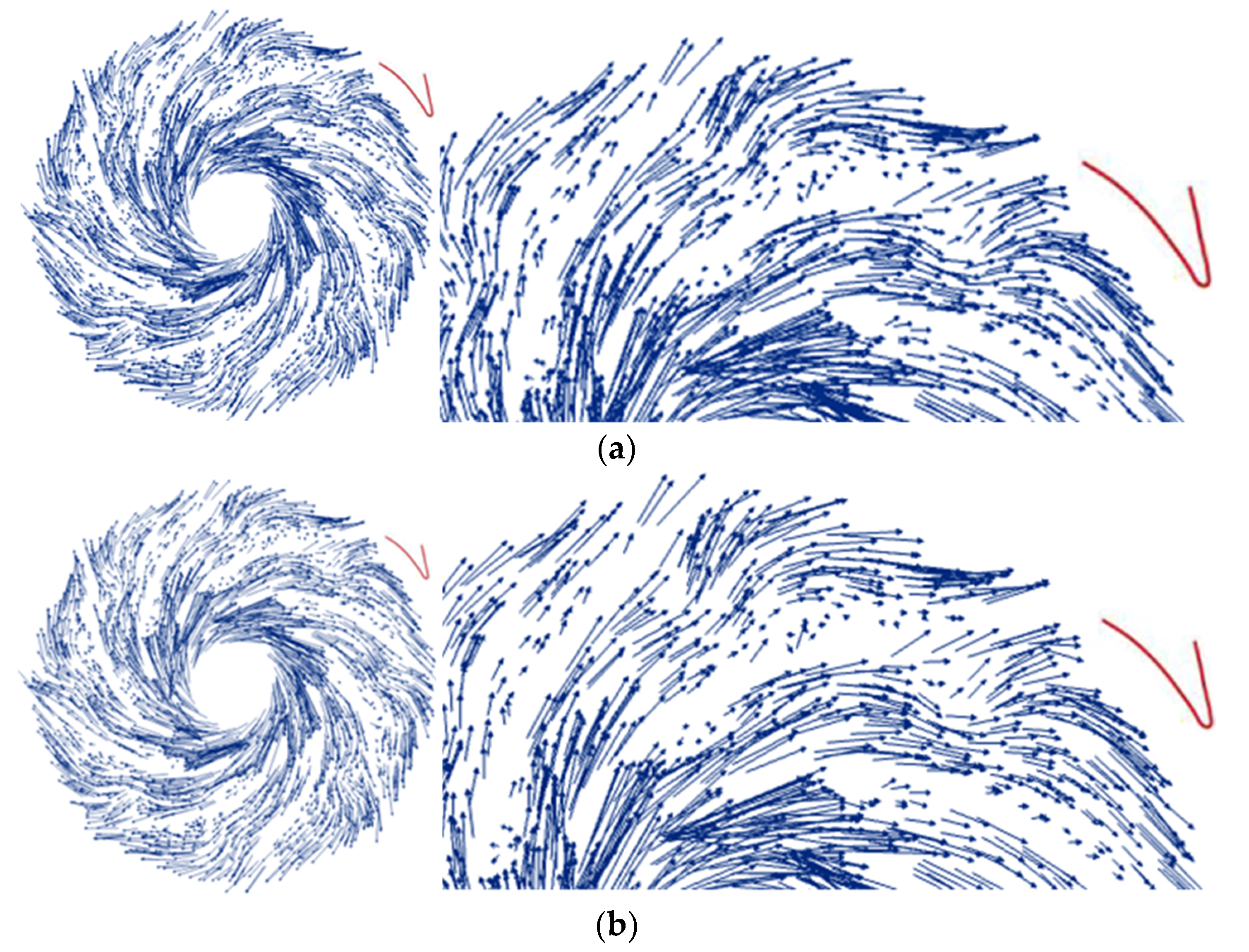
4.2. The Development of Cavitation in Inducer and Impeller
4.3. Pressure Pulsations in the Inducer
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| fv | mass fractions of the vapor |
| fg | mass fractions of the gas |
| fl | mass fractions of the liquid |
| ρm | mixed density |
| ρv | densities of the vapor |
| ρg | densities of the gas |
| ρl | densities of the liquid |
| αv | volume fractions of the vapor |
| αg | volume fractions of the gas |
| αl | volume fractions of the liquid |
| Re | vapor generation rates |
| Rc | vapor condensation rates |
| δij | shear stress |
| µT | turbulent viscosity |
| µm | vapor–liquid phase laminar viscosity |
| NPSHr | required net positive suction head |
| pin | pressure of the pump inlet |
| pv | pressure of the vapor |
| v1 | velocity of the pump inlet |
References
- Zhou, J.; Xing, G.L.; Zhou, S.P. Effects of Different Turbulence Models on Simulation Accuracy of the Miniature Super-low Specific Speed Centrifugal Pump. Eng. Technol. 2018, 31, 792–797. [Google Scholar] [CrossRef] [Green Version]
- Cao, R.; Yuan, J.; Deng, F.; Wang, L. Numerical method to predict vibration characteristics induced by cavitation in centrifugal pumps. Meas. Sci. Technol. 2021, 32, 115109. [Google Scholar] [CrossRef]
- Lei, T.; Shan, Z.B.; Liang, C.S.; Chuan, W.Y.; Bin, W.B. Numerical simulation of unsteady cavitation flow in a centrifugal pump at off-design conditions. Proc. Inst. Mech. Eng. C—J. Mech. Eng. Sci. 2013, 228, 1994–2006. [Google Scholar] [CrossRef]
- Fu, Q.; Zhang, F.; Zhu, R.; He, B. A systematic investigation on flow characteristics of impeller passage in a nuclear centrifugal pump under cavitation state. Ann. Nucl. Energy 2016, 97, 190–197. [Google Scholar] [CrossRef]
- Xu, W.; He, X.; Hou, X.; Huang, Z.; Wang, W. Influence of wall roughness on cavitation performance of centrifugal pump. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 314. [Google Scholar] [CrossRef]
- Fu, Y.; Yuan, J.; Yuan, S.; Pace, G.; D’Agostino, L.; Huang, P.; Li, X. Numerical and Experimental Analysis of Flow Phenomena in a Centrifugal Pump Operating Under Low Flow Rates. J. Fluids Eng. 2014, 137, 205–207. [Google Scholar] [CrossRef]
- Puplaa, S.; Coutier-Delgosha, O.; Dazin, A.; Roussette, O.; Bois, G.; Caignaert, G. Experimental Study of a Cavitating Centrifugal Pump During Fast Startups. J. Fluids Eng. 2010, 132, 021301. [Google Scholar]
- Fecser, N.; Lakatos, I. Cavitation Measurement in a Centrifugal Pump. Acta Polytech. Hung. 2021, 18, 63–77. [Google Scholar] [CrossRef]
- Bachert, R.; Stoffel, B.; Dular, M. Unsteady Cavitation at the Tongue of the Volute of a Centrifugal Pump. J. Fluids Eng. 2010, 132, 061301. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Investigation of effect of pump rotational speed on performance and detection of cavitation within a centrifugal pump using vibration analysis. Heliyon 2019, 5, e01910. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, J.; Yuan, S.; Siva, P.; Yuan, J.; Ren, X.; Zhou, B. The characteristics investigation under the unsteady cavitation condition in a centrifugal pump. J. Mech. Sci. Technol. 2017, 31, 1213–1222. [Google Scholar] [CrossRef]
- Jiang, J.; Li, Y.-H.; Pei, C.-Y.; Li, L.-L.; Fu, Y.; Cheng, H.-G.; Sun, Q.-Q. Cavitation performance of high-speed centrifugal pump with annular jet and inducer at different temperatures and void fractions. J. Hydrodyn. 2019, 31, 93–101. [Google Scholar] [CrossRef]
- Choi, C.H.; Kim, J. Study on the Cavitating Flows in a Turbopump Inducer. J. Propuls. Power 2015, 31, 537–542. [Google Scholar] [CrossRef]
- Guo, X.M.; Zhu, Z.C.; Cui, B.L.; Shi, G. Effects of the number of inducer blades on the anti-cavitation characteristics and external performance of a centrifugal pump. J. Mech. Sci. Technol. 2016, 30, 3173–3181. [Google Scholar] [CrossRef]
- Kang, B.Y.; Kang, S.H. Effect of the number of blades on the performance and cavitation instabilities of a turbopump inducer with an identical solidity. J. Mech. Sci. Technol. 2015, 29, 5251–5256. [Google Scholar] [CrossRef]
- Campos-Amezcua, R.; Khelladi, S.; Mazur-Czerwiec, Z.; Bakir, F.; Campos-Amezcua, A.; Rey, R. Numerical and experimental study of cavitating flow through an axial inducer considering tip clearance. Proc. Inst. Mech. Eng. A—J. Power Energy 2013, 227, 446. [Google Scholar] [CrossRef]
- Pace, G.; Valentini, D.; Pasini, A.; Torre, L.; Fu, Y.; d’Agostino, L. Geometry Effects on Flow Instabilities of Different Three-Bladed Inducers. J. Fluids Eng. 2015, 137, 041304. [Google Scholar] [CrossRef]
- Chern, M.J.; Hsu, P.H.; Cheng, Y.J.; Tseng, P.Y.; Hu, C.M. Numerical Study on Cavitation Occurrence in Globe Valve. J. Energy Eng. 2013, 139, 25–34. [Google Scholar] [CrossRef]




| Group | Elements | Head | Efficiency |
|---|---|---|---|
| Grid 1 | 1,289,484 | 34.25 m | 57.23% |
| Grid 2 | 1,786,352 | 34.52 m | 51.64% |
| Grid 3 | 3,275,154 | 35.58 m | 49.68% |
| Grid 4 | 5,065,316 | 35.60 m | 49.41% |
| Grid 5 | 6,148,215 | 35.61 m | 49.34% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, B.; Han, X.; An, Y. Numerical Simulation of Unsteady Cavitation Flow in a Low-Specific-Speed Centrifugal Pump with an Inducer. J. Mar. Sci. Eng. 2022, 10, 630. https://doi.org/10.3390/jmse10050630
Cui B, Han X, An Y. Numerical Simulation of Unsteady Cavitation Flow in a Low-Specific-Speed Centrifugal Pump with an Inducer. Journal of Marine Science and Engineering. 2022; 10(5):630. https://doi.org/10.3390/jmse10050630
Chicago/Turabian StyleCui, Baoling, Xiaotian Han, and Yinchu An. 2022. "Numerical Simulation of Unsteady Cavitation Flow in a Low-Specific-Speed Centrifugal Pump with an Inducer" Journal of Marine Science and Engineering 10, no. 5: 630. https://doi.org/10.3390/jmse10050630
APA StyleCui, B., Han, X., & An, Y. (2022). Numerical Simulation of Unsteady Cavitation Flow in a Low-Specific-Speed Centrifugal Pump with an Inducer. Journal of Marine Science and Engineering, 10(5), 630. https://doi.org/10.3390/jmse10050630






