A Comprehensive Star Rating Approach for Cruise Ships Based on Interactive Group Decision Making with Personalized Individual Semantics

Abstract

This article proposes a comprehensive star rating approach for cruise ships by the combination of subject and objective evaluation. To do that, it firstly established a index system of star rating for cruise ships. Then, the modified TOPSIS is adopted to tackle objective data for obtaining star ratings for basic cruise indicators and service capabilities of cruise ships. Thus, the concept of distributed linguistic star rating function (DLSRF) is defined to analyze the subjective evaluation from experts and users. Hence, a novel weight calculation method with interactive group decision making is presented to assign the importance of the main indicators. Particularly, in order to enable decision makers to effectively deal with the uncertainty in this star rating process, it adopts the personalized individual semantics (PIS) model. Finally, data of nine cruise ships is collected to obtain their final star rating results and some suggestions for improving cruise service capabilities and star indicators were put forward.

1. Introduction

The cruise industry has flourished in recent years to be one of the most rapidly developing segments of the global tourism industry, with millions of travelers cruising each year [1,2]. Cruise tourism is a universal type of tourism that combines all of its forms and contains of its types: recreational, sports, health improving, educational, congress etc., as well as combining various options for service and recreation [3]. As a new economic form, the cruise economy has broad prospects for development and is known as the ‘Golden Industry on Water’. Some research on cruise ships have been carried out from different perspectives [4,5]. However, the goal of most of them is how to improve user satisfaction and build the cruise brand. Few studies have looked at the star rating of cruise ships, but it is indeed significant to manage the product quality and prices of cruise lines, similar to a hotel star rating. Similar to some research about maritime evaluation [6], this is essentially a multi-attribute decision problem. However, there are two long-standing issues for the star rating of cruise ships. One is how to build a star rating system for cruise ships, and another is how to assign the weights of different indicators [7,8].

Then, the first issue is important to determine the index system of star rating for cruise ships. This article constructs a novel index system of star rating based on literature analysis and experts interviews, which involves four parts including a combination of subjective and objective evaluations: (1) basic indicators of cruise ships, such as, the number of crew and the tonnage of the cruise ship, etc.; (2) the service capacities of the cruise ships, including restaurants, bars, recreational facilities and children’s services, etc.; (3) subjective star ratings from experts and (4) subjective star ratings from users/potential users. The proposed star rating system not only refers to historical information, but also combines current experts’ advice, and then it has a higher reliability.

The second one, ‘how to determine the weights of the above four parts?’, is also another key issue. Thus, this article proposes a novel weight calculation approach of the index system of cruise ships star rating expressed by linguistic information from group experts. To resolve the disagreements among group experts, an interactive group decision making is investigated [9,10,11]. Additionally, the same term usually means different meanings for different experts, hence, the personalized individual semantics (PIS) is used to unify the linguistic scales of different experts [12]. In order to obtain the comprehensive scores of basic situations and service capacities for cruise ships, it uses the modified TOPSIS (The Technique for Order of Preference by Similarity to Ideal Solution) to the finish objective evaluations.

Therefore, this paper aims to contribute to the existing research in the following areas:

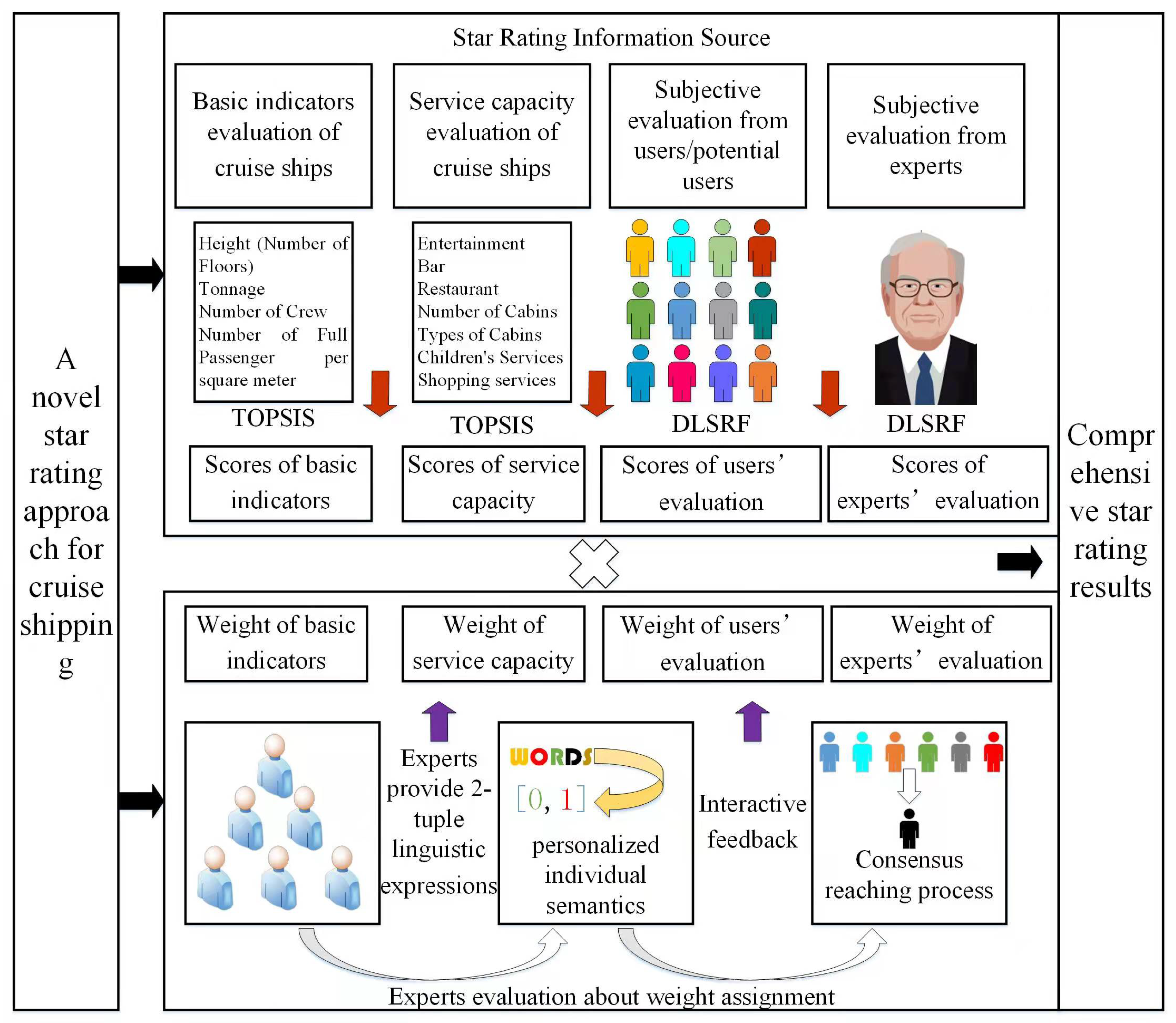
• In theory, this article proposes a index system of star rating for cruise ships and establishes a comprehensive star rating approach by subject and objective evaluation. To do that, it firstly utilizes the modified TOPSIS to evaluate the star rating of basic situations and service capacities for cruise ships and defines distributed linguistic star rating function (DLSRF) to express the preference about cruise ships from experts and users/potential users. Furthermore, a novel weight calculation based on interactive group decision making is proposed to assign the weights of evaluations from different sources;
• In practice, few studies discuss the methodology for star rating of cruise ships, our proposed work investigates the comprehensive star rating by the combination of basic indicators, service capacities for cruise ships, experts’ comments and users/potential users’ review. Moreover, it provides some managerial insights to standardize cruise industry standards.

The organization of the rest of this paper is as follows: The related literature is reviewed in Section 2. In Section 3, PIS model under 2-tuple linguistic and interactive group decision making are introduced, where these two methods can be combined to make up a novel weight calculation approach. Furthermore, the modified TOPSIS is presented for objective star rating and DLSRF is defined for subject star rating in this section. The approaches mentioned above was used flexibly to evaluate the star rating of nine cruise ships by combining objective and survey data in Section 4. In Section 5, the proposed method and evaluation results are validated and potential approaches to improve cruise service are discussed. Finally, we highlight the contribution of this paper in Section 6 and future research directions are indicated.

2. Literature Review

2.1. Literature Review of Cruise Products

This section will present the following research literature on cruise products. Usually, the basic attributes of cruise products involve accommodation, food, entertainment, health care, etc. and every attribute will have an impact on star rating of cruise ships. Some literature had analyzed the attributes of cruise ships from different perspectives. Such as, Xie et al. [13] found that there are seven dimensions of cruise onboard attributes based on the results of factor analysis, namely entertainment attributes, recreation and sport attributes, supplementary attributes, core attributes, fitness and health attributes, children attributes, and crew attributes. Hwang et al. [14] explored the effect of food quality, service quality, staff/crew attractiveness, entertainment, ship facilities, ports of call, programs/places for children, and cabin quality on brand prestige of cruise ships based on statistical analysis. Furthermore, Hosany et al. [15] believed that cruise marketers should emphasize the educational, esthetic, escapist, and entertaining values of the cruise vacation in their promotional campaigns. In addition, some other research have investigated the impact of different cruise attributes on user experience and satisfaction, listed as

Table 1. Important cruise ship attributes and its literature sources.

Literature Sources	Cruise Ship Attributes
Chua et al., 2015 [16]	Physical environment attributes (including ship size, navigation, hygiene, lighting, music, temperature, etc.), interactive attributes and outcome attributes (including catering, accommodation, sports, entertainment, wellness, children’s facilities and services, etc.)
Li and Kwortnik 2017 [17]	Catering, entertainment, cost, service and cabin, etc.
Swain and Barth 2002 [18]	Cabins, Crews, Cruise space, Cruise tonnage, Cruise length and sailing time, etc.
Teye and Leclerc 1998 [19]	Room service, food service, entertainment properties, bar service, food quality and staff service, etc.
Yi, Day, and Cai 2014 [20]	Onboard facilities, Meals, Entertainment and Employee, etc.
Zhang et al., 2012 [21]	Staff, Guest rooms, Public spaces, Catering, Services, Entertainment and Wellness and fitness, etc.

. Therefore, this article selects the following main indicators to evaluate the star rating of cruise ships: (1) basic indicators of cruise ships; (2) the service capacity of the cruise ship, (3) subjective star ratings from experts and (4) subjective star ratings from users/potential users.

2.2. Literature Review of Technical Methods

As mentioned earlier, the technical methods involved in this article include PIS linguistic model, interactive group decision making, DLSRF and the modified TOPSIS. Without a doubt, the design of PIS linguistic model comes from the development of group decision making, which is proposed by Dong and Li [12]. In recent years, it has been used by many experts in many fields involving group decision problems. Such as, Zhang et al. proposed a reliability management method based on failure modes and effects analysis by PIS linguistic model [22] and Wan et al. presented a consensus reaching process for large-scale group decision making based on PIS linguistic model and applied it into COVID-19 surveillance [23]. In addition to preference representations related PIS linguistic model, group decision making also involves the interaction mechanisms. In the past ten years, many interaction mechanisms for group decision making are discussed. Initially, it was mainly discussed from the cost perspective, Yu et al. [24] used a minimum adjustment-based consensus reaching to solve the multi-attribute group decision making and Wu et al. [25] developed a method of travel destination evaluation considering minimum adjustment cost feedback mechanism under the environment of online reviews. Later, more group consensus interaction mechanisms considering behavior were studied. Wang et al. [26] presented a two stage interaction mechanism considering different power structures in social network group decision making; Liang et al. [27] constructed a consensus reaching model with time constraints, where bounded confidence behavior is investigated to control the modification levels of decision makers; Dong et al. [28] and Cao et al. [29] designed a decentralized interaction mechanism for consensus in group decision making; Cao and Zha et al. [30,31] provided a personalized feedback mechanism to provide different feedback suggestions for decision makers with different consensus levels. DLSRF is an extension of distributed linguistic function in process of cruise evaluation. Distributed linguistic function is also a widely used linguistic representation and processing method in the field of decision-making, especially, group decision making. Jin et al. [32] proposed a fresh decision support model based on consistency and consensus adjustment algorithm in group decision-making problems with distribution linguistic data to evaluate of China’s state-owned enterprise equity incentive model. Tian et al. [33] develops an integrated multi-criteria group decision-making method within the context of multi-granular linguistic distribution assessments to evaluating tourism attractions. Finally, TOPSIS is a classic method for objective data evaluation, which has been used and extended in many studies. Zhang et al. [34] proposed a framework for evaluating the mined association rules based on TOPSIS method with combination weights under the theory of multiple criteria decision, which takes both objective interestingness measures and the users’ domain information into account; Liu et al. [35] establishes a modified TOPSIS method with cloud model to rank the new energy investment alternatives; Wu et al. [36] presented a new quality function deployment model based on the Kano model and TOPSIS method by considering the behavior of experts with prospect theory under interval type-2 fuzzy linguistic environment to measure the uncertainties and behavioral risk factors in e-commerce service design; and an extended TOPSIS model with Pythagorean fuzzy sets is proposed to assess risk of clearing and grading process of a natural gas pipeline project [37].

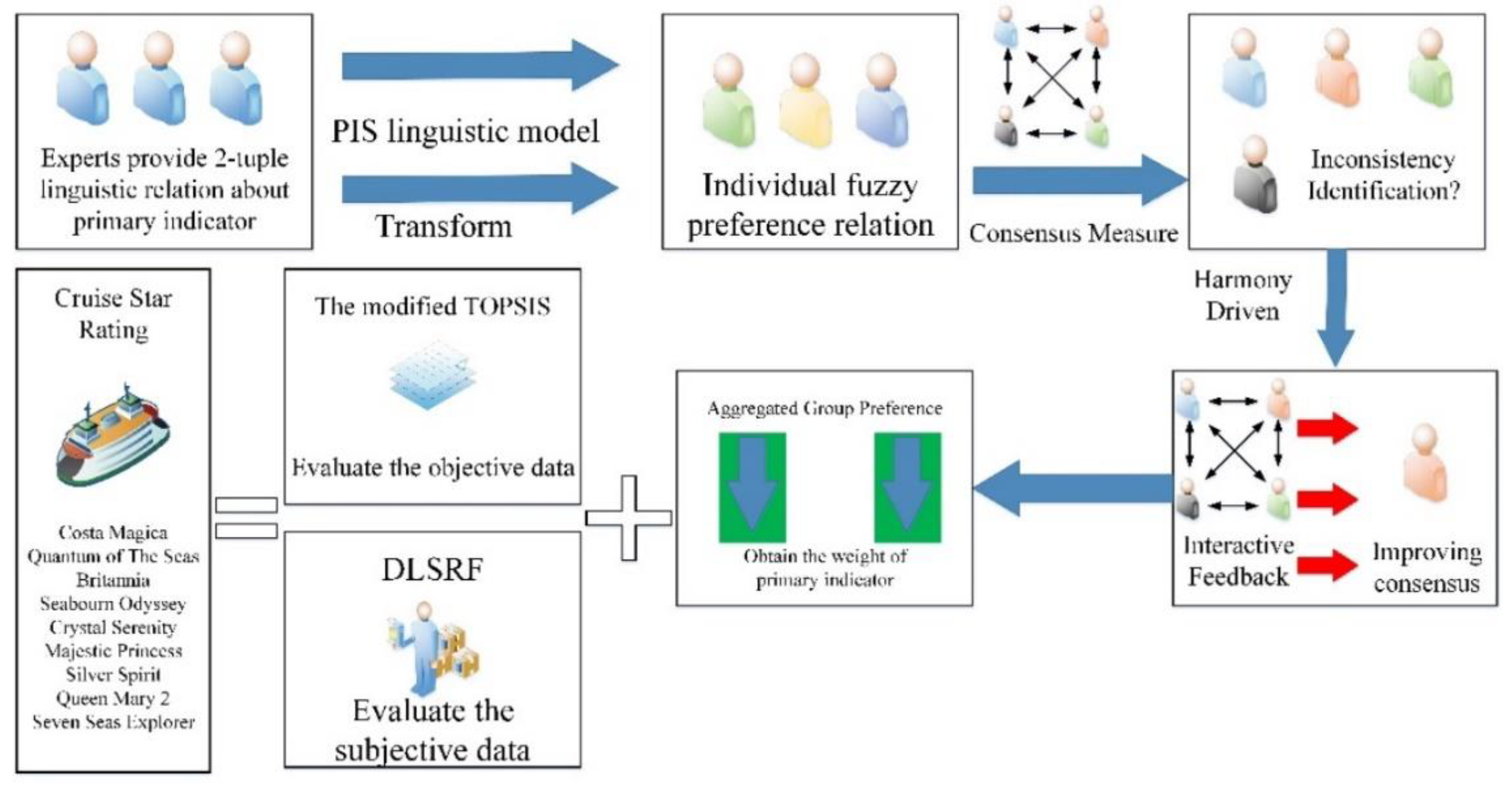
3. Comprehensive Star Rating Approach for Cruise Ships

Star rating of cruise ships is an extremely complicated issue because many factors involved are difficult to quantify, such as, the weights of some unrelated star rating indicators. The only feasible approach is to obtain the pairwise importance relationship by experts’ interviews. However, the terms from experts are also complicated, ‘how to compute these linguistic terms into weights’ and ‘how to identify the true meaning of each expert term’ have become challenges. Thus, PIS model under 2-tuple linguistic is presented to convert terms from experts into numerical value, which can not only obtain the true meanings of experts, but also facilitate the computing words to obtain weights. Simultaneously, there exists disagreement among experts in the process of obtaining weights, an interactive group decision making is introduced to improve the consensus among experts by a harmony approach. Furthermore, the modified TOPSIS is adopted to tackle the star rating derived from objective data and DLSRF is defined to help experts and users express their star rating preferences.

3.1. PIS Model under 2-Tuple Linguistic

Above all, Herrera and Martinez proposed the 2-tuple linguistic model in the framework of computing with words, which is a linguistic representation model widely used into different fields [38]. Here, we assumed $S=\left\{s_0,s_1,\cdots ,s_g\right\}$ be a linguistic term set, and $\beta \in \left[0,g\right]$ be a value representing the result of a symbolic aggregation operation. The 2-tuple linguistic model involves the transformation function between 2-tuples ($\overline{S}$) and numerical values ($\left[0,g\right]$) as follows [39]:

$$\Delta :\left[0,g\right]\to \overline{S}$$

(1)

$$\Delta \left(\beta \right)=\left(s_i,\alpha \right),with \{\begin{array}{c}{s}_i,i=round\left(\beta \right)\\ \alpha =\beta -i,\alpha \in \left[-0.5,0.5\right]\end{array}$$

(2)

where function $\Delta$ is a one-to-one mapping whose inverse function ${\Delta }^{-1}:\overline{S}\to \left[0,g\right]$ is equal to ${\Delta }^{-1}\left(s_i,\alpha \right)=i+\alpha$.

In the decision making process, the same term usually have different meanings for different experts, for example, when two experts evaluate the importance degree between basic indicators and service capacity of cruise ships, they both use the terms ‘more important’, i.e., they both believe the basic indicators are more important than service capacity, but one expert think the probability that basic indicators are more important than service capacity is 60%, while other expert think the probability that basic indicators are more important than service capacity is 70%.

While it is an effective tool for PIS model to tackle this situation the same word has different meanings for different experts, where numerical scale model and linguistic preference relations consistency are the basis of PIS model. The numerical scale model is introduced by Dong et al. [40].

Let $S=\left\{s_0,s_1,\cdots ,s_g\right\}$ be a linguistic term set and $R$ be the set of real numbers. A function $NS:S\to R$ is called a numerical scale of $S$, and $NS\left(s_i\right)$ is the numerical index of $s_i$, the numerical scale $NS:S\to R$ is as follows [41].

$$NS\left(s_i,\alpha \right)=\{\begin{array}{c}NS\left(s_i\right)+\alpha \times \left(NS\left(s_{i+1}\right)-NS\left(s_i\right)\right),\alpha \ge 0\\ NS\left(s_i\right)+\alpha \times \left(NS\left(s_i\right)-NS\left(s_{i-1}\right)\right),\alpha <0\end{array}$$

(3)

If $NS\left(s_i\right)<NS\left(s_{i+1}\right)$, ($\forall i=0,1,\cdots ,g-1$), then the numerical scale NS on S is ordered. The above is the numerical scale model, and the consistency of a linguistic preference relation based on the 2-tuple linguistic model under numerical scale is measured as follows.

Let $L={\left(l_{ij}^k\right)}_{n\times n}$ be a linguistic preference relation on a set of alternatives $X=\left\{x_1,x_2,\cdots ,x_n\right\}$, whose element $l_{ij}^k\in S$ denotes the preference degree of $x_i$ over $x_j$. A linguistic preference relation $L={\left(l_{ij}^k\right)}_{n\times n}$ is consistent linguistic preference relation based on numerical scales, if $NS\left(l_{ij}\right)\in \left[0,1\right]$ and $NS\left(l_{ij}\right)+NS\left(l_{jz}\right)-NS\left(l_{iz}\right)=0.5$, for $i<j<z$, thus, the consistency index of a linguistic preference matrix $L$ with respect to $NS$ is as follows, with $NS\left(l_{ij}\right)\in \left[0,1\right]$ [41].

$$CL\left(L\right)=1-\frac{4}{n\cdot \left(n-1\right)\cdot \left(n-2\right)}{\displaystyle \sum }_{i,j,z=1;i<j<z}^n\left(NS\left(l_{ij}\right)+NS\left(l_{jz}\right)-NS\left(l_{iz}\right)-0.5\right)$$

(4)

a larger value of $CL\left(L\right)\in \left[0,1\right]$ indicates a better consistency of $L$.

Furthermore, the PIS model is presented with the maximum consistency index of $L^k$ as objective function and the numerical scales of linguistic terms as restrictions. Usually, the numerical scales of linguistic terms are set as follows [39].

$$N{S}^k(s_i)\{\begin{array}{ll}=0& if i=0\\ \in [\frac{i-1}{g},\frac{i+1}{g}]& if i=1,2,\dots ,g-1;i\ne \frac{g}{2}\\ =0.5& if i=\frac{g}{2}\\ =1& if i=g\end{array}$$

Usually, a small constraint value $\lambda$ is predefined to guarantee the rank of $NS$, i.e., $NS\left(s_{i+1}\right)-NS\left(s_i\right)\ge \lambda$. Therefore, we use PIS model driven by consistency to obtain the personalized numerical scales as follows.

$$\{\begin{array}{c}max:CL(L)=1-\frac{4}{n·(n-1)·(n-2)}{\displaystyle \sum _{i,j,z=1;i<j<z}^n}\mid NS(l_{ij})+NS(l_{jz})-NS(l_{iz})-0.5\mid \\ s.t.\{\begin{array}{l}N{S}^k(s_0)=0\\ N{S}^k(s_i)\in [\frac{i-1}{g},\frac{i+1}{g}]\\ N{S}^k\left(s_{\frac{g}{2}}\right)=0.5\\ N{S}^k\left(s_g\right)=1\\ N{S}^k\left(s_{i+1}\right)-N{S}^k\left(s^i\right)\ge \lambda ,i=0,1,\dots ,g-1\end{array}\end{array}$$

(5)

The proposed PIS model can quantify the individual linguistic preference relation $L={\left(l_{ij}^k\right)}_{n\times n}$, $\left(k=1,2,\cdots ,m\right)$ to generate the individual fuzzy preference relation $F^k={\left(f_{ij}^k\right)}_{n\times n}$, $\left(k=1,2,\cdots ,m\right)$ by using the individual numerical scale $N{S}^k$. Here, $f_{ij}^k=N{S}^k\left(l_{ij}^k\right)$, where $i=1,\cdots ,n;j=i+1,\cdots ,m$.

3.2. Interactive Group Decision Making

When multiple experts evaluate the weights of indicators, the disagreement among experts may emerge, hence, an interactive group decision making is proposed to deal with this situation [11,42]. An interactive group decision making framework with bilateral negotiating mechanism is generally consisted by the four parts: (1) preference representation, (2) consensus measure, (3) inconsistency identification and (4) interaction mechanism [26,30,43]. As described in the previous, this article uses 2-tuple linguistic model to achieve the initial preference representation and they are transformed into fuzzy preference relations by PIS model.

The approach of consensus measure is presented as follows. Assuming a group of experts $E=\left\{e_1,\cdots ,e_k,\cdots ,e_m\right\}$ provide risk evaluations using fuzzy preference relations $\left\{F^1={\left(f_{ij}^1\right)}_{n\times n},\cdots ,F^k={\left(f_{ij}^k\right)}_{n\times n},\cdots ,F^m={\left(f_{ij}^m\right)}_{n\times n}\right\}$, the consensus degree between any two experts, $e_h$ and $e_k$, is measured as follows.

$$c{d}^{hk}=1-\frac{1}{n\cdot \left(n-1\right)}{\displaystyle \sum }_{i,j=1;j\ne i}^n\left|f_{ij}^h-f_{ij}^k\right|$$

(6)

where $c{d}^{hk}\in \left[0,1\right]$ and the symmetric consensus matrix $CM={\left(c{d}^{hk}\right)}_{m\times m}$ reflects the consensus situation among all the experts about the weights of indicators. The consensus level of every expert is presented as the average of his/her mutual consensus degrees with the rest of experts in the group, i.e.,

$$C{D}^h=\frac{1}{m-1}{\displaystyle \sum }_{k=1;k\ne h}^{m}c{d}^{hk}$$

(7)

Here, $\beta$ is assumed as the consensus threshold, the termination condition of the interaction process is $\forall C{D}^h\ge \beta$, i.e., the third step of consensus reaching process, inconsistency identification. If $C{D}^h<\beta$, the interaction mechanism in the consensus reaching process will be activated as follows, otherwise, the consensus about weights assignments among experts has been reached and the preferences can be used to assign weights directly.

Before describing the interactive consensus reaching model, the concept of harmony degree and its threshold is defined as follows, because it used to control the opinion modification level of experts in the consensus reaching process. Usually, harmony degree is defined to measure the agreement between $e_h$’s preferences before and after interaction with other experts.

The original weight preferences of $e_h$ and $e_k$ can be transformed into the fuzzy preference relation $F^h={\left(f_{ij}^h\right)}_{n\times n}$ and $F^k={\left(f_{ij}^k\right)}_{n\times n}$, respectively. In addition, the weight preferences after interaction for $e_h$ and $e_k$ are $f{f}_{ij}^{hk}=\left(1-{\delta }_h\right)·f_{ij}^h+{\delta }_h·f_{ij}^k$ and $f{f}_{ij}^{kh}=\left(1-{\delta }_k\right)·f_{ij}^k+{\delta }_k·f_{ij}^h$, respectively, where ${\delta }_h,{\delta }_k\in \left[0,1\right],\left({\delta }_h+{\delta }_k\in (0,1]\right)$ are the respective interaction parameters that represent how much change in weight evaluations one expert adopts from the weight evaluations of the other expert interacting with. The harmony degrees of experts $e_h$ and $e_k$ after their interaction are defined by [29]:

$$H{D}_k^h=1-\frac{1}{n\cdot \left(n-1\right)}\cdot {\displaystyle \sum }_{i,j=1;j\ne i}^n\left|f{f}_{ij}^{hk}-f_{ij}^h\right|=\left(1-{\delta }_h\right)+{\delta }_h\cdot c{d}_{hk}$$

(8)

$$H{D}_h^k=1-\frac{1}{n\cdot \left(n-1\right)}\cdot {\displaystyle \sum }_{i,j=1;j\ne i}^n\left|f{f}_{ij}^{kh}-f_{ij}^k\right|=\left(1-{\delta }_k\right)+{\delta }_k\cdot c{d}_{kh}$$

(9)

While there usually exists a harmony boundary for every expert in the interaction process between experts $e_h$ and $e_k$, thus, the concept of harmony threshold $\left(\gamma \right)$ is proposed to simulate limited compromise behavior of experts in the bargaining process, as follows [29].

$${\gamma }^{h,m}={\left(C{D}^h\right)}^{\frac{1}{m}}$$

(10)

In the consensus reaching process, if $\exists C{D}^h<\beta$, two experts $e_a$ and $e_b$ with minimum consensus degree, i.e., $c{d}_{ab}=\min \left\{c{d}_{hk};h,k=1,2,\cdots ,m\right\}$, will be asked to interaction with each other. Let $rc{d}_{ab}$ be the consensus degree between the identified experts $e_a$ and $e_b$, after their bilateral negotiating interaction process, that is,

$$rc{d}_{ab}=1-\frac{1}{n\cdot \left(n-1\right)}\cdot {\displaystyle \sum }_{i,j=1;j\ne i}^n\left(f{f}_{ij}^{ab}-f{f}_{ij}^{ba}\right)=\left({\delta }_a+{\delta }_b\right)+\left[1-\left({\delta }_a+{\delta }_b\right)\right]\cdot c{d}_{ab}$$

(11)

In order to optimize consensus after bilateral negotiation between the identified experts, the following interaction feedback optimization structure is proposed with the maximum consensus degree as objective function and the individual harmony degree as restrictions:

$$\{\begin{array}{l}\max :({\delta }_a+{\delta }_b)+[1-({\delta }_a+{\delta }_b\left)\right]·c{d}_{ab}\\ s.t.\{\begin{array}{l}c{d}_{ab}=\min \{c{d}_{hk};h,k=1,2,\cdots ,m\}\\ c{d}^{hk}=1-\frac{1}{n·(n-1)}{\displaystyle \sum _{i,j=1;j\ne 1}^n}\mid f_{ij}^h-f_{ij}^k\mid \\ (1-{\delta }_a)+{\delta }_a·c{d}_{ab}\ge {\gamma }^a\\ (1-{\delta }_b)+{\delta }_b·c{d}_{ab}\ge {\gamma }^b\\ {\delta }_a,{\delta }_b>0\\ {\delta }_a+{\delta }_b\in (0,1]\end{array}\end{array}$$

(12)

3.3. DLSRF

Usually, the star rating for cruise ships can be divided into seven star-levels, from one star to seven stars. Then it is difficult to determine whether a cruise ship is 5-star or 6-star, or even 7-star, when experts evaluate it, due to the uncertainty of human intuition. In this context, this article proposed the following definition of DLSRF. Suppose that $SR=\left\{s{r}_i|i=1,2,\cdots ,7\right\}$ is a star rating linguistic term set. A DLSRF is expressed as follows:

$$\Theta =\left\{\left(s{r}_i,{\phi }_i\right)|\left({\phi }_i>0,\forall i\right)\wedge {\sum }_{i=1}^7{\phi }_i=1\right\}$$

(13)

The set $\left\{{\phi }_1,\cdots ,{\phi }_7\right\}$ is the distributed assessment of SR. In order to aggregate the evaluations from experts or users, distributed linguistic star rating averaging operator (DLSRAO) is defined as follows, with q experts or users.

$$DLSRAO\left({\Theta }_1,\cdots ,{\Theta }_j,\cdots ,{\Theta }_q\right)=\left\{s{r}_i,\frac{1}{q}{\displaystyle \sum }_{i=1}^q{\phi }_i\right\}$$

(14)

And this article the definition of expectation degree of $\mathrm{DLSRF}$ $\Theta$ for obtaining the final evaluation results:

$$E\left(\Theta \right)={\displaystyle \sum }_{i=1}^{7}s{r}_i\cdot {\phi }_i$$

(15)

3.4. The Modified TOPSIS

TOPSIS is based on the fundamental premise that the best solution has the shortest distance from the positive-ideal solution, and the longest distance from the negative-ideal one [44,45]. Modified TOPSIS integrates the attribute weights with the performance ratings in a slightly different manner compared to the traditional TOPSIS method [46,47]. Similar to the traditional TOPSIS method, the overall performance score is obtained from the distance from positive and negative solutions, where the distance is related with the alternative weights. Supposed that the original decision matrices are constituted of the relevant indicator data of each cruise ship participating in the star rating evaluation, the modified TOPSIS method is explained through the following stages. As (16), where $x_{ij}$ means the data of cruise ship $i$ under indicator $j$ $\left(i=1,2,\cdots ,I;j=1,2,\cdots ,J\right)$.

$$X=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1J}\\ x_{21}& x_{22}& \cdots & x_{2J}\\ \cdots & \cdots & \cdots & \cdots \\ x_{I1}& x_{I2}& \cdots & x_{IJ}\end{array}\right]$$

(16)

• Stage 1: Normalize the original decision matrix. The normalize value $y_{ij}$ of original decision matrix is calculated through $x_{ij}$ in $X$ is divided by its norm, as follow.

  $$y_{ij}=x_{ij}/\sqrt{{\displaystyle \sum }_{i=1}^I{x}_{ij}^2}$$

  (17)

The normalize value $y_{ij}$ can be given as a matrix $Y$ as shown in Equation (18).

$$Y=\left[\begin{array}{cccc}{y}_{11}& y_{12}& \cdots & y_{1J}\\ y_{21}& y_{22}& \cdots & y_{2J}\\ \cdots & \cdots & \cdots & \cdots \\ y_{I1}& y_{I2}& \cdots & y_{IJ}\end{array}\right]$$

(18)

• Stage 2: Identify the ideal solutions: $P^{+}$ and $P^{-}$ are defined as the positive and negative ideal solutions, respectively, and can be obtained in terms of normalized value from Equation (18) as,

  $$P^{+}=\left[y_1^{+},y_2^{+},\cdots ,y_J^{+}\right]$$

  (19)

  $$P^{-}=\left[y_1^{-},y_2^{-},\cdots ,y_J^{-}\right]$$

  (20)

  where,

  $$y_j^{+}=\{\begin{array}{c}\max y_{ij};for benefit attribute\\ \min y_{ij};for cost attribute \end{array}$$

  $$y_j^{-}=\{\begin{array}{c}\min y_{ij};for benefit attribute\\ \max y_{ij};for cost attribute \end{array}$$

• Stage 3: Obtain the weighted Euclidean distance. The weighted Euclidean distances from the positive and negative ideal solutions for each cruise ship are obtained from Equations (18)–(20) as,

  $$D_i^{+}=\sqrt{{\displaystyle \sum }_{j=1}^J{W}_j{\left(y_{ij}-y_j^{+}\right)}^2}$$

  (21)

  $$D_i^{-}=\sqrt{{\displaystyle \sum }_{j=1}^J{W}_j{\left(y_{ij}-y_j^{-}\right)}^2}$$

  (22)

  where $W_j$ $\left(j=1,2,\cdots ,J\right)$ is weights for indicators $j$, the average operator is used in this article.

• Stage 4: Obtain the overall star rating score: The overall score for each cruise ship is obtained as:

$$V_i=\frac{D_i^{-}}{D_i^{-}+D_i^{+}}$$

(23)

Star rating score is utilized to convert and divide star rating levels of cruise ships. Usually, the evaluation of cruise ship is divided into seven stars, thus, we set the cruise ship with a score in the interval $\left[0,\frac{1}{7}\right]$ as one-star, the cruise ship with a score in the interval $\left[\frac{1}{7},\frac{2}{7}\right]$ as a two-star, and so on, let the cruise ship with a score in the interval $\left[\frac{6}{7},1\right]$ as a seven-star.

4. A Novel Star Rating Index System

This section constructs a novel star rating index system for luxury cruise ships and chooses nine luxury cruise ships as research objects, namely Costa Magica, Quantum of The Seas, Britannia, Seabourn Odyssey, Crystal Serenity, Majestic Princess, Silver Spirit, Queen Mary 2 and Seven Seas Explorer. The proposed star rating index system includes the four primary indicators mentioned in Section 1, which is shown as Figure 1. Firstly, the weights of four parts are obtained based on interactive consensus and evaluations of experts under 2-tuple linguistic. Secondly, this section determines a star rating system of basic indicators and service capacity for the cruise ship based on TOPSIS and some research data is presented including the ships’ tonnage, height, number of crew, full passenger number, ships’ cabins number, category, type and maximum area. Thirdly, it provides the star rating from experts and users/potential users by DLSRF. Finally, comprehensive star rating results are generated. In order to ensure the integrity of the proposed method, Figure 2 is embedded in this article to link or weave different techniques.

4.1. Weighting Calculation Based on Interactive Consensus

This subsection contributes to provide a weight calculation approach, where experts provide their evaluation by 2-tuple linguistic. However, on the one hand, the same words from different experts may usually have different meanings, thus, this article introduces PIS to deal with this problem. On the other hand, there usually exist disagreements among experts due to different educational background and social levels, so it will integrate the interactive group decision making to help experts improve consensus. To sum up, a weight assignment method integrating PIS model and interactive group decision making is proposed under 2-tuple linguistic. The five experts are required to provide the relative importance level for star rating of cruise ships about basic indicators, service capacity, subjective star ratings from experts and from users/potential users, by linguistic terms set S = {$s_0$ = extremely unimportant, $s_1$ = very unimportant, $s_2$ = unimportant, $s_3$ = fair, $s_4$ = important, $s_5$ = very important, $s_6$ = extremely important}, as follows.

$$\begin{array}{cc}{L}_1=\left\{\begin{array}{cccc}{s}_3& s_5& s_3& s_4\\ null& s_3& s_6& s_2\\ null& null& s_3& s_1\\ null& null& null& s_3\end{array}\right\}& L_2=\left\{\begin{array}{cccc}{s}_3& s_4& s_5& s_4\\ null& s_3& s_2& s_4\\ null& null& s_3& s_3\\ null& null& null& s_3\end{array}\right\}\\ L_3=\left\{\begin{array}{cccc}{s}_3& s_2& s_1& s_5\\ null& s_3& s_4& s_6\\ null& null& s_3& s_3\\ null& null& null& s_3\end{array}\right\}& L_4=\left\{\begin{array}{cccc}{s}_3& s_3& s_1& s_2\\ null& s_3& s_4& s_5\\ null& null& s_3& s_6\\ null& null& null& s_3\end{array}\right\}\\ L_5=\left\{\begin{array}{cccc}{s}_3& s_6& s_4& s_5\\ null& s_3& s_1& s_2\\ null& null& s_3& s_5\\ null& null& null& s_3\end{array}\right\}& \end{array}$$

Let $\lambda =0.01$ and $\beta =0.8$, PIS model is solved to obtain the personalized numerical scales of linguistic terms for each expert, $\left\{N{S}^k\left(s_0\right),N{S}^k\left(s_1\right),\cdots ,N{S}^k\left(s_6\right)\right\}$, $\left(k=1,2,\cdots ,5\right)$, which are listed in

Table 2. Personalized numerical scales of linguistic terms for each expert.

	$\mathit{N}{\mathit{S}}^{\mathit{k}}\left({\mathit{s}}_0\right)$	$\mathit{N}{\mathit{S}}^{\mathit{k}}\left({\mathit{s}}_1\right)$	$\mathit{N}{\mathit{S}}^{\mathit{k}}\left({\mathit{s}}_2\right)$	$\mathit{N}{\mathit{S}}^{\mathit{k}}\left({\mathit{s}}_3\right)$	$\mathit{N}{\mathit{S}}^{\mathit{k}}\left({\mathit{s}}_4\right)$	$\mathit{N}{\mathit{S}}^{\mathit{k}}\left({\mathit{s}}_5\right)$	$\mathit{N}{\mathit{S}}^{\mathit{k}}\left({\mathit{s}}_6\right)$
$e_1$	0	0.100	0.343	0.500	0.510	0.667	1
$e_2$	0	0.100	0.490	0.500	0.657	0.667	1
$e_3$	0	0.157	0.167	0.500	0.510	0.667	1
$e_4$	0	0.333	0.490	0.500	0.510	0.667	1
$e_5$	0	0.100	0.167	0.500	0.510	0.667	1

.

Then, the individual linguistic weight preferences are transformed into the individual fuzzy preference relation as follows.

$$\begin{array}{ll}{F}^1=\left(\begin{array}{cccc}0.500& 0.667& 0.500& 0.510\\ 0.333& 0.500& 1.000& 0.343\\ 0.500& 0.000& 0.500& 0.100\\ 0.490& 0.657& 0.900& 0.500\end{array}\right)& F^2=\left(\begin{array}{cccc}0.500& 0.657& 0.667& 0.657\\ 0.343& 0.500& 0.490& 0.657\\ 0.333& 0.510& 0.500& 0.500\\ 0.343& 0.343& 0.500& 0.500\end{array}\right)\\ F^3=\left(\begin{array}{cccc}0.500& 0.167& 0.157& 0.667\\ 0.833& 0.500& 0.510& 1.000\\ 0.843& 0.490& 0.500& 0.500\\ 0.333& 0.000& 0.500& 0.500\end{array}\right)& F^4=\left(\begin{array}{cccc}0.500& 0.500& 0.333& 0.490\\ 0.500& 0.500& 0.510& 0.667\\ 0.667& 0.490& 0.500& 1.000\\ 0.510& 0.333& 0.000& 0.500\end{array}\right)\\ F^5=\left(\begin{array}{cccc}0.500& 1.000& 0.510& 0.667\\ 0.000& 0.500& 0.100& 0.167\\ 0.490& 0.900& 0.500& 0.667\\ 0.333& 0.833& 0.333& 0.500\end{array}\right)& \end{array}$$

Here, the original consensus matrix $C{M}^0={\left(c{d}_{hk}^0\right)}_{m\times m}$ is calculated from Equation (6), the original CD value of each expert is obtained from Equation (7) (shown in column 2

Table 3. Consensus degrees of experts in each round of interaction.

	Original	1st Interaction	2nd Interaction	3rd Interaction	4th Interaction
$C{D}^1$	0	0.100	0.343	0.500	0.510
$C{D}^2$	0	0.100	0.490	0.500	0.657
$C{D}^3$	0	0.157	0.167	0.500	0.510
$C{D}^4$	0	0.333	0.490	0.500	0.510
$C{D}^5$	0	0.100	0.167	0.500	0.510

), which requires the application of an interactive group decision making to reach consensus as a result of all CD are below the predefined consensus threshold value. The minimum of all elements in $C{M}^0$ is $c{d}_{35}=0.568$, therefore, the interactive consensus feedback optimization model is applied to expert $e_3$ and $e_5$. Harmony thresholds of these experts are obtained as: ${\gamma }^3=0.921$ and ${\gamma }^5=0.918$ by Equation (10) (see column 3

Table 4. Related indicators in each round of negotiation.

Negotiation Round	Expert	Harmony Threshold	Interaction Parameter
1st negotiation	$e_3$	0.921	0.181
	$e_5$	0.918	0.191
2nd negotiation	$e_1$	0.926	0.194
	$e_3$	0.942	0.152
3rd negotiation	$e_1$	0.942	0.205
	$e_4$	0.949	0.182
4th negotiation	$e_3$	0.958	0.155
	$e_5$	0.946	0.199

). The optimum feedback parameters are generated as ${\delta }^3=0.181$ and ${\delta }^5=0.191$ (see column 4 Table 4) through Model (12) and this is 1 round of interaction. The 4 rounds of interaction need to be applied in the whole process, which is not repeated. The consensus status, harmony thresholds and interaction parameters of experts are incarnated in Table 3 and Table 4, respectively. When the consensus process is finished, the consensual weight evaluation of experts is generated after 4 round of interaction process, which are aggregated as follows.

$$F_{4^{th}}^c=\left(\begin{array}{cccc}0.500& 0.589& 0.428& 0.599\\ 0.411& 0.500& 0.519& 0.578\\ 0.572& 0.481& 0.500& 0.559\\ 0.401& 0.423& 0.441& 0.500\end{array}\right)$$

Then, the relative importance levels are calculated for star rating of cruise ships about basic indicators, service capacities, subjective star ratings from experts and from users/potential users, as following steps.

• Step 1: To calculate the mean of relative weight of each indicator:

$$w_j=\frac{1}{n-1}\cdot {\displaystyle \sum }_{i=1;i\ne j}^n{f}_{ij}^c$$

(24)

• Step 2: To normalize the mean of relative weight of each indicator:

$$W_j=\frac{w_{ij}}{{\sum }_{i=1}^n{w}_j}$$

(25)

Following the above two steps, the weight is obtained for star rating of cruise ships about basic indicators, service capacity, subjective star ratings from experts and from users/potential users: $W=\left(0.231,0.249,0.231,0.289\right)$.

4.2. Star Rating System of Indicators and Service Capacity

When evaluating cruise star ratings based on basic indicators, four secondary indicators, including tonnage, height, number of crew and full passengers’ number, are selected to measure the size of cruise ships. Since only when the size of a cruise ship reaches a certain level, it can be equipped with facilities and services to achieve some star rating. The data is sourced from the official website of ZYOULUN, which is shown as

Table 5. The basic indicators of cruise ships.

Cruise Ship	Tonnage	Height	Number of Crew	Full Passenger Number
Costa Magica	105,000	13	1027	3470
Quantum of The Seas	168,666	18	1500	4905
Britannia	143,370	17	1389	4324
Seabourn Odyssey	32,346	11	225	450
Crystal Serenity	68,870	13	655	1070
Majestic Princess	143,000	19	1350	3560
Silver Spirit	36,000	11	376	540
Queen Mary 2	148,528	13	2054	2594
Seven Seas Explorer	54,000	10	542	750

. On the other hand, we analyze the service capabilities of cruise ships from two aspects: accommodation conditions and service facilities, respectively. The evaluation indicators of accommodation conditions include cabins’ number, cabins’ category, cabins’ type and maximum cabin area, where there may be multiple cabin types in one cabins’ category, such as, there are seven different types of rooms located on different floors in Deluxe Stateroom with Verandah for Crystal Serenity. The accommodation conditions of nine cruise ships are described as

Table 6. The accommodation condition of cruise ships.

Cruise Ship	Cabins Number	Cabins Category	Cabins Type	Maximum Cabin Area
Costa Magica	1358	8	11	48.2
Quantum of The Seas	2094	21	68	203
Britannia	1819	5	34	31
Seabourn Odyssey	225	9	15	110
Crystal Serenity	535	5	13	121
Majestic Princess	1780	8	41	63.4
Silver Spirit	270	6	12	137
Queen Mary 2	1296	13	30	151
Seven Seas Explorer	810	10	16	281.1

, whose data is from the official website of ZYOULUN. The evaluation indicators of service facilities include the number of restaurants, shopping malls, entertainment center, bar, children care and other services, listed in

Table 7. The service facilities of cruise ships.

Cruise Ship	Restaurant	Shopping	Service	Entertainment	Bar	Children
Costa Magica	4	2	2	20	4	3
Quantum of The Seas	19	2	7	13	0	3
Britannia	12	1	3	5	4	0
Seabourn Odyssey	4	1	5	6	1	0
Crystal Serenity	10	7	3	18	8	2
Majestic Princess	10	1	9	20	0	3
Silver Spirit	7	0	2	5	2	0
Queen Mary 2	7	1	6	7	6	1
Seven Seas Explorer	8	0	5	7	3	0

, whose data is from the official website of ZYOULUN. According to the modified TOPSIS presented in Section 3.4, the evaluation results of basic indicators and service capacity are reflected in

Table 8. The evaluation results and rankings of basic indicators and service capacity for cruise ships.

Cruise Ship	Basic Indicators		Service Capacity
	Scores	Star Rating	Scores	Star Rating
Costa Magica	0.53484	3	0.38746	3
Quantum of The Seas	0.82695	6	0.58834	5
Britannia	0.75079	6	0.32646	3
Seabourn Odyssey	0.02598	1	0.21796	2
Crystal Serenity	0.22065	2	0.54297	4
Majestic Princess	0.69972	5	0.45509	4
Silver Spirit	0.05895	1	0.17193	2
Queen Mary 2	0.69175	5	0.42163	3
Seven Seas Explorer	0.13382	1	0.34265	3

(including scores and star rating).

4.3. A Star Rating System from Experts and Users

This article collects star ratings of experts on cruise ships through face-to-face interviews, the experts interviewed included five experts in the field of tourism management and in online travel company. In turn, the results of the interviews are brought into DLSRF for use in calculations. The evaluation results of individual experts are shown in Appendix A and the aggregated evaluation by Equation (14) results are shown in

Table 9. Aggregated cruise star rating results from five experts.

Cruise Ship	1-Star	2-Star	3-Star	4-Star	5-Star	6-Star	7-Star
Costa Magica	0	0	0.48	0.38	0.14	0	0
Quantum of The Seas	0	0	0	0	0.4	0.44	0.16
Britannia	0	0.02	0.24	0.22	0.36	0.16	0
Seabourn Odyssey	0.16	0.48	0.36	0	0	0	0
Crystal Serenity	0	0.14	0.56	0.28	0.02	0	0
Majestic Princess	0.02	0.06	0.36	0.38	0.14	0.04	0
Silver Spirit	0.14	0.24	0.4	0.22	0	0	0
Queen Mary 2	0	0	0.12	0.44	0.36	0.08	0
Seven Seas Explorer	0.02	0.32	0.42	0.24	0	0	0

. The total evaluation score for each cruise ship is calculated according to Equation (15) and the final cruise star rating results provided by experts are obtained according to the rounding principle and the above results, which shown as

Table 10. Scores and staring rating results of nine cruise ships from experts and users.

Cruise Ship	Experts		Users
	Scores	Star Rating	Scores	Star Rating
Costa Magica	3.66	4	6.38	6
Quantum of The Seas	5.76	6	5.29	5
Britannia	4.4	4	3.77	4
Seabourn Odyssey	2.2	2	3.37	3
Crystal Serenity	3.18	3	3.64	4
Majestic Princess	3.68	4	3.84	4
Silver Spirit	2.7	3	4.01	4
Queen Mary 2	4.4	4	3.95	4
Seven Seas Explorer	2.88	3	3.02	3

. Similarly, 15 users with cruise experience are invited to participate in interviews to evaluate the star rating of the nine cruise ships. In order to guarantee the validity of the interviews, 15 users were divided into three groups to conduct interviews led by researchers to obtain the final individual user evaluations, as Appendix B and the aggregated evaluation of 15 users by Equation (14) results are shown in

Table 11. Aggregated cruise star rating results from 15 users.

Cruise Ship	1-Star	2-Star	3-Star	4-Star	5-Star	6-Star	7-Star
Costa Magica	0.00	0.00	0.00	0.00	0.10	0.42	0.48
Quantum of The Seas	0.00	0.00	0.00	0.16	0.43	0.36	0.05
Britannia	0.00	0.08	0.31	0.43	0.16	0.03	0.00
Seabourn Odyssey	0.01	0.18	0.35	0.36	0.10	0.00	0.00
Crystal Serenity	0.00	0.04	0.40	0.44	0.12	0.00	0.00
Majestic Princess	0.03	0.10	0.24	0.34	0.23	0.07	0.00
Silver Spirit	0.00	0.12	0.21	0.30	0.29	0.08	0.00
Queen Mary 2	0.00	0.05	0.29	0.42	0.20	0.05	0.00
Seven Seas Explorer	0.06	0.21	0.43	0.25	0.05	0.00	0.00

. The total evaluation score and star rating results from users for each cruise ship is obtained based on Equation (15), reflected as Table 10.

4.4. Comprehensive Star Rating Results

According to the framework proposed in this paper, the comprehensive star rating results of nine cruise ships are calculated based on the weighted average of four indicators, including basic indicators, service capacity, the evaluation of experts and users, shown as

Table 12. The comprehensive star rating results of ten cruise ships.

Cruise Ship	Star Rating
	Basic Indicators	Service Capacity	Experts Evaluations	Users Evaluations	Comprehensive Scores	Star Rating
Weight	0.231	0.249	0.231	0.289	-	-
Costa Magica	3	3	4	6	4.099	4
Quantum of The Seas	6	5	6	5	5.462	5
Britannia	6	3	4	4	4.213	4
Seabourn Odyssey	1	2	2	3	2.059	2
Crystal Serenity	2	4	3	4	3.308	3
Majestic Princess	5	4	4	4	4.231	4
Silver Spirit	1	2	3	4	2.579	3
Queen Mary 2	5	3	4	4	3.982	4
Seven Seas Explorer	1	3	3	3	2.539	3

, where the weights and scores of four indicators have been introduced before.

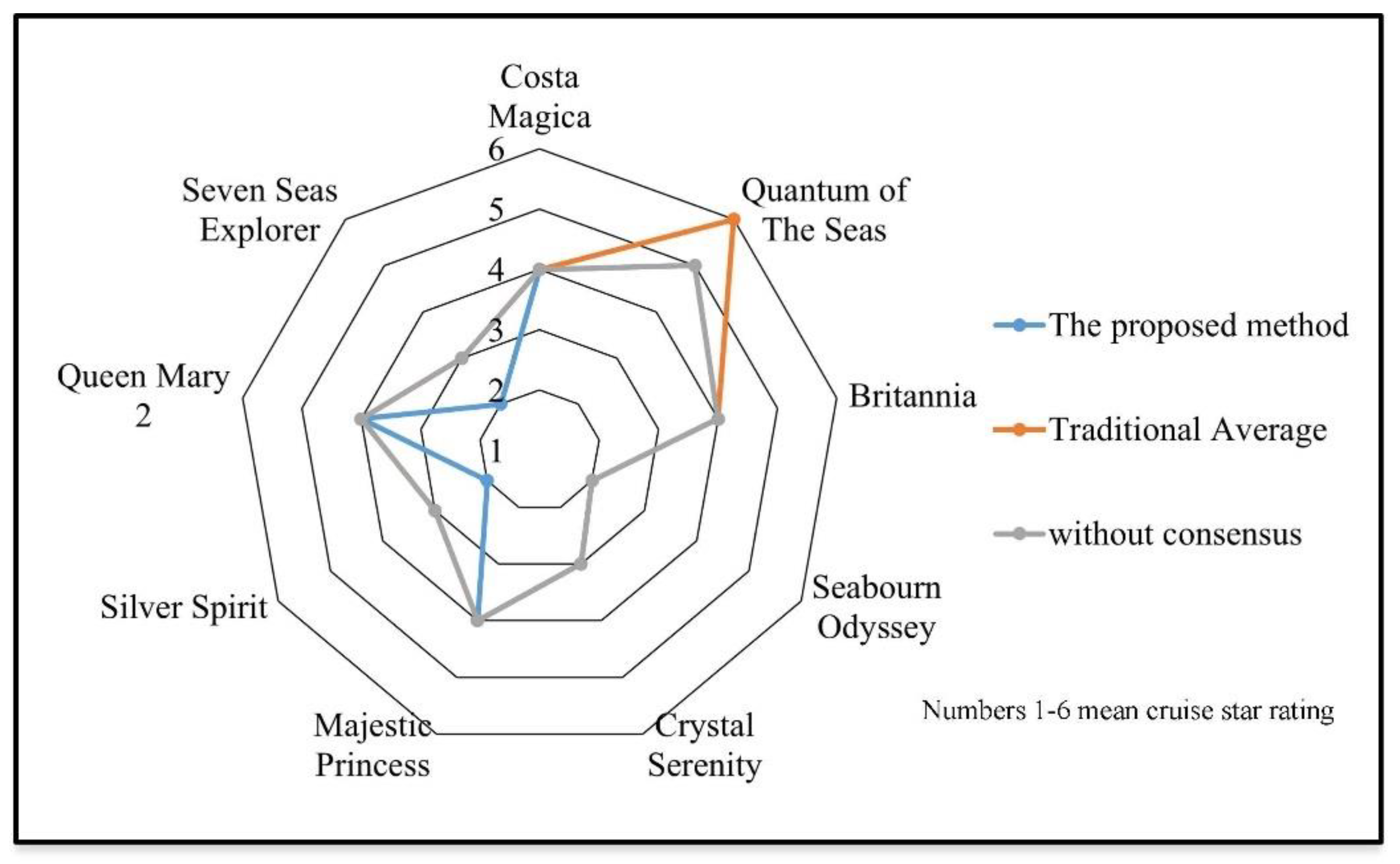
5. Discussion and Comparison Analysis

In order to verify the effectiveness of the proposed method, the correlation of the star ratings among the four indicators involving ${\mathrm{BI}}_i$ (basic indicators), ${\mathrm{SC}}_i$ (service capacity), ${\mathrm{EE}}_i$ (experts’ evaluations), ${\mathrm{UE}}_i$ (users evaluations) ($i=1,2,\dots ,10$) is analyzed based on Equation (24) as an example of the correlation between basic indicators and service capacity. And the results of correlation of the star ratings among the four indicators are shown as

Table 13. The correlation of the star ratings among the four indicators for nine cruises.

Cruise Ship	Basic Indicators	Service Capacity	Experts Evaluations	Users Evaluations
Basic Indicators	-	0.84	0.86	0.79
Service Capacity	0.84	-	0.93	0.90
Experts Evaluations	0.86	0.93	-	0.93
Users Evaluations	0.79	0.90	0.93	-

.

On the one hand, compared with the basic indicators of cruise ships, experts and users attach great importance to the service capabilities of cruise ships, because both expert ratings and user ratings have a high correlation with the service capabilities of cruise ships. However, compared with the fact that users ignore the basic indicators of cruise ships, experts seem to be more concerned about this factor, because they know that the basic indicators of cruise ships often determine service capabilities. For example, when there is not enough space on the cruise ship or there are not enough service personnel, it is impossible to provide high-quality service, which can also be confirmed by the high correlation between service capabilities and basic indicators. In addition, there is a strong correlation between user evaluations and expert evaluations, which can reflect the validity of our data and interviews.

On the other hand, a comparison analysis is presented to verify the effect of interactive group consensus process and PIS linguistic model on cruise star rating. It measures the generated weight and cruise star rating results under the condition of average weight and no consensus mechanism, respectively. The comparison results are shown in

Table 14. Indicator weights analysis under different mechanisms.

Cruise Ship	Basic Indicators	Service Capacity	Experts Evaluations	Users Evaluations
Traditional Average	0.250	0.250	0.250	0.250
Without Consensus	0.228	0.252	0.234	0.286
The proposed method	0.231	0.249	0.231	0.289

and Figure 3, which finds that weights obtained based on expert evaluations tend to assign more weights to the fourth primary indicator, users’ evaluations to cruise ships. When the consensus among experts assigning weights is not reached, the second primary indicator, service capacity of cruise ships, is also assigned more weight, while the more weight is transferred into the fourth primary indicator, users’ evaluations to cruise ships, after reaching consensus. Furthermore, the cruise star rating results by different methods are relatively stable based on Figure 3.

In addition, from Figure 3, the final star rating results of cruise ships by the proposed method are not very high than the traditional average method, most cruise ships are distributed on three-star and four-star, and very few cruise ships are rated as five-star, which also shows that the current luxury cruise ships still have room for improvement. Service capacity has more influence than basic indicators and users’ evaluations are more important than expert evaluations based on the analysis of weights. Thus, it is crucial to focus on improving the service capability and user satisfaction of cruise ships. But how to improve the above issue? we make the following recommendations from four aspects including accommodation, restaurant, entertainment and business based on the interviews.

• Firstly, it is best to develop more cabins categories by creating a theme, which can be achieved by purchasing intellectual property, such as, intellectual property in games and movies. Simultaneously, different types of cabins need to be developed in the same theme cabin category, such as whether there is a balcony, the size of the window, etc., to meet the needs of different levels of users. Furthermore, the maximum room size for some cruise ships is too small and it need to be refurbished to meet the demands of business events, such as business dinners and meetings.
• Secondly, it is necessary to have a well-known chef in charge for restaurants, which can increase the attractiveness to users. On the other hand, a good restaurant environment can not only improve user satisfaction, but also develop additional value beyond dining, for instance regularly inviting well-known bands to perform and displaying some high-value artworks. More importantly, keeping ingredients fresh is a huge challenge for restaurants on cruise ships, where users did say that the food quality on some cruise ships was not good enough in our interviews. Therefore, it is important for cruise ships to introduce some technology to ensure the freshness of ingredients.
• Thirdly, most of the cruise ships are doing relatively well in terms of entertainment facilities, each with its own characteristics, such as, Queen Mary 2 is the only cruise ship with its own planetarium, where visitors can experience a visual tour of space, watch the star or take an astronomy class. With new content every day, the planetarium can also be used as a cinema, lecture hall, or even a studio when needed. However, most cruise ships are also still lacking in entertainment. More ideas and games can be introduced beyond traditional casinos, bars and shows to in order to cater to the interests of the new consumer groups of cruise ships, such as, board role-playing games including murder mystery game, werewolves of Miller’s Hollow, which are popular recently. In addition, a library with a comfortable environment and a view of the sea is also necessary.
• Finally, in order to enhance satisfaction of users and improve humanized service, some necessary facilities for business activities need to be added, such as negotiations, meetings and team building and some necessary medical services need to be provided, such as trauma and seasickness treatment. More attention is needed that the basic indicators of the ships must be considered comprehensively when the ship is built, and the overall layout should take the type and quantity of services into account to build a high-star cruise ship.

6. Conclusions and Future Work

A star rating approach for cruise shipping by the combination the modified TOPSIS and interactive group decision making under PIS model. The main advantages for the proposed star rating approach are summarized as follows:

• Firstly, it has established a novel cruise star rating indicators system, that integrates subjective and objective evaluations, including four parts: (1) basic indicators of cruise ships, (2) service capacity of the cruise ship, (3) star rating from experts and (4) star rating provided by users/potential users, where the modified TOPSIS is adopted in subjective evaluation to obtain the star rating of cruise ships based on basic indicators and service capacity. Furthermore, DLSRF is defined in objective evaluation to help experts and users express the star rating of cruise ships.
• Secondly, it proposes a novel weight calculation method based on the weighted opinions from experts. Usually, it is difficult for experts to provide the value weights directly, so 2-tuple linguistic is adopted to obtain experts’ weight preferences. Simultaneously, PIS model is introduced to address the problem that the same term has different meanings for different experts. In addition, an interactive group decision making is presented to manage the weight preferences from experts for avoiding the conflicts among experts.
• Thirdly, it provides a complete cruise star rating system, which, in managerial insight, facilitates the development of industry standards and improves standardized management level of cruise companies in the digital and intelligent age. Furthermore, not only the validity of the proposed method is verified and discussed, but also some suggestions from four perspectives, including accommodations, restaurants, entertainment and humanized services, are also recommended to improve the service capability of cruise ships.

However, there are still two shortcomings in this article: one is users who participated in the interview are mainly concentrated in one city with similarities in income and consumption preferences, another is the method proposed in this article involves both subjective data and objective data, which is difficult to obtain, and calculation method is more complicated. In the future, we will further simplify the computational complexity of star ratings, online review information will be used to finish the star rating of cruise ships and the effect of social network among experts and users will be explored [48]. In addition, it lacks an effective verification mechanism for the same types of objective data, and similarity confirmation method will be discussed in the future by learn from [49].