Dose Rate Assessment Exercises with Stylized Phantom of Neon Flying Squid from Northwest Pacific
Abstract
:1. Introduction
2. Materials and Methods
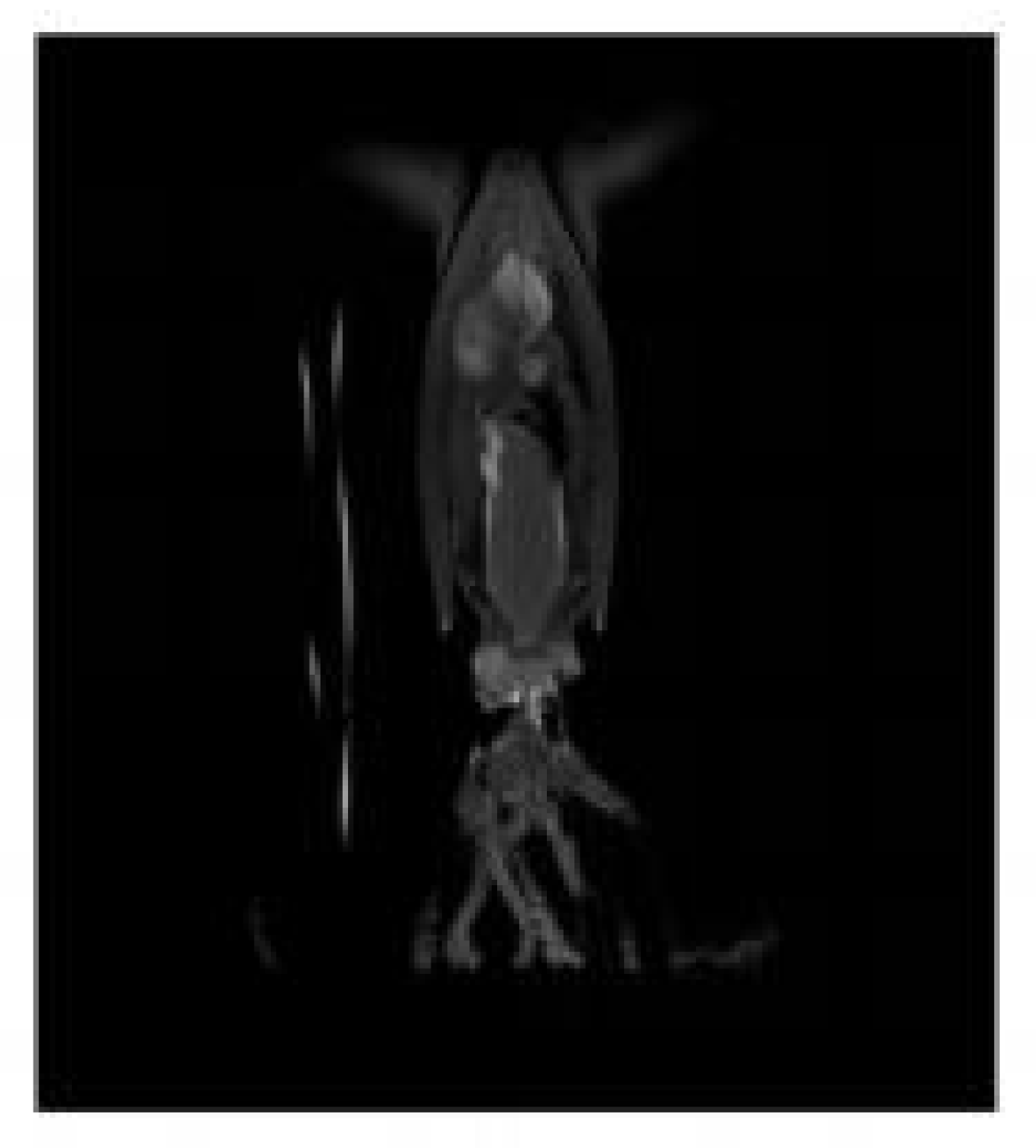
2.1. Scanning and Segmentation of the Sample
2.2. Stylized Phantom Establishment
2.3. Source Term
2.4. Dose Conversion Coefficient Simulation
2.5. Radiological Dose Assessment
3. Result and Discussion
3.1. Dose Conversion Coefficient of Individual Organs Obtained with Geant4
3.2. Comparison of DCCs Obtained with Geant4 and the ERICA Tool
3.3. Dose Rate for the Squid Sample in the FDNPP Accident Scenario
4. Conclusions and Prospect
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ICRP. Recommendations of the international commission on radiological protection. Ann. ICRP 1977, 1, 1–53. [Google Scholar]
- ICRP. A framework for assessing the impact of ionizing radiation on non-human species. Ann. ICRP 2003, 33, 1–6. [Google Scholar]
- ICRP. The 2007 recommendations of the international commission on radiological protection. Ann. ICRP 2007, 37, 2–4. [Google Scholar]
- ICRP. Environmental Protection: The Concept and Use of Reference Animals and Plants. Ann. ICRP 2008, 38, 4–6. [Google Scholar]
- Clement, C.H.; Strand, P.; Beresford, N.; Copplestone, D.; Godoy, J.; Jianguo, L.; Saxén, R.; Yankovich, T.; Brown, J. Environmental protection: Transfer parameters for reference animals and plants. Ann. ICRP 2009, 39, 6. [Google Scholar] [CrossRef]
- ICRP. Dose coefficients for non-human biota environmentally exposed to radiation. Ann. ICRP 2017, 46, 1–136. [Google Scholar] [CrossRef]
- Montgomery, D.A.; Martinez, N.E. Dosimetric modeling of Tc-99, Cs-137, Np-237, and U-238 in the grass species Andropogon Virginicus: Development and comparison of stylized, voxel, and hybrid phantom geometry. J. Environ. Radioact. 2020, 211, 106075. [Google Scholar] [CrossRef]
- Williams, C. Framework for assessment of environmental impact (FASSET) of ionising radiation in European ecosystems. J. Radiol. Prot. 2004, 24, A1–A12. [Google Scholar]
- Brown, J.E.; Alfonso, B.; Avila, R.; Beresford, N.A.; Copplestone, D.; Proehl, G.; Ulanovsky, A. The ERICA Tool. J. Environ. Radioact. 2008, 99, 1371–1383. [Google Scholar] [CrossRef] [Green Version]
- Pappa, K.F.; Tsabaris, C.; Ioannidou, A.; Patiris, L.D.; Kaberi, H. Radioactivity and metal concentrations in marine sediments associated with mining activities in Ierissos Gulf, North Aegean Sea, Greece. Appl. Radiat. Isot. 2016, 116, 22–33. [Google Scholar] [CrossRef]
- Pappa, K.F.; Tsabaris, C.; Patiris, L.D.; Androulakaki, E.G.; Vlastou, R. Historical trends and assessment of radionuclides and heavy metals in sediments near an abandoned mine, Lavrio, Greece. Environ. Sci. Pollut. Res. 2018, 25, 30084–30100. [Google Scholar] [CrossRef] [PubMed]
- Johansen, M.; Beresford, N.A.; Howard, B.; Hinton, T.; Bollhoefer, A.; Doering, C.; Twining, J. Recent developments in the modelling of radionuclide uptake, radiation dose and effects in wildlife. In Proceedings of the 13th South Pacific Environmental Radioactivity Association Conference (SPERA 2014), Darwin, Australia, 1–5 September 2014. [Google Scholar]
- ICRP. Protection of the environment under different exposure situations. ICRP Publication 124. Ann. ICRP 2014, 43, 2. [Google Scholar]
- Zaidi, H.; Tsui, B. Review of Computational Anthropomorphic Anatomical and Physiological Models. Proc. IEEE. 2009, 97, 1938–1953. [Google Scholar] [CrossRef]
- Martinez, N.E. Review of current methods in internal dosimetry of non-human biota. In Proceedings of the 15th International High-level Radioactive Waste Management Conference, Charleston, SC, USA, 12–16 April 2015. [Google Scholar]
- Xie, T.; Zaidi, H. Development of computational small animal models and their applications in preclinical imaging and therapy research. Med. Phys. 2016, 43, 111–131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zaidi, H. Computational Anatomical Animal Models; IOP Publishing: Bristol, UK, 2018; pp. 2053–2563. [Google Scholar]
- Martinez, N.E.; Johnson, T.E.; Capello, K.; Prinder, J.E. Development and comparison of computational models for estimation of absorbed organ radiation dose in rainbow trout (oncorhynchus mykiss) from uptake of iodine-131. J. Environ. Radioact. 2014, 138, 50–59. [Google Scholar] [CrossRef] [PubMed]
- Caffrey, E.A.; Higley, K.A. Creation of a voxel phantom of the ICRP reference crab. J. Environ. Radioact. 2013, 120, 14–18. [Google Scholar] [CrossRef]
- Caffrey, E.A.; Johansen, M.P.; Higley, K.A. Voxel modeling of rabbits for use in radiological dose rate calculations. J. Environ. Radioact. 2015, 151, 480–486. [Google Scholar] [CrossRef]
- Kinase, S. Voxel-based frog phantom for internal dose evaluation. J. Nucl. Sci. Technol. 2008, 45, 1049–1052. [Google Scholar] [CrossRef]
- Segars, W.P.; Tsui, B.M.W.; Frey, E.C.; Johnson, G.A.; Berr, S.S. Development of a 4-D digital mouse phantom for molecular imaging research. Mol. Imaging Biol. 2004, 6, 149–159. [Google Scholar] [CrossRef]
- Stabin, M.G.; Kost, S.D.; Segars, W.P.; Guilmette, R.A. Two realistic beagle models for dose assessment. Health Phys. 2015, 109, 198–204. [Google Scholar] [CrossRef]
- Martinez, N.E.; Johnson, T.E.; Pinder, J.E. Application of computational models to estimate organ radiation dose in rainbow trout from uptake of molybdenum-99 with comparison to iodine-131. J. Environ. Radioact. 2016, 151, 468–479. [Google Scholar] [CrossRef] [PubMed]
- Bustamante, P.; Teyssie, J.L.; Danis, B.; Fowler, S.W.; Miramand, P.; Coeret, O.; Warnau, M. Uptake, transfer and distribution of silver and cobalt in tissues of the common cuttlefish sepia officinalis at different stages of its life cycle. Mar. Ecol. Prog. 2004, 269, 185–195. [Google Scholar] [CrossRef]
- Miramand, P.; Bentley, B. Concentration and distribution of heavy metals in tissues of two cephalopods, eledone cirrhosa and sepia officinalis, from the french coast of the english channel. Mar. Biol. 1992, 114, 407–414. [Google Scholar] [CrossRef]
- Cannon, M.E.; Carpenter, S.L.; Elta, G.H.; Nostrant, T.T.; Scheiman, J.M. Eus compared with ct, magnetic resonance imaging, and angiography and the influence of biliary stenting on staging accuracy of ampullary neoplasms. Gastrointest. Endosc. 1999, 50, 27–33. [Google Scholar] [CrossRef]
- Koch, K.; Oellig, F.; Oberholzer, K.; Bender, P.; Kunz, P.; Mildenberger, P.; Hake, U.; Kreiter, K.F.; Thelen, M. Assessment of right ventricular function by 16-detector-row ct: Comparison with magnetic resonance imaging. Eur. Radiol. 2005, 15, 312–347. [Google Scholar] [CrossRef]
- Trefethen, L.N. Spectral Methods in MATLAB; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Ecabert, O.; Peters, J.; Weese, J. Modeling shape variability for full heart segmentation in cardiac computed-tomography images. Proc. SPIE Int. Soc. Opt. Eng. 2006, 6144, 1199–1210. [Google Scholar]
- Wenqiao, T. Development of a fish heterogeneous phantom for estimation of radiation dose rates. China Nucl. Sci. Technol. Rep. 1999, 1, 551–569. [Google Scholar]
- Jian, S.; Wen, Y.; Zhi, Z.; Hao, M.; Chen, L.; Cheng, J. Monte carlo calculation of artificial radionuclide radiation dose rates for marine species in the western pacific. Radiat. Prot. Dosim. 2013, 158, 479–486. [Google Scholar]
- Sefl, M. Geant4 simulation toolkit. Nucl. Instrum. Methods Phys. Res. 2012, 506, 250–303. [Google Scholar]
- Jianguo, L. A Manual of Radioecology Transfer Parameters; Atomic Energy Press: Beijing, China, 2006. [Google Scholar]
- Barendsen, G.W. Dose fractionation, dose rate and iso-effect relationships for normal tissue responses. Int. J. Radiat. Oncol. 1982, 8, 1981–1997. [Google Scholar] [CrossRef]
- IAEA. Effects of Ionizing Radiation on Plants and Animals at Levels Implied by Current Radiation Protection Standards; International Atomic Energy Agency: Vienna, Austria, 1992.
- Xiaoping, B. Study of ERICA Code Application in Radiological Impact Assessment of Terres- trial Biota Near Nuclear Power Plant. Radiat. Prot. Bull. 2012, 3, 4–9. [Google Scholar]
- Groen, R.S. Health effects due to radiation from the chernobyl accident. annex d of unscear 2008: Sources and effects of ionizing radiation. Volume 2: Effects. Arch. Neurol. 2011, 52, 373–378. [Google Scholar]

| Organs | Elements (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| C | H | O | N | Ca | Na | Mg | P | S | Cl | K | |
| Carcass | 14.3 | 10.2 | 71.0 | 3.4 | − | 0.1 | − | 0.2 | 0.3 | 0.1 | 0.4 |
| Foot | 14.3 | 10.2 | 71.0 | 3.4 | − | 0.1 | − | 0.2 | 0.3 | 0.1 | 0.4 |
| Head | 14.3 | 10.2 | 71.0 | 3.4 | − | 0.1 | − | 0.2 | 0.3 | 0.1 | 0.4 |
| Gladius | 15.2 | 3.0 | 41.8 | 2.5 | 21.0 | 3.5 | 0.2 | 10.3 | 0.3 | − | 2.2 |
| Ink-sac | 10.5 | 10.3 | 74.9 | 3.1 | − | 0.2 | − | 0.2 | 0.3 | 0.3 | 0.2 |
| Stomach | 12.1 | 10.3 | 73.4 | 3.2 | − | 0.1 | − | 0.2 | 0.2 | 0.3 | 0.2 |
| Liver | 13.2 | 10.2 | 72.4 | 3.0 | − | 0.2 | 0.3 | 0.2 | 0.2 | 0.2 | 0.1 |
| Gill | 10.5 | 10.3 | 74.9 | 3.1 | − | 0.2 | − | 0.2 | 0.3 | 0.3 | 0.2 |
| Glands | 10.1 | 9.1 | 69.0 | 11.0 | − | 0.2 | 0.1 | 0.2 | 0.1 | 0.1 | 0.1 |
| Gonad | 11.5 | 10.6 | 75.1 | 2.2 | − | 0.1 | − | 0.1 | 0.1 | 0.2 | 0.1 |
| Organs | Geometry | a1, b1, c1 | r1 | h, r2 | a2, b2, c2 | Density | Weight Coefficients |
|---|---|---|---|---|---|---|---|
| Carcass | ellipsoid | 13.4, 4.5, 3.5 | − | − | − | 1.020 | 0.699 |
| Foot | cylinder | − | − | 6.5, 1.8 | − | 1.025 | 0.053 |
| Head | cylinder | − | − | 6.0, 3.1 | − | 1.020 | 0.143 |
| Gladius | cuboid | − | − | − | 13.0, 3.0, 0.2 | 1.200 | 0.007 |
| Ink-sac | ellipsoid | 6.0, 1.2, 1.0 | − | − | − | 1.040 | 0.024 |
| Stomach | ellipsoid | 3.3, 1.4, 1.3 | − | − | − | 1.030 | 0.020 |
| Liver | ellipsoid | 4.7, 1.9, 1.0 | − | − | − | 1.030 | 0.030 |
| Gill | ellipsoid | 4.6, 1.3, 0.8 | − | − | − | 1.200 | 0.019 |
| Glands | sphere | − | 1.25 | − | − | 1.000 | 0.004 |
| Gonad | sphere | − | 0.62 | − | − | 1.000 | 0.001 |
| Element | H | O | Na | Cl | Mg | S | Ca | K |
|---|---|---|---|---|---|---|---|---|
| Mass fraction | 10.756 | 86.045 | 1.056 | 1.851 | 0.126 | 0.087 | 0.040 | 0.039 |
| Density (g cm−3) | 1.025 | |||||||
| CF(L Kg−1) | 54Mn | 60Co | 65Zn | 95Zr | 110mAg | 131I | 134Cs | 137Cs |
|---|---|---|---|---|---|---|---|---|
| Cephalopods Mollusks | 3000 − | 300 − | 60,000 − | 50 − | − 60,000 | − 10 | 9 − | 9 − |
| Nuclides | DCCs × 10−4 (µGy Kg h−1 Bq−1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Carc | Foot | Head | Glad. | Ink-s. | Stom. | Liver | Gill | Glands | Gona. | |
| 137Cs | 2.67 | 1.66 | 2.25 | 1.82 | 1.89 | 1.68 | 1.92 | 1.80 | 1.88 | 2.03 |
| 110mAg | 2.99 | 1.89 | 2.45 | 1.96 | 2.01 | 1.83 | 2.06 | 1.97 | 2.04 | 1.97 |
| 60Co | 5.96 | 3.74 | 4.89 | 2.92 | 4.22 | 3.74 | 4.32 | 4.04 | 4.14 | 4.69 |
| 134Cs | 2.81 | 1.80 | 2.42 | 2.01 | 1.95 | 2.00 | 2.12 | 1.76 | 1.93 | 1.85 |
| 131I | 1.54 | 0.89 | 1.28 | 1.43 | 1.05 | 1.03 | 1.08 | 9.90 | 1.06 | 0.92 |
| 54Mn | 3.89 | 2.45 | 3.25 | 2.29 | 2.76 | 2.27 | 2.75 | 2.44 | 2.65 | 2.54 |
| 65Zn | 2.55 | 1.58 | 2.14 | 1.28 | 1.73 | 1.63 | 1.81 | 1.76 | 1.84 | 1.48 |
| 95Zr | 1.96 | 1.16 | 1.63 | 1.17 | 1.34 | 1.10 | 1.41 | 1.24 | 1.30 | 1.47 |
| Nuclides | DCCs × 10−4 (µGy Kg h−1 Bq−1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Carc | Foot | Head | Glad. | Ink-s. | Stom. | Liver | Gill | Glands | Gona. | |
| 137Cs | 3.74 | 3.06 | 3.62 | 2.53 | 3.37 | 3.16 | 3.40 | 3.20 | 3.43 | 2.97 |
| 110mAg | 1.21 | 0.88 | 1.08 | 0.83 | 0.95 | 0.9 | 0.96 | 0.92 | 0.96 | 0.88 |
| 60Co | 3.97 | 3.06 | 3.68 | 2.51 | 3.35 | 3.15 | 3.37 | 3.20 | 3.38 | 2.97 |
| 134Cs | 3.59 | 2.79 | 3.46 | 2.22 | 3.17 | 2.90 | 3.22 | 2.96 | 3.24 | 2.66 |
| 131I | 3.68 | 2.99 | 3.61 | 2.44 | 3.36 | 3.12 | 3.40 | 3.17 | 3.45 | 2.91 |
| 54Mn | 1.16 | 0.71 | 0.98 | 0.59 | 0.08 | 0.75 | 0.82 | 0.76 | 0.83 | 0.7 |
| 65Zn | 0.81 | 0.49 | 0.69 | 0.37 | 0.57 | 0.53 | 0.58 | 0.53 | 0.58 | 0.5 |
| 95Zr | 1.83 | 1.50 | 1.74 | 1.30 | 1.63 | 1.54 | 1.63 | 1.56 | 1.64 | 1.48 |
| Nuclides | DCCs × 10−4 (µGy Kg h−1 Bq−1) | |||||||
|---|---|---|---|---|---|---|---|---|
| 137Cs | 110mAg | 60 Co | 134Cs | 131I | 54Mn | 65Zn | 95Zr | |
| Ext-ERICA | 2.90 | 1.42 | 13.00 | 7.99 | 1.95 | 4.30 | 3.01 | 3.80 |
| Int-ERICA | 1.78 | 2.18 | 1.96 | 1.92 | 1.36 | 0.55 | 0.40 | 1.14 |
| Ext-Geant4 | 2.47 | 2.75 | 5.49 | 2.61 | 1.42 | 3.58 | 2.35 | 1.80 |
| Int-Geant4 | 3.64 | 1.14 | 3.80 | 3.47 | 3.59 | 1.05 | 0.75 | 1.77 |
| Nuclide | Max-Radio [14] | ERICA | This Study | Recommended-EC |
|---|---|---|---|---|
| Tool | ||||
| 134Cs | 6.70 × 104 | 1.70 × 102 | 2.39 × 102 ± 0.85 | − |
| 137Cs | 6.80 × 104 | 1.30 × 102 | 2.27 × 102 ± 0.85 | − |
| 131I | 1.80 × 105 | 2.81 × 102 | 6.71 × 102 ± 1.14 | 10 |
| Total | − | 5.81 × 102 | 1.14 × 103 ± 1.66 | − |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Yu, W.; He, J.; Zeng, Z. Dose Rate Assessment Exercises with Stylized Phantom of Neon Flying Squid from Northwest Pacific. J. Mar. Sci. Eng. 2022, 10, 782. https://doi.org/10.3390/jmse10060782
Li J, Yu W, He J, Zeng Z. Dose Rate Assessment Exercises with Stylized Phantom of Neon Flying Squid from Northwest Pacific. Journal of Marine Science and Engineering. 2022; 10(6):782. https://doi.org/10.3390/jmse10060782
Chicago/Turabian StyleLi, Jia, Wen Yu, Jianhua He, and Zhi Zeng. 2022. "Dose Rate Assessment Exercises with Stylized Phantom of Neon Flying Squid from Northwest Pacific" Journal of Marine Science and Engineering 10, no. 6: 782. https://doi.org/10.3390/jmse10060782
APA StyleLi, J., Yu, W., He, J., & Zeng, Z. (2022). Dose Rate Assessment Exercises with Stylized Phantom of Neon Flying Squid from Northwest Pacific. Journal of Marine Science and Engineering, 10(6), 782. https://doi.org/10.3390/jmse10060782





