The Influence of Bathymetry on Regional Marine Geoid Modeling in Northern Europe
Abstract
:1. Introduction
2. Methods
2.1. From Discrete Gravity Data to a Gridded Gravity Field Representation
2.2. Quasigeoid Determination
3. Study Area and Data
Validation Datasets
4. Gravity Field Estimation and Geoid Modeling
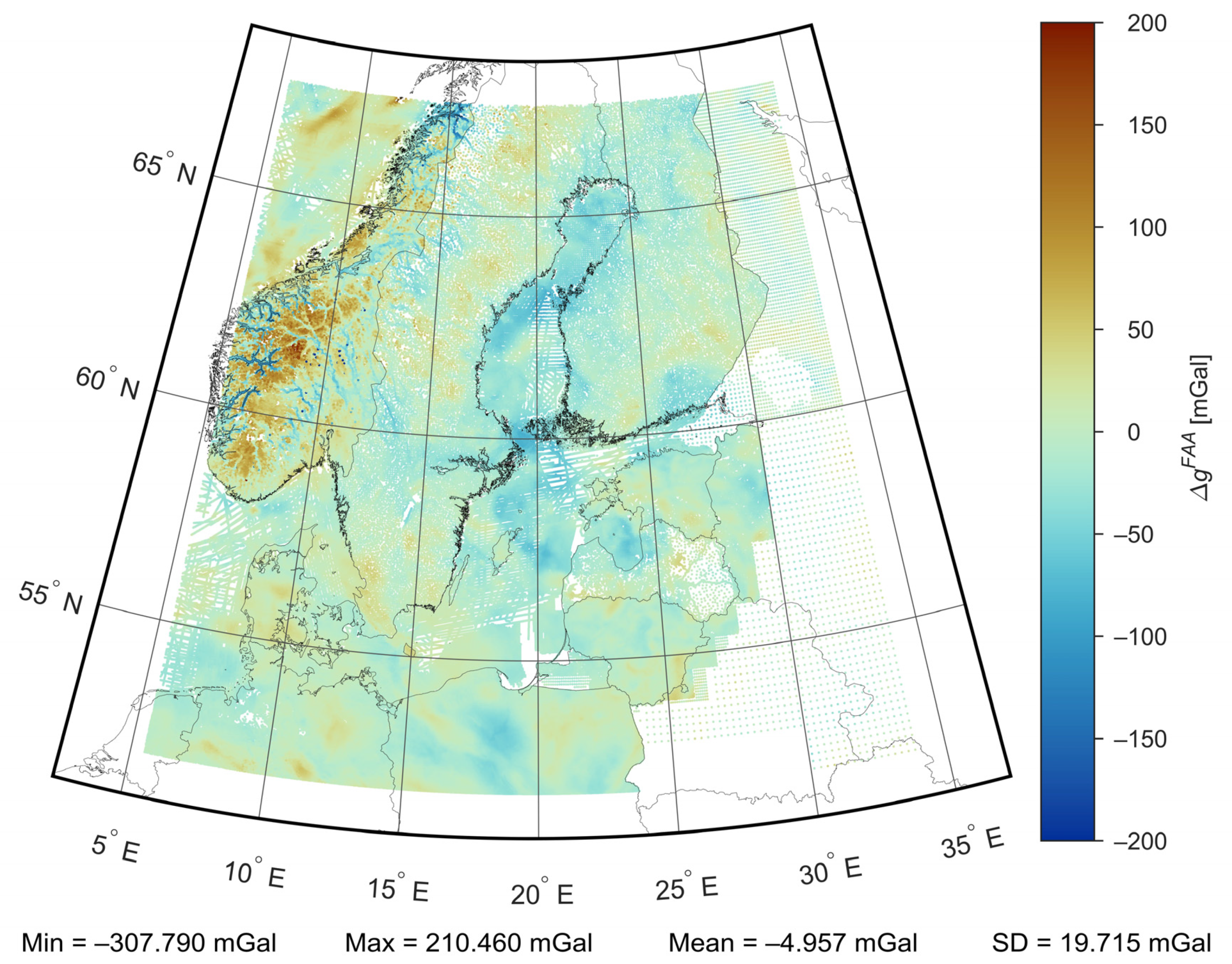
4.1. Preparation of Gravity Data
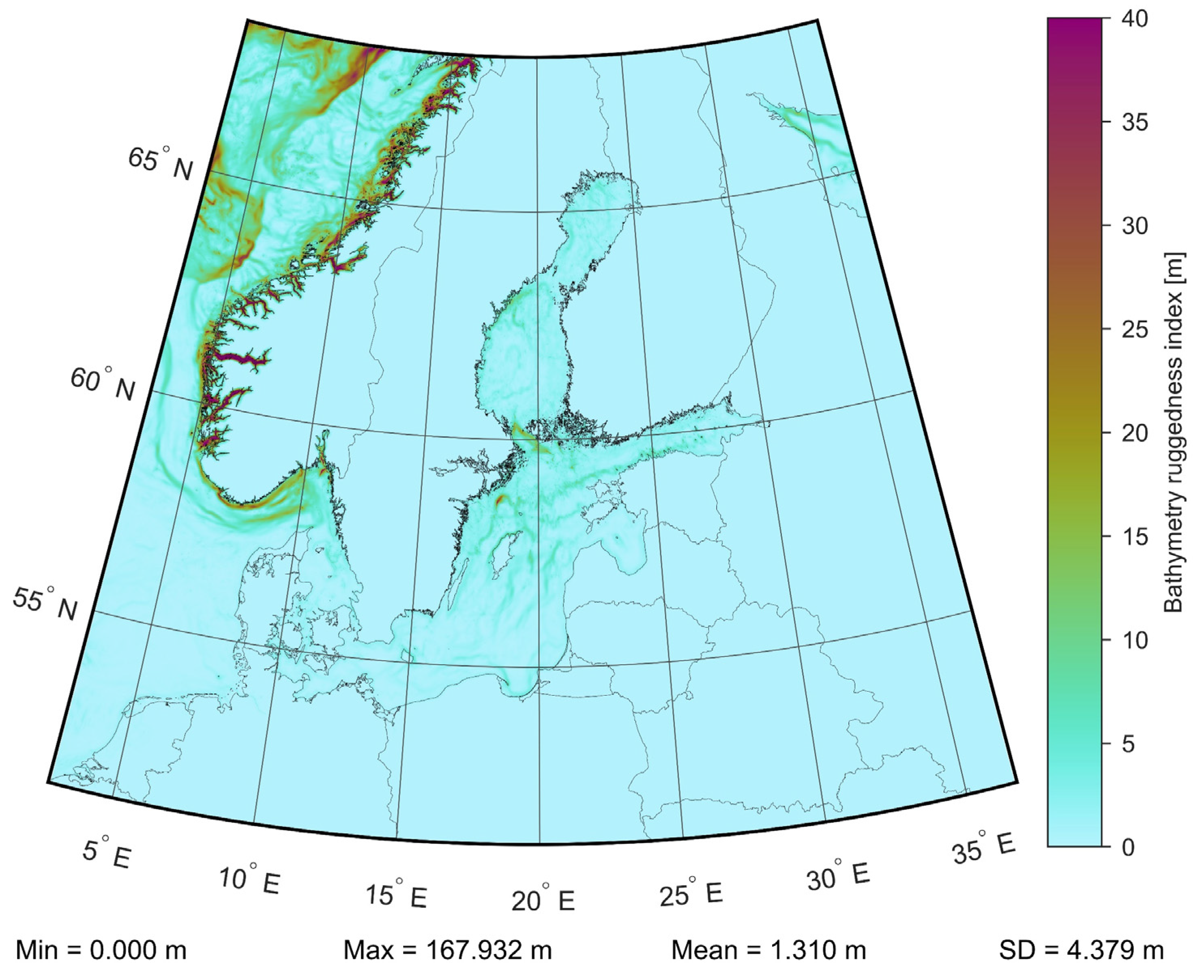
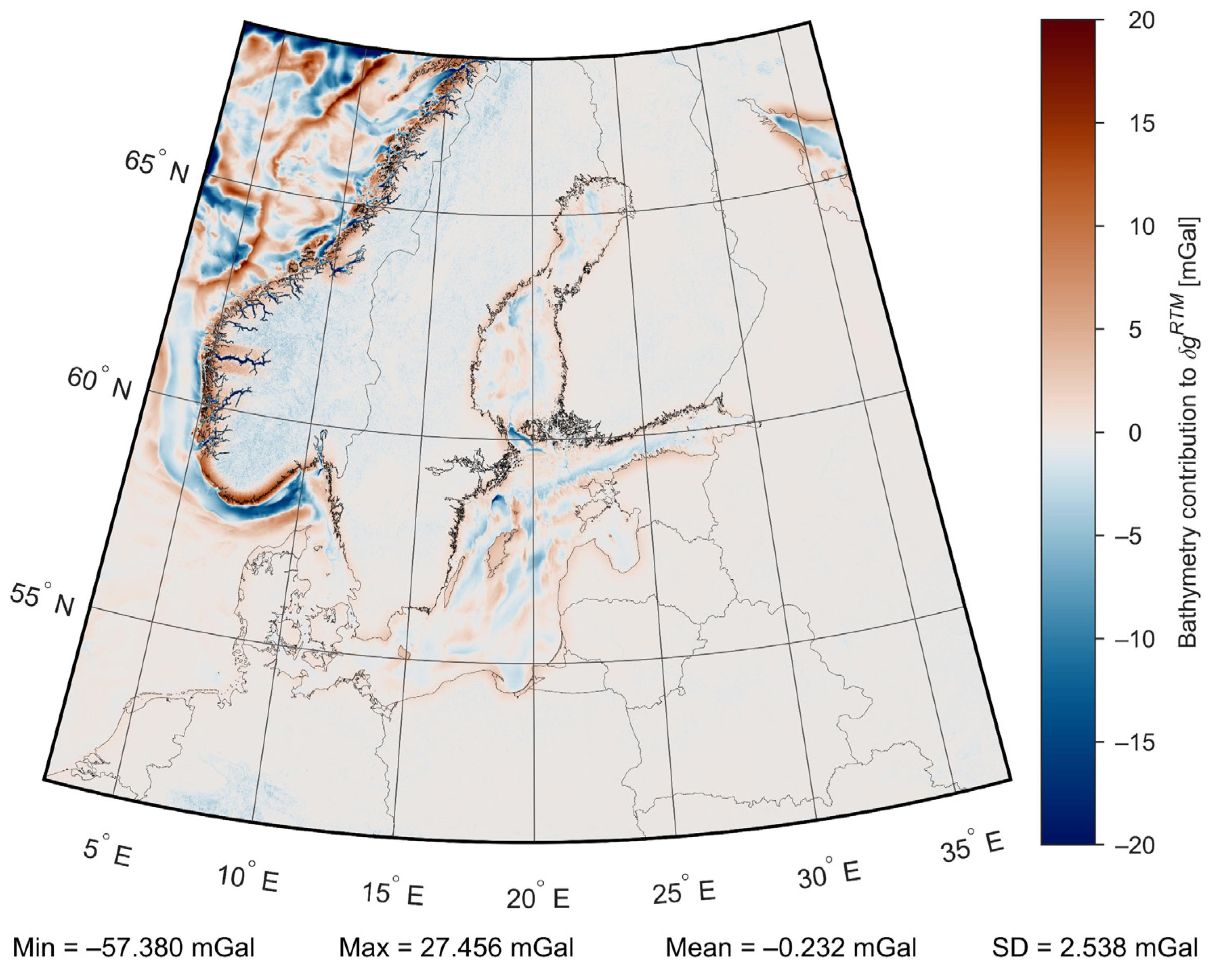
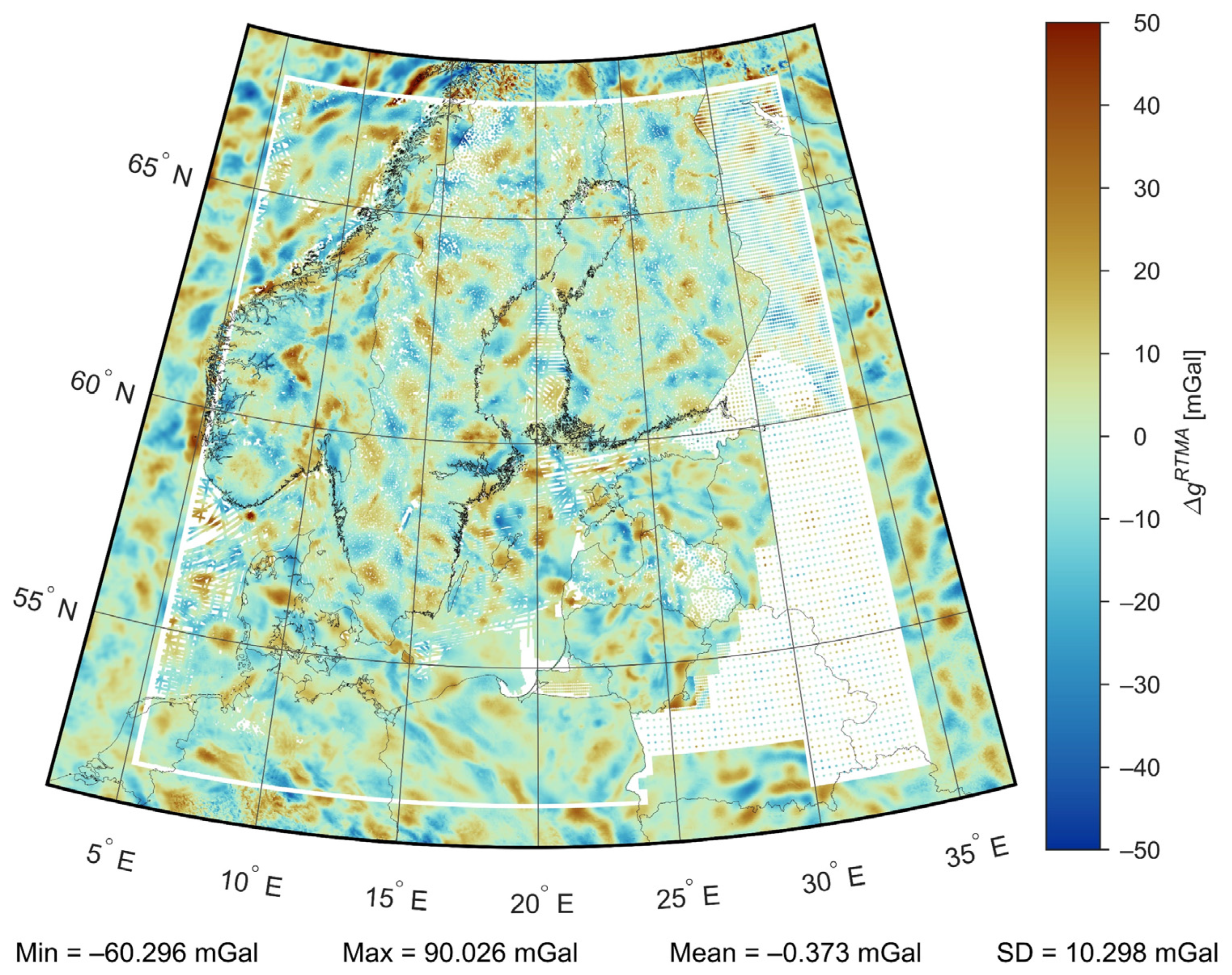
4.2. Determination of Residual Terrain Model Anomalies
4.3. Gravity Data Gridding
4.4. Results of Geoid Modeling
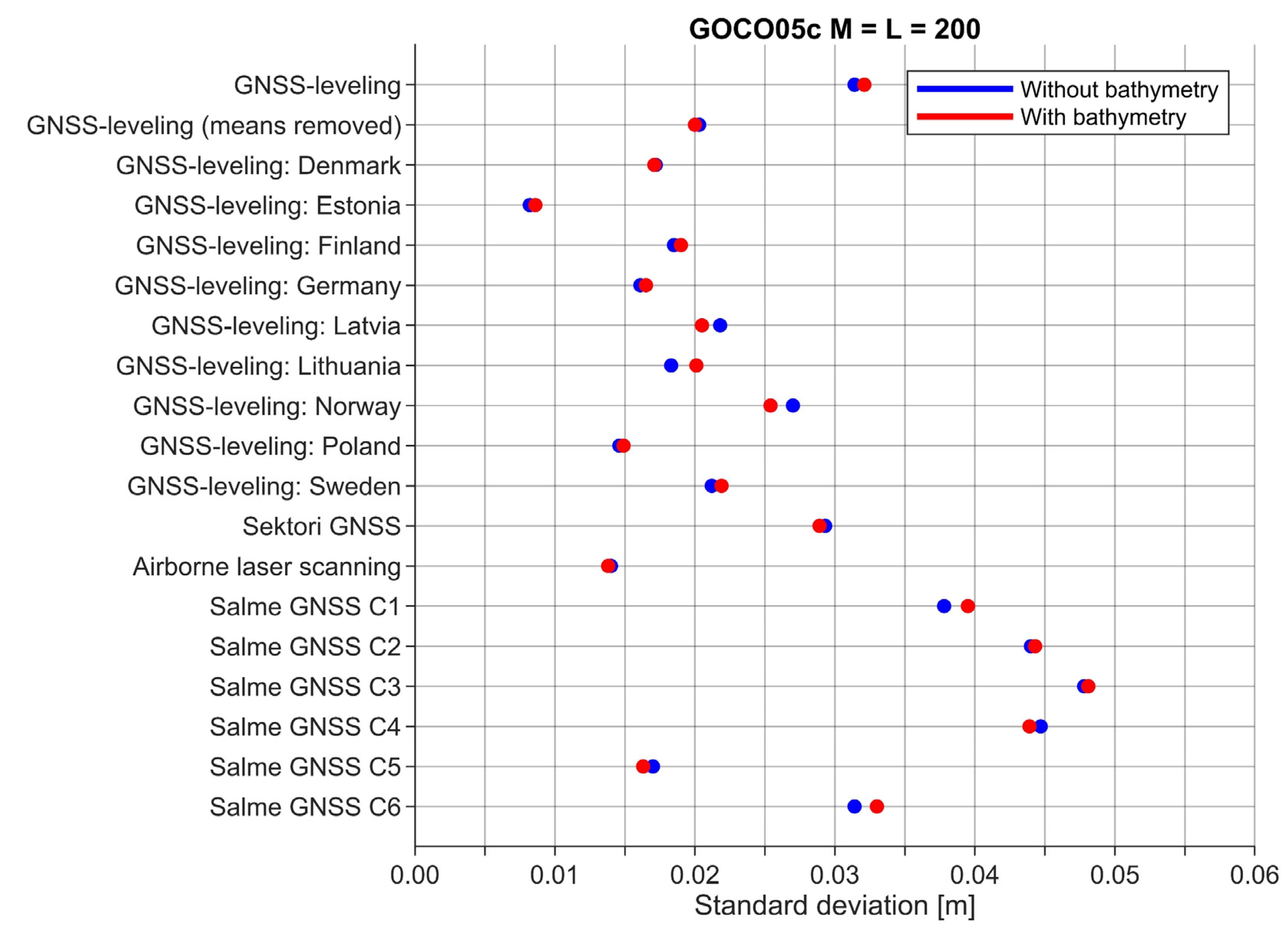
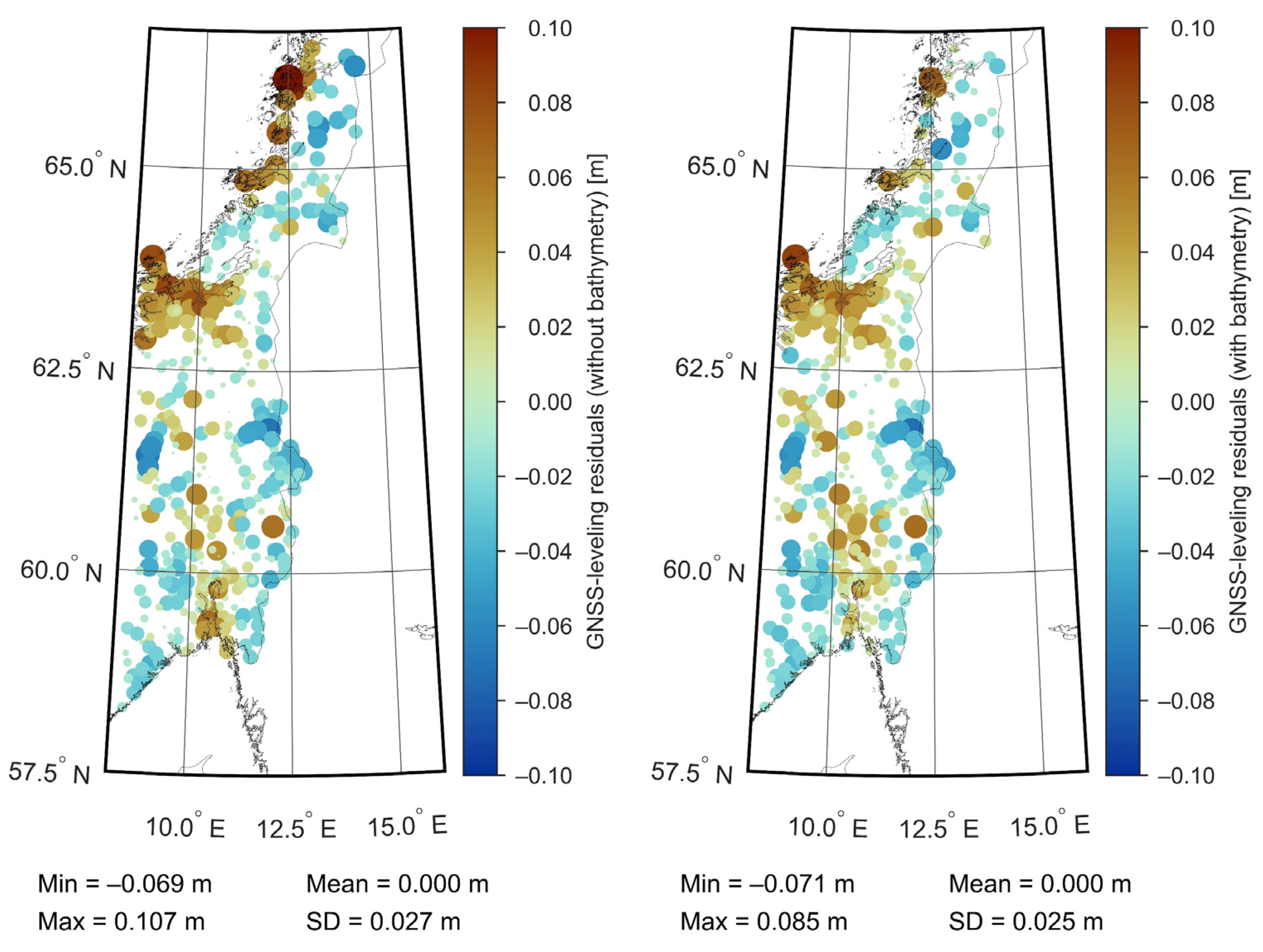
4.5. Bathymetry Influence on Geoid Modeling
5. Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gruber, T.; Willberg, M. Signal and error assessment of GOCE-based high resolution gravity field models. J. Geod. Sci. 2019, 9, 71–86. [Google Scholar] [CrossRef]
- Brockmann, J.M.; Schubert, T.; Schuh, W.-D. An improved model of the Earth’s static gravity field solely derived from reprocessed GOCE data. Surv. Geophys. 2021, 42, 277–316. [Google Scholar] [CrossRef]
- Huang, J. Determining coastal mean dynamic topography by geodetic methods. Geophys. Res. Lett. 2017, 44, 11125–11128. [Google Scholar] [CrossRef]
- Andersen, O.B.; Nielsen, K.; Knudsen, P.; Hughes, C.W.; Bingham, R.; Fenoglio-Marc, L.; Gravelle, M.; Kern, M.; Polo, S.P. Improving the coastal mean dynamic topography by geodetic combination of tide gauge and satellite altimetry. Mar. Geod. 2018, 41, 517–545. [Google Scholar] [CrossRef]
- Idžanović, M.; Ophaug, V.; Andersen, O.B. The coastal mean dynamic topography in Norway observed by CryoSat-2 and GOCE. Geophys. Res. Lett. 2017, 44, 5609–5617. [Google Scholar] [CrossRef] [Green Version]
- Knudsen, P.; Andersen, O.; Maximenko, N. A new ocean mean dynamic topography model, derived from a combination of gravity, altimetry and drifter velocity data. Adv. Space Res. 2021, 68, 1090–1102. [Google Scholar] [CrossRef]
- Stokes, G.G. On the variation of gravity on the surface of the Earth. Trans. Cambridge Philos. Soc. 1849, 8, 672–695. [Google Scholar]
- Molodenskii, M.S.; Eremeev, V.F.; Yurkina, M. Methods for Study of the External Gravitational Field and Figure of the Earth; Israel Program for Scientific Translations: Jerusalem, Israel, 1962. [Google Scholar]
- Sjöberg, L.E.; Hunegnaw, A. Some modifications of Stokes’ formula that account for truncation and potential coefficient errors. J. Geod. 2000, 74, 232–238. [Google Scholar] [CrossRef]
- Ellmann, A. Two deterministic and three stochastic modifications of Stokes’s formula: A case study for the Baltic countries. J. Geod. 2005, 79, 11–23. [Google Scholar] [CrossRef]
- Goyal, R.; Ågren, J.; Featherstone, W.E.; Sjöberg, L.E.; Dikshit, O.; Balasubramanian, N. Empirical comparison between stochastic and deterministic modifiers over the French Auvergne geoid computation test-bed. Surv. Rev. 2022, 54, 57–69. [Google Scholar] [CrossRef]
- Sjöberg, L.E. A computational scheme to model the geoid by the modified Stokes formula without gravity reductions. J. Geod. 2003, 77, 423–432. [Google Scholar] [CrossRef]
- Sjöberg, L.E.; Bagherbandi, M. (Eds.) Applications and comparisons of LSMSA and RCR. In Gravity Inversion and Integration; Springer: Cham, Switzerland, 2017; pp. 181–202. [Google Scholar] [CrossRef]
- Wang, Y.M.; Sánchez, L.; Ågren, J.; Huang, J.; Forsberg, R.; Abd-Elmotaal, H.A.; Ahlgren, K.; Barzaghi, R.; Bašić, T.; Carrion, D.; et al. Colorado geoid computation experiment: Overview and summary. J. Geod. 2021, 95, 127. [Google Scholar] [CrossRef]
- Märdla, S.; Ågren, J.; Strykowski, G.; Oja, T.; Ellmann, A.; Forsberg, R.; Bilker-Koivula, M.; Omang, O.; Paršeliūnas, E.; Liepinš, I.; et al. From discrete gravity survey data to a high-resolution gravity field representation in the Nordic-Baltic region. Mar. Geod. 2017, 40, 416–453. [Google Scholar] [CrossRef]
- Sakil, F.F.; Erol, S.; Ellmann, A.; Erol, B. Geoid modeling by the least squares modification of Hotine’s and Stokes’ formulae using non-gridded gravity data. Comput. Geosci. 2021, 156, 104909. [Google Scholar] [CrossRef]
- dos Santos, N.P.; Escobar, I.P. Discrete evaluation of Stokes’s integral by means of Voronoi and Delaunay structures. J. Geod. 2004, 78, 354–367. [Google Scholar] [CrossRef]
- Omang, O.C.D.; Forsberg, R. How to handle topography in practical geoid determination: Three examples. J. Geod. 2000, 74, 458–466. [Google Scholar] [CrossRef]
- Tscherning, C.C.; Forsberg, R. Geoid determination in the Nordic countries from gravity and height data. Boll. Geod. Sci. Affin. 1987, 46, 21–43. [Google Scholar]
- Forsberg, R. A new high-resolution geoid of the Nordic area. In Determination of the Geoid; Rapp, R.H., Sansò, F., Eds.; Springer: New York, NY, USA, 1991; pp. 241–250. [Google Scholar] [CrossRef]
- Forsberg, R.; Kaminskis, J.; Solheim, D. Geoid of the Nordic and Baltic region from gravimetry and satellite altimetry. In Gravity, Geoid and Marine Geodesy; Segawa, J., Fujimoto, H., Okubo, S., Eds.; Springer: Berlin, Germany, 1997; pp. 540–547. [Google Scholar] [CrossRef]
- Denker, H.; Torge, W. The European gravimetric quasigeoid EGG97—An IAG supported continental enterprise. In Geodesy on the Move; Forsberg, R., Feissel, M., Dietrich, R., Eds.; Springer: Berlin, Germany, 1998; pp. 249–254. [Google Scholar] [CrossRef]
- Omang, O.C.D.; Forsberg, R. The Northern European geoid: A case study on long-wavelength geoid errors. J. Geod. 2002, 76, 369–380. [Google Scholar] [CrossRef]
- Forsberg, R.; Strykowski, G.; Solheim, D. NKG-2004 geoid of the Nordic and Baltic area. In Proceedings of the International Association of Geodesy Symposium on Gravity, Geoid, and Space Missions, Porto, Portugal, 30 August–3 September 2004. [Google Scholar]
- Denker, H.; Barriot, J.-P.; Barzaghi, R.; Fairhead, D.; Forsberg, R.; Ihde, J.; Kenyeres, A.; Marti, U.; Sarrailh, M.; Tziavos, I.N. The development of the European gravimetric geoid model EGG07. In Observing our Changing Earth; Sideris, M.G., Ed.; Springer: Berlin, Germany, 2009; pp. 177–185. [Google Scholar] [CrossRef]
- Denker, H. Regional gravity field modeling: Theory and practical results. In Sciences of Geodesy—II.; Xu, G., Ed.; Springer: Berlin, Germany, 2013; pp. 185–291. [Google Scholar] [CrossRef] [Green Version]
- Ågren, J.; Strykowski, G.; Bilker-Koivula, M.; Omang, O.; Märdla, S.; Oja, T.; Ellmann, A.; Liepins, I.; Parseliunas, E.; Forsberg, R.; et al. On the development of the new Nordic gravimetric geoid model NKG2015. In Proceedings of the 26th International Union of Geodesy and Geophysics General Assembly, Prague, Czech Republic, 22 June–2 July 2015. [Google Scholar] [CrossRef]
- Denker, H. A new European gravimetric (quasi)geoid EGG2015. In Proceedings of the 26th International Union of Geodesy and Geophysics General Assembly, Prague, Czech Republic, 22 June–2 July 2015. [Google Scholar]
- Ågren, J.; Strykowski, G.; Bilker-Koivula, M.; Omang, O.; Märdla, S.; Forsberg, R.; Ellmann, A.; Oja, T.; Liepins, I.; Parseliunas, E.; et al. The NKG2015 gravimetric geoid model for the Nordic-Baltic region. In Proceedings of the International Symposium on Gravity, Geoid and Height Systems 2016, Thessaloniki, Greece, 19–23 September 2016. [Google Scholar] [CrossRef]
- Dahl, O.C.; Forsberg, R. Geoid models around Sognefjord using depth data. J. Geod. 1998, 72, 547–556. [Google Scholar] [CrossRef]
- Schwabe, J.; Ågren, J.; Liebsch, G.; Westfeld, P.; Hammarklint, T.; Mononen, J.; Andersen, O.B. The Baltic Sea Chart Datum 2000 (BSCD2000)—Implementation of a common reference level in the Baltic Sea. Int. Hydrogr. Rev. 2020, 23, 63–83. [Google Scholar]
- Varbla, S.; Ågren, J.; Ellmann, A.; Poutanen, M. Treatment of tide gauge time series and marine GNSS measurements for vertical land motion with relevance to the implementation of the Baltic Sea Chart Datum 2000. Remote Sens. 2022, 14, 920. [Google Scholar] [CrossRef]
- Bouin, M.-N.; Ballu, V.; Calmant, S.; Boré, J.-M.; Folcher, E.; Ammann, J. A kinematic GPS methodology for sea surface map-ping, Vanuatu. J. Geod. 2009, 83, 1203. [Google Scholar] [CrossRef]
- Saari, T.; Bilker-Koivula, M.; Koivula, H.; Nordman, M.; Häkli, P.; Lahtinen, S. Validating geoid models with marine GNSS measurements, sea surface models, and additional gravity observations in the Gulf of Finland. Mar. Geod. 2021, 44, 196–214. [Google Scholar] [CrossRef]
- Varbla, S.; Liibusk, A.; Ellmann, A. Shipborne GNSS-determined sea surface heights using geoid model and realistic dynamic topography. Remote Sens. 2022, 14, 2368. [Google Scholar] [CrossRef]
- Gruno, A.; Liibusk, A.; Ellmann, A.; Oja, T.; Vain, A.; Jürgenson, H. Determining sea surface heights using small footprint airborne laser scanning. In Proceedings of the Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions 2013, Dresden, Germany, 23–26 September 2013. [Google Scholar] [CrossRef]
- Zlinszky, A.; Timár, G.; Weber, R.; Székely, B.; Briese, C.; Ressl, C.; Pfeifer, N. Observation of a local gravity potential isosurface by airborne lidar of Lake Balaton, Hungary. Solid Earth 2014, 5, 355–369. [Google Scholar] [CrossRef] [Green Version]
- Varbla, S.; Ellmann, A.; Delpeche-Ellmann, N. Applications of airborne laser scanning for determining marine geoid and surface waves properties. Eur. J. Remote Sens. 2021, 54, 557–567. [Google Scholar] [CrossRef]
- Jahanmard, V.; Delpeche-Ellmann, N.; Ellmann, A. Realistic dynamic topography through coupling geoid and hydrodynamic models of the Baltic Sea. Cont. Shelf Res. 2021, 222, 104421. [Google Scholar] [CrossRef]
- Heiskanen, W.A.; Moritz, H. Physical Geodesy; W. H. Freeman and Company: San Francisco, CA, USA, 1967. [Google Scholar]
- Moritz, H. Geodetic Reference System 1980. J. Geod. 2000, 74, 128–133. [Google Scholar] [CrossRef]
- Forsberg, R.; Tscherning, C.C. The use of height data in gravity field approximation by collocation. J. Geophys. Res. Solid Earth 1981, 86, 7843–7854. [Google Scholar] [CrossRef]
- Forsberg, R. A Study of Terrain Reductions, Density Anomalies and Geophysical Inversion Methods in Gravity Field Modelling; Ohio State University: Columbus, OH, USA, 1984. [Google Scholar]
- Moritz, H. Advanced Physical Geodesy; Wichmann: Karlsruhe, Germany, 1980. [Google Scholar]
- Kasper, J.F. A second-order Markov gravity anomaly model. J. Geophys. Res. 1971, 76, 7844–7849. [Google Scholar] [CrossRef]
- Sjöberg, L.E. Refined least squares modification of Stokes’ formula. Manus. Geod. 1991, 16, 367–375. [Google Scholar]
- Ellmann, A. Computation of three stochastic modifications of Stokes’s formula for regional geoid determination. Comput. Geosci. 2005, 31, 742–755. [Google Scholar] [CrossRef]
- Ellmann, A. Using high-resolution spectral models of gravity anomaly for computing stochastic modifications of Stokes’s formula. Comput. Geosci. 2012, 39, 188–190. [Google Scholar] [CrossRef]
- Paul, M.K. A method of evaluating the truncation error coefficients for geoidal height. Bull. Géodésique 1973, 110, 413–425. [Google Scholar] [CrossRef]
- Hagiwara, Y. A new formula for evaluating the truncation error coefficient. Bull. Géodésique 1976, 50, 131–135. [Google Scholar] [CrossRef]
- Sjöberg, L.E. A solution to the downward continuation effect on the geoid determined by Stokes’ formula. J. Geod. 2003, 77, 94–100. [Google Scholar] [CrossRef]
- Sjöberg, L.E. The IAG approach to the atmospheric geoid correction in Stokes’ formula and a new strategy. J. Geod. 1999, 73, 362–366. [Google Scholar] [CrossRef]
- Sjöberg, L.E.; Nahavandchi, H. The atmospheric geoid effects in Stokes’ formula. Geophys. J. Int. 2000, 140, 95–100. [Google Scholar] [CrossRef] [Green Version]
- Sjöberg, L.E. Topographic and atmospheric corrections of gravimetric geoid determination with special emphasis on the effects of harmonics of degrees zero and one. J. Geod. 2001, 75, 283–290. [Google Scholar] [CrossRef]
- Sjöberg, L.E. Ellipsoidal corrections to order e2 of geopotential coefficients and Stokes’ formula. J. Geod. 2003, 77, 139–147. [Google Scholar] [CrossRef]
- Ellmann, A.; Sjöberg, L.E. Ellipsoidal correction for the modified Stokes formula. Boll. Geod. Sci. Affin. 2004, 63, 153–172. [Google Scholar]
- Sjöberg, L.E. A spherical harmonic representation of the ellipsoidal correction to the modified Stokes formula. J. Geod. 2004, 78, 180–186. [Google Scholar] [CrossRef]
- Ågren, J.; Sjöberg, L.E.; Kiamehr, R. The new gravimetric quasigeoid model KTH08 over Sweden. J. Appl. Geod. 2009, 3, 143–153. [Google Scholar] [CrossRef]
- Ellmann, A. A numerical comparison of different ellipsoidal corrections to Stokes’ formula. In A Window on the Future of Geodesy; Sansò, F., Ed.; Springer: Berlin, Germany, 2005; pp. 409–414. [Google Scholar] [CrossRef]
- Märdla, S.; Ellmann, A.; Ågren, J.; Sjöberg, L.E. Regional geoid computation by least squares modified Hotine’s formula with additive corrections. J. Geod. 2018, 92, 253–270. [Google Scholar] [CrossRef]
- Ekman, M. Impacts of geodynamic phenomena on systems for height and gravity. Bull. Géodésique 1989, 63, 281–296. [Google Scholar] [CrossRef]
- Poutanen, M.; Vermeer, M.; Mäkinen, J. The permanent tide in GPS positioning. J. Geod. 1996, 70, 499–504. [Google Scholar] [CrossRef]
- GEBCO_2021 Grid. Available online: https://doi.org/10.5285/c6612cbe-50b3-0cff-e053-6c86abc09f8f (accessed on 25 March 2022).
- Hao, R.; Wan, X.; Wang, Y.; Annan, R.F.; Sui, X. Evaluation of four global bathymetry models by shipborne depths data. J. Surv. Eng. 2022, 148, 04021033. [Google Scholar] [CrossRef]
- Leppäranta, M.; Myrberg, K. Physical Oceanography of the Baltic Sea; Springer: Berlin, Germany, 2009. [Google Scholar] [CrossRef]
- Riley, S.J.; DeGloria, S.D.; Elliot, R. A terrain ruggedness index that quantifies topographic heterogeneity. Intermt. J. Sci. 1999, 5, 23–27. [Google Scholar]
- Pail, R.; Gruber, T.; Fecher, T.; GOCO Project Team. The combined gravity model GOCO05c. GFZ Data Serv. 2016. [Google Scholar] [CrossRef]
- Fecher, T.; Pail, R.; Gruber, T.; the GOCO Consortium. GOCO05c: A new combined gravity field model based on full normal equations and regionally varying weighting. Surv. Geophys. 2017, 38, 571–590. [Google Scholar] [CrossRef]
- Förste, C.; Abrykosov, O.; Bruinsma, S.; Dahle, C.; König, R.; Lemoine, J.-M. ESA’s release 6 GOCE gravity field model by means of the direct approach based on improved filtering of the reprocessed gradients of the entire mission (GO_CONS_GCF_2_DIR_R6). GFZ Data Serv. 2019. [Google Scholar] [CrossRef]
- Kvas, A.; Mayer-Gürr, T.; Krauss, S.; Brockmann, J.M.; Schubert, T.; Schuh, W.-D.; Pail, R.; Gruber, T.; Jäggi, A.; Meyer, U. The satellite-only gravity field model GOCO06s. GFZ Data Serv. 2019. [Google Scholar] [CrossRef]
- Kvas, A.; Brockmann, J.M.; Krauss, S.; Schubert, T.; Gruber, T.; Meyer, U.; Mayer-Gürr, T.; Schuh, W.-D.; Jäggi, A.; Pail, R. GOCO06s—A satellite-only global gravity field model. Earth Syst. Sci. Data 2021, 13, 99–118. [Google Scholar] [CrossRef]
- Zingerle, P.; Pail, R.; Gruber, T.; Oikonomidou, X. The experimental gravity field model XGM2019e. GFZ Data Serv. 2019. [Google Scholar] [CrossRef]
- Zingerle, P.; Pail, R.; Gruber, T.; Oikonomidou, X. The combined global gravity field model XGM2019e. J. Geod. 2020, 94, 66. [Google Scholar] [CrossRef]
- Rüdja, A.; Varbla, S. Estonian GNSS-leveling dataset with relevance to the implementation of the Baltic Sea Chart Datum 2000. SEANOE 2022. [Google Scholar] [CrossRef]
- Vestøl, O.; Ågren, J.; Steffen, H.; Kierulf, H.; Tarasov, L. NKG2016LU: A new land uplift model for Fennoscandia and the Baltic region. J. Geod. 2019, 93, 1759–1779. [Google Scholar] [CrossRef] [Green Version]
- Varbla, S.; Ellmann, A.; Delpeche-Ellmann, N. Validation of marine geoid models by utilizing hydrodynamic model and shipborne GNSS profiles. Mar. Geod. 2020, 43, 134–162. [Google Scholar] [CrossRef]
- Liibusk, A.; Varbla, S.; Ellmann, A.; Vahter, K.; Uiboupin, R.; Delpeche-Ellmann, N. Shipborne GNSS acquisition of sea surface heights in the Baltic Sea. J. Geod. Sci. 2022. in print. [Google Scholar] [CrossRef]
- Forsberg, R.; Olesen, A.V.; Keller, K.; Møller, M.; Gidskehaug, A.; Solheim, D. Airborne gravity and geoid surveys in the Arctic and Baltic seas. In Proceedings of the International Symposium on Kinematic Systems in Geodesy, Geomatics and Navigation (KIS-2001), Banff, Canada, 5–8 June 2001. [Google Scholar]
- Ellmann, A. Downward continuation of airborne gravity data using high-resolution global geopotential models. In Proceedings of the 8th International Conference on Environmental Engineering, Vilnius, Lithuania, 19–20 May 2011. [Google Scholar]
- Förste, C.; Bruinsma, S.L.; Abrykosov, O.; Lemoine, J.-M.; Marty, J.C.; Flechtner, F.; Balmino, G.; Barthelmes, F.; Biancale, R. EIGEN-6C4 the latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse. GFZ Data Serv. 2014. [Google Scholar] [CrossRef]
- Oja, T.; Ellmann, A.; Märdla, S. Gravity anomaly field over Estonia. Estonian J. Earth Sci. 2019, 68, 55–75. [Google Scholar] [CrossRef]
- Mostafavi, M.; Delpeche-Ellmann, N.; Ellmann, A. Accurate sea surface heights from Sentinel-3A and Jason-3 retrackers by incorporating high-resolution marine geoid and hydrodynamic models. J. Geod. Sci. 2021, 11, 58–74. [Google Scholar] [CrossRef]





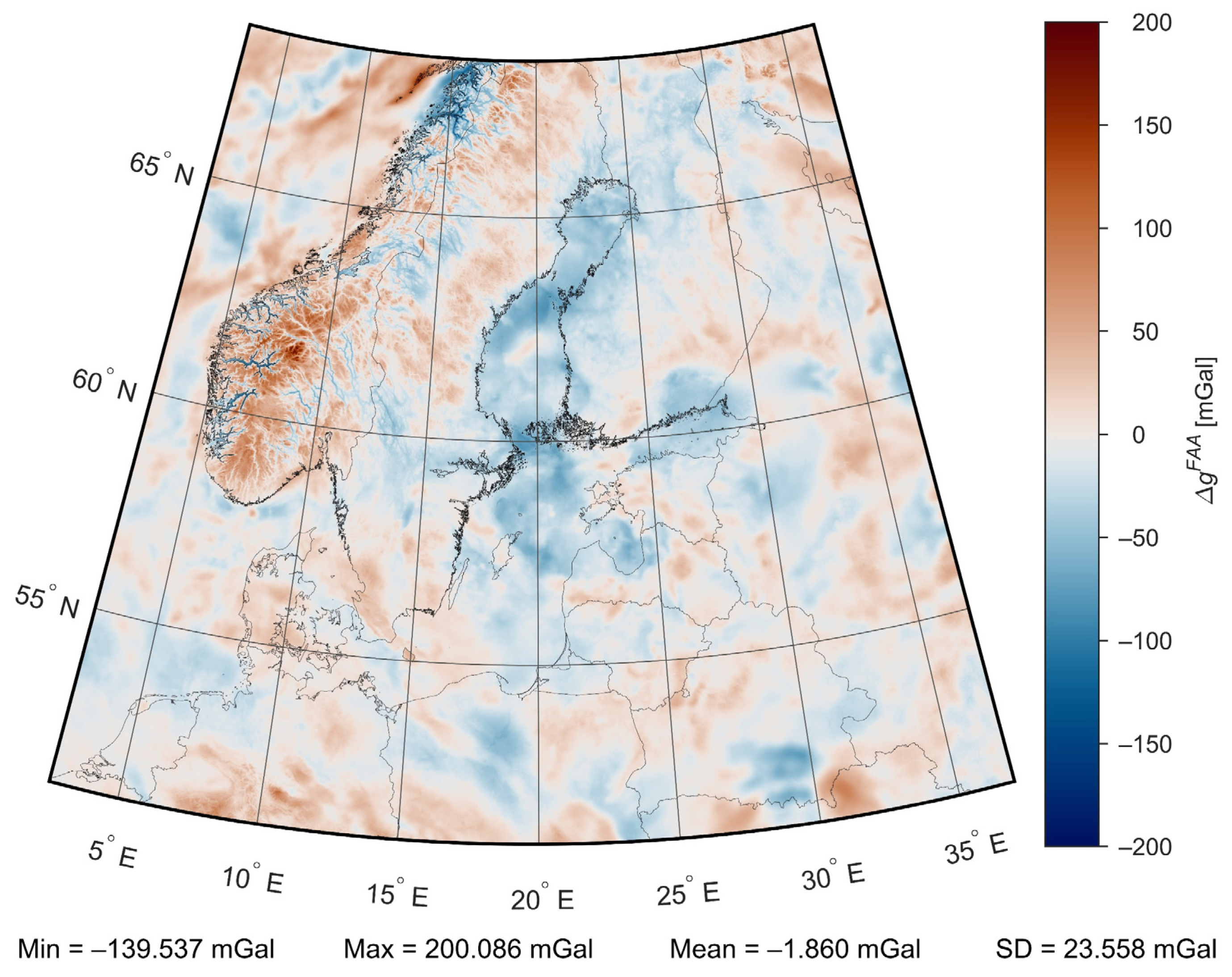
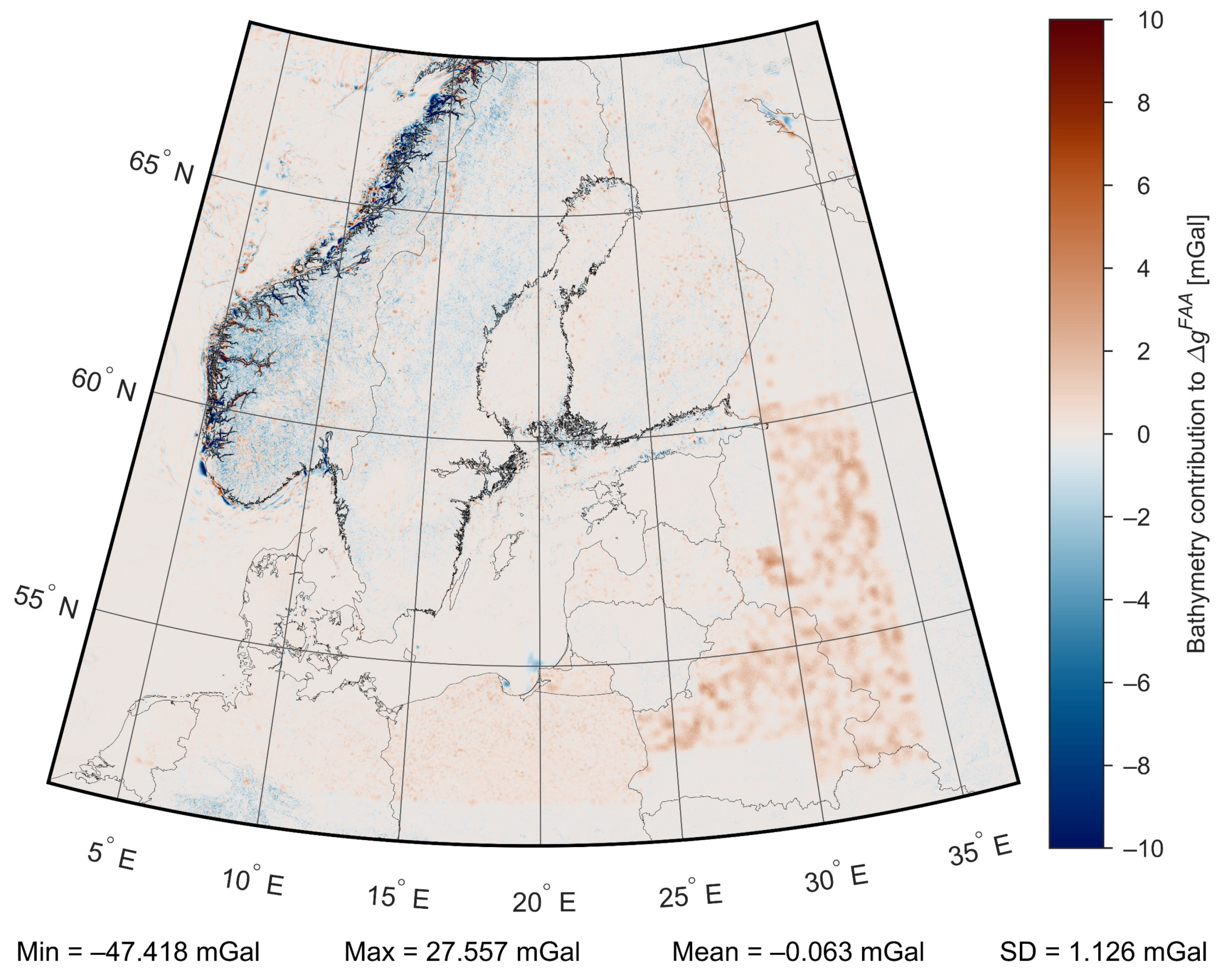
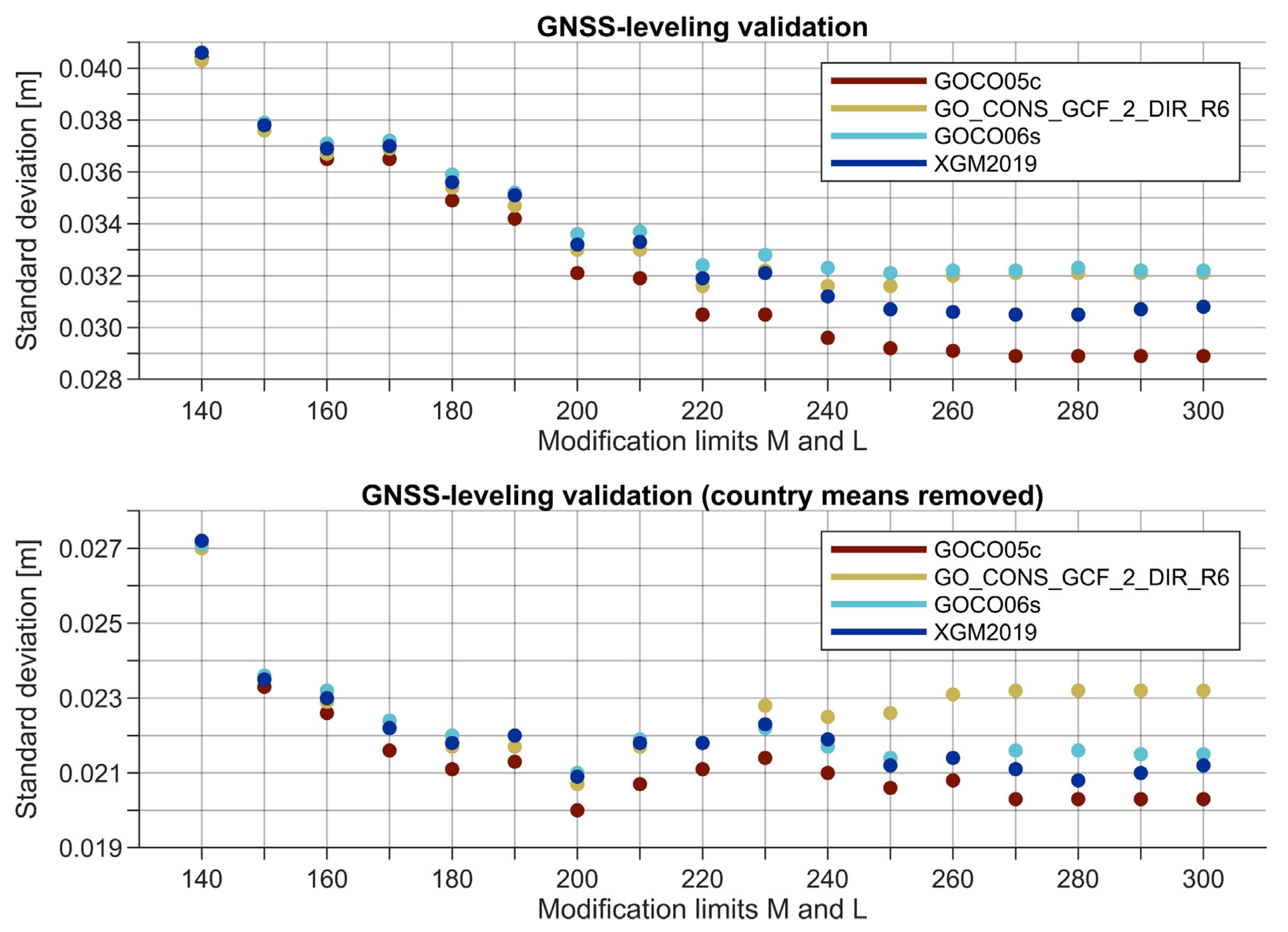

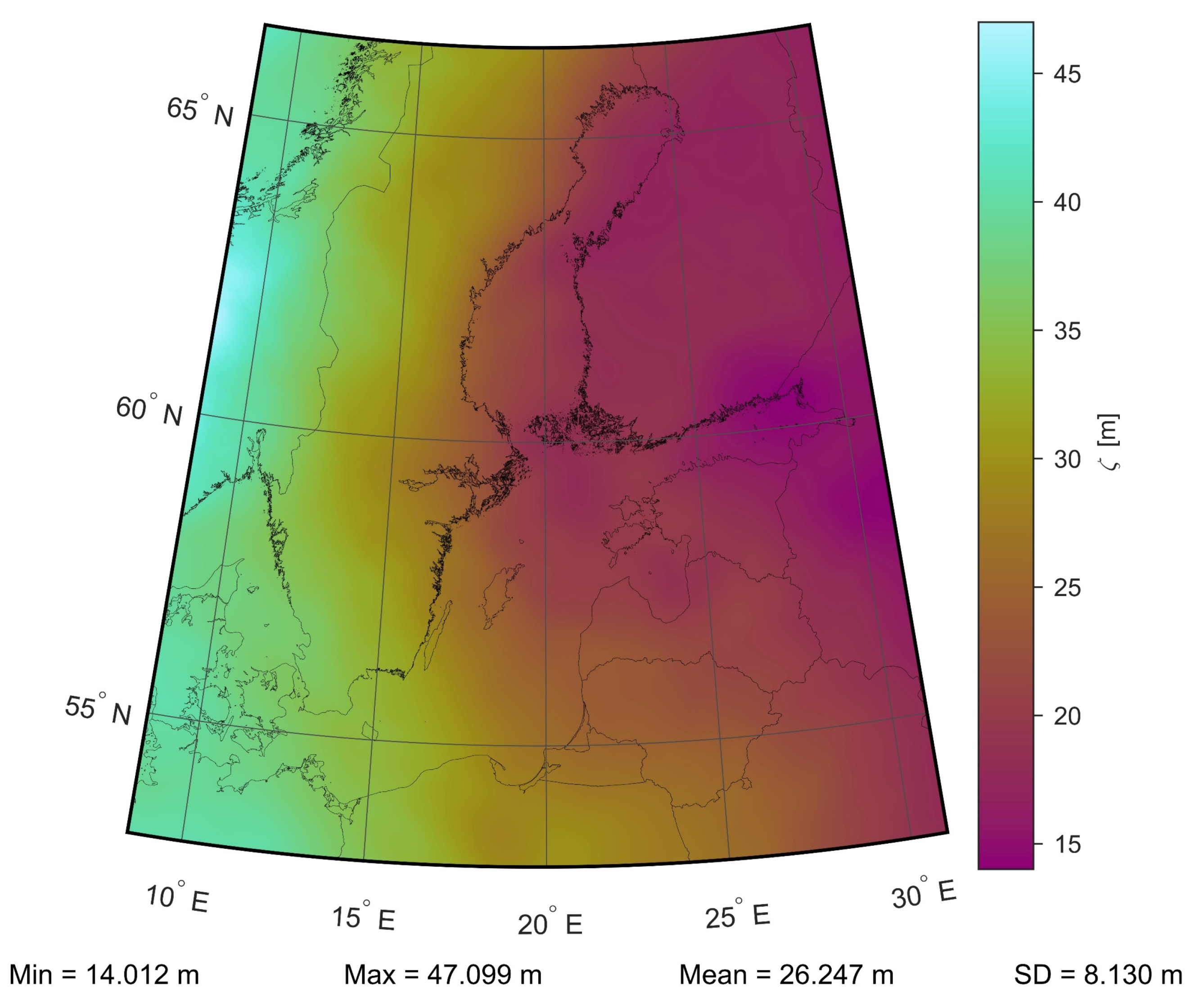


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varbla, S. The Influence of Bathymetry on Regional Marine Geoid Modeling in Northern Europe. J. Mar. Sci. Eng. 2022, 10, 793. https://doi.org/10.3390/jmse10060793
Varbla S. The Influence of Bathymetry on Regional Marine Geoid Modeling in Northern Europe. Journal of Marine Science and Engineering. 2022; 10(6):793. https://doi.org/10.3390/jmse10060793
Chicago/Turabian StyleVarbla, Sander. 2022. "The Influence of Bathymetry on Regional Marine Geoid Modeling in Northern Europe" Journal of Marine Science and Engineering 10, no. 6: 793. https://doi.org/10.3390/jmse10060793
APA StyleVarbla, S. (2022). The Influence of Bathymetry on Regional Marine Geoid Modeling in Northern Europe. Journal of Marine Science and Engineering, 10(6), 793. https://doi.org/10.3390/jmse10060793





