Lateral Variation of Tidal Mixing Asymmetry and Its Impact on the Longitudinal Sediment Transport in Turbidity Maximum Zone of Salt Wedge Estuary
Abstract
:1. Introduction
2. Materials and Methods
2.1. Field Observations
2.2. Potential Energy Anomaly
2.3. Asymmetry Degree of Tidal Mixing
2.3.1. Eddy Viscosity and Diffusivity
2.3.2. Vertical Mixing Coefficients
2.4. Longitudinal Sediment Transport
2.4.1. Longitudinal Net Water and Sediment Transports
2.4.2. Decomposition of Sediment Transport Rate
2.4.3. Decomposition of Sediment Flux
3. Result
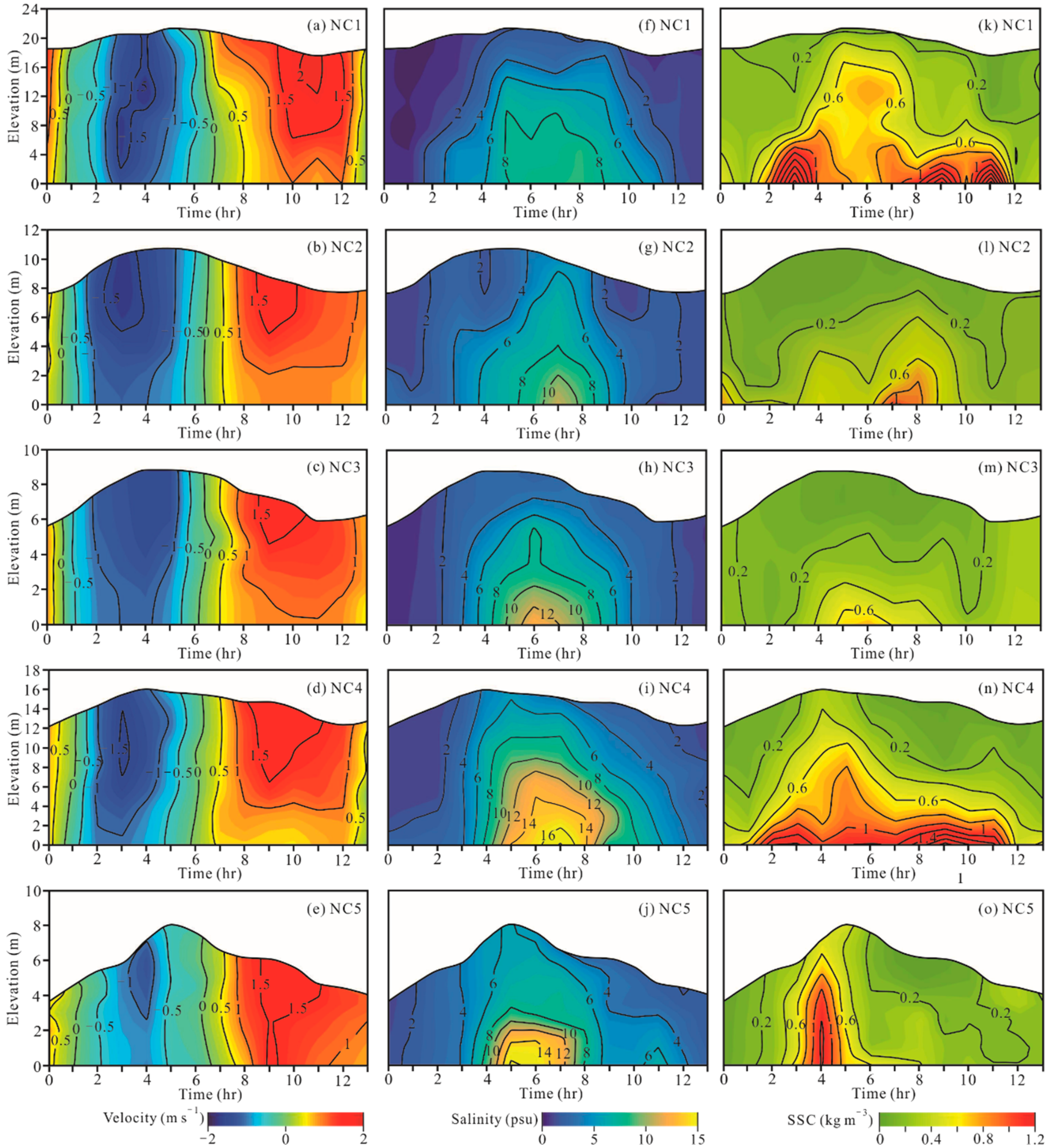
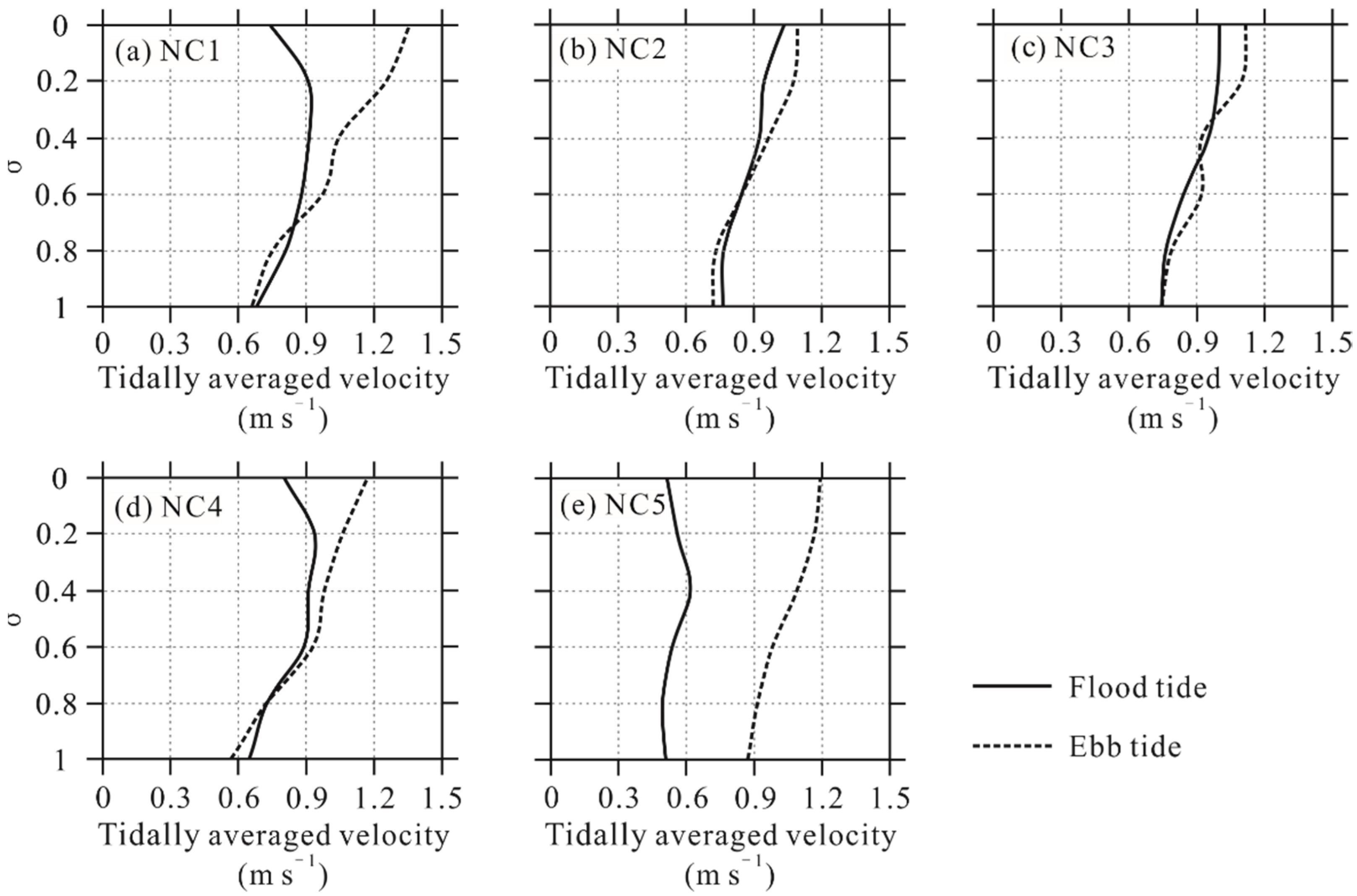
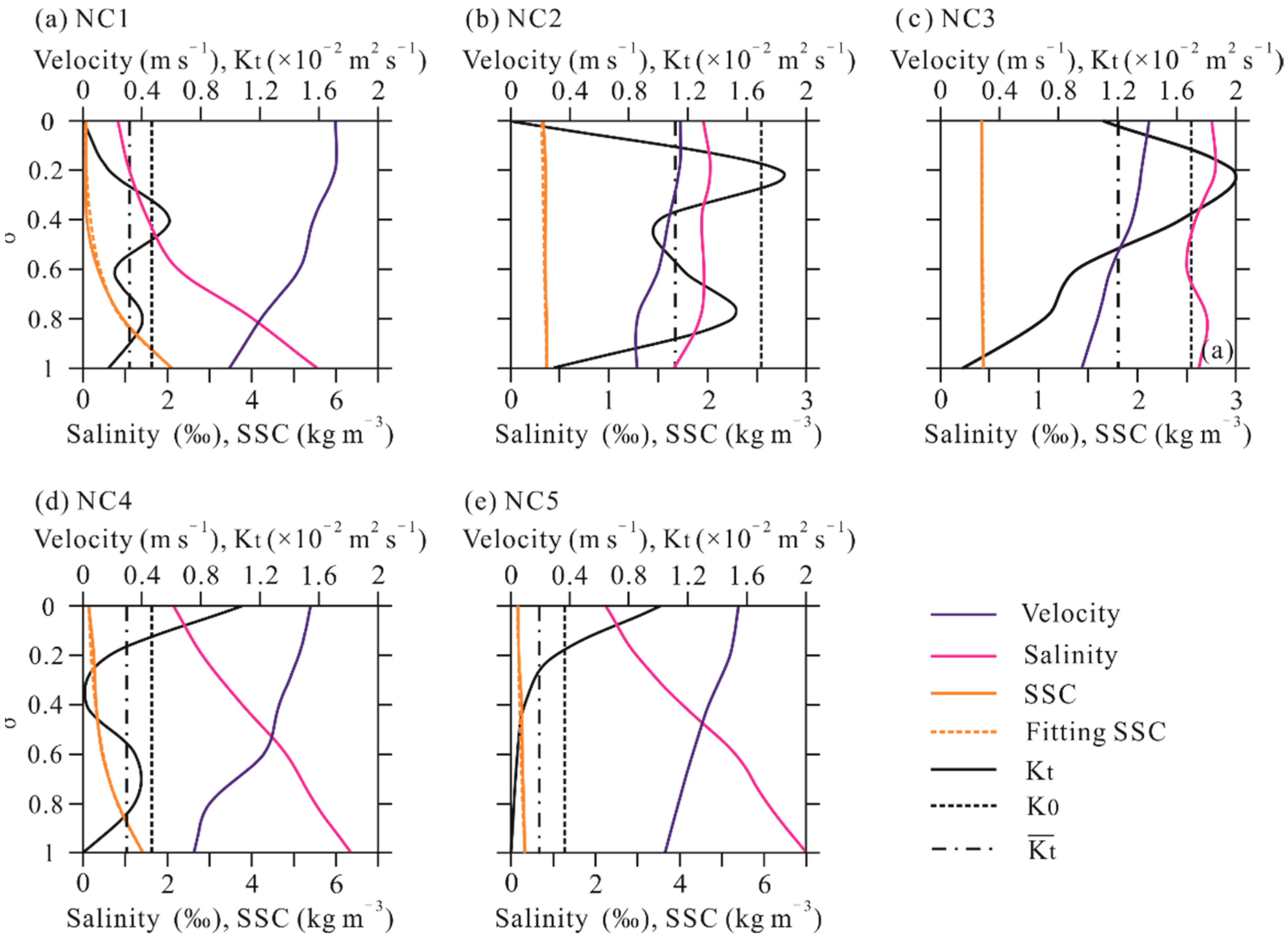
3.1. Lateral Variations of Velocity and Salinity
3.2. Temporal Variation of Stratification
3.3. Temporal Variations of Eddy Viscosity and Diffusivity
3.4. Lateral Variations of Tidal Mixing Asymmetry
3.5. Longitudinal Sediment Transport
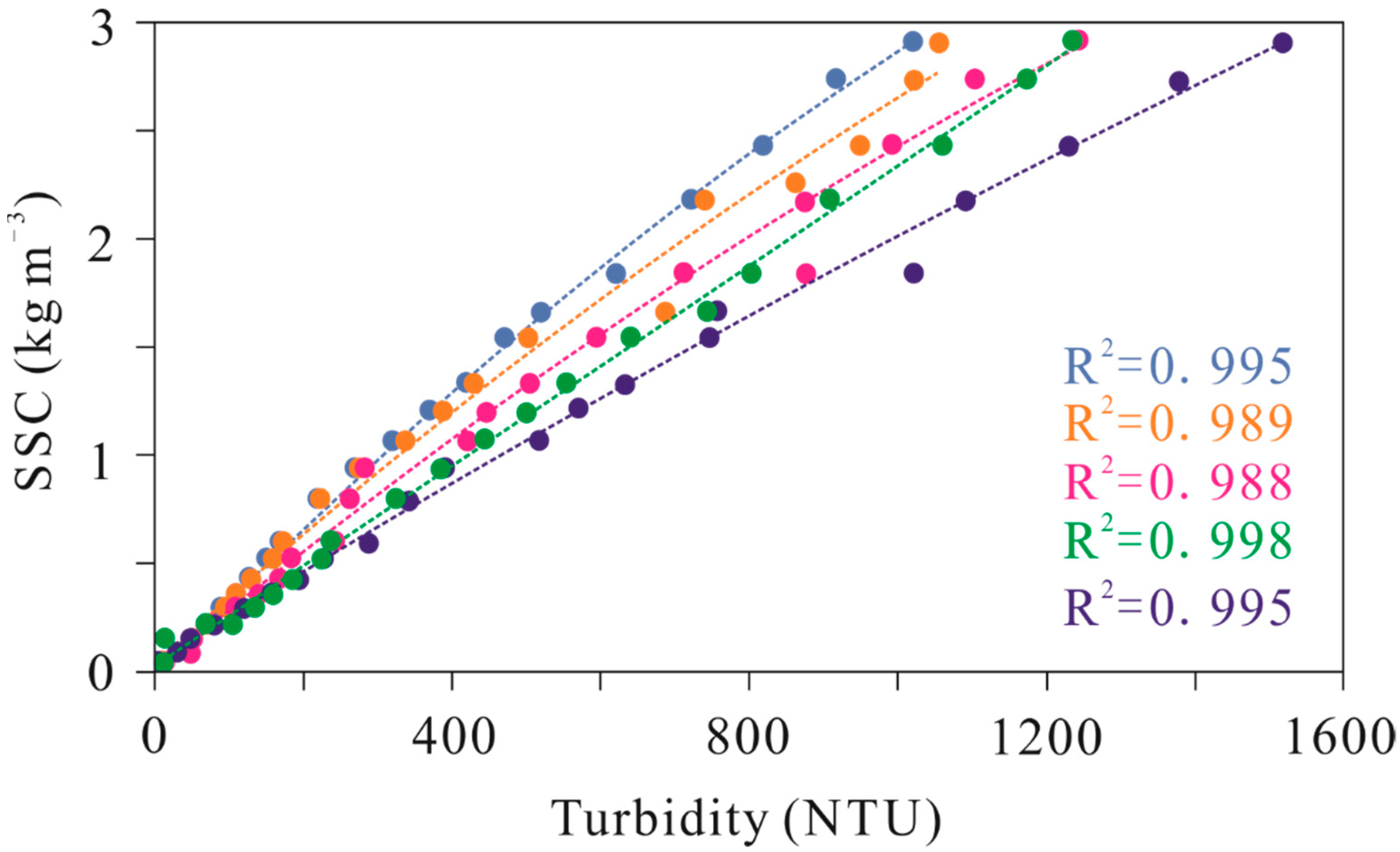
3.5.1. Lateral Variations of SSC
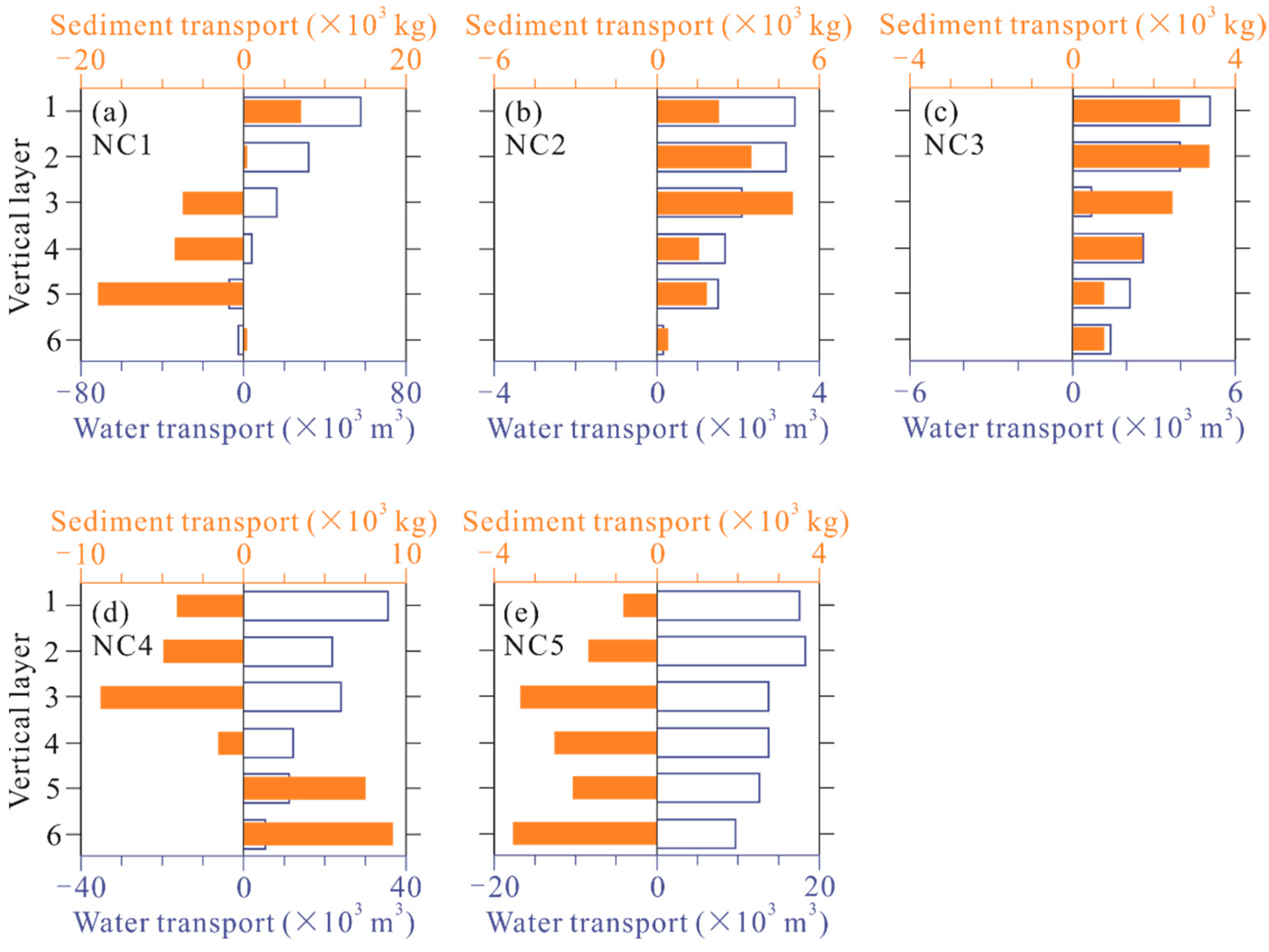
3.5.2. Lateral Variations of Longitudinal Net Water and Sediment Transports
3.5.3. Tidally Averaged Longitudinal Sediment Transport Rate
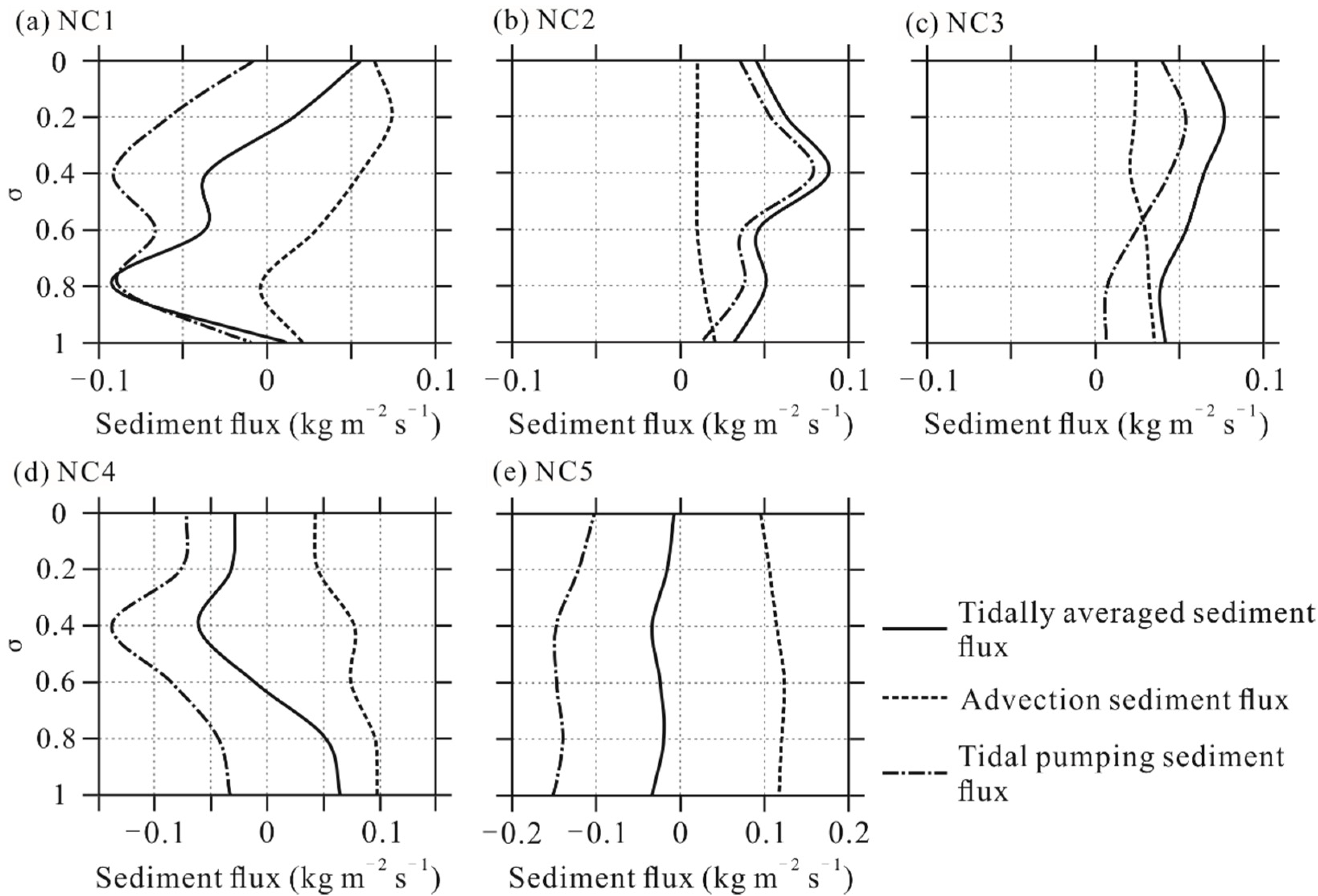
3.5.4. Tidally Averaged Longitudinal Sediment Flux
4. Discussion
4.1. Mechanism behind Lateral Variations of Tidal Mixing Asymmetry
4.2. Impact of Tidal Mixing Asymmetry on Longitudinal Net Sediment Transport
4.3. Impacts of Advection and Resuspension on Longitudinal Net Sediment Transport
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Simpson, J.H.; Brown, J.; Matthews, J.; Allen, G. Tidal Straining, Density Currents, and Stirring in the Control of Estuarine Stratification. Estuaries 1990, 13, 125–132. [Google Scholar] [CrossRef]
- Jay, D.A.; Musiak, J.M. Internal tidal asymmetry in channel flows. Origins and consequences. In Mixing Processes in Estuaries and Coastal Seas, Coastal Estuarine Studies Series; AGU: Washington, DC, USA, 1996; Volume 50, pp. 211–249. [Google Scholar] [CrossRef]
- Cheng, P.; Valle-Levinson, A.; De Swart, H.E. A numerical study of residual estuarine circulation induced by asymmetric tidal mixing in tidally dominated estuaries. J. Geophys. Res. Oceans 2011, 116, C01017. [Google Scholar] [CrossRef] [Green Version]
- Burchard, H.; Baumert, H. The Formation of Estuarine Turbidity Maxima Due to Density Effects in the Salt Wedge. A Hydrodynamic Process Study. J. Phys. Oceanogr. 1998, 28, 309–321. [Google Scholar] [CrossRef]
- Scully, M.E.; Friedrichs, C.T. Sediment pumping by tidal asymmetry in a partially mixed estuary. J. Geophys. Res. Oceans 2007, 112, C07028. [Google Scholar] [CrossRef] [Green Version]
- Geyer, W.R. The Importance of Suppression of Turbulence by Stratification on the Estuarine Turbidity Maximum. Estuaries 1993, 16, 113–125. [Google Scholar] [CrossRef]
- Scully, M.E.; Friedrichs, C.T. The influence of asymmetries in overlying stratification on near-bed turbulence and sediment suspension in a partially mixed estuary. Ocean Dyn. 2003, 53, 208–219. [Google Scholar] [CrossRef]
- Wan, Y.; Gu, F.; Wu, H.; Roelvink, D. Hydrodynamic evolutions at the Yangtze Estuary from 1998 to 2009. Appl. Ocean Res. 2014, 47, 291–302. [Google Scholar] [CrossRef]
- Sanford, L.P.; Suttles, S.E.; Halka, J.P. Reconsidering the Physics of the Chesapeake Bay Estuarine Turbidity Maximum. Estuaries 2001, 24, 655–669. [Google Scholar] [CrossRef]
- Li, L.; He, Z.; Xia, Y.; Dou, X. Dynamics of sediment transport and stratification in Changjiang River Estuary, China. Estuar. Coast. Shelf Sci. 2018, 213, 1–17. [Google Scholar] [CrossRef]
- Whitney, M.M.; Codiga, D.L.; Ullman, D.S.; McManus, P.M.; Jiorle, R. Tidal Cycles in Stratification and Shear and Their Relationship to Gradient Richardson Number and Eddy Viscosity Variations in Estuaries. J. Phys. Oceanogr. 2012, 42, 1124–1133. [Google Scholar] [CrossRef]
- Scully, M.E.; Friedrichs, C.T. The importance of tidal and lateral asymmetries in stratification to residual circulation in partially mixed estuaries. J. Phys. Oceanogr. 2007, 37, 1496–1511. [Google Scholar] [CrossRef] [Green Version]
- Fugate, D.C.; Friedrichs, C.T.; Sanford, L.P. Lateral dynamics and associated transport of sediment in the upper reaches of a partially mixed estuary, Chesapeake Bay, USA. Cont. Shelf Res. 2007, 27, 679–698. [Google Scholar] [CrossRef]
- Basdurak, N.B.; Valle-Levinson, A.; Cheng, P. Lateral structure of tidal asymmetry in vertical mixing and its impact on exchange flow in a coastal plain estuary. Cont. Shelf Res. 2013, 64, 20–32. [Google Scholar] [CrossRef]
- Ralston, D.K.; Geyer, W.R.; Warner, J.C. Bathymetric controls on sediment transport in the Hudson River estuary: Lateral asymmetry and frontal trapping. J. Geophys. Res. Oceans 2012, 117, C10013. [Google Scholar] [CrossRef] [Green Version]
- Geyer, W.R.; MacCready, P. The Estuarine Circulation. Annu. Rev. Fluid Mech. 2014, 46, 175–197. [Google Scholar] [CrossRef]
- Giddings, S.N.; Fong, D.A.; Monismith, S.G. Role of straining and advection in the intratidal evolution of stratification, vertical mixing, and longitudinal dispersion of a shallow, macrotidal, salt wedge estuary. J. Geophys. Res. Oceans 2011, 116, C03003. [Google Scholar] [CrossRef] [Green Version]
- Burchard, H.; Schuttelaars, H.M.; Ralston, D.K. Sediment Trapping in Estuaries. Annu. Rev. Mar. Sci. 2018, 10, 371–395. [Google Scholar] [CrossRef]
- Pu, X.; Shi, J.Z.; Hu, G.-D.; Xiong, L.-B. Circulation and mixing along the North Passage in the Changjiang River estuary, China. J. Mar. Syst. 2015, 148, 213–235. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, J.; Chen, Z.; Ruan, R.; Xu, G.; Zeng, G.; Zhu, J.; Dai, Z.; Chen, X.-Y.; Gu, S.; et al. Mapping Sea Level Rise Behavior in an Estuarine Delta System: A Case Study along the Shanghai Coast. Engineering 2018, 4, 156–163. [Google Scholar] [CrossRef]
- Jiang, C.; de Swart, H.E.; Li, J.; Liu, G. Mechanisms of along-channel sediment transport in the North Passage of the Yangtze Estuary and their response to large-scale interventions. Ocean Dyn. 2013, 63, 283–305. [Google Scholar] [CrossRef]
- Li, X.; Zhu, J.; Yuan, R.; Qiu, C.; Wu, H. Sediment trapping in the Changjiang Estuary: Observations in the North Passage over a spring-neap tidal cycle. Estuar. Coast. Shelf Sci. 2016, 177, 8–19. [Google Scholar] [CrossRef]
- Wu, S.; Cheng, H.; Xu, Y.; Li, J.; Zheng, S. Decadal changes in bathymetry of the Yangtze River Estuary: Human impacts and potential saltwater intrusion. Estuar. Coast. Shelf Sci. 2016, 182, 158–169. [Google Scholar] [CrossRef] [Green Version]
- Teng, L.Z.; Cheng, H.Q.; de Swart, H.E.; Dong, P.; Li, Z.H.; Li, J.F.; Wang, Y. On the mechanism behind the shift of the turbidity maximum zone in response to reclamations in the Yangtze (Changjiang) Estuary, China. Mar. Geol. 2021, 440, 106569. [Google Scholar] [CrossRef]
- Li, Z.H.; Jia, J.J.; Wu, Y.S.; Zong, H.B.; Zhang, G.A.; Wang, Y.P. Vertical distributions of suspended sediment concentrations in the turbidity maximum zone of the periodically and partially stratified Changjiang Estuary. Estuar. Coasts 2019, 42, 1475–1490. [Google Scholar] [CrossRef]
- Muste, M.; Yu, K.; Pratt, T.; Abraham, D. Practical aspects of ADCP data use for quantification of mean river flow characteristics; Part II: Fixed-vessel measurements. Flow Meas. Instrum. 2004, 15, 12–28. [Google Scholar] [CrossRef]
- Simpson, J.H.; Bowers, D. Models of stratification and frontal movement in shelf seas. Deep Sea Res. Part A Oceanogr. Res. Pap. 1981, 28, 727–738. [Google Scholar] [CrossRef]
- Burchard, H.; Hetland, R.; Schulz, E.; Schuttelaars, H.M. Drivers of Residual Estuarine Circulation in Tidally Energetic Estuaries: Straight and Irrotational Channels with Parabolic Cross Section. J. Phys. Oceanogr. 2011, 41, 548–570. [Google Scholar] [CrossRef]
- Wang, X.H.; Byun, D.S.; Wang, X.L.; Cho, Y.K. Modelling tidal currents in a sediment stratified idealized estuary. Continent. Shelf Res. 2005, 25, 655–665. [Google Scholar] [CrossRef]
- Stacey, M.T.; Rippeth, T.P.; Nash, J.D. Turbulence and stratification in estuaries and coastal Seas. In Treatise on Estuarine and Coastal Science; Academic Press: Waltham, MA, USA, 2011; pp. 9–35. [Google Scholar] [CrossRef]
- Lin, J.; van Prooijen, B.C.; Guo, L.; Zhu, C.; He, Q.; Wang, Z.B. Regime shifts in the Changjiang (Yangtze River) Estuary: The role of concentrated benthic suspensions. Mar. Geol. 2021, 433, 106403. [Google Scholar] [CrossRef]
- Pacanowski, R.C.; Philander, S.G.H. Parameterization of vertical mixing in numerical models of tropical oceans. J. Phys. Oceanogr. 1981, 11, 1443–1451. [Google Scholar] [CrossRef]
- Davies, A.M.; Kwong, S.C.; Flather, R.A. Formulation of a variable-function three-dimensional model, with applications to the M2 and M4 tide on the North-West European Continental Shelf. Cont. Shelf Res. 1997, 17, 165–204. [Google Scholar] [CrossRef]
- Wan, Y.; Wang, L. Numerical investigation of the factors influencing the vertical profiles of current, salinity, and SSC within a turbidity maximum zone. Int. J. Sediment Res. 2017, 32, 20–33. [Google Scholar] [CrossRef]
- Karimpour, F.; Venayagamoorthy, S.K. A simple turbulence model for stably stratified wall-bounded flows. J. Geophys. Res. Ocean 2014, 119, 870–880. [Google Scholar] [CrossRef]
- Wan, Y.; Wu, H.; Roelvink, D.; Gu, F. Experimental study on fall velocity of fine sediment in the Yangtze Estuary, China. Ocean Eng. 2015, 103, 180–187. [Google Scholar] [CrossRef]
- Orton, P.M.; Kineke, G.C. Comparing calculated and observed vertical suspended sediment distribution from a Hudson River Estuary turbidity maximum. Estuar. Coast. Shelf Sci. 2001, 52, 401–410. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Zhu, J.; Chen, B.; Chen, Y. Quantitative relationship of runoff and tide to saltwater spilling over from the North Branch in the Changjiang Estuary: A numerical study. Estuar. Coast. Shelf Sci. 2006, 69, 125–132. [Google Scholar] [CrossRef]
- Dyer, K.R. Fine sediment particle transport in estuaries. In Physical Processes in Estuaries; Springer: Berlin/Heidelberg, Germany, 1988; pp. 295–310. [Google Scholar]
- Zhou, Z.; Ge, J.; van Maren, D.S.; Wang, Z.B.; Kuai, Y.; Ding, P. Study of Sediment Transport in a Tidal Channel-Shoal System: Lateral Effects and Slack-Water Dynamics. J. Geophys. Res. Oceans 2021, 126, e2020JC016334. [Google Scholar] [CrossRef]
- Uncles, R.J.; Elliott RC, A.; Weston, S.A. Lateral distributions of water, salt and sediment transport in a partly mixed estuary. In Coastal Engineering; American Society of Civil Engineers: New York, NY, USA, 1985; pp. 3067–3077. [Google Scholar] [CrossRef]
- Lyu, H.; Zhu, J. Impacts of Tidal Flat Reclamation on Saltwater Intrusion and Freshwater Resources in the Changjiang Estuary. J. Coast. Res. 2019, 35, 314–321. [Google Scholar] [CrossRef]
- Stacey, M.T.; Fram, J.P.; Chow, F.K. Role of tidally periodic density stratification in the creation of estuarine subtidal circulation. J. Geophys. Res. Earth Surf. 2008, 113, C08016. [Google Scholar] [CrossRef] [Green Version]
- Zhu, L.; He, Q.; Shen, J.; Wang, Y. The influence of human activities on morphodynamics and alteration of sediment source and sink in the Changjiang Estuary. Geomorphology 2016, 273, 52–62. [Google Scholar] [CrossRef]





| Stations | Tidal-Mean Depth (m) | Flood Tide | Ebb Tide | ||||
|---|---|---|---|---|---|---|---|
| Flood Durations (h) | Mean Velocity * (m s−1) | Maximum Velocity * (m s−1) | Ebb Durations (h) | Mean Velocity * (m s−1) | Maximum Velocity * (m s−1) | ||
| NC1 | 19.63 | 5.7 | 0.95 | 1.50 | 6.6 | 1.00 | 1.59 |
| NC2 | 9.23 | 5.9 | 0.84 | 0.95 | 6.7 | 0.90 | 1.11 |
| NC3 | 7.42 | 5.7 | 0.84 | 1.30 | 7.2 | 0.93 | 1.31 |
| NC4 | 14.39 | 5.2 | 0.88 | 1.38 | 7.3 | 1.04 | 1.58 |
| NC5 | 5.82 | 5.3 | 0.54 | 1.20 | 7.7 | 0.91 | 1.42 |
| Station | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T1 + T2 | T3 + T4 + T5 | |
|---|---|---|---|---|---|---|---|---|---|---|
| NC1 | 1.31 | −0.43 | 0.02 | −1.10 | −0.06 | −0.54 | −0.20 | 0.88 | −1.14 | −0.59 |
| NC2 | 0.19 | −0.12 | 0.00 | 0.18 | 0.01 | −0.02 | 0.01 | 0.07 | 0.19 | 0.32 |
| NC3 | 0.31 | −0.22 | 0.00 | 0.16 | −0.02 | −0.02 | 0.03 | 0.09 | 0.14 | 0.25 |
| NC4 | 1.08 | −0.28 | 0.02 | −0.65 | −0.06 | −0.36 | −0.13 | 0.80 | −0.69 | −0.06 |
| NC5 | 0.70 | −0.15 | 0.05 | −0.78 | −0.12 | −0.03 | 0.02 | 0.55 | −0.85 | −0.30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, L.; Cheng, H.; Zhang, E.; Wang, Y. Lateral Variation of Tidal Mixing Asymmetry and Its Impact on the Longitudinal Sediment Transport in Turbidity Maximum Zone of Salt Wedge Estuary. J. Mar. Sci. Eng. 2022, 10, 907. https://doi.org/10.3390/jmse10070907
Teng L, Cheng H, Zhang E, Wang Y. Lateral Variation of Tidal Mixing Asymmetry and Its Impact on the Longitudinal Sediment Transport in Turbidity Maximum Zone of Salt Wedge Estuary. Journal of Marine Science and Engineering. 2022; 10(7):907. https://doi.org/10.3390/jmse10070907
Chicago/Turabian StyleTeng, Lizhi, Heqin Cheng, Erfeng Zhang, and Yajun Wang. 2022. "Lateral Variation of Tidal Mixing Asymmetry and Its Impact on the Longitudinal Sediment Transport in Turbidity Maximum Zone of Salt Wedge Estuary" Journal of Marine Science and Engineering 10, no. 7: 907. https://doi.org/10.3390/jmse10070907






