A Novel Integrated Gliding and Flapping Propulsion Biomimetic Manta-Ray Robot
Abstract
:1. Introduction
2. The Design of the Manta Ray Robot
2.1. The Shape Design of the Manta Ray Robot
2.2. The Structure Design of the Manta Ray Robot
2.3. The Gliding System Design of the Manta Ray Robot
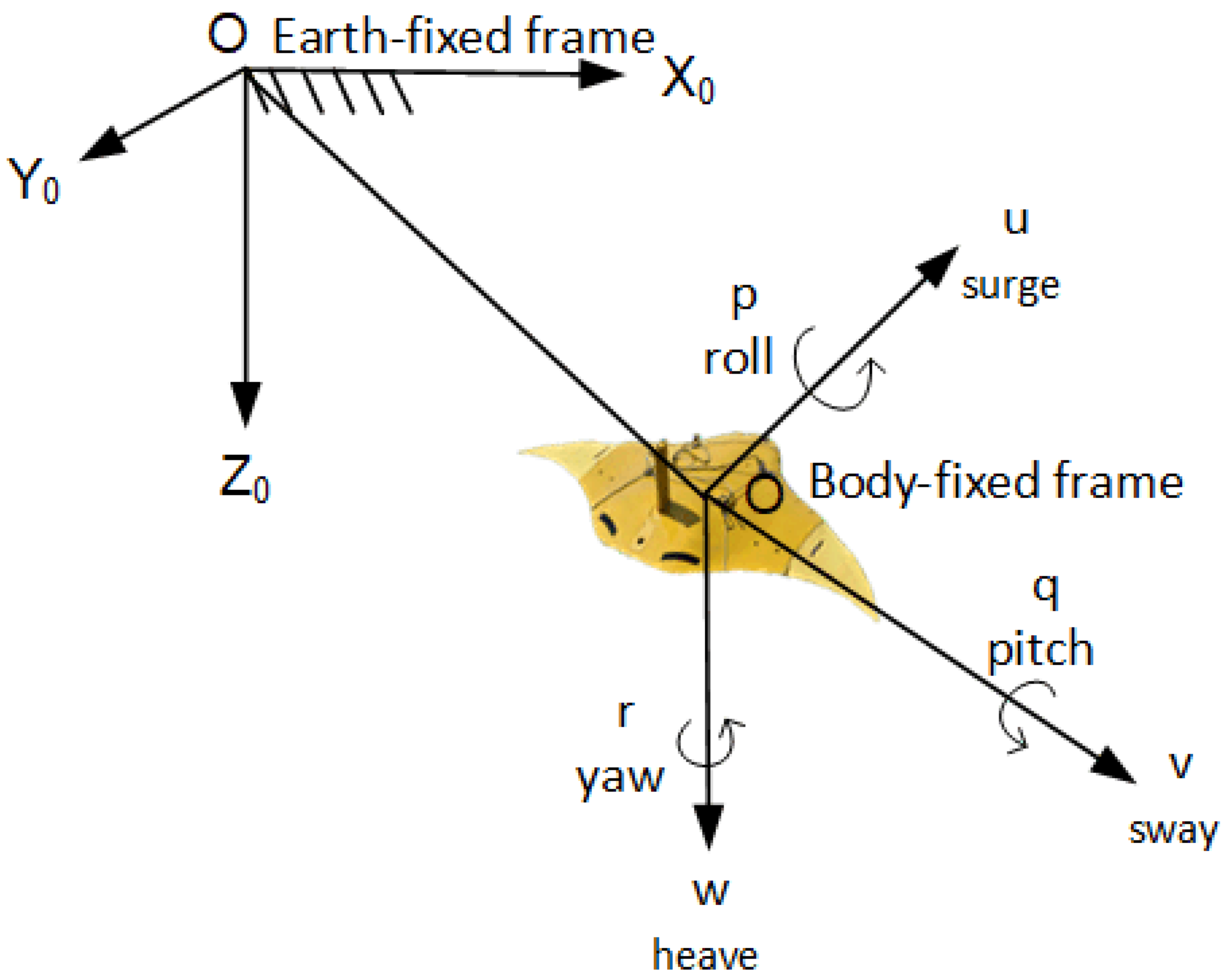
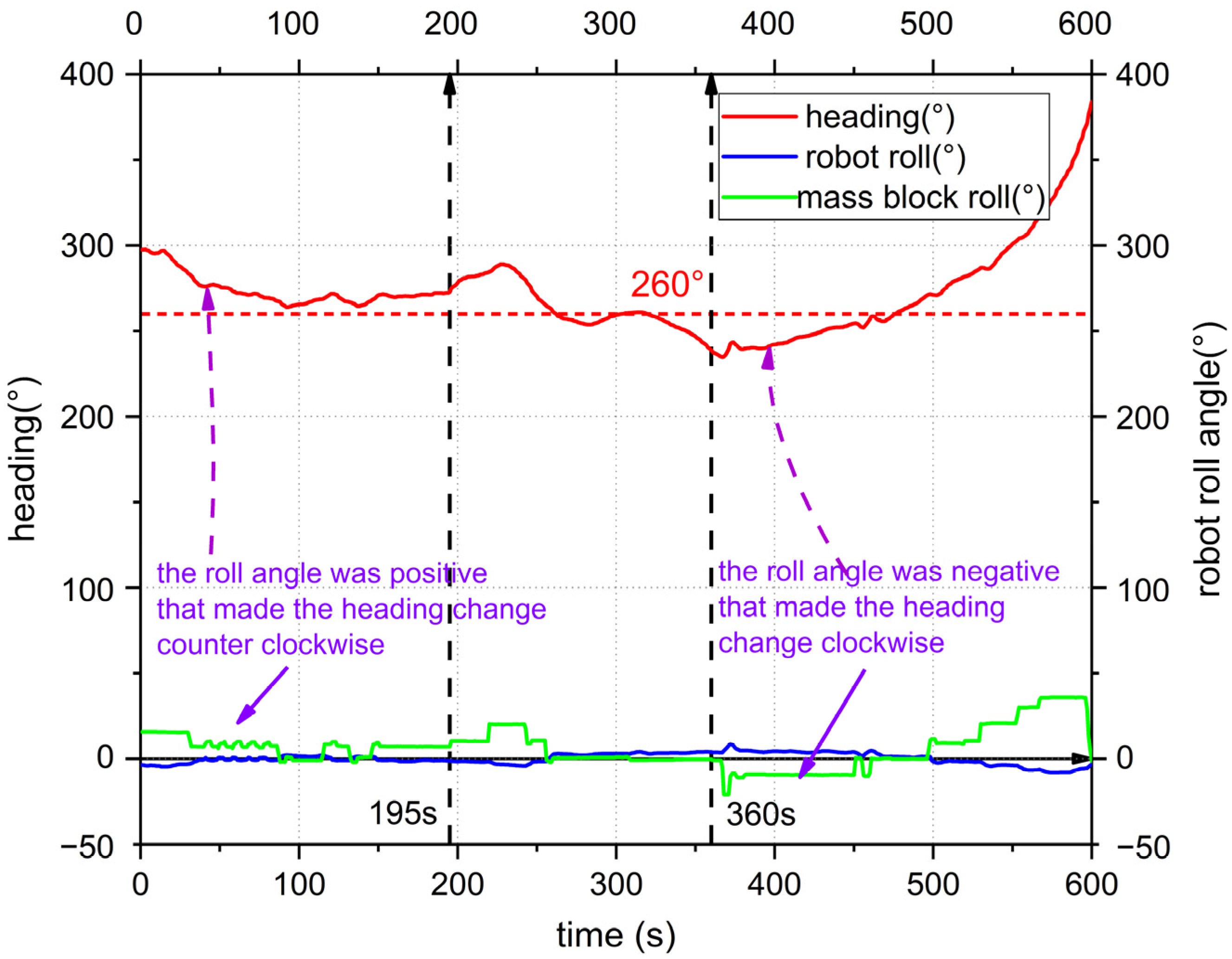
2.3.1. The Gliding Motion Analysis of the Manta Ray Robot
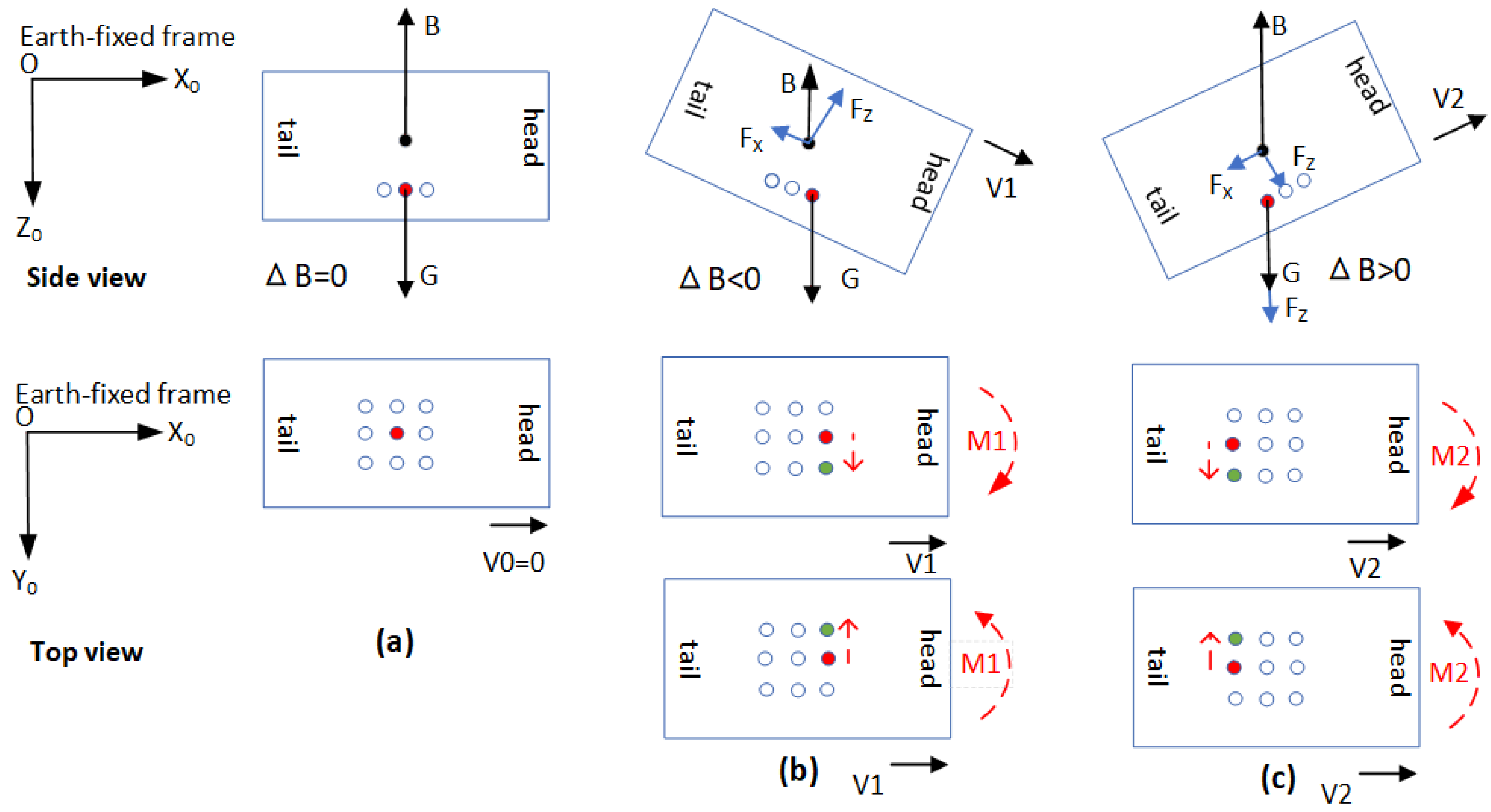
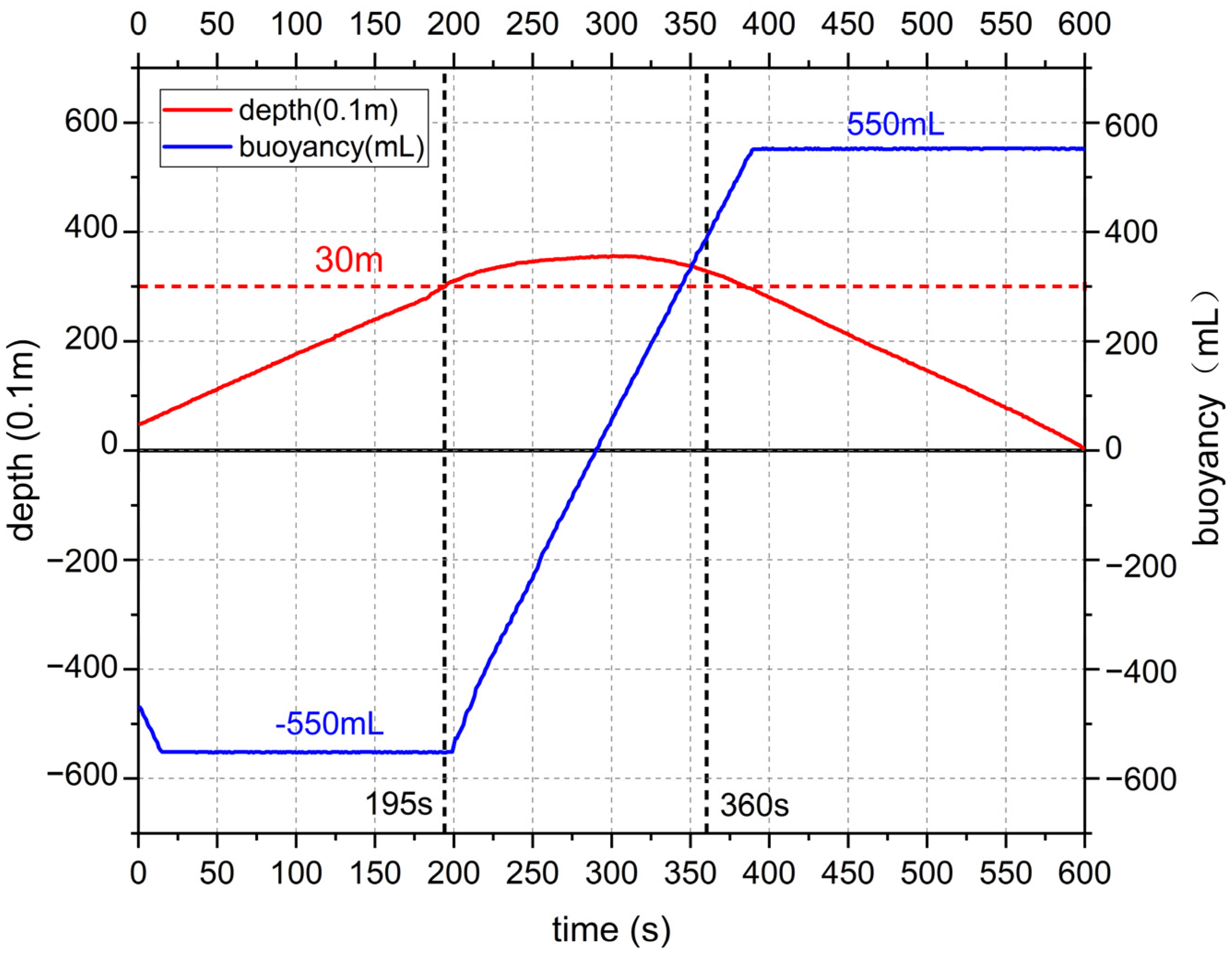
2.3.2. The Buoyancy-Adjustment System Design
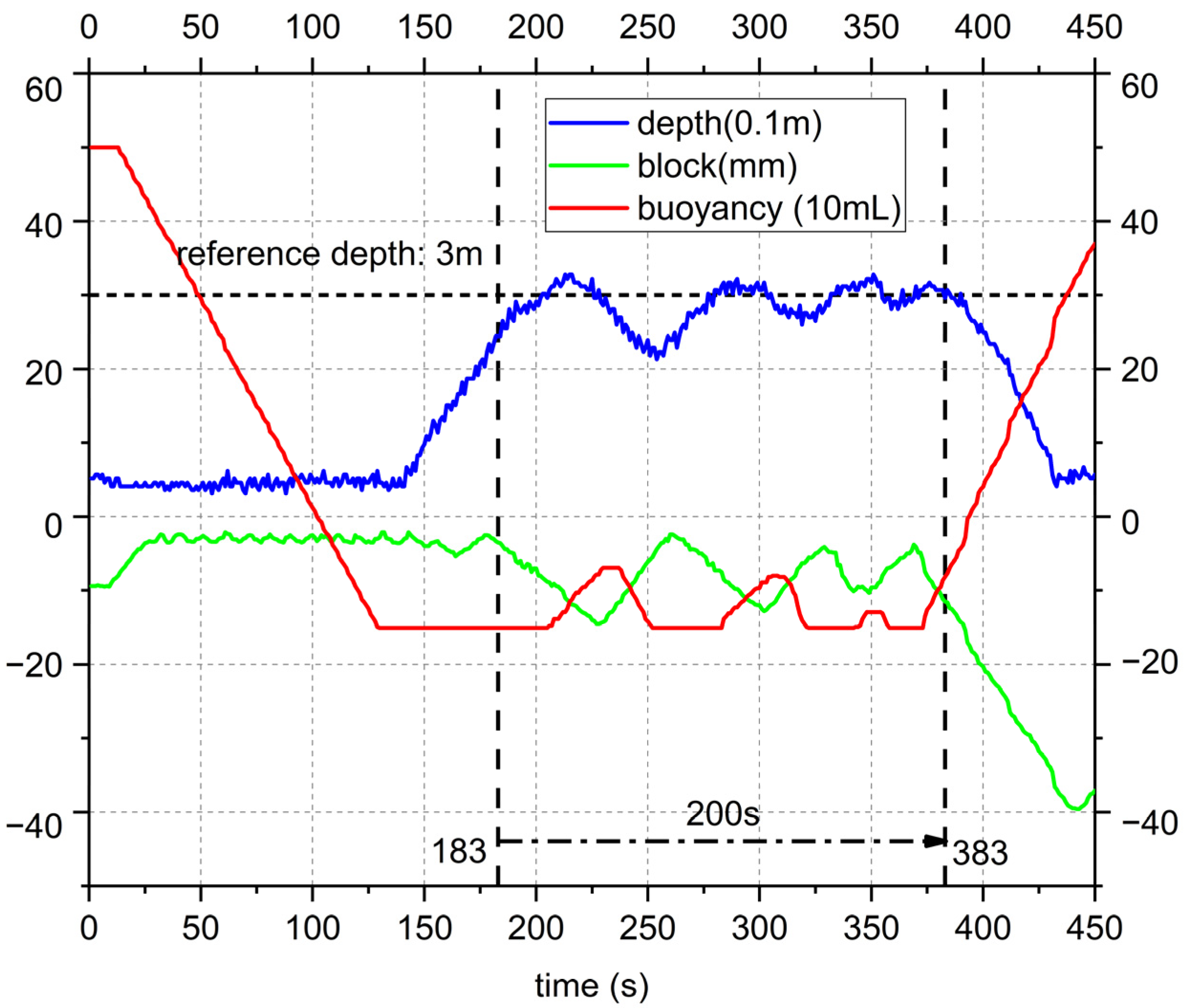
2.3.3. The Mass-Adjustment System Design
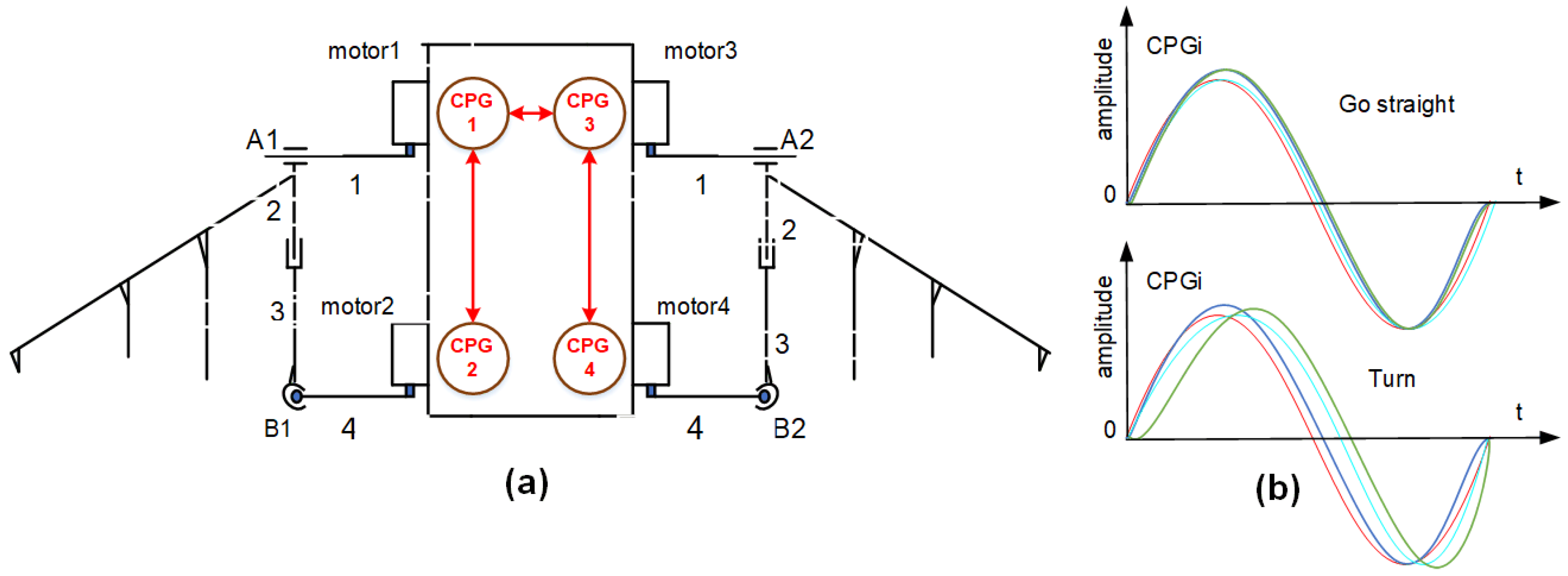
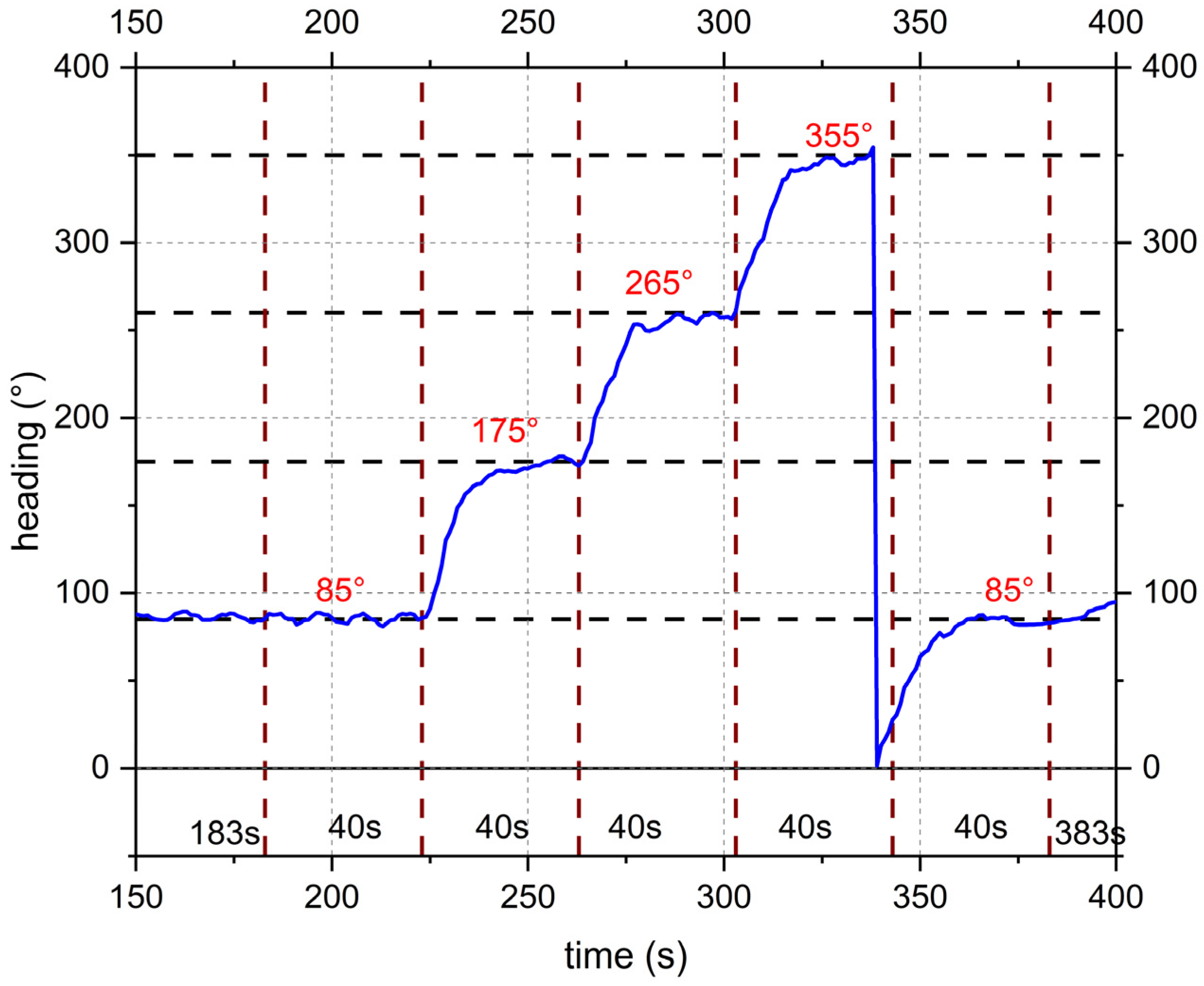
2.4. The Flapping Propulsion System Design
3. Experiments and Results
3.1. Setup of the Experiments
3.2. The Experiment Results
3.2.1. The Gliding Experiment Results
3.2.2. The Flapping Propulsion Experiment Results
4. Discussion
- (1)
- The accuracy of the heading control based on the centroid mechanism is not high, which affects the gliding speed.
- (2)
- The material of the flexible flapping wing is a skeleton plus fiber skin, leading to considerably more resistance compared with real fish during flutter propulsion.
- (3)
- The flapping propulsion model can achieve a highly maneuverable movement. The motor’s power is limited.
- (4)
- We located the buoyancy-adjustment system in the head of the prototype; the buoyancy changed with the alteration of the location of the centroid, which would affect the stability of the control system.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Domenici, P.; Blake, R.W. Review the Kinematics and Performance of Fish Fast-Start Swimming. J. Exp. Biol. 1997, 200, 1165–1178. [Google Scholar] [CrossRef] [PubMed]
- Colgate, J.E.; Lynch, K.M. Mechanics and Control of Swimming: A Review. IEEE J. Ocean. Eng. 2004, 29, 660–673. [Google Scholar] [CrossRef]
- Roper, D.T.; Sharma, S.; Sutton, R.; Culverhouse, P. A Review of Developments towards Biologically Inspired Propulsion Systems for Autonomous Underwater Vehicles. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2011, 225, 77–96. [Google Scholar] [CrossRef]
- Wu, T.Y. Fish Swimming and Bird/Insect Flight. Annu. Rev. Fluid Mech. 2011, 43, 25–58. [Google Scholar] [CrossRef]
- Gray, J. Studies in Animal Locomotion, VI. The Propulsive Powers of the Dolphin. J. Exp. Biol. 1936, 13, 192–199. [Google Scholar] [CrossRef]
- Triantafyllou, M.S.; Triantafyllou, G.S. An Efficient Swimming Machine. Sci. Am. 1995, 272, 64–70. [Google Scholar] [CrossRef]
- Stix, G. RoboTuna. Sci. Am. 1994, 270, 142. [Google Scholar] [CrossRef]
- Rus, D.; Tolley, M.T. Design, Fabrication and Control of Soft Robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Wang, S.; Wang, Y.; Cheng, L.; Tan, M. Development and Motion Control of Biomimetic Underwater Robots: A Survey. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 833–844. [Google Scholar] [CrossRef]
- Ahmed, F.; Waqas, M.; Javed, B.; Soomro, A.M.; Kumar, S.; Ashraf, H.; Khan, U.; Kim, K.H.; Choi, K.H. Decade of Bio-Inspired Soft Robots: A Review. Smart Mater. Struct. 2022, 31, 7. [Google Scholar] [CrossRef]
- Ahmed, F.; Waqas, M.; Shaikh, B.; Khan, U.; Soomro, A.M.; Kumar, S.; Ashraf, H.; Memon, F.H.; Choi, K.H. Multi-Material Bio-Inspired Soft Octopus Robot for Underwater Synchronous Swimming. J. Bionic Eng. 2022, 1–13. [Google Scholar] [CrossRef]
- Soomro, A.M.; Memon, F.H.; Lee, J.-W.; Ahmed, F.; Kim, K.H.; Kim, Y.S.; Choi, K.H. Fully 3D Printed Multi-Material Soft Bio-Inspired Frog for Underwater Synchronous Swimming. Int. J. Mech. Sci. 2021, 210, 106725. [Google Scholar] [CrossRef]
- Ahmed, F.; Muhammad, W.; Javed, B.; Soomro, A.M.; Kumar, S.; Hina, A.; Khan, U.; Kim, K.H.; Choi, K.H. Decade of Bio-Inspired Soft Robots: A Review. Smart Mater. Struct. 2022, 31, 073002. [Google Scholar] [CrossRef]
- Sfakiotakis, M.; Lane, D.M.; Davies, J. Review of Fish Swimming Modes for Aquatic Locomotion. IEEE J Ocean. Eng. 1999, 24, 237–252. [Google Scholar] [CrossRef] [Green Version]
- Xie, F.; Zuo, Q.; Chen, Q.; Fang, H.; He, K.; Du, R.; Zhong, Y.; Li, Z. Designs of the Biomimetic Robotic Fishes Performing Body and/or Caudal Fin (BCF) Swimming Locomotion: A Review. J. Intell. Robot. Syst. 2021, 102, 13. [Google Scholar] [CrossRef]
- Scaradozzi, D.; Palmieri, G.; Costa, D.; Pinelli, A. BCF Swimming Locomotion for Autonomous Underwater Robots: A Review and a Novel Solution to Improve Control and Efficiency. Ocean Eng. 2017, 130, 437–453. [Google Scholar] [CrossRef]
- Yu, J.; Wu, Z.; Su, Z.; Wang, T.; Qi, S. Motion Control Strategies for a Repetitive Leaping Robotic Dolphin. IEEE/ASME Trans. Mechatron. 2019, 24, 913–923. [Google Scholar] [CrossRef]
- Manta Ray FAQ. Available online: http://www.elasmo-research.org/education/topics/lh_manta_faq.htm (accessed on 23 March 2022).
- Xu, Y.; Zong, G.; Bi, S.; Gao, J. Initial Development of a Flapping Propelled Unmanned Underwater Vehicle (UUV). In Proceedings of the 2007 IEEE International Conference on Robotics and Biomimetics (ROBIO), Sanya, China, 15–18 December 2007; pp. 524–529. [Google Scholar]
- Cai, Y.; Bi, S.; Zhang, L.; Gao, J. Design of a Robotic Fish Propelled by Oscillating Flexible Pectoral Foils. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 2138–2142. [Google Scholar]
- Gao, J.; Bi, S.; Li, J.; Liu, C. Design and Experiments of Robot Fish Propelled by Pectoral Fins. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guilin, China, 19–23 December 2009; p. 6. [Google Scholar]
- Cai, Y.; Bi, S.; Zhang, L. Design and Implication of a Bionic Pectoral Fin Imitating Cow-Nosed Ray. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; p. 5. [Google Scholar]
- Zheng, L.; Bi, S.; Cai, Y.; Niu, C. Design and Optimization of a Robotic Fish Mimicking Cow-Nosed Ray. In Proceedings of the 2010 IEEE International Conference on Robotics and Biomimetics, Tianjin, China, 14–18 December 2010; pp. 1075–1080. [Google Scholar]
- Ma, H.; Cai, Y.; Wang, Y.; Bi, S.; Gong, Z. A Biomimetic Cownose Ray Robot Fish with Oscillating and Chordwise Twisting Flexible Pectoral Fins. Ind. Robot Int. J. 2015, 42, 214–221. [Google Scholar] [CrossRef]
- BOSS Project|EvoLogics. Available online: https://evologics.de/projects/boss (accessed on 23 March 2022).
- Glushko, I.; Olenew, E.; Komar, M.; Kniese, L.; Sokolovskyi, R.; Kebkal, O.; Bannasch, R.; Kebkal, K. Software Control Architecture for the BOSS Manta Ray AUV Actuation System. In Proceedings of the 2018 IEEE/OES Autonomous Underwater Vehicle Workshop (AUV), Porto, Portugal, 6–9 November 2018; pp. 1–5. [Google Scholar]
- Teubler, T.; Hellbruck, H. Design of Expert Systems for Autonomous Underwater Vehicle Control. In Proceedings of the OCEANS 2016 MTS/IEEE Monterey, Monterey, CA, USA, 19–23 September 2016; pp. 1–6. [Google Scholar]
- Wang, Z.; Wang, Y.; Li, J.; Hang, G. A Micro Biomimetic Manta Ray Robot Fish Actuated by SMA. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guilin, China, 19–23 December 2009; pp. 1809–1813. [Google Scholar]
- Zhu, Y.; Liu, Y.; Zhang, L.; Wang, Y.; Niu, W.; Huang, C. Dynamic Model and Motion Characteristics of an Underwater Glider with Manta-Inspired Wings. J. Bionic Eng. 2022, 19, 1–15. [Google Scholar] [CrossRef]
- Zhou, C.; Low, K.-H. Better Endurance and Load Capacity: An Improved Design of Manta Ray Robot (RoMan-II). J. Bionic Eng. 2010, 7, S137–S144. [Google Scholar] [CrossRef]
- Zhou, C.; Low, K.H. Design and Locomotion Control of a Biomimetic Underwater Vehicle With Fin Propulsion. IEEE/ASME Trans. Mechatron. 2012, 17, 25–35. [Google Scholar] [CrossRef]
- Cao, Y.; Lu, Y.; Cai, Y.; Bi, S.; Pan, G. CPG-Fuzzy-Based Control of a Cownose-Ray-like Fish Robot. Ind. Robot Int. J. Robot. Res. Appl. 2019, 46, 779–791. [Google Scholar] [CrossRef]
- Bal, C.; Ozmen Koca, G.; Korkmaz, D.; Akpolat, Z.H.; Ay, M. CPG-Based Autonomous Swimming Control for Multi-Tasks of a Biomimetic Robotic Fish. Ocean Eng. 2019, 189, 106334. [Google Scholar] [CrossRef]
- Sherman, J.; Davis, R.E.; Owens, W.B.; Valdes, J. The Autonomous Underwater Glider “Spray”. IEEE J. Ocean. Eng. 2001, 26, 437–446. [Google Scholar] [CrossRef] [Green Version]
- Hao, Y.; Cao, Y.; Cao, Y.; Huang, Q.; Pan, G. Course Control of a Manta Robot Based on Amplitude and Phase Differences. J. Mar. Sci. Eng. 2022, 10, 285. [Google Scholar] [CrossRef]
- Xing, C.; Cao, Y.; Cao, Y.; Pan, G.; Huang, Q. Asymmetrical Oscillating Morphology Hydrodynamic Performance of a Novel Bionic Pectoral Fin. J. Mar. Sci. Eng. 2022, 10, 289. [Google Scholar] [CrossRef]
- Ijspeert, A.J. Central Pattern Generators for Locomotion Control in Animals and Robots: A Review. Neural Netw. 2008, 21, 642–653. [Google Scholar] [CrossRef]
- Crespi, A.; Ijspeert, A.J. Online Optimization of Swimming and Crawling in an Amphibious Snake Robot. IEEE Trans. Robot. 2008, 24, 75–87. [Google Scholar] [CrossRef] [Green Version]
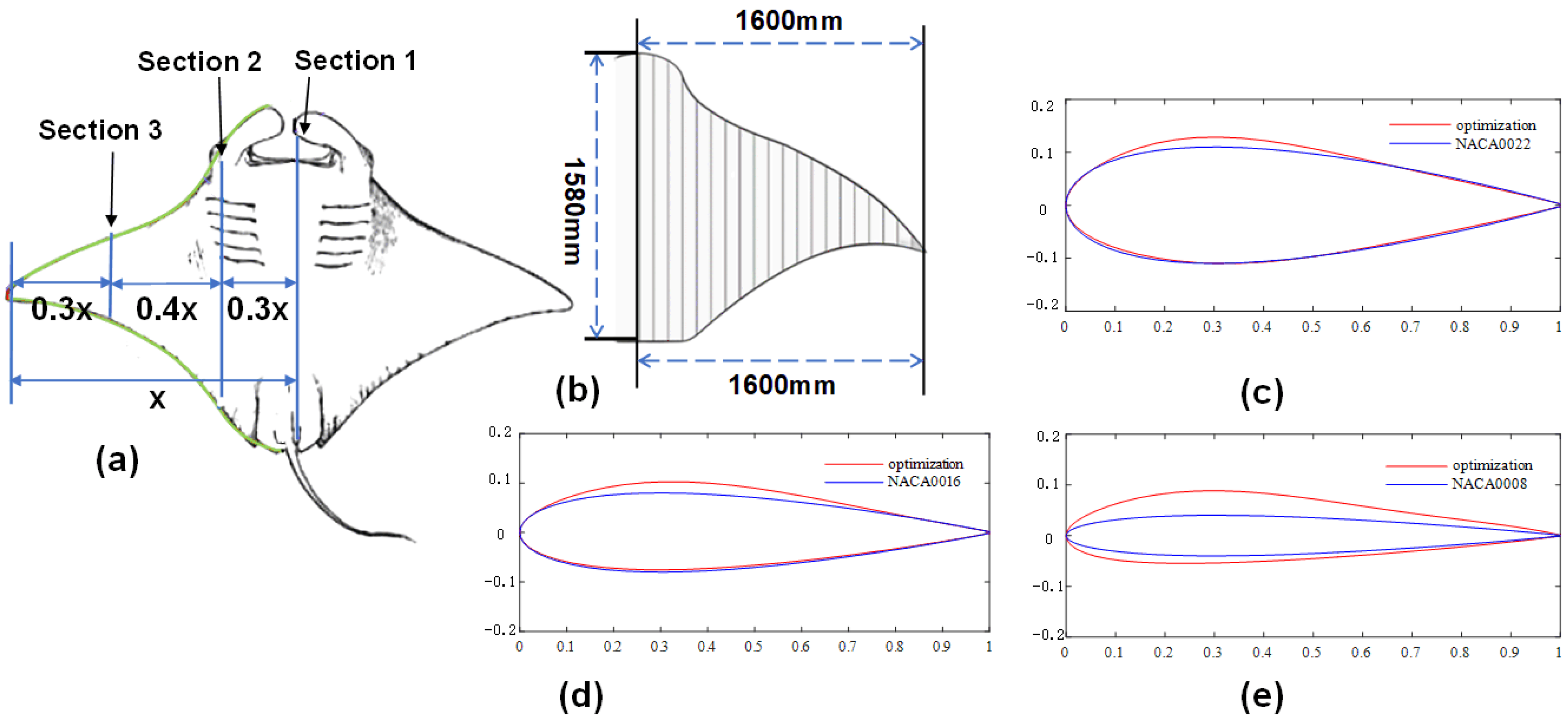



| Term | Spray [34] | BWUG [29] | Robotic Manta [35] | Robot Dolphin [17] | Proposed Robot |
|---|---|---|---|---|---|
| Length × Width × height | 2 m × 1.2 m × 0.3 m | 2.3 m × 1.3 m | 0.6 m × 0.8 m × 0.15 m | 0.72 m × 0.12 m × 0.13 m | 1.5 m × 3.2 m × 0.5 m |
| Payload capacity | Yes | Yes | No | No | Yes |
| Multiple propulsion modes | No | Yes | No | No | Yes |
| Bionic shape | No | No | Yes | Yes | Yes |
| Adapts to harsh underwater environment | Yes | Yes | No | No | Yes |
| DOF | Inertial Position and Euler Angles | Body-Fixed Velocities | Forces and Moments |
|---|---|---|---|
| Motion in the x-direction(surge) | x | X | |
| Motion in the y-direction(sway) | y | Y | |
| Motion in the z-direction(heave) | z | Z | |
| Rotation about the x-axis | p | K | |
| Rotation about the y-axis | q | M | |
| Rotation about the y-axis | r | n |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Pan, G.; Cao, Y.; Huang, Q.; Cao, Y. A Novel Integrated Gliding and Flapping Propulsion Biomimetic Manta-Ray Robot. J. Mar. Sci. Eng. 2022, 10, 924. https://doi.org/10.3390/jmse10070924
Zhang D, Pan G, Cao Y, Huang Q, Cao Y. A Novel Integrated Gliding and Flapping Propulsion Biomimetic Manta-Ray Robot. Journal of Marine Science and Engineering. 2022; 10(7):924. https://doi.org/10.3390/jmse10070924
Chicago/Turabian StyleZhang, Daili, Guang Pan, Yonghui Cao, Qiaogao Huang, and Yong Cao. 2022. "A Novel Integrated Gliding and Flapping Propulsion Biomimetic Manta-Ray Robot" Journal of Marine Science and Engineering 10, no. 7: 924. https://doi.org/10.3390/jmse10070924






