Ship’s Wake on a Finite Water Depth in the Presence of a Shear Flow
Abstract
:1. Introduction
- 1.
- Collinear (Section 3.1),
- 2.
- Cross (Section 3.2),
- 3.
- Inclined (Section 3.3).
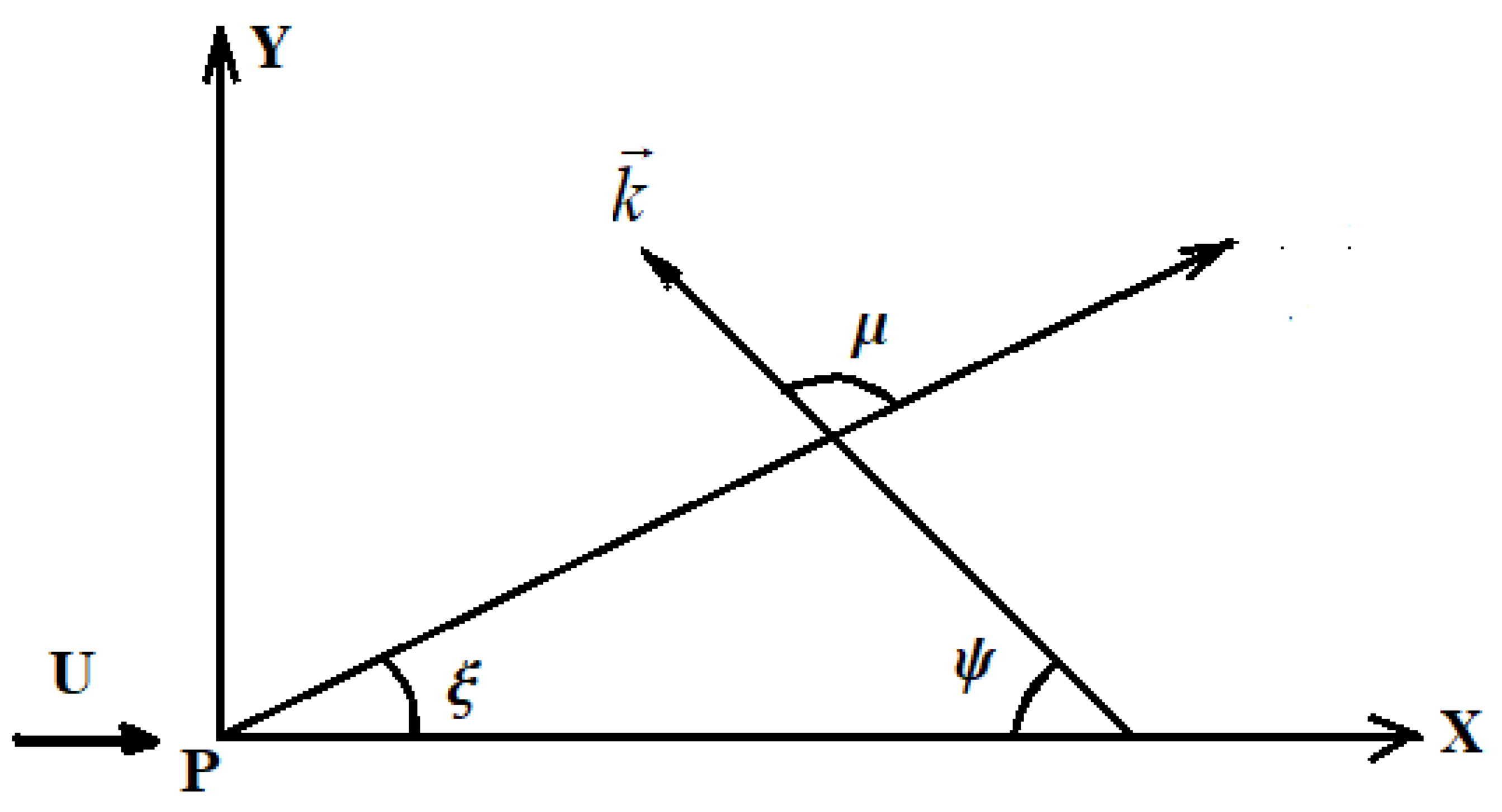
2. Ship Wake Model
3. Results
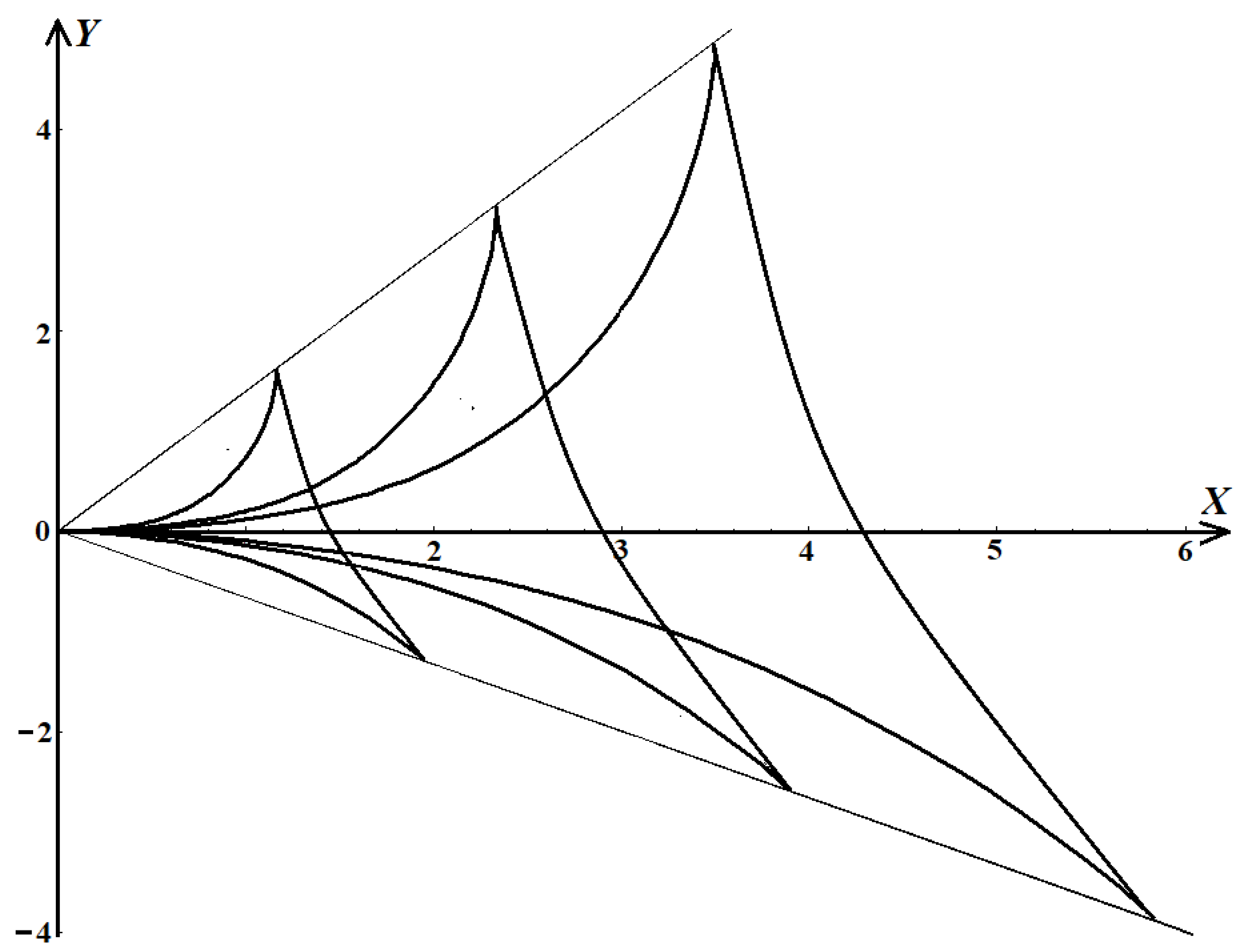
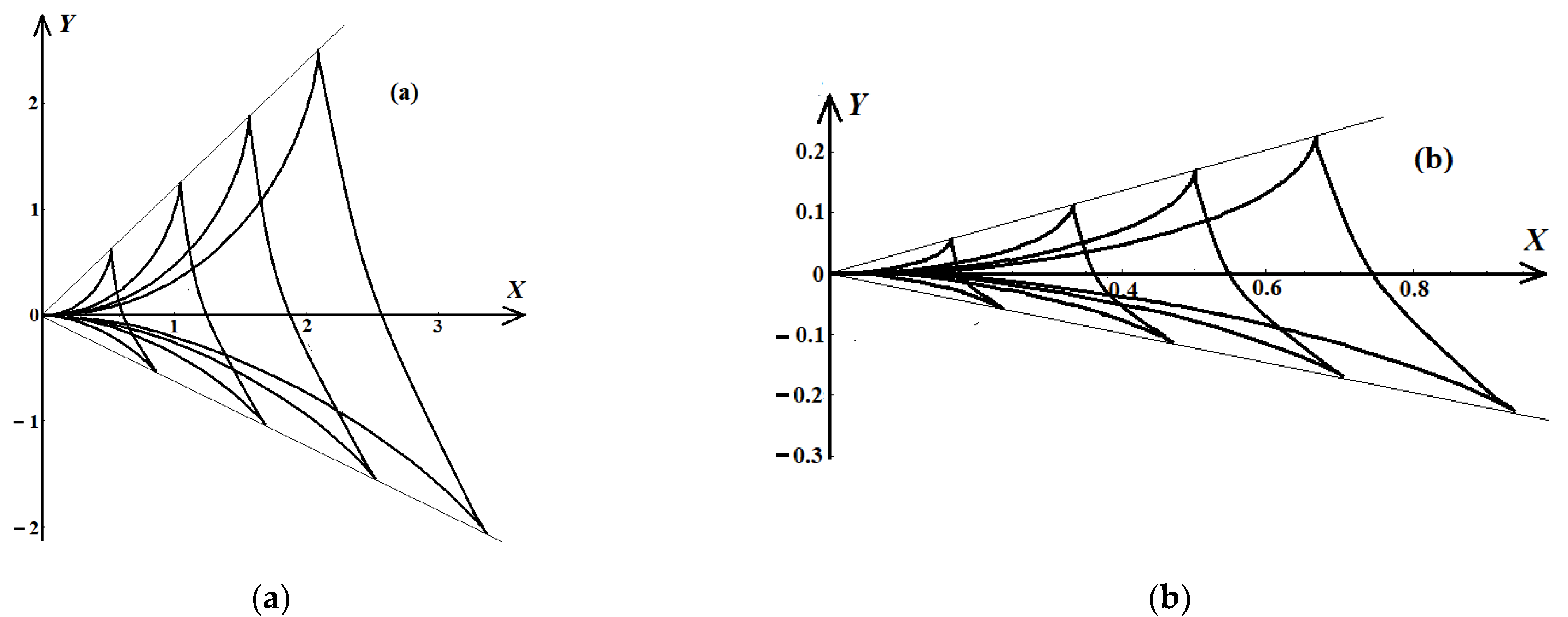
3.1. Ship Wake at Finite Water Depth
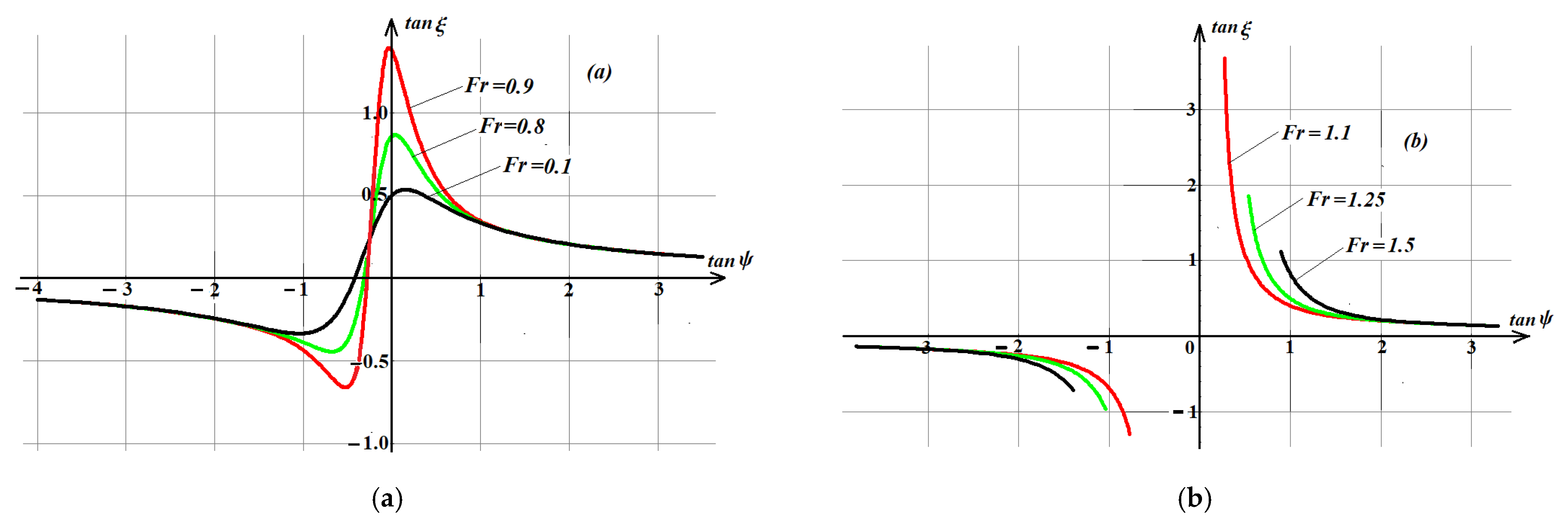
3.2. Collinear Propagation of the Ship and Shear Flow
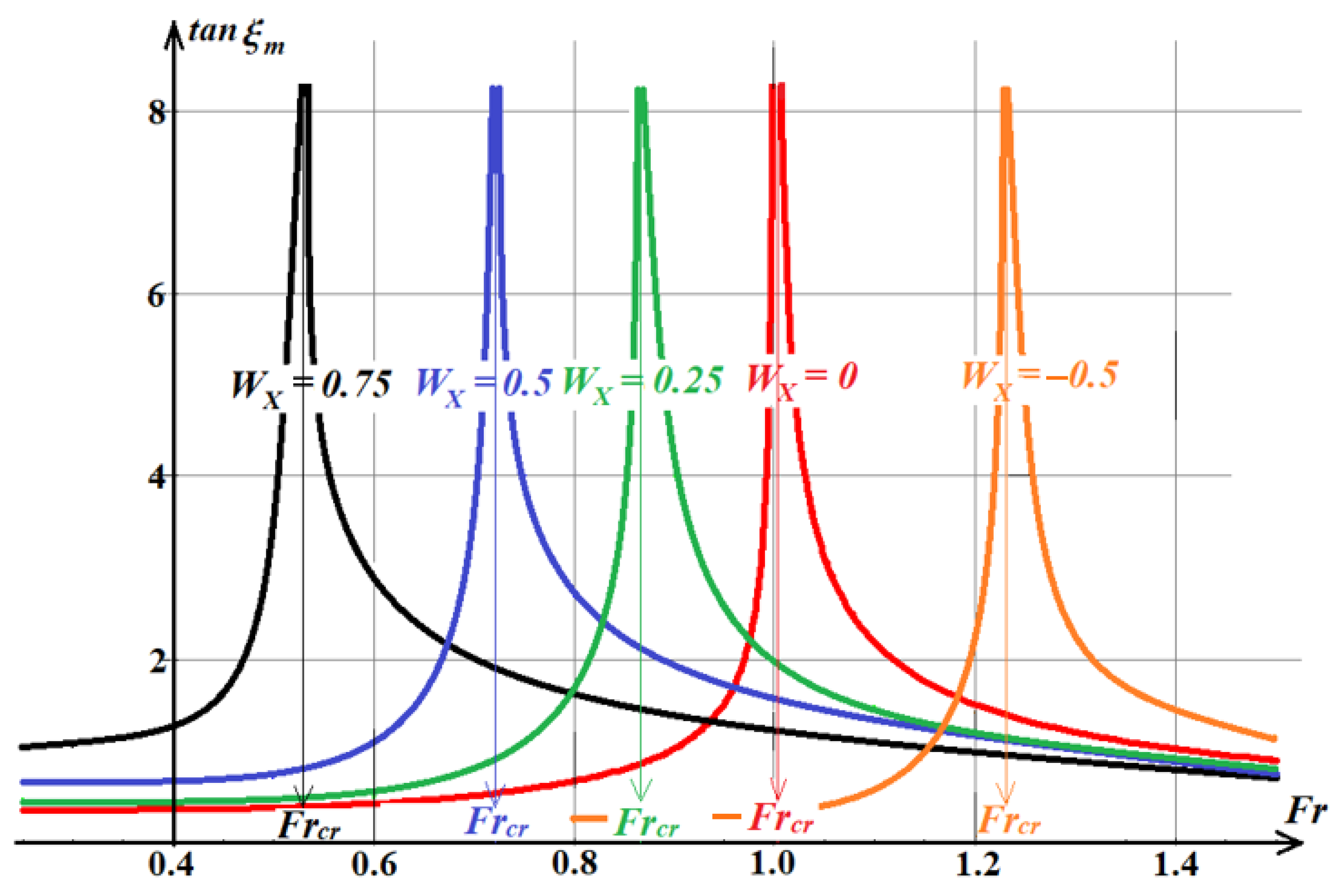
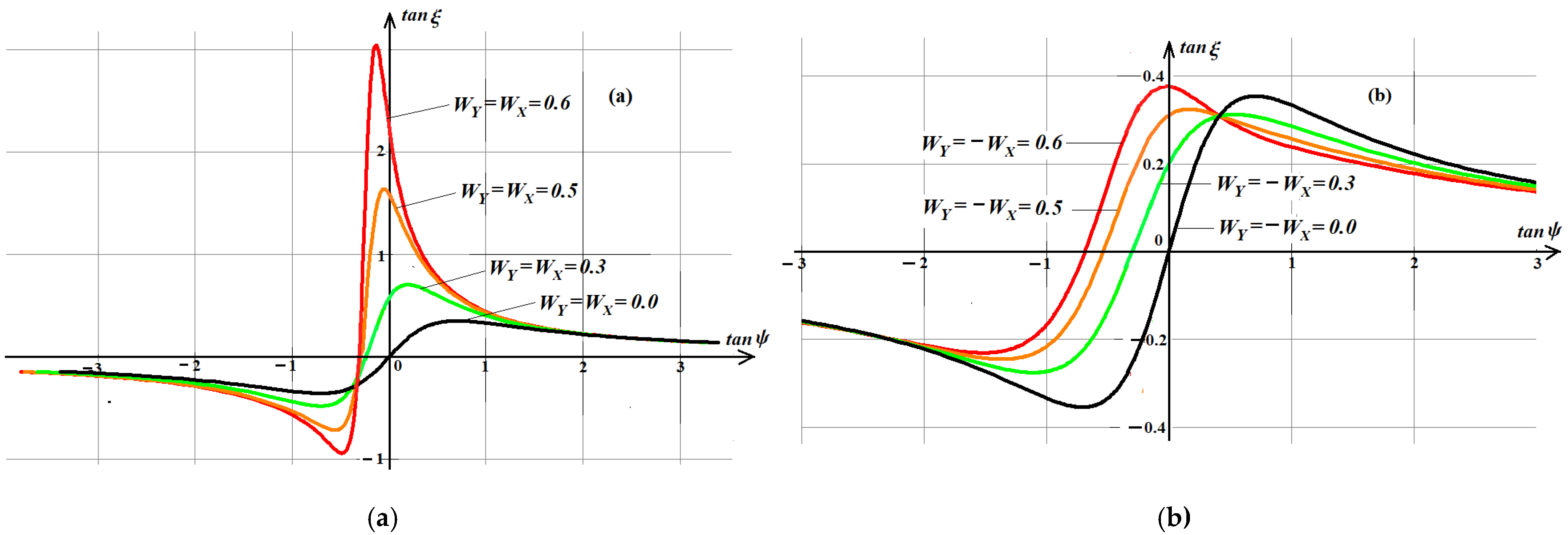
3.3. Cross Shear Flow
3.4. Inclined Direction of the Shear Current
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eldhuset, K. An Automatic Ship and Ship Wake Detection System for Spaceborne SAR images in Coastal Regions. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1010–1019. [Google Scholar] [CrossRef]
- Kuo, J.M.; Chen, K.S. The Application of Wavelets Correlator for Ship Wake Detection in SAR Images. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1506–1511. [Google Scholar]
- Tings, B.; Velotto, D. Comparison of ship wake detectability on C-band and X-band SAR. Int. J. Remote Sens. 2018, 39, 4451–4468. [Google Scholar] [CrossRef] [Green Version]
- Graziano, M.D.; D’Errico, M.; Rufino, G. Wake component detection in X-band SAR images for ship heading and velocity estimation. Remote Sens. 2016, 8, 498. [Google Scholar] [CrossRef] [Green Version]
- Karakuş, O.; Rizaev, I.; Achim, A. Ship Wake Detection in SAR Images via Sparse Regularization. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1665–1677. [Google Scholar] [CrossRef] [Green Version]
- Faltinsen, O.M. Hydrodynamics of High-Speed Marine Vehicles; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Li, Y.; Ellingsen, S.E. Ship waves on uniform shear current at finite depth: Wave resistance and critical velocity. J. Fluid Mech. 2016, 791, 539–567. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Smeltzer, B.K.; Ellingsen, S.E. Transient wave resistance upon a shear current. Eur. J. Mech. B Fluids 2019, 73, 180–192. [Google Scholar] [CrossRef] [Green Version]
- Thomson, S.W. On ship waves. Proc. Inst. Mech. Eng. 1887, 38, 409–434. [Google Scholar] [CrossRef]
- Reed, A.; Milgram, J. Ship Wakes and Their Radar Images. Annu. Rev. Fluid Mech. 2002, 34, 469–502. [Google Scholar] [CrossRef] [Green Version]
- Shemdin, O.H. Synthetic Aperture Radar Imaging of Ship Wakes in the Gulf of Alaska. J. Geophys. Res. Oceans 1990, 95, 16319–16338. [Google Scholar] [CrossRef]
- Hennings, I.; Romeiser, R.; Alpers, W.; Viola, A. Radar Imaging of Kelvin Arms of Ship Wakes. Int. J. Remote Sens. 1999, 20, 2519–2543. [Google Scholar] [CrossRef]
- Melsheimer, C.; Lim, H.; Shen, C. Observation and Analysis of Ship Wakes in ERS-SAR and SPOT Images. In Proceedings of the 20th Asian Conference on Remote Sensing, Hong Kong, China, 22–25 November 1999; pp. 554–559. [Google Scholar]
- Alpers, W.; Romeiser, R.; Hennings, I. On the Radar Imaging Mechanism of Kelvin Arms of Ship Wakes. In Proceedings of the IGARSS ‘98, Piscataway, NJ, USA, 6–10 July 1998; pp. 1932–1934. [Google Scholar]
- Tunaley, J.K.E.; Buller, E.H.; Wu, K.H.; Rey, M.T. The Simulation of the SAR Images of a Ship Wake. IEEE Trans. Geosci. Remote Sens. 1991, 29, 149–155. [Google Scholar] [CrossRef]
- Tunaley, J. The Unsteady Wake from a Body Moving Near an Internal Layer. In Proceedings of the 5th Canadian Conference on Marine Hydromechanics and Structures, St. Johns, NL, Canada, 16–17 October 1999; pp. 5–13. [Google Scholar]
- Shugan, I.V.; Lee, K.J.; Sun, A.J. Kelvin wake in the presence of surface waves. Phys. Lett. A 2006, 357, 232–235. [Google Scholar] [CrossRef]
- Fang, M.C.; Yang, R.Y.; Shugan, I.V. Kelvin Ship Wake in the Wind Waves Field and on the Finite Sea Depth. J. Mech. 2011, 27, 71–77. [Google Scholar] [CrossRef]
- Akylas, T. Unsteady and nonlinear effects near the cusp lines of the Kelvin ship-wave pattern. J. Fluid Mech. 1987, 175, 333–342. [Google Scholar] [CrossRef]
- Chen, H.; Zou, Q. Effects of following and opposing vertical current shear on nonlinear wave interactions. Appl. Ocean Res. 2019, 89, 23–35. [Google Scholar] [CrossRef]
- Peregrine, D.H. Interaction of water waves and currents. In Advances in Applied Mechanics; Elsevier: Amsterdam, The Netherlands, 1976; Volume 16, pp. 9–117. [Google Scholar]
- Teles da Silva, A.F.; Peregrine, D.H. Steep, steady surface waves on water of finite depth with constant vorticity. J. Fluid Mech. 1988, 195, 281–302. [Google Scholar] [CrossRef]
- Ellingsen, S.E.; Brevik, I. How linear surface waves are affected by a current with constant vorticity. Eur. J. Phys. 2014, 35, 025005. [Google Scholar] [CrossRef] [Green Version]
- Nwogu, O.G. Interaction of finite-amplitude waves with vertically sheared current fields. J. Fluid Mech. 2009, 627, 179–213. [Google Scholar] [CrossRef] [Green Version]
- Shrira, V.I. Surface waves on shear currents: Solution of the boundary-value problem. J. Fluid Mech. 1993, 252, 565–584. [Google Scholar] [CrossRef]
- Ellingsen, S.E. Initial surface disturbance on a shear current: The Cauchy-Poisson problem with a twist. Phys. Fluids 2014, 26, 082104. [Google Scholar] [CrossRef] [Green Version]
- Ellingsen, S.E.; Li, Y. Approximate dispersion relations for waves on arbitrary shear flows. J. Geophys. Res. Oceans 2017, 122, 9889–9905. [Google Scholar] [CrossRef] [Green Version]
- Ellingsen, S.E. Ship waves in the presence of uniform vorticity. J. Fluid Mech. 2014, 742, R2. [Google Scholar] [CrossRef] [Green Version]
- Smeltzer, B.; Ellingsen, S.E. Surface waves on currents with arbitrary vertical shear. Phys. Fluids 2017, 29, 047102. [Google Scholar] [CrossRef] [Green Version]
- Smeltzer, B.; Æsøy, E.; Ellingsen, S. Observation of surface wave patterns modified by sub-surface shear currents. J. Fluid Mech. 2019, 873, 508–530. [Google Scholar] [CrossRef] [Green Version]
- Lighthill, M.J.; Whitham, G.B. On Kinematic Waves: I. Flood Movement in Long Rivers; II. Theory of Traffic Flow on Long Crowded Roads. Proc. R. Soc. Lond. A 1955, 229, 281–345. [Google Scholar]
- Whitham, G.B. Linear and Nonlinear Waves; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Shugan, I.V.; Chen, Y.-Y. Kinematics of the Ship’s Wake in the Presence of a Shear Flow. J. Mar. Sci. Eng. 2021, 9, 7. [Google Scholar] [CrossRef]
- Phillips, O.M. The Dynamics of the Upper Ocean, 2nd ed.; Cambridge University Press: Cambridge, UK, 1977. [Google Scholar]
- Caplier, C.; Rousseaux, G.; Calluaud, D.; David, L. Energy distribution in shallow water ship wakes from a spectral analysis of the wave field. Phys. Fluids 2016, 28, 107104. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shugan, I.; Chen, Y.-Y. Ship’s Wake on a Finite Water Depth in the Presence of a Shear Flow. J. Mar. Sci. Eng. 2022, 10, 926. https://doi.org/10.3390/jmse10070926
Shugan I, Chen Y-Y. Ship’s Wake on a Finite Water Depth in the Presence of a Shear Flow. Journal of Marine Science and Engineering. 2022; 10(7):926. https://doi.org/10.3390/jmse10070926
Chicago/Turabian StyleShugan, Igor, and Yang-Yih Chen. 2022. "Ship’s Wake on a Finite Water Depth in the Presence of a Shear Flow" Journal of Marine Science and Engineering 10, no. 7: 926. https://doi.org/10.3390/jmse10070926
APA StyleShugan, I., & Chen, Y.-Y. (2022). Ship’s Wake on a Finite Water Depth in the Presence of a Shear Flow. Journal of Marine Science and Engineering, 10(7), 926. https://doi.org/10.3390/jmse10070926





