Development History of the Numerical Simulation of Tides in the East Asian Marginal Seas: An Overview
Abstract
:1. Introduction
2. Tidal Modeling without Data Assimilation
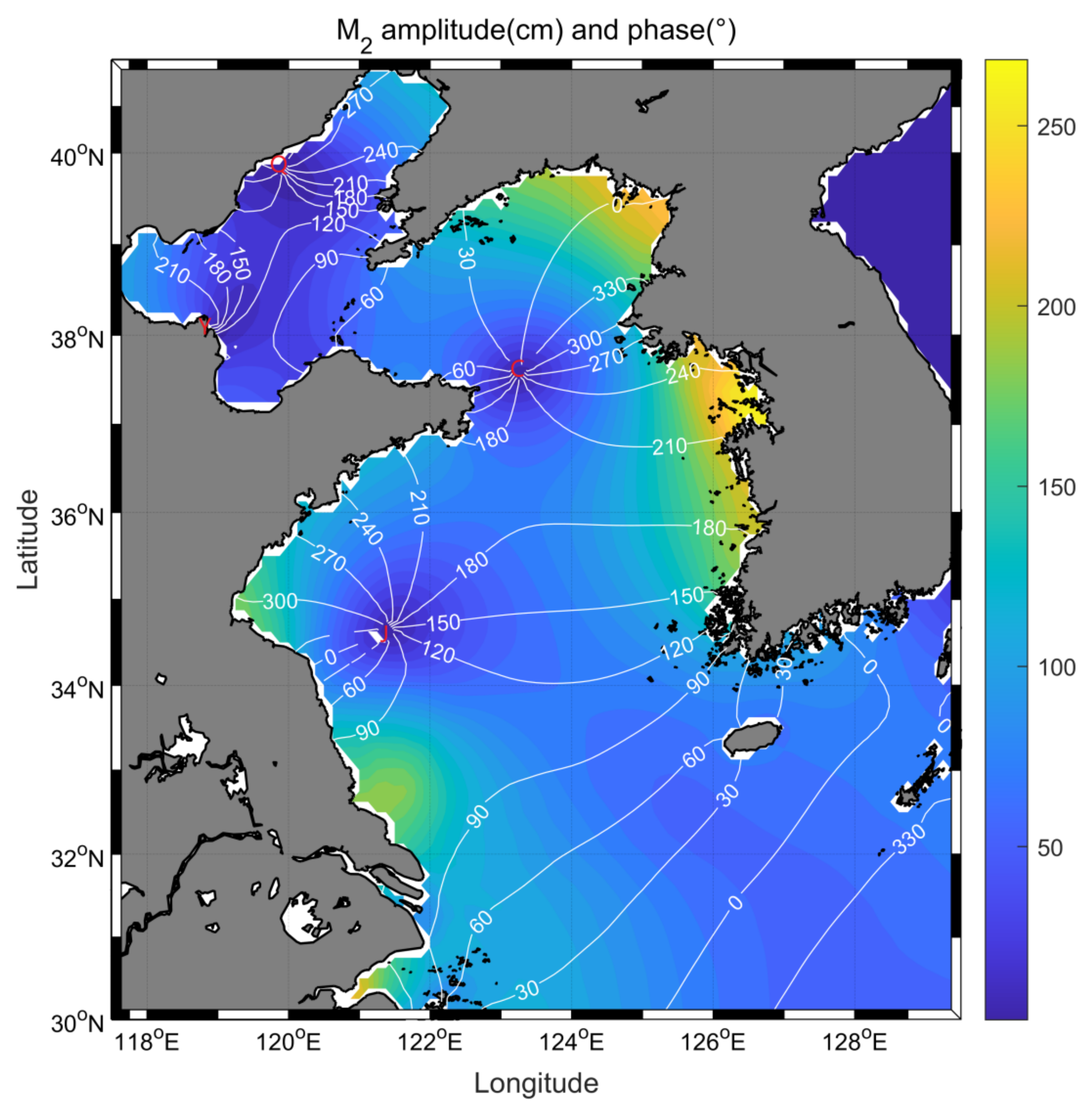
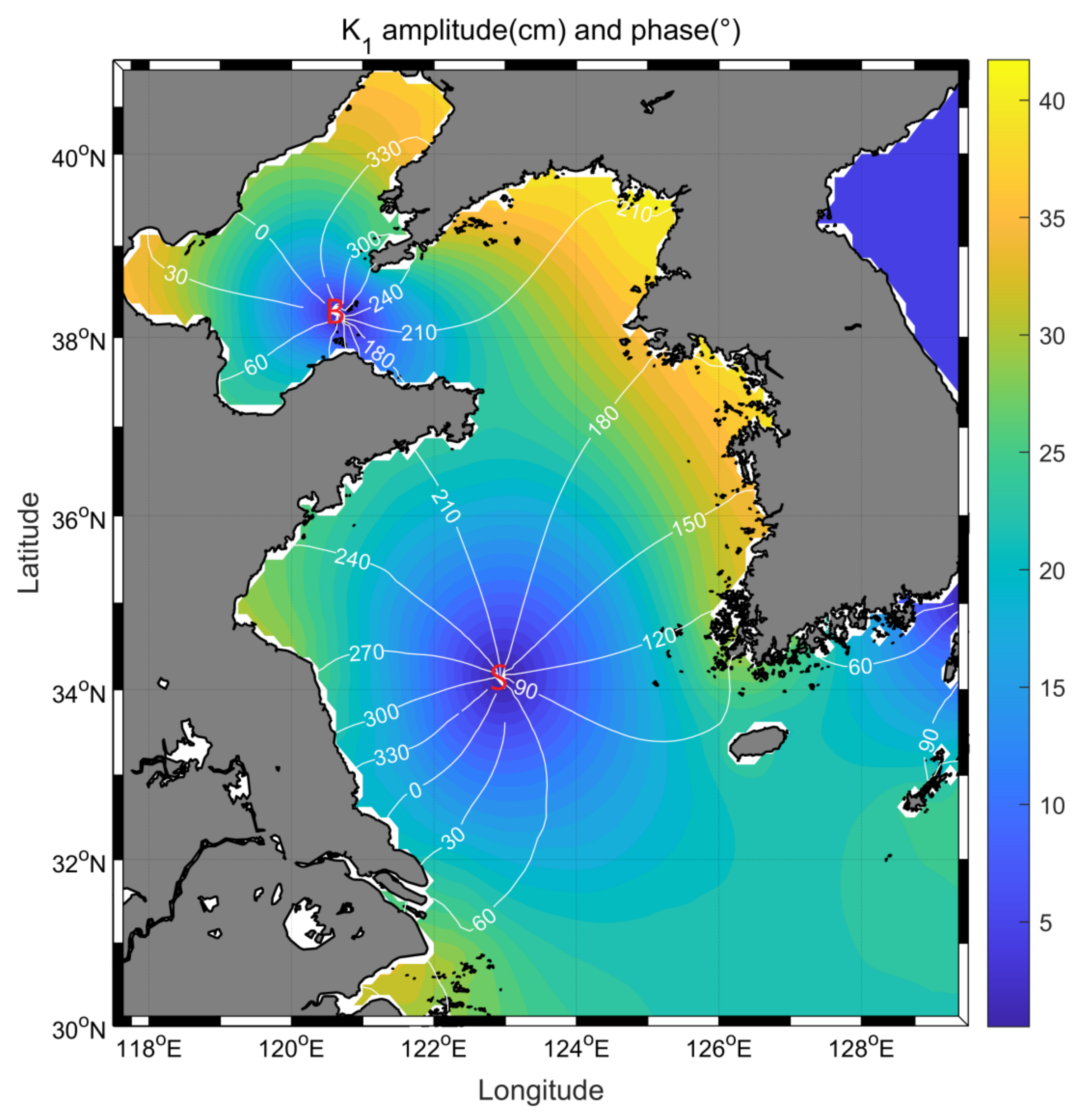

3. Tidal Modeling with Data Assimilation
4. Changing Tides under Natural Variability and Human Activities
5. Tidal Influence on the Ocean Environment
6. Numerical Studies of Internal Tides
7. Summary and Prospect
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gan, M.; Pan, H.; Chen, Y.; Pan, S. Application of the Variational Mode Decomposition (VMD) Method to River Tides. Estuar. Coast. Shelf Sci. 2021, 261, 107570. [Google Scholar] [CrossRef]
- Pan, H.; Guo, Z.; Lv, X. Inversion of Tidal Open Boundary Conditions of the M2 Constituent in the Bohai and Yellow Seas. J. Atmos. Ocean. Technol. 2017, 34, 1661–1672. [Google Scholar] [CrossRef]
- Choi, B.H.; Ko, J.S. Modeling of tides in the East Asian Marginal Seas. J. Korean Soc. Coast. Ocean Eng. 1994, 6, 94–108. [Google Scholar]
- Choi, B.H. Tides in the East Asian Marginal Seas; Hanrimwon Publishing Co.: Seoul, Korea, 2015; pp. 1–15. [Google Scholar]
- Shen, Y. Numerical Computation of Tides in the East China Sea. J. Shandong Coll. Oceanol. 1980, 10, 26–35. [Google Scholar]
- Choi, B.H. Development of fine-grid numerical tidal models of the Yellow Sea and the East China Sea. J. Korean Soc. Coast. Ocean Eng. 1990, 2, 231–234. [Google Scholar] [CrossRef]
- Zhu, L.; Hu, R.; Zhu, H.; Jiang, S.; Xu, Y.; Wang, N. Modeling Studies of Tidal Dynamics and the Associated Responses to Coastline Changes in the Bohai Sea, China. Ocean Dyn. 2018, 68, 1625–1648. [Google Scholar] [CrossRef]
- Feng, X.; Feng, H.; Li, H.; Zhang, F.; Feng, W.; Zhang, W.; Yuan, J. Tidal Responses to Future Sea Level Trends on the Yellow Sea Shelf. J. Geophys. Res. Ocean. 2019, 124, 7285–7306. [Google Scholar] [CrossRef]
- Lin, S.; Liu, G.; Niu, J.; Wei, X.; Cai, S. Responses of Hydrodynamics to Changes in Shoreline and Bathymetry in the Pearl River Estuary, China. Cont. Shelf Res. 2021, 229, 104556. [Google Scholar] [CrossRef]
- An, H.S. A Numerical Experiment of the M2 Tide in the Yellow Sea. J. Oceanogr. Soc. Jpn. 1977, 33, 103–110. [Google Scholar] [CrossRef]
- Pelling, H.E.; Uehara, K.; Green, J.A.M. The Impact of Rapid Coastline Changes and Sea Level Rise on the Tides in the Bohai Sea, China. J. Geophys. Res. Ocean. 2013, 118, 3462–3472. [Google Scholar] [CrossRef] [Green Version]
- Gao, X.; Wei, Z.; Lv, X.; Wang, Y.; Fang, G. Numerical Study of Tidal Dynamics in the South China Sea with Adjoint Method. Ocean Model. 2015, 92, 101–114. [Google Scholar] [CrossRef]
- Wang, D.; Pan, H.; Jin, G.; Lv, X. Seasonal Variation of the Principal Tidal Constituents in the Bohai Sea. Ocean Sci. 2020, 16, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Lv, X.; Zhang, J. Numerical Study on Spatially Varying Bottom Friction Coefficient of a 2D Tidal Model with Adjoint Method. Cont. Shelf Res. 2006, 26, 1905–1923. [Google Scholar] [CrossRef]
- Guo, Z.; Pan, H.; Fan, W.; Lv, X. Application of Surface Spline Interpolation in Inversion of Bottom Friction Coefficients. J. Atmos. Ocean. Technol. 2017, 34, 2021–2028. [Google Scholar] [CrossRef]
- Jan, S.; Lien, R.C.; Ting, C.H. Numerical Study of Baroclinic Tides in Luzon Strait. J. Oceanogr. 2008, 64, 789–802. [Google Scholar] [CrossRef]
- Liu, K.; Sun, J.; Guo, C.; Yang, Y.; Yu, W.; Wei, Z. Seasonal and Spatial Variations of the M2 Internal Tide in the Yellow Sea. J. Geophys. Res. Ocean. 2019, 124, 1115–1138. [Google Scholar] [CrossRef]
- Yan, T.; Qi, Y.; Jing, Z.; Cai, S. Seasonal and Spatial Features of Barotropic and Baroclinic Tides in the Northwestern South China Sea. J. Geophys. Res. Ocean. 2020, 125, e2018JC014860. [Google Scholar] [CrossRef] [Green Version]
- Wei, Z.; Sun, J.; Teng, F.; Xu, T.; Wang, Y.; Xu, X.; Fang, G. A Harmonic Analyzed Parameterization of Tide-Induced Mixing for Ocean Models. Acta Oceanol. Sin. 2018, 37, 1–7. [Google Scholar] [CrossRef]
- Susanto, R.D.; Pan, J.; Devlin, A.T. Tidal Mixing Signatures in the Hong Kong Coastal Waters from Satellite-Derived Sea Surface Temperature. Remote Sens. 2018, 11, 5. [Google Scholar] [CrossRef] [Green Version]
- Xing, Q.; Yu, H.; Yu, H.; Wang, H.; Ito, S.I.; Yuan, C. Evaluating the Spring-Neap Tidal Effects on Chlorophyll-a Variations Based on the Geostationary Satellite. Front. Mar. Sci. 2021, 8, 758538. [Google Scholar] [CrossRef]
- Fang, G. A Two-Dimensional Numerical Model for Tidal, Motion in the Taiwan Strait. Mar. Geophys. Res. 1984, 7, 267–276. [Google Scholar] [CrossRef]
- Fang, G.; Yang, J. A Two-Dimensional Numerical Model of the Tidal Motions in the Bohai Sea. Chin. J. Oceanol. Limnol. 1985, 3, 135–152. [Google Scholar] [CrossRef]
- Fang, G. A Finite Difference-Least Square Technique for Solving Tidal Wave Equations with Specific Application to the Modeling of M2 Tide in the Huanghai Sea. Sci. Sin. 1985, 28, 1110–1120. [Google Scholar]
- Fang, G. Tide and Tidal Current Charts for the Marginal Seas Adjacent to China. Chin. J. Oceanol. Limnol. 1986, 4, 1–16. [Google Scholar] [CrossRef]
- Fang, G.; Yang, J. Modeling and Prediction of Tidal Currents in the Korea Strait. Prog. Oceanogr. 1988, 21, 307–318. [Google Scholar] [CrossRef]
- Odamaki, M. Co-Oscillating and Independent Tides of the Japan Sea. J. Oceanogr. Soc. Jpn. 1989, 45, 217–232. [Google Scholar] [CrossRef]
- Cao, D.; Fang, G. A Numerical Model of the Tides and Tidal Currents in Beibu Bay. Oceanol. Limnol. Sin. 1990, 21, 105–113. [Google Scholar]
- Choi, B.H.; Fang, G. A Review of Tidal Models for the East China and Yellow Seas. J. Korean Soc. Coast. Ocean Eng. 1993, 5, 151–171. [Google Scholar]
- Zhao, B.; Fang, G.; Cao, D. Characteristics of Tidal Residual Currents and Their Relations with Coastal Current Transports in the Bohai Sea, Yellow Sea and East China Sea. Stud. Mar. Sin. 1995, 36, 1–11. [Google Scholar]
- Fang, G.; Kwok, Y.K.; Yu, K.; Zhu, Y. Numerical Simulation of Principal Tidal Constituents in the South China Sea, Gulf of Tonkin and Gulf of Thailand. Cont. Shelf Res. 1999, 19, 845–869. [Google Scholar] [CrossRef]
- Hart-Davis, M.G.; Piccioni, G.; Dettmering, D.; Schwatke, C.; Passaro, M.; Seitz, F. EOT20: A Global Ocean Tide Model from Multi-Mission Satellite Altimetry. Earth Syst. Sci. Data 2021, 13, 3869–3884. [Google Scholar] [CrossRef]
- Lin, M.C.; Juang, W.J.; Tsay, T.K. Anomalous Amplifications of Semidiurnal Tides along the Western Coast of Taiwan. Ocean Eng. 2001, 28, 1171–1198. [Google Scholar] [CrossRef]
- Jan, S.; Chern, C.S.; Wang, J. Transition of Tidal Waves from the East to South China Seas over the Taiwan Strait: Influence of the Abrupt Step in the Topography. J. Oceanogr. 2002, 58, 837–850. [Google Scholar] [CrossRef]
- Teng, F.; Fang, G.; Xu, X. Effects of Internal Tidal Dissipation and Self-Attraction and Loading on Semidiurnal Tides in the Bohai Sea, Yellow Sea and East China Sea: A Numerical Study. Chin. J. Oceanol. Limnol. 2017, 35, 987–1001. [Google Scholar] [CrossRef]
- Zhang, Q.; Su, M.; Yao, P.; Chen, Y.; Stive, M.J.F.; Wang, Z.B. Dynamics of a Tidal Current System in a Marginal Sea: A Case Study of the Yellow Sea, China. Front. Mar. Sci. 2020, 7, 596388. [Google Scholar] [CrossRef]
- Zhu, Y.; Fang, G. A Combined Two-and-Three Dimensional Numerical Hydrodynamical Model with Application to Simulation of Tidal Motions in the Beibuwan Gulf (Gulf of Tonkin). Oceanol. Limnol. Sin. 1993, 24, 117–125. [Google Scholar]
- Guo, X.; Yanagi, T. Three-Dimensional Structure of Tidal Current in the East China Sea and the Yellow Sea. J. Oceanogr. 1998, 54, 651–668. [Google Scholar] [CrossRef]
- Wang, K.; Fang, G.; Feng, S. A 3-D numerical simulation of M2 tides and tidal currents in the Bohai Sea, the Huanghai Sea and the East China Sea. ACTA Oceanol. Sin. 1999, 21, 1–13. [Google Scholar]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 2015, 9, 347–404. [Google Scholar] [CrossRef]
- Wu, R.; Jiang, Z.; Li, C. Revisiting the Tidal Dynamics in the Complex Zhoushan Archipelago Waters: A Numerical Experiment. Ocean Model. 2018, 132, 139–156. [Google Scholar] [CrossRef]
- Chu, D.; Niu, H.; Wang, Y.P.; Cao, A.; Li, L.; Du, Y.; Zhang, J. Numerical Study on Tidal Duration Asymmetry and Shallow-Water Tides within Multiple Islands: An Example of the Zhoushan Archipelago. Estuar. Coast. Shelf Sci. 2021, 262, 107576. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Beardsley, R.C. An unstructured grid, finite-volume, threedimensional, primitive equations ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Han, G.; Fang, G.; Ma, J.; Liu, K.; Li, D. Optimizing Open Boundary Conditions of Nonlinear Tidal Model Using Adjoint Method. ACTA Oceanol. Sin. 2001, 23, 25–31. [Google Scholar]
- He, Y.; Lu, X.; Qiu, Z.; Zhao, J. Shallow Water Tidal Constituents in the Bohai Sea and the Yellow Sea from a Numerical Adjoint Model with TOPEX/POSEIDON Altimeter Data. Cont. Shelf Res. 2004, 24, 1521–1529. [Google Scholar] [CrossRef]
- Wu, Z.; Tian, J.; Zhao, Q. 3-D Numerical Simulation of the South China Sea Tidal Waves with Assimilation Method. J. Hydrodyn. 2004, 19, 501–506. [Google Scholar] [CrossRef]
- Blumberg, A.F.; Mellor, G.F. Three-Dimensional Coastal Ocean Models. Coast. Estuar. Stud. 1987, 4, 1–16. [Google Scholar]
- Book, J.W.; Pistek, P.; Perkins, H.; Thompson, K.R.; Teague, W.J.; Jacobs, G.A.; Suk, M.S.; Chang, K.I.; Lee, J.C.; Choi, B.H. Data Assimilation Modeling of the Barotropic Tides in the Korea/Tsushima Strait. J. Oceanogr. 2004, 60, 977–993. [Google Scholar] [CrossRef]
- Jan, S.; Wang, Y.H.; Wang, D.P.; Chao, S.Y. Incremental Inference of Boundary Forcing for a Three-Dimensional Tidal Model: Tides in the Taiwan Strait. Cont. Shelf Res. 2004, 24, 337–351. [Google Scholar] [CrossRef]
- Zu, T.; Gan, J.; Erofeeva, S.Y. Numerical Study of the Tide and Tidal Dynamics in the South China Sea. Deep Sea Res. Part I Oceanogr. Res. Pap. 2008, 55, 137–154. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, X. Inversion of Three-Dimensional Tidal Currents in Marginal Seas by Assimilating Satellite Altimetry. Comput. Methods Appl. Mech. Eng. 2010, 199, 3125–3136. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, X.; Wang, P.; Wang, Y.P. Study on Linear and Nonlinear Bottom Friction Parameterizations for Regional Tidal Models Using Data Assimilation. Cont. Shelf Res. 2011, 31, 555–573. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.P. A Method for Inversion of Periodic Open Boundary Conditions in Two-Dimensional Tidal Models. Comput. Methods Appl. Mech. Eng. 2014, 275, 20–38. [Google Scholar] [CrossRef]
- Jiang, D.; Chen, H.; Jin, G.; Lv, X. Estimating Smoothly Varying Open Boundary Conditions for a 3D Internal Tidal Model with an Improved Independent Point Scheme. J. Atmos. Ocean. Technol. 2018, 35, 1299–1311. [Google Scholar] [CrossRef]
- Zheng, J.; Mao, X.; Lv, X.; Jiang, W. The M2 Cotidal Chart in the Bohai, Yellow, and East China Seas from Dynamically Constrained Interpolation. J. Atmos. Ocean. Technol. 2020, 37, 1219–1229. [Google Scholar] [CrossRef]
- Qian, S.; Wang, D.; Zhang, J.; Li, C. Adjoint Estimation and Interpretation of Spatially Varying Bottom Friction Coefficients of the M2 Tide for a Tidal Model in the Bohai, Yellow and East China Seas with Multi-Mission Satellite Observations. Ocean Model. 2021, 161, 101783. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, J.; Wang, Y.P. Estimation of Bottom Friction Coefficient in Multi-Constituent Tidal Models Using the Adjoint Method: Temporal Variations and Spatial Distributions. J. Geophys. Res. Ocean. 2021, 126, 1–20. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, J.; Mu, L. A Feature Point Scheme for Improving Estimation of the Temporally Varying Bottom Friction Coefficient in Tidal Models Using Adjoint Method. Ocean Eng. 2021, 220, 108481. [Google Scholar] [CrossRef]
- Li, M.; Liang, S.; Sun, Z. Optimization Inversion Method for Tidal Model under Open Boundary Condition: A Case Study of K1 Constituent Amplitude. Adv. Water Sci. 2009, 20, 129–134. [Google Scholar] [CrossRef]
- Li, M.; Si, Q.; Liang, S.; Sun, Z.; You, X. Applied Data Driven Model for Current Field Calibration under the Condition of Open Boundary. J. Water Resour. Water Eng. 2011, 22, 7–10. [Google Scholar]
- Moon, J.H.; Hirose, N.; Morimoto, A. Green’s Function Approach for Calibrating Tides in a Circulation Model for the East Asian Marginal Seas. J. Oceanogr. 2012, 68, 345–354. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, Y.; Gao, X.; Fang, G. Improved Nudging Assimilation Schemes and Their Applications in Simulating M2 Tide in the Northwest Pacific. Adv. Mar. Sci. 2015, 33, 431–438. [Google Scholar]
- Zhu, Z.N.; Zhu, X.H.; Zhang, C.; Chen, M.; Wang, M.; Dong, M.; Liu, W.; Zheng, H.; Kaneko, A. Dynamics of Tidal and Residual Currents Based on Coastal Acoustic Tomography Assimilated Data Obtained in Jiaozhou Bay, China. J. Geophys. Res. Ocean. 2021, 126, 1–26. [Google Scholar] [CrossRef]
- Pan, H.; Lv, X.; Wang, Y.; Matte, P.; Chen, H.; Jin, G. Exploration of Tidal-Fluvial Interaction in the Columbia River Estuary Using S_TIDE. J. Geophys. Res. Ocean. 2018, 123, 6598–6619. [Google Scholar] [CrossRef]
- Pan, H.; Lv, X. Is There a Quasi 60-Year Oscillation in Global Tides? Cont. Shelf Res. 2021, 222, 104433. [Google Scholar] [CrossRef]
- Lu, S.; Tong, C.; Lee, D.Y.; Zheng, J.; Shen, J.; Zhang, W.; Yan, Y. Propagation of Tidal Waves up in Yangtze Estuary during the Dry Season. J. Geophys. Res. Ocean. 2015, 120, 6445–6473. [Google Scholar] [CrossRef] [Green Version]
- WL Delft Hydraulics. User Manual Delft3D-FLOW; WL Delft Hydraulics: Delft, The Netherlands, 1999. [Google Scholar]
- Zhang, M.; Townend, I.; Zhou, Y.; Cai, H. Seasonal Variation of River and Tide Energy in the Yangtze Estuary, China. Earth Surf. Process. Landforms 2015, 41, 98–116. [Google Scholar] [CrossRef]
- Zhang, M.; Townend, I.H.; Cai, H.; Zhou, Y. Seasonal Variation of Tidal Prism and Energy in the Changjiang River Estuary: A Numerical Study. Chin. J. Oceanol. Limnol. 2016, 34, 219–230. [Google Scholar] [CrossRef]
- Hervouet, J.M. Hydrodynamics of Free Surface Flows: Modelling with the Finite Element Method; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Zhang, H.; Cheng, W.; Qiu, X.; Feng, X.; Gong, W. Tide-Surge Interaction along the East Coast of the Leizhou Peninsula, South China Sea. Cont. Shelf Res. 2017, 142, 32–49. [Google Scholar] [CrossRef]
- Zhang, F.; Sun, J.; Lin, B.; Huang, G. Seasonal Hydrodynamic Interactions between Tidal Waves and River Flows in the Yangtze Estuary. J. Mar. Syst. 2018, 186, 17–28. [Google Scholar] [CrossRef]
- Devlin, A.T.; Zaron, E.D.; Jay, D.A.; Talke, S.A.; Pan, J. Seasonality of Tides in Southeast Asian Waters. J. Phys. Oceanogr. 2018, 48, 1169–1190. [Google Scholar] [CrossRef]
- Phan, H.M.; Ye, Q.; Reniers, A.J.H.M.; Stive, M.J.F. Tidal Wave Propagation along The Mekong Deltaic Coast. Estuar. Coast. Shelf Sci. 2019, 220, 73–98. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, J.; Wu, Y.; Wang, K.H.; Zhang, Q.; Wu, S.; You, Z.J.; Ma, Y. A Modelling Study of Ice Effect on Tidal Damping in the Bohai Sea. Ocean Eng. 2019, 173, 748–760. [Google Scholar] [CrossRef]
- Guo, L.; Zhu, C.; Wu, X.; Wan, Y.; Jay, D.A.; Townend, I.; Wang, Z.B.; He, Q. Strong Inland Propagation of Low-Frequency Long Waves in River Estuaries. Geophys. Res. Lett. 2020, 47, 1–11. [Google Scholar] [CrossRef]
- Marshall, J.; Adcroft, A.; Hill, C.; Perelman, L.; Heisey, C. A finite-volume, incompressible Navier Stokes model for studies of the ocean on parallel computers. J. Geophys. Res. Ocean. 1997, 102, 5753–5766. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Sun, Z.; Huang, S.; Liu, X.; Hu, Z. Numerical Study of the Tidal Refraction Effect on the Open Coast in Southeastern Zhejiang. J. Oceanogr. 2020, 76, 43–56. [Google Scholar] [CrossRef]
- Choi, B.H.; Eum, H.M.; Woo, S.B. Modeling of coupled tide-wave-surge process in the Yellow Sea. Ocean Eng. 2003, 30, 739–759. [Google Scholar] [CrossRef]
- Choi, B.H.; Eum, H.M.; Woo, S.B. A synchronously coupled tide-wave-surge model of the Yellow Sea. Coast. Eng. 2003, 47, 381–398. [Google Scholar] [CrossRef]
- Feng, X.; Feng, H. On the Role of Anthropogenic Activity and Sea-Level-Rise in Tidal Distortion on the Open Coast of the Yellow Sea Shelf. J. Geophys. Res. Ocean. 2021, 126, 1–27. [Google Scholar] [CrossRef]
- Zhu, C.; Guo, L.; van Maren, D.S.; Wang, Z.B.; He, Q. Exploration of Decadal Tidal Evolution in Response to Morphological and Sedimentary Changes in the Yangtze Estuary. J. Geophys. Res. Ocean. 2021, 126, 1–19. [Google Scholar] [CrossRef]
- Susanto, R.D.; Ray, R.D. Seasonal and Interannual Variability of Tidal Mixing Signatures in Indonesian Seas from High-Resolution Sea Surface Temperature. Remote Sens. 2022, 14, 1934. [Google Scholar] [CrossRef]
- Lee, H.J.; Park, J.H.; Wimbush, M.; Jung, K.T.; Jang, C.J.; Cho, Y.K.; Seo, Y.K.; Nam, J.H. Tidal Effects on Intermediate Waters: A Case Study in the East/Japan Sea. J. Phys. Oceanogr. 2011, 41, 234–240. [Google Scholar] [CrossRef]
- Zhang, W.; Feng, H.; Hoitink, A.J.F.; Zhu, Y.; Gong, F.; Zheng, J. Tidal Impacts on the Subtidal Flow Division at the Main Bifurcation in the Yangtze River Delta. Estuar. Coast. Shelf Sci. 2017, 196, 301–314. [Google Scholar] [CrossRef]
- Ji, X.; Zhang, W. Tidal Impacts on Downstream Hydraulic Geometry of a Tide-Influenced Delta. Ocean Dyn. 2020, 70, 1239–1252. [Google Scholar] [CrossRef]
- Yuan, S.; Xu, X.; Deng, J.; Qiu, Z. A Numerical Study on Internal Tides in the Northeast of South China Sea. Trop. Oceanol. 1995, 14, 15–23. [Google Scholar]
- Fang, G.; Li, H.; Du, T. A Layered 3-D Numerical Ocean Model for Simulation of Internal Tides. Stud. Mar. Sin. 1997, 38, 1–15. [Google Scholar]
- Cai, S.; Huang, Q.; Qiu, Z.; Mai, B. A Numerical Study on Dynamic Mechanism of Internal Tide. Trop. Oceanol. 2000, 19, 27–32. [Google Scholar]
- Miao, C.; Chen, H.; Lv, X. An Isopycnic-Coordinate Internal Tide Model and Its Application to the South China Sea. Chin. J. Oceanol. Limnol. 2011, 29, 1339–1356. [Google Scholar] [CrossRef]
- Wang, D.P. Diurnal Modulation of Semidiurnal Internal Tides in Luzon Strait. Ocean Model. 2012, 59–60, 1–10. [Google Scholar] [CrossRef]
- Wu, L.; Miao, C.; Zhao, W. Patterns of K1 and M2 Internal Tides and Their Seasonal Variations in the Northern South China Sea. J. Oceanogr. 2013, 69, 481–494. [Google Scholar] [CrossRef]
- Guo, Z.; Cao, A.; Lv, X.; Song, J. Impacts of Stratification Variation on the M2 Internal Tide Generation in Luzon Strait. Atmos.-Ocean 2020, 58, 206–218. [Google Scholar] [CrossRef]
- Guo, Z.; Cao, A.; Wang, S. Influence of Remote Internal Tides on the Locally Generated Internal Tides upon the Continental Slope in the South China Sea. J. Mar. Sci. Eng. 2021, 9, 1268. [Google Scholar] [CrossRef]
- Wang, S.; Cao, A.; Li, Q.; Chen, X. Reflection of K1 Internal Tides at the Continental Slope in the Northern South China Sea. J. Geophys. Res. Ocean. 2021, 126, 1–20. [Google Scholar] [CrossRef]
- Li, B.; Du, L.; Peng, S.; Yuan, Y.; Meng, X.; Lv, X. Modulation of Internal Tides by Turbulent Mixing in the South China Sea. Front. Mar. Sci. 2021, 8, 772979. [Google Scholar] [CrossRef]
- Jiang, B.; Lv, X. Three-Dimensional Numerical Simulation of Internal Tides in the Bohai Sea, the Yellow Sea and the East China Sea. Trans. Oceanol. Limnol. 2007, 1, 30–37. [Google Scholar]
- Jeon, C.; Park, J.; Varlamov, S.M.; Yoon, J.; Kim, Y.H.; Seo, S.; Park, Y.; Min, H.S.; Lee, J.H.; Kim, C. Seasonal variation of semidiurnal internal tides in the East/Japan Sea. J. Geophys. Res. Ocean. 2014, 119, 2843–2859. [Google Scholar] [CrossRef]
- Lin, F.; Asplin, L.; Wei, H. Summertime M2 Internal Tides in the Northern Yellow Sea. Front. Mar. Sci. 2021, 8, 1–15. [Google Scholar] [CrossRef]
- Yu, Q.; Pan, H.; Gao, Y.; Lv, X. The Impact of the Mesoscale Ocean Variability on the Estimation of Tidal Harmonic Constants Based on Satellite Altimeter Data in the South China Sea. Remote Sens. 2021, 13, 2736. [Google Scholar] [CrossRef]
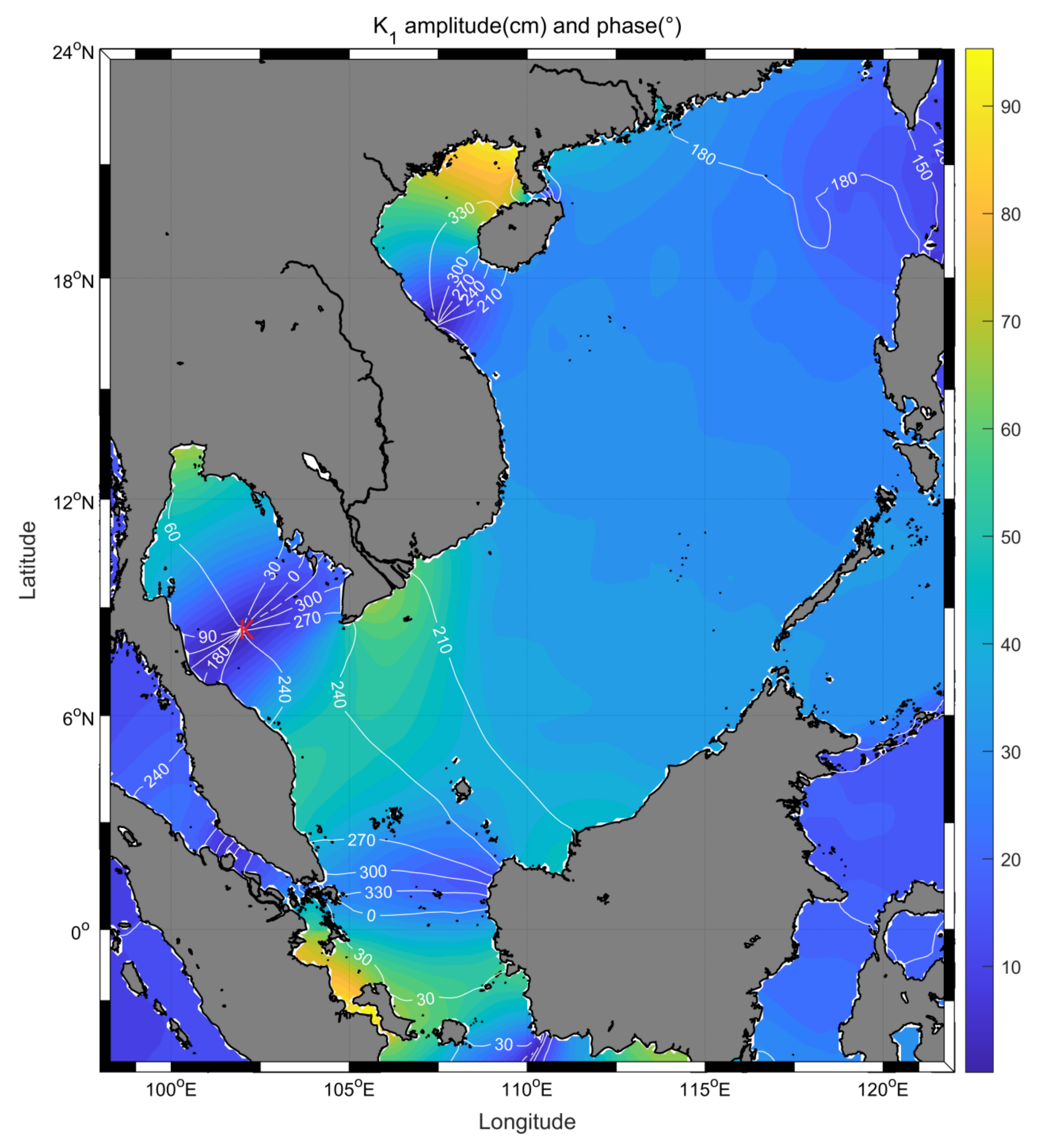
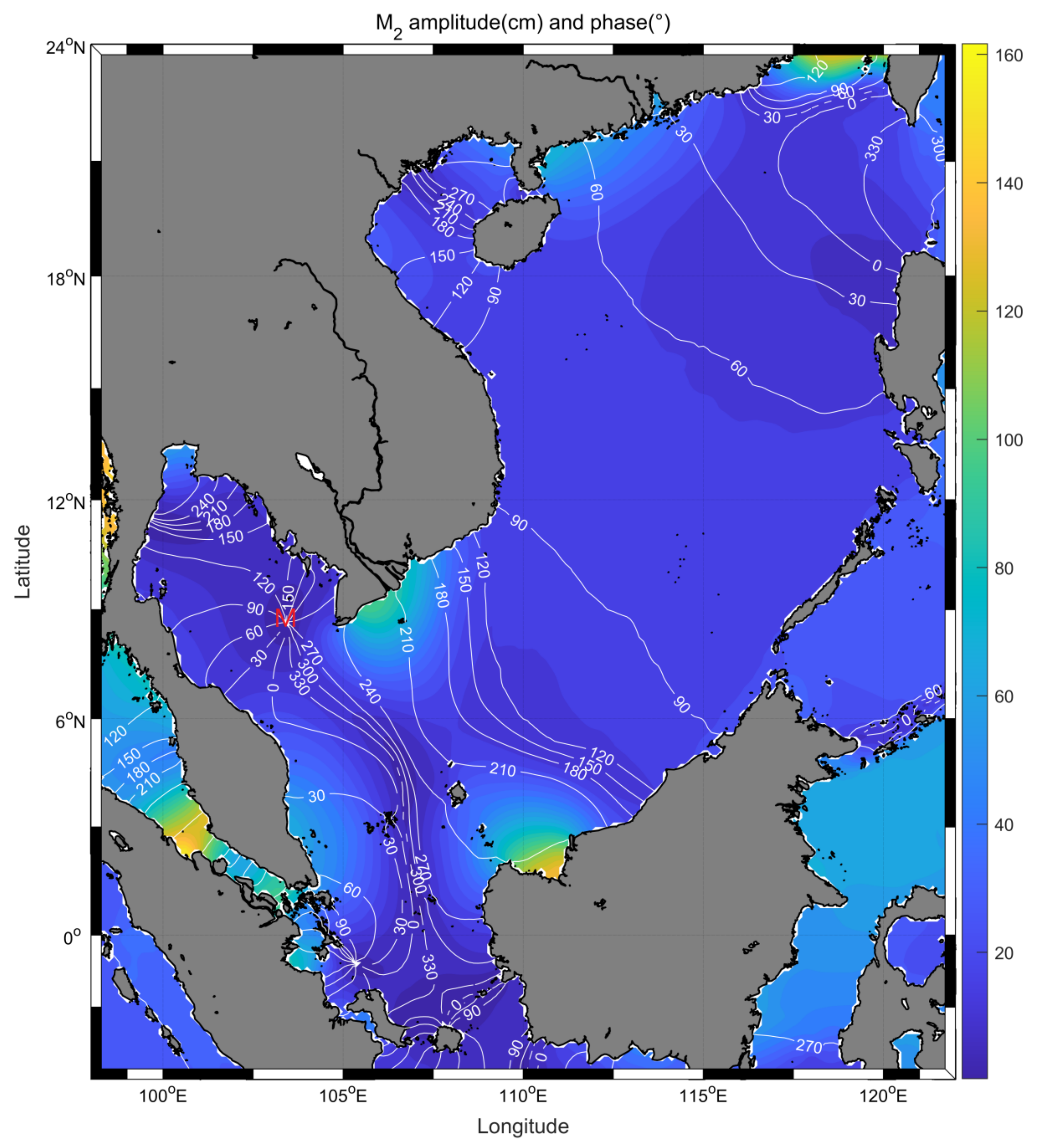

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Z.; Pan, H.; Xu, T.; Wang, Y.; Wang, J. Development History of the Numerical Simulation of Tides in the East Asian Marginal Seas: An Overview. J. Mar. Sci. Eng. 2022, 10, 984. https://doi.org/10.3390/jmse10070984
Wei Z, Pan H, Xu T, Wang Y, Wang J. Development History of the Numerical Simulation of Tides in the East Asian Marginal Seas: An Overview. Journal of Marine Science and Engineering. 2022; 10(7):984. https://doi.org/10.3390/jmse10070984
Chicago/Turabian StyleWei, Zexun, Haidong Pan, Tengfei Xu, Yonggang Wang, and Jian Wang. 2022. "Development History of the Numerical Simulation of Tides in the East Asian Marginal Seas: An Overview" Journal of Marine Science and Engineering 10, no. 7: 984. https://doi.org/10.3390/jmse10070984
APA StyleWei, Z., Pan, H., Xu, T., Wang, Y., & Wang, J. (2022). Development History of the Numerical Simulation of Tides in the East Asian Marginal Seas: An Overview. Journal of Marine Science and Engineering, 10(7), 984. https://doi.org/10.3390/jmse10070984






