Dynamic Analysis on Pile Group Supported Offshore Wind Turbine under Wind and Wave Load
Abstract
:1. Introduction
- (1)
- The barycenter of blades and the turbine might slightly shift from the rotating shaft, which will produce eccentric force, and its frequency is equal to the frequency of the turbine rotation frequency. This frequency is called the 1P frequency [5,6,7]. Since an OWT has different rotation speeds, the 1P frequency is not a single frequency but a frequency range, which is related to the highest and lowest value of the rotation speed.
- (2)
- Rotating blades will produce the air turbulence load. Once a blade runs across a certain location, a turbulence load will be created. This load is usually called 2P or 3P load. Most OWTs are three-blade structures, and the model used in this paper is the same, so it is a 3P frequency.
2. Proposed Calculation Method
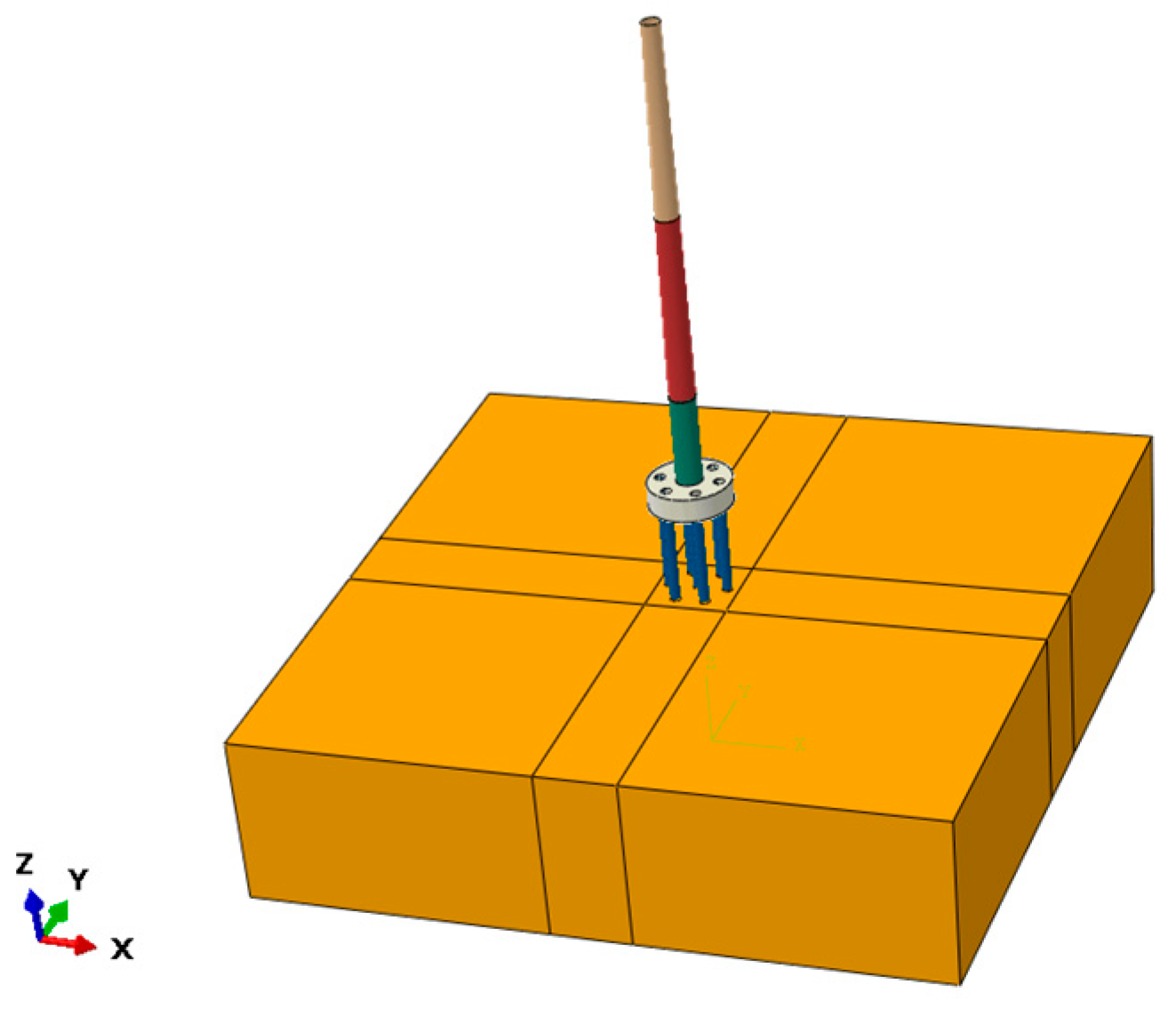
2.1. Model Establishment
2.2. Pile Submerged in the Seawater
- (1)
- When , the maximum total wave force happens when , and the maximum total wave force equals .
- (2)
- When , the maximum total wave force happens when , .
2.3. Pile Embedded in the Soil
2.3.1. Pile–Soil Interaction
- (1)
- The horizonal displacement of the active pile under the pile top dynamic load;
- (2)
- The passive pile is influenced by the incident wave from the active pile displacement after the soil attenuation;
- (3)
- The horizontal displacement of the passive pile;
- (4)
- The active pile is influenced by the secondary wave from the passive pile displacement after soil attenuation.
2.3.2. Active Pile Displacement
2.3.3. Soil Attenuation Function and Soil Displacement
2.3.4. Passive Pile Displacement
2.3.5. Active Pile Displacement Due to Secondary Wave
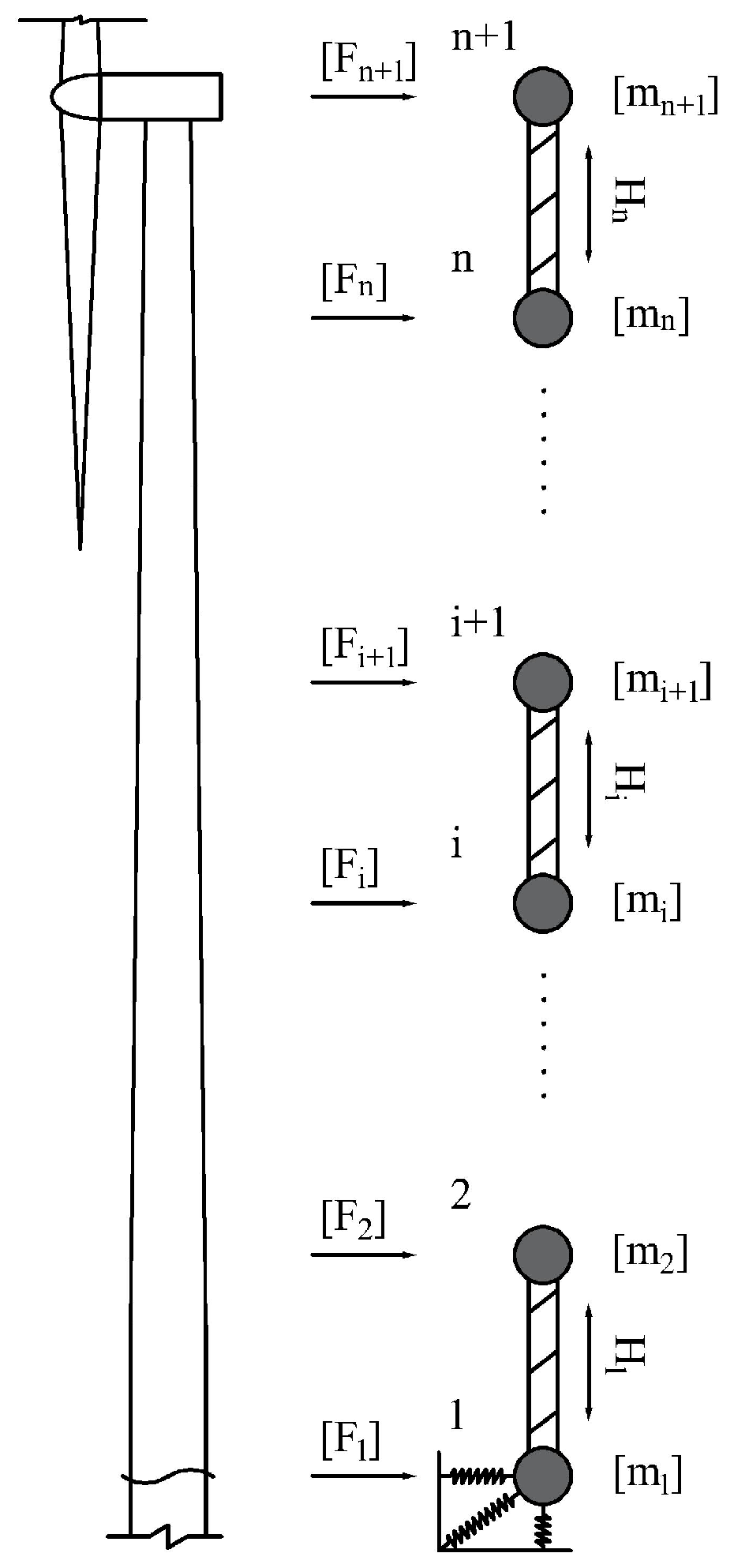
2.4. Overall Dynamic Response of the Pile Group
2.4.1. Active Pile
2.4.2. Passive Pile
2.4.3. Active Pile under Secondary Wave
2.4.4. Pile–Pile Interaction and Pile Group Dynamic Response
2.5. Superstructure Dynamic Response
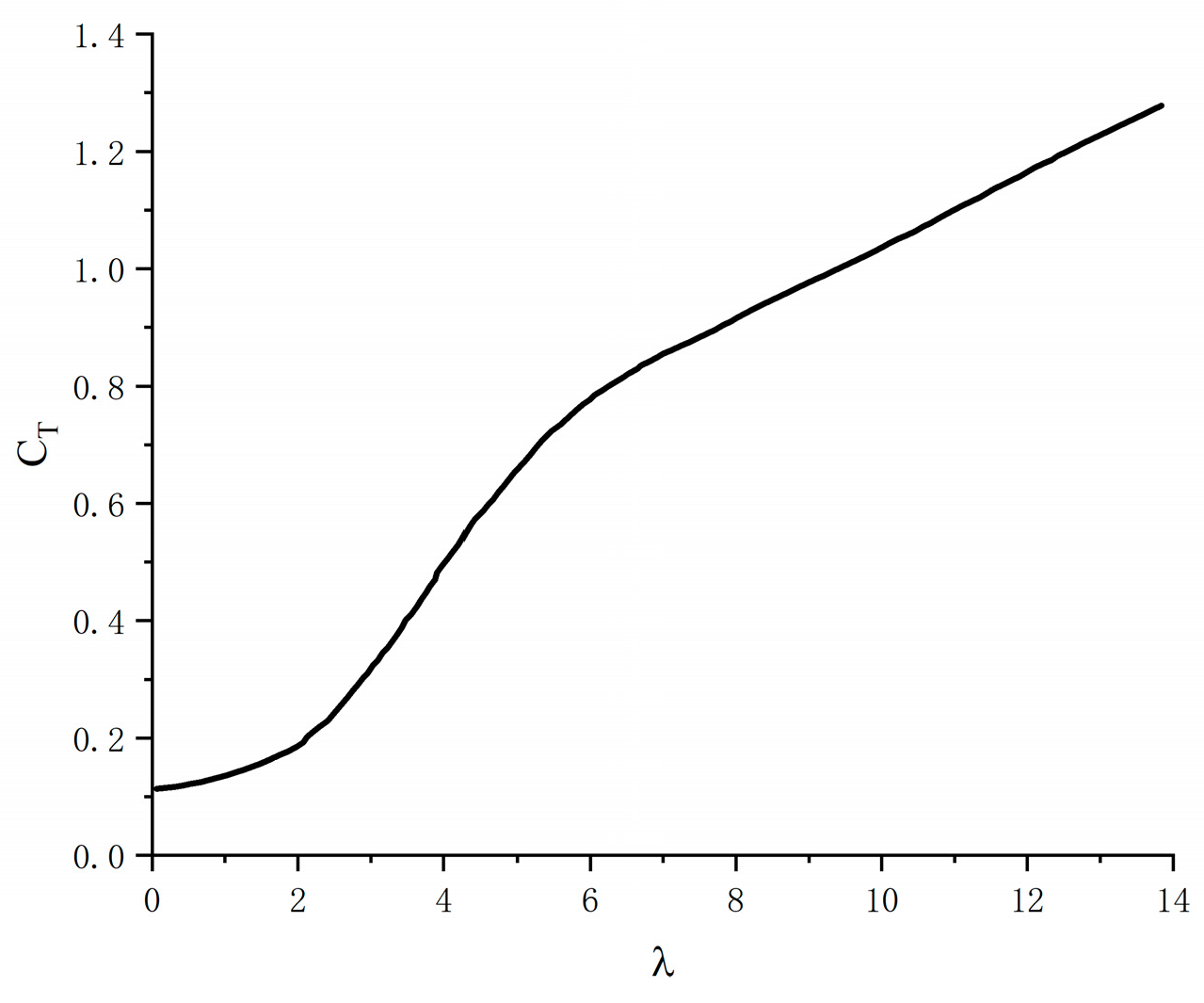
2.5.1. Distributed Wind Load
2.5.2. Thrust Wind Load
2.5.3. Tower Dynamic Response
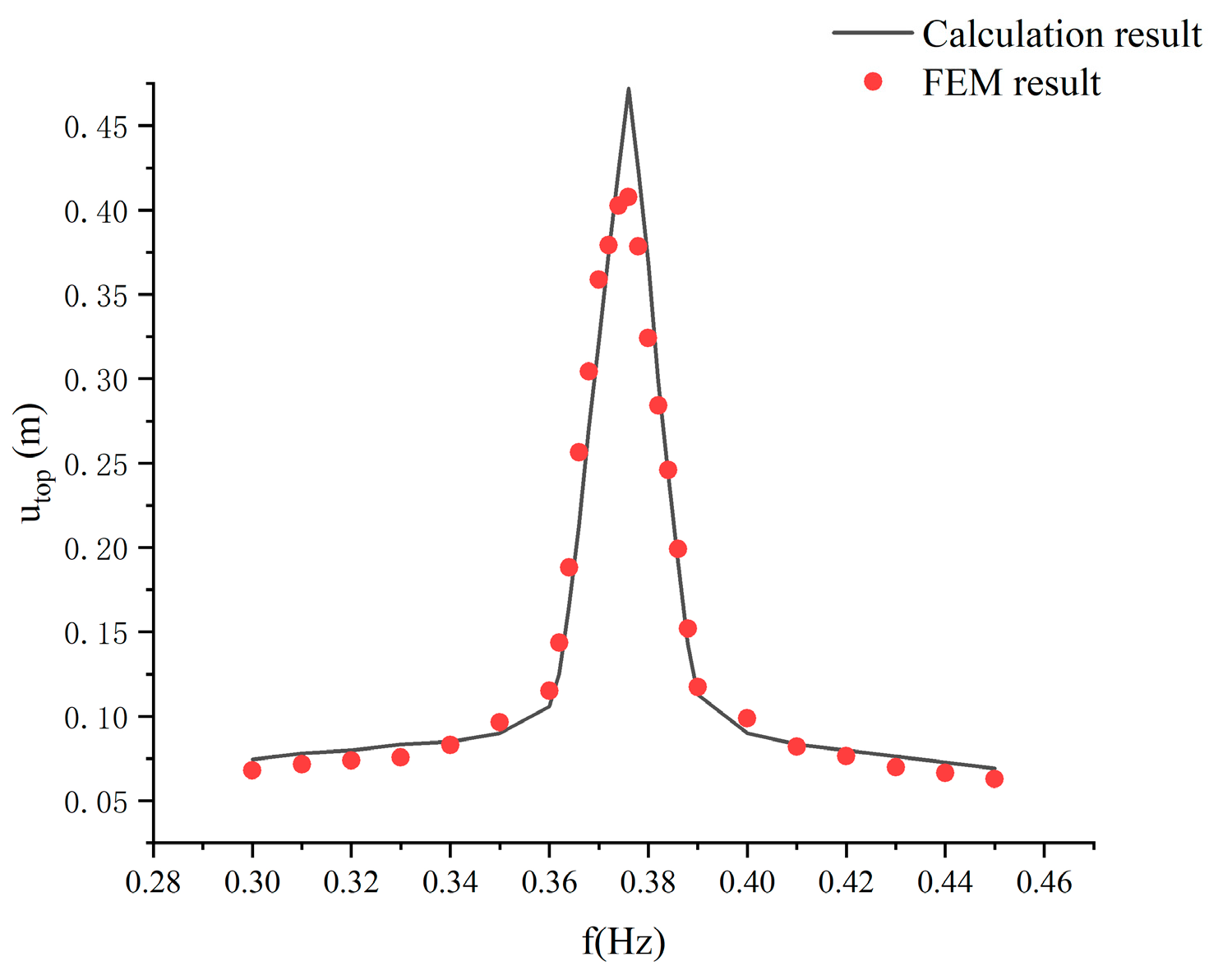
3. Validation
4. Parametric Analysis
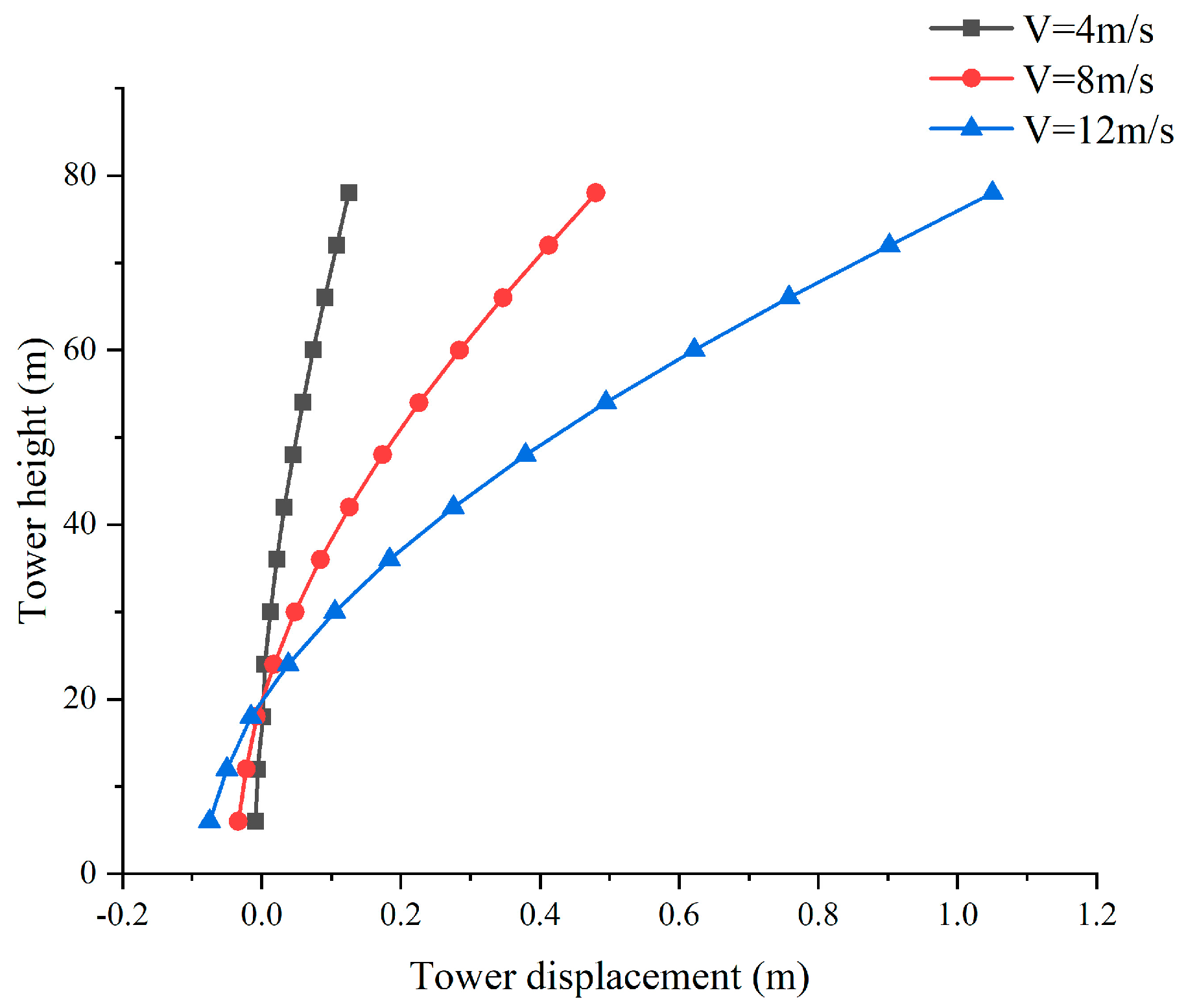
4.1. Tower Displacement
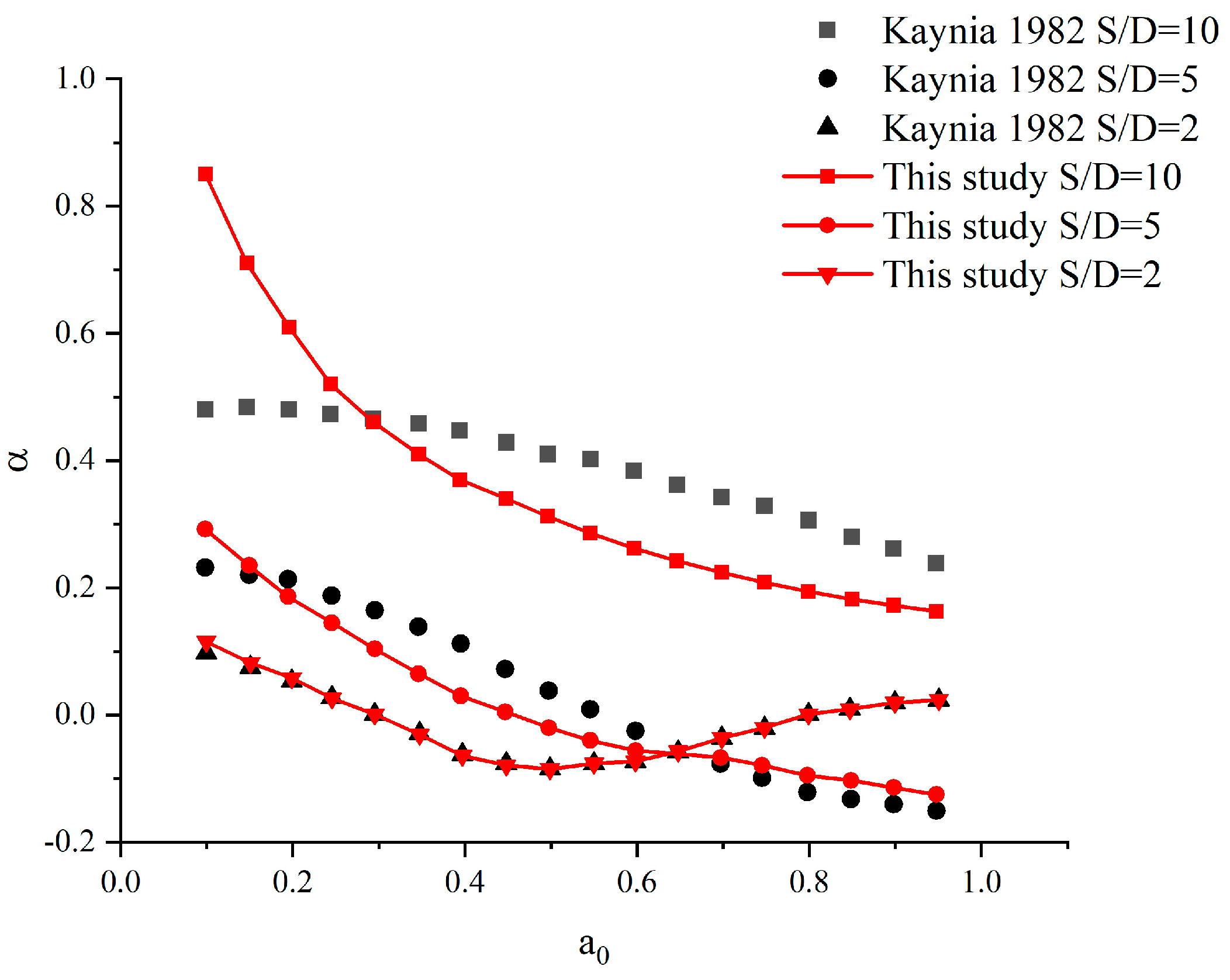
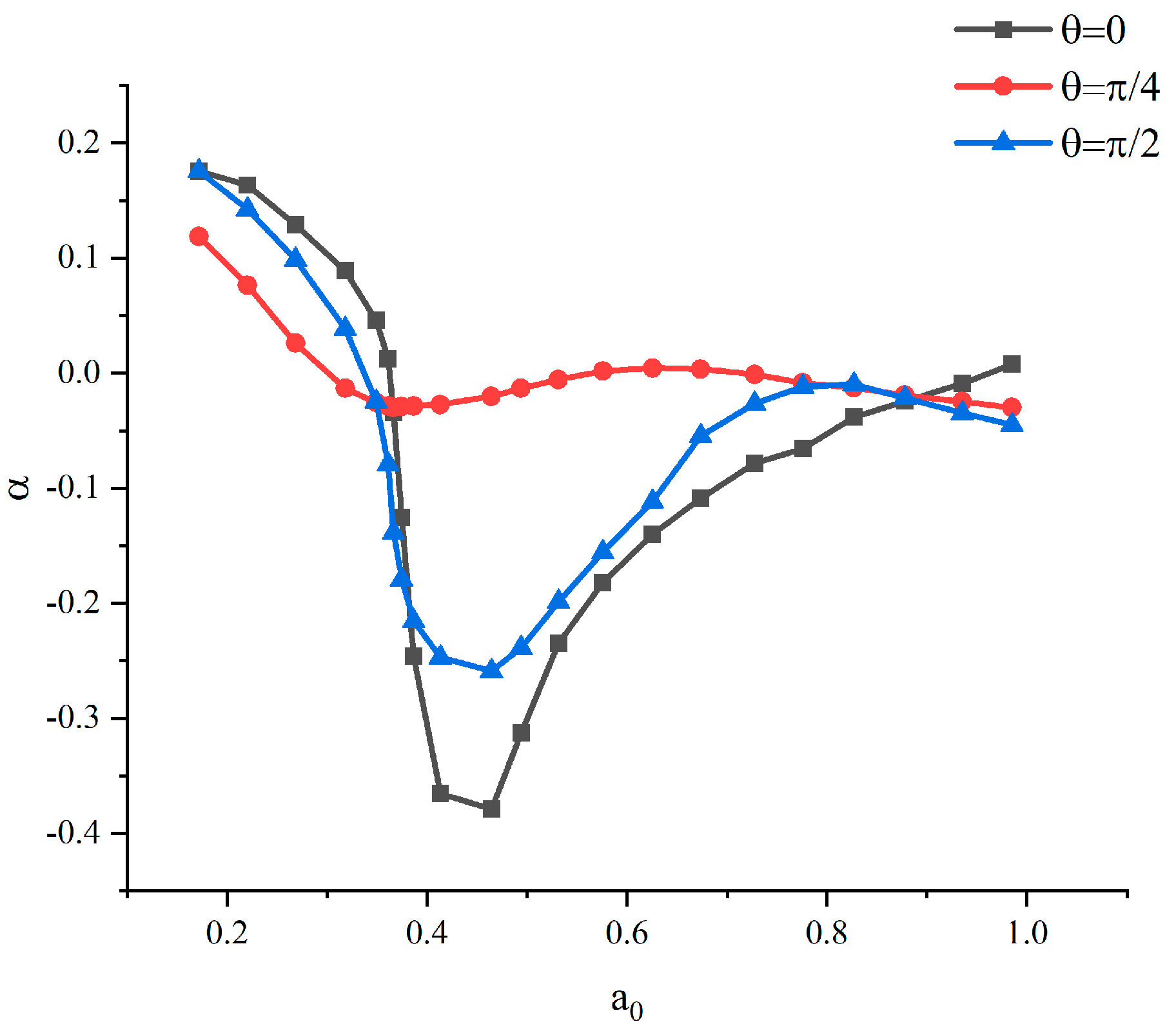
4.2. Pile–Pile Interaction Factor
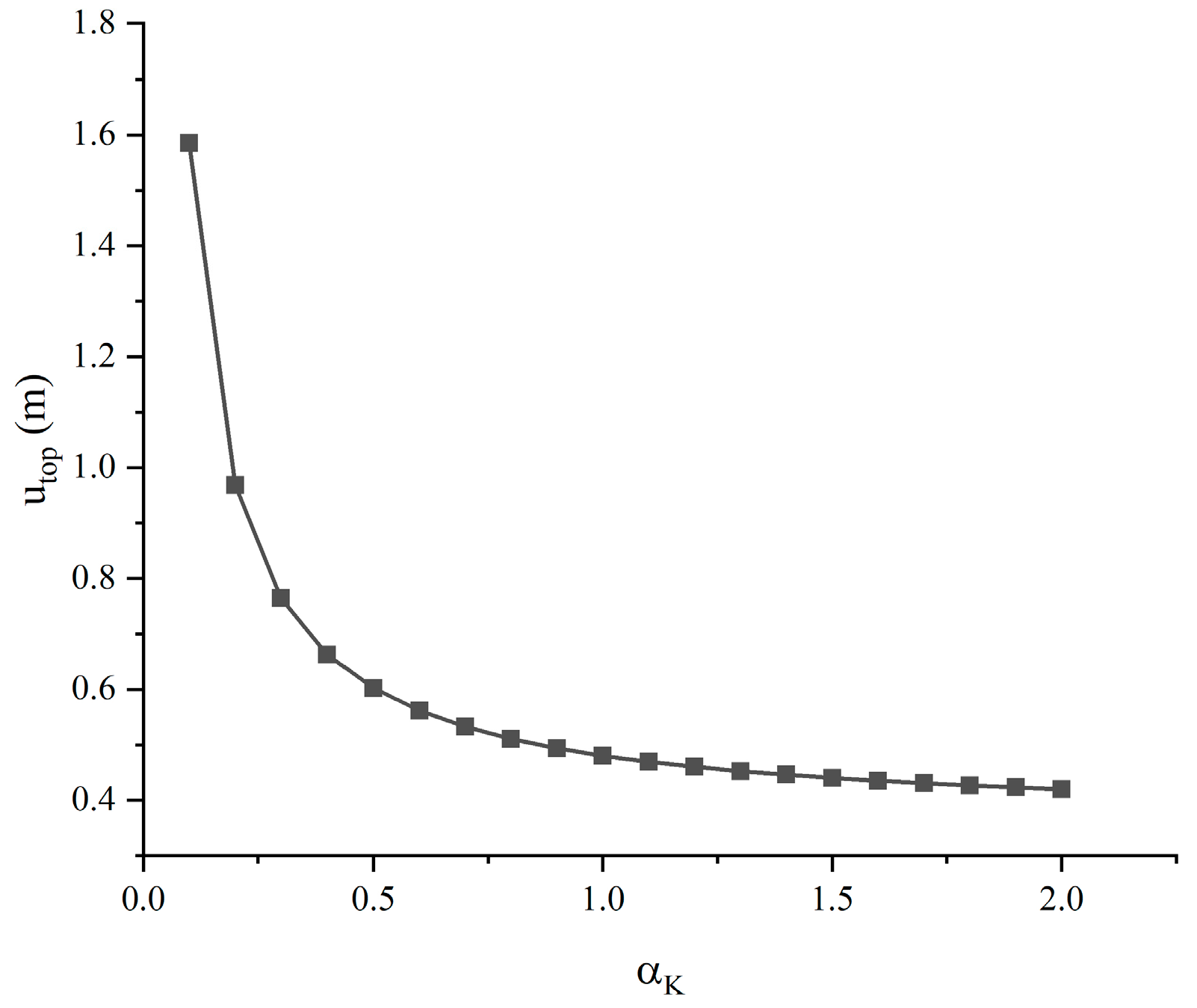
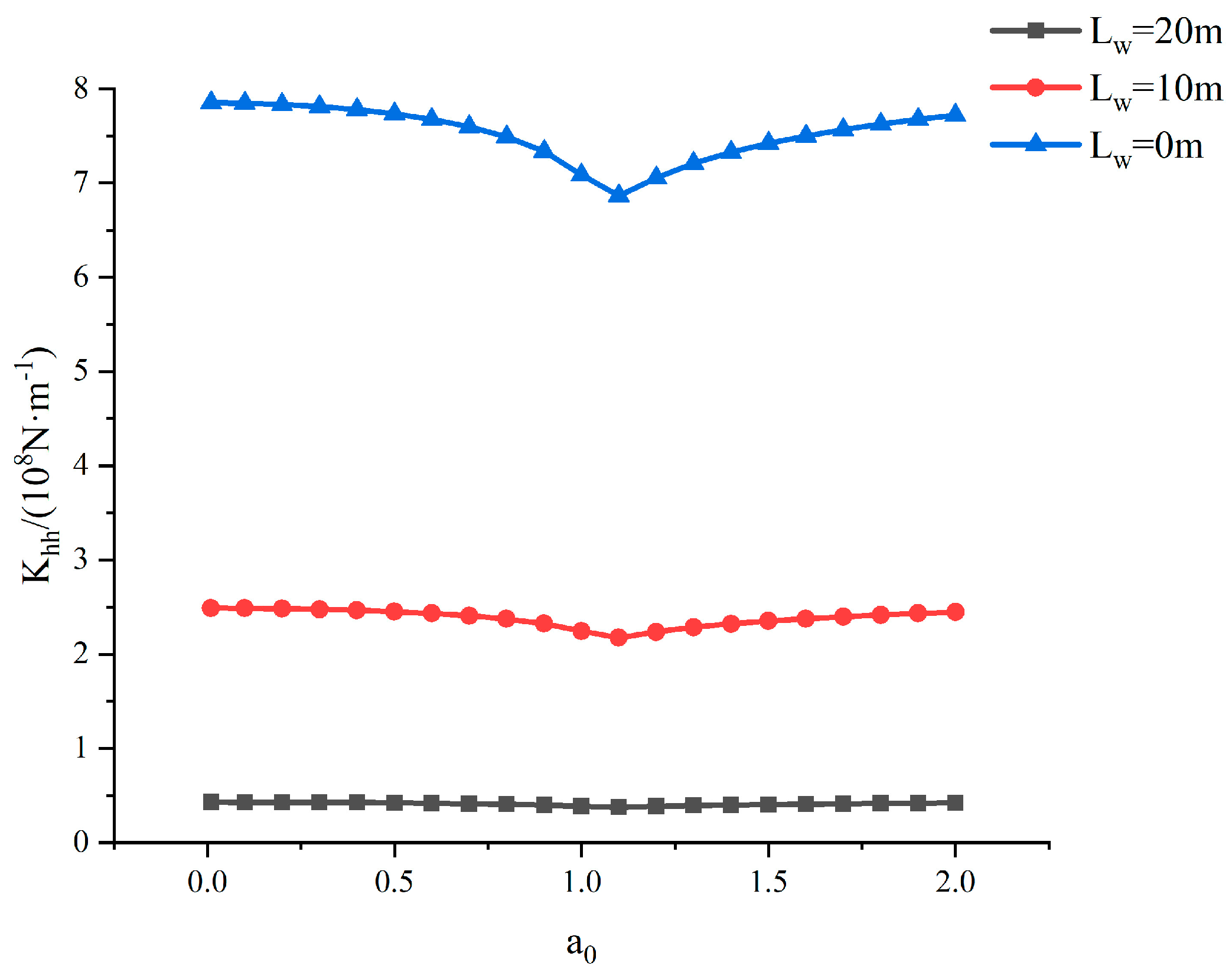
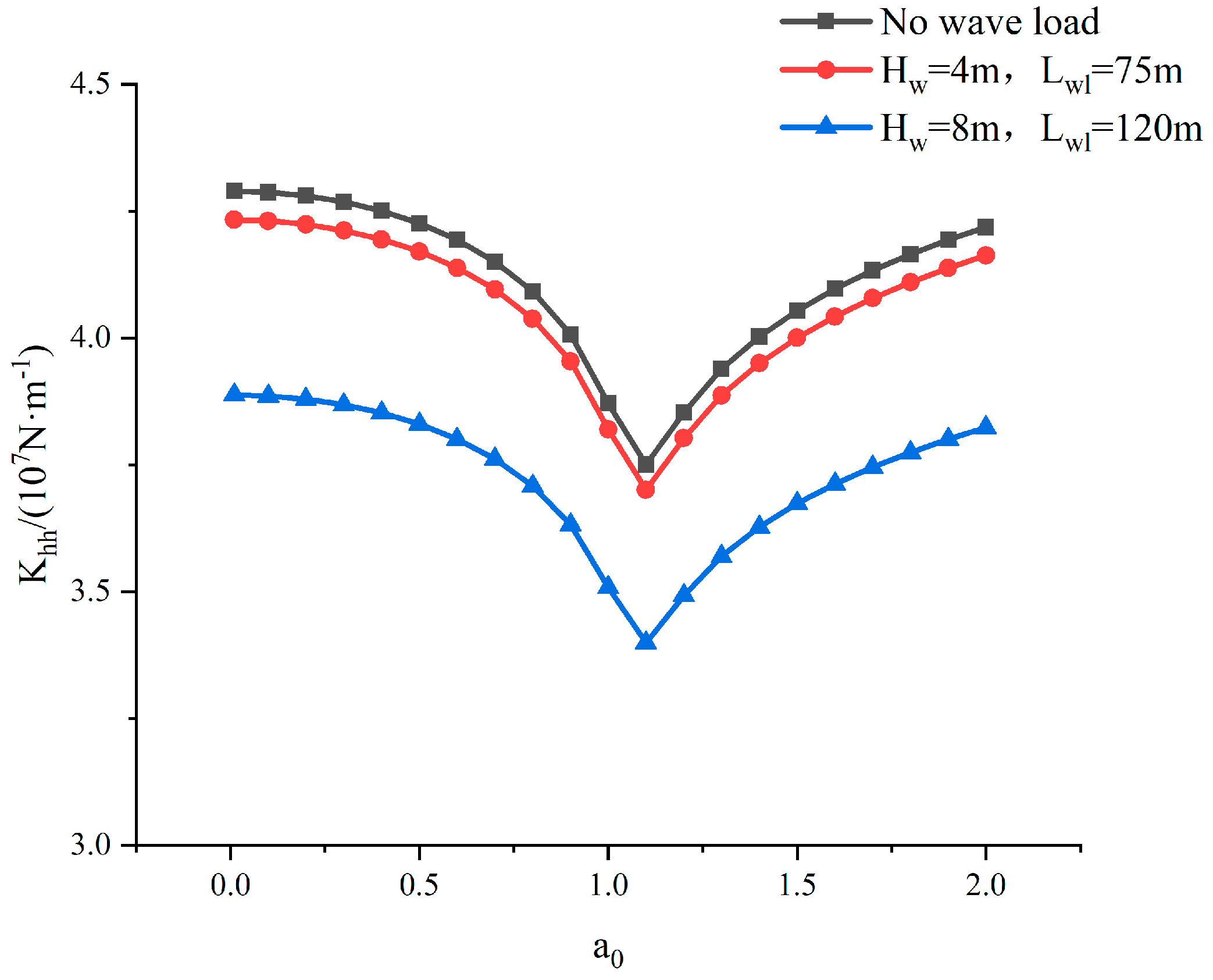
4.3. Dynamic Foundation Impedance
5. Conclusions
- (1)
- With increasing wind speed, the tower displacement increases significantly. The influence of foundation impedance on the tower displacement is more significant when the foundation impedance is relatively small.
- (2)
- The pile–pile interaction factor depends largely on the pile spacing. When the pile spacing is large, the influence of the passive pile on the active pile can be ignored; when the pile spacing is small, a secondary wave effect should be considered for the pile–pile interaction factor.
- (3)
- When the pile embedded ratio is large, the pile–pile interaction is more obvious. When the incidence angle is , the pile–pile interaction is less significant compared with that of and .
- (4)
- The foundation impedance decreases significantly with an increasing pile embedment ratio.
- (5)
- The influence of wave load on the foundation impedance is more obvious when the wave load is large.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Feyzollahzadeh, M.; Mahmoodi, M.; Yadavar-Nikravesh, S.; Jamali, J. Wind load response of offshore wind turbine tow-ers with fixed monopile platform. J. Wind Eng. Ind. Aerodyn. 2016, 158, 122–138. [Google Scholar] [CrossRef]
- Zheng, X.Y.; Li, H.; Rong, W.; Li, W. Joint earthquake and wave action on the monopile wind turbine foundation: An experimental study. Mar. Struct. 2015, 44, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Gupta, B.K.; Basu, D. Offshore wind turbine monopile foundations: Design perspectives. Ocean Eng. 2020, 213, 107514. [Google Scholar] [CrossRef]
- Bhattacharya, S. Challenges in Design of Foundations for Offshore Wind Turbines. Eng. Technol. Ref. 2014, 1, 922. [Google Scholar] [CrossRef]
- Lombardi, D.; Bhattacharya, S.; Wood, D.M. Dynamic soil–structure interaction of monopile supported wind turbines in cohesive soil. Soil Dyn. Earthq. Eng. 2013, 49, 165–180. [Google Scholar] [CrossRef]
- Damgaard, M.; Bayat, M.; Andersen, L.; Ibsen, L. Assessment of the dynamic behaviour of saturated soil subjected to cyclic loading from offshore monopile wind turbine foundations. Comput. Geotech. 2014, 61, 116–126. [Google Scholar] [CrossRef]
- Bouzid, D.A.; Bhattacharya, S.; Otsmane, L. Assessment of natural frequency of installed offshore wind turbines using nonlinear finite element model considering soil-monopile interaction. J. Rock Mech. Geotech. Eng. 2018, 10, 333–346. [Google Scholar] [CrossRef]
- Alkhoury, P.; Soubra, A.H.; Rey, V.; Aït-Ahmed, M. A full three-dimensional model for the estimation of the natural fre-quencies of an offshore wind turbine in sand. Wind Energy 2021, 24, 699–719. [Google Scholar] [CrossRef]
- Kjørlaug, R.A.; Kaynia, A.M. Vertical earthquake response of megawatt-sized wind turbine with soil-structure interaction effects. Earthq. Eng. Struct. Dyn. 2015, 44, 2341–2358. [Google Scholar] [CrossRef]
- Corciulo, S.; Zanoli, O.; Pisanò, F. Transient response of offshore wind turbines on monopiles in sand: Role of cyclic hy-dro–mechanical soil behaviour. Comput. Geotech. 2017, 83, 221–238. [Google Scholar] [CrossRef] [Green Version]
- Zuo, H.; Bi, K.; Hao, H. Dynamic analyses of operating offshore wind turbines including soil-structure interaction. Eng. Struct. 2018, 157, 42–62. [Google Scholar] [CrossRef]
- Galvín, P.; Romero, A.; Solís, M.; Domínguez, J. Dynamic characterisation of wind turbine towers account for a monopile foundation and different soil conditions. Struct. Infrastruct. Eng. 2017, 13, 942–954. [Google Scholar] [CrossRef]
- Kausel, E. Early history of soil–structure interaction. Soil Dyn. Earthq. Eng. 2010, 30, 822–832. [Google Scholar] [CrossRef] [Green Version]
- Reese, L.C. Non-dimensional solutions for laterally loaded piles with soil modulus assumed proportional to depth. In Proceedings of the 8th Texas Conference on Soil Mechanics and Foundation Engineering, Austin, TX, USA, 14–15 September 1956. [Google Scholar]
- McClelland, B.; Focht, J. Soil modulus for laterally loaded piles. J. Soil Mech. Found. Div. 1956, 82, 1081-1–1081-22. [Google Scholar] [CrossRef]
- Darvishi-Alamouti, S.; Bahaari, M.R.; Moradi, M. Natural frequency of offshore wind turbines on rigid and flexible monopiles in cohesionless soils with linear stiffness distribution. Appl. Ocean Res. 2017, 68, 91–102. [Google Scholar] [CrossRef]
- Andersen, L.V.; Vahdatirad, M.; Sichani, M.T.; Sørensen, J.D. Natural frequencies of wind turbines on monopile founda-tions in clayey soils—A probabilistic approach. Comput. Geotech. 2012, 43, 1–11. [Google Scholar] [CrossRef]
- Adhikari, S.; Bhattacharya, S. Vibrations of wind-turbines considering soil-structure interaction. Wind Struct. Int. J. 2011, 14, 85–112. [Google Scholar] [CrossRef] [Green Version]
- Adhikari, S.; Bhattacharya, S. Dynamic Analysis of Wind Turbine Towers on Flexible Foundations. Shock Vib. 2012, 19, 37–56. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Adhikari, S. Experimental validation of soil–structure interaction of offshore wind turbines. Soil Dyn. Earthq. Eng. 2011, 31, 805–816. [Google Scholar] [CrossRef]
- Nogami, T.; Paulson, S.K. Transfer matrix approach for nonlinear pile group response analysis. Int. J. Numer. Anal. Methods Geomech. 1985, 9, 299–316. [Google Scholar] [CrossRef]
- Zhang, L.; Gong, X.-N.; Yang, Z.-X.; Yu, J.-L. Elastoplastic solutions for single piles under combined vertical and lateral loads. J. Cent. South Univ. Technol. 2011, 18, 216–222. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, M.; Zou, X. Behavior of Laterally Loaded Piles in Multilayered Soils. Int. J. Géoméch. 2015, 15, 06014017. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Z.; Zhao, H. Analysis of Wind-Turbine Steel Tower by Transfer Matrix. In Proceedings of the 2009 International Conference on Energy and Environment Technology, Guilin, China, 16–18 October 2009. [Google Scholar]
- Huang, M.; Zhong, R. Coupled horizontal-rocking vibration pf partially embedded pile groups and its effect on resonance of offshore wind turbine structures. Chinsese J. Geotech. Eng. 2014, 36, 286–294. [Google Scholar]
- Anoyatis, G.; Mylonakis, G.; Lemnitzer, A. Soil reaction to lateral harmonic pile motion. Soil Dyn. Earthq. Eng. 2016, 87, 164–179. [Google Scholar] [CrossRef] [Green Version]
- Anoyatis, G.; Lemnitzer, A. Dynamic pile impedances for laterally–loaded piles using improved Tajimi and Winkler for-mulations. Soil Dyn. Earthq. Eng. 2017, 92, 279–297. [Google Scholar] [CrossRef] [Green Version]
- Shuqing, W.; Bingchen, L. Wave Mechanics for Ocean Engineering; China Ocean University Press: Qingdao, China, 2013. (In Chinese) [Google Scholar]
- Xin-xin, L.; Da-peng, S.; Xue-jiao, X.; Hao, W.; Yu-cheng, L. Experimental study of irregular wave force loads on high rise pile platform. J. Waterw. Harb. 2013, 34, 277–284. (In Chinese) [Google Scholar]
- Dobry, R.; Gazetas, G. Dynamic Response of Arbitrarily Shaped Foundations. J. Geotech. Eng. 1986, 112, 109–135. [Google Scholar] [CrossRef]
- Mylonakis, G.; Gazetas, G. Lateral Vibration and Internal Forces of Grouped Piles in Layered Soil. J. Geotech. Geoenvironmental Eng. 1999, 125, 16–25. [Google Scholar] [CrossRef]
- Luan, L.; Zheng, C.; Kouretzis, G.; Ding, X. Dynamic analysis of pile groups subjected to horizontal loads considering coupled pile-to-pile interaction. Comput. Geotech. 2020, 117, 103276. [Google Scholar] [CrossRef]
- Van Binh, L.; Ishihara, T.; Van Phuc, P.; Fujino, Y. A peak factor for non-Gaussian response analysis of wind turbine tower. J. Wind Eng. Ind. Aerodyn. 2008, 96, 2217–2227. [Google Scholar] [CrossRef]
- Veritas, N. Environmental Conditions and Environmental Loads; Det Norske Veritas Oslo: Høvik, Norway, 2000. [Google Scholar]
- Jara, F.A.V. Model Testing of Foundations for Offshore Wind Turbines; Oxford University: Oxford, UK, 2006. [Google Scholar]
- Kaynia, A.M. Dynamic Stiffness and Seismic Response of Pile Groups; Massachusetts Institute of Technology: Cambridge, MA, USA, 1982. [Google Scholar]

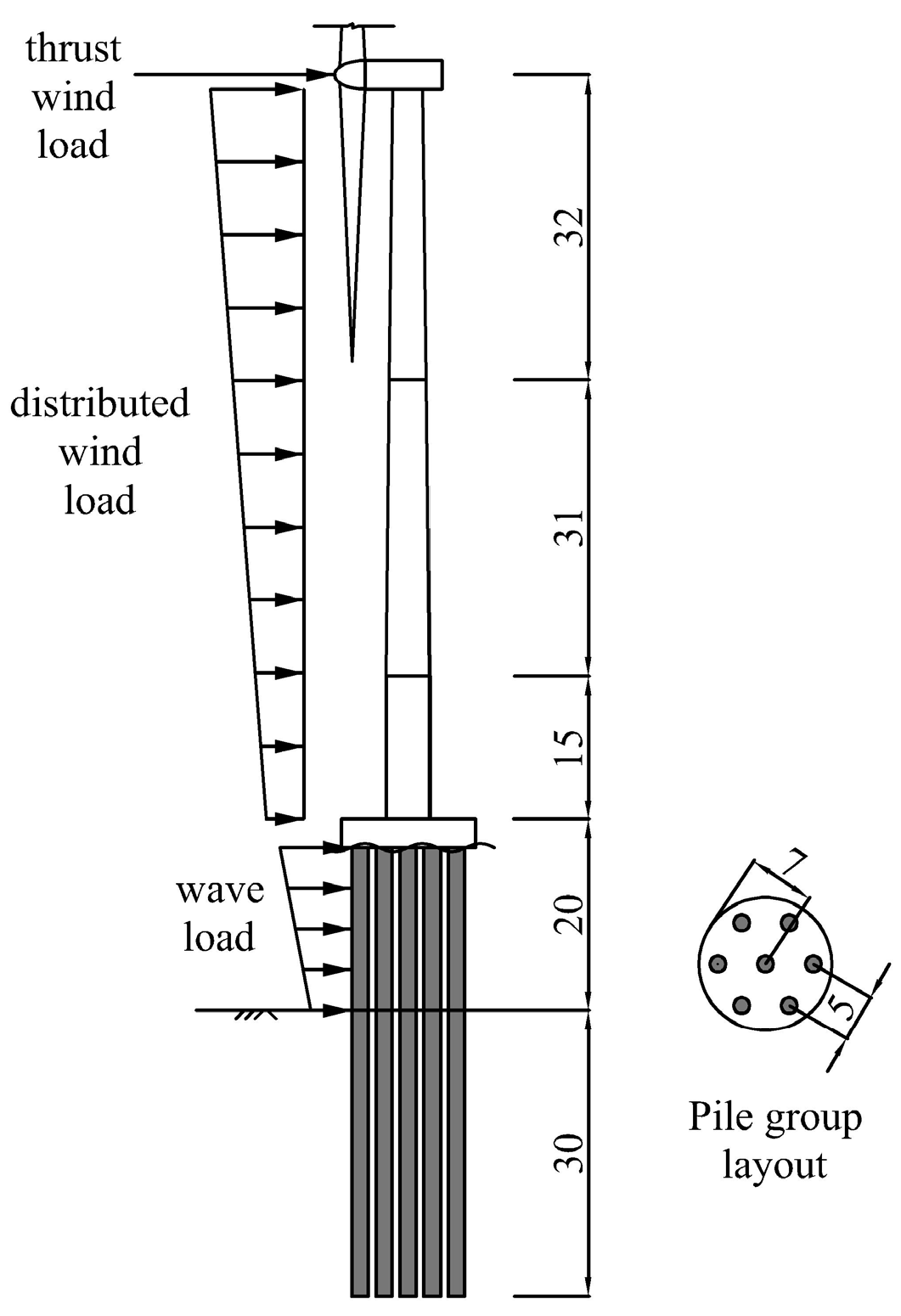


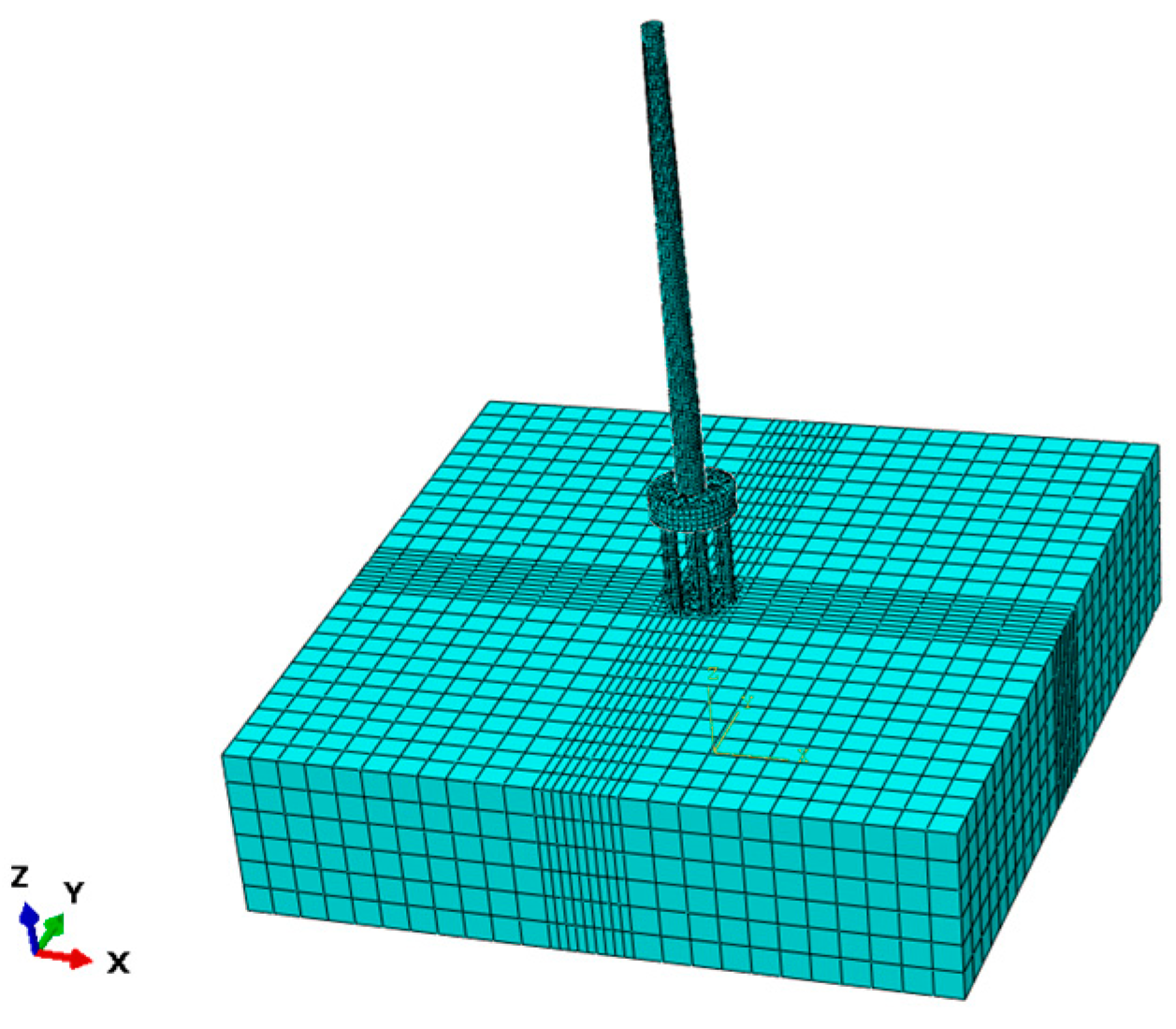

| Tower Parts | Length (m) | Bottom Diameter | Top Diameter | Tower Wall Thickness |
|---|---|---|---|---|
| Upper segment | 32 | 3.9 | 3.1 | 50 |
| Middle segment | 31 | 4.5 | 3.9 | 50 |
| Bottom segment | 15 | 4.5 | 4.5 | 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Yao, W.; Yu, G. Dynamic Analysis on Pile Group Supported Offshore Wind Turbine under Wind and Wave Load. J. Mar. Sci. Eng. 2022, 10, 1024. https://doi.org/10.3390/jmse10081024
Shi Y, Yao W, Yu G. Dynamic Analysis on Pile Group Supported Offshore Wind Turbine under Wind and Wave Load. Journal of Marine Science and Engineering. 2022; 10(8):1024. https://doi.org/10.3390/jmse10081024
Chicago/Turabian StyleShi, Yusha, Wenjuan Yao, and Guoliang Yu. 2022. "Dynamic Analysis on Pile Group Supported Offshore Wind Turbine under Wind and Wave Load" Journal of Marine Science and Engineering 10, no. 8: 1024. https://doi.org/10.3390/jmse10081024
APA StyleShi, Y., Yao, W., & Yu, G. (2022). Dynamic Analysis on Pile Group Supported Offshore Wind Turbine under Wind and Wave Load. Journal of Marine Science and Engineering, 10(8), 1024. https://doi.org/10.3390/jmse10081024






