Abstract
An experimental investigation of the vertical structure characteristics of internal solitary waves (ISWs) was systematically carried out in a large gravitationally stratified fluid flume. Four different stratifications were established, and basic elements of ISWs were measured by a conductivity probe array. The vertical distributions of the amplitude, characteristic frequency and waveform of two types of ISWs under different stratifications were obtained, and the experimental results were compared with the theoretical model. The study shows that most vertical structures of the amplitude under different stratifications agree with those of the theoretical model, while there are some deviations for ISWs with large amplitudes. Neither the two-layer model nor the continuously stratified model can effectively describe the variation in the characteristic frequency at different depths with amplitude. For a single small-amplitude ISW, the characteristic frequency first increases and then decreases with increasing depth. The characteristic frequency is largest at the depth of the maximum buoyancy frequency. For an ISW with a relatively large amplitude, there is likely to be a local minimum of the characteristic frequency near the depth where the maximum buoyancy frequency lies. In different stratifications, the function of KdV theory can describe the waveforms of ISWs at different depths well.
1. Introduction
Internal solitary waves (ISWs), which are a kind of nonlinear internal wave, are ubiquitous in marginal sea areas [1,2,3]. Based on the balance between nonlinearity and dispersion, ISWs can maintain a stable shape for long distances in the horizontal direction [4]. Due to the opposite flow direction induced by the upper and lower layers of the wave, a strong shear flow can be vertically induced, which can have a significant impact on the safety of marine structures and underwater platforms [5,6,7,8,9,10]. In addition, ISWs with large amplitudes, which are often accompanied by relatively large vertical velocities, can have an important impact on seawater mixing [11], nutrient transport [12] and sediment resuspension [13] in the ocean. Therefore, studying the vertical structure characteristics of ISWs is greatly significant.
Vertical structures of ISWs usually refer to the distribution of amplitudes at different depths [14]. A large amount of information can be obtained from the vertical structure of ISWs, including the depth of the maximum amplitude and the vertical scale of ISWs. Additionally, vertical structures can reflect the evolution of ISWs to a certain extent [15]. Many theoretical studies on vertical structures of ISWs have been carried out thus far [16,17,18,19,20,21,22]. Fliegel and Hunkins [18] first calculated the dispersion relation of internal waves by using the Thomson–Haskell method and obtained vertical structures of internal waves in different modes. Based on the Thomson–Haskell method, Cai and Gan [19] calculated the internal wave dispersion relation without using the Boussinesq approximation and theoretically analyzed the vertical structure characteristics of different modes at two stations in the South China Sea. Zhang and Gao [20] obtained vertical structures and the dispersion relation of internal waves by using the transformation method of Russian scholars. Based on a numerical method, Deng et al. [21] analyzed the vertical structures of different modes of internal waves in background currents. Kurkina et al. [22] solved the theoretical vertical structures of first-mode and second-mode ISWs with nonlinear corrections in two-layer and three-layer fluids.
The propagation and evolution characteristics of ISWs have been investigated in several studies by using in situ observational data [23,24,25,26,27]. Vlasenko et al. [28] obtained measured data of ISWs in the Strait of Messina and found that the observed vertical structures of ISWs are consistent with numerical simulation results. Geng et al. [29] obtained the vertical structures of ISWs near the Dongsha Atoll of the South China Sea using seismic technology and found that the observational vertical structures of ISWs are generally consistent with the theoretical results except when ISWs interact with the topography. Similarly, Gong et al. [14] compared the vertical structures of ISWs obtained by the seismic method with two theories. The results show that ISWs with low nonlinearity can be described by a linear vertical structure function, while ISWs with high nonlinearity are in agreement with the first-order nonlinear vertical structure function. Because obtaining refined vertical structure data from field observations is difficult, the verification of the theoretical vertical structure of ISWs based on observational data is relatively limited. In terms of laboratory experiments, many experimental methods have been used to study the characteristics of ISWs [30,31,32,33,34,35]. At present, experimental research objects of ISWs are not limited to the first mode. Many experimental studies on the generation mechanism and evolution characteristics of second-mode ISWs have been carried out [36,37,38]. However, most experimental studies focus on the propagation and evolution characteristics of ISWs at the interface (position of maximum amplitude), while there are few studies on the vertical structure of ISWs in stratified fluids.
Korteweg de Vries’ (KdV) theory is the most commonly used theoretical model to describe the propagation and evolution characteristics of ISWs in laboratory experiments [39,40,41]. Since weak nonlinearity is an important condition for validating the KdV model, KdV theory is not applicable to describe ISWs with large amplitudes [42,43,44]. Michallet and Barthelemy [45] compared the theoretical and experimental results of the waveform, phase velocity and frequency–amplitude relationship of ISWs and found that KdV theory can describe small-amplitude solitary waves in different stratified fluids well. Grue et al. [46] analyzed the propagation characteristics of ISWs in two-layer fluids and found that KdV theory can provide predictions that are consistent with the experimental results of small-amplitude ISWs. Du et al. [47] compared the experimental results of the elevation- and depression-type ISWs with the results from the following three different theoretical models: KdV, extended KdV (eKdV) and Miyata–Choi–Camassa (MCC). The results show that the experimental results conform to those of KdV theory when the ratio of the amplitude of ISWs to the total water depth is less than 0.04. However, KdV theory is presently used to describe the characteristics of ISWs at the interface in laboratory experiments, and the validity of KdV theory describing the properties of ISWs at different depths in stratified fluids is not clear.
In view of the above discussion, an experimental method is used in this paper to study the vertical structure of the amplitude of ISWs in a large, gravitationally stratified fluid flume and to analyze the domain of validity of KdV theory by comparing the characteristics of ISWs at different depths with theoretical models. The influence of environmental factors on the vertical structure characteristics of ISWs is further analyzed by setting different stratifications and amplitudes. This paper is organized in the following manner: The KdV model is introduced in Section 2, including the two-layer model and the continuously stratified model. The experimental techniques and methods are presented in Section 3. The results and discussion are provided in Section 4, and the conclusion is presented in Section 5.
2. Theoretical Models
Considering a stratified fluid of a finite depth with rigid boundaries where buoyancy frequency is a continuous function of the depth, the eigenfunction is determined by the solution of the boundary value problem:
where is the buoyancy frequency, which is determined by the formula ; is the linear phase speed of ISWs; and is the total water depth. Equation (1) can be solved by using the Thomson–Haskell method [18], and can be obtained. Then, can be calculated under the normalization condition of .
For ISWs with a maximum amplitude in a stratified fluid, their amplitude at different depths can be calculated by the following expression (with the nonlinear terms removed):
Under the Boussinesq approximation, the vertical isopycnal displacement of ISWs propagating in the positive direction of axis can be described by the classical KdV equations:
where is the time, and is the horizontal coordinate along the propagation direction of ISWs. The parameters and are called the nonlinear coefficient and the dispersion coefficient, respectively.
The well-known solitary wave solution to Equation (3) is
where is the amplitude of ISWs, and the nonlinear velocity and the characteristic width of this soliton can be calculated by:
The characteristic frequency of the soliton can be obtained by . Since and are both relative to , the characteristic frequency will change with . Moreover, the obtained frequency–amplitude relationship varies for the two-layer fluid model and the continuously stratified fluid model due to the different calculation methods of , and in these two models.
In the continuously stratified model, can also be obtained when the eigenfunction is calculated by the Thomson–Haskell method. The terms , can be determined by the following formula:
In the two-layer model, , and can be determined by the following expressions:
where and are the thicknesses of the upper and lower layers, respectively, and and are the densities of the upper and lower layers, respectively.
3. Experimental Device and Method
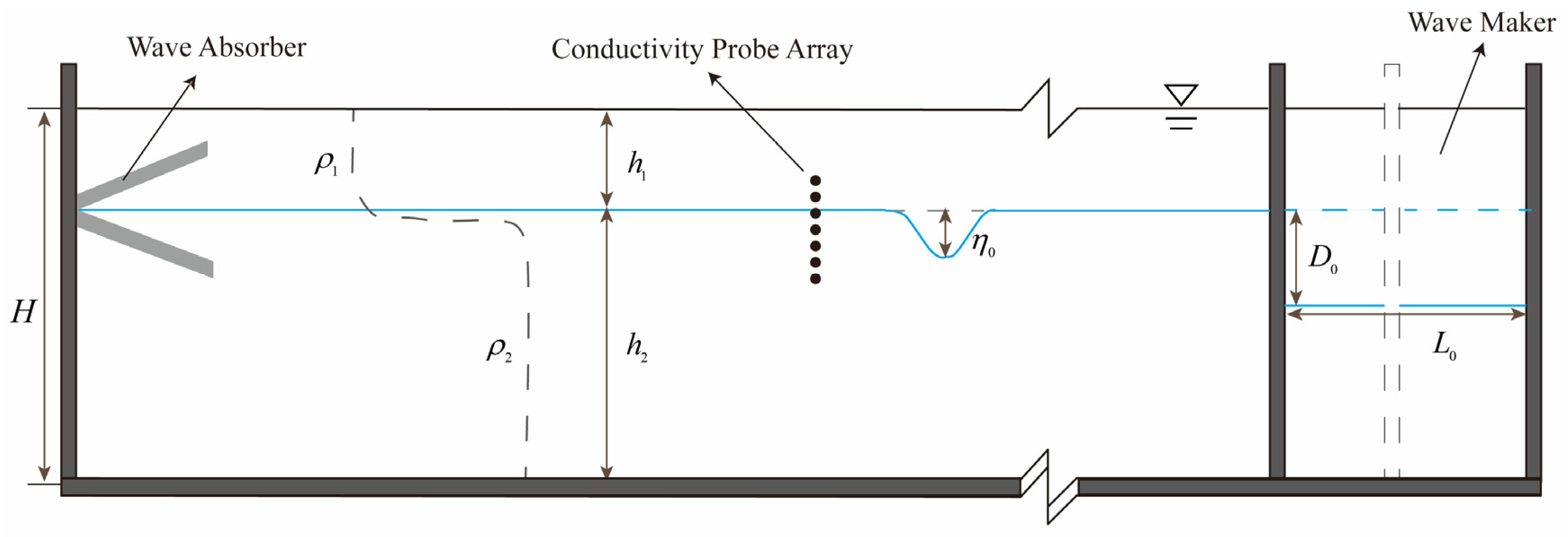
The experiments were performed in a gravitationally stratified fluid flume that is 1200 cm long, 120 cm wide and 100 cm high. At the right end of the flume, the wave maker aimed to achieve gravity collapse in the stratified fluid, which is presented in Figure 1. The step length and depth are and , respectively, in the experimental generation principle of ISWs. This device can produce high-quality elevation- or depression-type ISWs at arbitrary pycnocline depths. At the left end of the flume, a wedge-shaped wave absorber was installed. According to the amplitude of ISWs and interface depth, the wedge angle can be adjusted to effectively eliminate the reflected waves. A stratified fluid was created by using the classic “double-tank” method. At first, the flume was filled with fresh water of density to the depth . Then a brine solution of density was slowly injected beneath the fresh water through two small openings along the bottom of the flume until the brine depth reached , and the total depth was . Due to the mixing of fresh water in the upper layer and brine solution in the lower layer, a continuous density distribution structure with a certain thickness was formed at the interface, namely the pycnocline, which can simulate the actual vertical density distribution of the ocean with the characteristics of a typical pycnocline.
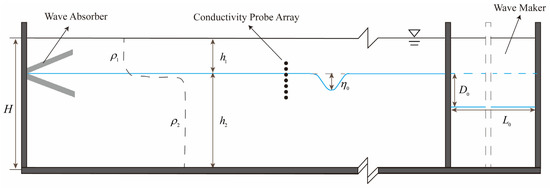
Figure 1.
Schematic diagram of the experimental apparatus.
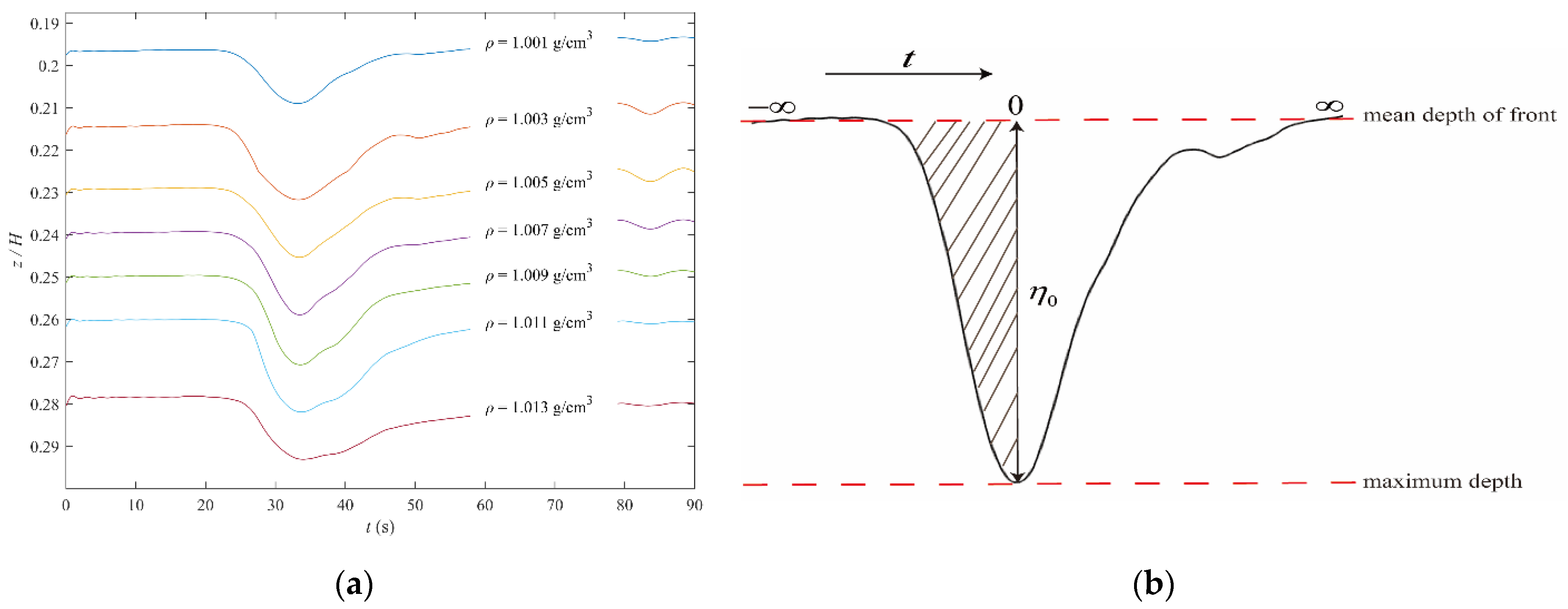
The vertical distribution of density in stratified fluids and vertical structures of ISWs was measured by an internal wave dynamic measurement system. This system consists of a conductivity probe array, signal control circuit and data processing system. A vertically displaceable probe was used to measure the vertical density distribution of the fluid. A conductivity probe array consisting of seven probes vertically arranged at equal intervals was used to measure the vertical structure of ISWs. The horizontal distance between the probes and the wave maker is 6 m, so the fully developed ISWs can be detected (Figure 1). Adjusting the position of the conductivity probe array to cover the whole pycnocline according to the stratification conditions and amplitude of ISWs, the fluctuation of ISWs at different depths can be completely captured. The origin of the axis is set at the surface with the positive axis running downward. Figure 2a shows the vertical distribution of isopycnic lines of ISWs in a certain stratification. The back portion of the wave was contaminated by the small-amplitude disturbances in the tail. Therefore, as shown in Figure 2b, only the forward portion of the wave was used to calculate the amplitude and characteristic length of ISWs [40,41]. The characteristic length and frequency of ISWs can be experimentally calculated by the following expressions (Equations (10) and (11), respectively):
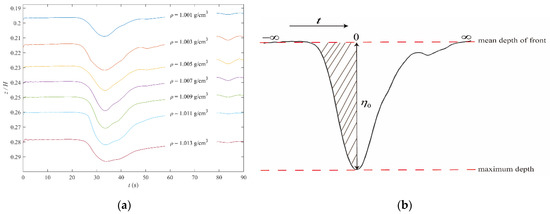
Figure 2.
Vertical distribution of isopycnic lines of ISWs in a certain stratification (a) and experimental method of calculating the amplitude and characteristic frequency of ISWs (b).
4. Results and Discussion
To fully study the vertical structure characteristics of ISWs, four stratification conditions were set in the experiment, and two types of ISWs (elevation- and depression-type) were generated during operation. The specific experimental conditions are summarized in Table 1. S1 is a representative of the stratification in the deep sea. S2–S4 are used to simulate the different stratifications in the continental shelves. Both elevation-type () and depression-type () ISWs exist in real oceans. Compared with the depression-type ISWs, the amplitudes of the elevation-type ISWs are generally smaller. During the experiment, the total water depth and the densities of upper and lower layers ( and , respectively) remained unchanged. Additionally, the dimensionless maximum amplitude ranged from 0.008 to 0.120.

Table 1.
Summary of experimental conditions.
4.1. Vertical Structure of the Amplitude
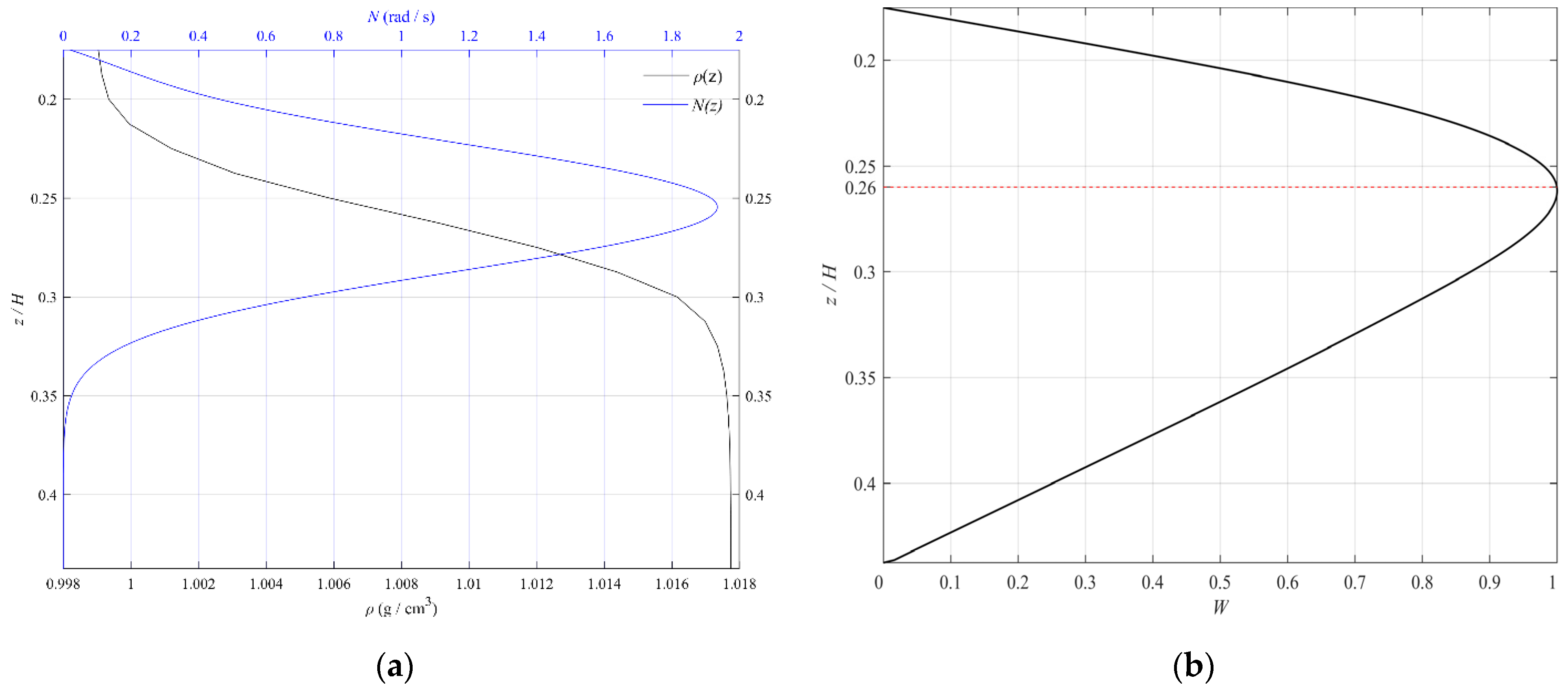
According to the theoretical model, the distribution of the buoyancy frequency can be obtained from the experimental density profile , and the vertical modal function of the internal wave can be subsequently calculated. Figure 3 illustrates the vertical distribution of ISWs in S3, with Figure 3a showing the density profile and buoyancy frequency distribution and Figure 3b presenting the vertical modal function of ISWs obtained by the Thomson–Haskell method. Figure 3 shows that under the condition of this density stratification, the variation in the buoyancy frequency and internal wave vertical modal function with depth are consistent, which show a trend of first increasing and then decreasing with an increasing depth. The maximum value of the buoyancy frequency profile is at a depth of , and the maximum value of the corresponding vertical modal function is at a depth of approximately (red line in Figure 3b). There is a small deviation between the depth of the maximum value of the buoyancy frequency profile and the depth of the maximum value of the vertical modal function that is obtained by the Thomson–Haskell method, which can also be found from the theoretical results of Kurkina et al. [22].
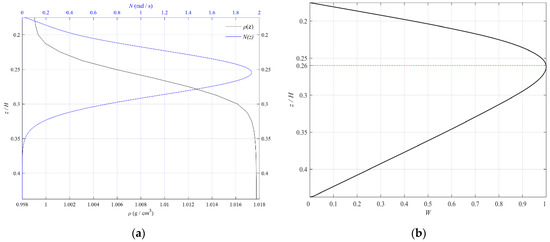
Figure 3.
Profile of the density and buoyancy frequency in S3 (a) and the vertical modal function calculated by the Thomson–Haskell method in S3 (b).
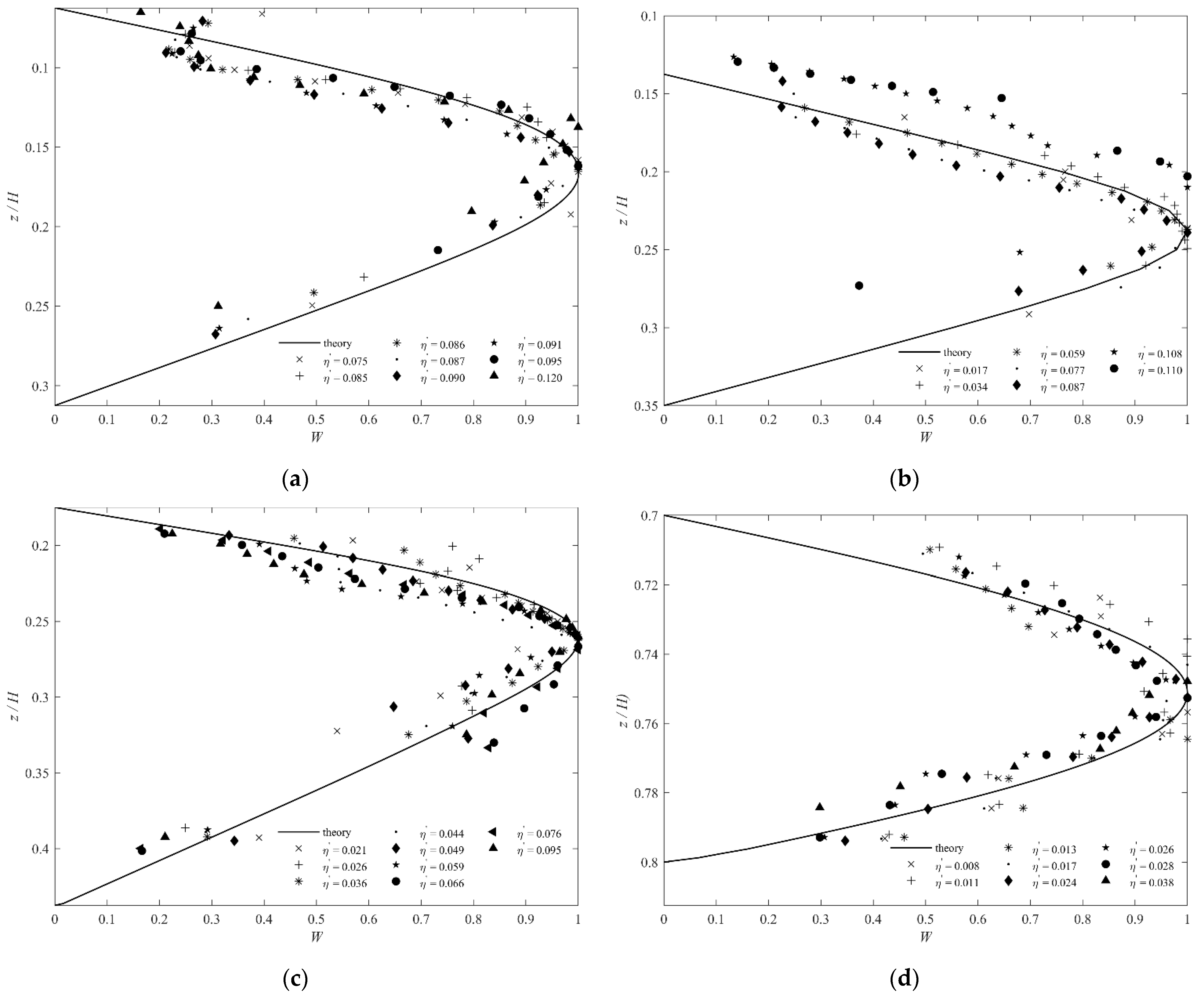
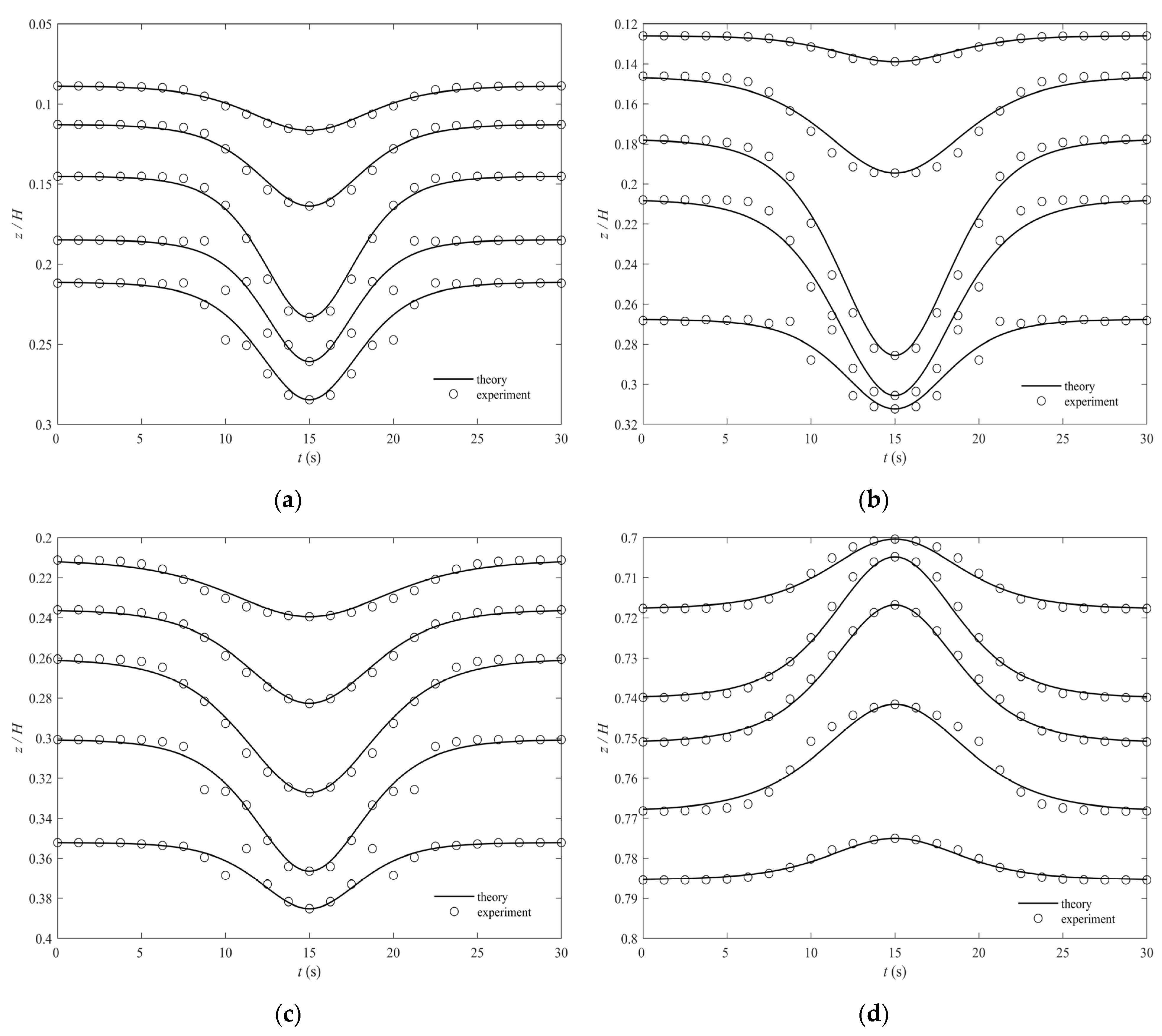
Figure 4 demonstrates a comparison between the theoretical and experimental results of the vertical structure of the amplitude of ISWs in four stratification conditions. Under different stratification conditions, whether elevation-type or depression-type, the theoretical vertical structure of the amplitude is basically consistent with most of the experimental results. In addition, the amplitude initially increases and then decreases with an increasing depth both theoretically and experimentally. For S1, the depths of the maximum amplitudes of ISWs under different cases are basically the same, while the depth of the maximum amplitude of ISW with large amplitude () moves up. For S2, most of the vertical distributions of the amplitude conform to the theory, while the vertical amplitude structure of ISWs with relatively large amplitudes ( and ) moves up. For S3, the depths of the maximum amplitudes under different cases and the vertical structure of the amplitude are consistent with the theory. For S4, similar to S3, the theory can describe the vertical structure of ISWs under different cases well. Figure 5 shows the variation in root mean square error with increasing under different stratification conditions. Root mean square errors in different stratifications are relatively small when . However, once , the root mean square errors start to increase significantly and exceed the allowable range.
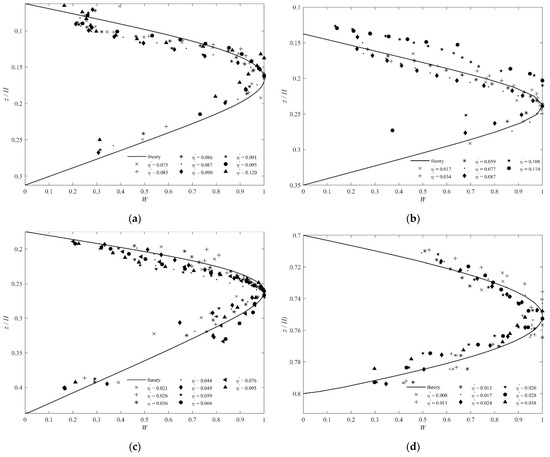
Figure 4.
Experimental vertical structure of the amplitude and theoretical vertical mode function: (a) S1; (b) S2; (c) S3; (d) S4.
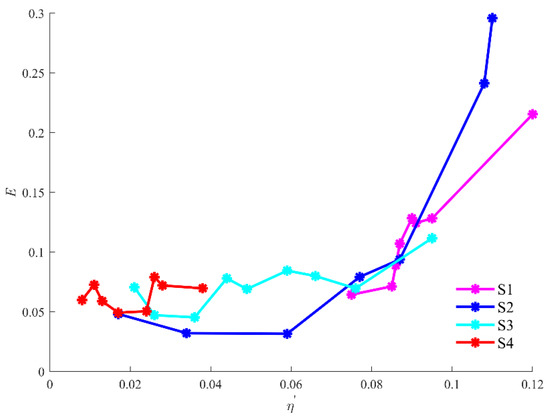
Figure 5.
Variation in with in different stratifications.
For S1 and S2, the vertical structures of ISWs basically conform to the theory in most cases, while for ISWs with large amplitudes (), the experimental vertical structures deviate from the theoretical model. These results occur because the effect of the nonlinear terms will be more significant with an increasing amplitude. In addition, with an increasing , the difference between the theoretical and experimental vertical structures of ISWs with large amplitudes is more obvious. However, for S3 and S4, the vertical structures of ISWs are consistent with the theoretical value due to the relatively small amplitudes ().
4.2. Vertical Distribution of the Characteristic Frequency
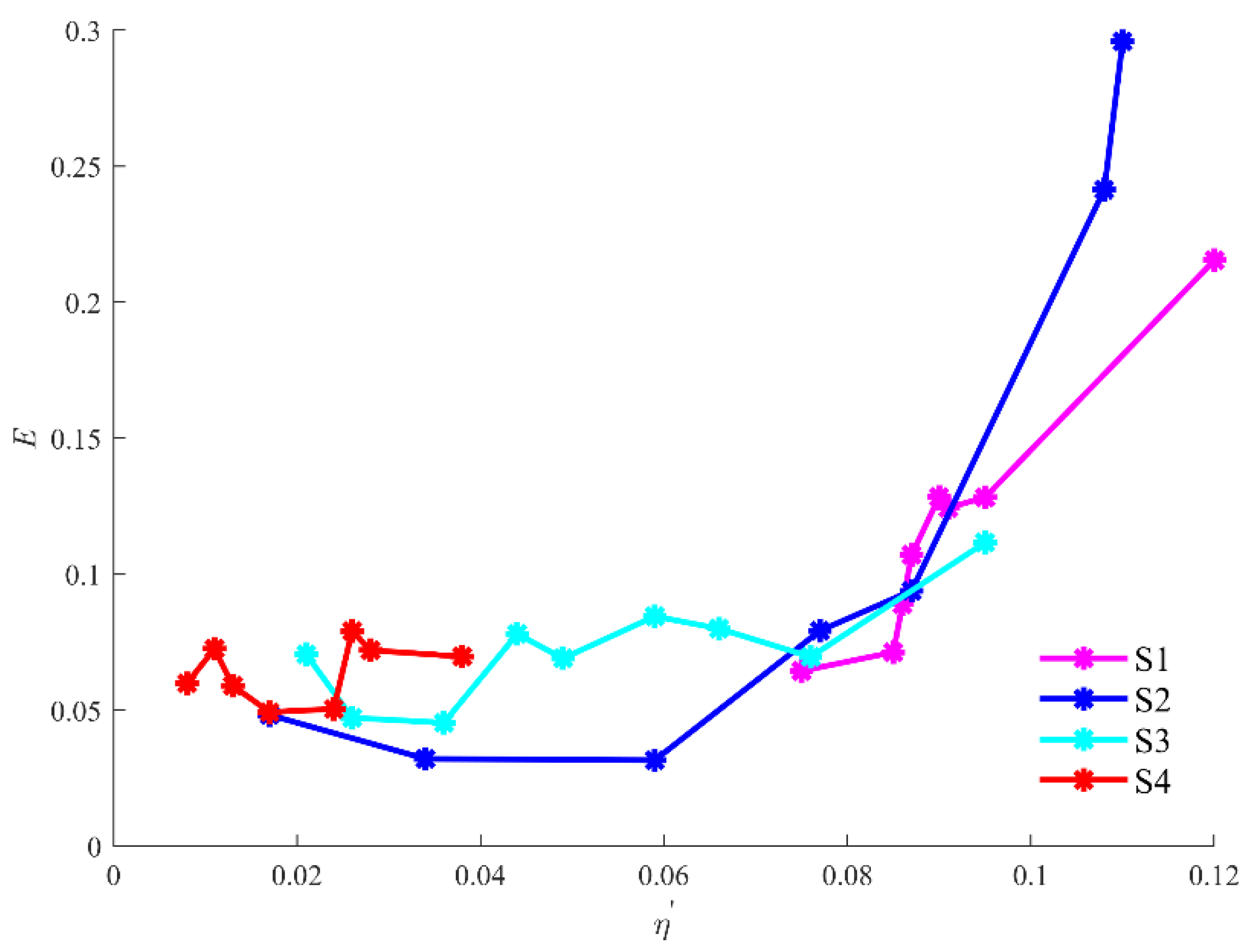
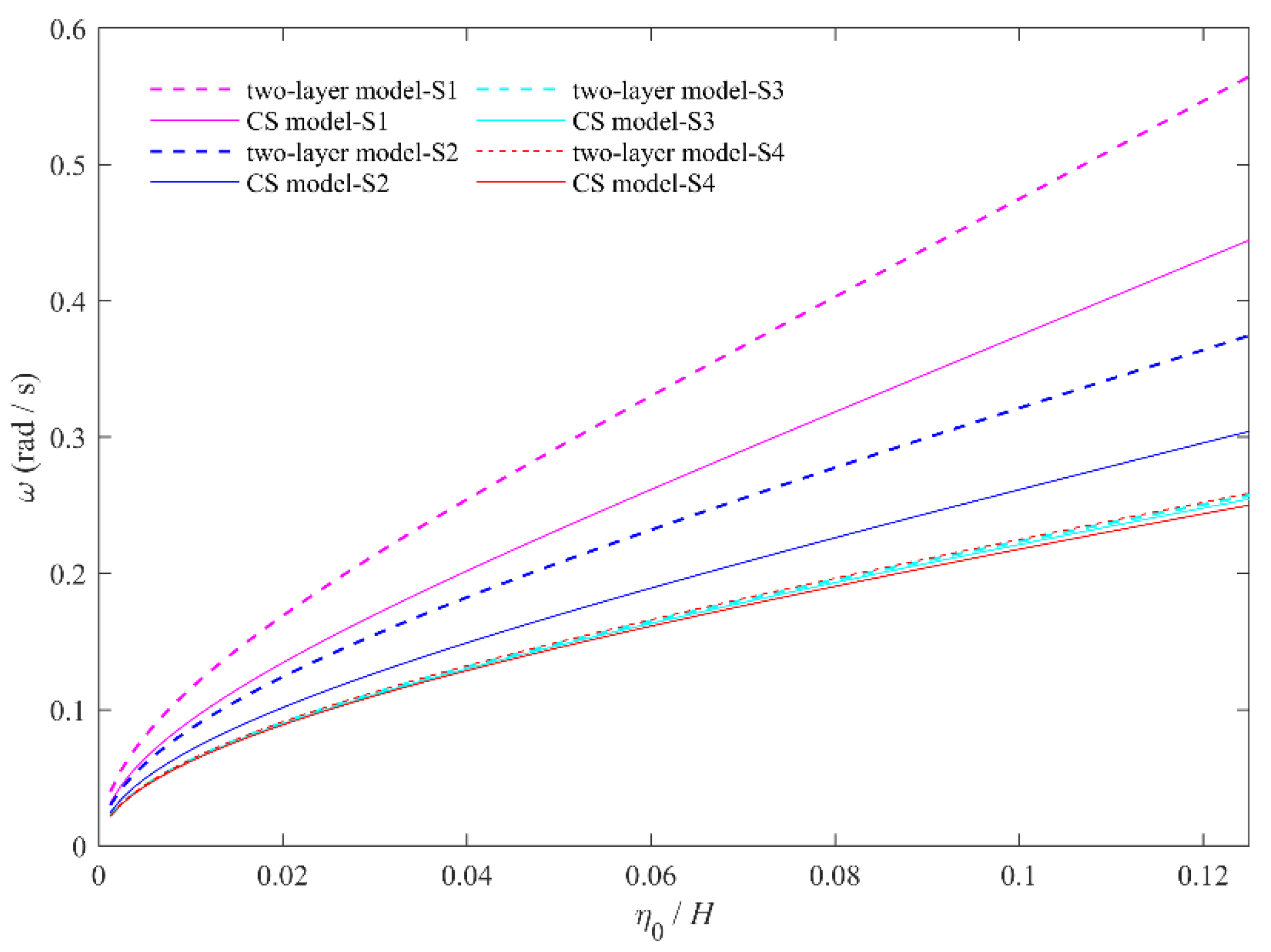
As shown in Figure 6, the variation in the theoretical characteristic frequency of ISWs with amplitudes in continuously stratified fluid and two-layer fluid can be obtained according to the expression of the characteristic frequency . The results show that the characteristic frequency of ISWs increases with an increasing amplitude whether it is for the continuously stratified fluid or the two-layer fluid. The theoretical value of the characteristic frequency in the two-layer fluid is larger than that in the continuously stratified fluid at the same amplitude. Generally, this is mainly due to smaller absolute values of and larger values of in the continuously stratified model for different stratifications. In addition, the variation in characteristic frequency is closely related to the stratification conditions. For the depression-type ISWs, both the characteristic frequency under the same amplitude and the difference in the theoretical values between the two-layer model and the continuously stratified model will correspondingly decrease with an increasing . The variation in the characteristic frequency of the elevation-type ISWs with the amplitude in S4 is basically consistent with that in S3. These trends are also closely linked to values of and in different stratification conditions.
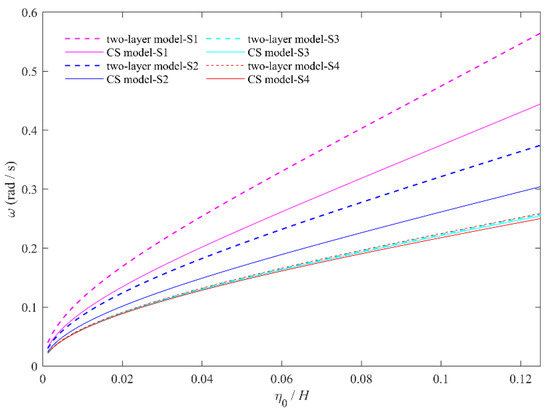
Figure 6.
The theoretical frequency–amplitude relationship in S1–S4, where CS refers to continuously stratified.
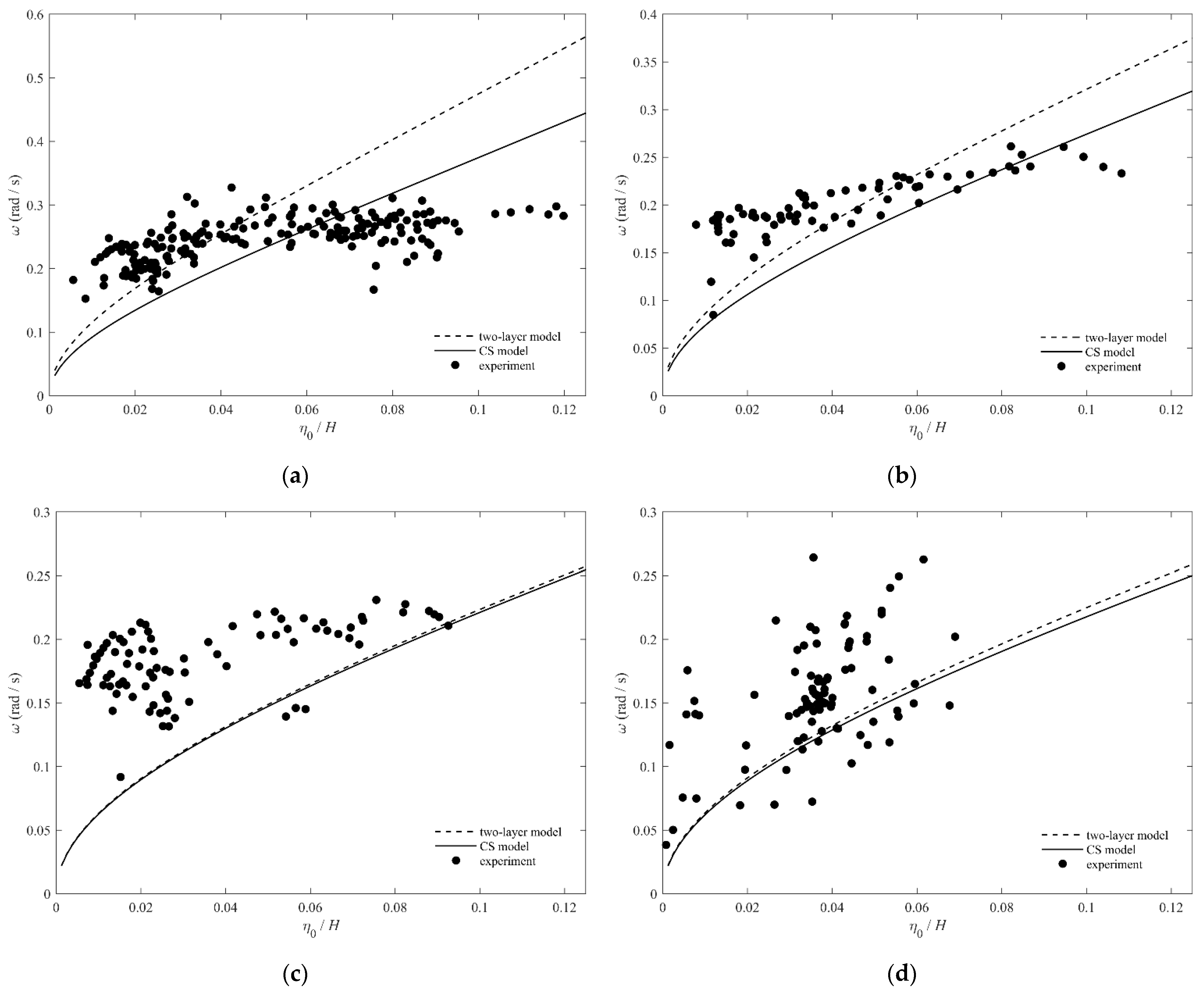
The theoretical and experimental results of the frequency–amplitude relationship of ISWs in S1–S4 are presented in Figure 7. For S1, the experimental characteristic frequencies at small amplitudes () are slightly larger than their theoretical values. The characteristic frequencies of ISWs are close to the theoretical values of the two-layer model under the condition of . When is satisfied, the experimental characteristic frequencies approach the theoretical values of the continuously stratified model. The characteristic frequencies of ISWs are smaller than the theoretical frequencies for relatively large amplitudes (). For S2, which is similar to S1, the experimental characteristic frequencies at small amplitudes () are larger than their theoretical values. Regarding the amplitude that satisfies , the characteristic frequencies of ISWs are basically between the theoretical values of the two models but closer to the continuously stratified model. The characteristic frequencies of ISWs are still smaller than the theoretical frequencies for relatively large amplitudes (). For S3, the theoretical values of the two models are coinciding, but the characteristic frequencies of most ISWs obtained by experiments are larger. For S4, the theoretical values of the two models are also close, and the characteristic frequencies obtained experimentally are dispersed with the amplitude. Different from other stratification conditions, the experimental values of the characteristic frequencies can be larger or smaller than the theoretical ones under the same amplitude.
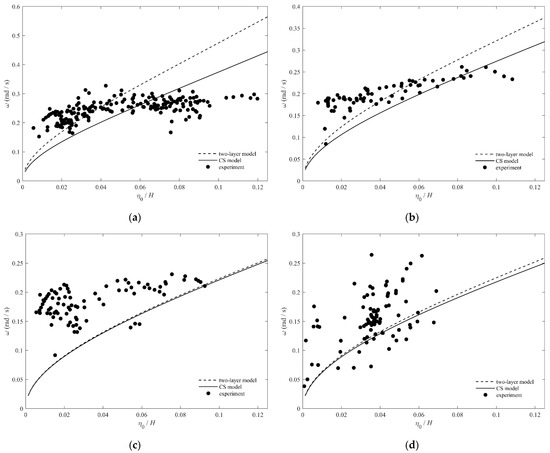
Figure 7.
Experimental and theoretical frequency–amplitude relationship of ISWs: (a) S1; (b) S2; (c) S3; (d) S4.
Comparing different stratification conditions, the characteristic frequency of ISWs increases with an increasing amplitude for the four stratifications, which is consistent with the trend of the theoretical model. Among these stratifications, S1 and S2 can describe the variation in the characteristic frequency with the amplitude to some extent by the two-layer model or the continuously stratified model. For S3 and S4, these two models have difficulty describing the frequency–amplitude relationship. For the depression-type ISWs (S1–S3), the characteristic frequency distribution is more concentrated with the amplitude, while the characteristic frequency distribution of elevation-type ISWs (S4) is relatively dispersed with the amplitude. One possible reason may be that the characteristic frequencies do not change much with the amplitude due to the interactive relationship of the waveforms at different depths. Therefore, the experimental characteristic frequency does not increase with an increasing amplitude as fast as that in models. In addition, we also consider that the waveforms of elevation-type ISWs can be easily affected by some disturbances due to the small amplitudes, which results in the dispersive amplitude–frequency relationship in S4. Another explanation for the discrepancy is that the density profile of the fluid may change with the extension of time, leading to the difference between the experimental characteristic frequency and the theoretical values.
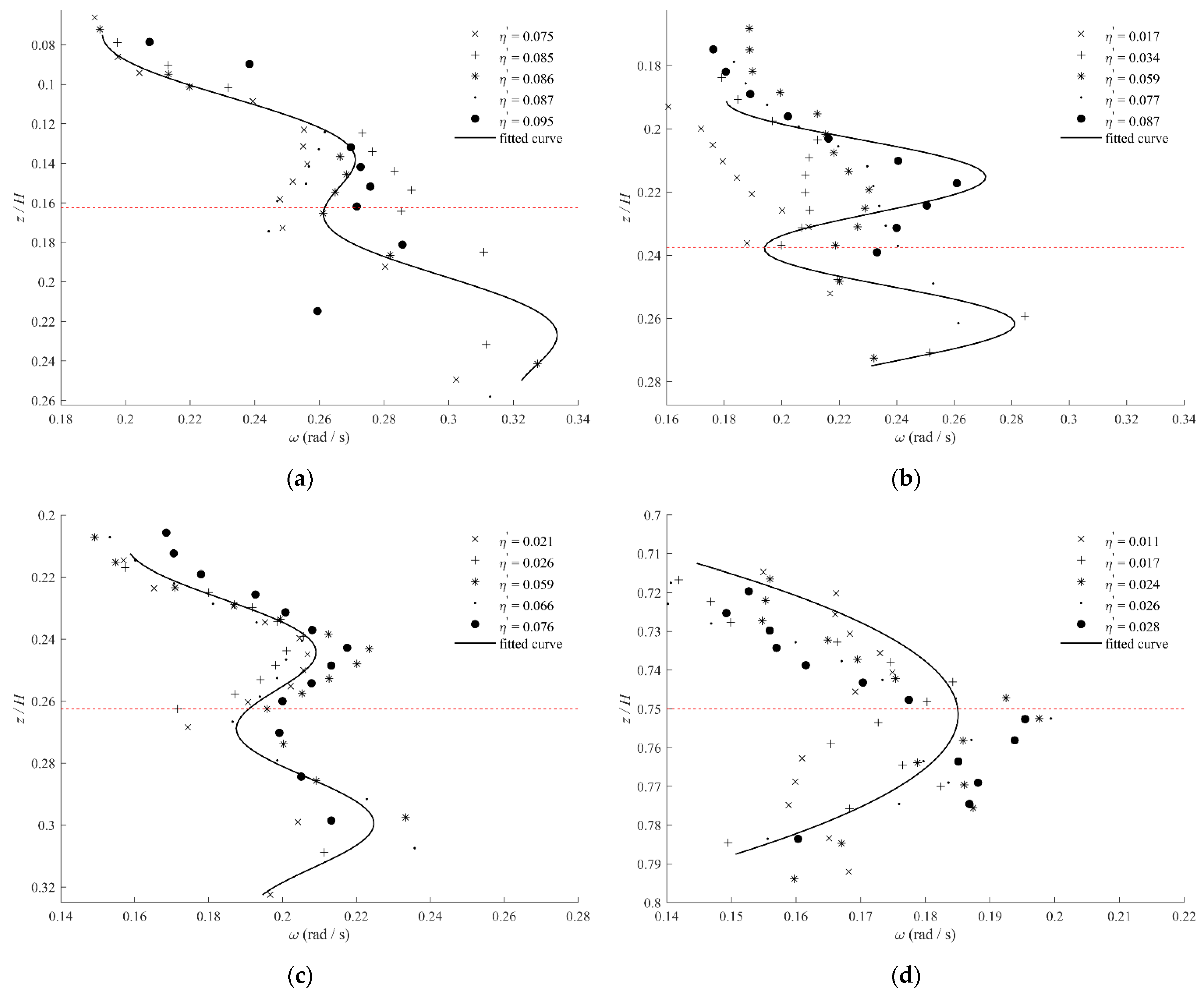
Figure 8 shows the vertical variation in the characteristic frequency under different stratifications and cases, where the solid line is the fitted curve reflecting the variation in the characteristic frequency with depth. Figure 8a–c show that the variation in the characteristic frequency with depth can be divided into two stages. In the first stage, the characteristic frequency increases with an increasing depth and then begins to decrease when it reaches a certain value. Then, there is a local minimum of the characteristic frequency. In the second stage, the characteristic frequency initially increases with an increasing depth and then decreases when it reaches a certain value. Some studies have shown that the characteristic frequency initially increases with an increasing amplitude. When the amplitude reaches a certain value, the characteristic frequency will stop increasing and begin to decrease [46]. Since the amplitude first increases and then decreases with an increasing depth, such variation in the characteristic frequency with the amplitude is formed. The red line in Figure 7 represents the depth where the maximum amplitude of ISWs lies (position of the maximum buoyancy frequency in the stratified fluid), which corresponds to the depth where the local minimum of the characteristic frequency lies. Figure 8d shows that the characteristic frequency first increases and then decreases with an increasing depth under different cases in S4, and the characteristic frequency reaches the maximum near the depth of the maximum buoyancy frequency. This is mainly because the amplitudes in this stratification are relatively small. Therefore, the characteristic frequency only increases with an increasing amplitude in S4. In summary, for a single small-amplitude ISW, the characteristic frequency initially increases and then decreases with an increasing depth. The characteristic frequency is the largest at the depth where the maximum buoyancy frequency lies. For an ISW with relatively large amplitude, there is likely to be a local minimum of the characteristic frequency near the depth where the maximum buoyancy frequency is located.
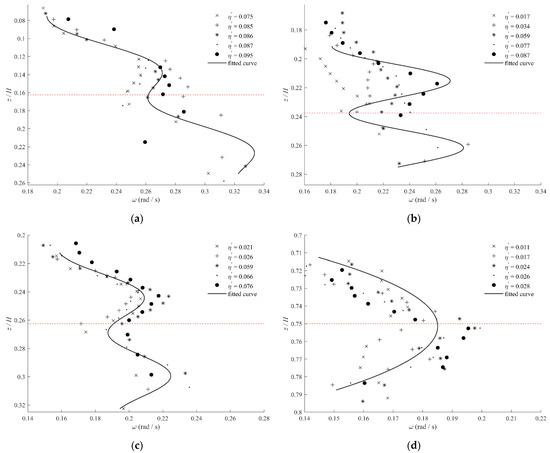
Figure 8.
Experimental vertical distributions of the characteristic frequencies: (a) S1; (b) S2; (c) S3; (d) S4. The red line represents the depth of the maximum amplitude of ISWs.
4.3. Vertical Distribution of the Waveform
The ISW solution obtained by KdV theory is . This ISW solution contains three basic elements (amplitude, characteristic frequency and function). The amplitude and characteristic frequency of ISWs have been discussed above. To investigate whether the function in KdV theory can describe waveforms of ISWs at different vertical depths, the amplitude and characteristic frequency obtained by experiments are used to calculate the theoretical waveform distribution of ISWs. Then, the theoretical waveform distribution is compared with the experimental results to verify the validity of the function. Figure 9 illustrates the theoretical and experimental results of the vertical distribution of waveforms in four different stratification conditions. Figure 9 shows that in four different stratification conditions, the experimental distribution of solitary wave waveforms at different depths is consistent with the theory. Since some errors may occur when the conductivity probes are used to measure the density in the flume, the experimental waveforms of the ISWs at some depths deviate from the theory to some extent. Generally, the deviations are within the allowable range. Thus, the function in KdV theory can describe the waveforms of ISWs at different depths well.
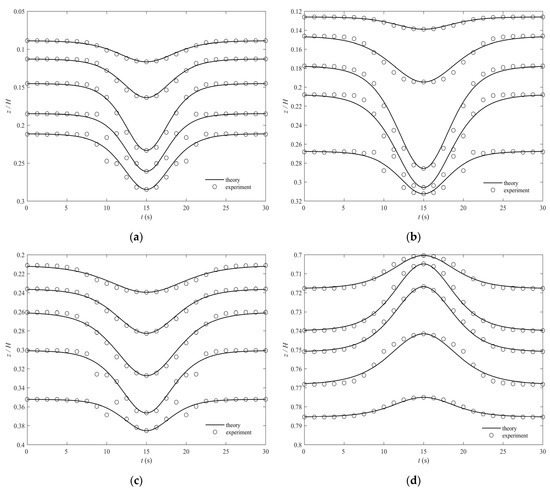
Figure 9.
Experimental and theoretical waveforms of ISWs at different depths: (a) S1; (b) S2; (c) S3; (d) S4.
5. Conclusions
In this paper, four stratifications are established by using a gravitationally stratified fluid flume. The experimental results of the vertical structure characteristics of ISWs in each stratification are compared with the theoretical model, and the influence of different stratifications and different maximum amplitudes on the agreement between the theoretical and experimental results is analyzed. The conclusions are as follows:
Under different stratification conditions, the vertical amplitude structures of most ISWs with relatively small amplitudes are in good agreement with the theoretical model, whether it is elevation-type or depression-type. Additionally, with the increase in the maximum amplitude of ISWs, the influence of the nonlinear terms of the vertical structure function will be more significant, which leads to deviations between the experimental results and the theoretical model.
For the same stratification and the same wave amplitude, the theoretical value of the characteristic frequency in a two-layer fluid is larger than that in a continuously stratified fluid. For the depression-type ISWs, with the increase in , the theoretical values of the characteristic frequency in the two models are both larger, and the difference between the theoretical values of the two models is more significant under the same amplitude. The frequency–amplitude relationship in experiments indicates that the frequency–amplitude relationship can be described to a certain extent by the two-layer model or the continuously stratified model only when is relatively small.
The vertical distribution of the characteristic frequency of a single ISW in the experiment indicates that the characteristic frequency of a single small-amplitude ISW initially increases and then decreases with an increasing depth. The characteristic frequency is largest at the depth where the maximum buoyancy frequency lies. For an ISW with a relatively large amplitude, there is likely to be a local minimum of the characteristic frequency near the depth where the maximum buoyancy frequency is located.
Under different stratification conditions, the function of KdV theory can be in good agreement with the waveforms of ISWs at different depths regardless of whether the ISWs are depression-type or elevation-type.
Author Contributions
Conceptualization, P.P. and H.D.; methodology, P.P. and H.D.; software, H.D. and G.W.; validation, P.P., H.D., S.W. and P.X.; formal analysis, P.P.; investigation, P.P., H.D. and P.X.; resources, H.D., S.C. and J.X.; data curation, H.D. and S.W.; writing—original draft preparation, P.P.; writing—review and editing, H.D., S.C. and J.X.; visualization, P.P.; supervision, H.D., G.W., S.C. and J.X.; project administration, H.D. and G.W.; funding acquisition, S.W., H.D. and G.W. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was supported by the National Natural Science Foundation of China (Grant 11902352) and the Postgraduate Scientific Research Innovation Project of Hunan Province (Grant CX20210042).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors would like to thank the reviewers for their valuable comments, which helped to improve the quality of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cai, S.; Xie, J.; He, J. An overview of internal solitary waves in the South China sea. Surv. Geophys. 2012, 33, 927–943. [Google Scholar] [CrossRef]
- Cai, S.; Xie, J.; Xu, J.; Wang, D.; Chen, Z.; Deng, X.; Long, X. Monthly variation of some parameters about internal solitary waves in the South China sea. Deep-Sea. Res. Part I 2014, 84, 73–85. [Google Scholar] [CrossRef]
- Alford, M.H.; Peacock, T.; MacKinnon, J.A.; Nash, J.D.; Buijsman, M.C.; Centurioni, L.R.; Chao, S.-Y.; Chang, M.-H.; Farmer, D.M.; Tang, T.Y. The formation and fate of internal waves in the South China Sea. Nature 2015, 521, 65–69. [Google Scholar] [CrossRef] [PubMed]
- Grimshaw, R.; Pelinovsky, E.; Talipova, T.; Kurkin, A. Simulation of the Transformation of Internal Solitary Waves on Oceanic Shelves. J. Phys. Oceanogr. 2004, 34, 2774–2791. [Google Scholar] [CrossRef] [Green Version]
- Cai, S.; Wang, S.; Long, X. A simple estimation of the force exerted by internal solitons on cylindrical piles. Ocean Eng. 2006, 33, 974–980. [Google Scholar] [CrossRef]
- Cai, S.; Long, X.; Wang, S. Forces and torques exerted by internal solitons in shear flows on cylindrical piles. Appl. Ocean Res. 2008, 30, 72–77. [Google Scholar] [CrossRef]
- Guo, H.; Zhang, L.; Li, X.; Lou, M. Dynamic responses of top tensioned riser under combined excitation of internal solitary wave, surface wave and vessel motion. J. Ocean Univ. China 2013, 12, 6–12. [Google Scholar] [CrossRef]
- Fan, H.; Li, C.; Wang, Z.; Xu, L.; Wang, Y.; Feng, X. Dynamic analysis of a hang-off drilling riser considering internal solitary wave and vessel motion. J. Nat. Gas. Sci. Eng. 2017, 37, 512–522. [Google Scholar] [CrossRef] [Green Version]
- Gong, Y.; Xie, J.; Xu, J.; Chen, Z.; He, Y.; Cai, S. Oceanic internal solitary waves at the Indonesian submarine wreckage site. Acta Oceanol. Sin. 2022, 41, 109–113. [Google Scholar] [CrossRef]
- Wang, T.; Huang, X.; Zhao, W.; Zheng, S.; Yang, Y.; Tian, J. Internal Solitary Wave Activities near the Indonesian Submarine Wreck Site Inferred from Satellite Images. J. Mar. Sci. Eng. 2022, 10, 197. [Google Scholar] [CrossRef]
- La Forgia, G.; Cavaliere, D.; Adduce, C.; Falcini, F. Mixing Efficiency for Breaking Internal Solitary Waves. J. Geophys. Res. Oceans 2021, 126, e2021JC017275. [Google Scholar] [CrossRef]
- Woodson, C.B. The Fate and Impact of Internal Waves in Nearshore Ecosystems. Ann. Rev. Mar. Sci. 2018, 10, 421–441. [Google Scholar] [CrossRef]
- Boegman, L.; Stastna, M. Sediment Resuspension and Transport by Internal Solitary Waves. Annu. Rev. Fluid Mech. 2019, 51, 129–154. [Google Scholar] [CrossRef]
- Gong, Y.; Song, H.; Zhao, Z.; Guan, Y.; Kuang, Y. On the vertical structure of internal solitary waves in the northeastern South China Sea. Deep-Sea. Res. Part I 2021, 173, 103550. [Google Scholar] [CrossRef]
- Vlasenko, V.; Hutter, K. Numerical Experiments on the Breaking of Solitary Internal Waves over a Slope–Shelf Topography. J. Phys. Oceanogr. 2002, 32, 1779–1793. [Google Scholar] [CrossRef]
- Pelinovksy, E.; Talipova, T.; Ivanov, V. Estimations of the nonlinear properties of the internal wave field off the Israel coast. Nonlinear Proc. Geoph. 1995, 2, 80–88. [Google Scholar] [CrossRef]
- Shi, X.; Fan, Z.; Liu, H. A Numerical Calculation Method for Eigenvalue Problems of Nonlinear Internal Waves. J. Hydrodyn. 2009, 21, 373–378. [Google Scholar] [CrossRef]
- Fliegel, M.; Hunkins, K. Internal Wave Dispersion Calculated Using the Thomson-Haskell Method. J. Phys. Oceanogr. 1975, 5, 541–548. [Google Scholar] [CrossRef] [Green Version]
- Cai, S.; Gan, Z. A numerical method of internal waves dispersion relation. J. Trop. Oceanogr. 1995, 1, 22–30. (In Chinese) [Google Scholar]
- Keben, Z.; Hushan, G. A numerical method for vertical structure of internal waves in ocean. J. Trop. Oceanogr. 1997, 4, 62–67. (In Chinese) [Google Scholar]
- Bing, D.; Xiang, Z.; Ming, Z. Calculation and Analysis of Vertical Structure of Internal Wave in Background Current. Adv. Mar. Sci. 2014, 2, 121–129. (In Chinese) [Google Scholar]
- Kurkina, O.; Rouvinskaya, E.; Kurkin, A.; Giniyatullin, A.; Pelinovsky, E. Vertical structure of the velocity field induced by mode-I and mode-II solitary waves in a stratified fluid. Eur. Phys. J. E Soft Matter. 2018, 41, 47. [Google Scholar] [CrossRef]
- Zhao, Z.; Alford, M.H. Source and propagation of internal solitary waves in the northeastern South China Sea. J. Geophys. Res. 2006, 111, C11012. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, E.; Talipova, T.; Kurkina, O. Internal solitary waves: Propagation, deformation and disintegration. Nonlinear Proc. Geoph. 2010, 17, 633–649. [Google Scholar] [CrossRef] [Green Version]
- Xudong, Z.; Jing, W.; Lina, S.; Junmin, M. Study on the amplitude inversion of internal waves at Wenchang area of the South China Sea. Acta Oceanol. Sin. 2016, 7, 14–19. [Google Scholar]
- Chang, M.H.; Lien, R.C.; Lamb, K.G.; Diamessis, P.J. Long-Term Observations of Shoaling Internal Solitary Waves in the Northern South China Sea. J. Geophys. Res. 2021, 126, 2169–9275. [Google Scholar] [CrossRef]
- Song, H.; Gong, Y.; Yang, S.; Guan, Y. Observations of Internal Structure Changes in Shoaling Internal Solitary Waves Based on Seismic Oceanography Method. Front. Mar. Sci. 2021, 8, 2296–7745. [Google Scholar] [CrossRef]
- Vlasenko, V.; Brandt, P.; Rubino, A. Structure of Large-Amplitude Internal Solitary Waves. J. Phys. Oceanogr. 2000, 30, 2172–2185. [Google Scholar] [CrossRef] [Green Version]
- Geng, M.; Song, H.; Guan, Y.; Bai, Y. Analyzing amplitudes of internal solitary waves in the northern South China Sea by use of seismic oceanography data. Deep-Sea. Res. Part I 2019, 146, 1–10. [Google Scholar]
- Wang, S.-D.; Wei, G.; Du, H.; Wu, J.-L.; Wang, X.-L. Experimental investigation of the wave-flow structure of an oblique internal solitary wave and its force exerted on a slender body. Ocean Eng. 2020, 201, 107057. [Google Scholar] [CrossRef]
- Zhi, C.; Wang, H.; Chen, K.; You, Y. Theoretical and experimental investigation on strongly nonlinear internal solitary waves moving over slope-shelf topography. Ocean Eng. 2021, 223, 108645. [Google Scholar] [CrossRef]
- Du, H.; Wang, S.-D.; Wang, X.-L.; Xu, J.-N.; Guo, H.-L.; Wei, G. Experimental investigation of elevation internal solitary wave propagation over a ridge. Phys. Fluids 2021, 33, 1–9. [Google Scholar] [CrossRef]
- Tian, Z.; Jia, Y.; Du, Q.; Zhang, S.; Guo, X.; Tian, W.; Zhang, M.; Song, L. Shearing stress of shoaling internal solitary waves over the slope. Ocean Eng. 2021, 241, 0029–8018. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, M.; Mei, Y.; Lu, K.; Chen, X. Study on Inversion Amplitude of Internal Solitary Waves Applied to Shallow Sea in the Laboratory. IEEE. Geosci. Remote. Sens. Lett. 2021, 18, 577–581. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, J.; Li, Z.; Liang, K.; Chen, X. Laboratory Study of the Impact of the Surface Solitary Waves Created by the Internal Solitary Waves on Optical Imaging. J. Geophys. Res. 2022, 127, 2169–9275. [Google Scholar] [CrossRef]
- Vlasenko, V.; Hutter, K. Generation of second mode solitary waves by the interaction of a sill. Nonlinear Proc. Geoph. 2001, 8, 223–239. [Google Scholar] [CrossRef]
- Brandt, A.; Shipley, K.R. Laboratory experiments on mass transport by large amplitude mode-2 internal solitary waves. Phys. Fluids 2014, 26, 046601. [Google Scholar] [CrossRef]
- Deepwell, D.; Stastna, M.; Carr, M.; Davies, P.A. Wave generation through the interaction of a mode-2 internal solitary wave and a broad, isolated ridge. Phys. Rev. Fluids 2019, 4, 094802. [Google Scholar] [CrossRef] [Green Version]
- Walker, L.R. Interfacial solitary waves in a two-fluid medium. Phys. Fluids 1974, 16, 1796. [Google Scholar] [CrossRef]
- Koop, C.G.; Butler, G. An investigation of internal solitary waves in a two-fluid system. J. Fluid Mech. 1981, 112, 225–251. [Google Scholar] [CrossRef]
- Kao, T.W.; Pan, F.-S.; Renouard, D. Internal solitons on the pycnocline: Generation, propagation, and shoaling and breaking over a slope. J. Fluid Mech. 1985, 159, 19–53. [Google Scholar] [CrossRef]
- Ostrovsky, L.A.; Stepanyants, Y.A. Internal solitons in laboratory experiments: Comparison with theoretical models. Chaos 2005, 15, 37111. [Google Scholar] [CrossRef]
- Chen, M.; Chen, K.; You, Y.-X. Experimental investigation of internal solitary wave forces on a semi-submersible. Ocean Eng. 2017, 141, 205–214. [Google Scholar] [CrossRef]
- Barros, R.; Choi, W.; Milewski, P.A. Strongly nonlinear effects on internal solitary waves in three-layer flows. J. Fluid Mech. 2020, 883, A16. [Google Scholar] [CrossRef]
- Michallet, H.; Barthelemy, E. Experimental study of interfacial solitary waves. J. Fluid Mech. 1998, 366, 159–177. [Google Scholar] [CrossRef]
- Grue, J.; Jensen, A.; Rusas, P.-O.; Sveen, J.K. Properties of large-amplitude internal waves. J. Fluid Mech. 1999, 380, 257–278. [Google Scholar] [CrossRef] [Green Version]
- Du, H.; Wei, G.; Wang, S.-D.; Wang, X.-L. Experimental study of elevation- and depression-type internal solitary waves generated by gravity collapse. Phys. Fluids 2019, 31, 102104. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).