A Recognition Algorithm of Seismic Signals Based on Wavelet Analysis
Abstract
:1. Introduction
2. Principle
3. Parameter Setting
3.1. Decomposition Layer
3.2. Wavelet Basis
4. Data Processing
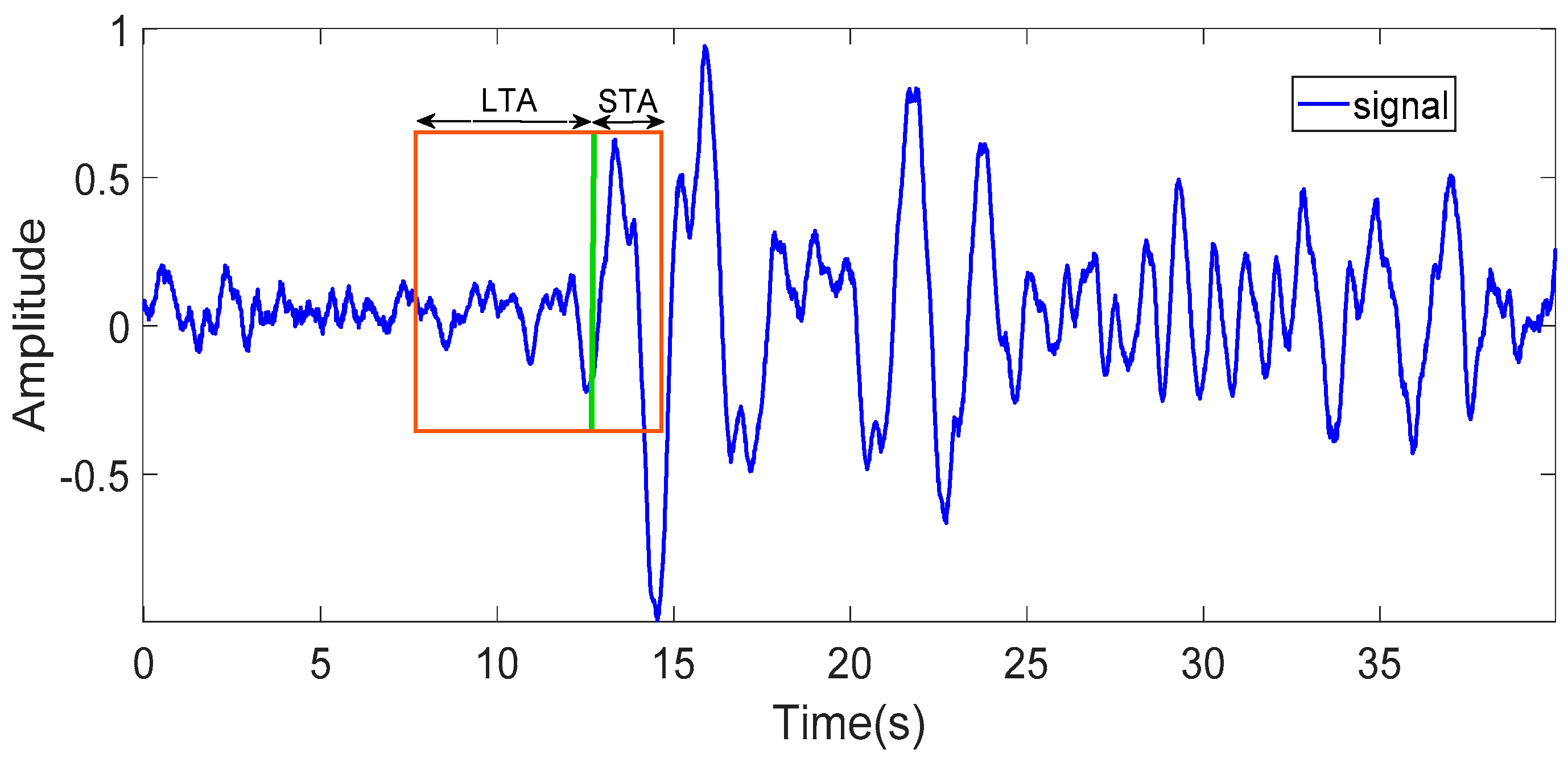
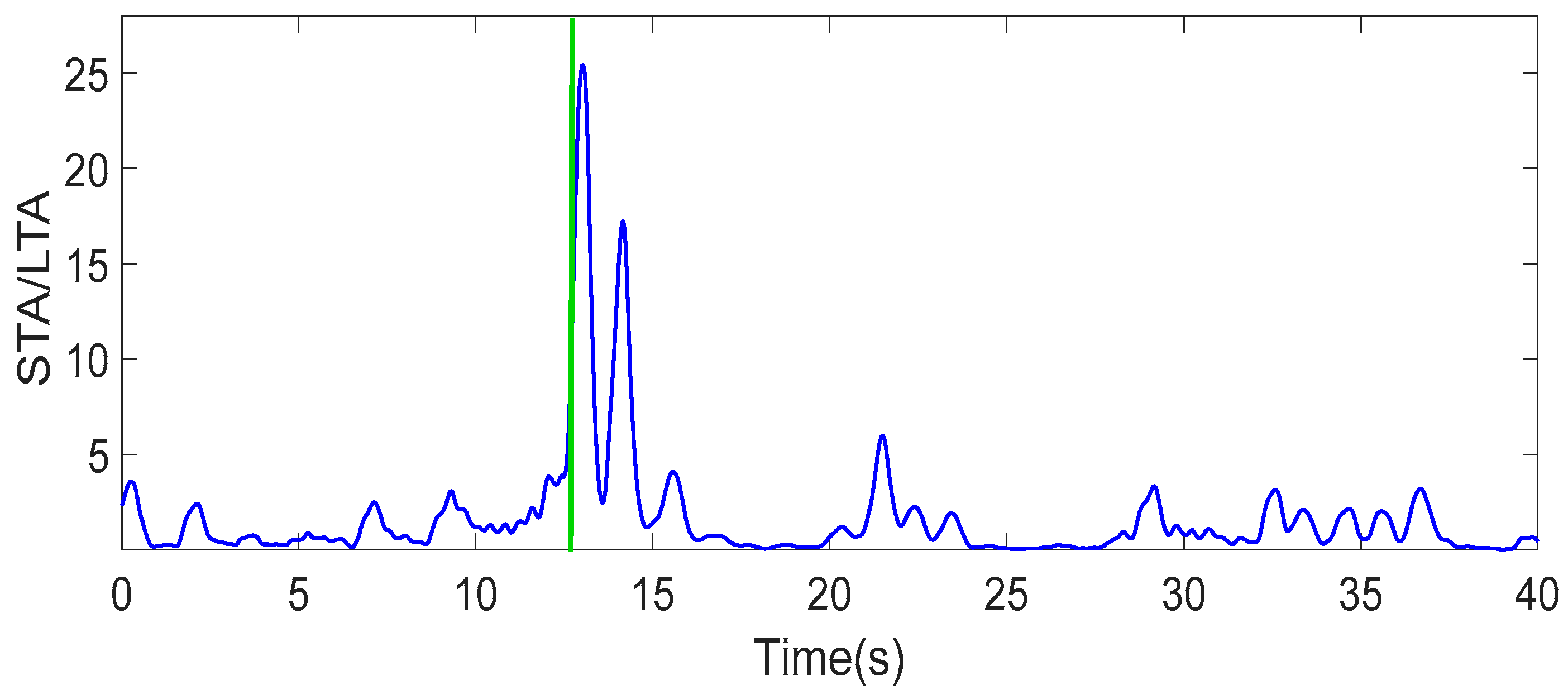
4.1. Pre-Detection
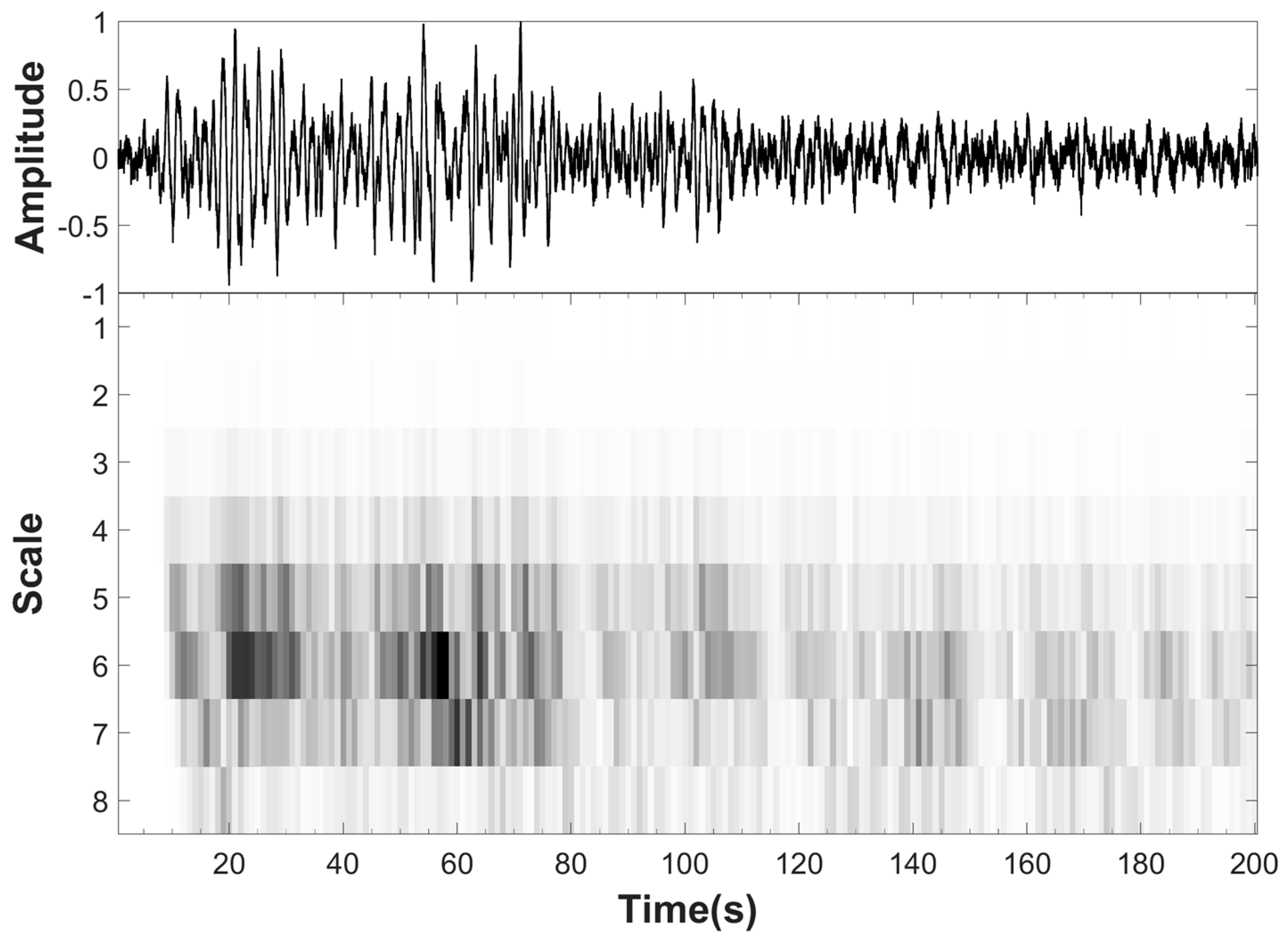
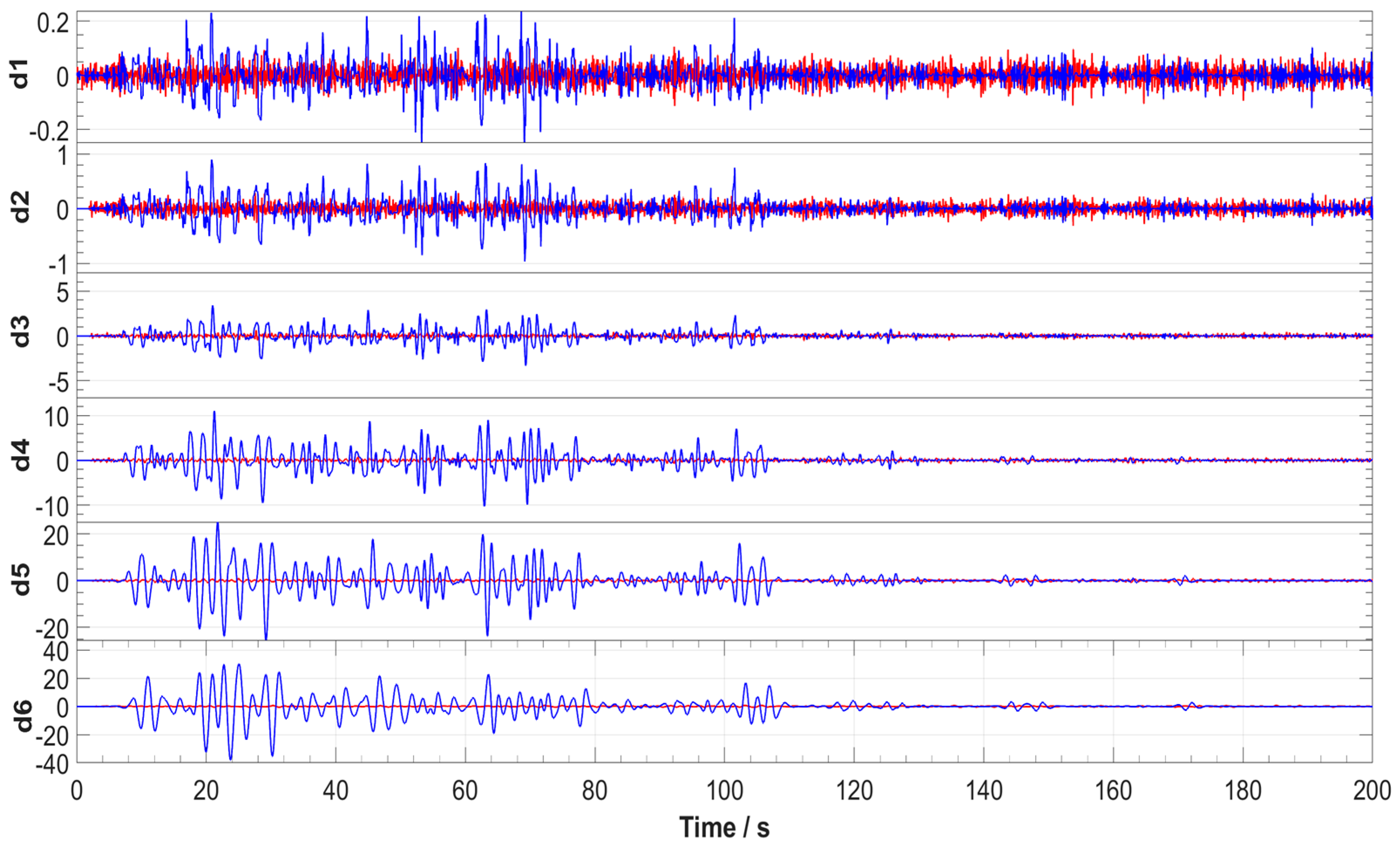
4.2. Wavelet Transformation
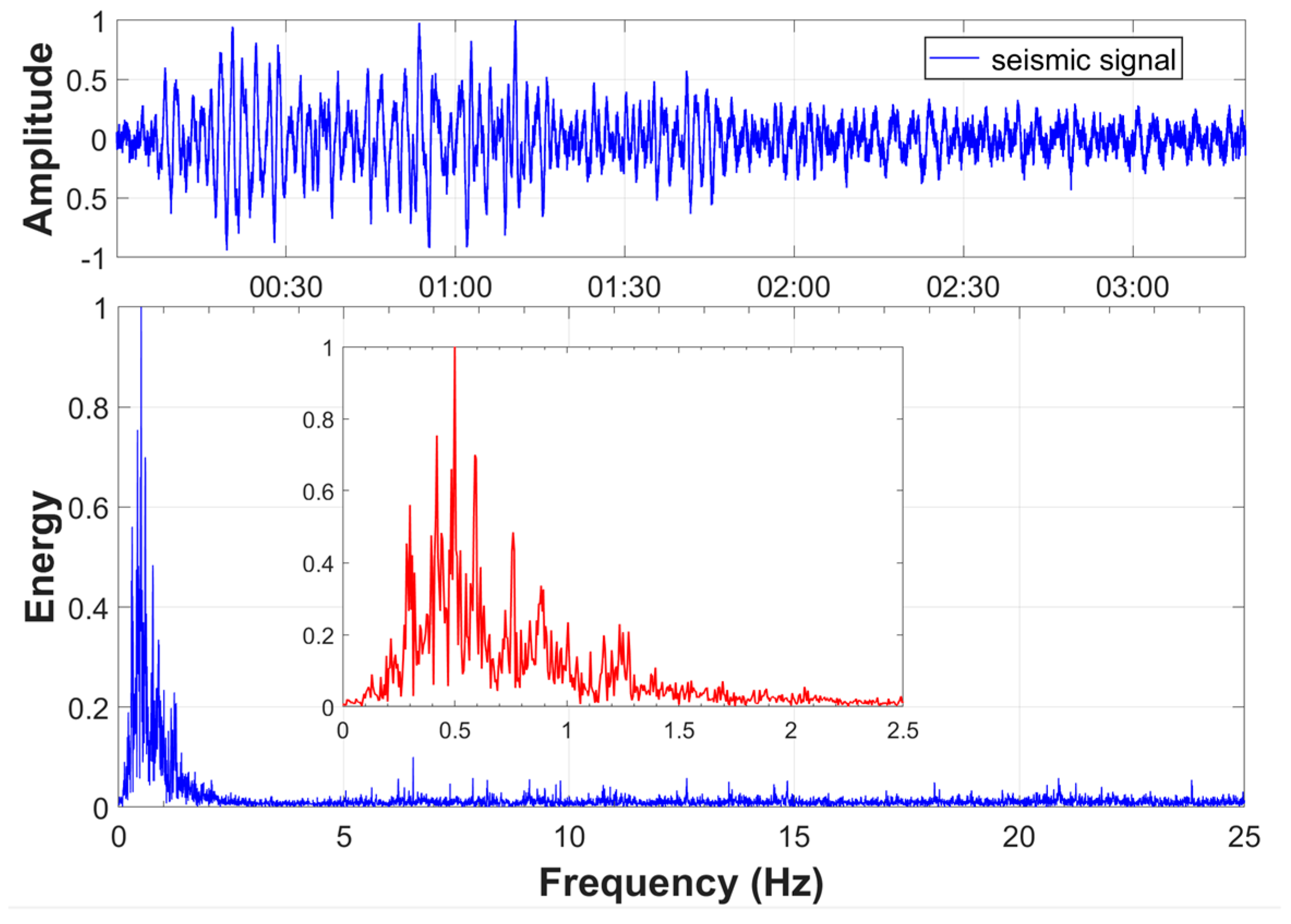
4.3. Power Calculation
5. Validation and Analysis
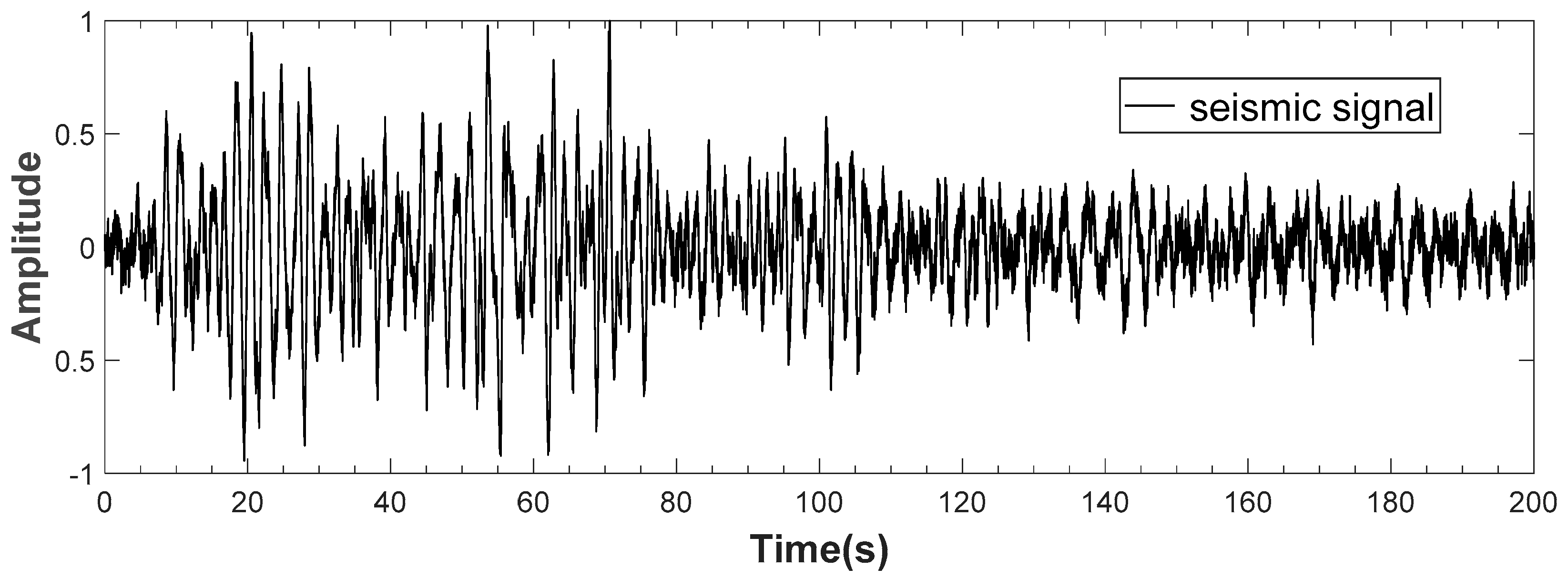
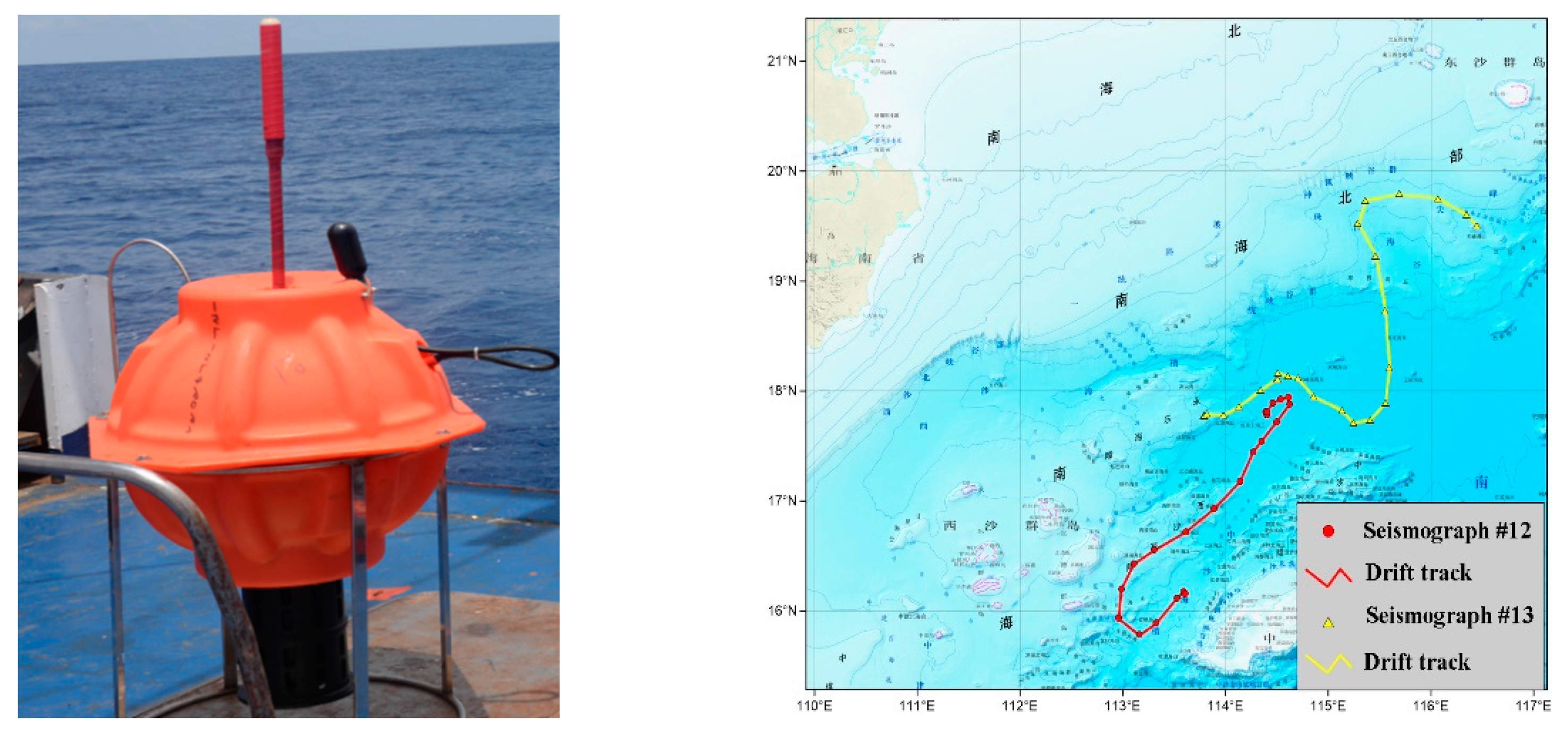
5.1. Data Sources
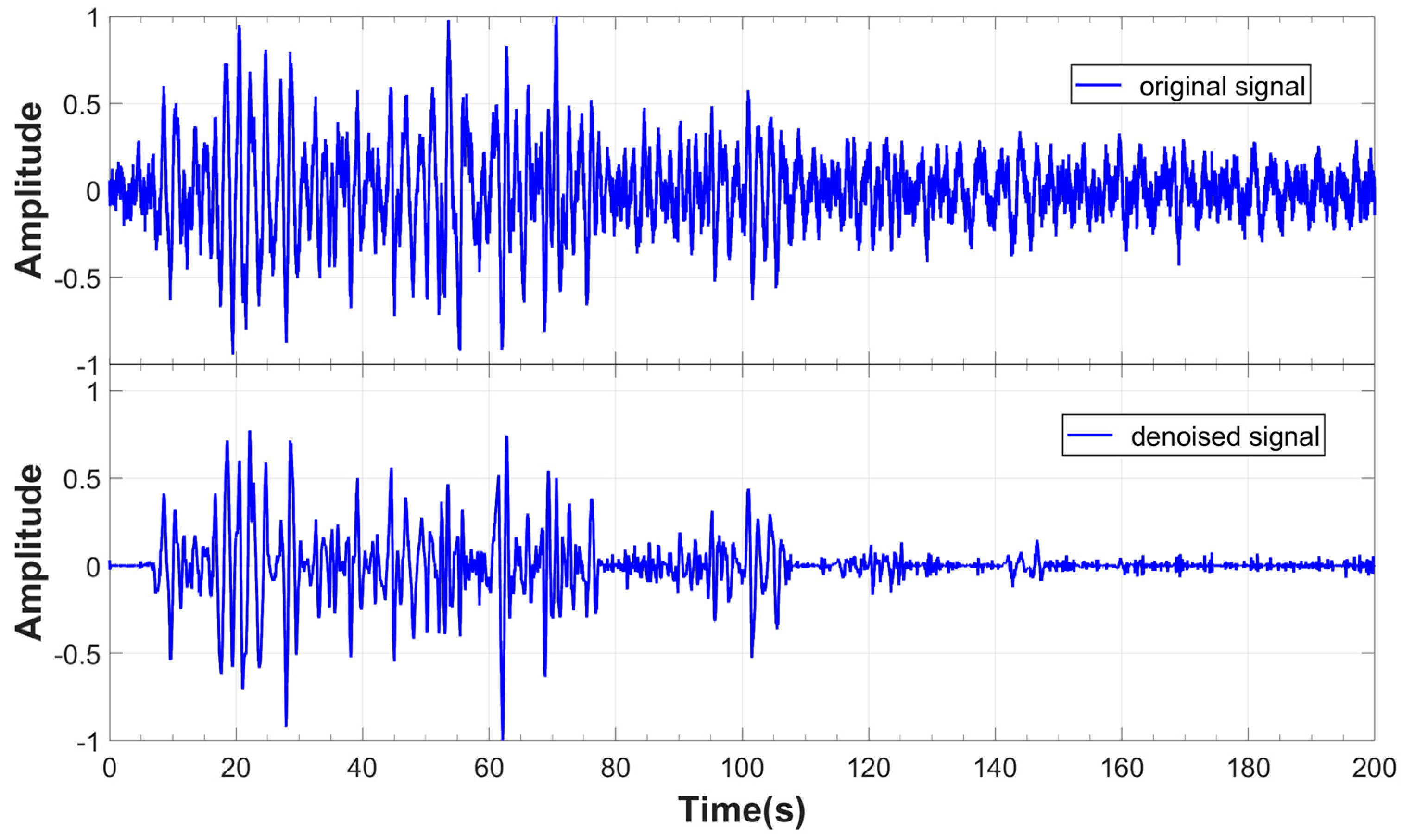
5.2. Result
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sukhovich, A.; Bonnieux, S.; Hello, Y.; Irisson, J.-O.; Simons, F.J.; Nolet, G. Seismic monitoring in the oceans by autonomous floats. Nat. Commun. 2015, 6, 8027. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nolet, G.; Hello, Y.; van Der Lee, S.; Bonnieux, S.; Ruiz, M.C.; Pazmino, N.A.; Deschamps, A.; Regnier, M.M.; Font, Y.; Chen, Y.J.; et al. Imaging the Galapagos mantle plume with an unconventional application of floating seismometers. Sci. Rep. 2019, 9, 1326. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Simons, F.J.; Nolet, G.; Georgief, P.; Babcock, J.M.; Regier, L.A.; Davis, R.E. On the potential of recording earthquakes for global seismic tomography by low-cost autonomous instruments in the oceans. J. Geophys. Res. 2009, 114, B5307. [Google Scholar] [CrossRef] [Green Version]
- Ding, W.; Huang, H.; Zhu, X.; Sun, G.; Niu, X. New mobile oceanic seismic recording system and its application in marine seismic exploration. Prog. Geophys. 2019, 34, 292–296. [Google Scholar]
- Stevenson, P.R. Microearthquakes at Flathead Lake, Montana: A Study using automatic earthquake processing. Bull. Seism. Soc. Am. 1976, 66, 61–80. [Google Scholar] [CrossRef]
- Murat, M.E.; Rudman, A.J. Automated first arrival picking: A neural network approach. Geophys. Prospect. 1992, 40, 587–604. [Google Scholar] [CrossRef]
- Leonard, M. Comparison of manual and automatic onset time picking. Bull. Seism. Soc. Am. 2000, 90, 1384–1390. [Google Scholar] [CrossRef]
- Anant, K.S.; Dowla, F.U. Wavelet transform method for phase identification in three-component seismograms. Bull. Seism. Soc. Am. 1997, 87, 1598–1612. [Google Scholar] [CrossRef]
- Bai, C.; Kennett, B.L.N. Phase identification and attribute analysis of broadband seismograms at far-regional distances. J. Seismol. 2001, 5, 217–231. [Google Scholar] [CrossRef]
- Wang, C.; Bai, C.; Wang, X. Review of automatic onset time picking for seismic arrivals. Prog. Geophys. 2013, 28, 2363–2375. [Google Scholar]
- Zhao, R.; Song, G. An improved method for white noise reduction based on wavelet transform. J. Xidian Univ. 2000, 5, 619–622. [Google Scholar]
- Sweldens, W. The lifting scheme: A custom-design construction of biorthogonal wavelets. Appl. Comput. Harmon. Anal. 1996, 3, 186–200. [Google Scholar] [CrossRef] [Green Version]
- Sukhovich, A.; Irisson, J.-O.; Simons, F.J.; Ogé, A.; Hello, Y.M.; Deschamps, A.; Nolet, G. Automatic discrimination of underwater acoustic signals generated by teleseismic P–waves: A probabilistic approach. Geophys. Res. Lett. 2011, 38, L18605. [Google Scholar] [CrossRef] [Green Version]
- Grossmann, A.; Morlet, J. Decomposition of Hardy functions into square integrable wavelets of constant shape. SIAM. J. Math. Anal. 1984, 15, 723–736. [Google Scholar] [CrossRef]
- Goupillaud, P.; Grossmann, A.; Morlet, J. Cycle-octave and related transforms in seismic signal analysis. Geoexploration 1984, 23, 85–102. [Google Scholar] [CrossRef]
- Li, G. Application of wavelet analysis technology in turbine fault diagnosis. Mech. Eng. 2012, 12, 41–42. [Google Scholar]
- Chen, S.; Zhu, J.; Meng, Q. Identification of sedimentary cycles using multi-scale wavelet transform based on seismic data. Glob. Geol. 2021, 40, 140–145. [Google Scholar]
- Gao, Y.; Wang, H.; You, S.; Feng, L.; He, Y.; Liu, K. A pulsar signal denoising algorithm based on wavelet basis function selection and improved threshold function. Electron. Opt. Control. 2020, 27, 15–19. [Google Scholar]
- Zeng, Y.; Wu, Y.; Song, R.; Hu, W. Study on Wavelet De-noising Parameters of Track Vibration Signal for Metro with the Train Traveling on at Low Speed. Noise Vib. Control. 2019, 39, 151–155. [Google Scholar]
- Luo, L. Application Research of Wavelet Transform in Deformation Monitoring Data Denoising and Information Extraction. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2017. [Google Scholar]
- McGuire, J.J.; Simons, F.J.; Collins, J.A. Analysis of seafloor seismograms of the 2003 Tokachi-Oki earthquake sequence for earthquake early warning. Geophys. Res. Lett. 2008, 35, L14310. [Google Scholar] [CrossRef] [Green Version]





| Wavelet Function | Haar | Daubechies | Biorthogonal | Coiflets | Symlets |
|---|---|---|---|---|---|
| Wavelet abbreviation | haar | db | bior | coif | sym |
| Orthogonality | Yes | Yes | No | Yes | Yes |
| Biorthogonality | Yes | Yes | Yes | Yes | Yes |
| Tight support | Yes | Yes | Yes | Yes | Yes |
| Support length | 1 | 2N-1 | reconstruction: 2Nr + 1 | 6N-1 | 2N-1 |
| decomposition: 2Nd + 1 | |||||
| Filter length | 2 | 2N | Max (2Nr, 2Nd) + 2 | 6N | 2N |
| Symmetry | Yes | Approximate symmetry | No | Approximate symmetry | Approximate symmetry |
| Regularity | No | No | No | No | No |
| The order of the vanishing moment | 1 | N | Nr-1 | 2N | N |
| Scale | Frequency Range |
|---|---|
| 1 | 6.3~12.5 Hz |
| 2 | 3.2~6.3 Hz |
| 3 | 1.7~3.2 Hz |
| 4 | 0.9~1.7 Hz |
| 5 | 0.5~0.9 Hz |
| 6 | 0.3~0.5Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, W.; Ding, W.; Zhu, X.; Hou, F. A Recognition Algorithm of Seismic Signals Based on Wavelet Analysis. J. Mar. Sci. Eng. 2022, 10, 1093. https://doi.org/10.3390/jmse10081093
Jiang W, Ding W, Zhu X, Hou F. A Recognition Algorithm of Seismic Signals Based on Wavelet Analysis. Journal of Marine Science and Engineering. 2022; 10(8):1093. https://doi.org/10.3390/jmse10081093
Chicago/Turabian StyleJiang, Wensheng, Weiwei Ding, Xinke Zhu, and Fei Hou. 2022. "A Recognition Algorithm of Seismic Signals Based on Wavelet Analysis" Journal of Marine Science and Engineering 10, no. 8: 1093. https://doi.org/10.3390/jmse10081093
APA StyleJiang, W., Ding, W., Zhu, X., & Hou, F. (2022). A Recognition Algorithm of Seismic Signals Based on Wavelet Analysis. Journal of Marine Science and Engineering, 10(8), 1093. https://doi.org/10.3390/jmse10081093






