Numerical and Experimental Study on the Effect of Rotor–Stator Distance on Rotor–Stator Interaction Strength within Mixed-Flow Centrifugal Pumps
Abstract
:1. Introduction
2. Geometry and Parameters
3. Numerical Modeling
3.1. Mathematical Model
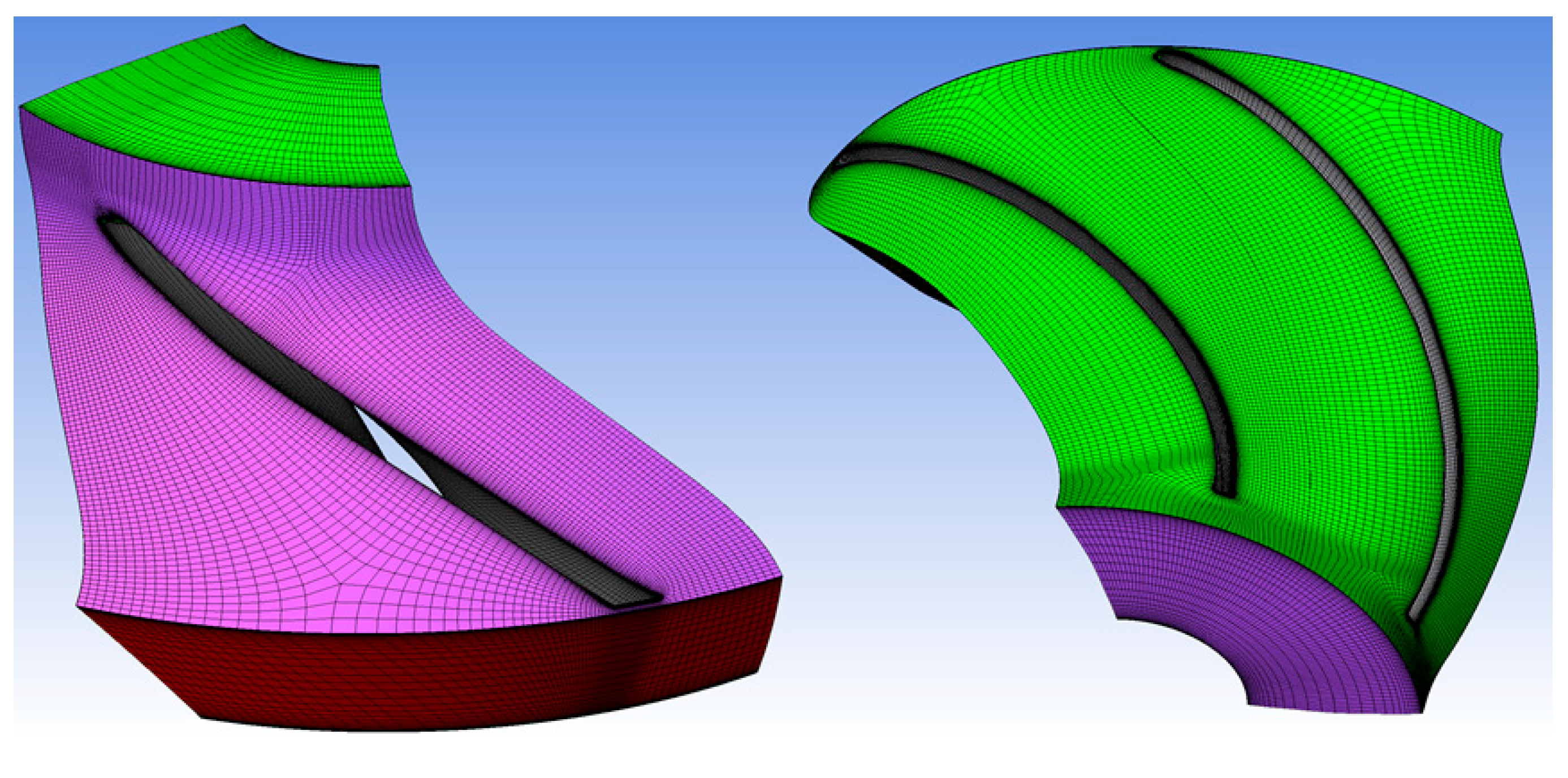
3.2. Grids
3.3. Boundary Conditions
4. Results and Discussion
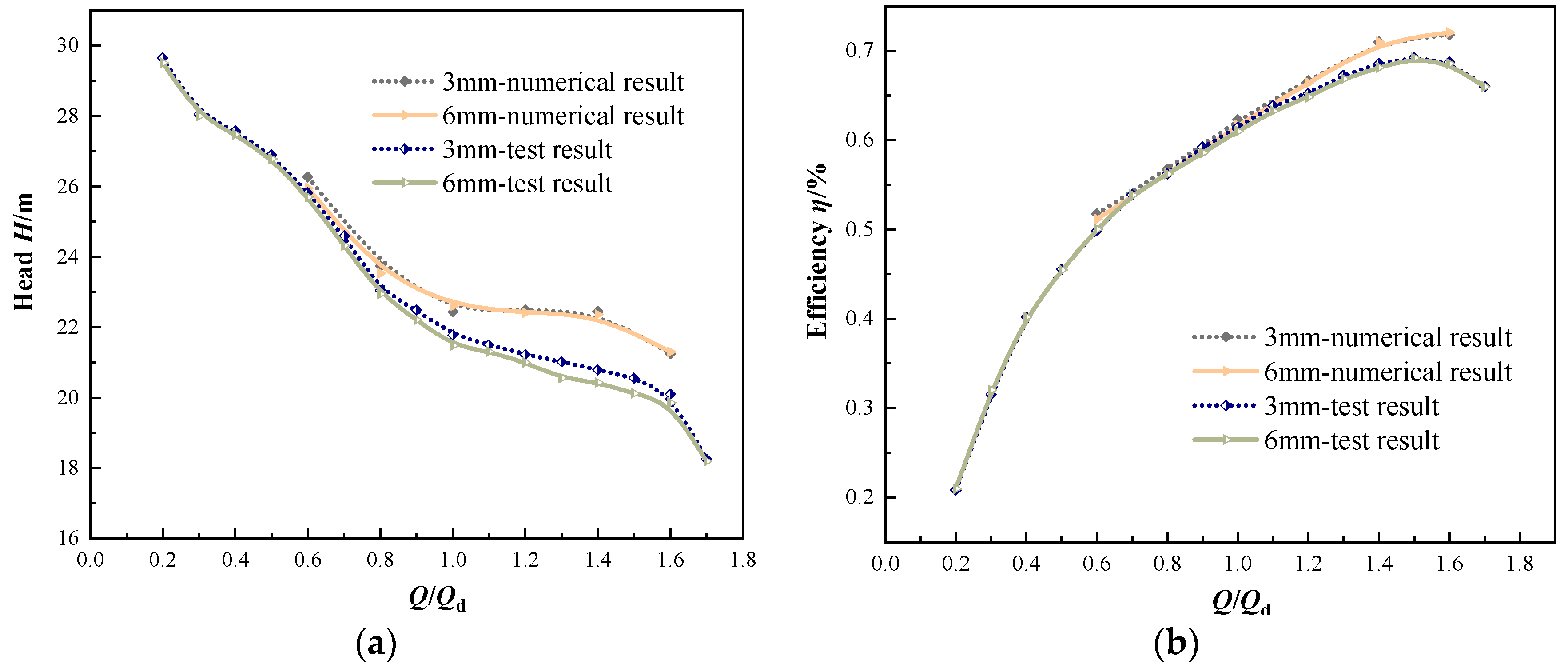
4.1. Pump Performance Validation
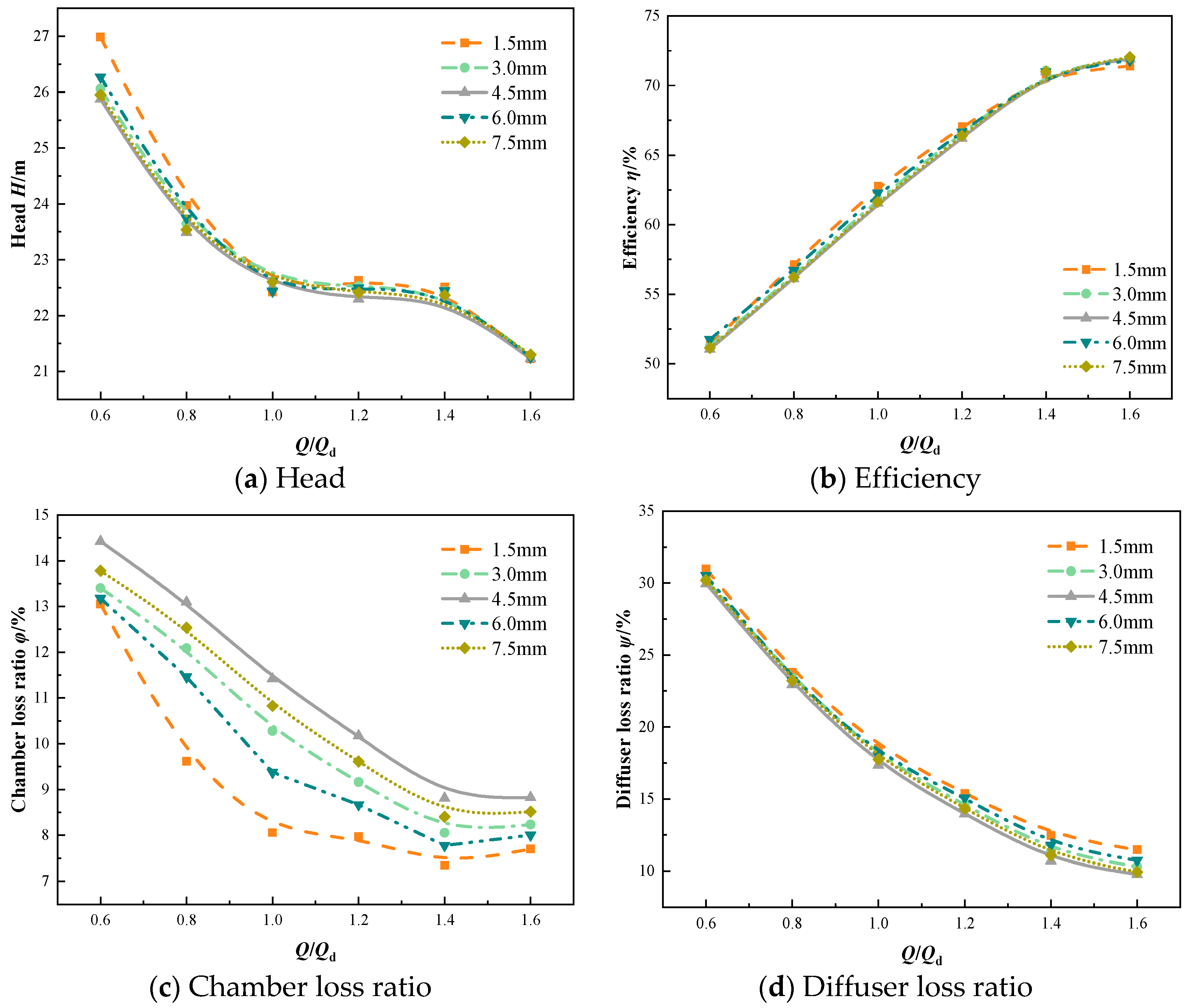
4.2. Performance Comparison with Different Rotor–Stator Distances
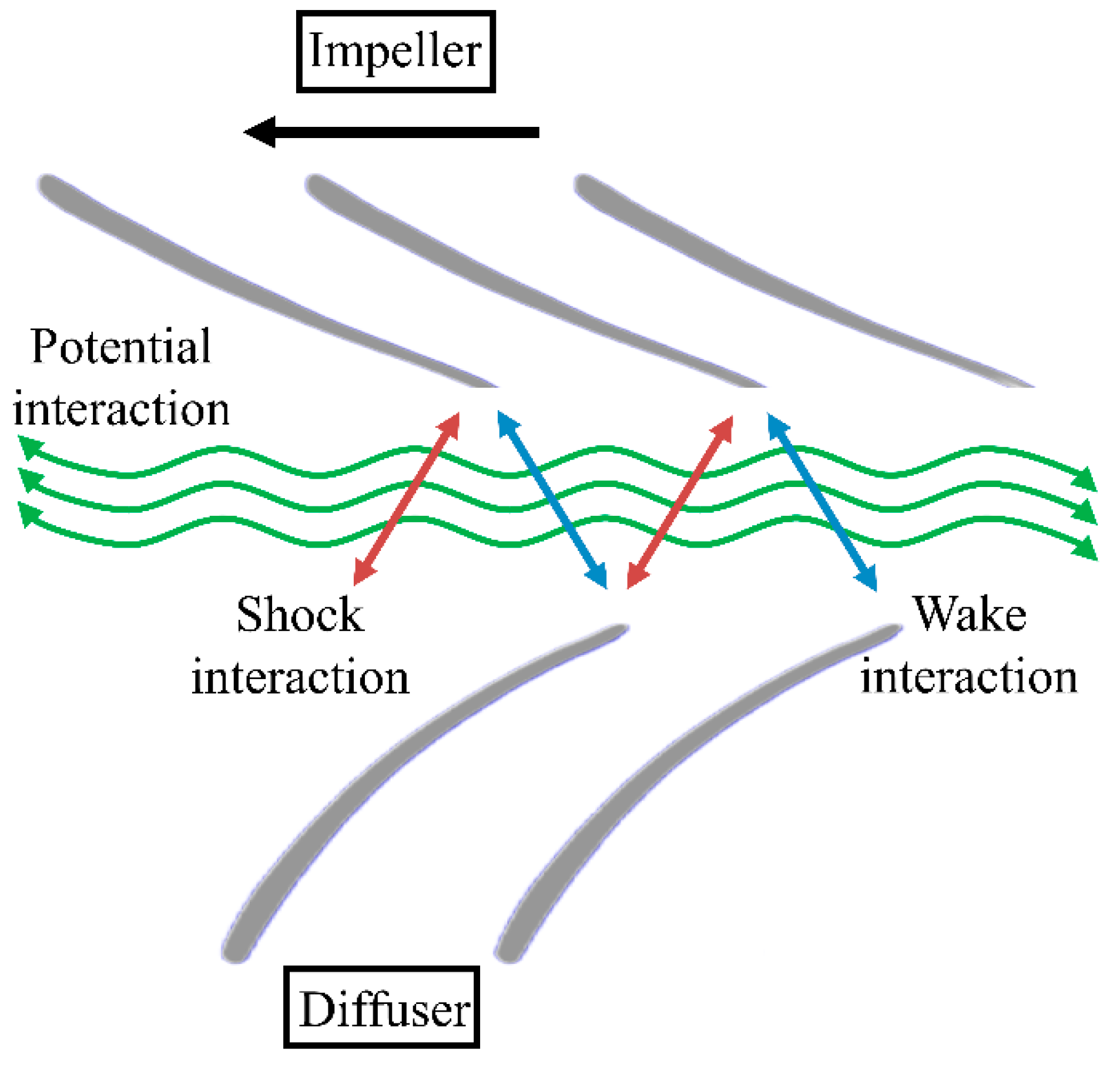
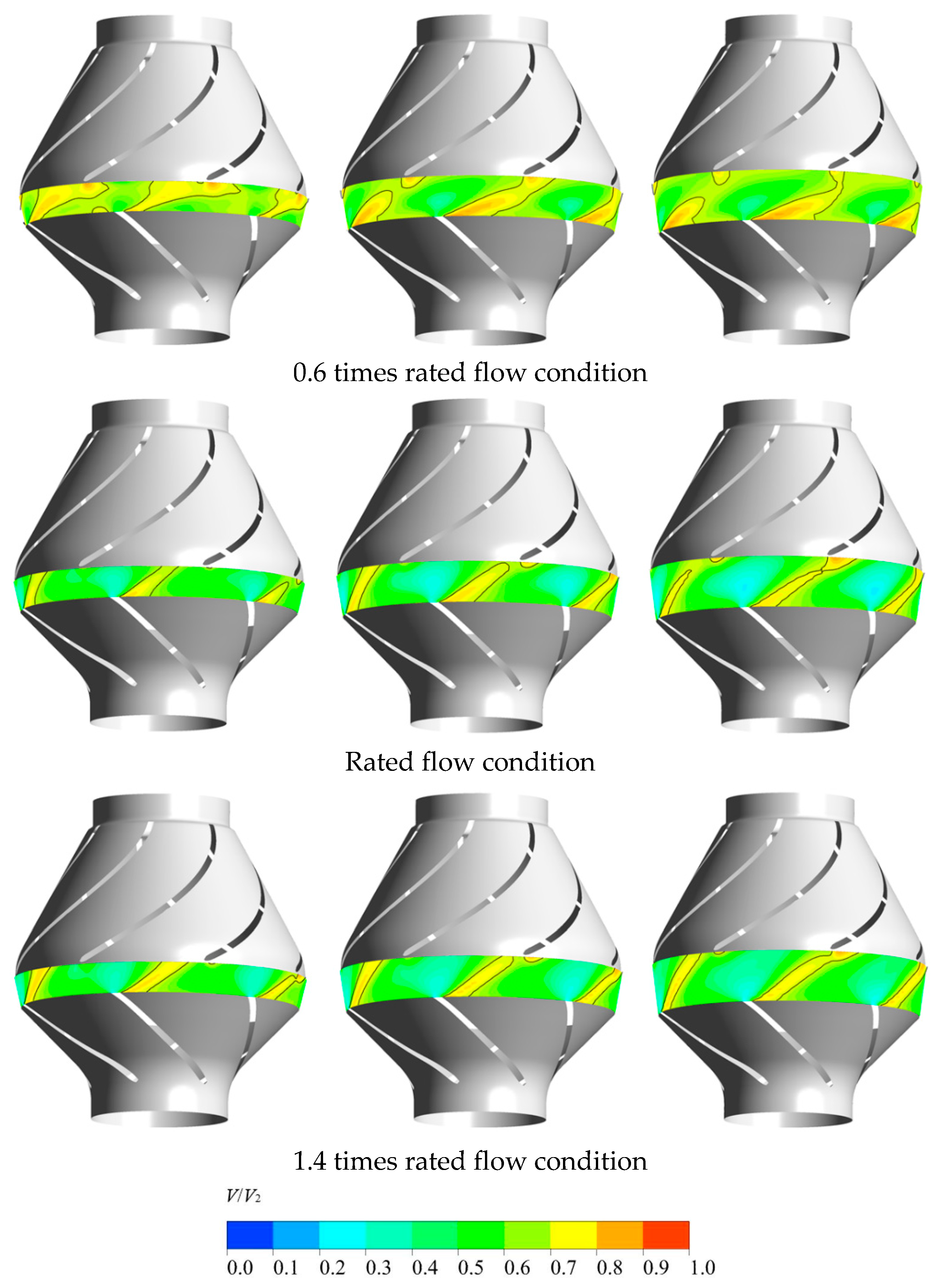
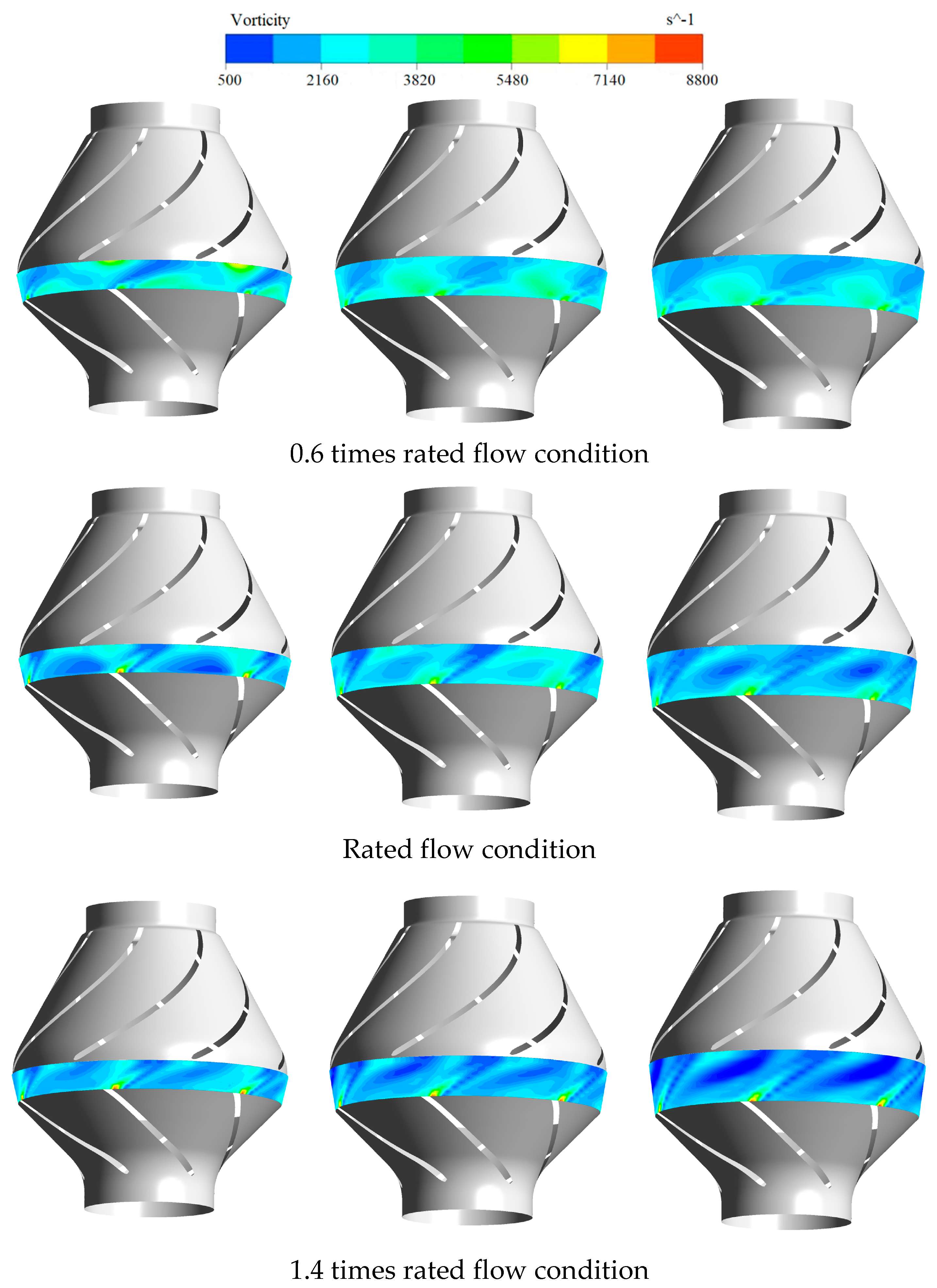
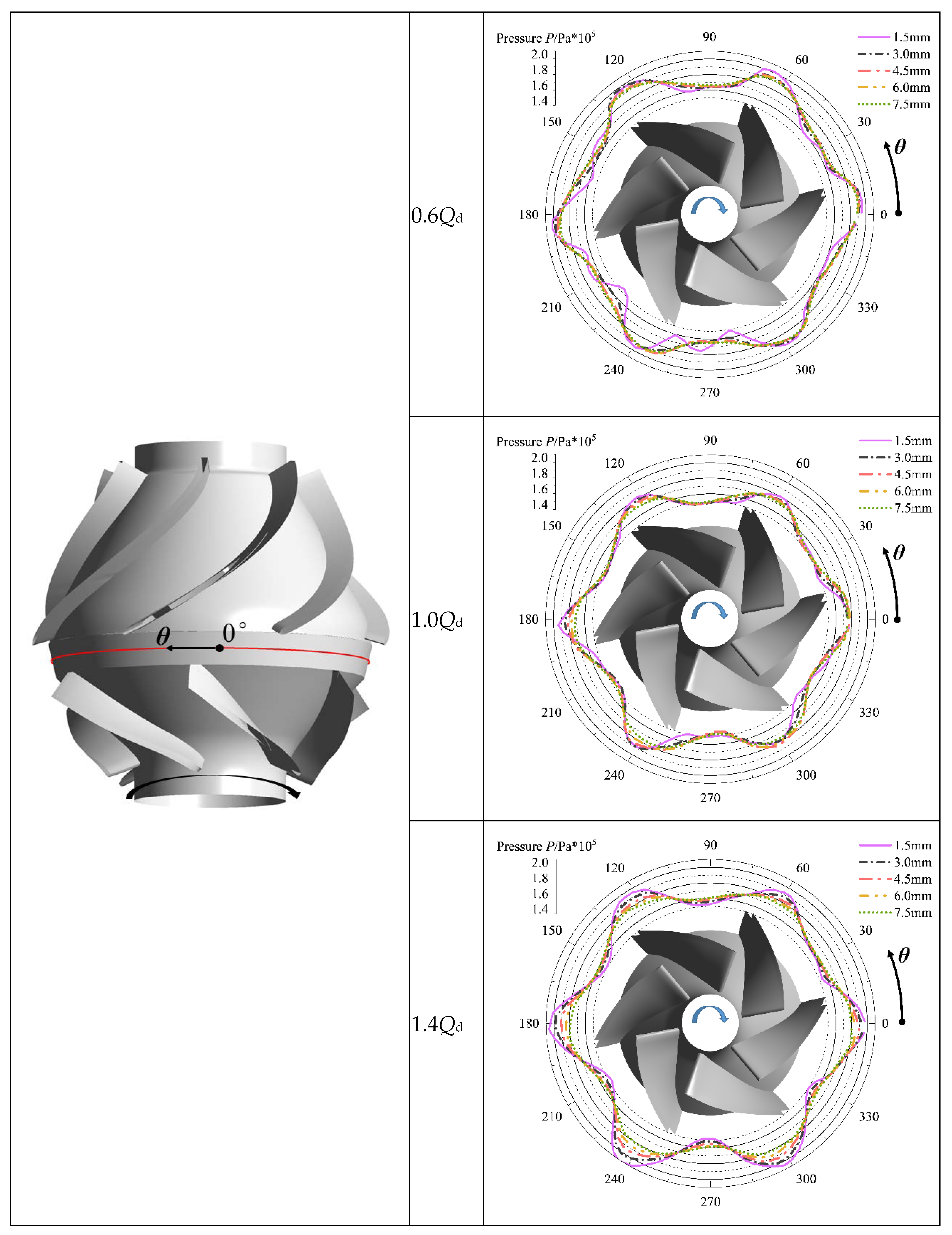
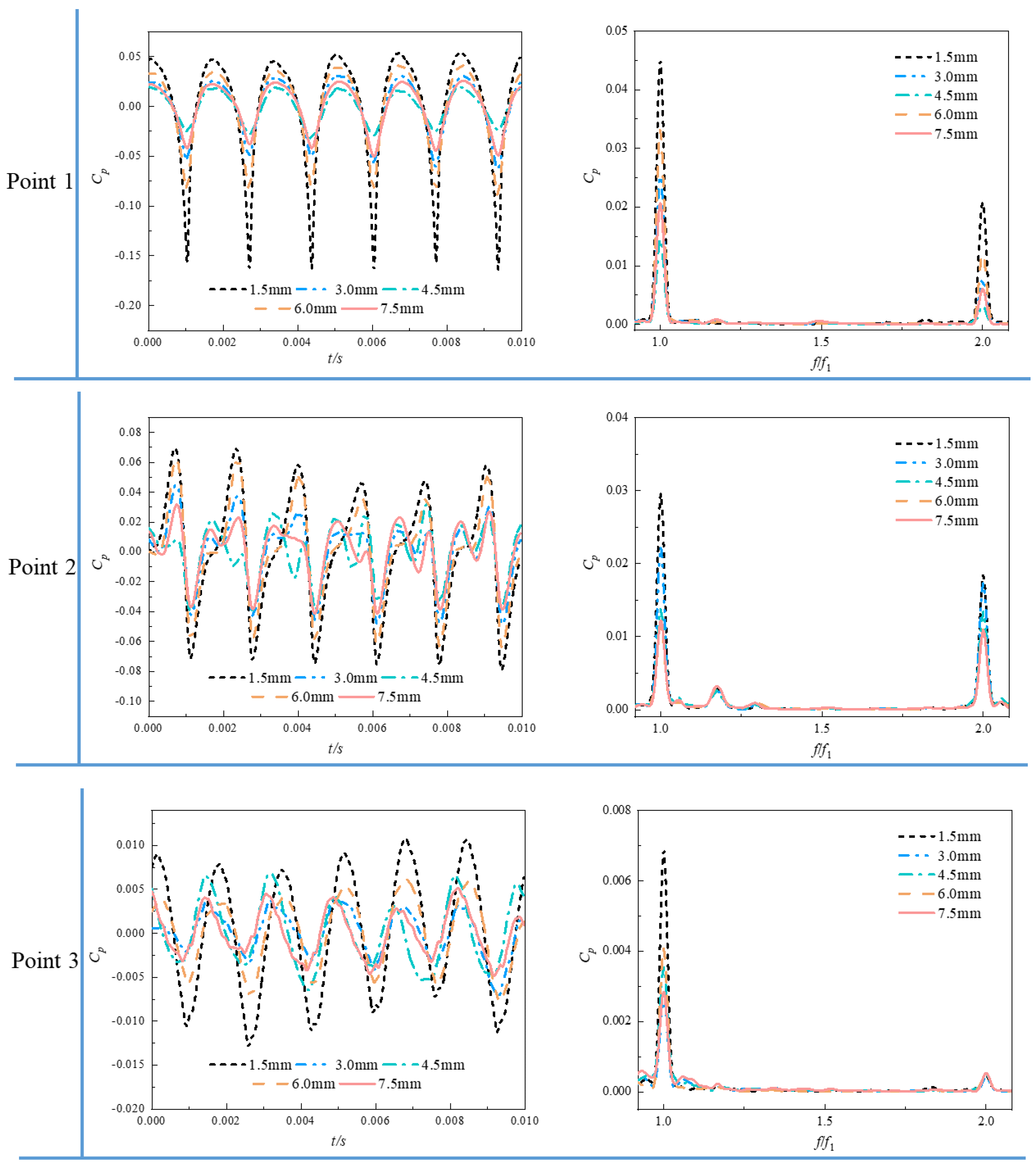
4.3. Flowfield Pattern with Different Rotor–Stator Distances
5. Conclusions
- (1)
- The performance of the mixed-flow centrifugal pump at 3 mm and 6 mm rotor–stator distances was obtained experimentally. The comparison with the numerical prediction results shows that the numerical prediction results of the performance of the mixed-flow centrifugal pump at full flow conditions are in high agreement with the experimental results, and the numerical prediction of the head and efficiency at full flow conditions maintain the same variation pattern as the experimental results. This proves that the CFD method in this paper is highly accurate in obtaining the performance and flow pattern within the mixed-flow centrifugal pump.
- (2)
- As the rotor–stator distance increases, the flow loss ratio in the chamber of the mixed-flow centrifugal pump increases, which leads to a slight reduction in the shut-off point head and rated efficiency. The head and efficiency of the mixed-flow centrifugal pump at each rotor–stator distance under full flow conditions do not vary greatly; therefore, its performance is less affected by the rotor–stator distance at full flow conditions.
- (3)
- The jet velocity at the impeller outlet decays rapidly in the axial direction, so the impact strength of the jet on the diffuser blades decreases significantly with the increase in the rotor–stator distance. At the same time, the strength of the impeller outlet wake also decreases continuously during the propagation downstream. However, the wake interaction caused by low flow conditions is much stronger, which is consistent with the engineering practice of the pump system in the low flow conditions prone to vibration and noise. Therefore, avoiding the partial working condition operation of the pump device and appropriately enhancing the rotor–stator distance can significantly reduce the shock interaction and wake interaction intensity in the pump, which is conducive to the safe and stable operation of the pump device.
- (4)
- When the rotor–stator distance is 1.5 mm, the amplitude of pressure changes in the circumferential direction of the rotor–stator interaction zone is significantly greater than the amplitude of pressure change under other rotor–stator distances. When the rotor–stator distance is raised, the number of pressure change cycles is consistent with the number of impeller blades, and the amplitude of pressure change in the circumferential direction is significantly reduced. Therefore, the rotor–stator distance elevation can reduce the intensity of potential interaction in the pump. In engineering practice, too-small rotor–stator distances should be avoided to prevent the induction of high-frequency resonance in the pump system.
- (5)
- Based on the present study, we believe that increasing the rotor–stator distance can reduce the rotor–stator interaction intensity in the pump, weaken the internal pressure pulsation phenomenon, and thus, improve the operational stability of the pump system while keeping the pump system performance basically unchanged. The results of this study can be extended to all centrifugal pumps using diffusers in the form of vanes as the pressure chamber, which has strong practical application and theoretical value.
- (6)
- However, the work conducted so far in this paper is still insufficient for revealing the detailed mechanism of rotor–stator interference in mixed-flow centrifugal pumps. For example, the local energy loss due to unsteady interference flow caused by different rotor–stator distances is not yet clear. At the same time, the coupling relationship between the rotor–stator interference of the pump chamber and the flow characteristics of the medium has not been studied. Therefore, the above deficiencies will be the target of future research to explore the energy and flow characteristics of the pump device under different rotor–stator interference conditions, and continue to improve the theory related to rotor–stator interference of pumps.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Symbols
| Q | flow rate |
| Qd | designed flow rate |
| H | head |
| n | rotating speed |
| φ | chamber loss ratio |
| Zi | blade number of impeller |
| Zd | vane number of diffuser |
| ε | maximum grid control size |
| μt | turbulence viscosity |
| k | turbulent kinetic energy |
| ω | turbulent frequency |
| P | pressure |
| Pkb | influence of the buoyancy forces in turbulent kinetic energy |
| Pωb | influence of the buoyancy forces in turbulent frequency |
| Pk | production rate of turbulence |
Abbreviations
| CFD | computational fluid dynamics |
| FFT | fast Fourier transform |
| BPF | blade passing frequency |
References
- Kim, J.H.; Ahn, H.J.; Kim, K.Y. High-efficiency design of a mixed-flow centrifugal pump. Sci. China Ser. E Technol. Sci. 2010, 53, 24–27. [Google Scholar] [CrossRef]
- Muggli, F.A.; Holbein, P.; Dupont, P. CFD calculation of a mixed flow pump characteristic from shutoff to maximum flow. J. Fluids Eng. 2002, 124, 798–802. [Google Scholar] [CrossRef]
- Li, W.; Li, E.; Ji, L.; Zhou, L. Mechanism and propagation characteristics of rotating stall in a mixed-flow centrifugal pump. Renew. Energy 2020, 153, 74–92. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Detection of cavitation phenomenon within a centrifugal pump based on vibration analysis technique in both time and frequency domains. Exp. Tech. 2020, 44, 329–347. [Google Scholar] [CrossRef]
- Wang, C.L.; Jia, F.; Wu, Z.W.; Liu, D. Pressure fluctuation of unsteady flow in high specific speed mixed-flow centrifugal pump. J. Drain. Irrig. Mach. Eng. 2013, 31, 103–108. [Google Scholar]
- Miyabe, M.; Maeda, H.; Umeki, I.; Jittani, Y. Unstable head-flow characteristic generation mechanism of a low specific speed mixed flow pump. J. Therm. Sci. 2006, 15, 115–120. [Google Scholar] [CrossRef]
- Wang, K.; Liu, H.; Zhou, X.; Wang, W. Experimental research on pressure fluctuation and vibration in a mixed flow pump. J. Mech. Sci. Technol. 2016, 30, 179–184. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R.; Mishra, R. Experimental investigation of the effect of air injection on performance and detection of cavitation in the centrifugal pump based on vibration technique. Arab. J. Sci. Eng. 2020, 45, 5657–5671. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Experimental comparative investigations to evaluate cavitation conditions within a centrifugal pump based on vibration and acoustic analyses techniques. Arch. Acoust. 2020, 45, 541–556. [Google Scholar]
- Al-Obaidi, A.R. Experimental investigation of the effect of suction valve opening on the performance and detection of cavitation in the centrifugal pump based on acoustic analysis technique. Arch. Acoust. 2019, 44, 59–69. [Google Scholar]
- Miyabe, M.; Furukawa, A.; Maeda, H.; Umeki, I.; Jittani, Y. A behavior of the diffuser rotating stall in a low specific speed mixed-flow centrifugal pump. Int. J. Fluid Mach. Syst. 2009, 2, 31–39. [Google Scholar] [CrossRef]
- Liu, M.; Tan, L.; Liu, Y.; Xu, Y.; Cao, S. Large eddy simulation of cavitation vortex interaction and pressure fluctuation around hydrofoil ALE 15. Ocean Eng. 2018, 163, 264–274. [Google Scholar] [CrossRef]
- Wang, C.; He, X.; Shi, W.; Wang, X.; Wang, X.; Qiu, N. Numerical study on pressure fluctuation of a multistage centrifugal pump based on whole flow field. AIP Adv. 2019, 9, 035118. [Google Scholar] [CrossRef]
- Miyabe, M.; Furukawa, A.; Maeda, H.; Umeki, I. Investigation of internal flow and characteristic instability of a mixed flow pump. In Proceedings of the Fluids Engineering Division Summer Meeting, Vail, CO, USA, 2–6 August 2009; Volume 43727, pp. 315–321. [Google Scholar]
- Al-Obaidi, A.R. Investigation of effect of pump rotational speed on performance and detection of cavitation within a centrifugal pump using vibration analysis. Heliyon 2019, 5, e01910. [Google Scholar] [CrossRef] [PubMed]
- Van Esch, B.; Cheng, L. Unstable operation of a mixed-flow centrifugal pump and the influence of tip clearance. In Proceedings of the ASME-JSME-KSME Joint Fluids Engineering Conference, Shizuoka, Japan, 24–29 July 2011; Volume 44403, pp. 79–87. [Google Scholar]
- Funakoshi, H.; Tsukamoto, H.; Miyazaki, K.; Miyagawa, K. Experimental study on unstable characteristics of mixed-flow centrifugal pump at low flow-rates. In Proceedings of the ASME/JSME 2003 4th Joint Fluids Summer Engineering Conference, Honolulu, HI, USA, 6–10 July 2003; Volume 36975, pp. 609–614. [Google Scholar]
- Nagahara, T. Application of PIV for the flow field measurement in a mixed-flow centrifugal pump. In IOP Conference Series. Earth and Environmental Science; IOP Publishing: Bristol, UK, 2012; p. 15. [Google Scholar]
- Dring, R.; Joslyn, H.; Hardin, L.; Wagner, J.H. Turbine rotor-stator interaction. ASME J. Eng. Gas. Turbines Power 1982, 104, 729–742. [Google Scholar] [CrossRef]
- Joslyn, D.; Dring, R. Three-dimensional flow in an axial turbine: Part 1—Aerodynamic mechanisms. ASME J. Turbomach. 1992, 114, 61–70. [Google Scholar] [CrossRef]
- Iino, T.; Kasai, K. An analysis of unsteady flow induced by interaction between a centrifugal impeller and a vaned diffuser. Trans. Jpn. Soc. Mech. Eng. 1985, 51, 154–159. [Google Scholar]
- Al-Obaidi, A.R. Numerical investigation of flow field behaviour and pressure fluctuations within an axial flow pump under transient flow pattern based on CFD analysis method. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; Volume 1279, p. 012069. [Google Scholar]
- Shi, F.; Tsukamoto, H. Numerical study of pressure fluctuations caused by impeller-diffuser interaction in a diffuser pump stage. ASME J. Fluids Eng. 2001, 123, 466–474. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R.; Mohammed, A.A. Numerical Investigations of Transient Flow Characteristic in Axial Flow Pump and Pressure Fluctuation Analysis Based on the CFD Technique. J. Eng. Sci. Technol. Rev. 2019, 12, 70–79. [Google Scholar] [CrossRef]
- Zhang, M.; Tsukamoto, H. Unsteady hydrodynamic forces due to rotor-stator interaction on a diffuser pump with identical number of vanes on the impeller and diffuser. ASME J. Fluids Eng. 2005, 127, 743–751. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Investigation of the influence of various numbers of impeller blades on internal flow field analysis and the pressure pulsation of an axial pump based on transient flow behavior. Heat Transf. 2020, 49, 2000–2024. [Google Scholar] [CrossRef]
- Barrio, R.; Parrondo, J.; Blanco, E. Numerical analysis of the unsteady flow in the near-tongue region in a volute-type centrifugal pump for different operating points. Comput. Fluids 2010, 39, 859–870. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, L.; Shi, W.; He, Z.; Han, Y.; Xiao, Y. Interstage difference of pressure pulsation in a three-stage electrical submersible pump. J. Pet. Sci. Eng. 2021, 196, 107653. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, L.; Han, Y.; Hang, J.; Lv, W.; Shi, W.; He, Z.; Pan, B. Pressure pulsation investigation in an electrical submersible pump based on Morlet continuous wavelet transform. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 6069–6079. [Google Scholar] [CrossRef]
- Karassik, I.J.; Messina, J.P.; Cooper, P.; Heald, C.C. Pump Handbook; McGraw-Hill Education: New York, NY, USA, 2008. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: London, UK, 2007. [Google Scholar]
- Bradshaw, P. An Introduction to Turbulence and Its Measurement: Thermodynamics and Fluid Mechanics Series; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Dhakal, T.P.; Walters, D.K. A three-equation variant of the SST k-ω model sensitized to rotation and curvature effects. J. Fluids Eng. 2011, 133, 111201. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, H.; Liu, J.; Wang, C.; Ge, J.; Zhu, Y.; Chen, X.; Hu, B. Flow characteristics of oblique submerged impinging jet at various impinging heights. J. Mar. Sci. Eng. 2022, 10, 399. [Google Scholar] [CrossRef]
- Hu, B.; Wang, H.; Liu, J.; Zhu, Y.; Wang, C.; Ge, J.; Zhang, Y. A numerical study of a submerged water jet impinging on a stationary wall. J. Mar. Sci. Eng. 2022, 10, 228. [Google Scholar] [CrossRef]
- Li, W.; Yang, Z.; Shi, W.; Li, E.; Ji, L. Research progress of non-uniform inflow of water jet pump. J. Drain. Irrig. Mach. Eng. 2022, 40, 757–765. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, F.; Chen, X.; Yang, Y.; Wang, C. Numerical and Experimental Study on the Effect of Rotor–Stator Distance on Rotor–Stator Interaction Strength within Mixed-Flow Centrifugal Pumps. J. Mar. Sci. Eng. 2022, 10, 1114. https://doi.org/10.3390/jmse10081114
Han F, Chen X, Yang Y, Wang C. Numerical and Experimental Study on the Effect of Rotor–Stator Distance on Rotor–Stator Interaction Strength within Mixed-Flow Centrifugal Pumps. Journal of Marine Science and Engineering. 2022; 10(8):1114. https://doi.org/10.3390/jmse10081114
Chicago/Turabian StyleHan, Feng, Xionghuan Chen, Yang Yang, and Chuan Wang. 2022. "Numerical and Experimental Study on the Effect of Rotor–Stator Distance on Rotor–Stator Interaction Strength within Mixed-Flow Centrifugal Pumps" Journal of Marine Science and Engineering 10, no. 8: 1114. https://doi.org/10.3390/jmse10081114
APA StyleHan, F., Chen, X., Yang, Y., & Wang, C. (2022). Numerical and Experimental Study on the Effect of Rotor–Stator Distance on Rotor–Stator Interaction Strength within Mixed-Flow Centrifugal Pumps. Journal of Marine Science and Engineering, 10(8), 1114. https://doi.org/10.3390/jmse10081114






