Waste Heat Source Profiles for Marine Application of Organic Rankine Cycle

Abstract

The maritime industry will continue to see increasing regulatory requirements to reduce carbon emissions from ships’ operations. Improving the energy efficiency of ships with waste heat recovery systems based on the organic Rankine cycle (ORC) is an attractive way to meet these tightening requirements. The operational profile of a ship has a huge influence on the feasibility of installing ORC onboard as it affects the waste heat source profile from the diesel engines. However, to date, scant attention has been paid to examining the effects that the operational profile has on the marine application of ORC as it is both difficult and expensive to obtain. The present paper aims to describe a methodology that can overcome this problem by developing a generic ship speed profile that defines the ship’s operational profile. This speed profile works together with a fit-for-purpose diesel engine waste heat model to derive a waste heat source profile that is used as the input to a thermoeconomic analysis that can justify the installation of ORC. The proposed methodology allows for an objective comparison of the feasibility of ORC subjected to variations in the operational profile. Furthermore, the optimum ORC design can be identified to meet payback time expectations of different shipowners.

1. Introduction

In recent International Maritime Organization (IMO) Marine Environment Protection Committee (MEPC) meetings, several new requirements like the Energy Efficiency Existing Ship Index (EEXI) and Carbon Intensity Indicator (CII) were made mandatory for existing ships in an attempt to reduce carbon dioxide emissions from the international maritime industry [1].

The EEXI is a design index that is to be calculated once for each existing ship and verified to be lower than the required EEXI specific for each ship type that has been deemed to meet the requirements. The CII is an operational index that needs to be calculated annually to ascertain that the actual carbon emission intensity of each ship remains in the acceptable band, otherwise corrective actions need to be implemented by the shipowners. Enhancing the ship’s efficiency with waste heat recovery systems can improve both EEXI and CII by reducing the carbon emissions from the ship’s operations. Recently, waste heat recovery systems based on the organic Rankine cycle (ORC) have been shown in several studies to be very promising [2,3,4,5,6] for marine applications. Indeed, several actual marine applications have been reported (Refer to Appendix A for a compilation).

Unlike land-based ORC systems in the geothermal and biomass industry, the heat source for the ORC that recovers waste heat from the diesel engines onboard a ship varies due to its operational profile that concerns the ship at berth, manoeuvring, transit, or on anchor. In the current literature, several methods have been proposed to represent this variation in heat source profiles. Machinery operational data have been obtained from a passenger ferry with measurements of the engine exhaust gas temperature and engine load that allowed the exhaust mass flow rate to be estimated [7]. However, it is rare to be provided with these data due to the confidential nature of the ship’s operations. The more common way taken by [8,9,10] will be to assume a speed distribution curve or histogram that shows the percentage of time at each speed the ship is sailing, as shown in Figure 1.

The problem with this method is that discrete speed baskets (12, 14, 16 knots, etc.) will have to be defined. However, in reality, speed variation is a continuous function. For a meaningful comparison, it is also difficult to justify changes in a particular ship’s speed profile for each specific ship.

The isolated effects of diesel engine load on heat source profile for marine ORC have also been presented in [11]. However, the exhaust gas data are obtained from the engine maker’s database for the identified engine.

This paper presents a novel methodology that is outlined in Figure 2 to define the waste heat source profile from diesel engines onboard a ship. It utilises a generic ship speed profile and a fit-for-purpose diesel engine waste heat model, taking into account a ship’s operational profile in the thermoeconomic analysis, in order to justify the marine application of ORC. The analysis will be performed using the multi-domain system modelling and commercial simulation software, Amesim [12]. Furthermore, the proposed methodology can also be applied to the feasibility assessment of other novel green technologies for marine applications where the ship’s operational profile is needed.

2. Generic Ship Speed Profiles

A generic ship speed profile can be defined to represent the actual operational profile for each ship. This can be expressed as the cumulative distribution of ship speed with time and is convenient to be used directly in time-domain analysis software like Amesim [13].

The cumulative distribution curve simplifies this representation as it starts at 0% and eventually ends at 100%. The operational profile of the ship determines the shape of the speed cumulative distribution curve, as shown in Figure 3, which presents five basic generic ship speed profiles. For computational simplicity, the basic generic ship speed profile equation is based on a quadratic equation of the form shown in Equation (1):

$$\frac{V}{V_{max}}={\left(\frac{t}{t_{max}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}$$

(1)

where V and t refer to the ship speed and time, subscript, max refers to the maximum, and superscript n refers to the generic ship speed profile load factor.

The generic ship speed load profile factor n can take values between 0.25 to 4. For example, when n is equal to 1, speed is equally distributed in time. For a lightly loaded ship spending most of the time at lower speeds, its n value will be less than 1, for example, 0.25 or 0.5. The converse applies for heavily loaded ships where their n values will be greater than 1 usually 2 or 4. For more complex representations, S-curve cumulative distributions that correspond to normal speed distributions could be adopted but this will increase the complexity of the equations used.

The proposed generic ship speed profile is suitable for quasi-static thermodynamic analyses, where the heat source input varies with time without consideration for transients like accelerations and decelerations. For dynamic analyses, the order of the changes in ship speed is important and hence such a method will be less useful.

The proposed generic ship speed profile is compared with actual speed profiles derived by calculating the ship speed by means of the Automated Identification System (AIS) data of eight ship types operating in Norwegian waters [14] and plotted in Figure 4 and Figure 5 below for coastal and ocean-going ships respectively.

An interesting observation can be seen when most of the actual speed profiles for coastal ships (shown in Figure 4) are quite close to the lightly-loaded generic speed profiles where n is 0.25 or 0.5, while for ocean-going ships (shown in Figure 5), they are closer to that of heavily-loaded speed profiles when n equals 2 or 4.

The above shows that the seemingly complicated ship operational profile that is only available by the shipowner or AIS data can be approximated by means of the simplified generic ship speed profiles. One just needs to know the maximum ship speed and the total time duration for the study. Then, operational profiles can be studied by just varying the generic ship speed profile load factor, n.

3. Fit-For-Purpose Diesel Engine Waste Heat Model

As mentioned above, most researchers in the current literature use waste heat data from engine makers in their studies. Some of them have proposed detailed engine models based on the mean value engine model (MVEM) or more advanced ones like zero and one-dimensional models [15]. However, in the preliminary stages of assessing the feasibility of ORC, many engine parameters are not available to support the building of advanced diesel engine models. To this end, a simpler and fit-for-purpose waste heat model for the diesel engine is required to be developed. Such engine models based on regression analysis have been used in industry research such as, for example, the Fourth IMO GHG Study [16], based on earlier studies by [17]. In these studies, correlations for specific fuel consumption varying with engine load have been derived.

As the diesel engine exhaust gas has the highest potential for waste heat recovery, correlations concerning the engine-specific exhaust flow and temperature were proposed in [13] for the slow-speed diesel (SSD) and medium-speed diesel (MSD) based on a regression analysis from over seventy diesel engines, utilising engine performance data available in the public domain. The proposed correlations are stated below in Equations (2) and (3).

For the specific exhaust flow, which is the ratio between exhaust gas mass flow and engine maximum continuous power, a linear correlation was proposed as in Equation (2):

$$\frac{{\dot{m}}_{exh}}{P_{MCR}}=a\lambda +b$$

(2)

where λ is the engine load factor and the constants a and b are coefficients found for each engine type.

For the exhaust gas temperature, a quadratic relation with engine load was proposed, in the form of Equation (3):

$$T_{exh}=c{\lambda }^2+d\lambda +e$$

(3)

where c, d, and e are coefficients found for each engine type.

The values for the various constants found for the SSD and MSD engines are listed in

Table 1. Summary of coefficients for engine exhaust gas correlations.

Engine Type	Specific Exhaust Gas Flow (kg/s/kW)		Exhaust Gas Temperature (°C)
	a	b	c	d	e
SSD	0.0017	0.0004	290.45	−384.53	341.68
MSD	0.0015	0.0004	210.53	−272.8	401.31

:

The proposed correlations were verified with the performance data of the reference engines. The correlations for SSD showed a good fit with average deviations of −2 and +2%, while for MSD this was −8% and −3%, respectively, for specific exhaust gas flow and exhaust temperature, respectively [13].

The proposed diesel engine exhaust gas correlations allow for a quick and reliable estimation of the exhaust gas flow and temperature varying with engine load with minimal input data and are especially useful in the preliminary design stage of the marine ORC.

4. Marine Application of ORC Onboard an Offshore Service Vessel

A 5200 deadweight tonnage (DWT) multipurpose platform supply vessel (MPSV) is considered a case study to demonstrate how the proposed waste heat profile can be defined and used in a thermoeconomic analysis to assess the feasibility of waste heat recovery using ORC for marine applications. The principal specifications of the MPSV are summarised in

Table 2. Principal specifications of the MPSV.

Specifications
Length waterline, LWL	88.4 m
Breadth, B	20 m
Design draught, T	5.5 m
Deadweight	5200 ton
Service speed	12 knots
Design	Wartsila WSD 1000 MPSV
Classification	American Bureau of Shipping +A1, (E) Offshore Support Vessel, Supply-HNLS, FFV 1, OSR-S1, +DPS-2, SPS, +AMS, HAB(WB), UWILD, CRC
Main machinery	4 × Wartsila 6L26 diesel engines rated at 1950 kW 2 × azimuthing thrusters at 2500 kW 2 × tunnel bow thrusters (Dia:2m) at 1000 kW

.

The MPSV was designed by Wartsila Ship Design [18] to carry supplies like fuel oil, drilling fluids, and chemicals to offshore rigs. It can also operate as a standby firefighting vessel and oil spill recovery vessel in case of accidents occurring on the oil rig.

4.1. Generic Operational Profile

The navigation data is derived from the AIS dataset from one of the maritime data providers. For the first ten months of operation, ship speed is plotted against the time stamp to obtain the ship speed profile shown in Figure 6.

The usual way to visualise variations in ship speed, is by using a speed distribution diagram like that shown in Figure 7, from which it can be identified that MPSV spends the majority of its time at the low-speed range of fewer than 2 knots.

The MPSV speed profile shown in Figure 6 is re-organised into a cumulative curve and is overlaid with the proposed generic speed profiles with n values, 0.25, 0.5, and 1, as shown in Figure 8.

It can be observed that the generic speed profile with n = 0.25 (yellow line) best matches the actual speed profile with an even distribution of errors. Hence, the generic speed profile with n = 0.25 will be used for the rest of the analysis for the MPSV.

Unlike other conventional cargo ships like a tanker, bulker, or containership, the MPSV does not carry bulk cargo between ports but serves offshore rigs. Three operational modes can be identified: transit, harbour, and offshore. For transit mode, the MPSV is deemed to be moving at speeds greater than 2 knots, while the harbour mode can be identified by its proximity to land. The offshore mode may consist of three further categories, namely, standby, dynamic positioning (light), and dynamic positioning (heavy).

Based on information from the designers [19], the percentage spent at each sub-category, as well as the corresponding load factor on the thrusters, are shown in

Table 3. Offshore mode definition.

Percentage of Time	Offshore Mode (100%)
	DP Heavy	DP Light	Standby
	20%	60%	20%
Propulsion thruster load factor	0.6	0.36	0.12
Bow thruster load factor	0.7	0.4	0.2

. With this information, the power requirement for propulsion and manoeuvering can be calculated specifically for the offshore mode, as described in the following section.

4.2. Estimating Propulsion, Manoeuvring and Auxiliary Loads

The energy balance between the power provided by the engines and the various loads onboard the MPSV can be described by Equation (4) below. The engine power demand consists of two main kinds of components, namely propulsion and manoeuvering, which make up the mechanical load (m), and auxiliary ones, which are related to the electrical load (el).

$${\displaystyle \sum }_{i=1}^{k_{ME}}{\lambda }_i·P_{ME,i}={\displaystyle \sum }_{i=0}^k\frac{P_{el,i}}{{\eta }_{etr}{\eta }_g{\eta }_m}+{\displaystyle \sum }_{i=0}^k\frac{P_{m,i}}{{\eta }_m}$$

(4)

During transit mode, when the MPSV moves with a speed greater than 2 knots, the power required to move the ship, P_D is estimated with the Holtrop and Mennen method [20], using the design parameters listed in

Table 4. Hull form coefficients.

Block Coefficient, CB.	0.7
Prismatic coefficient, CP	0.71
Midship section coefficient, CM	0.99
Waterplane area coefficient, CWP	0.83
Windage coefficient	0.7

and

Table 5. Specifications of major components.

Area	Measured
Area of appendages, Sapp	78 m2
Transom area, AT	9.65 m2
Bulb transverse area, ABT	10.43 m2
Height of bulb, hB	4 m
Windage area, Aw	472.93 m2

, based on measurements from the ship’s arrangement drawings.

The generally widely accepted assumptions for the various efficiencies are shown in

Table 6. Assumed values of efficiencies.

Efficiencies
Sea margin, 1 + x	1.2
Propulsive efficiency, ηD	70%
Mechanical/electrical transmission efficiency, ηs/ηetr	99%
Motor/generator efficiency, ηmtr/ηgen	96.5%

.

The auxiliary power requirement at sea, P_el is estimated with a correlation presented in [21] as shown in Equation (5) and is found to be in good agreement at the lower power range [13].

$$P_{el}=100+0.55{\left(P_{MCR,ME}\right)}^{0.7}$$

(5)

By using the definition of the operational modes shown earlier, the power demand for propulsion and manoeuvring in harbour and offshore modes are summarised in

Table 7. Propulsion, manoeuvring and auxiliary loads during different modes.

Operational Mode:	Speed Range	Prop. & Manoeuvring Loads	Auxiliary Loads
Transit	>2 knots	PD	PEL
Harbour	0–2 knots	0	0.3PEL
Offshore	0–2 knots	0.36Pp + 0.44PBT	1.3PEL

, where P_p and P_BT are the rated power of the propellers and bow thrusters. The propulsion and manoeuvring power for the offshore modes are estimated based on the distribution in Table 3 accounting for the proportion of time and load factor at each of the offshore mode sub-categories.

4.3. Exhaust Waste Heat Profile

The main diesel engine exhaust mass flow and temperature are calculated by Equations (2) and (3) and compared in Figure 9 against their listed values as stated in the corresponding published engine project guide [22].

It is found that the correlations predict the exhaust mass flow rate very accurately, within 5%, while the exhaust gas temperature is estimated less accurately with discrepancies up to 13%. This is inevitable as the exhaust temperature is influenced mainly by the turbocharger performance, which can differ much between different engines. Nonetheless, this is considered acceptable in the preliminary design stage, as the variations will not exceed the uncertainty in capital costs that are estimated between −24% and +36% [23].

When the number of operating main engines is considered to meet the required propulsion, manoeuvring, and auxiliary power requirements, the total heat source profile in terms of mass flow and temperature can be derived. The waste heat source can be represented by the three operational profiles, namely the actual AIS, generic one, and design profile. The latter has been based on the operational mode distribution and is derived from a study by the designer [19]. These three profiles are compared in Figure 10. According to this figure, the cumulative distribution of exhaust heat is close for the operational profile derived from actual AIS (dotted) and generic profile with an n value equal to 0.25 (full line). There is a greater departure from the former if the designer’s operational profile is used.

This indicates that the proposed generic ship speed profile together with the fit-for-purpose diesel engine waste heat model can be used to approximate the actual waste heat profile very well.

4.4. Design of Marine Organic Rankine Cycle

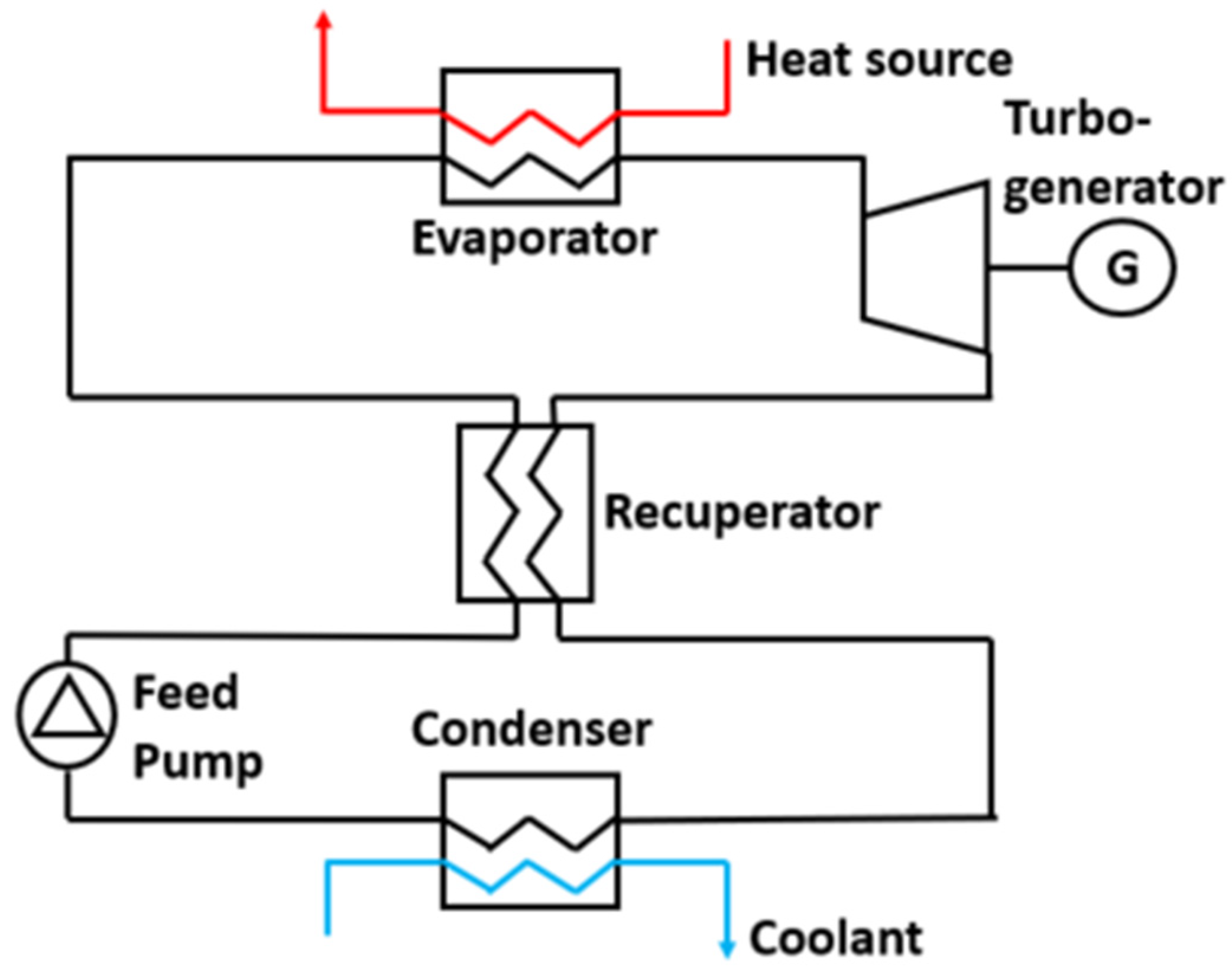
There are various design options in ORC that include the selection of suitable cycle configurations, working fluids, heat exchangers, and fluid machinery. Two main cycle configurations had been studied most in the literature, namely the simple (sORC) and the recuperative (rcORC) cycle configurations, shown in Figure 11 and Figure 12, respectively.

By applying relevant selection constraints involving critical and condensing pressures, evaporating and condensing temperatures, on the full list of working fluids available in the thermophysical property library, Coolprop [24], a shortlist of 19 working fluids suitable for marine ORC was identified in [13]. Based on the availability of working fluid properties in Amesim, cyclopentane and ethanol were selected as representative working fluids of the dry and wet types, respectively. A brief comparison of these two working fluids with water in terms of their properties is shown in

Table 8. Properties of selected working fluids compared with water.

Fluids	Cyclopentane	Ethanol	Water
Molecular formula	C5H10	C2H5OH	H2O
Tboiling (°C)	49.3	78.3	100.0
Tcrit (°C)	238.6	240.8	374.0
Pcrit (bar)	45.1	61.5	220.6
GWP	Low	Low	Low
ODP	0	0	0
Flash-point (°C)	−37.2	12.9	NA
Autoignition temperature (°C)	361	422.9	NA

.

The heat exchangers are modelled herein with the effectiveness-Number of Transfer Unit (ε-NTU) method [25] through the Equations (6)–(11):

$$\epsilon =\frac{{\dot{Q}}_{actual}}{{\dot{Q}}_{max}}$$

(6)

$${\dot{Q}}_{actual}=C_h\left(T_{h,i}-T_{h,o}\right)=C_c\left(T_{c,o}-T_{c,i}\right)$$

(7)

$${\dot{Q}}_{max}=C_{min}\left(T_{h,i}-T_{c,i}\right)$$

(8)

$$\epsilon =f\left(C_r, NTU, flow arrangement\right)$$

(9)

$$NTU=\frac{1}{1-C_r}ln\frac{1-\epsilon C_r}{1-\epsilon }$$

(10)

$$NTU=\frac{UA}{C_{min}}$$

(11)

The overall heat transfer coefficient is estimated by using typical values from [26] shown in

Table 9. Assumed values of overall heat transfer coefficient.

Heat Exchanger	U-Value (W/m2K)
Evaporator	99
Condenser	764
Recuperator	524
Preheater	524

.

The performance of fluid machinery, like the expander and pump, is modelled using their isentropic efficiency, according to Equations (12) and (13). Prior research had assumed isentropic efficiencies of about 80% [13]. For the present study, a more conservative value of 70% is assumed that takes into account variations in the performance of machinery at part-load operations.

$${\eta }_{is,exp}=\raisebox{1ex}{$({\mathrm{h}}_{exp,o}-{\mathrm{h}}_{exp,i})$}\!\left/ \!\raisebox{-1ex}{${\left({\mathrm{h}}_{exp,o}-{\mathrm{h}}_{exp,i}\right)}_{is}$}\right.$$

(12)

$${\eta }_{is,pp}=\raisebox{1ex}{${({\mathrm{h}}_{pp,o}-{\mathrm{h}}_{pp,i})}_{is}$}\!\left/ \!\raisebox{-1ex}{$\left({\mathrm{h}}_{pp, o}-{\mathrm{h}}_{pp,i}\right)$}\right.$$

(13)

To assess the thermal performance, the net work output, ${\dot{W}}_{net}$, is defined below, which substracts the work input of all pumps (used in the working fluid or the heat source or the heat sink circuits) from the gross work output from the expander.

$${\dot{W}}_{net}={\dot{W}}_{exp}-{\displaystyle \sum }_{j=1}^n{\dot{W}}_{pp,j}$$

(14)

Unless otherwise stated, the assumptions summarised in

Table 10. Assumptions for ORC designs.

Assumption	Value
Exhaust gas minimum temperature, Texh,o	150 °C
Evaporating pressure, Pevap	20 bar
Condensing temperature, Tcond	45 °C
Expander and pump isentropic efficiency, ηexp/ηpp	70%

are used for the ORC thermodynamic analysis.

4.5. Economic Analysis

The economic analysis of the ORC is not trivial. Its reliability depends on the assumptions made, as well as on the actual costs of equipment (to the degree that they are available from makers since they are not available in literature due to confidentiality). In this study, the capital cost of the ORC is estimated using the module costing technique presented in [23], which defines a bare module cost, C_BM:

$$C_{BM}=C_p^0{F}_{BM}$$

(15)

where $C_p^0$ is the purchased equipment cost with basic conditions at ambient operating pressure using carbon steel construction and can be estimated by the formula:

$$lo{g}_{10}{C}_p^0=K_1+K_{2}lo{g}_{10}\left(A\right)+K_3{\left[lo{g}_{10}\left(A\right)\right]}^2$$

(16)

where A is the capacity or size parameter of the equipment, while K₁, K₂, and K₃ are empirical coefficients that vary with equipment type.

F_BM is the bare module cost factor that takes into account the specific material and pressure and is found by the following formula:

$$F_{BM}=\left(B_1+B_2{F}_M{F}_P\right)$$

(17)

where F_M is the material factor, and F_P is the pressure factor. The latter is calculated from the following:

$$lo{g}_{10}{F}_p=C_1+C_{2}lo{g}_{10}P+C_3{\left(lo{g}_{10}P\right)}^2$$

(18)

where P is the gauge pressure in barg.

The expander bare module cost, C_BM has a simpler relation, does not require the pressure factor, and just takes into account the material factor:

$$C_{BM}=C_p^0{F}_{M2}$$

(19)

The various costing factors related to the above correlations are summarised in

Table 11. Costing factors used for ORC components.

Equipment	Heat Exchanger	Pump	Expander
Type	Shell and Tube	Positive displacement	Centrifugal, axial and reciprocating
Material	Carbon steel/Copper tube	Carbon steel	Carbon steel
Range for A	10 < A < 1000 m2	1 < A < 100 kW	100 < A < 4000 kW
K1	4.3247	3.4771	2.2897
K2	−0.303	0.1350	1.3604
K3	0.1634	0.1438	−0.127
B1	1.63	1.89	-
B2	1.66	1.35	-
Range for P (barg)	5 < P < 140	10 < P < 100	-
C1	0.03881	−0.245382	-
C2	−0.11272	0.259016	-
C3	0.08183	−0.01363	-
FM	1.4	1.4	3.5

taken from [23].

The total module cost can be derived by summing all the bare module costs of various components and providing a margin of 15% and 3% for contingency costs and other fees [23] as per Equation (20):

$$C_{TM}=1.18{\displaystyle \sum }_{i=1}^n{C}_{BM,i}$$

(20)

The total capital investment cost, C_TI can be estimated by adding an additional 2% margin to account for the additional fire protection system needed to deal with flammable fluids in the ORC system.

To account for inflation between the years 2001 and 2020, the Chemical Engineering Plant Cost Index (CEPSI) is used as below:

$$C_{TI}=\frac{CEPCI\left(2020\right)}{CEPCI \left(2001\right)}{C}_{TI\left(2001\right)}$$

(21)

where CEPCI for the years 2020 and 2001 is 596.2 and 397, respectively [23,27].

The specific investment cost (SIC) in $/kW can be derived as below:

$$SIC=\frac{C_{TI}}{{\dot{W}}_{net}}$$

(22)

where ${\dot{W}}_{net}$ is the net work output from the ORC system.

Shipowners will be interested in the benefits that can be generated by investing in an ORC system. The way to measure this is the annual fuel savings in mass, M_FS, calculated as follows, taking into account the time spent at each engine load annually:

$$M_{FS}={\displaystyle \sum }_{load}{\dot{W}}_{net}\times t_{load}\times SFOC$$

(23)

where t_load is the time spent at each engine load and SFOC is the specific fuel oil consumption of the diesel engine generator, which is assumed to be 200 g/kWh.

The annual fuel cost savings in dollars, E_j will then depend on the Unit Cost of the Fuel, UFC used onboard the ship. The price development of marine fuels from the year 2014 can be obtained from [28] for LNG, Intermediate Fuel Oil (IFO), Marine Gas Oil (MGO), and methanol. The UFC of MGO is taken to be $610/ton.

$$E_j=M_{FS}\times UFC$$

(24)

The discounted payback time (DPT) for the installation of ORC can be estimated by considering the time value of money for annual fuel savings that will occur in the future to give a better indication of the actual payback time of the investment in-line with general accounting principles, considering interest rate per year, i of 4% per year [13]. DPT is calculated as:

$$DPT=-\frac{\ln \left[1-\frac{C_{TI}}{E_j}\left(e^i-1\right)\right]}{i}$$

(25)

A sample calculation is performed and presented in Appendix B for SIC and DPT.

5. Results and Discussions

The generic ship speed profile and fit-for-purpose diesel engine waste heat model are used to derive the operational profile for the case ship under consideration. This section shows how results produced by the proposed methodology can be used to find the optimised design that will meet the payback time expectations of the shipowners.

The choice of working fluids affects the thermal performance of ORC, as it can be seen in Figure 13, which presents the net work output against evaporating pressure for the sORC operating with two different working fluids: cyclopentane and ethanol.

At 20 bar of evaporating pressure with ethanol as the working fluid, almost 140 kW of power could be recovered, where the maximum continuous rating (MCR) of the diesel engine is 1950 kW. The ethanol-sORC provides about 20% more power than the corresponding cyclopentane-sORC.

As the ORC using ethanol exhibits a better thermal performance than the one using cyclopentane, the variation in performance due to cycle configuration is examined next. The net work output plot against the evaporating pressure is compared between two cycle configurations, namely sORC and rcORC, as in Figure 14. As it can be seen, rcORC offers an additional 16% extra net work output over sORC.

While the rcORC offers a better thermal performance compared to the sORC, it requires an additional heat exchanger that will lead to a higher capital cost. This is shown in Figure 15, according to which rcORC is more expensive than sORC by about 20%.

The tradeoff between the thermal performance and cost of different ORC designs can be assessed through the Specific Installation Cost (SIC) as shown in Figure 16, which presents the SIC for the sORC and rcORC configurations, utilising ethanol as the working fluid. For comparison, the calculated SIC is compared with the SIC proposed by Quoilin [29]. Although the estimated values of SIC for the ethanol sORC and rcORCs are lower than the reference one by 20 to 30%, the present results are considered satisfactory and promising for a preliminary stage estimation.

The total capital costs are broken down into components as shown in Figure 17. As it can be seen, the major cost component is due to expander (Exp) which can range from 35% to 45%. This could be attributed to the fact that expanders are specialised machinery that require precise fabrication. The components with the next highest cost are those of the heat exchangers, namely the evaporator (Evap), condenser (Cond), and recuperator (Recp) with a total from about 45% to 60%. The pumps, both the working fluid pump (Wfp) and cooling water pump (Cwp) contribute only a minor component of the total cost as these are mainly off-the-shelf items.

The results shown earlier were derived from thermodynamic analyses based on the waste heat from a single diesel engine at 100% load in order to assess the impact of various ORC design options on the thermoeconomic performance of the system. Next, to account for the operational profile of the ship, the discounted payback time (DPT) of the sORC and rcORC running on either cyclopentane or ethanol are shown in Figure 18, based on the waste heat profile from the generic ship speed profile with a n value of 0.25.

It can be observed that there is a minimum DPT for each ORC design. The sORC cycle configuration provides the lowest DPT of 7.5 and 8.3 years for ethanol and cyclopentane, respectively. Overall, the ethanol-sORC has the lowest DPT for a 100 kW ORC at 7.5 years, but this is still higher than the desired 5.2 years of payback preferred by most shipowners [30]. Hence, the assumed operational profile may not encourage the shipowner to invest in a new ORC to improve fuel savings.

Then, using the generic ship speed profile, the effect of changes in the operational profile on the payback time was examined. The results are shown in Figure 19, in which the payback time of an ethanol-sORC is plotted against the ORC net work output for different n values from 0.25 to 4 to account for different ship speed profiles.

If the generic operational profile increases from n = 0.25 to 4, which is more like that of a sea-going cargo ship sailing at higher speeds, most of the operating time, the DPT falls to a minimum of 4.3 years at a maximum work output of 250 to 300 kW. If the desired payback time of the shipowner is less than 5.2 years, the options meeting this will be below the red dotted line. This means that the ship needs to be loaded at a higher speed with n values greater than 1. It is noted that the actual operational profile based on AIS and the assumed generic profile with the n value of 0.25, 0.5, and 1 will not be able to meet this at all power outputs.

6. Conclusions

A method to define the operational profile of a ship by using a generic ship speed profile and fit-for-purpose diesel engine waste heat model was described. This method was applied to a thermoeconomic analysis of ORC application onboard an offshore service vessel to identify the optimum designs with the lowest payback time for the shipowners.

A thermoeconomic analysis based on the assumed ship speed profile with an n value of 0.25 was performed for the case ship. It was found that the lowest discounted payback time is achievable at 7.5 years for a 100 kW ethanol simple ORC. If the payback time expectation is less than 5.2 years, as is the likely case for many shipowners, the proposed ORC design will not be feasible. However, if the operational profile changes in a way such that the ship sails with higher speed more often, the payback time for the ORC will fall below 5.2 years for some ORC designs that can make them attractive for installation by the shipowner.

The present study has contributed to the knowledge base by proposing and testing a method of representing the operational profile of a ship that can be used to generate the waste heat profile to run a marine ORC and produce additional energy that leads to fuel savings and reductions in emissions. It was shown that with the generic ship speed profile and the fit-for-purpose diesel engine waste heat model, the waste heat profile can be modelled satisfactorily when compared to data obtained from the actual operational profile from an AIS system. Hence, the difficulty in obtaining the reliable and costly operational profile of a ship can be reduced.

Several study areas can be built upon this research. A stochastic approach can be developed to characterise the operational profile of different ship types relying on big data from an AIS system. The diesel engine waste heat model can be extended to other alternative fuels like LNG, methanol, ammonia, or even hydrogen. Lastly, the application of energy storage systems such as batteries to store excess energy recovered by the ORC could be examined.