Prediction of Overpressure Zones in Marine Sediments Using Rock-Physics and Other Approaches
Abstract
:1. Introduction
2. Overview
2.1. Geological Setting
2.2. Data
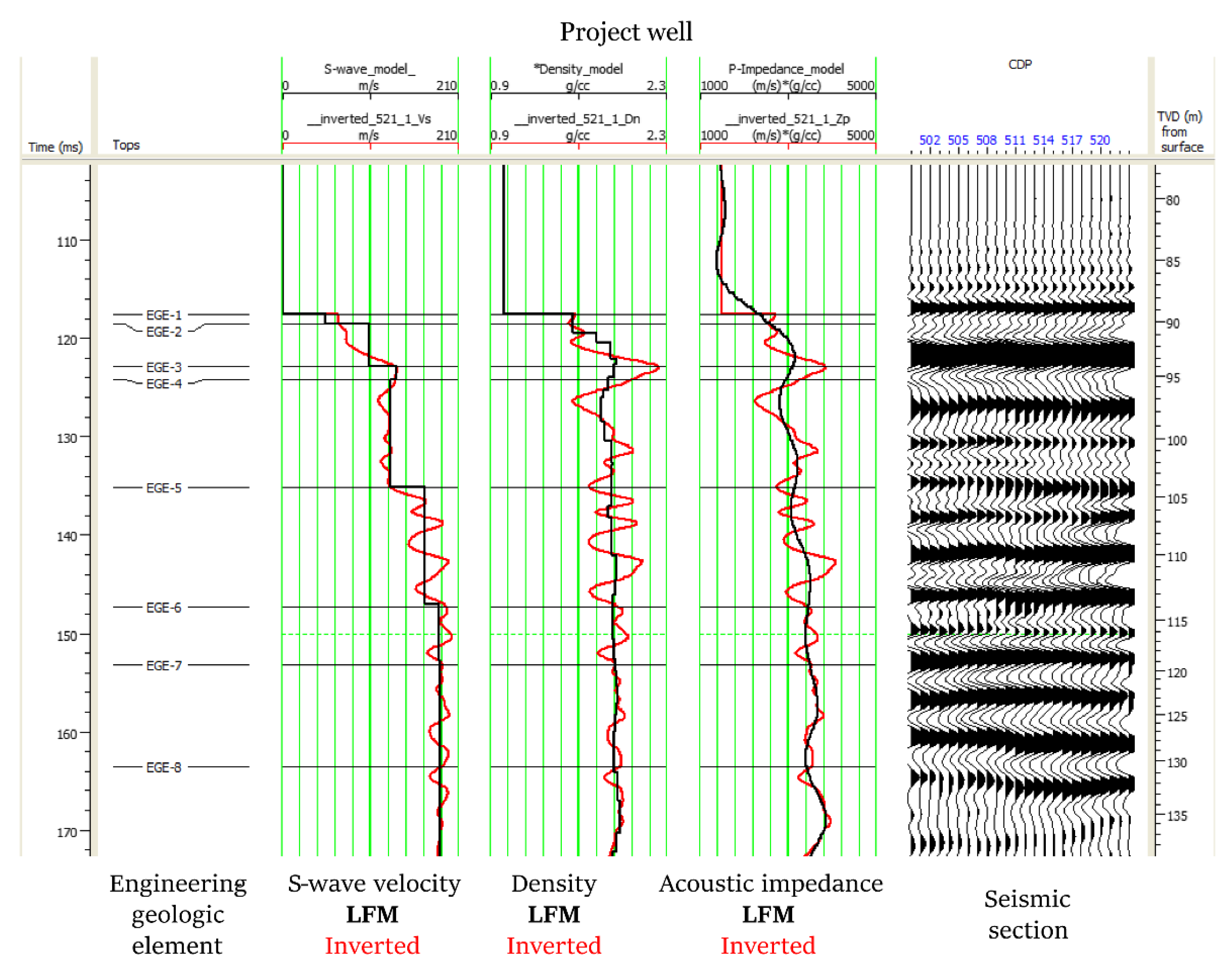
2.3. Seismic Inversion
2.4. Model of Mechanical Properties
3. Results
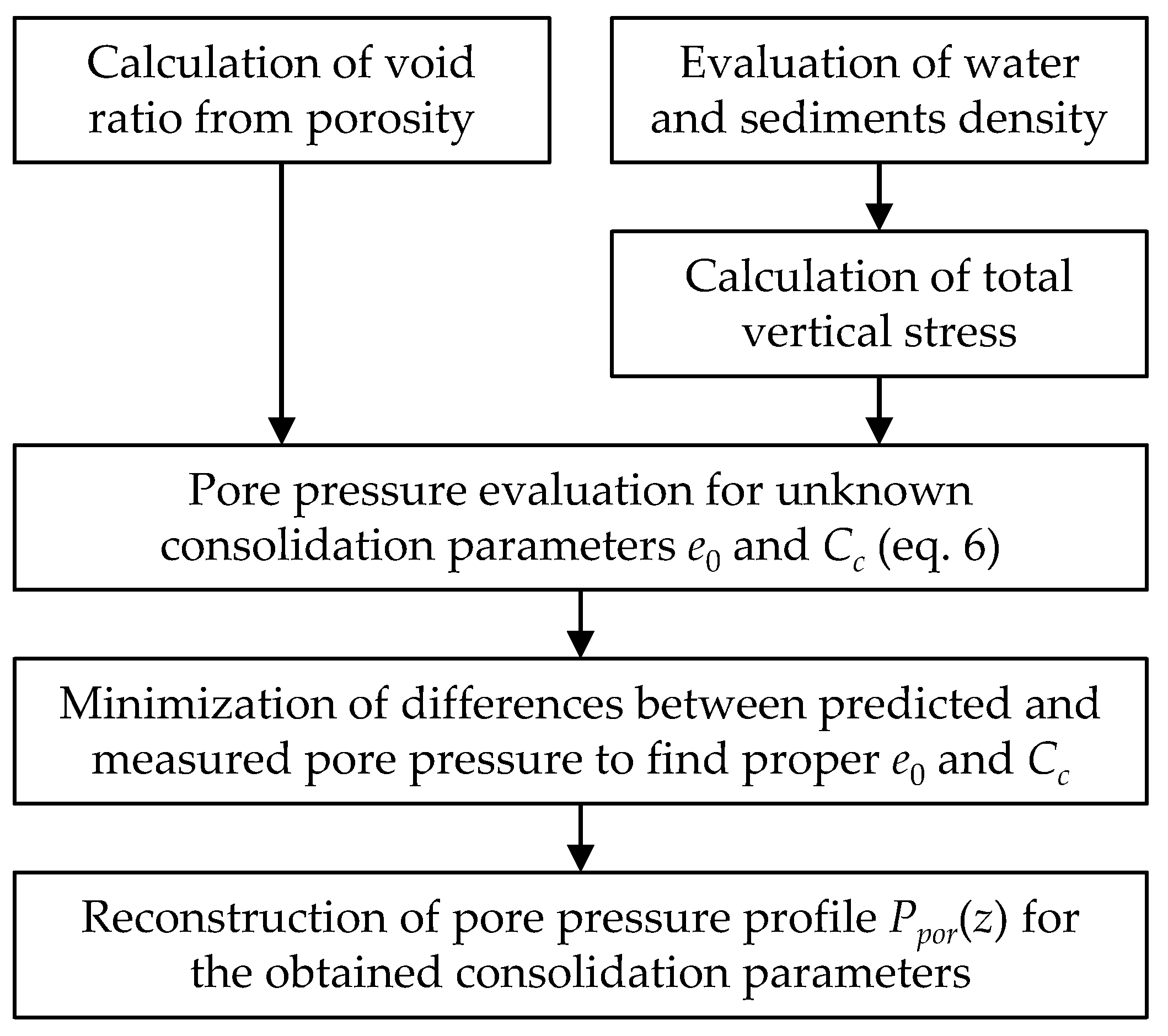
3.1. Pore Pressure Prediction from Void Ratio
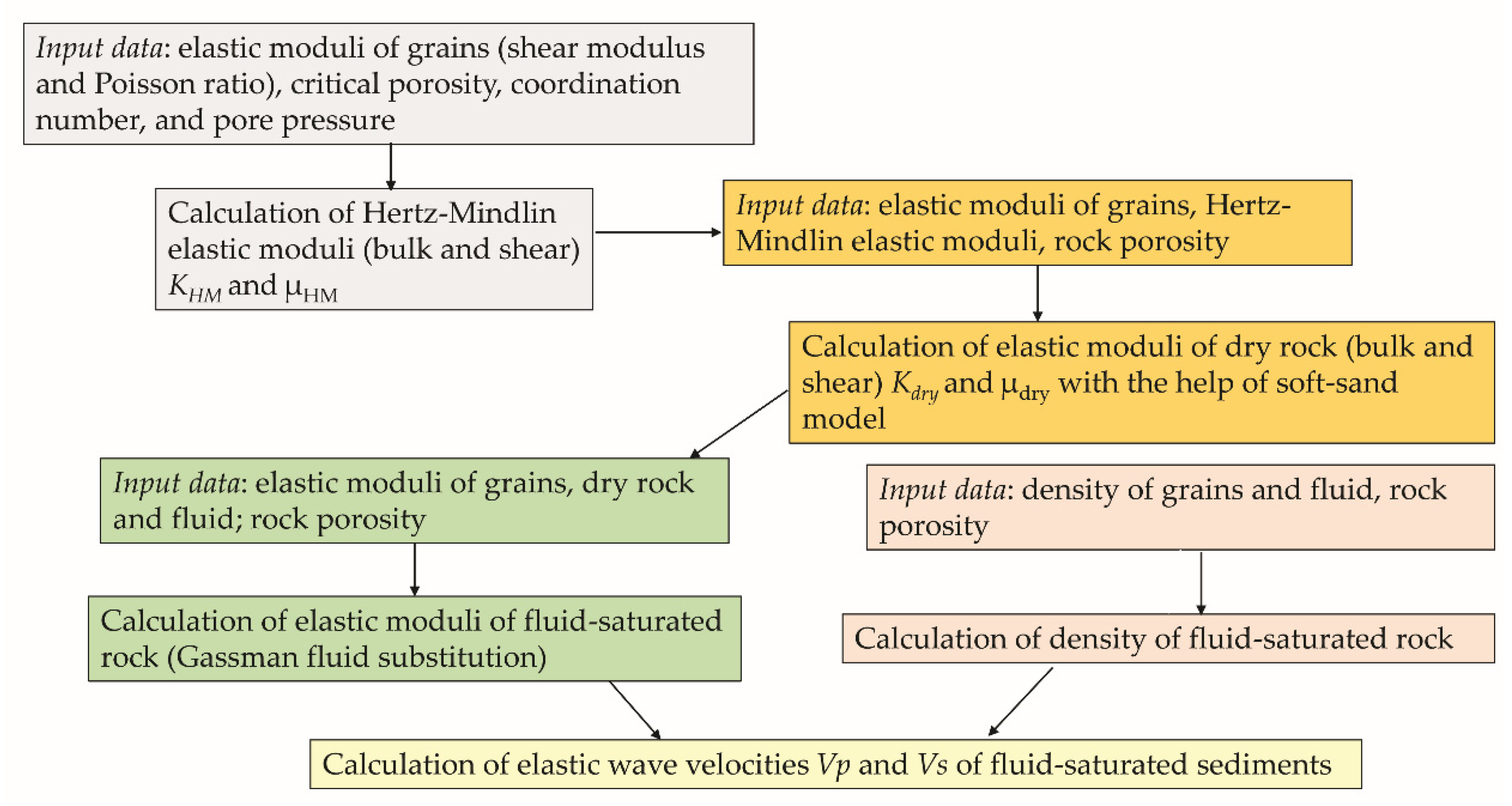
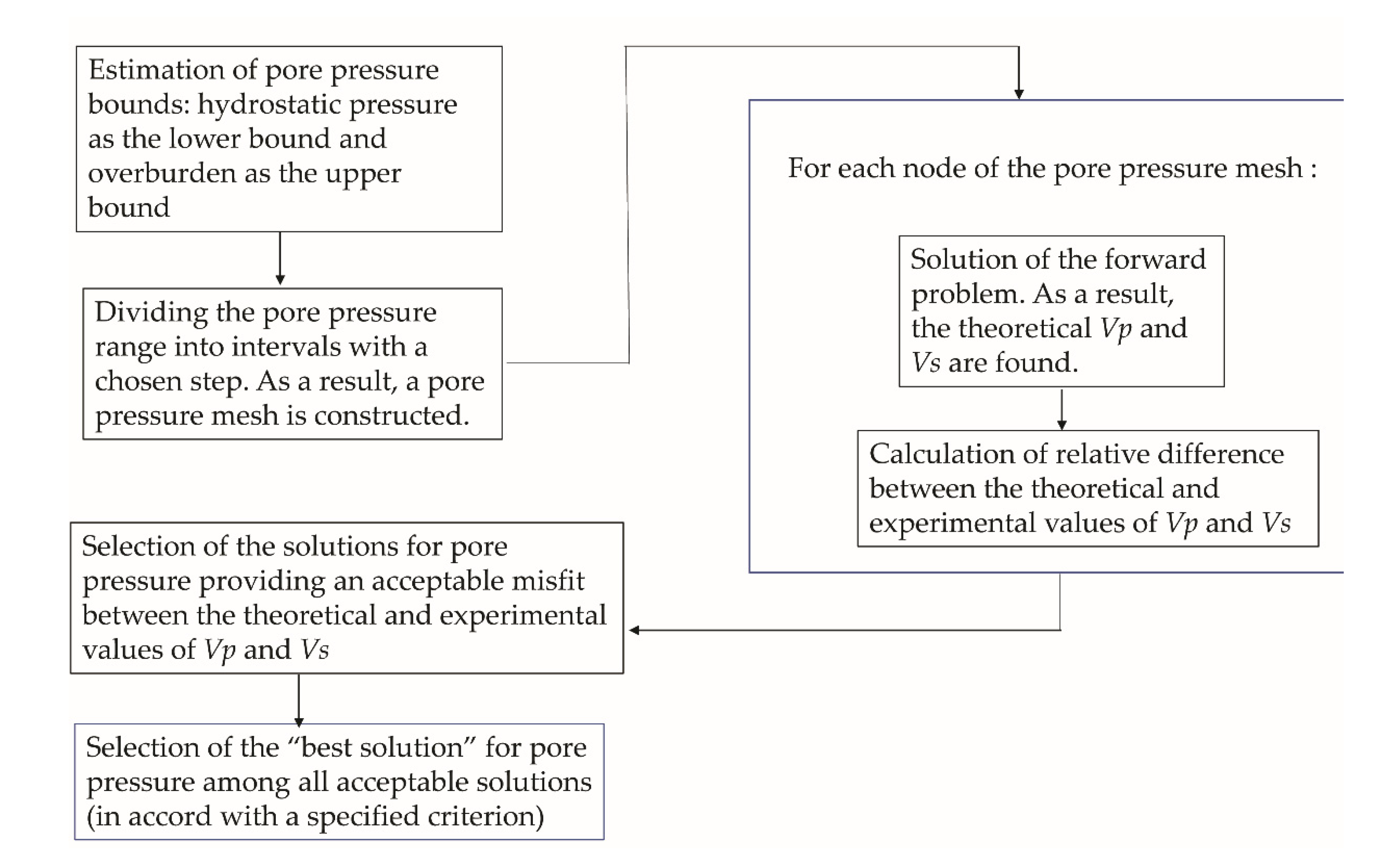
3.2. Pore Pressure Prediction from Rock-Physics Modeling
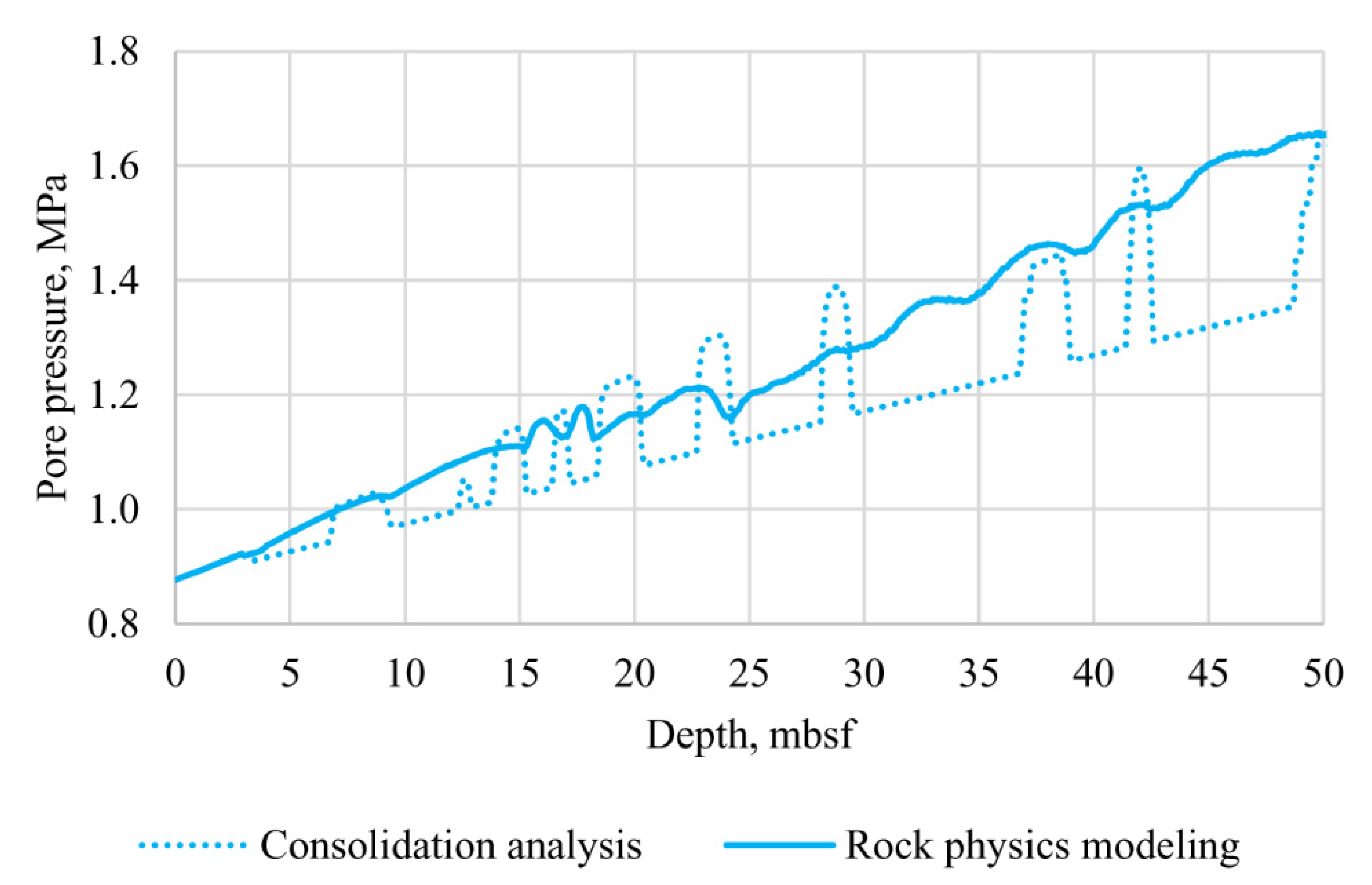
3.3. Pore pressure Prediction Comparison
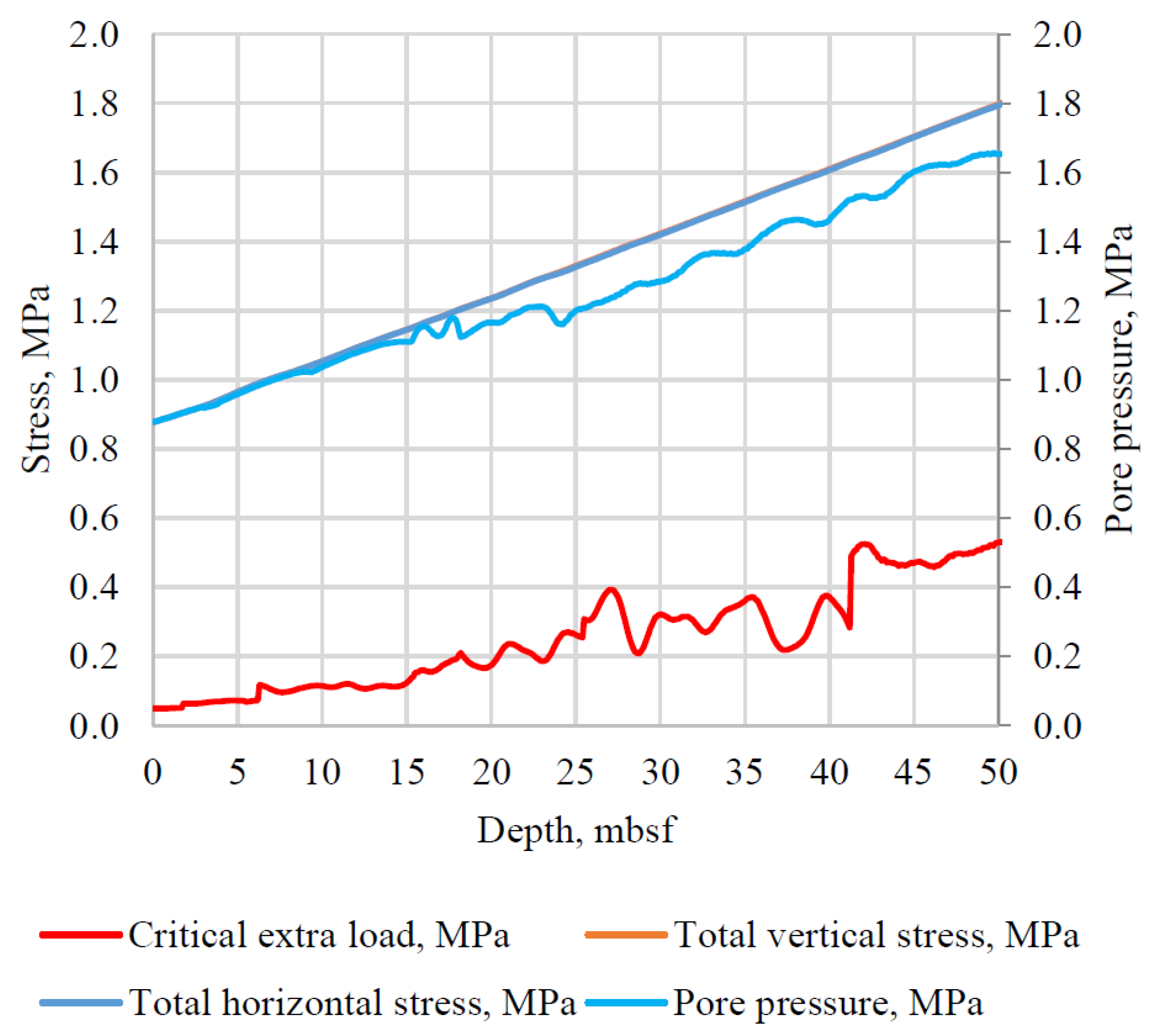
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Zhang, J. Effective stress, porosity, velocity and abnormal pore pressure prediction accounting for compaction disequilibrium and unloading. Mar. Pet. Geol. 2013, 45, 2–11. [Google Scholar] [CrossRef]
- Holand, P.; Skalle, P. Deepwater Kicksand and BOP Performance; SINTEF Report for U.S.; Minerals Management Service: Washington, DC, USA, 2001; 123p. [Google Scholar]
- Skalle, P.; Podio, A.L. Trends extracted from 1200 Gulf Coast blowouts during 1960–1996. World Oil 1998, 219, 67–72. [Google Scholar]
- Tobin, H.J.; Saffer, D.M. Elevated fluid pressure and extreme mechanical weakness of a plate boundary thrust, Nankai Trough subduction zone. Geology 2009, 37, 679–682. [Google Scholar] [CrossRef]
- Tingay, M.R.P.; Hillis, R.R.; Swarbrick, R.E.; Morley, C.K.; Damit, A.R. Origin of overpressure and pore-pressure prediction in the Baram province, Brunei. AAPG Bull. 2009, 93, 51–74. [Google Scholar] [CrossRef]
- Yin, Z.; Linga, P. Methane hydrates: A future clean energy source. Chin. J. Chem. Eng. 2019, 27, 2026–2036. [Google Scholar] [CrossRef]
- Bhatnagar, G.; Chapman, W.G.; Hirasaki, G.J.; Dickens, G.R.; Dugan, B. Effect of Overpressure on Gas Hydrate Distribution. In Proceedings of the 6th International Conference on Gas Hydrates (ICGH 2008), Vancouver, BC, Canada, 6–10 July 2008. [Google Scholar]
- Ren, J.; Liu, X.; Niu, M.; Yin, Z. Effect of sodium montmorillonite clay on the kinetics of CH4 hydrate-implication for energy recovery. Chem. Eng. J. 2022, 437, 135368. [Google Scholar] [CrossRef]
- York, P.; Prithard, D.; Dodson, J.K.; Dodson, T.; Rosenberg, S.; Gala, D.; Utama, B. Eliminating Non-productive Time Associated Drilling Trouble Zone. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 4–7 May 2009. [Google Scholar] [CrossRef]
- Holand, P.; Awan, H. Reliability of Deepwater Subsea BOP Systems and Well Kicks; ExproSoft AS Report no. 201252/02; Exprosoft: Trondheim, Norway, 2012; 164p. [Google Scholar]
- Hottmann, C.E.; Johnson, R.K. Estimation of Formation Pressures from Log-Derived Shale Properties. J. Pet. Technol. 1965, 17, 717–722. [Google Scholar] [CrossRef]
- Eaton, B.A. The Effect of Overburden Stress on Geopressures Prediction from Well Logs. J. Pet. Technol. 1972, 24, 929–934. [Google Scholar] [CrossRef]
- Eaton, B.A. The Equation for Pore Pressure Prediction from Well Logs. In Proceedings of the Fall Meeting of the Society of Petroleum Engineers of AIME, Dallas, TX, USA, 28 September–1 October 1975. [Google Scholar]
- Bowers, G.L. Pore Pressure Estimation from Velocity Data; Accounting for Overpressure Mechanisms Besides Undercompaction. SPE Drill. Compl. 1995, 10, 89–95. [Google Scholar] [CrossRef]
- Zhang, J. Pore pressure prediction from well logs: Methods, modifications, and new approaches. Earth-Sci. Rev. 2011, 108, 50–63. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, R. Pore pressure prediction using geophysical methods in carbonate reservoirs: Current status, challenges and way ahead. J. Nat. Gas Sci. Eng. 2015, 27, 986–993. [Google Scholar] [CrossRef]
- Mondol, N.H.; Bjorlykke, K.; Jahren, J.; Hoeg, K. Experimental mechanical compaction of clay mineral aggregates–changes in physical properties of mudstones during burial. Mar. Pet. Geol. 2007, 24, 289–311. [Google Scholar] [CrossRef]
- Schneider, J.; Flemings, P.B.; Dugan, B.; Long, H.; Germaine, J.T. Overpressure and consolidation near the seafloor of Brazos-Trinity Basin IV, northwest deepwater Gulf of Mexico. J. Geophys. Res. 2009, 114, B05102. [Google Scholar] [CrossRef]
- Long, H.; Flemings, P.B.; Germaine, J.T. Interpreting in situ pressure and hydraulic properties with borehole penetrometers in ocean drilling: DVTPP and Piezoprobe deployments at southern Hydrate Ridge, offshore Oregon. J. Geophys. Res. 2007, 112, B04101. [Google Scholar] [CrossRef]
- Sultan, N.; Lafuerza, S. In situ equilibrium pore-water pressures derived from partial piezoprobe dissipation tests in marine sediments. Can. Geotech. J. 2013, 50, 1294–1305. [Google Scholar] [CrossRef]
- Radwan, A.E.; Abudeif, A.M.; Attia, M.M.; Mohammed, M.A. Pore and fracture pressure modeling using direct and indirect methods in Badri Field, Gulf of Suez, Egypt. J. Afr. Earth Sci. 2019, 156, 133–143. [Google Scholar] [CrossRef]
- Rostami, S.A.; Kinik, K.; Gumus, F.; Kirchhoff, M. Dynamic Calibration of the Empirical Pore Pressure Estimation Methods Using MPD Data. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 4–7 May 2015. [Google Scholar] [CrossRef]
- Ganguli, S.S.; Sen, S. Investigation of present-day in-situ stresses and pore pressure in the south Cambay Basin, western India: Implications for drilling, reservoir development and fault reactivation. Mar. Pet. Geol. 2020, 118, 104422. [Google Scholar] [CrossRef]
- Long, H.; Flemings, P.B.; Germaine, J.T.; Saffer, D.M. Consolidation and overpressure near the seafloor in the Ursa Basin, Deepwater Gulf of Mexico. Earth Planet. Sci. Let. 2011, 305, 11–20. [Google Scholar] [CrossRef]
- Han, T.; Pervukhina, M.; Clennell, M.B.; Dewhurst, D.N. Model-based pore-pressure prediction in shales: An example from the Gulfof Mexico, North America. Geophysics 2017, 82, M37–M42. [Google Scholar] [CrossRef]
- Ziegler, F.E.; Jones, J.F. Predrill pore-pressure prediction and pore pressure and fluid loss monitoring during drilling: A case study for a deepwater subsalt Gulf of Mexico well and discussion on fracture gradient, fluid losses, and wellbore breathing. Interpretation 2014, 2, SB45–SB55. [Google Scholar] [CrossRef]
- Zhang, J.; Yin, S. Real-Time Pore Pressure Detection: Indicators and Improved Methods. Geofluids 2017, 2017, 3179617. [Google Scholar] [CrossRef]
- Oloruntobi, O.; Adedigba, S.; Khan, F.; Chunduru, R.; Butt, S. Overpressure prediction using the hydro-rotary specific energy concept. J. Nat. Gas Sci. Eng. 2018, 55, 243–253. [Google Scholar] [CrossRef]
- Tanikawa, W.; Hirose, T.; Hamada, Y.; Gupta, L.P.; Ahagon, N.; Masaki, Y.; Abe, N.; Wu, H.Y.; Sugihara, T.; Nomura, S.; et al. Porosity, permeability, and grain size of sediment cores from gas-hydrate-bearing sites and their implication for overpressure in shallow argillaceous formations: Results from the national gas hydrate program expedition 02, Krishna-Godavari Basin, India. Mar. Pet. Geol. 2019, 108, 332–347. [Google Scholar] [CrossRef]
- Mindlin, R.D. Compliance of elastic bodies in contact. J. Appl. Mech. 1949, 16, 259–268. [Google Scholar] [CrossRef]
- Brandt, H. A study of the speed of sound in porous granular media. J. Appl. Mech. 1955, 22, 479–486. [Google Scholar] [CrossRef]
- Digby, P.J. The effective elastic moduli of porous granular rocks. J. Appl. Mech. 1981, 48, 803–808. [Google Scholar] [CrossRef]
- Walton, K. The effective elastic moduli of a random packing of spheres. J. Mech. Phys. Sol. 1987, 35, 213–226. [Google Scholar] [CrossRef]
- Jenkins, J.; Johnson, D.; La Ragione, L.; Makse, H. Fluctuations and the effective moduli of an isotropic, random aggregate of identical, frictionless spheres. J. Mech. Phys. Sol. 2005, 53, 197–225. [Google Scholar] [CrossRef]
- Dvorkin, J.; Prasad, M.; Sakai, A.; Lavoie, D. Elasticity of marine sediments. Geophys. Res. Lett. 1999, 26, 1781–1784. [Google Scholar] [CrossRef]
- Mavko, G.; Mukerdji, T.; Dvorkin, J. Rock Physics Handbook, 3rd ed.; Cambridge University Press: Cambridge, UK, 2020; pp. 220–308. [Google Scholar]
- Hashin, Z.; Shtrikman, S. A variational approach to the elastic behavior of multiphase materials. J. Mech. Phys. Sol. 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Polukhtovich, V.M.; Popadok, I.V.; Samarski, A.D.; Khnykin, V.I. Features of the geological structure and prospects for oil and gas potential in the southwestern part of the Indolo-Kuban trough. Geol. Oil Gas 1981, 1, 43–47. [Google Scholar]
- Gorshkov, A.S.; Meisner, L.B.; Soloviev, V.V.; Tugolesov, D.A.; Khakhalev, E.M. Album of Structural Maps and Thickness Maps of the Cenozoic Deposits of the Black Sea Depression, m 1:1,500,000; Tugolesov, D. A.M., GUGK pri CM USSR: Moscow, Russia, 1989. [Google Scholar]
- Bogaets, A.T.; Bondarchuk, G.K.; Les’kiv, I.V.; Novociletskiy, R.M.; Pavlyuk, M.I.; Paliy, A.M.; Panchenko, D.E.; Samarski, A.D.; Khnykin, V.I.; Chir, N.M.; et al. Geology of the Shelf of the Ukrainian SSR. Oil and Gas Potential; Naukova Dumka: Kyiv, Ukraine, 1986; 152p. [Google Scholar]
- Terekhov, A.A.; Shimkus, K.M. Young sediments and thrust structures in the Prikrymskaya and the Caucasian zones of the Black Sea depression. Geotectonics 1989, 1, 72–79. [Google Scholar]
- Bagriy, I.D.; Voitsitsky, Z.I.; Maslun, N.V.; Naumenko, U.Z.; Aksem, S.D.; Grieg, M.Y. Integrated geological-structural-thermo-atmo-geochemical studies—A tool for forecasting and searching for hydrocarbons and methane hydrates on the continental slope of the Black Sea. In Geology and Mineral Resources of the World Ocean; National Academy of Sciences of Ukraine: Kyiv, Ukraine, 2014; Volume 4, pp. 24–47. [Google Scholar]
- Gozhik, P.F.; Maslun, N.V.; Plotnikova, L.F.; Ivanik, M.M.; Yakushin, L.M.; Ishchenko, I.I. Stratigraphy of the Meso-Cenozoic Clades of the Peninsular-Western Shelf of the Black Sea; Institute of Geological Sciences of the National Academy of Sciences of Ukraine: Kyiv, Ukraine, 2006; 171p. [Google Scholar]
- Maslun, N.V.; Ivanik, M.M.; Tsikhotska, N.N.; Klyushina, G.V. Detailed Stratification of Maikop Clade in the Peninsula-Zahodny Shelf of the Black Sea; Biostratigraphic Criteria for the Analysis and Correlations in the Clade of the Phanerozoic of Ukraine; Institute of Geological Sciences of the National Academy of Sciences of Ukraine: Kyiv, Ukraine, 2005; pp. 153–159. [Google Scholar]
- Tsytovich, N.A. Soil Mechanics; Gosstroiizdat: Moscow, Russia, 1963; pp. 73–76. (In Russian) [Google Scholar]
- Vardy, M.E. Deriving shallow-water sediment properties using post-stack acoustic impedance inversion. Near Surf. Geophys. 2014, 13, 143–154. [Google Scholar] [CrossRef]
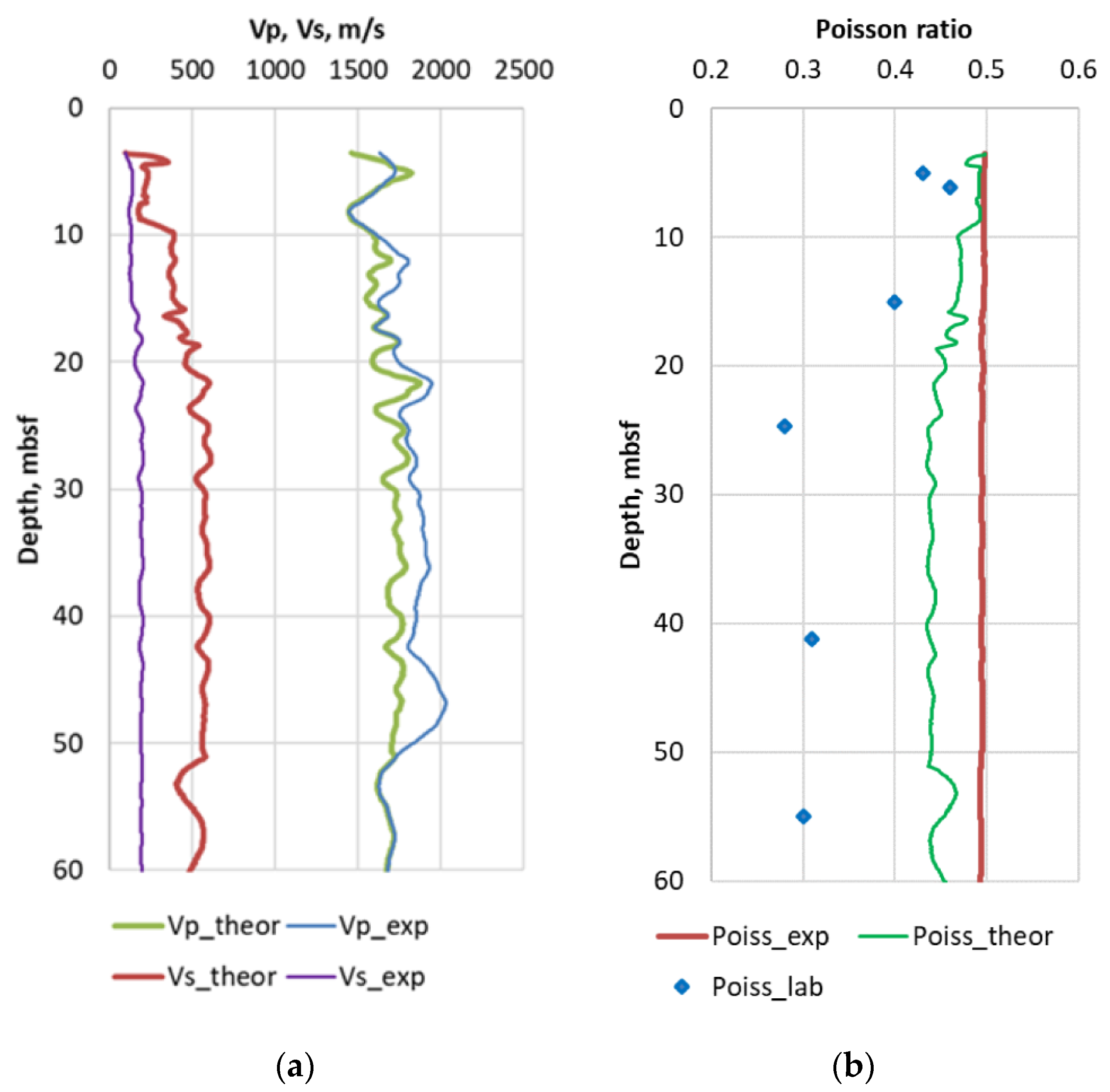
- Pirogova, A.S.; Tikhotskii, S.A.; Tokarev, M.Y.; Suchkova, A.V. Estimation of Elastic Stress-Related Properties of Bottom Sediments via the Inversion of Very- and Ultra-High-Resolution Seismic Data. Izv. Atmos. Ocean. Phys. 2019, 55, 1755–1765. [Google Scholar] [CrossRef]
- Zoback, M.D. Reservoir Geomechanics, 1st ed.; Cambridge University Press: Cambridge, UK, 2007; 490p. [Google Scholar]
- Dubinya, N.V.; Vershinin, A.V.; Pirogova, A.S.; Tikhotsky, S.A. Usage of Imitational Geological-Petrophysical Models to Reduce Drilling Risks for Offshore Reservoirs Exploration. In Proceedings of the SPE Russian Petroleum Technology Conference 2020, Moscow, Russia, 26–29 October 2020. [Google Scholar] [CrossRef]
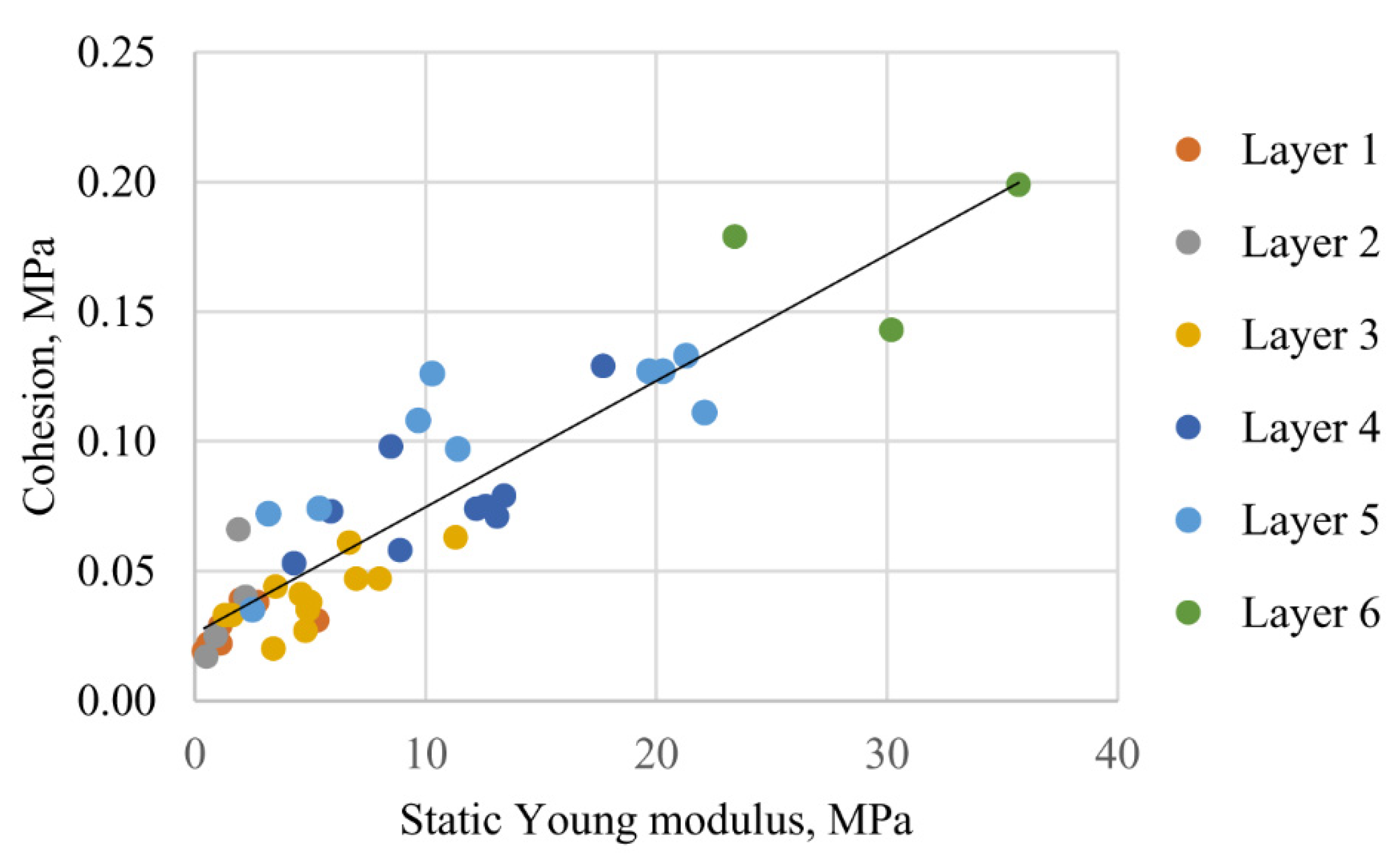
- Becker, D.E.; Crooks, J.H.A.; Been, K.; Jefferies, M.G. Work as a criterion for determining in situ and yield stresses in clays. Can. Geotech. J. 1987, 24, 549–564. [Google Scholar] [CrossRef]
- Saffer, D.M.; Silver, E.A.; Fisher, A.T.; Tobin, H.; Moran, K. Inferred pore pressures at the Costa Rica subduction zone: Implications for dewatering processes. Earth Planet. Sci. Lett. 2000, 177, 193–207. [Google Scholar] [CrossRef]
- Dugan, B.; Germaine, J. Near-seafloor overpressure in the deep-water Mississippi Canyon, northern Gulf of Mexico. Geophys. Res. Lett. 2008, 35, L02304. [Google Scholar] [CrossRef]
- Jamiolkowski, M. New Developments in Field and Laboratory Testing of Soils. In Proceedings of the 11th International Conference on Soil Mechanics and Foundation Engineering, San Francisco, CA, USA, 12–16 August 1985. [Google Scholar]
- Gassmann, F. Über die Elastizität Poröser Medien; Vierteljahrsschrift der Naturforschenden Gesellschaft in Zurich: Zurich, Switzerland, 1951; Volume 96, pp. 1–23. [Google Scholar]
- Bayuk, I.; Ammerman, M.; Chesnokov, E. Elastic moduli of anisotropic clay. Geophysics 2007, 72, D107–D117. [Google Scholar] [CrossRef]
- Katahara, K.W. Clay minerals elastic properties. SEG Tech. Program Exp. Abstr. 1996, 1691–1694. [Google Scholar] [CrossRef]
- Vasilev, I.; Dubinya, N.; Tikhotskiy, S.; Nachev, V.; Alekseev, D. Numerical model of jack-up rig’s mechanical behavior under seismic loading. Comput. Res. Model. 2022, 14. accepted. [Google Scholar]

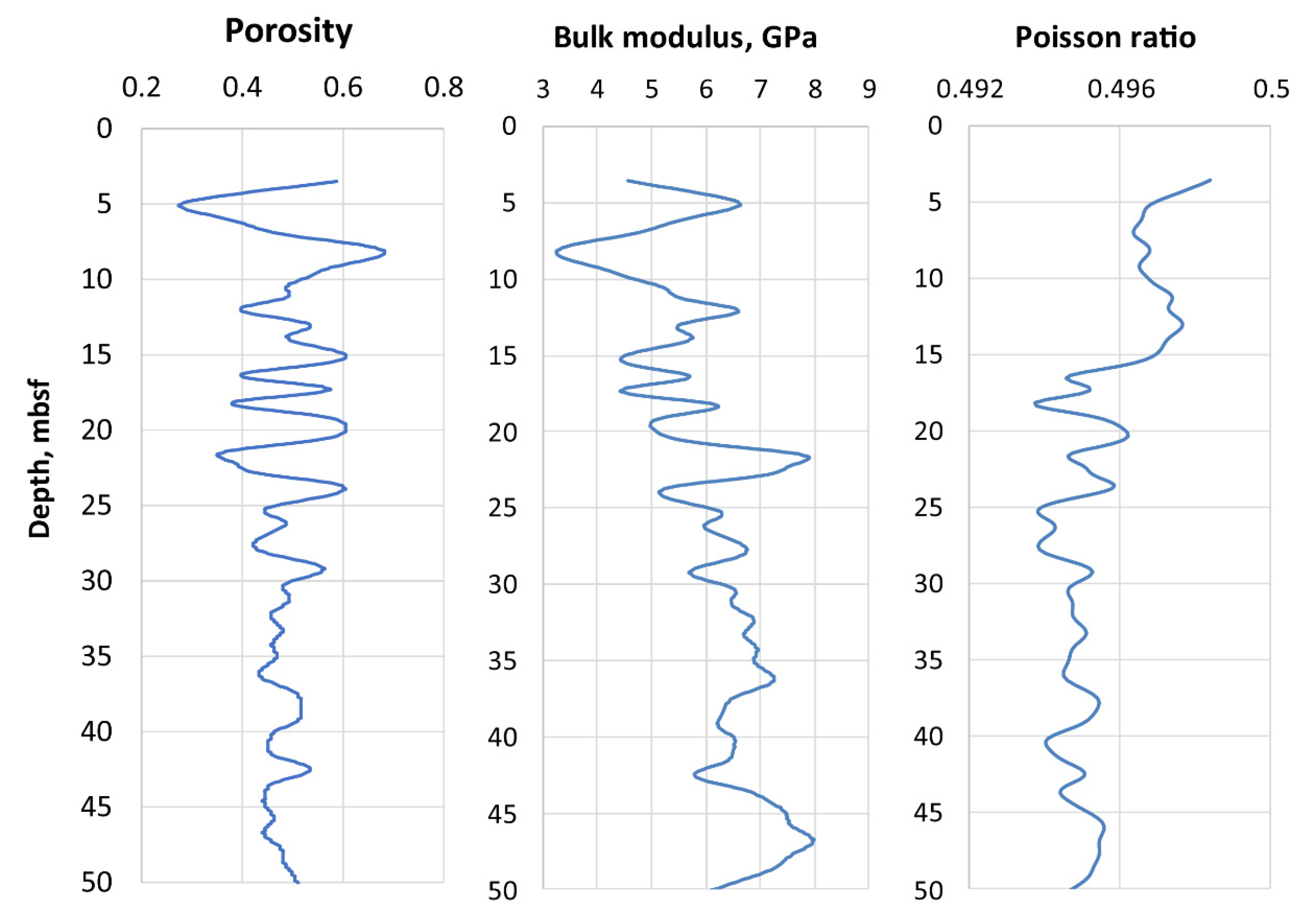
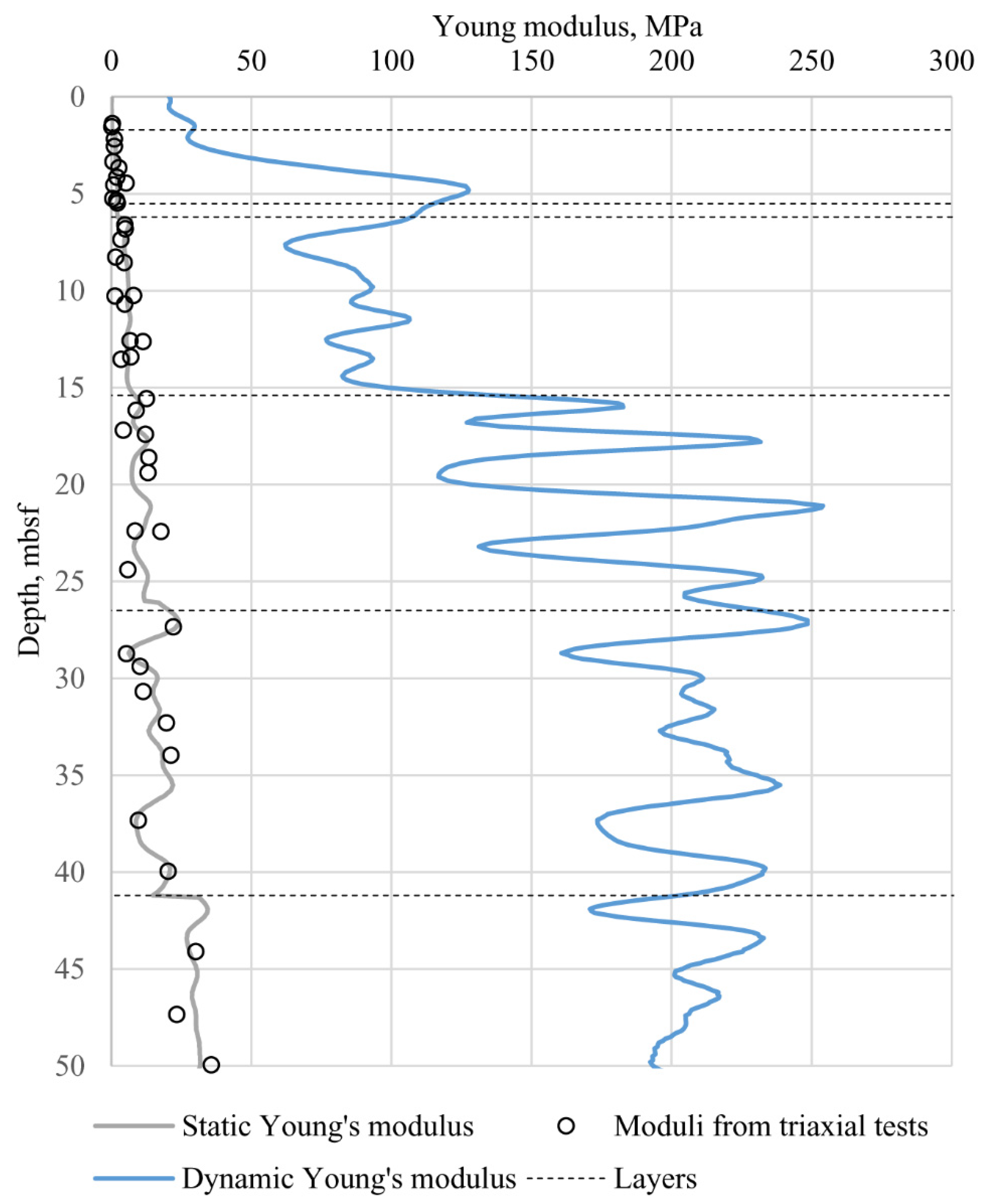

| Engineering Geologic Element (EGE) | Depth (from the Seafloor), m | Thick-Ness, m | Description | Poisson’s Ratio | Den-sity, g/cc | Young’s Modulus, MPa |
|---|---|---|---|---|---|---|
| EGE 1 | 0.15–1.7 | 0.15–1.80 | Silt | - | 1.54 | 1 |
| EGE 2 | 4.65–5.50 | 3.0–3.90 | Fluid-saturated plastic clay with an admixture of organic matter | 0.43 | 1.87 | 3 |
| EGE 3 | 5.90–6.20 | 0.40–1.55 | Fluid-saturated plastic clay loam with an admixture of organic matter | 0.46 | 1.86 | 6 |
| EGE 4 | 14.75–15.40 | 8.80–9.40 | Calcareous fluid-saturated plastic clay with an admixture of organic matter | 0.40 | 1.81 | 4 |
| EGE 5 | 24.50–24.90 | 9.40–10.15 | Calcareous high-plastic clay with an admixture of organic matter | 0.28 | 1.85 | 7 |
| EGE 6 | 41.25 | 16.55 | Calcareous high-plastic clay with an admixture of organic matter | 0.31 | 1.90 | 9 |
| EGE 7 | >50.5 | >9.25 | Calcareous high-plastic clay with an admixture of organic matter | 0.30 | 1.91 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubinya, N.; Bayuk, I.; Hortov, A.; Myatchin, K.; Pirogova, A.; Shchuplov, P. Prediction of Overpressure Zones in Marine Sediments Using Rock-Physics and Other Approaches. J. Mar. Sci. Eng. 2022, 10, 1127. https://doi.org/10.3390/jmse10081127
Dubinya N, Bayuk I, Hortov A, Myatchin K, Pirogova A, Shchuplov P. Prediction of Overpressure Zones in Marine Sediments Using Rock-Physics and Other Approaches. Journal of Marine Science and Engineering. 2022; 10(8):1127. https://doi.org/10.3390/jmse10081127
Chicago/Turabian StyleDubinya, Nikita, Irina Bayuk, Alexei Hortov, Konstantin Myatchin, Anastasia Pirogova, and Pavel Shchuplov. 2022. "Prediction of Overpressure Zones in Marine Sediments Using Rock-Physics and Other Approaches" Journal of Marine Science and Engineering 10, no. 8: 1127. https://doi.org/10.3390/jmse10081127
APA StyleDubinya, N., Bayuk, I., Hortov, A., Myatchin, K., Pirogova, A., & Shchuplov, P. (2022). Prediction of Overpressure Zones in Marine Sediments Using Rock-Physics and Other Approaches. Journal of Marine Science and Engineering, 10(8), 1127. https://doi.org/10.3390/jmse10081127






