Prediction Method for Ocean Wave Height Based on Stacking Ensemble Learning Model
Abstract
:1. Introduction
2. Materials and Method Analysis
2.1. Experimental Data Source
2.2. XGBoost Algorithm
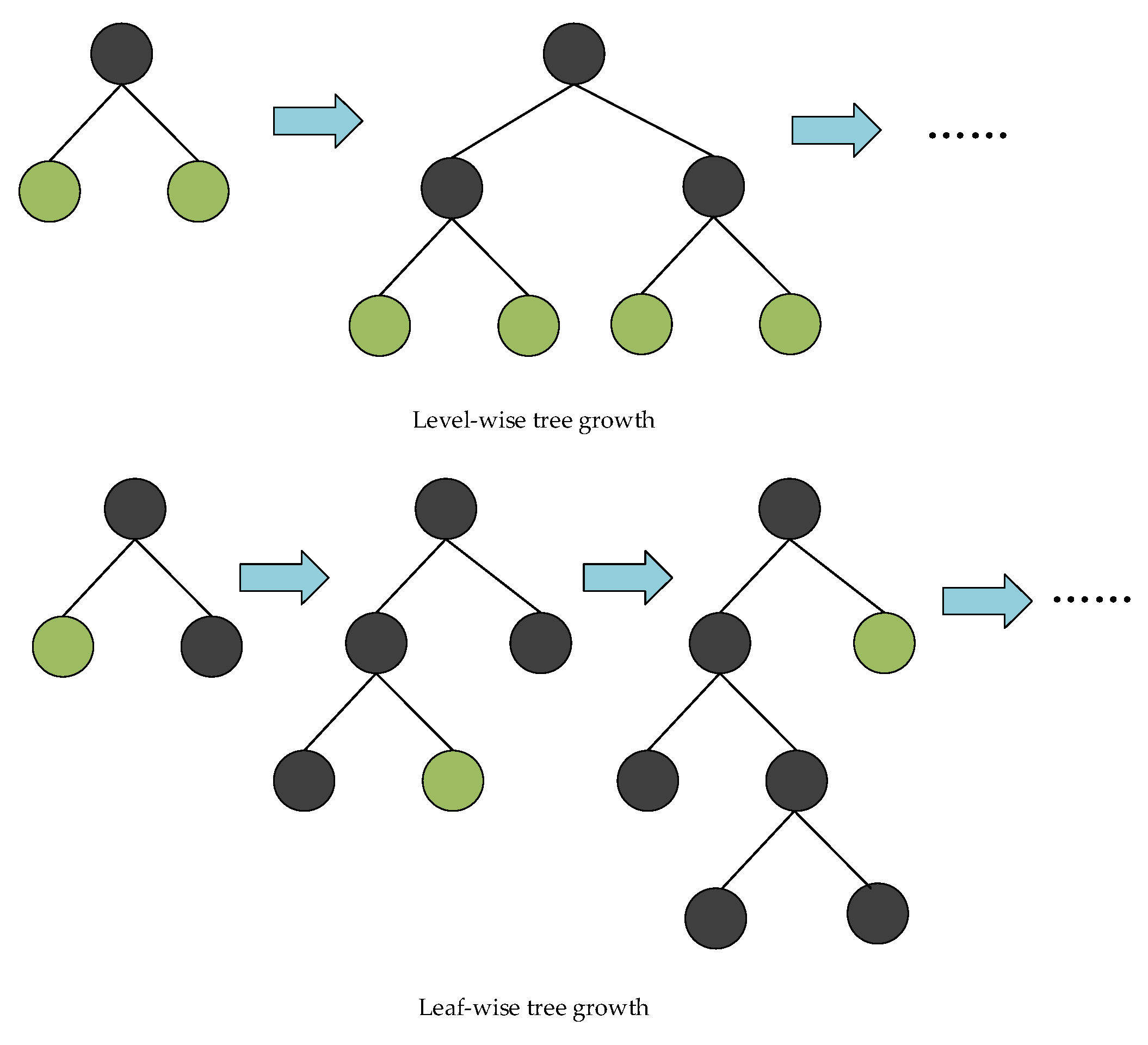
2.3. LightGBM Algorithm
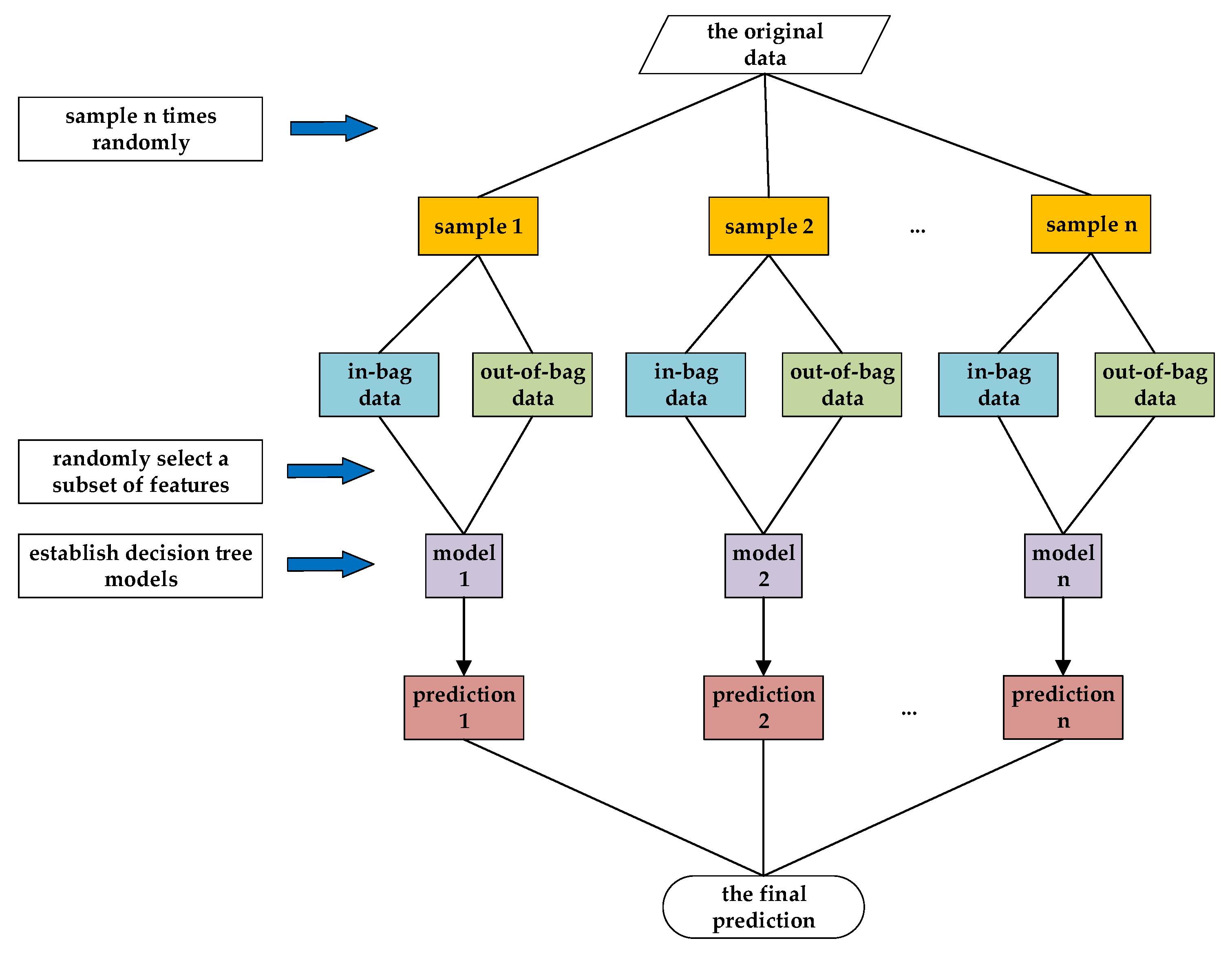
2.4. Random Forest Algorithm
- Self-service sampling;
- Determine the optimal number of features of the decision tree;
- Establish a random forest algorithm model.
2.5. AdaBoost Algorithm
- Initialize the weight distribution of the training data;
- Train the learners and calculate the error parameters;
- Update sample weights;
- Obtain the final algorithm model.
3. Experimental Steps and Model Building
3.1. Data Preprocessing
3.2. Data Analysis
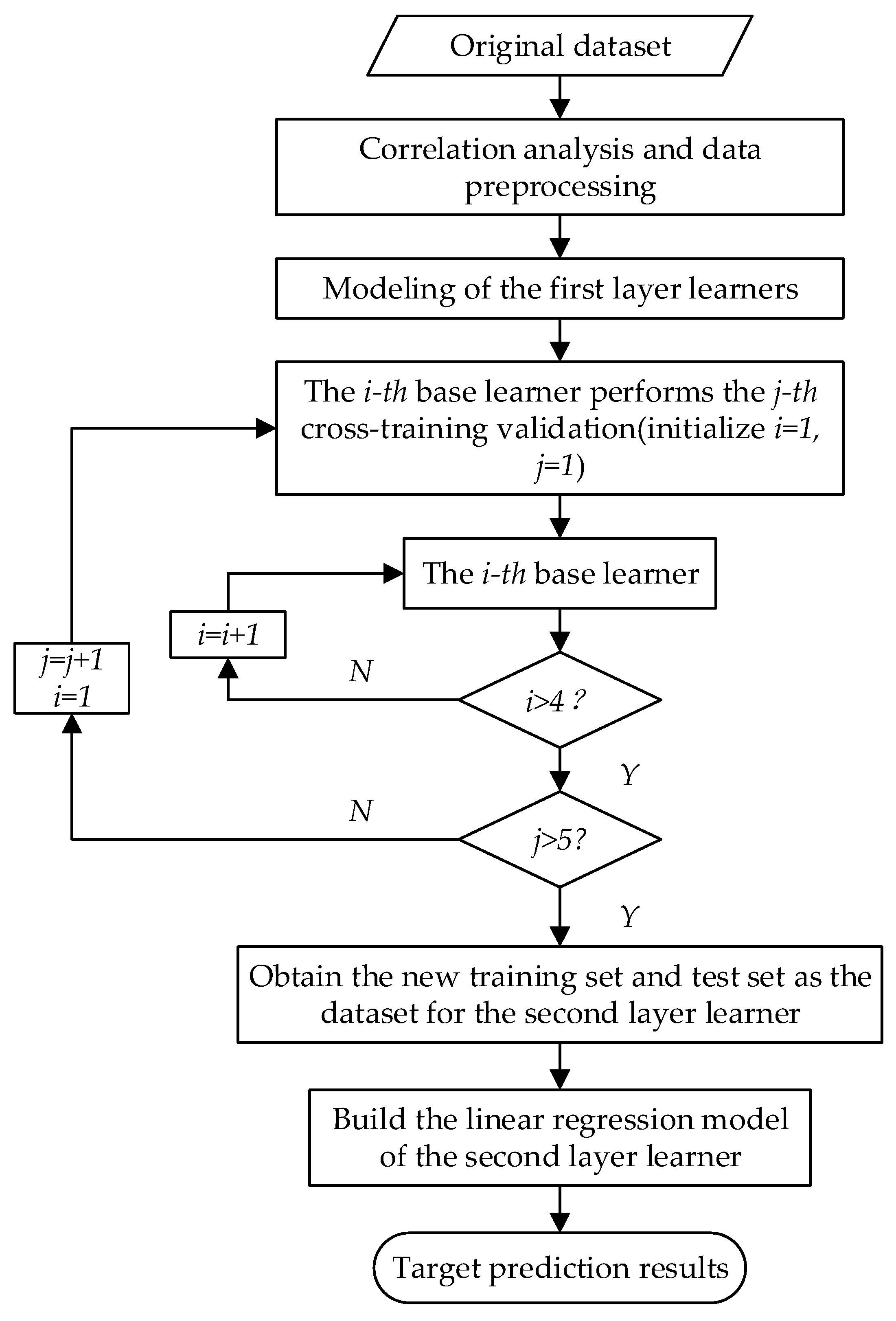
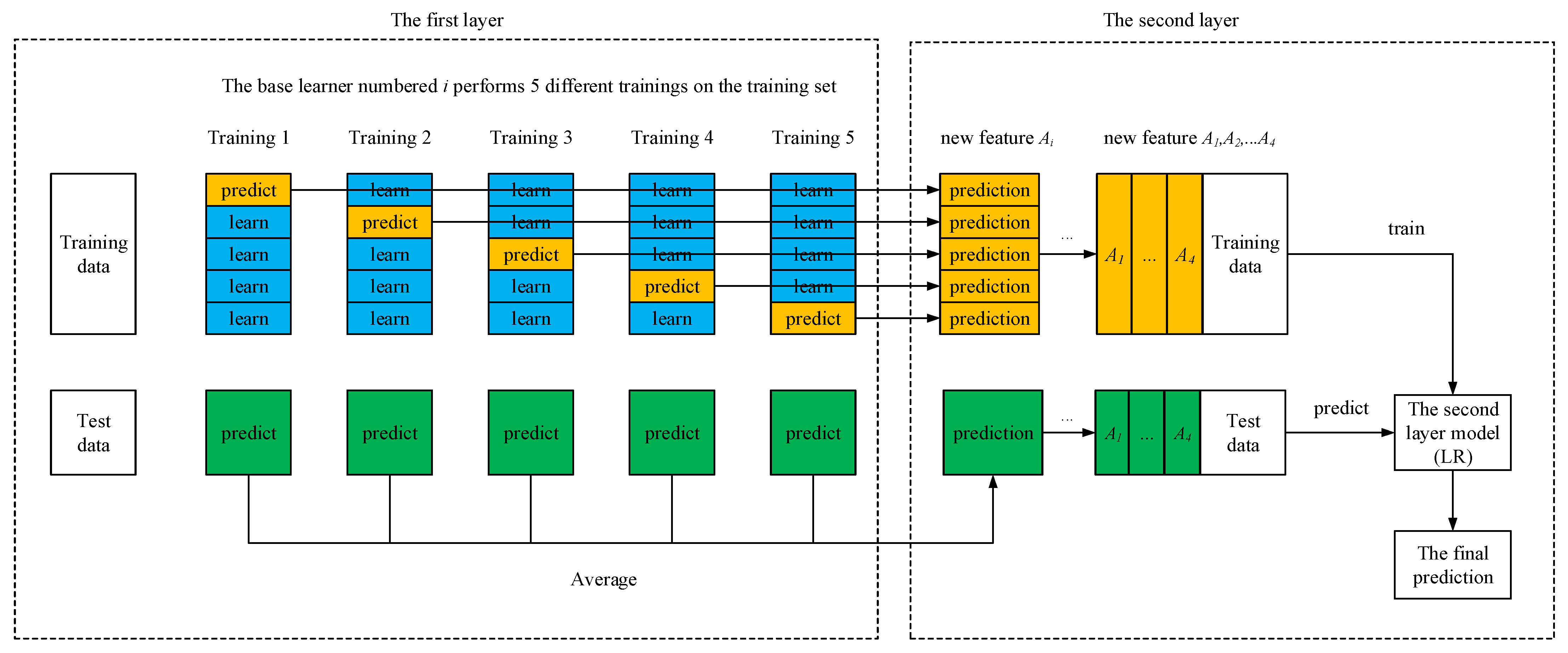
3.3. Establishment of Stacking Model
| Algorithm 1: The stacking algorithm pseudocode. |
| Stacking model algorithm |
| initialization: Set the first layer learner: the second-layer learner: |
| data input |
| for |
| end |
| for |
| for |
| end |
| end |
| model output |
- Choice of learners;
- Division of the first-layer dataset;
- Training and prediction of the first-layer base model;
- Dataset of the second-layer learners;
- Training and prediction of the second-layer learners.
4. Results and Discussion
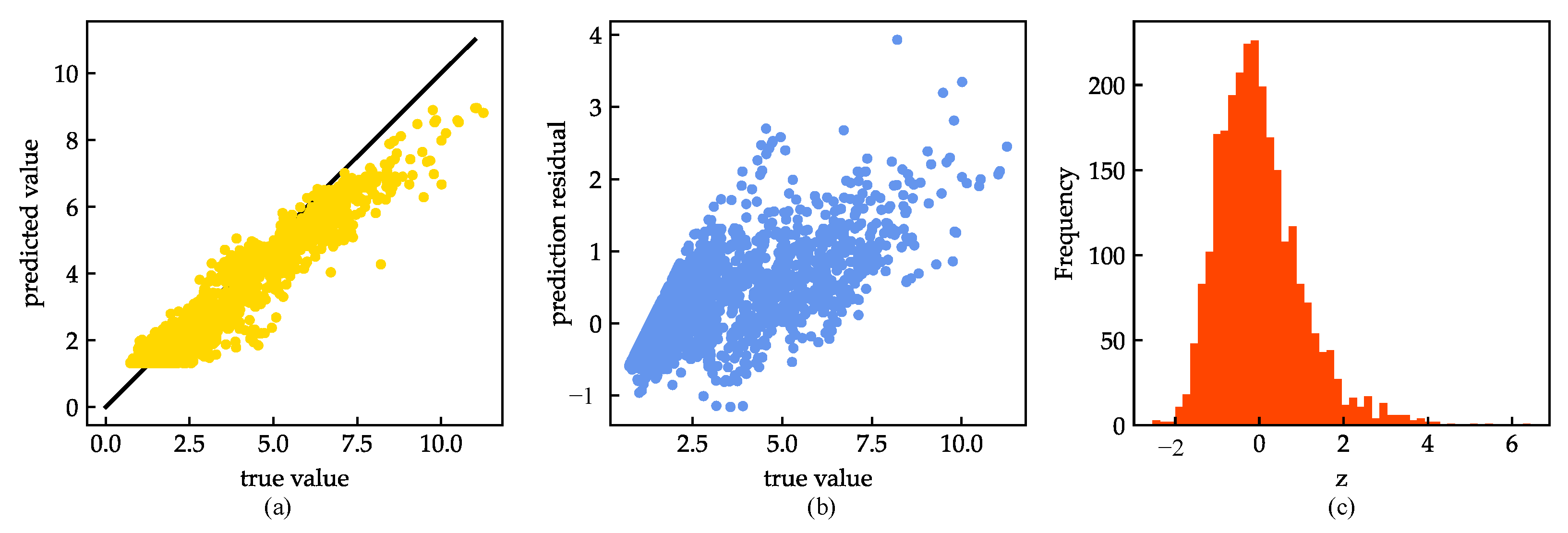
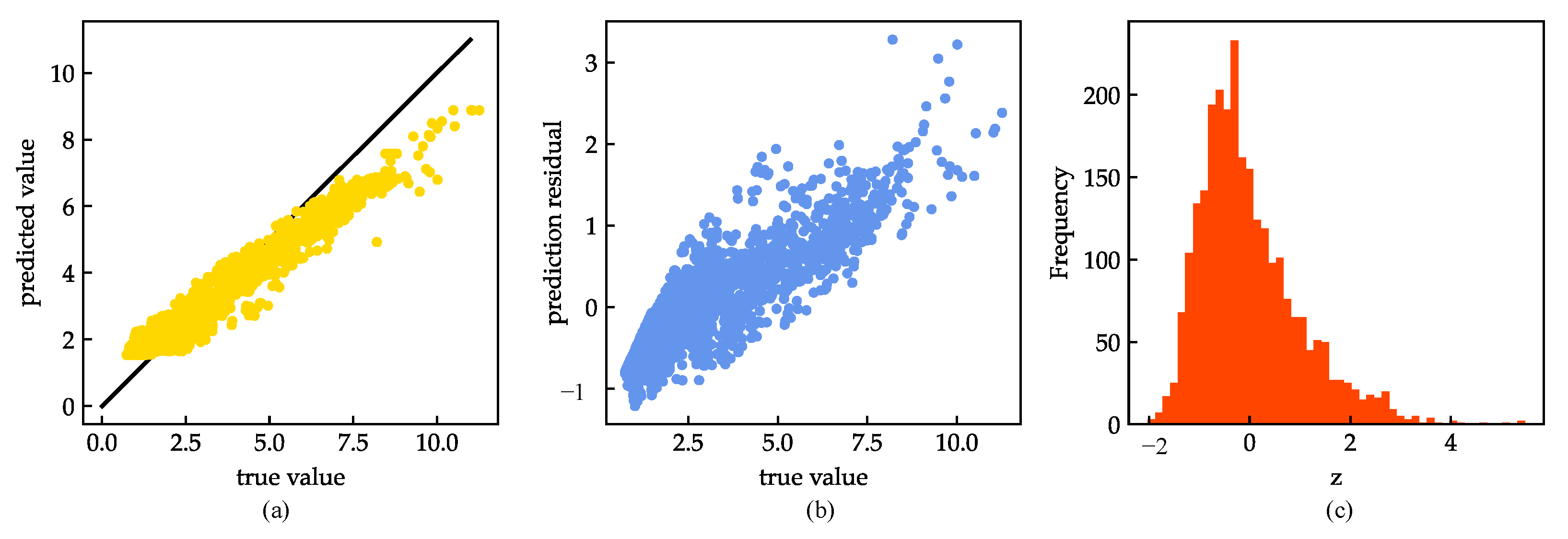
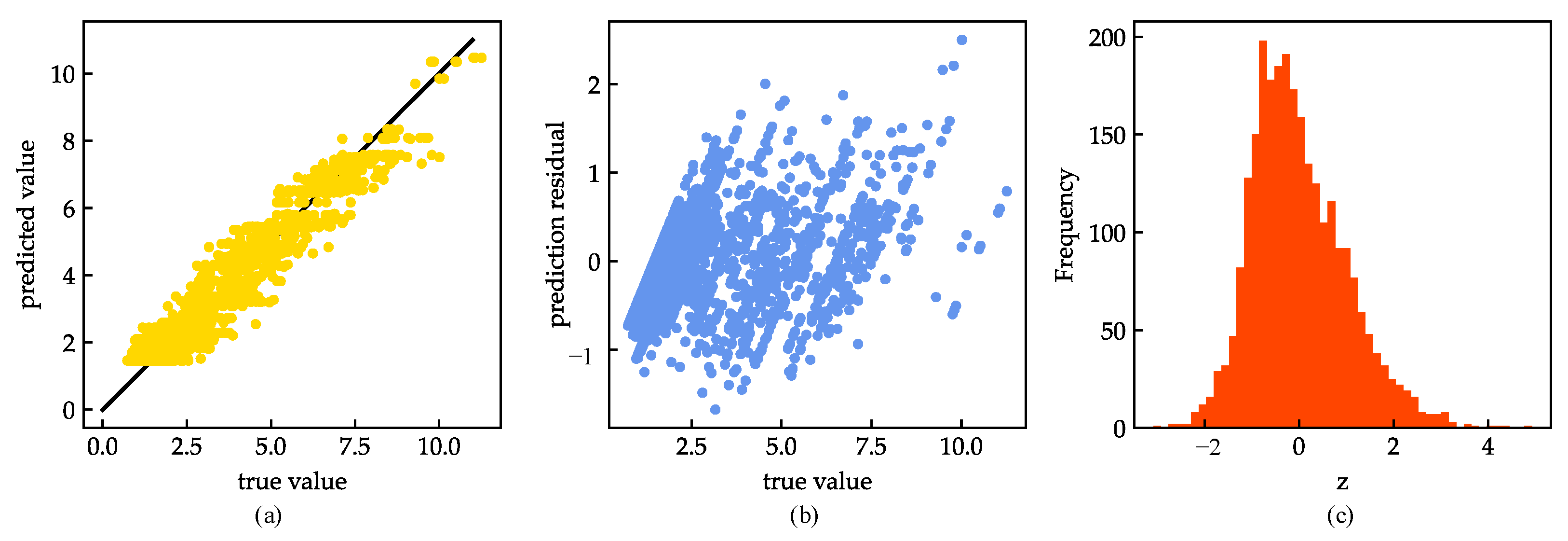
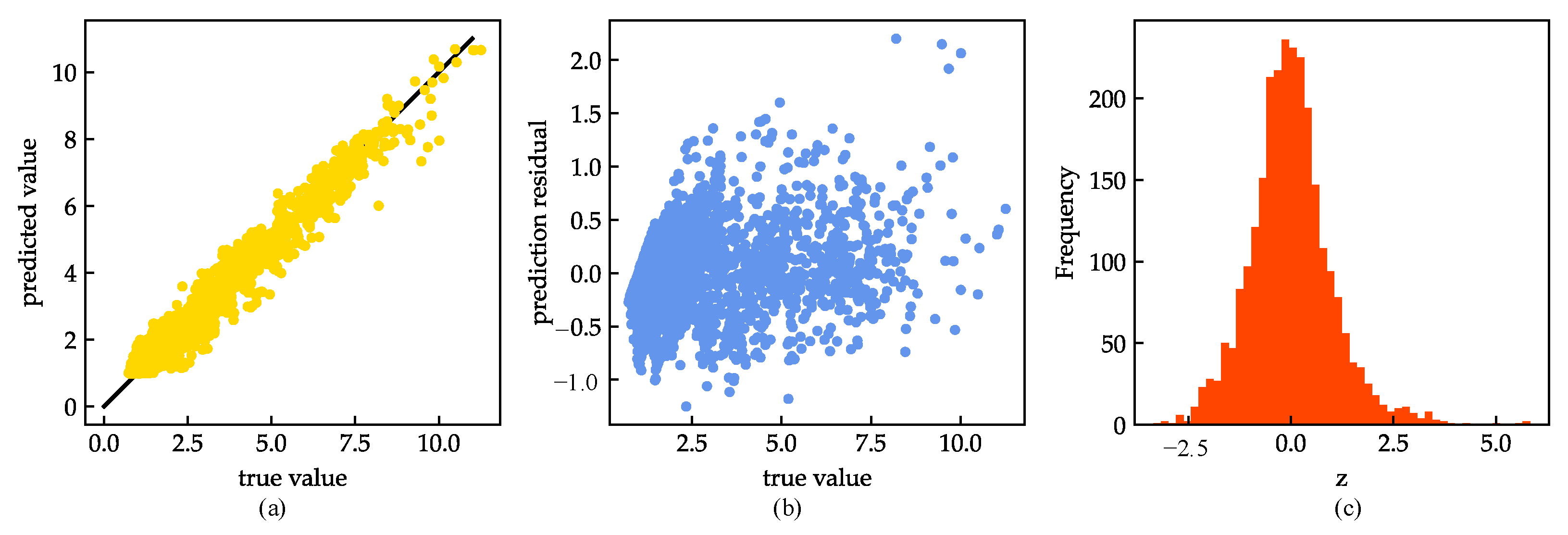
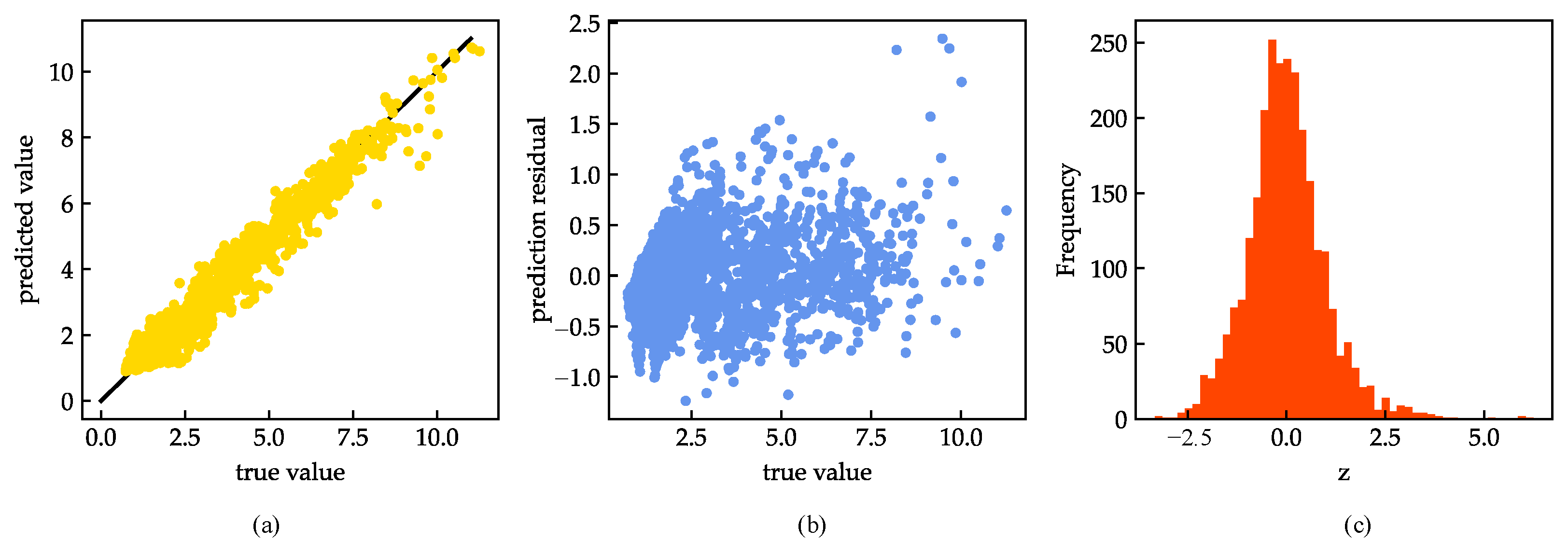
4.1. Model Evaluation and Analysis
4.2. Model Improvements
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Z. Towards the “Blue Water Navy”. Xinmin Weekly 2017, 35, 58–59. [Google Scholar]
- Wan, F.; Liu, Y.; Chen, W. The Design of Regional Cultural Service of the Maritime Silk Road Based on Symbolic Semantics. Front. Art Res. 2022, 4, 1–6. [Google Scholar] [CrossRef]
- Song, A.Y.; Fabinyi, M. China’s 21st century maritime silk road: Challenges and opportunities to coastal livelihoods in ASEAN countries. Mar. Policy 2022, 136, 104923. [Google Scholar] [CrossRef]
- Daniel, D.; Ryszard, W. The Impact of Major Maritime Accidents on the Development of International Regulations Concerning Safety of Navigation and Protection of the Environment. Sci. J. Pol. Nav. Acad. 2017, 211, 23–44. [Google Scholar]
- Poznanska, I.V. Organizational-Economic Aspects of the Implementation of International Standards for Safety of Maritime Navigation. Probl. Ekon. 2016, 3, 68–73. [Google Scholar]
- Rolf, J.B.; Asbjørn, L.A. Maritime navigation accidents and risk indicators: An exploratory statistical analysis using AIS data and accident reports. Reliab. Eng. Syst. Saf. 2018, 176, 174–186. [Google Scholar]
- Hanzu-Pazara, R.; Varsami, C.; Andrei, C.; Dumitrache, R. The influence of ship’s stability on safety of navigation. IOP Conf. Ser. Mater. Sci. Eng. 2016, 145, 082019. [Google Scholar] [CrossRef]
- Mahjoobi, J.; Etemad-Shahidi, A.; Kazeminezhad, M.H. Hindcasting of wave parameters using different soft computing methods. Appl. Ocean. Res. 2008, 30, 28–36. [Google Scholar] [CrossRef]
- Deo, M.C.; Jha, A.; Chaphekar, A.S.; Ravikant, K. Neural networks for wave forecasting. Ocean Eng. 2001, 28, 889–898. [Google Scholar] [CrossRef]
- Makarynskyy, O. Improving wave predictions with artificial neural networks. Ocean Eng. 2003, 31, 709–724. [Google Scholar] [CrossRef]
- Makarynskyy, O.; Pires-Silva, A.A.; Makarynska, D.; Ventura-Soares, C. Artificial neural networks in wave predictions at the west coast of Portugal. Comput. Geosci. 2005, 31, 415–424. [Google Scholar] [CrossRef]
- Ahmadreza, Z.; Dimitri, S.; Ahmadreza, A.; Arnold, H. Learning from data for wind-wave forecasting. Ocean Eng. 2008, 35, 953–962. [Google Scholar]
- Deka, P.C.; Prahlada, R. Discrete wavelet neural network approach in significant wave height forecasting for multistep lead time. Ocean Eng. 2012, 43, 32–42. [Google Scholar] [CrossRef]
- Castro, A.; Carballo, R.; Iglesias, G.; Rabuñal, J.R. Performance of artificial neural networks in nearshore wave power prediction. Appl. Soft Comput. 2014, 23, 194–201. [Google Scholar] [CrossRef]
- Mehmet, Ö.; Zekai, Ş. Prediction of wave parameters by using fuzzy logic approach. Ocean Eng. 2007, 34, 460–469. [Google Scholar]
- Adem, A.; Mehmet, Ö.; Murat, İ.K. Prediction of wave parameters by using fuzzy inference system and the parametric models along the south coasts of the Black Sea. J. Mar. Sci. Technol. 2014, 19, 1–14. [Google Scholar]
- Gaur, S.; Deo, M.C. Real-time wave forecasting using genetic programming. Ocean Eng. 2008, 35, 1166–1172. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J. Precipitation forecasting using wavelet-genetic programming and wavelet-neuro-fuzzy conjunction models. Water Resour. Manag. 2011, 25, 3135–3152. [Google Scholar] [CrossRef]
- Nitsure, S.P.; Londhe, S.N.; Khare, K.C. Wave forecasts using wind information and genetic programming. Ocean Eng. 2012, 54, 61–69. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Leaning Theory; Springer: New York, NY, USA, 1995; p. 314. [Google Scholar]
- Mohandes, M.A.; Halawani, T.O.; Rehman, S.; Hussain, A. Support vector machines for wind speed prediction. Renew. Energy 2004, 29, 939–947. [Google Scholar] [CrossRef]
- Tirusew, A.; Mariush, K.; Mac, M.; Abedalrazq, K. Multi-time scale stream flow predictions: The support vector machines approach. J. Hydrol. 2006, 318, 7–16. [Google Scholar]
- Sancho, S.; Emilio, G.O.; Ángel, M.P.; Antonio, P.; Luis, P. Short term wind speed prediction based on evolutionary support vector regression algorithms. Expert Syst. Appl. 2011, 38, 4052–4057. [Google Scholar]
- Sujay, R.N.; Paresh, C.D. Support vector machine applications in the field of hydrology: A review. Appl. Soft Comput. 2014, 19, 372–386. [Google Scholar]
- Mahjoobi, J.; Mosabbeb, E.A. Prediction of significant wave height using regressive support vector machines. Ocean Eng. 2009, 36, 339–347. [Google Scholar] [CrossRef]
- Zhu, Z.; Cao, Q.; Xu, J. Application of neural networks to wave prediction in coastal areas of Shanghai. Mar. Forecast. 2018, 35, 25–33. [Google Scholar]
- Sinha, M.; Rao, A.; Basu, S. Forecasting space: Time variability of wave heights in the bay of Bengal: A genetic algorithm approach. J. Oceanogr. 2013, 69, 117–128. [Google Scholar] [CrossRef]
- Mohammad, R.N.; Reza, K. Wave Height Prediction Using Artificial Immune Recognition Systems (AIRS) and Some Other Data Mining Techniques. Iran. J. Sci. Technol. Trans. Civ. Eng. 2017, 41, 329–344. [Google Scholar]
- Wu, Z.; Jiang, C.; Conde, M.; Deng, B.; Chen, J. Hybrid improved empirical mode decomposition and BP neural network model for the prediction of sea surface temperature. Ocean Sci. 2019, 15, 349–360. [Google Scholar] [CrossRef]
- Ali, M.; Pasad, R. Significant wave height forecasting via an extreme learning machine model integrated with improved complete ensemble empirical mode decomposition. Renew. Sustain. Energy Rev. 2019, 104, 281–295. [Google Scholar] [CrossRef]
- James, S.C.; Zhang, Y.; O’Donncha, F. A machine learning framework to forecast wave conditions. Coastal Eng. 2018, 137, 1–10. [Google Scholar] [CrossRef]
- Yang, Y.; Tu, H.; Song, L.; Chen, L.; Xie, D.; Sun, J. Research on Accurate Prediction of the Container Ship Resistance by RBFNN and Other Machine Learning Algorithms. J. Mar. Sci. Eng. 2021, 9, 376. [Google Scholar] [CrossRef]
- Wu, M.; Stefanakos, C.; Gao, Z. Multi-Step-Ahead Forecasting of Wave Conditions Based on a Physics-Based Machine Learning (PBML) Model for Marine Operations. J. Mar. Sci. Eng. 2020, 8, 992. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Gao, S.; Ren, P. Ocean Wave Height Series Prediction with Numerical Long Short-Term Memory. J. Mar. Sci. Eng. 2021, 9, 514. [Google Scholar] [CrossRef]
- Xu, P.; Han, C.; Cheng, H.; Cheng, C.; Ge, T. A Physics-Informed Neural Network for the Prediction of Unmanned Surface Vehicle Dynamics. J. Mar. Sci. Eng. 2022, 10, 148. [Google Scholar] [CrossRef]
- Valera, M.; Walter, R.K.; Bailey, B.A.; Castillo, J.E. Machine Learning Based Predictions of Dissolved Oxygen in a Small Coastal Embayment. J. Mar. Sci. Eng. 2020, 8, 1007. [Google Scholar] [CrossRef]
- He, J.; Hao, Y.; Wang, X. An Interpretable Aid Decision-Making Model for Flag State Control Ship Detention Based on SMOTE and XGBoost. J. Mar. Sci. Eng. 2021, 9, 156. [Google Scholar] [CrossRef]
- Tian, R.; Chen, F.; Dong, S.; Amezquita-Sanchez, J.P. Compound Fault Diagnosis of Stator Interturn Short Circuit and Air Gap Eccentricity Based on Random Forest and XGBoost. Math. Probl. Eng. 2021, 2021, 2149048. [Google Scholar] [CrossRef]
- Gan, M.; Pan, S.; Chen, Y.; Cheng, C.; Pan, H.; Zhu, X. Application of the Machine Learning LightGBM Model to the Prediction of the Water Levels of the Lower Columbia River. J. Mar. Sci. Eng. 2021, 9, 496. [Google Scholar] [CrossRef]
- Wang, L.; Guo, Y.; Fan, M.; Li, X. Wind speed prediction using measurements from neighboring locations and combining the extreme learning machine and the AdaBoost algorithm. Energy Rep. 2022, 8, 1508–1518. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]



| Symbol | Illustration | Units |
|---|---|---|
| u10 | the horizontal speed of air moving toward the east, at a height of ten meters above the surface of the earth | m/s |
| v10 | the horizontal speed of air moving toward the north, at a height of ten meters above the surface of the earth | m/s |
| airMass | the mass of air per cubic meter over the oceans | kg/m3 |
| cdww | the resistance that ocean waves exert on the atmosphere | dimensionless |
| vertV | an estimate of the vertical velocity of updraughts generated by free convection | m/s |
| mpww | the average time for two consecutive wave crests, on the surface of the sea generated by local winds, to pass through a fixed point | s |
| msl | the pressure (force per unit area) of the atmosphere at the surface of the earth | Pa |
| wind | the horizontal speed of the “neutral wind”, at a height of ten meters above the surface of the earth | m/s |
| sst | the temperature of seawater near the surface | K |
| sp | the pressure (force per unit area) of the atmosphere at the surface of land, sea, and inland water | Pa |
| hmax | an estimate of the height of the expected highest individual wave within a 20 min window | m |
| Features | Minimum Value | Maximum Value | Median Value |
|---|---|---|---|
| u10 (m/s) | −17.940 | 11.734 | −3.174 |
| v10 (m/s) | −18.111 | 12.139 | 0.705 |
| airMass (kg/m3) | 1.132 | 1.211 | 1.160 |
| cdww (dimensionless) | 0.0006 | 0.003 | 0.0011 |
| vertV (m/s) | 0.000 | 11.734 | 0.713 |
| mpww (s) | 1.517 | 9.298 | 3.476 |
| msl (Pa) | 99,522.455 | 102,522.813 | 101,082.747 |
| wind (m/s) | 2.000 | 18.141 | 6.621 |
| sst (K) | 296.405 | 304.136 | 300.774 |
| sp (Pa) | 99,522.562 | 102,523.899 | 101,083.687 |
| hmax (m) | 0.727 | 11.263 | 2.253 |
| Abbreviation | Illustration |
|---|---|
| XGBoost | The extreme gradient boosting |
| LightGBM | The light gradient boosting machine |
| RF | The random forest |
| AdaBoost | The adaptive boosting |
| LR | The linear regression |
| MAE | The mean absolute error |
| MSE | The mean squared error |
| R2 | The r2 score |
| Datasets | Parameters | XGBoost | LightGBM | RF | AdaBoost | Stacking | Improved Stacking |
|---|---|---|---|---|---|---|---|
| training sets | MAE | 0.446 | 0.447 | 0.445 | 0.417 | 0.284 | 0.281 |
| MSE | 0.372 | 0.321 | 0.344 | 0.259 | 0.154 | 0.150 | |
| R2 | 0.895 | 0.909 | 0.902 | 0.926 | 0.956 | 0.957 | |
| test sets | MAE | 0.459 | 0.464 | 0.461 | 0.433 | 0.278 | 0.278 |
| MSE | 0.399 | 0.359 | 0.375 | 0.285 | 0.141 | 0.140 | |
| R2 | 0.888 | 0.899 | 0.895 | 0.920 | 0.960 | 0.961 |
| Parameters | XGBoost | LightGBM | RF | AdaBoost |
|---|---|---|---|---|
| corr | 0.964 | 0.978 | 0.947 | 0.962 |
| std_resid | 0.567 | 0.600 | 0.612 | 0.521 |
| number of samples z > 3 | 34 | 22 | 36 | 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, Y.; Zhang, H.; Li, J.; Li, G. Prediction Method for Ocean Wave Height Based on Stacking Ensemble Learning Model. J. Mar. Sci. Eng. 2022, 10, 1150. https://doi.org/10.3390/jmse10081150
Zhan Y, Zhang H, Li J, Li G. Prediction Method for Ocean Wave Height Based on Stacking Ensemble Learning Model. Journal of Marine Science and Engineering. 2022; 10(8):1150. https://doi.org/10.3390/jmse10081150
Chicago/Turabian StyleZhan, Yu, Huajun Zhang, Jianhao Li, and Gen Li. 2022. "Prediction Method for Ocean Wave Height Based on Stacking Ensemble Learning Model" Journal of Marine Science and Engineering 10, no. 8: 1150. https://doi.org/10.3390/jmse10081150
APA StyleZhan, Y., Zhang, H., Li, J., & Li, G. (2022). Prediction Method for Ocean Wave Height Based on Stacking Ensemble Learning Model. Journal of Marine Science and Engineering, 10(8), 1150. https://doi.org/10.3390/jmse10081150





