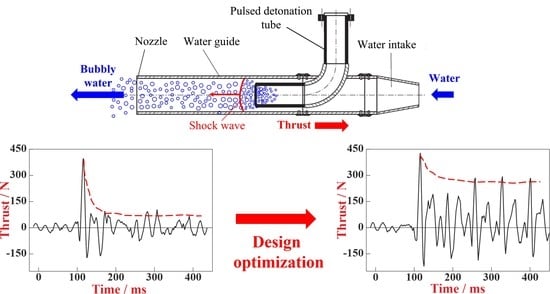
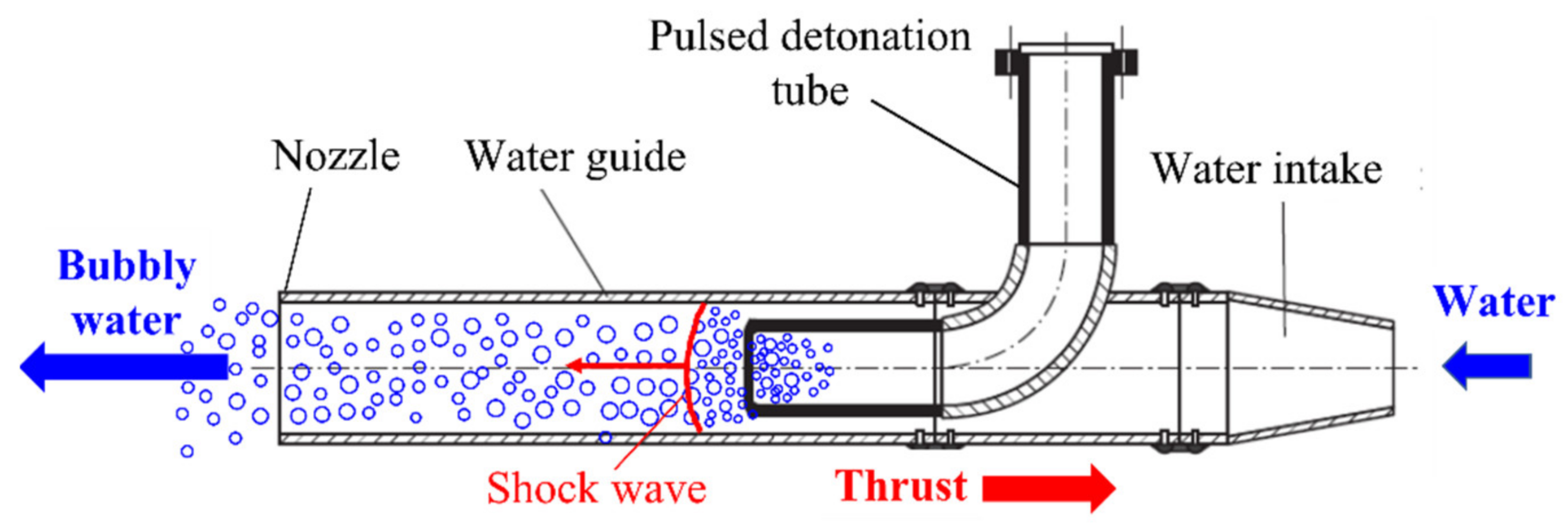
Pulsed Detonation Hydroramjet: Design Optimization
Abstract
:1. Introduction
2. Materials and Methods
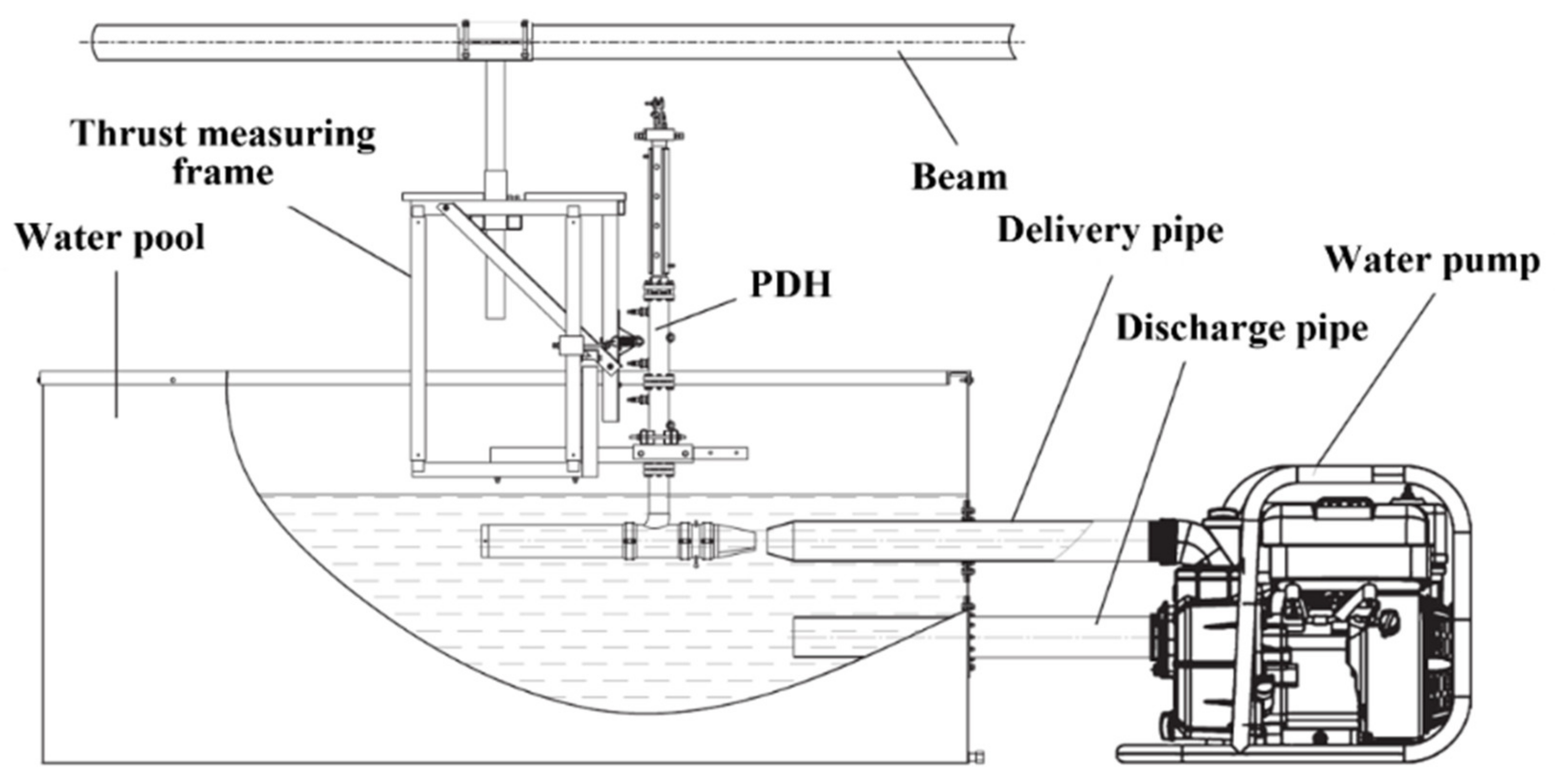
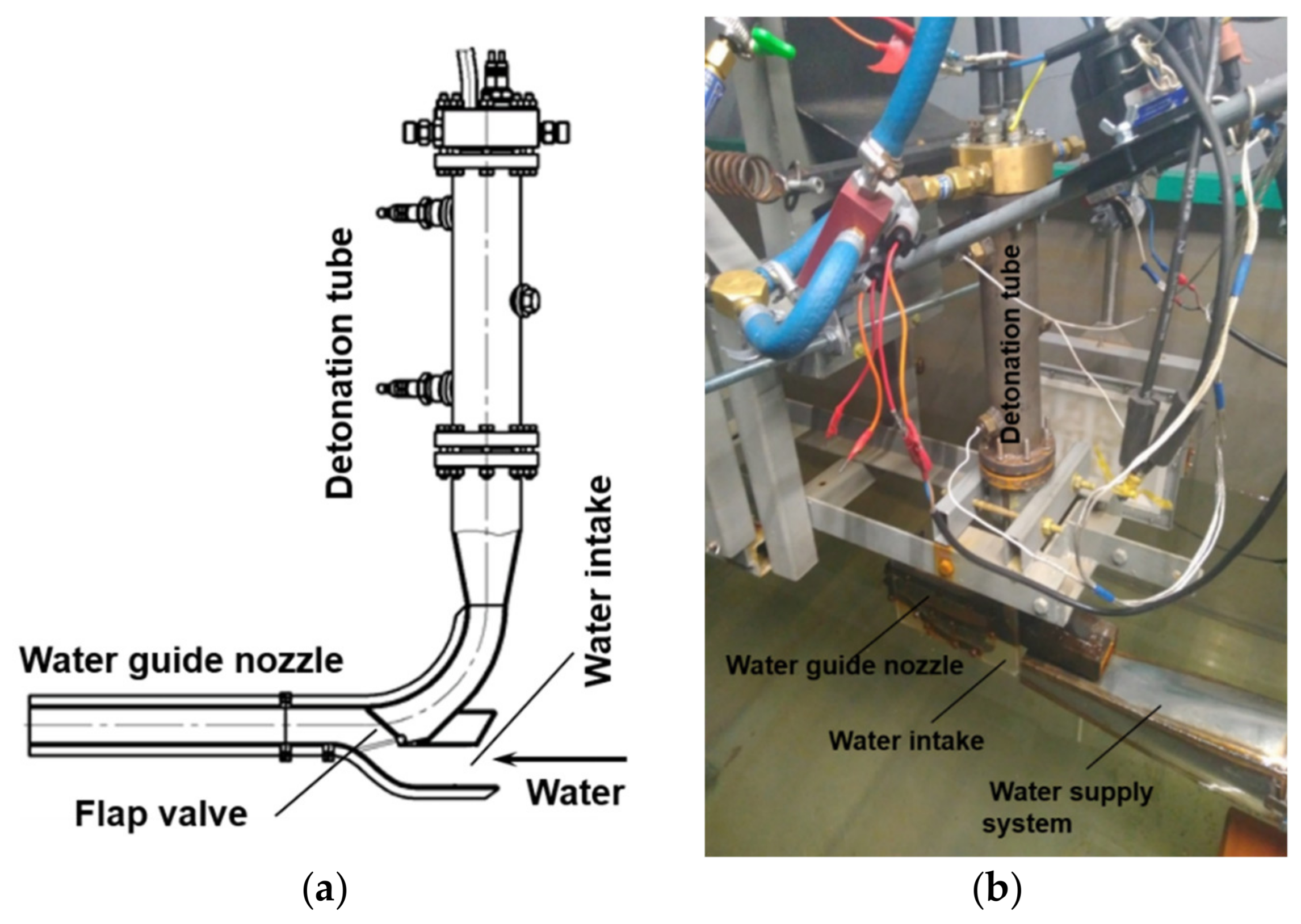
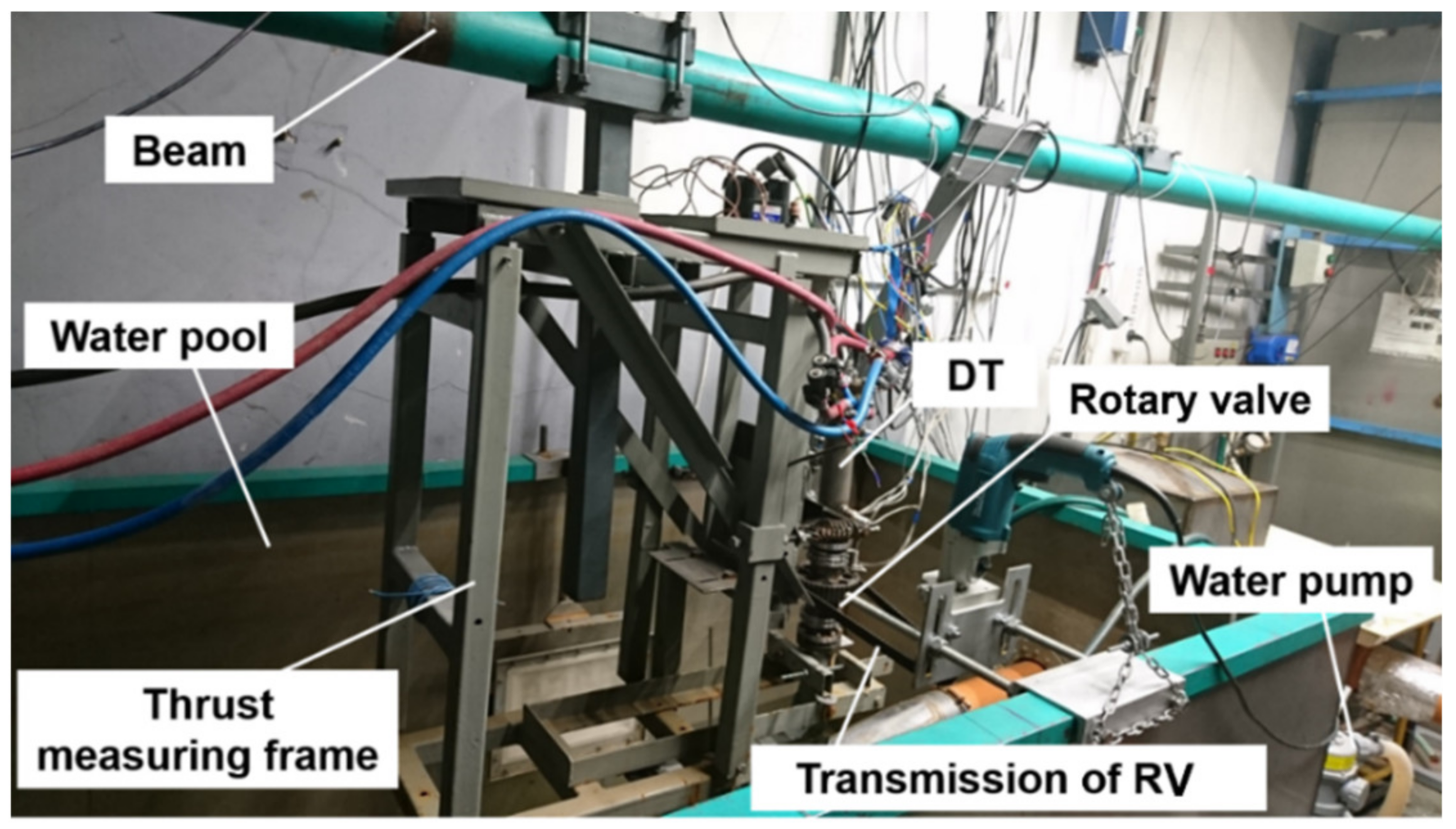
2.1. Test Rig
2.2. Baseline PDH Model
- -
- purging the DT with nitrogen gas;
- -
- filling the DT with the explosive mixture;
- -
- spark ignition of the explosive mixture followed by deflagration-to-detonation transition and combustion of the mixture in the propagating detonation wave; and
- -
- momentum transfer from the propagating shock wave and expanding detonation products to bubbly water in the water guide, and outflow of bubbly water from the water guide.
3. Results and Discussion
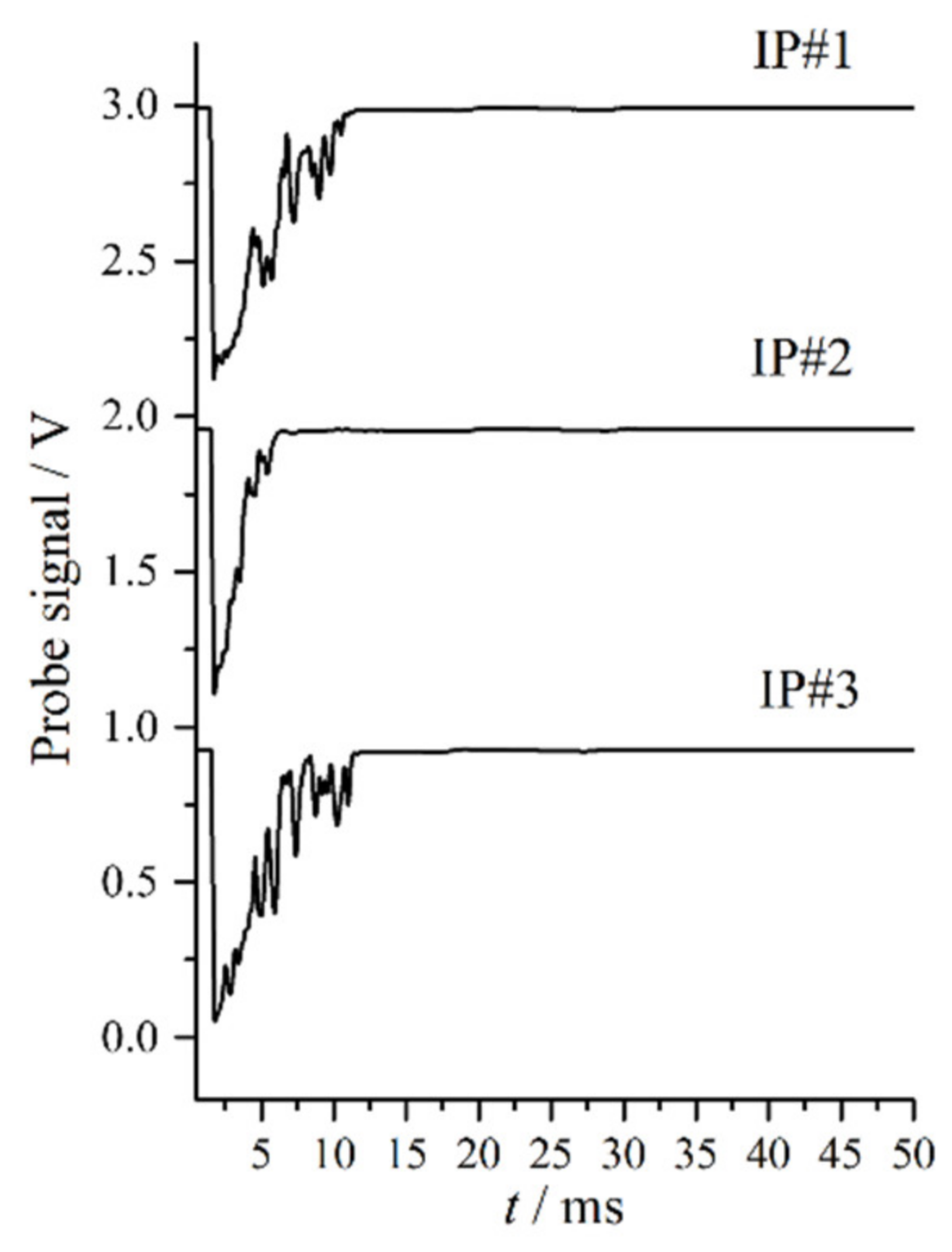
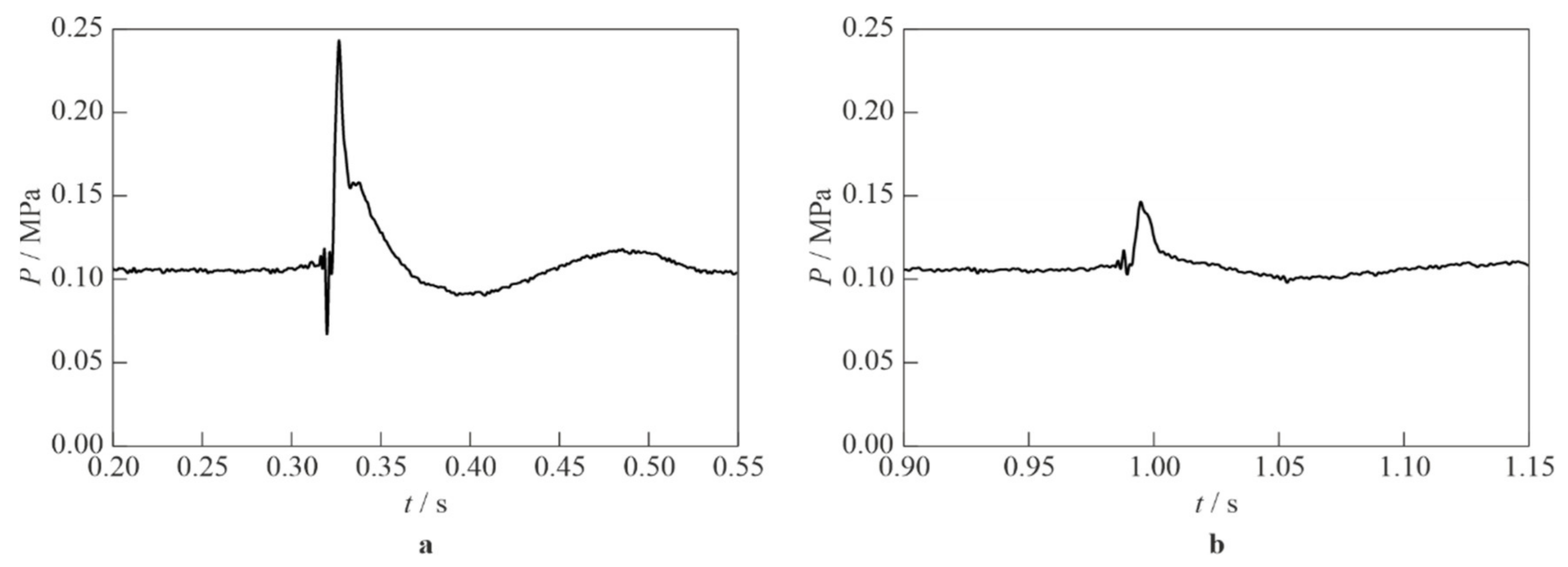
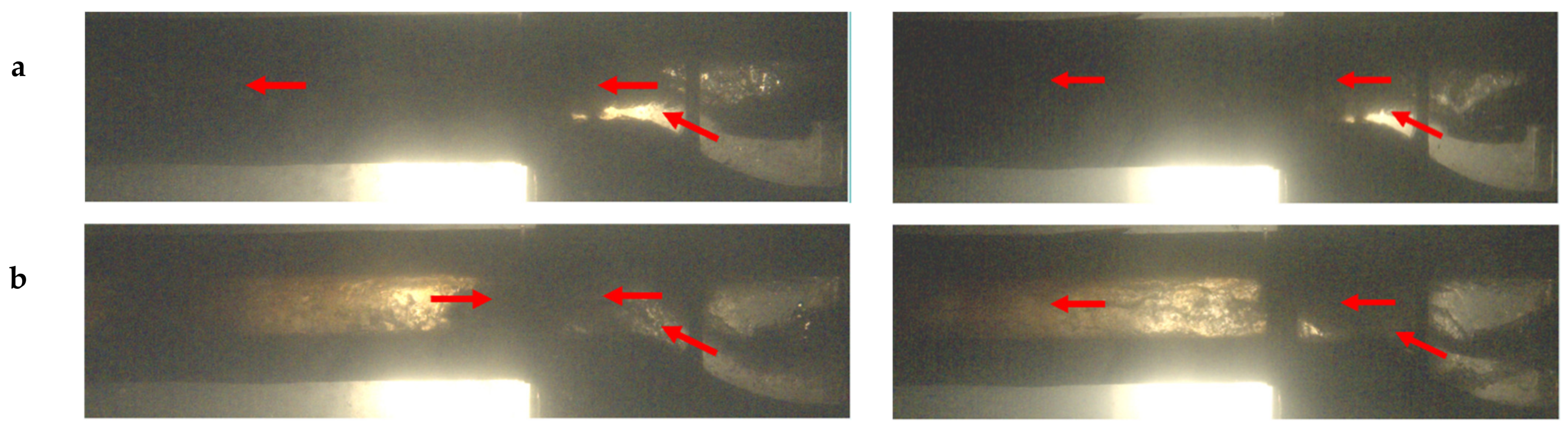
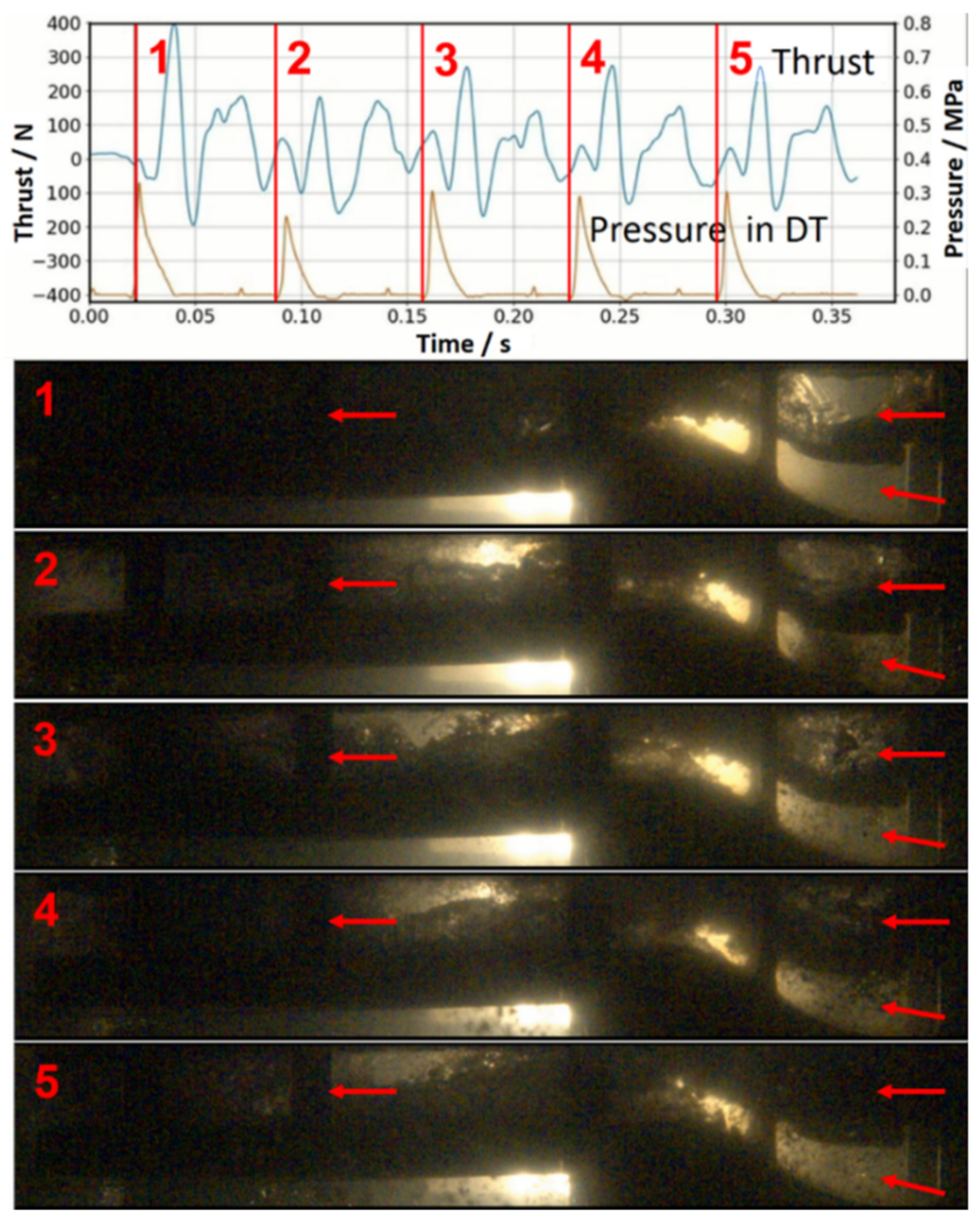
3.1. Cycle-to-Cycle Variability
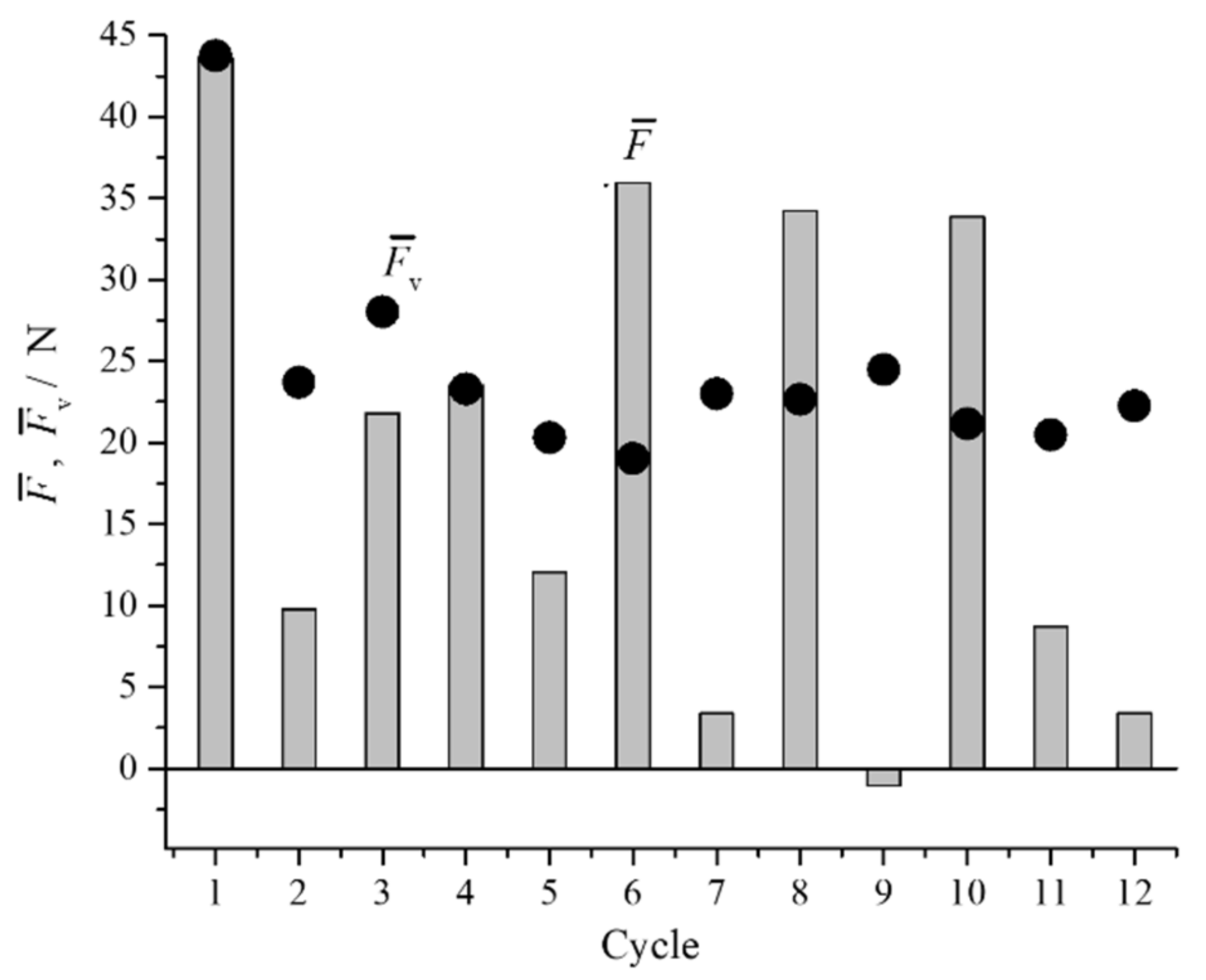
3.2. PDH Model with Passive Flap Valve
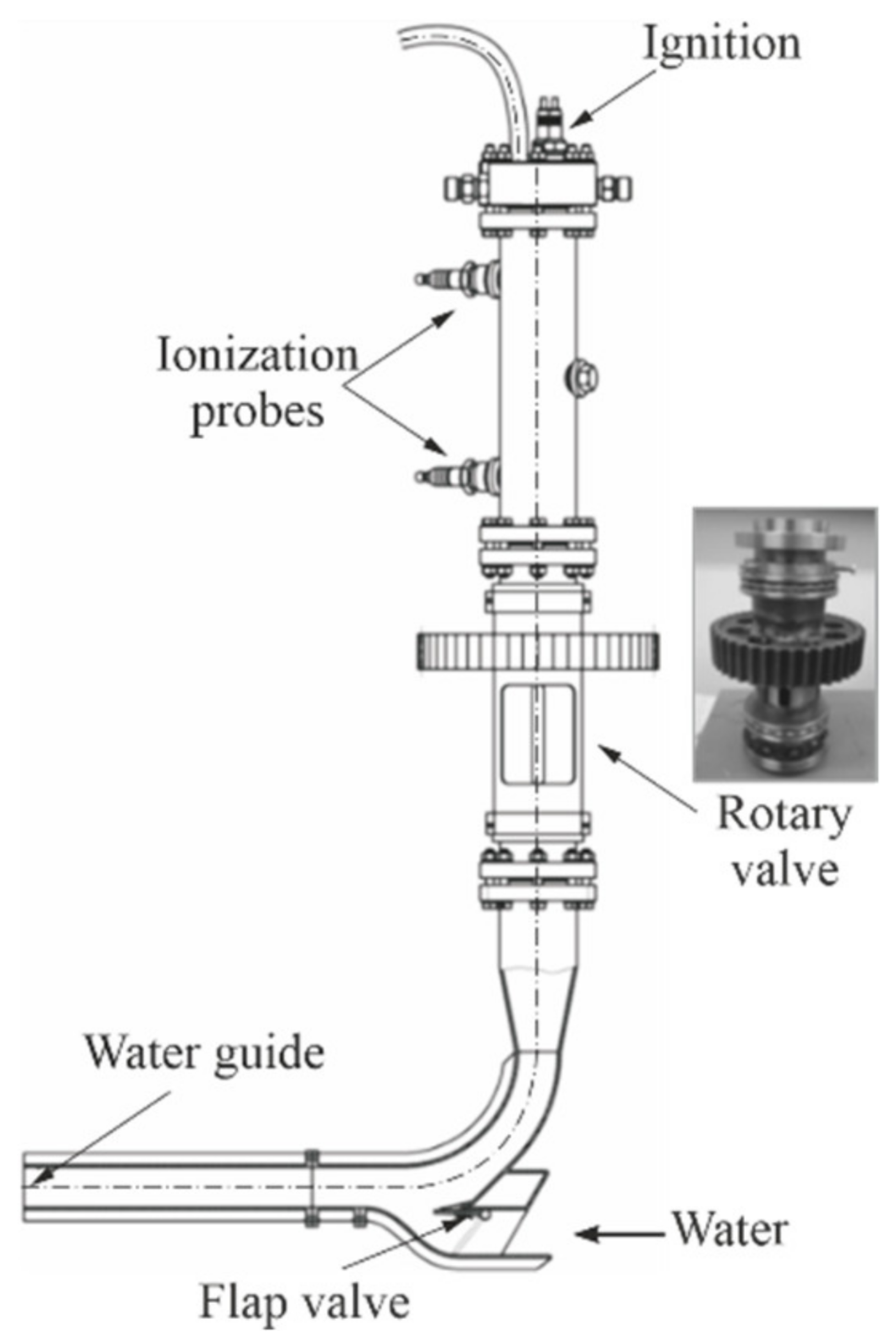
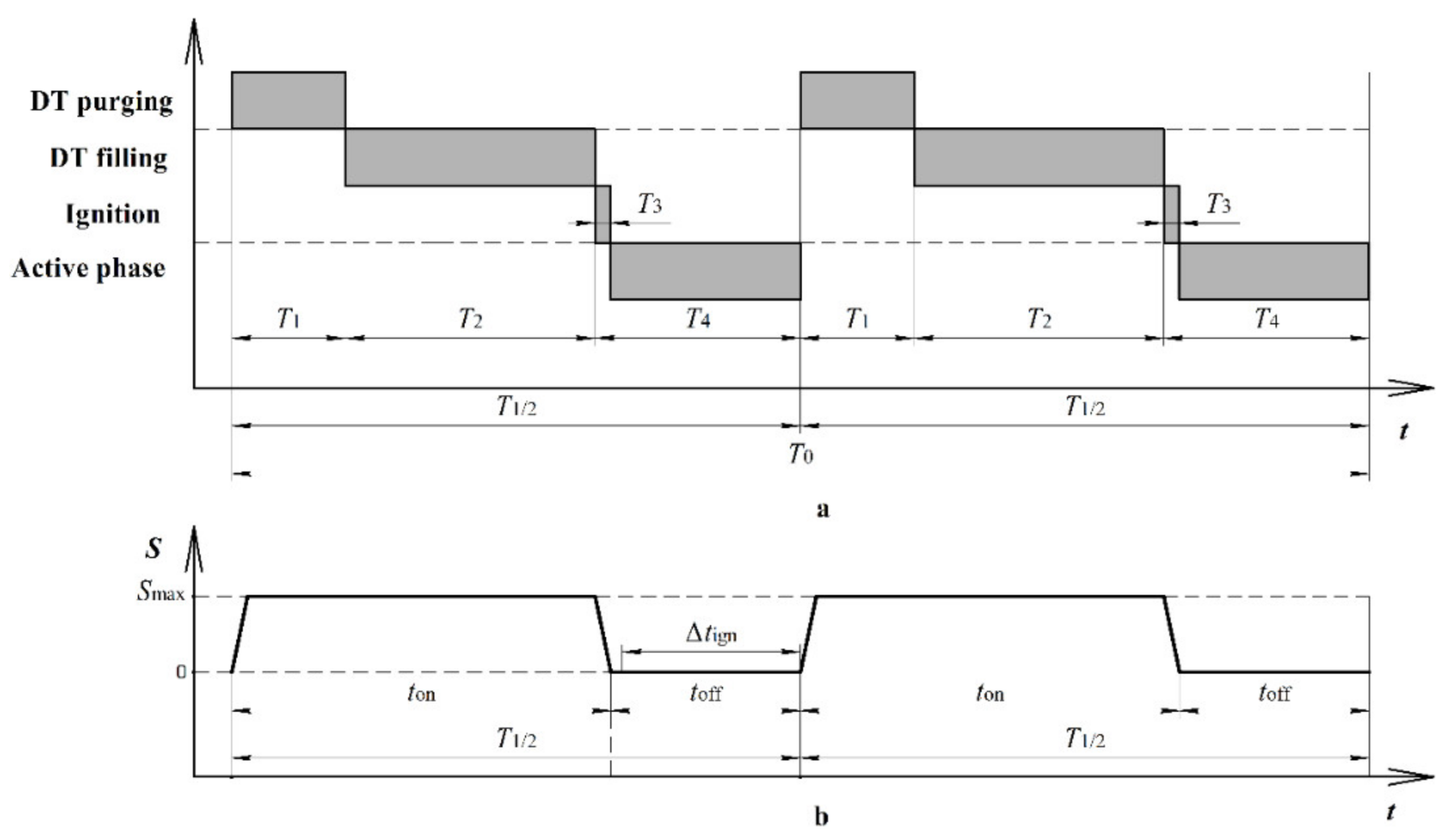
3.3. PDH Model with Passive Flap Valve and Active Rotary Valve
- (1)
- purging the DT with nitrogen gas (time interval T1);
- (2)
- filling the DT with the explosive mixture (time interval T2);
- (3)
- spark ignition of the explosive mixture followed by deflagration-to-detonation transition and combustion of the mixture in the propagating detonation wave (time interval T3); and
- (4)
- momentum transfer from the propagating shock wave and expanding detonation products to bubbly water in the water guide, outflow of bubbly water from the water guide (time interval T4).
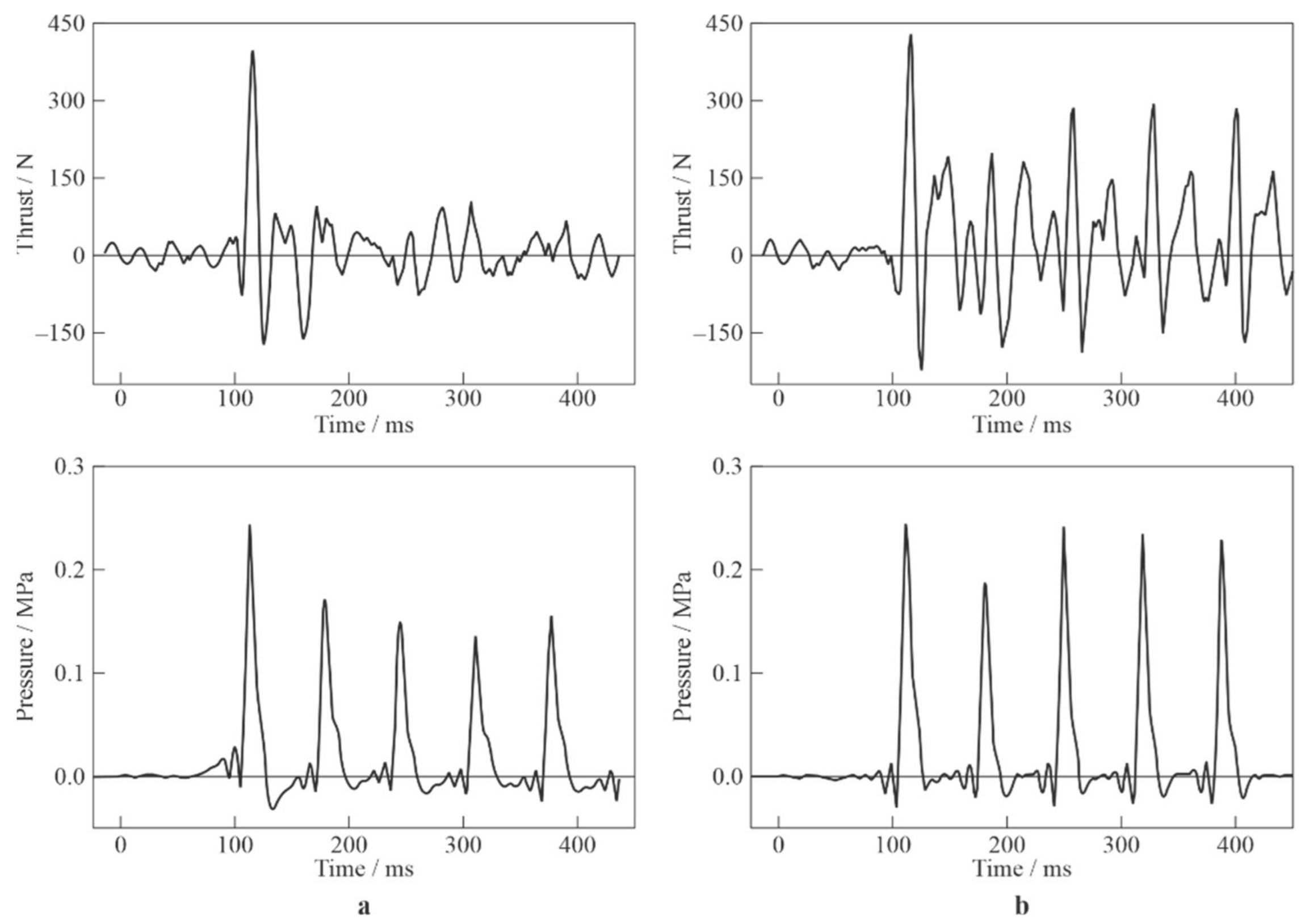
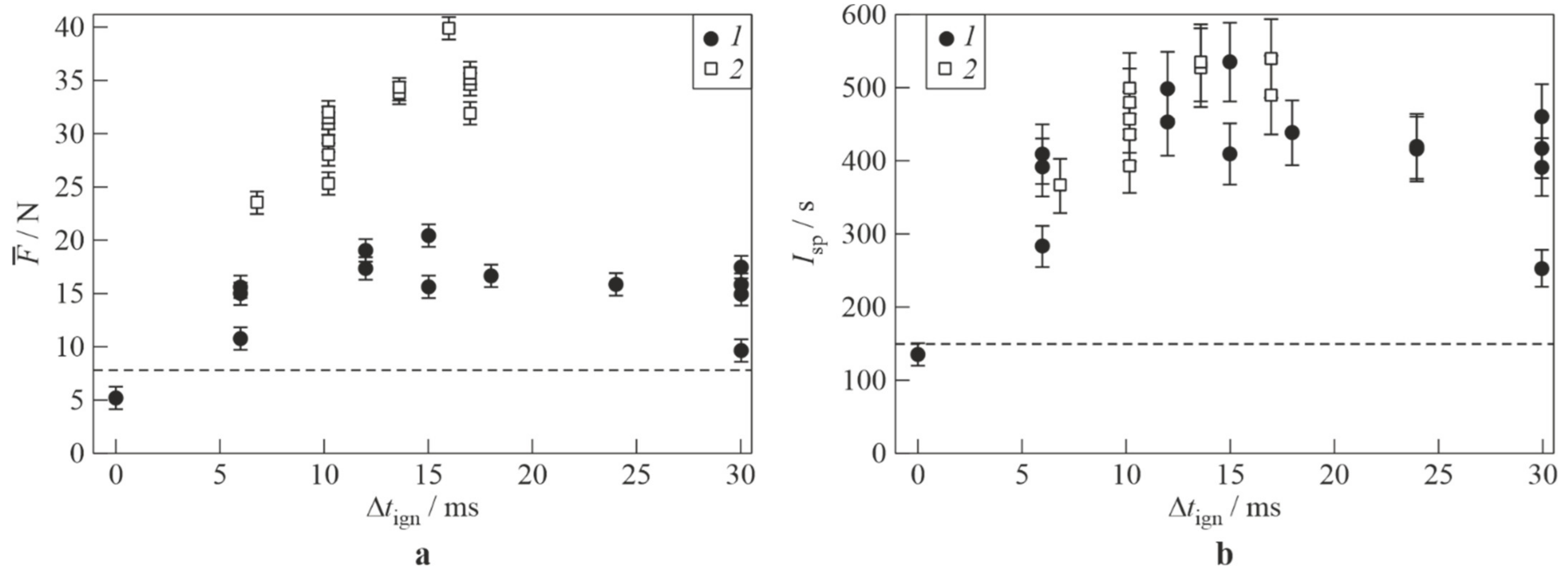
3.4. Effect of Ignition Delay on PDH Thrust Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational fluid dynamics |
| DT | Detonation tube |
| FV | Flap valve |
| IP | Ionization probe |
| PDH | Pulsed detonation hydroramjet |
| PS | Position sensor |
| R&D | Research and development |
| RV | Rotary valve |
| Nomenclature | |
| Time-averaged thrust of PDH | |
| F(t) | Thrust of PDH |
| Time-averaged thrust of PDH with a passive flap valve | |
| g | Acceleration of gravity |
| Isp | Time-averaged specific impulse of PDH |
| Isp,v | Time-averaged specific impulse of PDH with a passive flap valve |
| Mass flow rate of the explosive mixture | |
| P | Pressure pulse amplitude |
| P(t) | Measured pressure at DT exit |
| S | Cross-sectional area of water guide |
| t | Time |
| toff | Time interval when the RV is closed |
| ton | Time interval when the RV is open |
| T1, T2, T3, T4 | Time intervals in PDH operation cycle |
| T1/2 | half time of RV revolution |
| Vm | Fill volume of the DT with the explosive mixture |
| Δtign | Ignition delay |
References
- Zeldovich, Y.B. To the question of energy use of detonation combustion. J. Propul. Power 2006, 22, 588–592. [Google Scholar] [CrossRef]
- Frolov, S.M.; Aksenov, V.S.; Ivanov, V.S. Experimental proof of Zel’dovich cycle efficiency gain over cycle with constant pressure combustion for hydrogen-oxygen fuel mixture. Int. J. Hydrog. Energy 2015, 40, 6970–6975. [Google Scholar] [CrossRef]
- Bussing, T.R.A.; Pappas, G. An introduction to pulse detonation engines. In Proceedings of the 32nd Aerospace Sciences Meeting and Exhibit, AIAA Paper 94-0263, Reno, NV, USA, 10–13 January 1994. [Google Scholar]
- Kailasanath, K. Recent developments in the research on pulse detonation engines. AIAA J. 2003, 41, 145–159. [Google Scholar] [CrossRef]
- Roy, G.D.; Frolov, S.M.; Borisov, A.A.; Netzer, D.W. Pulse detonation propulsion: Challenges, current status, and future perspective. Prog. Energy Combust. Sci. 2004, 30, 545–672. [Google Scholar] [CrossRef]
- Voitsekhovskii, B.V. Stationary spin detonation. Sov. J. Appl. Mech. Tech. Phys. 1960, 3, 157–164. [Google Scholar]
- Bykovskii, F.A.; Zhdan, S.A.; Vedernikov, E.F. Continuous spin detonations. J. Propul. Power 2006, 22, 1204–1216. [Google Scholar] [CrossRef]
- Lu, F.K.; Braun, E.M. Rotating detonation wave propulsion: Experimental challenges, modeling, and engine concepts. J. Propul. Power 2014, 30, 1125–1142. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Kompaneets, A.S. The Theory of Detonation; Gostekhteorizdat: Moscow, Russia, 1955. [Google Scholar]
- Shchelkin, K.I. Fast Combustion and Spin Detonation of Gases; Voenizdat: Moscow, Russia, 1949. [Google Scholar]
- Lee, J.H. The Detonation Phenomenon; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Borisov, A.A.; Gelfand, B.E. Review of papers on detonation of two-phase systems. Arch. Thermodyn. Spalania 1976, 7, 273–287. [Google Scholar]
- Benedick, W.B.; Tieszen, S.R.; Knystautas, R.; Lee, J.H.S. Detonation of unconfined large-scale fuel spray–air clouds. In Dynamics of Detonations and Explosions: Detonations; Kuhl, A.L., Leyer, J.-C., Borisov, A.A., Sirignano, W.A., Eds.; 133, Progress in Astronautics and Aeronautics; AIAA: New York, NY, USA, 1991; pp. 297–310. [Google Scholar]
- Kailasanath, K. Liquid-fueled detonations in tubes. J. Propul. Power 2006, 22, 1261–1268. [Google Scholar] [CrossRef]
- Frolov, S.M.; Aksenov, V.S.; Frolov, F.S.; Avdeev, K.A. Pumpjet Pulse Detonation Engine (Variants) and Method for Creating Hydro-Jet. Patent WO/2015/099552, 23 December 2013. Available online: https://patentscope.wipo.int/search/en/detail.jsf?docId=WO2015099552&cid=P10-KLWBNQ-86226-1 (accessed on 4 August 2022).
- Frolov, S.M.; Avdeev, K.A.; Aksenov, V.S.; Frolov, F.S.; Sadykov, I.A.; Shamshin, I.O.; Tukhvatullina, R.R. Direct conversion of fuel chemical energy into the energy of water motion. In Nonequilibrium Processes in Physics and Chemistry; Starik, A.M., Frolov, S.M., Eds.; Torus Press: Moscow, Russia, 2016; Volume 2, pp. 251–262. [Google Scholar]
- Frolov, S.; Avdeev, K.; Aksenov, V.; Frolov, F.; Sadykov, I.; Shamshin, I.; Tukhvatullina, R. Pulse-detonation hydrojet. In Scientific-Practical Conference “Research and Development-2016; Springer: Berlin/Heidelberg, Germany, 2016; p. 709. [Google Scholar]
- Frolov, S.M.; Aksenov, V.S.; Sadykov, I.A.; Avdeev, K.A.; Shamshin, I.O. Testing of experimental models of a hydrojet with pulsed-detonation combustion of liquid fuel. Combust. Explos. 2017, 10, 73–82. [Google Scholar]
- Frolov, S.M.; Aksenov, V.S.; Sadykov, I.A.; Avdeev, K.A.; Shamshin, I.O. Hydrojet engine with pulse detonation combustion of liquid fuel. Dokl. Phys. Chem. 2017, 475, 129–133. [Google Scholar] [CrossRef]
- Frolov, S.M.; Avdeev, K.A.; Aksenov, V.S.; Borisov, A.A.; Frolov, F.S.; Shamshin, I.O.; Tukhvatullina, R.R.; Basara, B.; Edelbauer, W.; Pachler, K. Experimental and computational studies of shock wave-to-bubbly water momentum transfer. Int. J. Multiph. Flow 2017, 92, 20–38. [Google Scholar] [CrossRef]
- Frolov, S.M.; Avdeev, K.A.; Aksenov, V.S.; Frolov, F.S.; Sadykov, I.A.; Shamshin, I.O.; Tukhvatullina, R.R. Pulsed detonation hydroramjet. In Advances in Pulsed and Continuous Detonations; Frolov, S.M., Ed.; Torus Press: Moscow, Russia, 2019; pp. 372–396. [Google Scholar]
- Frolov, S.M.; Aksenov, V.S.; Avdeev, K.A.; Sadykov, I.A.; Shamshin, I.O.; Tukhvatullina, R.R. Pulsed-detonation hydroramjet. In Recent Progress in Detonation for Propulsion; Frolov, S.M., Kasahara, J., Eds.; Torus Press: Moscow, Russia, 2019; pp. 68–70. [Google Scholar]
- Frolov, S.M.; Avdeev, K.A.; Aksenov, V.S.; Frolov, F.S.; Sadykov, I.A.; Shamshin, I.O.; Tukhvatullina, R.R. Pulsed detonation hydroramjet: Simulations and experiments. Shock Waves 2020, 30, 221–234. [Google Scholar] [CrossRef]
- Ando, K.; Colonius, T.; Brennen, C.E. Numerical simulation of shock propagation in a polydisperse bubbly liquid. Int. J. Multiph. Flow 2011, 37, 596–608. [Google Scholar] [CrossRef]
- Jourdan, G.; Mariani, C.; Houas, L.; Chinnayya, A.; Hadjadj, A.; Del Prete, E.; Haas, J.F.; Rambert, N.; Counilh, D.; Faure, S. Analysis of shock-wave propagation in aqueous foams using shock tube experiments. Phys. Fluids 2015, 27, 056101. [Google Scholar] [CrossRef]
- Borisov, A.A.; Gelfand, B.E.; Timofeev, E.I. Shock waves in liquids containing gas bubbles. Int. J. Multiph. Flow 1983, 9, 531–543. [Google Scholar] [CrossRef]
- Zhang, X.; Li, S.; Yu, D.; Yang, B.; Wang, N. The evolution of interfaces for underwater supersonic gas jets. Water 2020, 12, 488. [Google Scholar] [CrossRef]
- Wang, C.; Li, N.; Huang, X.; Liu, W.; Weng, C. Shock wave and bubble pulsation characteristics in a field generated by single underwater detonation. Phys. Fluids 2022, 34, 066108. [Google Scholar] [CrossRef]
- Wang, C.; Li, N.; Huang, X.; Weng, C. Investigation of the effect of nozzle on underwater detonation shock wave and bubble pulsation. Energies 2022, 15, 3194. [Google Scholar] [CrossRef]
- Hou, Z.; Li, N.; Huang, X.; Li, C.; Kang, Y.; Weng, C. Three-dimensional numerical simulation on near-field pressure evolution of dual-tube underwater detonation. Phys. Fluids 2022, 34, 033304. [Google Scholar] [CrossRef]
- Avdeev, K.A.; Aksenov, V.S.; Borisov, A.A.; Frolov, S.M.; Sadykov, I.A.; Frolov, F.S.; Shamshin, I.O. Propagation of high-frequency sequence of shock waves in water with gas bubbles. Combust. Explos. 2016, 9, 83–95. [Google Scholar]
- Liu, W.; Li, N.; Huang, X.; Kang, Y.; Li, C.; Qiang, W.; Weng, C. Experimental study of underwater pulse detonation gas jets: Bubble velocity field and time–frequency characteristics of pressure field. Phys. Fluids 2021, 33, 083324. [Google Scholar] [CrossRef]
- Liu, W.; Li, N.; Weng, C.; Huang, X.; Kang, Y. Bubble dynamics and pressure field characteristics of underwater detonation gas jet generated by a detonation tube. Phys. Fluids 2021, 33, 023302. [Google Scholar] [CrossRef]
- Nguyen, V.; Phan, H.; Duy, T.; Park, W. Numerical modeling for compressible two-phase flows and application to near-field underwater explosions. Comput. Fluids 2021, 215, 104805. [Google Scholar] [CrossRef]
- Phan, T.; Nguyen, V.; Park, W. Numerical study on dynamics of an underwater explosion bubble based on compressible homogeneous mixture model. Comput. Fluids 2019, 191, 104262. [Google Scholar] [CrossRef]
- Phan, H.; Nguyen, V.; Duy, T.; Kim, D.; Park, W. Numerical study on simultaneous thermodynamic and hydrodynamic mechanisms of underwater explosion. Int. J. Heat Mass Transfer 2021, 178, 121581. [Google Scholar] [CrossRef]
- Zhang, A.; Wang, S.; Huang, C.; Wang, B. Influences of initial and boundary conditions on underwater explosion bubble dynamics. Eur. J. Mech. B 2013, 42, 69. [Google Scholar] [CrossRef]
- Liu, N.N.; Zhang, A.M.; Liu, Y.L.; Li, T. Numerical analysis of the interaction of two underwater explosion bubbles using the compressible Eulerian finite-element method. Phys. Fluids 2020, 32, 046107. [Google Scholar]
- Liu, N.N.; Zhang, A.M.; Cui, P.; Wang, S.P.; Li, S. Interaction of two out-of-phase underwater explosion bubbles. Phys. Fluids 2021, 33, 106103. [Google Scholar] [CrossRef]
- Wu, W.; Liu, Y.; Zhang, A.; Liu, N.; Liu, L. Numerical investigation on underwater explosion cavitation characteristics near water wave. Ocean Eng. 2020, 205, 107321. [Google Scholar] [CrossRef]
- Wu, W.; Zhang, A.; Liu, Y.; Liu, M. Interaction between shock wave and a movable sphere with cavitation effects in shallow water. Phys. Fluids 2020, 32, 016103. [Google Scholar]
- Yu, J.; Liu, J.; Wang, H.; Wang, J.; Zhang, L.; Liu, G. Numerical simulation of underwater explosion cavitation characteristics based on phase transition model in compressible multicomponent fluids. Ocean Eng. 2021, 240, 109934. [Google Scholar] [CrossRef]
- Phan, H.; Nguyen, V.; Park, W. Numerical study on strong nonlinear interactions between spark-generated underwater explosion bubbles and a free surface. Int. J. Heat Mass Transfer 2020, 163, 120506. [Google Scholar] [CrossRef]
- Klaseboer, E.; Hung, K.C.; Wang, C.; Khoo, B.C.; Boyce, P.; Debono, S.; Charlier, H. Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure. J. Fluid Mech. 2005, 537, 387–413. [Google Scholar] [CrossRef]
- Nguyen, A. The application of CEL technique to simulate the behavior of an underwater explosion bubble in the vicinity of a rigid wall. Appl. Mech. Mater. 2020, 902, 126. [Google Scholar] [CrossRef]
- Li, S.; Liu, Y.; Wang, Q.; Zhang, A. Dynamics of a buoyant pulsating bubble near two crossed walls. Phys. Fluids 2021, 33, 073310. [Google Scholar] [CrossRef]
- Frolov, S.M.; Aksenov, V.S.; Dubrovskii, A.V.; Zangiev, A.E.; Ivanov, V.S.; Medvedev, S.N.; Shamshin, I.O. Chemiionization and acoustic diagnostics of the process in continuous- and pulse detonation combustors. Dokl. Phys. Chem. 2015, 465, 273. [Google Scholar] [CrossRef]
- Frolov, S.M.; Platonov, S.V.; Avdeev, K.A.; Aksenov, V.S.; Ivanov, V.S.; Zangiev, A.E.; Sadykov, I.A.; Tukhvatullina, R.R.; Frolov, F.S.; Shamshin, I.O. Pulsed combustion of fuel–air mixture in a cavity above water surface: Modeling and experiments. Shock Waves 2022, 32, 1–10. [Google Scholar] [CrossRef]







| Test Fire | P#1/P#2/P#3, MPa | Isp,#1/Isp,#2/Isp,#3, s |
|---|---|---|
| 1 | 0.35/0.20/0.21 | 1160/200/250 |
| 2 | 0.33/0.19/0.17 | 980/510/390 |
| 3 | 0.33/0.18/0.16 | 1040/390/300 |
| Mean | 0.34/0.19/0.18 | 1060/360/310 |
| Test Fire | Vm, dm3 | N | Isp, s | Isp,v, s | |
|---|---|---|---|---|---|
| 1 | 0.4 | 17 | 20 | 340 | 390 |
| 2 | 0.5 | 18 | 23 | 310 | 440 |
| 3 | 0.6 | 19 | 22 | 270 | 340 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frolov, S.M.; Avdeev, K.A.; Aksenov, V.S.; Frolov, F.S.; Sadykov, I.A.; Shamshin, I.O. Pulsed Detonation Hydroramjet: Design Optimization. J. Mar. Sci. Eng. 2022, 10, 1171. https://doi.org/10.3390/jmse10091171
Frolov SM, Avdeev KA, Aksenov VS, Frolov FS, Sadykov IA, Shamshin IO. Pulsed Detonation Hydroramjet: Design Optimization. Journal of Marine Science and Engineering. 2022; 10(9):1171. https://doi.org/10.3390/jmse10091171
Chicago/Turabian StyleFrolov, Sergey M., Konstantin A. Avdeev, Viktor S. Aksenov, Fedor S. Frolov, Ilias A. Sadykov, and Igor O. Shamshin. 2022. "Pulsed Detonation Hydroramjet: Design Optimization" Journal of Marine Science and Engineering 10, no. 9: 1171. https://doi.org/10.3390/jmse10091171
APA StyleFrolov, S. M., Avdeev, K. A., Aksenov, V. S., Frolov, F. S., Sadykov, I. A., & Shamshin, I. O. (2022). Pulsed Detonation Hydroramjet: Design Optimization. Journal of Marine Science and Engineering, 10(9), 1171. https://doi.org/10.3390/jmse10091171