Thermohaline Dynamics in the Northern Continental Slope of the South China Sea: A Case Study in the Qiongdongnan Slope
Abstract
:1. Introduction
2. Data and Methods
2.1. Numerical Model
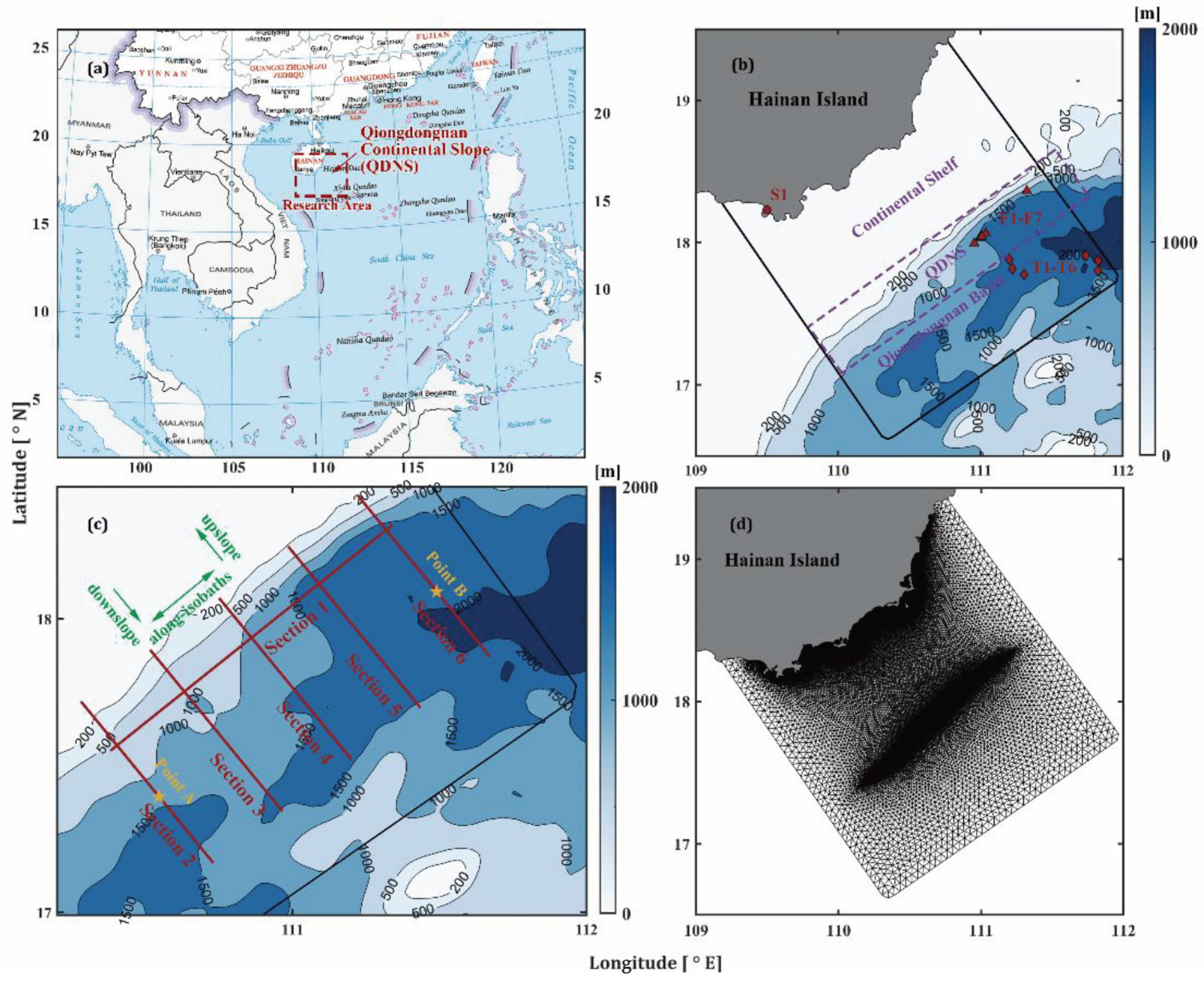
2.1.1. Model Domain
2.1.2. Model Configurations
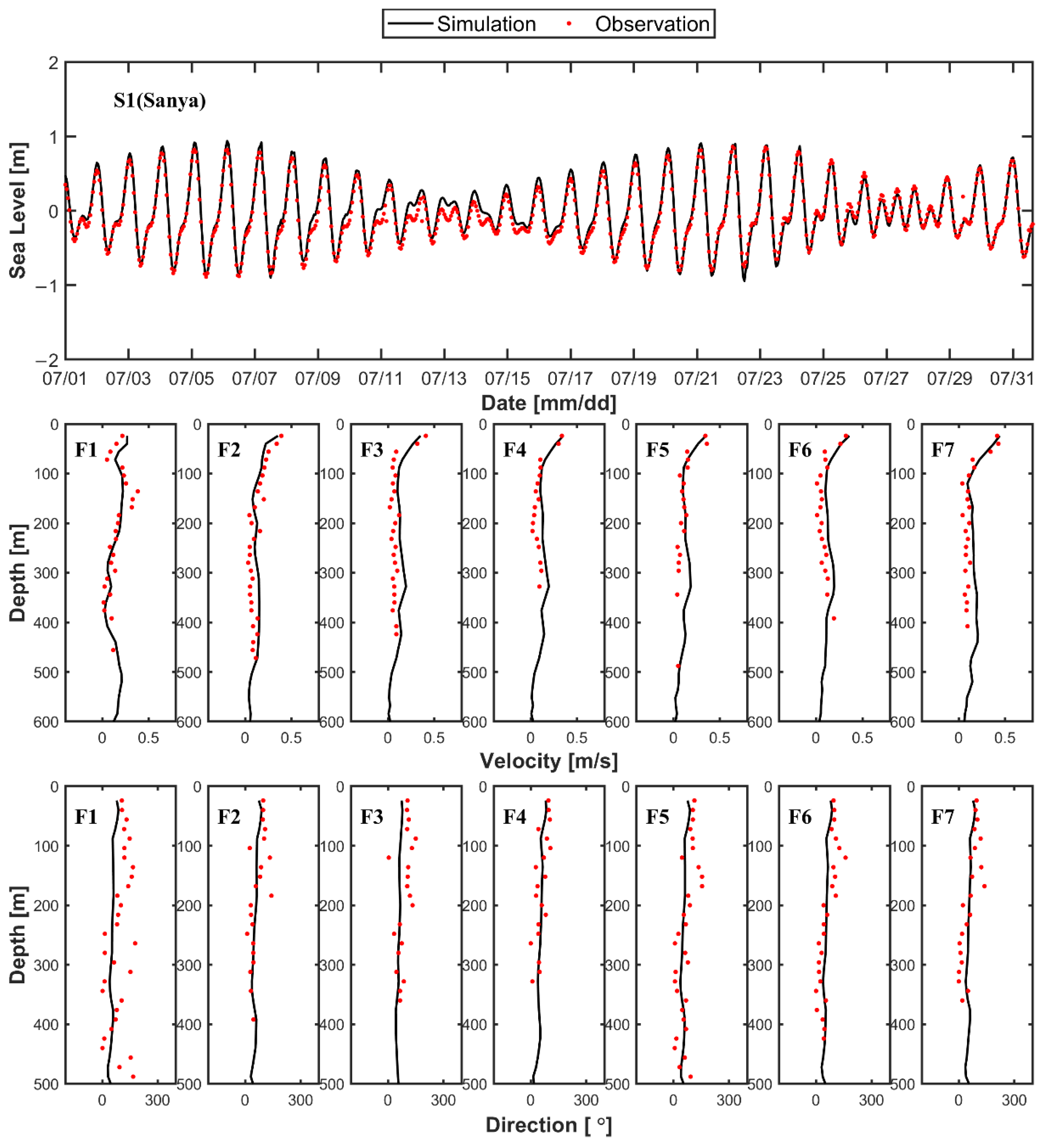
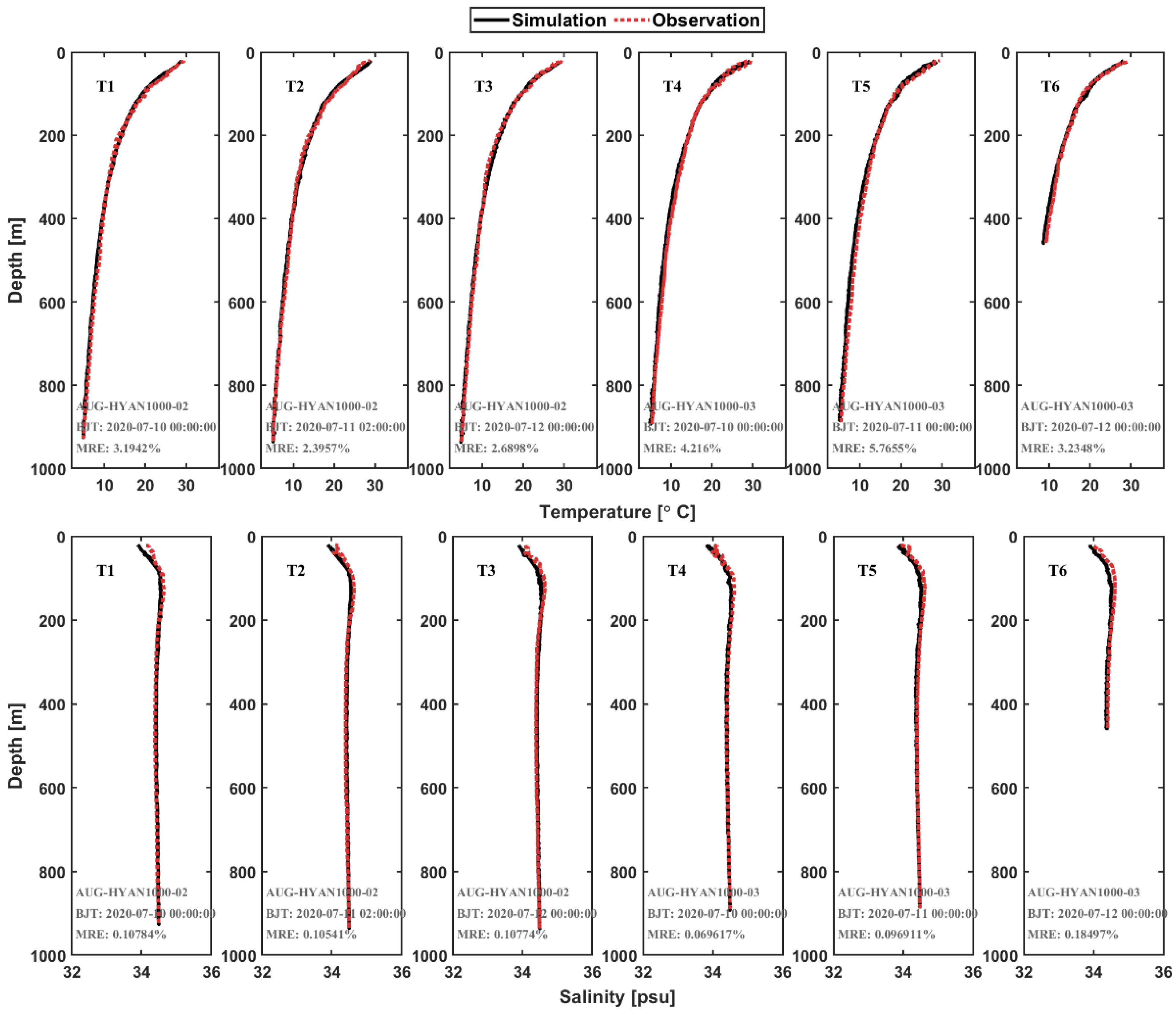
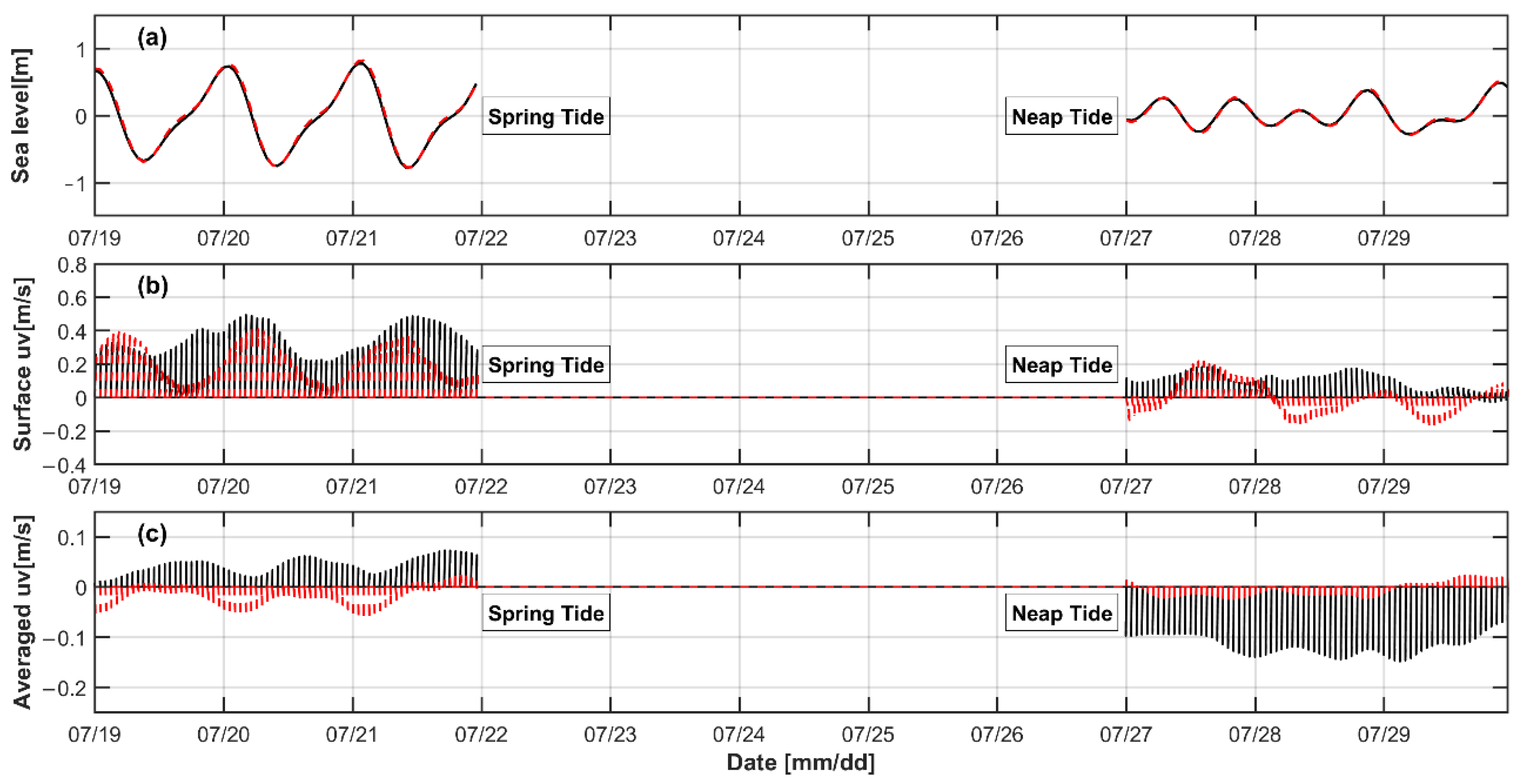
2.1.3. Model Validation
2.2. Thermohaline Balance
3. Results and Discussions
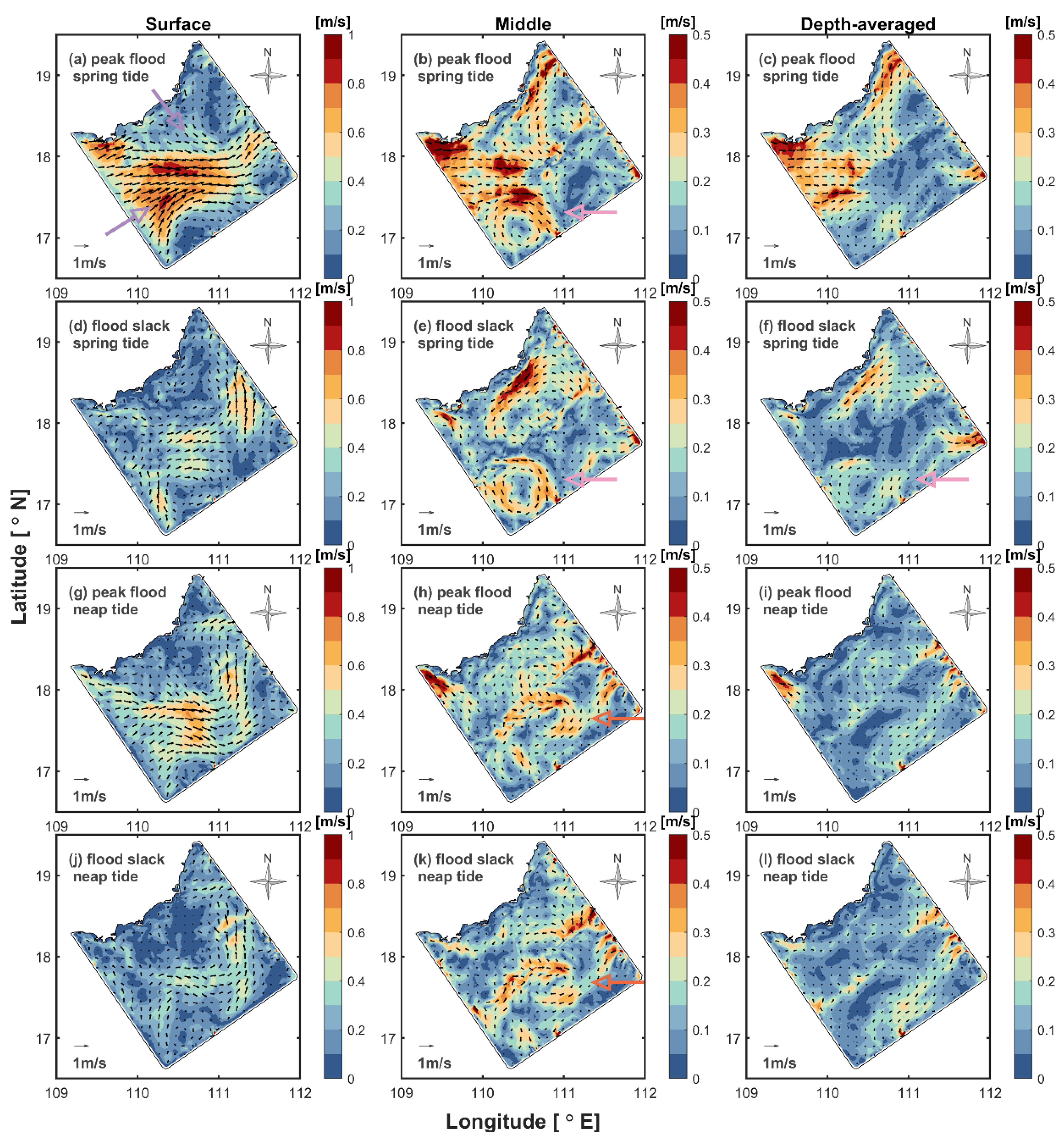
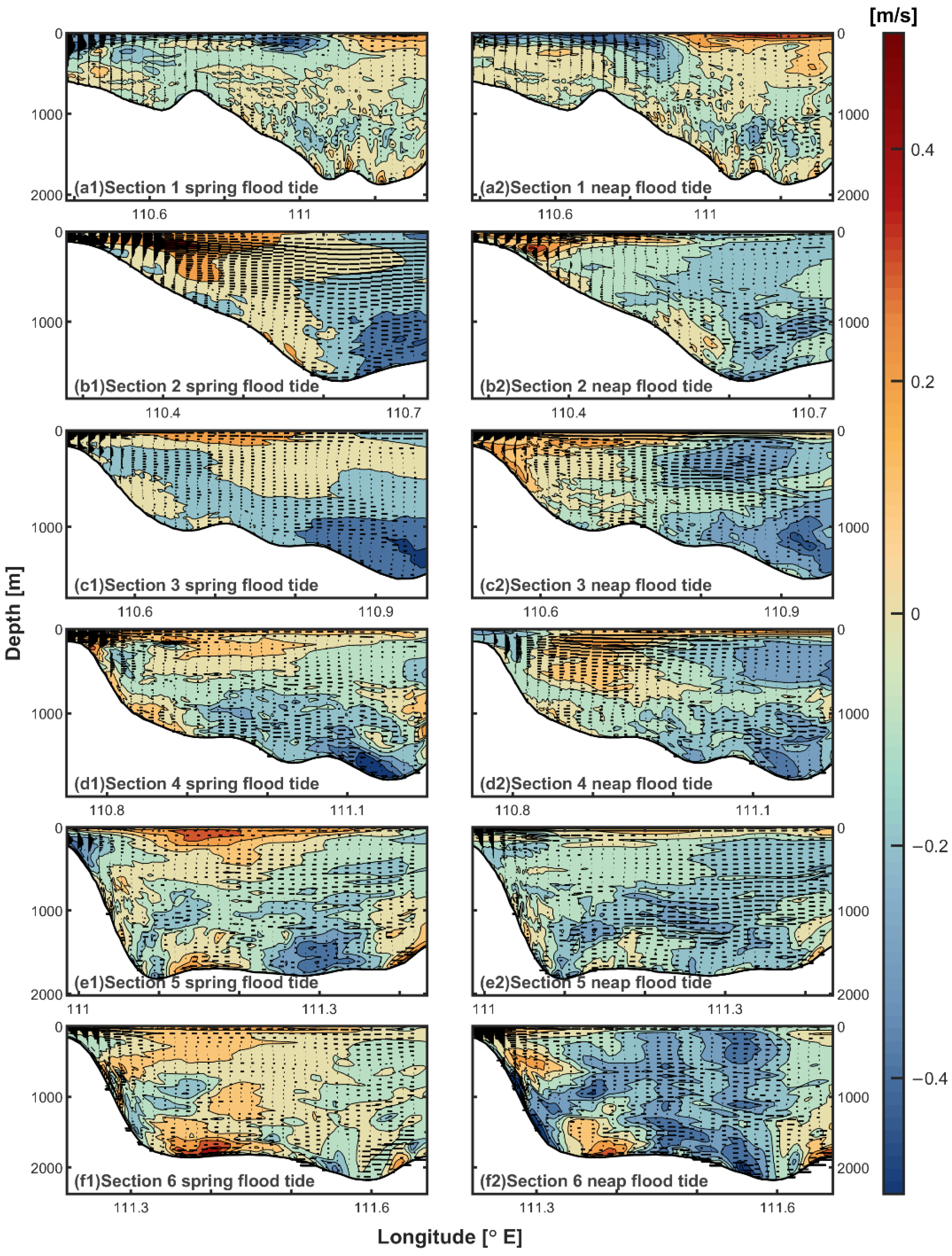
3.1. Hydrodynamic Structure
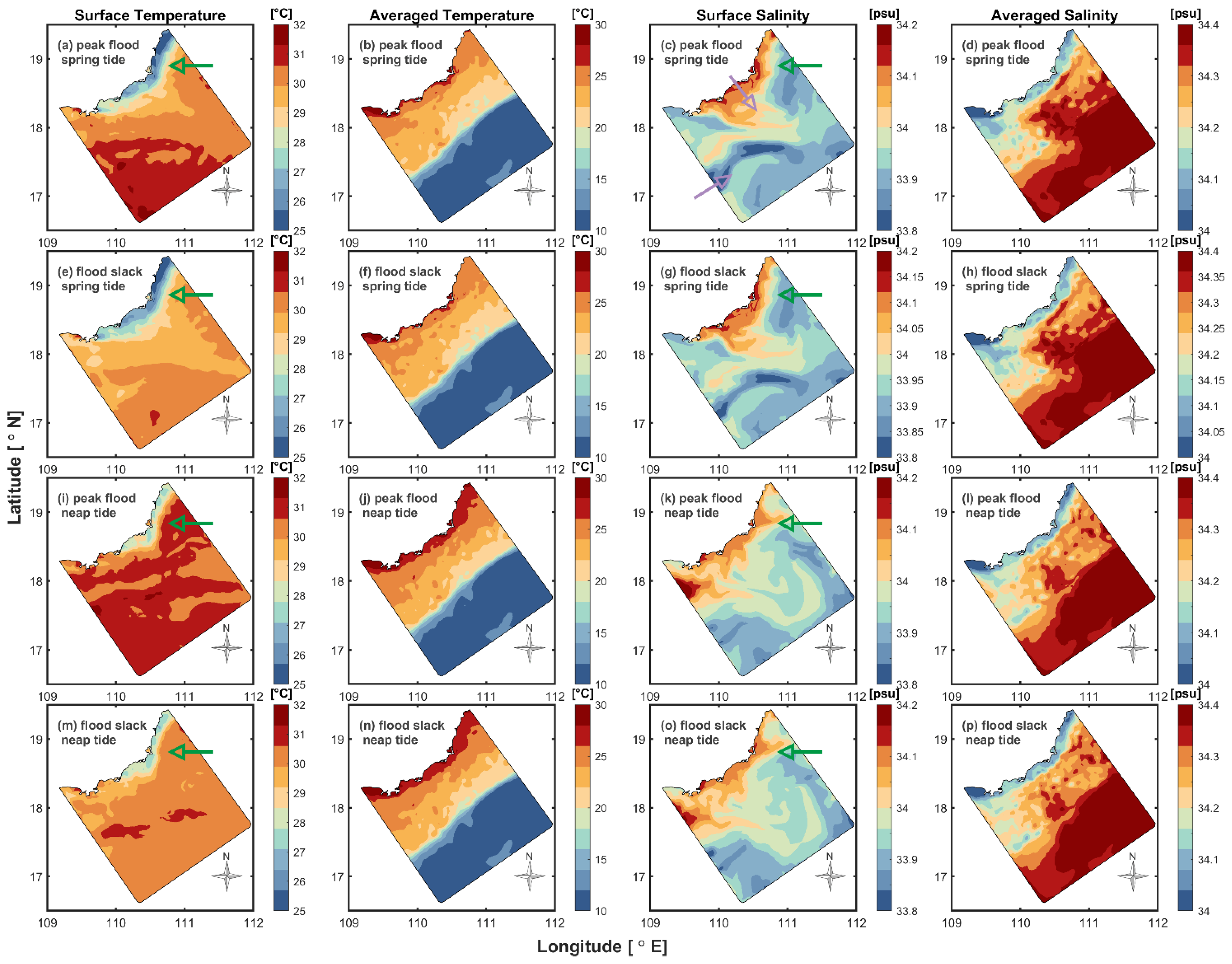
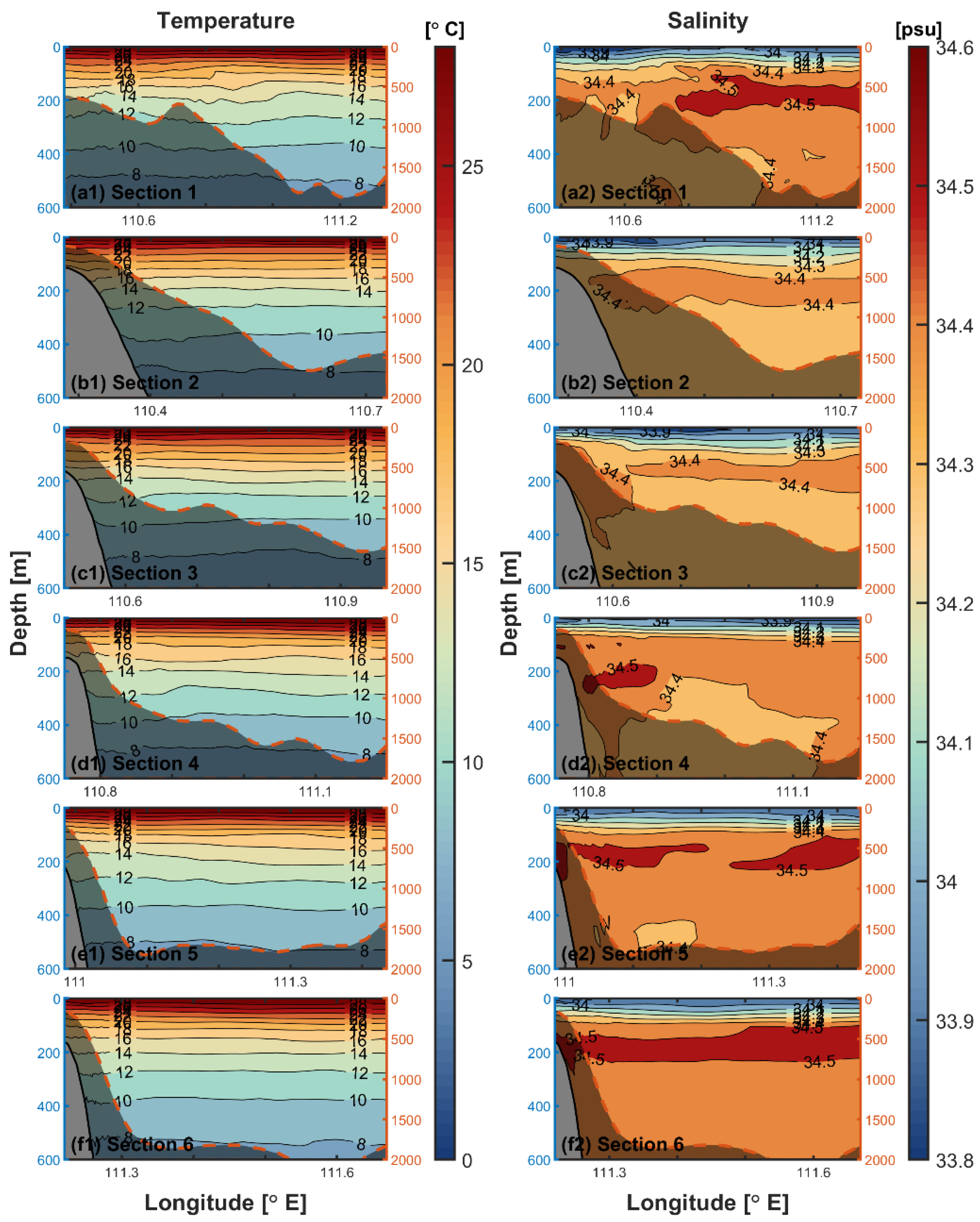
3.2. Thermohaline Structure
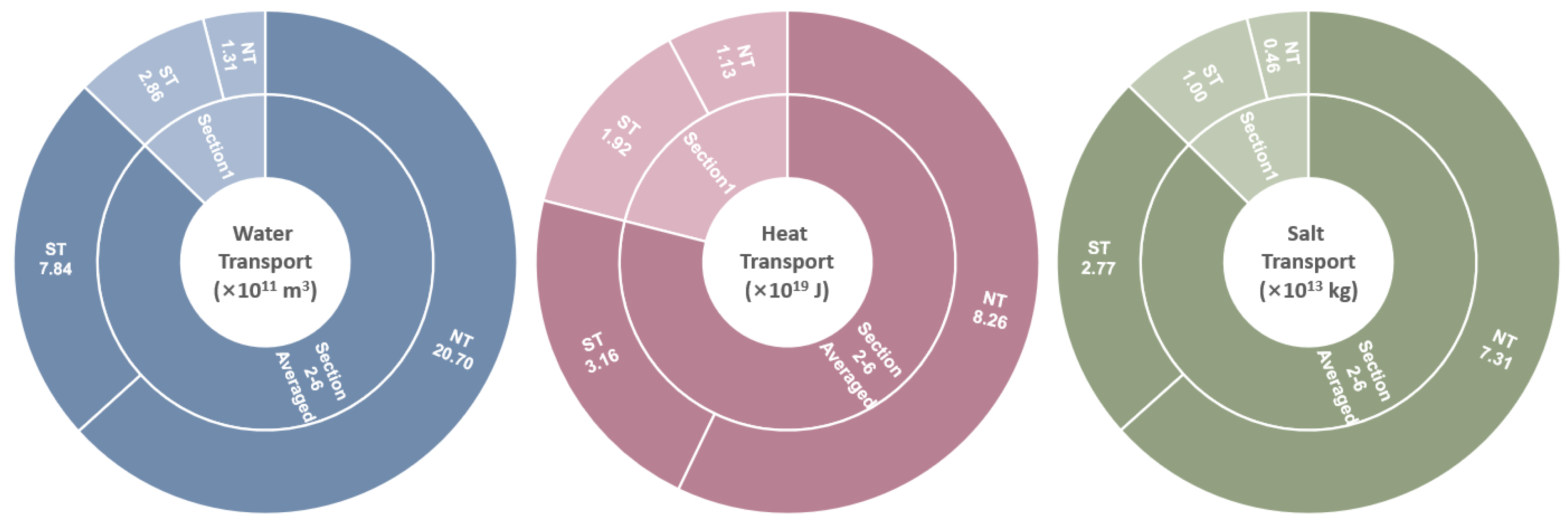
3.3. Water, Heat, and Salt Fluxes
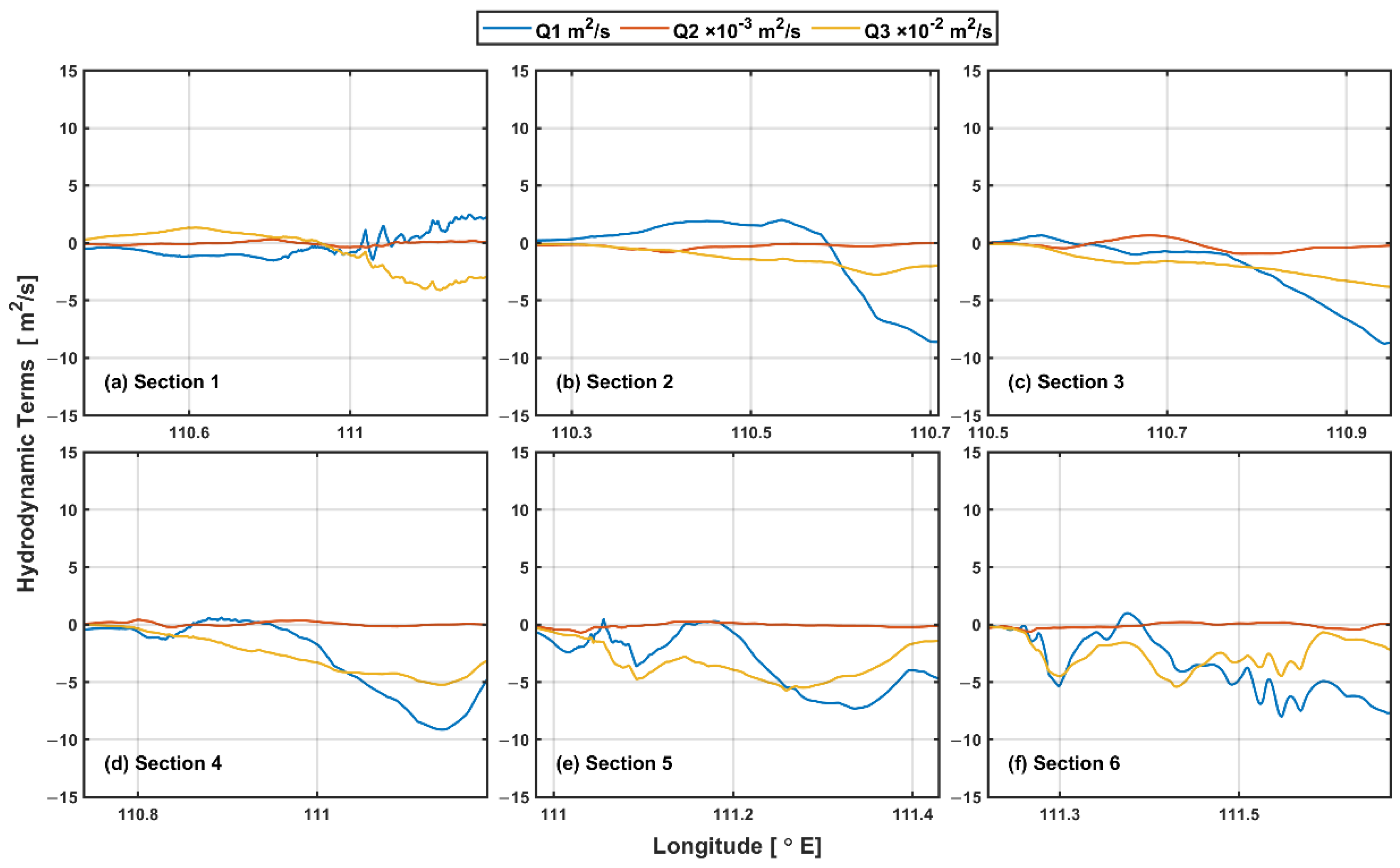
3.4. Thermohaline Balance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jing, Z.; Qi, Y.; Hua, Z.; Zhang, H. Numerical study on the summer upwelling system in the northern continental shelf of the south china sea. Cont. Shelf Res. 2009, 29, 467–478. [Google Scholar] [CrossRef]
- Wang, D.; Yang, Y.; Wang, J.; Bai, X. A modeling study of the effects of river runoff, tides, and surface wind-wave mixing on the eastern and western hainan upwelling systems of the south china sea, china. Ocean Dyn. 2015, 65, 1143–1164. [Google Scholar] [CrossRef]
- Li, Y.; Peng, S.; Wang, J.; Yan, J.; Huang, H. On the mechanism of the generation and interannual variations of the summer upwellings west and southwest off the hainan island. J. Geophys. Res. Ocean. 2018, 123, 8247–8263. [Google Scholar] [CrossRef]
- Fan, W.; Song, J.; Li, S. A numerical study on seasonal variations of the thermocline in the south china sea based on the roms. Acta Oceanol. Sin. 2014, 33, 56–64. [Google Scholar] [CrossRef]
- Johari, A.; Akhir, M.F. Exploring thermocline and water masses variability in southern south china sea from the world ocean database (wod). Acta Oceanol. Sin. 2019, 38, 38–47. [Google Scholar] [CrossRef]
- Chen, G.; Hou, Y.; Chu, X. Mesoscale eddies in the south china sea: Mean properties, spatiotemporal variability, and impact on thermohaline structure. J. Geophys. Res. 2011, 116, C06018. [Google Scholar] [CrossRef]
- Chen, G.; Gan, J.; Xie, Q.; Chu, X.; Wang, D.; Hou, Y. Eddy heat and salt transports in the south china sea and their seasonal modulations. J. Geophys. Res. Ocean. 2012, 117, C05021. [Google Scholar] [CrossRef]
- Li, D. Analysis of Water Masses in the Continental Slope of the Northern South China Sea; Shanghai Jiao Tong University: Shanghai, China, 2017. [Google Scholar]
- Lopes, P.F.M.; Verba, J.T.; Begossi, A.; Pennino, M.G. Predicting species distribution from fishers’ local ecological knowledge: A new alternative for data-poor management. Can. J. Fish. Aquat. Sci. 2019, 76, 1423–1431. [Google Scholar] [CrossRef]
- Falardeau, M.; Bennett, E.M.; Else, B.; Fisk, A.; Mundy, C.J.; Choy, E.S.; Ahmed, M.M.M.; Harris, L.N.; Moore, J.-S. Biophysical indicators and indigenous and local knowledge reveal climatic and ecological shifts with implications for arctic char fisheries. Glob. Environ. Chang. 2022, 74, 102469. [Google Scholar] [CrossRef]
- Muringai, R.T.; Mafongoya, P.L.; Lottering, R. Climate change and variability impacts on sub-saharan african fisheries: A review. Rev. Fish. Sci. Aquac. 2021, 29, 706–720. [Google Scholar] [CrossRef]
- Cai, M.; He, H.; Liu, M.; Li, S.; Tang, G.; Wang, W.; Huang, P.; Wei, G.; Lin, Y.; Chen, B.; et al. Lost but can’t be neglected: Huge quantities of small microplastics hide in the south china sea. Sci. Total Environ. 2018, 633, 1206–1216. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, H.; Chen, B.; Sun, X.; Qu, K.; Xia, B. Microplastic ingestion in deep-sea fish from the south china sea. Sci. Total Environ. 2019, 677, 493–501. [Google Scholar] [CrossRef]
- Kuo, Y.; Tseng, Y. Impact of enso on the south china sea during enso decaying winter–spring modeled by a regional coupled model (a new mesoscale perspective). Ocean Model. 2020, 152, 101655. [Google Scholar] [CrossRef]
- Xie, J.; He, Y.; Cai, S. Bumpy topographic effects on the transbasin evolution of large-amplitude internal solitary wave in the northern south china sea. J. Geophys. Res. Ocean. 2019, 124, 4677–4695. [Google Scholar] [CrossRef]
- Li, W.; Alves, T.M.; Wu, S.; Völker, D.; Zhao, F.; Mi, L.; Kopf, A. Recurrent slope failure and submarine channel incision as key factors controlling reservoir potential in the south china sea (qiongdongnan basin, south hainan island). Mar. Pet. Geol. 2015, 64, 17–30. [Google Scholar] [CrossRef]
- Estrade, P.; Marchesiello, P.; De Verdière, A.C.; Roy, C. Cross-shelf structure of coastal upwelling: A two-dimensional extension of ekman’s theory and a mechanism for inner shelf upwelling shut down. J. Mar. Res. 2008, 66, 589–616. [Google Scholar] [CrossRef]
- Chen, Z.; Yan, X.; Jiang, Y.; Jiang, L. Roles of shelf slope and wind on upwelling: A case study off east and west coasts of the us. Ocean Model. 2013, 69, 136–145. [Google Scholar] [CrossRef]
- Jacox, M.G.; Edwards, C.A. Effects of stratification and shelf slope on nutrient supply in coastal upwelling regions. J. Geophys. Res. 2011, 116, C03019. [Google Scholar] [CrossRef]
- Oke, P.R.; Middleton, J.H. Topographically induced upwelling off eastern australia. J. Phys. Oceanogr. 2000, 30, 512–531. [Google Scholar] [CrossRef]
- Su, J.; Pohlmann, T. Wind and topography influence on an upwelling system at the eastern hainan coast. J. Geophys. Res. 2009, 114, C06017. [Google Scholar] [CrossRef] [Green Version]
- Gan, J.; Liu, Z.; Hui, C.R. A three-layer alternating spinning circulation in the south china sea. J. Phys. Oceanogr. 2016, 46, 2309–2315. [Google Scholar] [CrossRef]
- Xu, F.-H.; Oey, L.-Y. State analysis using the local ensemble transform kalman filter (letkf) and the three-layer circulation structure of the luzon strait and the south china sea. Ocean Dyn. 2014, 64, 905–923. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, W.; Tian, J.; Liang, X. A mesoscale eddy pair southwest of taiwan and its influence on deep circulation. J. Geophys. Res. Ocean. 2013, 118, 6479–6494. [Google Scholar] [CrossRef]
- Liu, C.; Li, X.; Wang, S.; Tang, D.; Zhu, D. Interannual variability and trends in sea surface temperature, sea surface wind, and sea level anomaly in the south china sea. Int. J. Remote Sens. 2020, 41, 4160–4173. [Google Scholar] [CrossRef]
- Zhang, H.; Cheng, W.; Chen, Y.; Yu, L.; Gong, W. Controls on the interannual variability of hypoxia in a subtropical embayment and its adjacent waters in the guangdong coastal upwelling system, northern south china sea. Ocean Dyn. 2018, 68, 923–938. [Google Scholar] [CrossRef]
- Daryabor, F.; Ooi, S.H.; Samah, A.A.; Akbari, A. Dynamics of the water circulations in the southern south china sea and its seasonal transports. PLoS ONE 2016, 11, e0158415. [Google Scholar] [CrossRef]
- Chen, C.S.; Liu, H.D.; Beardsley, R.C. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H.F. A global, self-consistent, hierarchical, high-resolution shoreline database. J. Geophys. Res. Solid Earth 1996, 101, 8741–8743. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B.W. Etopo1 1 arc-minute global relief model: Procedures, data sources and analysis. In NOAA Technical Memorandum NESDIS NGDC-24; Barry, E., Ed.; National Geophysical Data Center: Boulder, CO, USA, 2009. [Google Scholar] [CrossRef]
- Wang, J. Global linear stability of the two-dimensional shallow-water equations: An application of the distributive theorem of roots for polynomials on the unit circle. Mon. Weather. Rev. 1996, 124, 1301–1310. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Hurlburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcraft, A.J.; Baraille, R.; Bleck, R. The hycom (hybrid coordinate ocean model) data assimilative system. J. Mar. Syst. 2007, 65, 60–83. [Google Scholar] [CrossRef]
- Foreman, M.G.G.; Bennett, A.F.; Egbert, G.D. Topex/poseidon tides estimated using a global inverse model. J. Geophys. Res. Ocean. 1994, 99, 24821–24852. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.-Y.; Iredell, M.; et al. The ncep climate forecast system version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Onken, R. Forecast skill score assessment of a relocatable ocean prediction system, using a simplified objective analysis method. Ocean Sci. 2017, 13, 925–945. [Google Scholar] [CrossRef]
- Dyer, K.R. Estuaries: A Physical Introduction; University of Plymouth: Plymouth, UK, 1997. [Google Scholar]
- Bai, P.; Gu, Y.; Li, P.; Wu, K. Modelling the upwelling off the east hainan island coast in summer 2010. Chin. J. Oceanol. Limnol. 2016, 34, 1358–1373. [Google Scholar] [CrossRef]
- He, Q.; Zhan, H.; Cai, S.; He, Y.; Huang, G.; Zhan, W. A new assessment of mesoscale eddies in the south china sea: Surface features, three-dimensional structures, and thermohaline transports. J. Geophys. Res. Ocean. 2018, 123, 4906–4929. [Google Scholar] [CrossRef]


| Forcing Condition | Forcing Type | Source |
|---|---|---|
| Initial | Tide | 0 |
| Flow | 0 | |
| Temperature | HYCOM GOFS 3.1 [32] | |
| Salinity | HYCOM GOFS 3.1 [32] | |
| Open boundary | Tide | TPXO 7.2 [33] |
| Flow | 0 | |
| Temperature | HYCOM GOFS 3.1 [32] | |
| Salinity | HYCOM GOFS 3.1 [32] | |
| Free Surface | wind | NCEP CFSv2 [34] |
| heat flux | NCEP CFSv2 [34] |
| Sea Level | 0.99 | 0.99 | |
| Flow | 0.81 | 0.77 | |
| Temperature | - | 3.58 | |
| Salinity | - | 0.11 |
| Units | Section 1 | Section 2 | Section 3 | Section 4 | Section 5 | Section 6 | |
|---|---|---|---|---|---|---|---|
| Max water flux (ST) | ×106 m3/s ≡ Sv | −3.59 | −5.06 | −9.70 | −12.83 | −10.87 | 8.03 |
| Max water flux (NT) | ×106 m3/s ≡ Sv | −2.11 | −6.39 | −7.19 | −8.00 | −11.61 | −17.59 |
| Net water transport (ST) | ×1011 m3 | −2.86 | −2.70 | −13.55 | −18.28 | −15.44 | 10.78 |
| Net water transport (NT) | ×1011 m3 | −1.31 | −11.79 | −14.24 | −15.07 | −23.88 | −38.50 |
| Max heat flux (ST) | ×1014 W | −1.89 | −1.98 | −4.40 | −5.42 | −4.59 | 3.30 |
| Max heat flux (NT) | ×1014 W | −1.18 | −2.45 | −3.07 | −3.39 | −4.82 | −6.87 |
| Net heat transport (ST) | ×1019 J | −1.92 | −0.11 | −5.93 | −7.55 | −6.63 | 4.44 |
| Net heat transport (NT) | ×1019 J | −1.13 | −4.36 | −5.70 | −6.30 | −9.89 | −15.06 |
| Max salt flux (ST) | ×108 kg/s | −1.26 | −1.78 | −3.42 | −4.53 | −3.84 | 2.84 |
| Max salt flux (NT) | ×108 kg/s | −0.74 | −2.25 | −2.54 | −2.83 | −4.10 | −6.22 |
| Net salt transport (ST) | ×1013 kg | −1.00 | −0.96 | −4.78 | −6.45 | −5.45 | 3.81 |
| Net salt transport (NT) | ×1013 kg | −0.46 | −4.16 | −5.03 | −5.32 | −8.44 | −13.61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Hu, W.; Li, L.; Pähtz, T.; Li, J. Thermohaline Dynamics in the Northern Continental Slope of the South China Sea: A Case Study in the Qiongdongnan Slope. J. Mar. Sci. Eng. 2022, 10, 1221. https://doi.org/10.3390/jmse10091221
He Z, Hu W, Li L, Pähtz T, Li J. Thermohaline Dynamics in the Northern Continental Slope of the South China Sea: A Case Study in the Qiongdongnan Slope. Journal of Marine Science and Engineering. 2022; 10(9):1221. https://doi.org/10.3390/jmse10091221
Chicago/Turabian StyleHe, Zhiguo, Wenlin Hu, Li Li, Thomas Pähtz, and Jianlong Li. 2022. "Thermohaline Dynamics in the Northern Continental Slope of the South China Sea: A Case Study in the Qiongdongnan Slope" Journal of Marine Science and Engineering 10, no. 9: 1221. https://doi.org/10.3390/jmse10091221







