Effect of Service Priority on the Integrated Continuous Berth Allocation and Quay Crane Assignment Problem after Port Congestion
Abstract
:1. Introduction
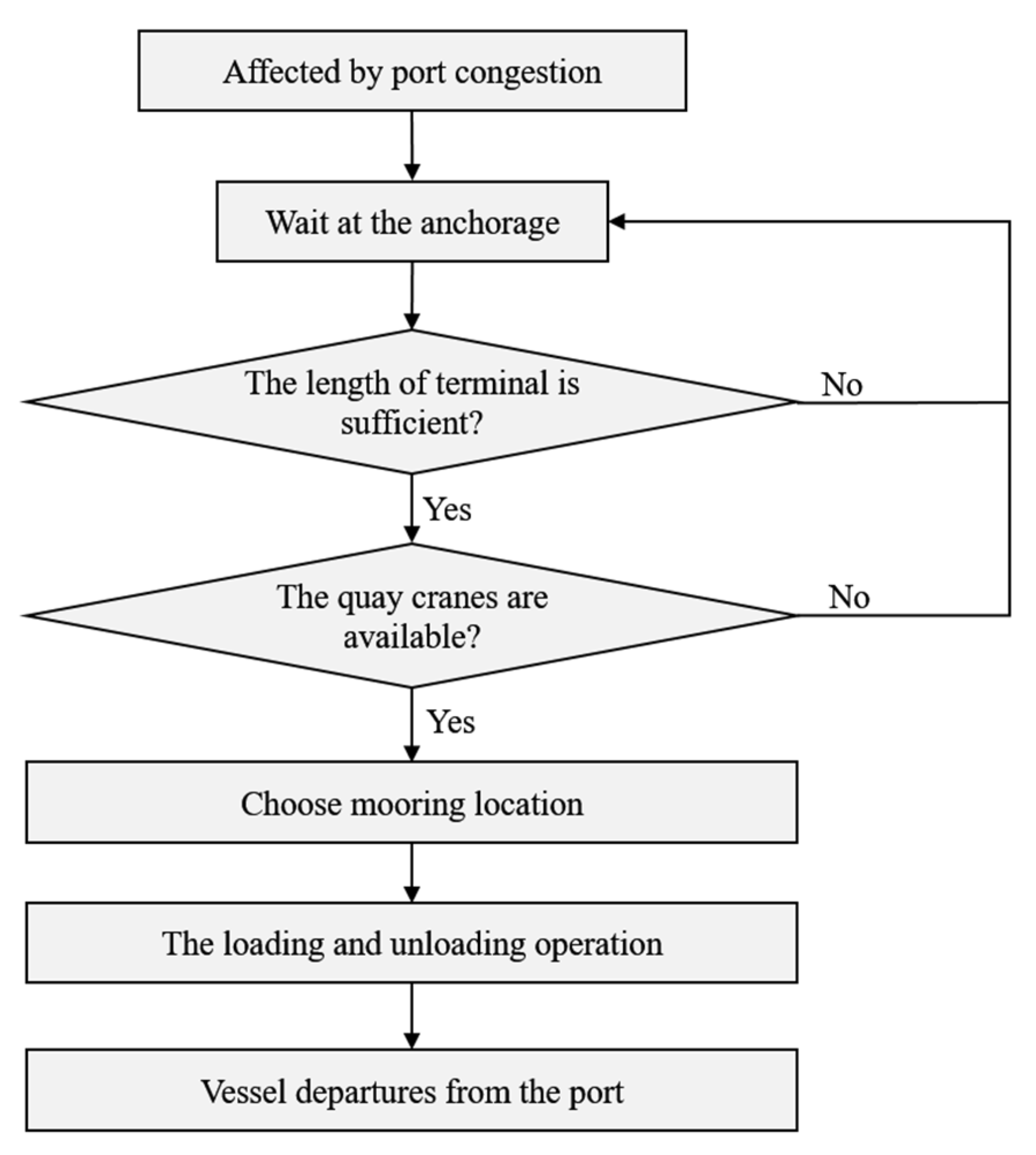
2. Problem Description and Model Formulation
2.1. Parameters
2.2. Basic Assumptions
2.3. Model Formulation
3. Solution Method
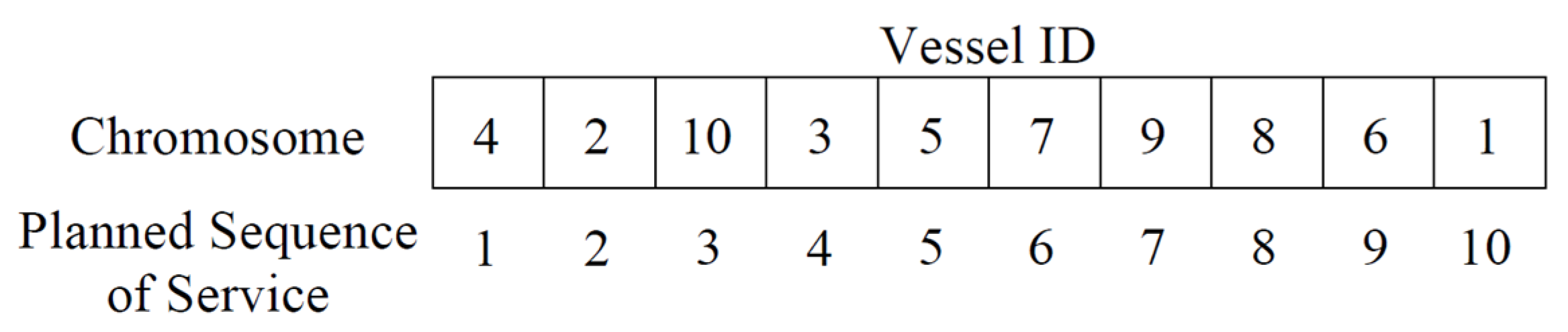
3.1. Chromosome Structure and Initialization
3.2. Fitness Evaluation
3.3. Crossover
3.4. Mutation
3.5. Selection
4. Results
4.1. Computational Experiments
4.2. Parameter Setting
4.3. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Statistics Bulletin of Transportation Industry Development in 2021. Available online: http://www.gov.cn/shuju/2022-05/25/content_5692174.htm (accessed on 20 July 2022).
- Muren; Meng, W.Y.; Li, G.R.; Hua, L.L. A goal-programming based optimal port docking scheme under COVID-19. Ocean. Coast. Manag. 2022, 225, 11. [Google Scholar] [CrossRef]
- Gui, D.P.; Wang, H.Y.; Yu, M. Risk Assessment of Port Congestion Risk during the COVID-19 Pandemic. J. Mar. Sci. Eng. 2022, 10, 150. [Google Scholar] [CrossRef]
- Christodoulou, A.; Kappelin, H. Determinant factors for the development of maritime supply chains: The case of the Swedish forest industry. Case Stud. Transp. Policy 2020, 8, 711–720. [Google Scholar] [CrossRef]
- Kontovas, C.; Psaraftis, H.N. Reduction of emissions along the maritime intermodal container chain: Operational models and policies. Marit. Policy Manag. 2011, 38, 451–469. [Google Scholar] [CrossRef]
- Winnes, H.; Styhre, L.; Fridell, E. Reducing GHG emissions from ships in port areas. Res. Transp. Bus. Manag. 2015, 17, 73–82. [Google Scholar] [CrossRef]
- Poulsen, R.T.; Sampson, H. A swift turnaround? Abating shipping greenhouse gas emissions via port call optimization. Transp. Res. Part D Transp. Environ. 2020, 86, 102460. [Google Scholar] [CrossRef]
- Christodoulou, A.; Gonzalez-Aregall, M.; Linde, T.; Vierth, I.; Cullinane, K. Targeting the reduction of shipping emissions to air A global review and taxonomy of policies, incentives and measures. Marit. Bus. Rev. 2019, 4, 16–30. [Google Scholar] [CrossRef]
- Poulsen, R.T.; Sampson, H. ‘Swinging on the anchor’: The difficulties in achieving greenhouse gas abatement in shipping via virtual arrival. Transport. Res. Part D Transport. Environ. 2019, 73, 230–244. [Google Scholar] [CrossRef]
- Imai, A.; Nishimura, E.; Hattori, M.; Papadimitriou, S. Berth allocation at indented berths for mega-containerships. Eur. J. Oper. Res. 2007, 179, 579–593. [Google Scholar] [CrossRef]
- Gharehgozli, A.H.; Roy, D.; de Koster, R. Sea container terminals: New technologies and OR models. Marit. Econ. Logist. 2016, 18, 103–140. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A survey of berth allocation and quay crane scheduling problems in container terminals. Eur. J. Oper. Res. 2010, 202, 615–627. [Google Scholar] [CrossRef]
- Iris, Ç.; Pacino, D.; Ropke, S. Improved formulations and an adaptive large neighborhood search heuristic for the integrated berth allocation and quay crane assignment problem. Transp. Res. Part E Logist. Transp. Rev. 2017, 105, 123–147. [Google Scholar] [CrossRef]
- Malekahmadi, A.; Alinaghian, M.; Hejazi, S.R.; Saidipour, M.A.A. Integrated continuous berth allocation and quay crane assignment and scheduling problem with time-dependent physical constraints in container terminals. Comput. Ind. Eng. 2020, 147, 106672. [Google Scholar] [CrossRef]
- Zheng, F.F.; Li, Y.; Chu, F.; Liu, M.; Xu, Y.F. Integrated berth allocation and quay crane assignment with maintenance activities. Int. J. Prod. Res. 2019, 57, 3478–3503. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Shahbazzade, S. The improved AFSA algorithm for the berth allocation and quay crane assignment problem. Clust. Comput. 2019, 22, 3665–3672. [Google Scholar] [CrossRef]
- Correcher, J.F.; Alvarez-Valdes, R.; Tamarit, J.M. New exact methods for the time-invariant berth allocation and quay crane assignment problem. Eur. J. Oper. Res. 2019, 275, 80–92. [Google Scholar] [CrossRef]
- Tang, M.; Ji, B.; Fang, X.P.; Yu, S.S. Discretization-strategy-based solution for berth allocation and quay crane assignment problem. J. Mar. Sci. Eng. 2022, 10, 495. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A follow-up survey of berth allocation and quay crane scheduling problems in container terminals. Eur. J. Oper. Res. 2015, 244, 675–689. [Google Scholar] [CrossRef]
- Wang, T.S.; Wang, X.C.; Meng, Q. Joint berth allocation and quay crane assignment under different carbon taxation policies. Transp. Res. Part B Methodol. 2018, 117, 18–36. [Google Scholar] [CrossRef]
- Agra, A.; Oliveira, M. MIP approaches for the integrated berth allocation and quay crane assignment and scheduling problem. Eur. J. Oper. Res. 2018, 264, 138–148. [Google Scholar] [CrossRef] [Green Version]
- Türkoğulları, Y.B.; Taskin, Z.C.; Aras, N.; Altınel, K. Optimal berth allocation and time-invariant quay crane assignment in container terminals. Eur. J. Oper. Res. 2014, 235, 88–101. [Google Scholar] [CrossRef]
- Li, F.; Yang, D.; Wang, S.; Weng, J.X. Ship routing and scheduling problem for steel plants cluster alongside the Yangtze River. Transp. Res. Part E Logist. Transp. Rev. 2019, 122, 198–210. [Google Scholar] [CrossRef]
- Lujan, E.; Vergara, E.; Rodriguez-Melquiades, J.; Jiménez-Carrión, M.; Sabino-Escobar, C.; Gutierrez, F. A fuzzy optimization model for the berth allocation problem and quay crane allocation problem (BAP + QCAP) with n quays. J. Mar. Sci. Eng. 2021, 9, 15. [Google Scholar] [CrossRef]
- Shang, X.T.; Cao, J.X.; Ren, J. A robust optimization approach to the integrated berth allocation and quay crane assignment problem. Transp. Res. Part E Logist. Transp. Rev. 2016, 94, 44–65. [Google Scholar] [CrossRef]
- Correcher, J.F.; Alvarez-Valdes, R. A biased random-key genetic algorithm for the time-invariant berth allocation and quay crane assignment problem. Expert Syst. Appl. 2017, 89, 112–128. [Google Scholar] [CrossRef]
- Liu, D.D.; Shi, G.Y.; Kang, Z. Fuzzy scheduling problem of vessels in one-way waterway. J. Mar. Sci. Eng. 2021, 9, 1064. [Google Scholar] [CrossRef]
- Fatemi-Anaraki, S.; Tavakkoli-Moghaddam, R.; Abdolhamidi, D.; Vahedi-Nouri, B. Simultaneous waterway scheduling, berth allocation, and quay crane assignment: A novel matheuristic approach. Int. J. Prod. Res. 2020, 59, 7576–7593. [Google Scholar] [CrossRef]
- Imai, A.; Chen, H.C.; Nishimura, E.; Papadimitriou, S. The simultaneous berth and quay crane allocation problem. Transp. Res. Part E Logist. Transp. Rev. 2008, 44, 900–920. [Google Scholar] [CrossRef]
- Giallombardo, G.; Moccia, L.; Salani, M.; Vacca, I. Modeling and solving the tactical berth allocation problem. Transp. Res. Part B Methodol. 2010, 44, 232–245. [Google Scholar] [CrossRef]
- Lin, S.W.; Ting, C.J. Solving the dynamic berth allocation problem by simulated annealing. Eng. Optim. 2014, 46, 308–327. [Google Scholar] [CrossRef]
- Hsu, H.P. A HPSO for solving dynamic and discrete berth allocation problem and dynamic quay crane assignment problem simultaneously. Swarm Evol. Comput. 2016, 27, 156–168. [Google Scholar] [CrossRef]
- Wang, K.; Zhen, L.; Wang, S.; Laporte, G. Column generation for the integrated berth allocation, quay crane assignment, and yard assignment problem. Transp. Sci. 2018, 52, 812–834. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, W.Y.; Jiang, Y.; Xu, X.L.; Xu, Y.Z.; Guo, Z.J. Joint berth allocation and ship loader scheduling under the rotary loading mode in coal export terminals. Transp. Res. Part B Methodol. 2022, 162, 229–260. [Google Scholar] [CrossRef]
- Jiang, M.X.; Zhou, J.; Feng, J.J.; Zhou, L.; Ma, F.Z.; Wu, G.H. Integrated berth and crane scheduling problem considering crane coverage in multi-terminal tidal ports under uncertainty. J. Mar. Sci. Eng. 2022, 10, 506. [Google Scholar] [CrossRef]
- Cheong, C.Y.; Tan, K.C.; Liu, D.K.; Lin, C.J. Multi-objective and prioritized berth allocation in container ports. Ann. Oper. Res. 2010, 180, 63–103. [Google Scholar] [CrossRef]
- Tang, L.M.; Dai, L.L. Berth allocation with service priority for container terminal of hub port. In Proceedings of the 4th International Conference on Wireless Communications, Networking and Mobile Computing, Dalian, China, 12–14 October 2018; pp. 8490–8493. [Google Scholar]
- Imai, A.; Nishimura, E.; Papadimitriou, S. Berth allocation with service priority. Transp. Res. Part B Methodol. 2003, 37, 437–457. [Google Scholar] [CrossRef]
- Zhang, Y.T.; Zhao, G. Dynamic distribution of berth-quay crane based on ship’s priority. In Proceedings of the 2018 6th International Conference on Machinery, Materials and Computing Technology, Osaka, Japan, 6–8 January 2018; Zuo, M., Ed.; Atlantis Press: Paris, France, 2018; Volume 152, pp. 141–146. [Google Scholar]
- Xu, D.; Li, C.-L.; Leung, J.Y.T. Berth allocation with time-dependent physical limitations on vessels. Eur. J. Oper. Res. 2012, 216, 47–56. [Google Scholar] [CrossRef]
- Stergiopoulos, G.; Valvis, E.; Mitrodimas, D.; Lekkas, D.; Gritzalis, D. Analyzing Congestion Interdependencies of Ports and Container Ship Routes in the Maritime Network Infrastructure. IEEE Access 2018, 6, 63823–63832. [Google Scholar] [CrossRef]
- Xu, B.W.; Li, J.J.; Liu, X.Y.; Yang, Y.S. System Dynamics Analysis for the Governance Measures Against Container Port Congestion. IEEE Access 2021, 9, 13612–13623. [Google Scholar] [CrossRef]
- Dulebenets, M.A. An adaptive island evolutionary algorithm for the berth scheduling problem. Memetic Comput. 2020, 12, 51–72. [Google Scholar] [CrossRef]
- Jia, S.; Li, C.L.; Xu, Z. A simulation optimization method for deep-sea vessel berth planning and feeder arrival scheduling at a container port. Transp. Res. Part B Methodol. 2020, 142, 174–196. [Google Scholar] [CrossRef]
- Song, Y.T.; Wang, N.U. On probability distributions of the time deviation law of container liner ships under interference uncertainty. J. R. Stat. Soc. Ser. A 2021, 184, 354–367. [Google Scholar] [CrossRef]
- Transport, C.W. Lianyungang MSA Makes Every Effort to Ensure the Navigation Safety of Ships. Available online: http://www.zgsyb.com/news.html?aid=373443 (accessed on 20 July 2022).
- Xiang, X.; Liu, C.C.; Miao, L.X. A bi-objective robust model for berth allocation scheduling under uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2017, 106, 294–319. [Google Scholar] [CrossRef]
- Meisel, F.; Bierwirth, C. Heuristics for the integration of crane productivity in the berth allocation problem. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 196–209. [Google Scholar] [CrossRef]
- Wang, T.S.; Du, Y.Q.; Fang, D.B.; Li, Z.C. Berth allocation and quay crane assignment for the trade-off between service efficiency and operating cost considering carbon emission taxation. Transp. Sci. 2020, 54, 1307–1331. [Google Scholar] [CrossRef]
- Lim, A. The berth planning problem. Oper. Res. Lett. 1998, 22, 105–110. [Google Scholar] [CrossRef]
- Chang, D.F.; Jiang, Z.H.; Yan, W.; He, J.L. Integrating berth allocation and quay crane assignments. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 975–990. [Google Scholar] [CrossRef]
- Wang, Q.J. Using genetic algorithms to optimise model parameters. Environ. Modell. Softw. 1997, 12, 27–34. [Google Scholar] [CrossRef]
- Ganji, S.R.S.; Babazadeh, A.; Arabshahi, N. Analysis of the continuous berth allocation problem in container ports using a genetic algorithm. J. Mar. Sci. Technol. 2010, 15, 408–416. [Google Scholar] [CrossRef]
- Tan, C.M.; He, J.L. Integrated proactive and reactive strategies for sustainable berth allocation and quay crane assignment under uncertainty. Ann. Oper. Res. 2021, 1–32. [Google Scholar] [CrossRef]
- Yu, J.J.; Tang, G.L.; Song, X.Q. Collaboration of vessel speed optimization with berth allocation and quay crane assignment considering vessel service differentiation. Transp. Res. Part E Logist. Transp. Rev. 2022, 160, 102651. [Google Scholar] [CrossRef]
- Liu, J.; Huang, W.; Shi, X. Damage Diagnosis for Offshore Platform Based on Genetic Algorithm. J. Vib. Meas. Diagn. 2012, 32, 327–331. [Google Scholar]
- Nishimura, E.; Imai, A.; Papadimitriou, S. Berth allocation planning in the public berth system by genetic algorithms. Eur. J. Oper. Res. 2001, 131, 282–292. [Google Scholar] [CrossRef]
- Tao, Z. TSP problem solution based on improved genetic algorithm. In Proceedings of the Icnc 2008: Fourth International Conference on Natural Computation, Jinan, China, 18–20 October 2008; Volume 1, pp. 686–690. [Google Scholar]
- Lazzerini, B.; Marcelloni, F. A genetic algorithm for generating optimal assembly plans. Artif. Intell. Eng. 2000, 14, 319–329. [Google Scholar] [CrossRef]
- Pongcharoen, P.; Hicks, C.; Braiden, P.M. The development of genetic algorithms for the finite capacity scheduling of complex products, with multiple levels of product structure. Eur. J. Oper. Res. 2004, 152, 215–225. [Google Scholar] [CrossRef]
- Yu, T.; Qiang, Z.; Benfei, Z. A genetic algorithm based on spatiotemporal conflict between continuous berth-allocation and time-varying specific crane assignment. Eng. Optim. 2019, 51, 390–411. [Google Scholar] [CrossRef]



| DWT(t) | 20,000 | 100,000 |
|---|---|---|
| (m) | U[129, 219] | U[294, 353] |
| (TEU) | ||
| 3 | 5 | |
| 2 | 4 | |
| (h) | ||
| Percentage | 80% | 20% |
| Vessel Number | Ship Length (m) | Loading and Unloading Volume (TEU) | Assigned Quay Cranes Number | Planned Departure Time (h) |
|---|---|---|---|---|
| 1 | 173 | 638 | 2 | 11 |
| 2 | 193 | 780 | 3 | 12 |
| 3 | 190 | 758 | 3 | 12 |
| 4 | 140 | 405 | 2 | 10 |
| 5 | 160 | 546 | 3 | 11 |
| 6 | 197 | 808 | 2 | 12 |
| 7 | 192 | 773 | 3 | 12 |
| 8 | 178 | 673 | 2 | 12 |
| 9 | 309 | 1600 | 5 | 18 |
| 10 | 342 | 1834 | 4 | 20 |
| Index | Vessel Type | Case 1: 1 | Case 2: C | Case 3: C2 |
|---|---|---|---|---|
| Average Operating Sequence | Large | 9.3 | 7.5 | 5.1 |
| Small | 4.6 | 5.0 | 5.6 | |
| Average Delay Departure Time (h) | Large | 7.049 | 3.189 | 0.553 |
| Small | 1.417 | 2.577 | 6.035 | |
| Average Time of Vessels at Port (h) | Large | 25.874 | 22.062 | 17.087 |
| Small | 11.601 | 11.977 | 16.366 | |
| Total Delay Departure Time of Vessels (h) | 25.436 | 26.992 | 49.390 | |
| Total Time of Vessels at Port (h) | 144.555 | 139.937 | 165.099 | |
| Total Waiting Time for Berthing (h) | 43.364 | 50.991 | 66.171 | |
| Vessel ID | The Berthing Order of Vessels with Different Service Priorities | ||
|---|---|---|---|
| Case 1: 1 | Case 2: C | Case 3: C2 | |
| 1 | 6 | 9 | 9 |
| 2 | 8 | 3 | 7 |
| 3 | 3 | 10 | 1 |
| 4 | 1 | 5 | 2 |
| 5 | 2 | 2 | 10 |
| 6 | 4 | 1 | 5 |
| 7 | 7 | 8 | 3 |
| 8 | 5 | 4 | 8 |
| 9 | 10 | 6 | 6 |
| 10 | 9 | 7 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, S.; Xu, S.; Gao, J.; Ma, M.; Liao, P. Effect of Service Priority on the Integrated Continuous Berth Allocation and Quay Crane Assignment Problem after Port Congestion. J. Mar. Sci. Eng. 2022, 10, 1259. https://doi.org/10.3390/jmse10091259
Tang S, Xu S, Gao J, Ma M, Liao P. Effect of Service Priority on the Integrated Continuous Berth Allocation and Quay Crane Assignment Problem after Port Congestion. Journal of Marine Science and Engineering. 2022; 10(9):1259. https://doi.org/10.3390/jmse10091259
Chicago/Turabian StyleTang, Shuang, Sudong Xu, Jianwen Gao, Mengdi Ma, and Peng Liao. 2022. "Effect of Service Priority on the Integrated Continuous Berth Allocation and Quay Crane Assignment Problem after Port Congestion" Journal of Marine Science and Engineering 10, no. 9: 1259. https://doi.org/10.3390/jmse10091259
APA StyleTang, S., Xu, S., Gao, J., Ma, M., & Liao, P. (2022). Effect of Service Priority on the Integrated Continuous Berth Allocation and Quay Crane Assignment Problem after Port Congestion. Journal of Marine Science and Engineering, 10(9), 1259. https://doi.org/10.3390/jmse10091259






