On the Non-Gaussianity of Sea Surface Elevations
Abstract
:1. Introduction
- a, more general, Weibull distribution [13],
- a Forristall distribution [1],
- a Naess distribution [14],
- a Boccotti distribution [15],
- a Klopman distribution [16],
- a van Vledder distribution [17],
- a Battjes–Groenendijk distribution [18],
- a Mendez distribution [19], or
- a LoWiSh II distribution [20].
2. Datasets
3. Methodology
- for all where E denotes the expectation function,
- for all where denotes the covariance function and
- for all where denotes the variance.
3.1. Tests for Stationarity
- 1.
- Ljung-Box test [41],
- 2.
- Augmented Dickey-Fuller test [42],
- 3.
- Phillips-Perron test [43] and
- 4.
- kpps test [44].
3.2. Tests for Gaussianity
Random Projection Test
- 1.
- Letdenote a beta distribution with parameters
- 2.
- Let be drawn from the distribution Note that
- 3.
- For any the natural numbers, let be the result of multiplyingand an element drawn independently from he distribution Note that
3.3. False Discovery Rate
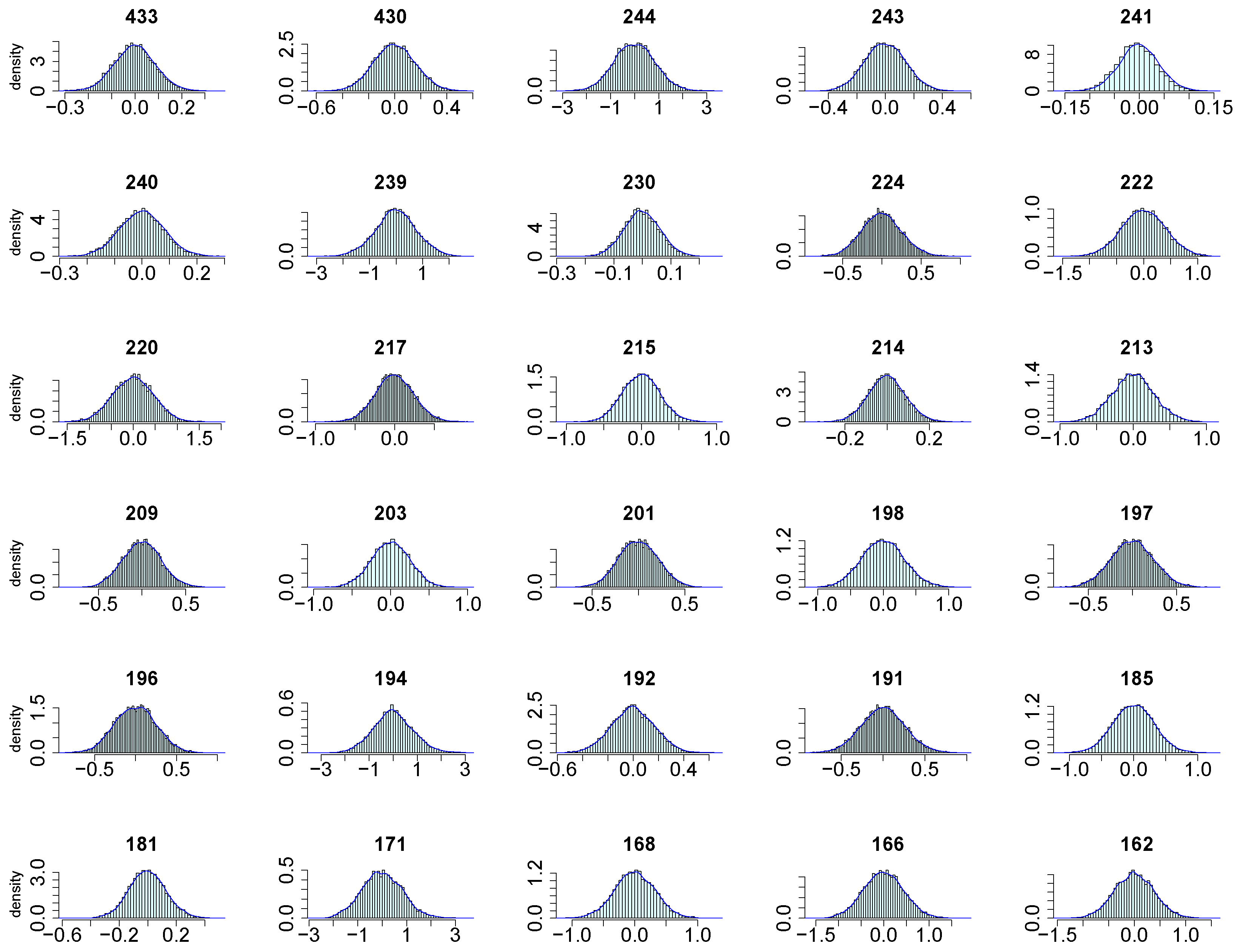
4. Results of the Analysis
5. Conclusions
- The sea surface elevations are generally not Gaussian as the time period increases, from time series recorded in just 4 to 10 min to time series recorded in 10 to 21 h.
- In a few of the cases the one-dimensional marginal is Gaussian for small and moderate time periods. For instance, for time series recorded in just 4 to 10 min, in 14 to 30 min and those recorded in 1 to 2 h.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FDR | False discovery rate |
| UTC | Coordinated universal time |
| iid | independent identically distributed |
Appendix A
| Buoy | Start Time (GMT) | End Time (GMT) | ||
|---|---|---|---|---|
| Date (yyyy-mm-dd) | Time | Date (yyyy-mm-dd) | Time | |
| 028 | 2021-04-29 | 19:00:00 | 2022-08-20 | 08:59:57 |
| 029 | 2022-01-26 | 21:00:00 | 2022-08-20 | 08:59:58 |
| 036 | 2022-05-25 | 23:00:00 | 2022-08-20 | 08:59:58 |
| 045 | 2022-03-01 | 20:00:00 | 2022-08-20 | 08:59:58 |
| 067 | 2020-12-02 | 21:00:00 | 2022-08-20 | 08:59:57 |
| 071 | 2022-08-02 | 19:32:13 | 2022-08-20 | 08:59:58 |
| 076 | 2022-06-02 | 18:00:00 | 2022-08-20 | 08:59:58 |
| 092 | 2021-08-04 | 21:00:00 | 2022-08-20 | 08:59:57 |
| 094 | 2020-10-08 | 21:00:00 | 2022-08-20 | 08:59:57 |
| 098 | 2022-02-04 | 21:00:00 | 2022-08-20 | 08:59:58 |
| 100 | 2021-02-19 | 18:00:00 | 2022-08-20 | 08:59:57 |
| 106 | 2022-01-20 | 23:00:00 | 2022-08-20 | 08:59:58 |
| 121 | 2021-06-21 | 13:32:13 | 2022-04-10 | 22:59:58 |
| 132 | 2020-09-15 | 22:30:00 | 2022-03-01 | 01:22:48 |
| 134 | 2022-01-15 | 15:00:00 | 2022-08-20 | 08:59:58 |
| 139 | 2021-11-14 | 20:00:00 | 2022-08-20 | 08:59:58 |
| 142 | 2022-03-02 | 15:00:00 | 2022-05-20 | 08:22:49 |
| 143 | 2022-08-16 | 23:00:00 | 2022-08-20 | 08:59:58 |
| 144 | 2021-11-11 | 17:00:00 | 2022-08-20 | 09:29:58 |
| 147 | 2022-03-21 | 15:00:00 | 2022-08-20 | 08:59:58 |
| 150 | 2021-11-18 | 15:00:00 | 2022-08-20 | 08:59:58 |
| 154 | 2021-01-12 | 17:00:00 | 2022-06-27 | 21:59:57 |
| 157 | 2020-06-20 | 20:00:00 | 2022-08-20 | 08:59:57 |
| 158 | 2022-07-06 | 02:02:13 | 2022-08-20 | 08:59:58 |
| 160 | 2022-05-02 | 21:02:13 | 2022-08-20 | 08:59:58 |
| 162 | 2021-11-20 | 18:00:00 | 2022-08-20 | 08:59:58 |
| 166 | 2022-05-16 | 21:00:00 | 2022-05-18 | 03:29:58 |
| 168 | 2022-03-25 | 20:00:00 | 2022-08-20 | 08:59:58 |
| 171 | 2022-01-14 | 16:00:00 | 2022-05-12 | 07:52:49 |
| 181 | 2022-08-11 | 21:02:13 | 2022-08-20 | 08:59:58 |
| 185 | 2022-08-06 | 02:00:00 | 2022-08-20 | 09:29:58 |
| 188 | 2021-11-03 | 10:23:10 | 2022-08-20 | 09:20:55 |
| 189 | 2021-10-20 | 20:02:13 | 2022-08-20 | 08:59:58 |
| 191 | 2021-12-13 | 20:00:00 | 2022-08-20 | 08:59:58 |
| 192 | 2022-08-04 | 17:00:00 | 2022-08-20 | 08:59:58 |
| 194 | 2021-11-05 | 15:00:00 | 2022-02-06 | 23:52:49 |
| 196 | 2022-07-19 | 04:02:13 | 2022-08-20 | 09:29:58 |
| 197 | 2022-07-19 | 04:02:13 | 2022-08-20 | 08:59:58 |
| 198 | 2021-06-16 | 21:00:00 | 2022-08-20 | 08:59:57 |
| 201 | 2021-11-10 | 21:00:00 | 2022-08-20 | 08:59:58 |
| 202 | 2021-07-21 | 08:02:13 | 2022-05-04 | 23:59:58 |
| 203 | 2021-05-12 | 19:00:00 | 2022-08-20 | 08:59:57 |
| 204 | 2021-08-20 | 23:00:00 | 2022-05-10 | 02:52:49 |
| 209 | 2022-06-10 | 18:32:13 | 2022-08-20 | 08:59:58 |
| 213 | 2022-03-15 | 17:00:00 | 2022-08-20 | 08:59:58 |
| 214 | 2022-06-28 | 04:02:13 | 2022-08-20 | 08:59:58 |
| 215 | 2022-04-14 | 19:00:00 | 2022-08-20 | 08:59:58 |
| 217 | 2022-08-08 | 23:02:13 | 2022-08-20 | 08:59:58 |
| 220 | 2022-04-26 | 22:00:00 | 2022-08-20 | 08:59:58 |
| 222 | 2021-11-15 | 15:00:00 | 2022-08-20 | 08:59:58 |
| 224 | 2020-07-16 | 15:00:00 | 2022-08-20 | 08:59:57 |
| 230 | 2022-05-19 | 17:00:00 | 2022-08-20 | 08:59:58 |
| 239 | 2022-07-17 | 19:05:10 | 2022-08-20 | 09:03:56 |
| 240 | 2022-07-22 | 19:02:13 | 2022-08-20 | 08:59:58 |
| 241 | 2022-08-02 | 00:00:00 | 2022-08-20 | 08:29:58 |
| 243 | 2021-09-13 | 20:00:00 | 2022-08-20 | 08:59:57 |
| 244 | 2022-03-31 | 04:30:00 | 2022-03-31 | 10:12:49 |
| 430 | 2022-07-15 | 18:02:13 | 2022-08-20 | 08:59:58 |
| 433 | 2022-08-05 | 17:00:00 | 2022-08-20 | 08:59:58 |
| Buoy | Length | Studied | Buoy | Length | Studied |
|---|---|---|---|---|---|
| 028 | 52,817,065 | 412,278 | 185 | 1,583,018 | 216,438 |
| 029 | 22,722,218 | 423,968 | 188 | 32,062,463 | 2304 |
| 036 | 9,557,162 | 458,528 | 189 | 33,569,279 | 6912 |
| 045 | 18,966,698 | 488,480 | 191 | 27,592,874 | 419,360 |
| 067 | 69,170,857 | 334,112 | 192 | 1,732,778 | 451,754 |
| 071 | 1,942,272 | 394,016 | 194 | 20,652,288 | 162,047 |
| 076 | 8,695,466 | 317,984 | 196 | 3,564,288 | 396,288 |
| 092 | 42,080,425 | 500,000 | 197 | 3,561,984 | 463,136 |
| 094 | 75,258,025 | 412,448 | 198 | 47,499,433 | 306,294 |
| 098 | 21,726,890 | 444,704 | 201 | 31,237,802 | 476,960 |
| 100 | 60,447,913 | 453,920 | 202 | 31,813,631 | 2304 |
| 106 | 23,376,554 | 145,322 | 203 | 51,379,369 | 403,232 |
| 121 | 32,447,231 | 29,952 | 204 | 57,986,303 | 6912 |
| 132 | 117,484,797 | 14,592 | 209 | 7,808,256 | 426,272 |
| 134 | 23,966,378 | 474,656 | 213 | 17,432,234 | 446,838 |
| 139 | 30,800,042 | 347,766 | 214 | 5,884,416 | 301,856 |
| 142 | 17,403,648 | 10,752 | 215 | 14,109,866 | 481,855 |
| 143 | 378,026 | 336,554 | 217 | 1,262,592 | 403,232 |
| 144 | 31,147,946 | 447,008 | 220 | 12,768,938 | 449,142 |
| 147 | 16,777,898 | 476,960 | 222 | 30,712,490 | 430,880 |
| 150 | 30,380,714 | 412,448 | 224 | 84,575,400 | 449,312 |
| 154 | 58,742,953 | 479,264 | 230 | 10,248,362 | 481,568 |
| 157 | 87,427,752 | 467,574 | 239 | 3,714,125 | 352,544 |
| 158 | 5,008,896 | 479,264 | 240 | 3,161,088 | 375,584 |
| 160 | 12,109,824 | 467,744 | 241 | 2,029,994 | 456,224 |
| 162 | 30,145,706 | 435,488 | 243 | 37,661,353 | 467,744 |
| 166 | 140,714 | 126,890 | 244 | 52,992 | 29,952 |
| 168 | 16,312,490 | 453,920 | 430 | 3,939,840 | 426,272 |
| 171 | 26,015,999 | 205,088 | 433 | 1,622,186 | 410,144 |
| 181 | 940,032 | 493,088 |
| buoy | 028 | 029 | 036 | 045 | 067 | 071 | 076 | 092 | 094 | 098 | 100 |
| bandwidtd | 0.04 | 0.12 | 0.05 | 0.04 | 0.06 | 0.08 | 0.07 | 0.04 | 0.06 | 0.08 | 0.04 |
| buoy | 106 | 121 | 132 | 134 | 139 | 142 | 143 | 144 | 147 | 150 | 154 |
| bandwidtd | 0.1 | 0.14 | 0.08 | 0.03 | 0.09 | 0.13 | 0.02 | 0.03 | 0.01 | 0.03 | 0.04 |
| buoy | 157 | 158 | 160 | 162 | 166 | 168 | 171 | 181 | 185 | 191 | 192 |
| bandwidtd | 0.04 | 0.01 | 0.03 | 0.05 | 0.07 | 0.05 | 0.11 | 0.02 | 0.06 | 0.04 | 0.03 |
| buoy | 194 | 196 | 197 | 198 | 201 | 203 | 209 | 213 | 214 | 215 | 217 |
| bandwidtd | 0.13 | 0.04 | 0.04 | 0.05 | 0.04 | 0.04 | 0.04 | 0.03 | 0.02 | 0.04 | 0.04 |
| buoy | 220 | 222 | 224 | 230 | 239 | 240 | 241 | 243 | 244 | 430 | 433 |
| bandwidtd | 0.08 | 0.07 | 0.04 | 0.01 | 0.13 | 0.01 | 0.01 | 0.02 | 0.13 | 0.03 | 0.02 |
References
- Forristall, G.Z. On the statistical distribution of wave heights in a storm. J. Geophys. Res. Ocean. 1978, 83, 2353–2358. [Google Scholar] [CrossRef]
- Azaïs, J.M.; León, J.R.; Ortega, J. Geometrical characteristics of Gaussian sea waves. J. Appl. Probab. 2005, 42, 407–425. [Google Scholar] [CrossRef]
- Karmpadakis, I.; Swan, C.; Christou, M. Assessment of wave height distributions using an extensive field database. Coast. Eng. 2020, 157, 103630. [Google Scholar] [CrossRef]
- Haver, S. On the joint distribution of heights and periods of sea waves. Ocean. Eng. 1987, 14, 359–376. [Google Scholar] [CrossRef]
- Mendes, S.; Scotti, A. The Rayleigh-Haring-Tayfun distribution of wave heights in deep water. Appl. Ocean. Res. 2021, 113, 102739. [Google Scholar] [CrossRef]
- Tayfun, M.A. Distribution of Large Wave Heights. J. Waterw. Port Coastal Ocean. Eng. 1990, 116, 686–707. [Google Scholar] [CrossRef]
- Mori, N.; Liu, P.C.; Yasuda, T. Analysis of freak wave measurements in the Sea of Japan. Ocean. Eng. 2002, 29, 1399–1414. [Google Scholar] [CrossRef]
- Stansell, P. Distributions of freak wave heights measured in the North Sea. Appl. Ocean. Res. 2004, 26, 35–48. [Google Scholar] [CrossRef]
- Stansell, P. Distributions of extreme wave, crest and trough heights measured in the North Sea. Ocean. Eng. 2005, 32, 1015–1036. [Google Scholar] [CrossRef]
- Casas-Prat, M.; Holthuijsen, L. Short-term statistics of waves observed in deep water. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Longuet-Higgins, M.S. On the distribution of the heights of sea waves: Some effects of nonlinearity and finite band width. J. Geophys. Res. Ocean. 1980, 85, 1519–1523. [Google Scholar] [CrossRef]
- Jishad, M.; Yadhunath, E.; Seelam, J.K. Wave height distribution in unsaturated surf zones. Reg. Stud. Mar. Sci. 2021, 44, 101708. [Google Scholar] [CrossRef]
- Muraleedharan, G.; Rao, A.; Kurup, P.; Nair, N.U.; Sinha, M. Modified Weibull distribution for maximum and significant wave height simulation and prediction. Coast. Eng. 2007, 54, 630–638. [Google Scholar] [CrossRef]
- Naess, A. On the distribution of crest to trough wave heights. Ocean. Eng. 1985, 12, 221–234. [Google Scholar] [CrossRef]
- Boccotti, P. On Mechanics of Irregular Gravity Waves. Atti Accad. Naz. Lincei Mem. 1989, 19, 110–170. [Google Scholar]
- Klopman, G. Extreme Wave Heights in Shallow Water; Report H2486; WL|Delft Hydraulics: Delft, The Netherlands, 1996. [Google Scholar]
- van Vledder, G.P. Modification of the Glukhovskiy Distribution; Technical Report H1203; Delft Hydraulics: Delft, The Netherlands, 1991. [Google Scholar]
- Battjes, J.A.; Groenendijk, H.W. Wave height distributions on shallow foreshores. Coast. Eng. 2000, 40, 161–182. [Google Scholar] [CrossRef]
- Mendez, F.J.; Losada, I.J.; Medina, R. Transformation model of wave height distribution on planar beaches. Coast. Eng. 2004, 50, 97–115. [Google Scholar] [CrossRef]
- Wu, Y.; Randell, D.; Christou, M.; Ewans, K.; Jonathan, P. On the distribution of wave height in shallow water. Coast. Eng. 2016, 111, 39–49. [Google Scholar] [CrossRef]
- Nieto-Reyes, A. On the Non-Gaussianity of the Height of Sea Waves. J. Mar. Sci. Eng. 2021, 9, 1446. [Google Scholar] [CrossRef]
- Srokosz, M. On the joint distribution of surface elevation and slopes for a nonlinear random sea, with an application to radar altimetry. J. Geophys. Res. Ocean. 1986, 91, 995–1006. [Google Scholar] [CrossRef]
- Srokosz, M.; Longuet-Higgins, M. On the skewness of sea-surface elevation. J. Fluid Mech. 1986, 164, 487–497. [Google Scholar] [CrossRef]
- Hokimoto, T.; Shimizu, K. A non-homogeneous hidden Markov model for predicting the distribution of sea surface elevation. J. Appl. Stat. 2014, 41, 294–319. [Google Scholar] [CrossRef]
- Pena-Sanchez, Y.; Mérigaud, A.; Ringwood, J.V. Short-term forecasting of sea surface elevation for wave energy applications: The autoregressive model revisited. IEEE J. Ocean. Eng. 2018, 45, 462–471. [Google Scholar] [CrossRef]
- Schulz-Stellenfleth, J.; Lehner, S. Measurement of 2-D sea surface elevation fields using complex synthetic aperture radar data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1149–1160. [Google Scholar] [CrossRef]
- Collins, C.O.; Lund, B.; Waseda, T.; Graber, H.C. On recording sea surface elevation with accelerometer buoys: Lessons from ITOP (2010). Ocean. Dyn. 2014, 64, 895–904. [Google Scholar] [CrossRef]
- Reichert, K.; Dannenberg, J.; van den Boom, H. X-Band radar derived sea surface elevation maps as input to ship motion forecasting. In Proceedings of the IEEE OCEANS’10, Sydney, NSW, Australia, 24–27 May 2010; pp. 1–7. [Google Scholar]
- Hessner, K.; Reichert, K.; Hutt, B.L. Sea surface elevation maps obtained with a nautical X-Band radar–Examples from WaMoS II stations. In Proceedings of the 10th International Workshop on Wave Hindcasting and Forecasting and Coastal Hazard Symposium, North Shore, Oahu, HI, USA, 11–16 November 2007; pp. 11–16. [Google Scholar]
- Cherneva, Z.; Guedes Soares, C. Non-linearity and non-stationarity of the New Year abnormal wave. Appl. Ocean. Res. 2008, 30, 215–220. [Google Scholar] [CrossRef]
- Rodriguez, G.; Soares, C.G.; Pacheco, M.; Pe´rez-Martell, E. Wave Height Distribution in Mixed Sea States. J. Offshore Mech. Arct. Eng. 2001, 124, 34–40. [Google Scholar] [CrossRef]
- Tayfun, M.A. Narrow-band nonlinear sea waves. J. Geophys. Res. Ocean. 1980, 85, 1548–1552. [Google Scholar] [CrossRef]
- Petrova, P.G.; Aziz Tayfun, M.; Guedes Soares, C. The Effect of Third-Order Nonlinearities on the Statistical Distributions of Wave Heights, Crests and Troughs in Bimodal Crossing Seas. J. Offshore Mech. Arct. Eng. 2013, 135, 021801. [Google Scholar] [CrossRef]
- Nieto-Reyes, A.; Cuesta-Albertos, J.A.; Gamboa, F. A Random-Projection Based Test of Gaussianity for Stationary Processes. Comput. Stat. Data Anal. 2014, 75, 124–141. [Google Scholar] [CrossRef]
- Epps, T.W. Testing That a Stationary Time Series is Gaussian. Ann. Stat. 1987, 15, 1683–1698. [Google Scholar] [CrossRef]
- Lobato, I.; Velasco, C. A simple Test of Normality for Time Series. Econom. Theory 2004, 20, 671–689. [Google Scholar] [CrossRef]
- Benetazzo, A.; Barbariol, F.; Bergamasco, F.; Torsello, A.; Carniel, S.; Sclavo, M. Observation of Extreme Sea Waves in a Space–Time Ensemble. J. Phys. Oceanogr. 2015, 45, 2261–2275. [Google Scholar] [CrossRef]
- Coleman, R. What is a Stochastic Process? In Stochastic Processes; Springer: Dordrecht, The Netherlands, 1974; pp. 1–5. [Google Scholar] [CrossRef]
- Rozanov, Y.A. Stationary Random Processes; Holden-Day: San Francisco, CA, USA, 1967. [Google Scholar]
- Kozachenko, Y.; Pogorilyak, O.; Rozora, I.; Tegza, A. 2-Simulation of Stochastic Processes Presented in the Form of Series. In Simulation of Stochastic Processes with Given Accuracy and Reliability; Kozachenko, Y., Pogorilyak, O., Rozora, I., Tegza, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 71–104. [Google Scholar] [CrossRef]
- Box, G.; Pierce, D.A. Distribution of Residual Autocorrelations in Autoregressive-Integrated Moving Average Time Series Models. J. Am. Stat. Assoc. 1970, 65, 1509–1526. [Google Scholar] [CrossRef]
- Said, S.E.; Dickey, D.A. Testing for Unit Roots in Autoregressive-Moving Average Models of Unknown Order. Biometrika 1984, 71, 599–607. [Google Scholar] [CrossRef]
- Perron, P. Trends and Random Walks in Macroeconomic Time Series: Further Evidence From a New Approach. J. Econ. Dyn. Control. 1988, 12, 297–332. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.; Schmidt, P.; Shin, Y. Testing the Null Hypothesis of Stationarity Against the Alternative of a Unit Root: How sure Are We that Economic Time Series Have a Unit Root? J. Econom. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- D’Agostino, R.B.; Stephens, M.A. Goodness-of-fit techniques. Qual. Reliab. Eng. Int. 1986, 3, 71. [Google Scholar] [CrossRef]
- Cuesta-Albertos, J.; del Barrio, E.; Fraiman, R.; Matrán, C. The Random Projection Method in Goodness of Fit for Functional Data. Comput. Stat. Data Anal. 2007, 51, 4814–4831. [Google Scholar] [CrossRef]
- Pitman, J. Combinatorial Stochastic Processes. In Lectures from the 32nd Summer School on Probability Theory Held in Saint-Flour; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Benjamini, Y.; Yekutieli, D. The Control of the False Discovery Rate in Multiple Testing under Dependency. Ann. Stat. 2001, 29, 1165–1188. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J. R. Stat. Soc. Ser. Methodol. 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Rudemo, M. Empirical Choice of Histograms and Kernel Density Estimators. Scand. J. Stat. 1982, 9, 65–78. [Google Scholar]
- Bowman, A.W. An Alternative Method of Cross-Validation for the Smoothing of Density Estimates. Biometrika 1984, 71, 353–360. [Google Scholar] [CrossRef]

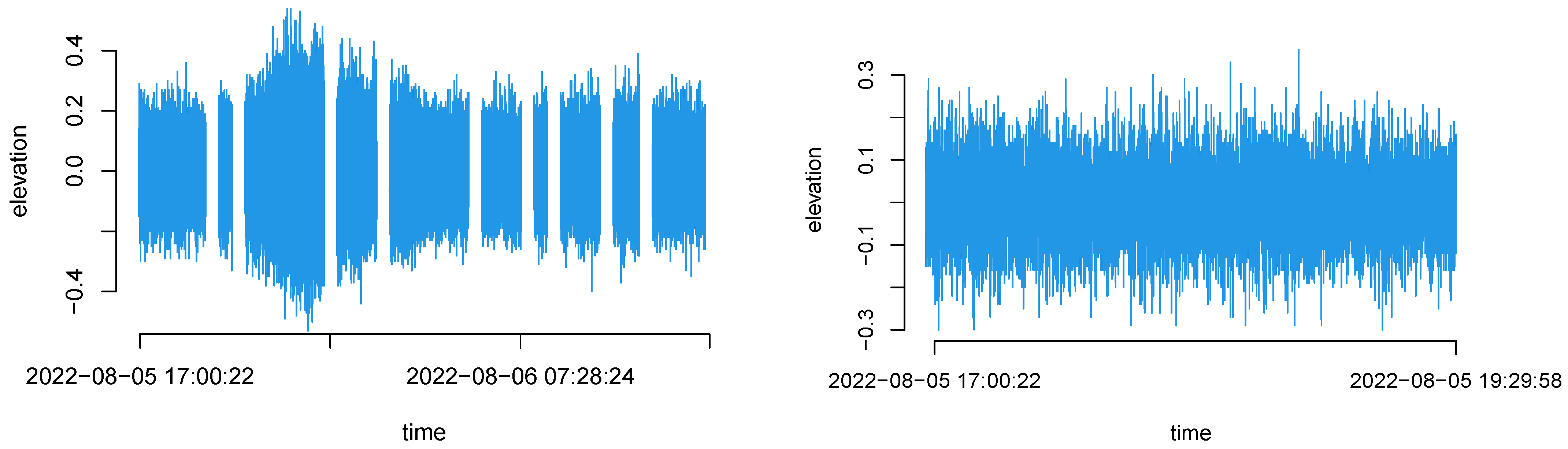



| Buoy | Latitude | Longitude | Buoy | Latitude | Longitude |
|---|---|---|---|---|---|
| 028 | 33.86° | −118.64° | 185 | 36.7° | −122.34° |
| 029 | 37.94° | −123.46° | 188 | 19.78° | −154.97° |
| 036 | 46.86° | −124.24° | 189 | −14.27° | −170.5° |
| 045 | 33.18° | −117.47° | 191 | 32.52° | −117.43° |
| 067 | 33.22° | −119.87° | 192 | 35.75° | −75.33° |
| 071 | 34.45° | −120.78° | 194 | 30° | −81.08° |
| 076 | 35.2° | −120.86° | 196 | 13.68° | 144.81° |
| 092 | 33.62° | −118.32° | 197 | 15.27° | 145.66° |
| 094 | 40.29° | −124.73° | 198 | 21.48° | −157.75° |
| 098 | 21.41° | −157.68° | 201 | 32.87° | −117.27° |
| 100 | 32.93° | −117.39° | 202 | 22.28° | −159.57° |
| 106 | 21.67° | −158.12° | 203 | 33.77° | −119.56° |
| 121 | 13.35° | 144.79° | 204 | 59.6° | −151.83° |
| 132 | 30.71° | −81.29° | 209 | 39.77° | −73.77° |
| 134 | 27.55° | −80.22° | 213 | 33.58° | −118.18° |
| 139 | 43.77° | −124.55° | 214 | 27.59° | −82.93° |
| 142 | 37.79° | −122.63° | 215 | 33.7° | −118.2° |
| 143 | 28.4° | −80.53° | 217 | 34.21° | −76.95° |
| 144 | 27.34° | −84.27° | 220 | 32.75° | −117.5° |
| 147 | 36.92° | −75.72° | 222 | 34.77° | −121.5° |
| 150 | 34.14° | −77.72° | 224 | 37.75° | −75.33° |
| 154 | 40.97° | −71.13° | 230 | 48.03° | −87.73° |
| 157 | 36.33° | −122.1° | 239 | 20.75° | −157° |
| 158 | 36.63° | −121.91° | 240 | 37.02° | −76.15° |
| 160 | 42.8° | −70.17° | 241 | 64.47° | −165.48° |
| 162 | 46.22° | −124.13° | 243 | 36° | −75.42° |
| 166 | 50.03° | −145.2° | 244 | 24.41° | −81.97° |
| 168 | 40.9° | −124.36° | 430 | 36.26° | −75.59° |
| 171 | 36.61° | −74.84° | 433 | 36.2° | −75.71° |
| 181 | 18.38° | −67.28° |
| Length | UTC | GMT | ||
|---|---|---|---|---|
| General | B | General | B | |
| 647.17 s | 260.23 s | 10.79 min | 4.34 min | |
| 2.5 × | 1819.04 s | 846.1719 s | 30.32 min | 14.10 min |
| 7678.42 s | 3775.86 s | 2.13 h | 1.05 h | |
| 2 × | 15,490.92 s | 7682.11 s | 4.30 h | 2.13 h |
| 4 × | 31,115.92 s | 15,494.61 s | 8.64 h | 4.30 h |
| 6 × | 46,740.92 s | 23,307.11 s | 12.98 h | 6.47 h |
| 8 × | 62,365.92 s | 31,119.61 s | 17.32 h | 8.64 h |
| 77,990.92 s | 38,932.11 s | 21.66 h | 10.81 h | |
| Time Period | Tests | ||||
|---|---|---|---|---|---|
| General | B | Augmented Dickey-Fuller | Phillips-Perron | Ljung-Box | kpps |
| 10.79 min | 4.34 min | <0.01 | <0.01 | 8.66 × | >0.1 |
| 30.32 min | 14.10 min | <0.01 | <0.01 | 6.09 × | >0.1 |
| 2.13 h | 1.05 h | <0.01 | <0.01 | 1.48 × | >0.1 |
| 4.30 h | 2.13 h | <0.01 | <0.01 | 0 | >0.1 |
| 8.64 h | 4.30 h | <0.01 | <0.01 | 2.60 × | >0.1 |
| 12.98 h | 6.47 h | <0.01 | <0.01 | 0 | >0.1 |
| 17.32 h | 8.64 h | <0.01 | <0.01 | 0.18 | >0.1 |
| 21.66 h | 10.81 h | <0.01 | <0.01 | 0.36 | >0.1 |
| Buoy | Epps | L.-V. | FDR | Buoy | Epps | L.-V. | FDR |
|---|---|---|---|---|---|---|---|
| 028 | 0.91 | 0.05 | 0.09 | 171 | 0.66 | 7.14 × | 1.43 × 10−10 |
| 029 | 0.42 | 0.61 | 0.61 | 181 | 1.61 × | 1.54 × | 3.07 × 10−4 |
| 036 | 0.15 | 0.14 | 0.15 | 185 | 0.91 | 0.6 | 0.91 |
| 045 | 0.97 | 0.28 | 0.56 | 191 | 0.52 | 0.31 | 0.52 |
| 067 | 0.28 | 0.15 | 0.28 | 192 | 0.88 | 0.07 | 0.14 |
| 071 | 0.47 | 0.61 | 0.61 | 194 | 8.07 × | 2.76 × | 5.53 × 10−9 |
| 076 | 0.20 | 0.24 | 0.24 | 196 | 0.07 | 0.35 | 0.15 |
| 092 | 0.09 | 0.01 | 0.03 | 197 | 0.81 | 0.16 | 0.33 |
| 094 | 0.87 | 0.27 | 0.54 | 198 | 0.49 | 1.58 × | 3.17 × 10−4 |
| 098 | 0.39 | 0.79 | 0.77 | 201 | 0.01 | 0.31 | 0.02 |
| 100 | 0.58 | 0.99 | 0.99 | 203 | 0.93 | 0.74 | 0.93 |
| 106 | 3.29 × | 0.02 | 6.58 × 10−4 | 209 | 0.73 | 0.01 | 0.01 |
| 121 | 0.41 | 1.43 × | 2.86 × 10−6 | 213 | 0.43 | 0.42 | 0.43 |
| 132 | 0.08 | 3.08 × | 6.16 × 10−11 | 214 | 0.04 | 6.35 × | 1.27 × 10−5 |
| 134 | 0.76 | 0.76 | 0.76 | 215 | 0.81 | 0.04 | 0.09 |
| 139 | 0.82 | 0.22 | 0.43 | 217 | 0.03 | 0.00 | 0.01 |
| 142 | 3.56 × | 1.59 × | 3.18 × 10−8 | 220 | 0.56 | 0.77 | 0.77 |
| 143 | 0.02 | 1.49 × | 2.98 × 10−4 | 222 | 0.86 | 0.60 | 0.86 |
| 144 | 0.01 | 5.51 × | 1.10 × 10−3 | 224 | 0.01 | 3.13 × | 6.27 × 10−9 |
| 147 | 0.48 | 0.36 | 0.48 | 230 | 0.66 | 0.04 | 0.09 |
| 150 | 0.33 | 0.47 | 0.47 | 239 | 0.22 | 0.77 | 0.44 |
| 154 | 0.63 | 0.06 | 0.11 | 240 | 0.74 | 0.64 | 0.74 |
| 157 | 0.16 | 0.45 | 0.33 | 241 | 0.10 | 0.20 | 0.19 |
| 158 | 0.60 | 0.67 | 0.67 | 243 | 0.06 | 0.01 | 0.01 |
| 160 | 0.18 | 0.02 | 0.04 | 244 | 0.51 | 0.02 | 0.04 |
| 162 | 0.92 | 0.20 | 0.40 | 430 | 0.17 | 0.32 | 0.32 |
| 166 | 0.68 | 6.87 × | 1.37 × 10−3 | 433 | 0.19 | 0.08 | 0.15 |
| 168 | 0.72 | 0.96 | 0.96 |
| Buoy | Epps (100,1) | Epps (2,7) | L.-V. (100,1) | L.-V. (2,7) | FDR |
|---|---|---|---|---|---|
| 028 | 0.89 | 0.62 | 0.04 | 0.01 | 0.04 |
| 029 | 0.42 | 0.46 | 0.61 | 0.65 | 0.65 |
| 036 | 0.20 | 0.26 | 0.16 | 0.26 | 0.26 |
| 045 | 0.98 | 0.98 | 0.27 | 0.26 | 0.81 |
| 067 | 0.34 | 0.26 | 0.15 | 0.16 | 0.34 |
| 071 | 0.46 | 0.53 | 0.62 | 0.78 | 0.78 |
| 076 | 0.21 | 0.73 | 0.24 | 0.62 | 0.73 |
| 094 | 0.87 | 0.81 | 0.27 | 0.76 | 0.87 |
| 098 | 0.39 | 0.56 | 0.79 | 0.85 | 0.85 |
| 100 | 0.62 | 0.84 | 1.00 | 1.00 | 1.00 |
| 134 | 0.72 | 0.24 | 0.76 | 0.32 | 0.76 |
| 139 | 0.80 | 0.56 | 0.24 | 0.39 | 0.80 |
| 147 | 0.54 | 0.75 | 0.36 | 0.55 | 0.75 |
| 150 | 0.19 | 0.53 | 0.48 | 0.61 | 0.61 |
| 154 | 0.60 | 0.50 | 0.07 | 0.29 | 0.30 |
| 157 | 0.19 | 0.16 | 0.43 | 0.52 | 0.52 |
| 158 | 0.59 | 0.51 | 0.69 | 0.76 | 0.76 |
| 162 | 0.91 | 0.98 | 0.19 | 0.24 | 0.72 |
| 168 | 0.73 | 0.76 | 0.96 | 0.87 | 0.96 |
| 185 | 0.91 | 0.77 | 0.60 | 0.60 | 0.91 |
| 191 | 0.50 | 0.47 | 0.33 | 0.63 | 0.63 |
| 192 | 0.69 | 0.09 | 0.08 | 0.08 | 0.18 |
| 196 | 0.10 | 0.32 | 0.36 | 0.45 | 0.39 |
| 197 | 0.58 | 0.07 | 0.14 | 0.01 | 0.04 |
| 203 | 0.93 | 0.95 | 0.74 | 0.72 | 0.95 |
| 213 | 0.43 | 0.65 | 0.42 | 0.87 | 0.87 |
| 215 | 0.67 | 0.50 | 0.05 | 0.11 | 0.19 |
| 220 | 0.60 | 0.88 | 0.78 | 0.35 | 0.88 |
| 222 | 0.84 | 0.62 | 0.59 | 0.64 | 0.84 |
| 230 | 0.79 | 0.83 | 0.02 | 0.08 | 0.08 |
| 239 | 0.22 | 0.29 | 0.77 | 0.79 | 0.79 |
| 240 | 0.78 | 0.93 | 0.76 | 0.96 | 0.96 |
| 241 | 0.11 | 0.18 | 0.26 | 0.11 | 0.26 |
| 430 | 0.21 | 0.41 | 0.34 | 0.63 | 0.63 |
| 433 | 0.31 | 0.72 | 0.14 | 0.65 | 0.58 |
| General | 10.79 m | 30.32 m | 2.13 h | 4.30 h | 8.64 h | 12.98 h | 17.32 h | 21.66 h | |
| Time Period | B | 4.34 m | 14.10 m | 1.05 h | 2.13 h | 4.30 h | 6.47 h | 8.64 h | 10.81 h |
| no projection | 15.25 | 19.30 | 36.36 | 58.49 | 78.43 | 80.39 | 90.20 | 96.08 | |
| witd projection | 22.03 | 22.81 | 40.00 | 58.49 | 78.43 | 82.35 | 92.16 | 96.08 | |
| minimum | 30.51 | 24.56 | 43.64 | 66.04 | 80.39 | 82.35 | 92.16 | 96.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nieto-Reyes, A. On the Non-Gaussianity of Sea Surface Elevations. J. Mar. Sci. Eng. 2022, 10, 1303. https://doi.org/10.3390/jmse10091303
Nieto-Reyes A. On the Non-Gaussianity of Sea Surface Elevations. Journal of Marine Science and Engineering. 2022; 10(9):1303. https://doi.org/10.3390/jmse10091303
Chicago/Turabian StyleNieto-Reyes, Alicia. 2022. "On the Non-Gaussianity of Sea Surface Elevations" Journal of Marine Science and Engineering 10, no. 9: 1303. https://doi.org/10.3390/jmse10091303
APA StyleNieto-Reyes, A. (2022). On the Non-Gaussianity of Sea Surface Elevations. Journal of Marine Science and Engineering, 10(9), 1303. https://doi.org/10.3390/jmse10091303







