Data-Driven Parameter Estimation of Nonlinear Ship Manoeuvring Model in Shallow Water Using Truncated Least Squares Support Vector Machines
Abstract
:1. Introduction
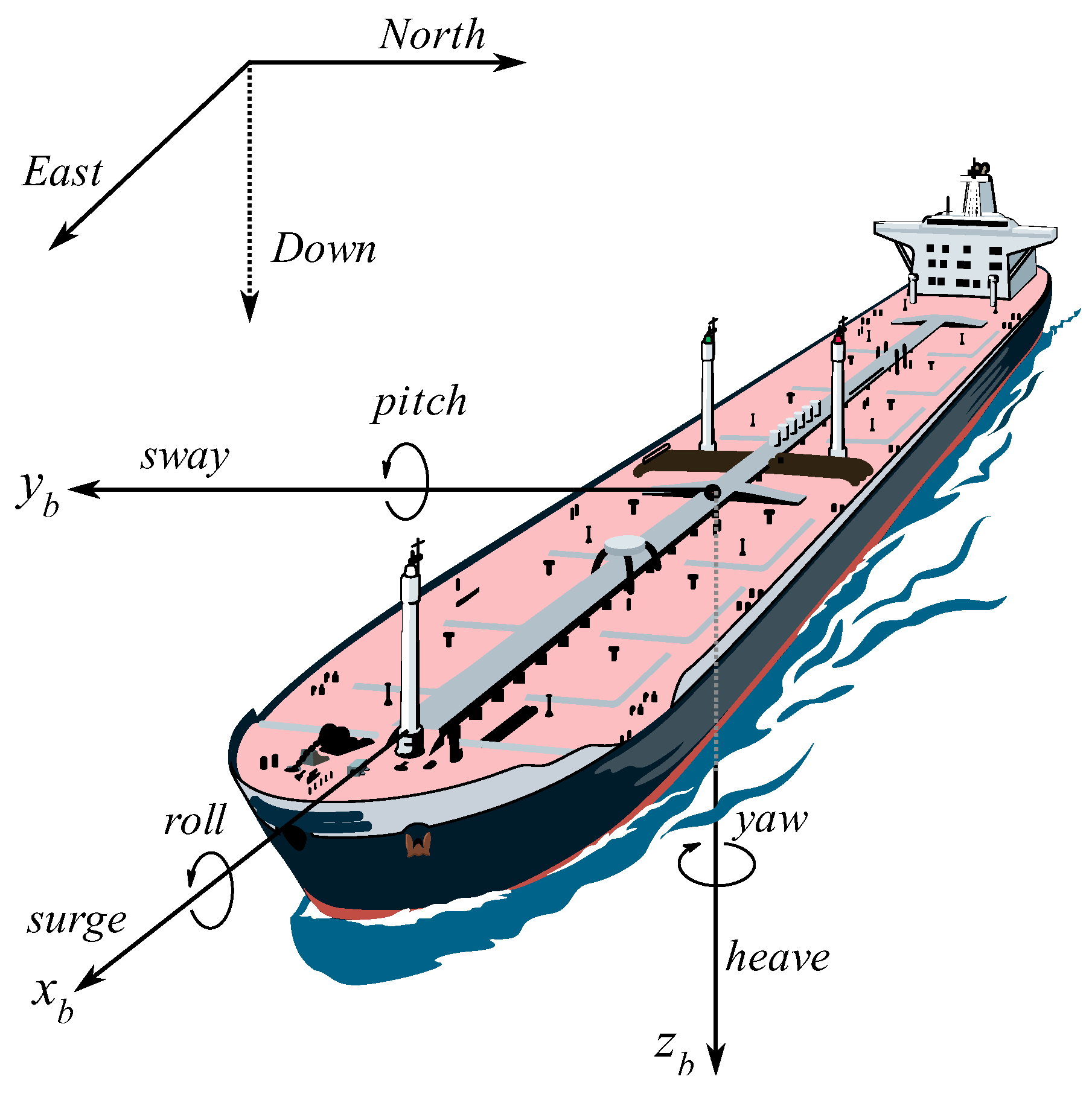
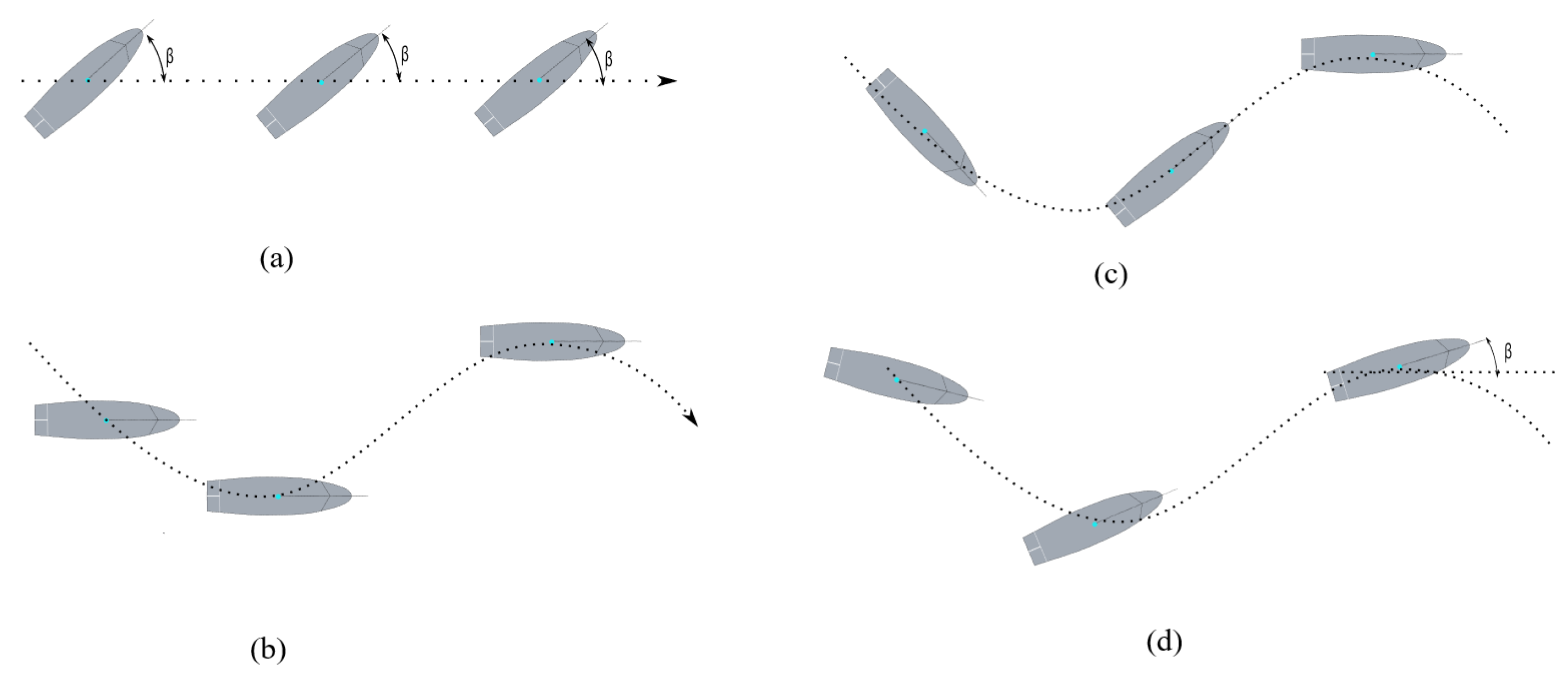
2. Ship Manoeuvring Model
3. Duisburg Model Tested in Shallow Water
4. Truncated LS-SVM
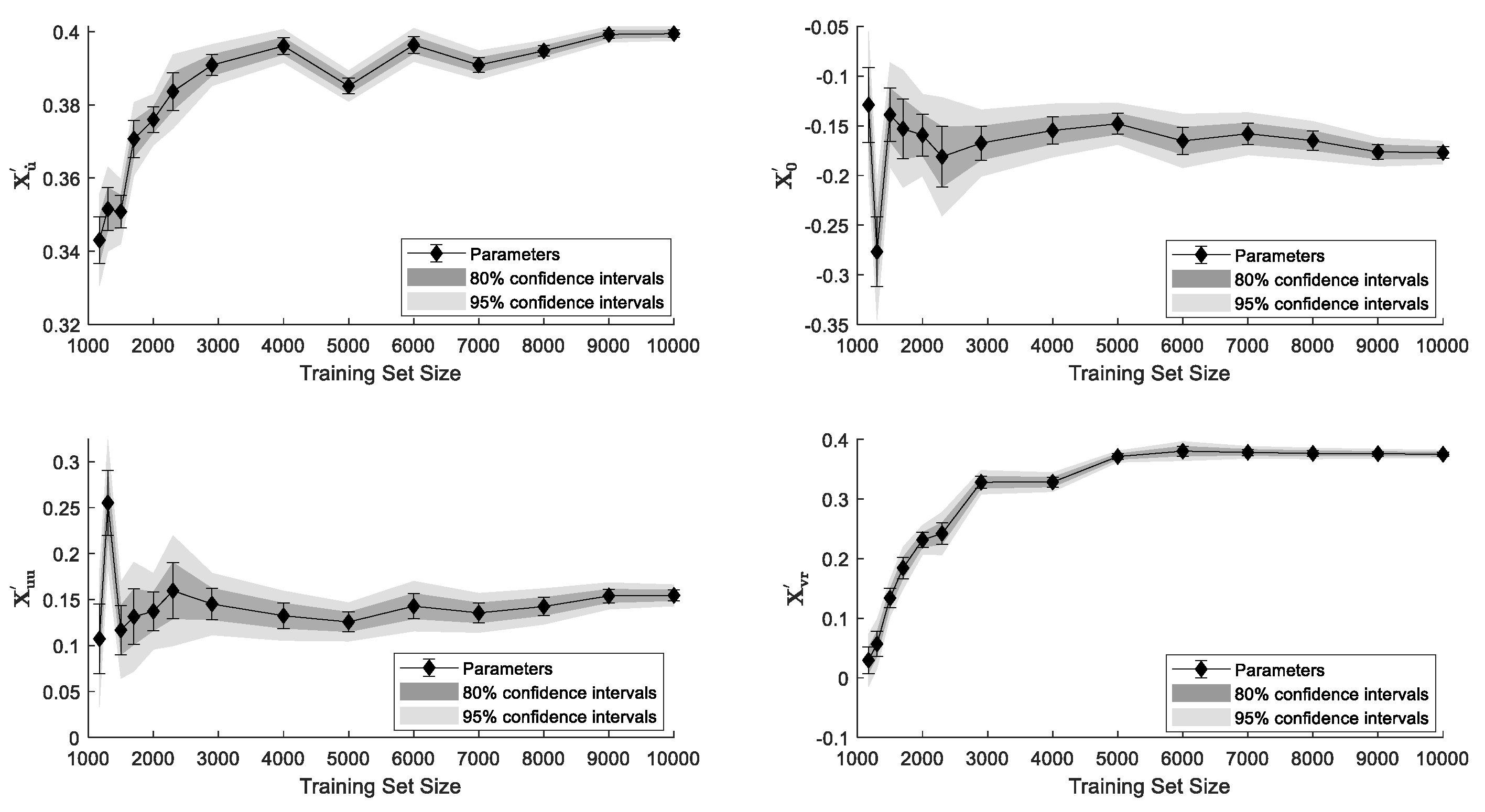
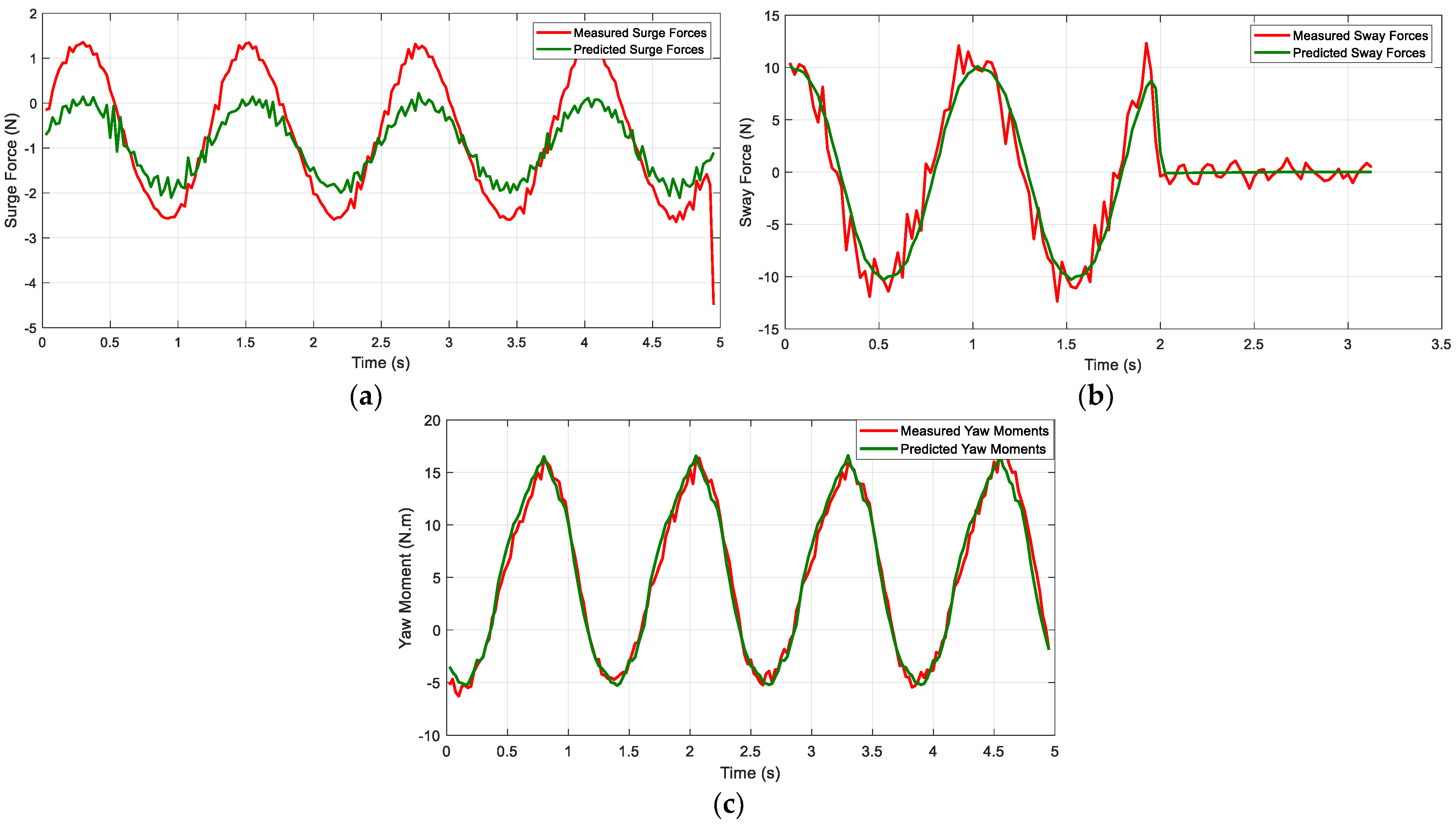
5. Data-Driven Manoeuvring Modelling of DTC Model
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| LS-SVM | Least-squares support vector machine |
| RMS | Root mean square |
| MMG | Manoeuvring Modelling Group |
| LSTM | Long short-term memory network |
| GA | Genetic Algorithm |
| CFD | Computational fluid dynamics |
| SVM | Support vector machine |
| PMM | Planar Motion Mechanism |
| DOF | Degrees of Freedom |
| DTC | Duisburg Test Case |
| FHR | Flanders Hydraulics Research |
| QP | Quadratic programming |
| R | Correlation coefficient |
References
- Yoshimura, Y.; Sakurai, H. Mathematical Model for the Manoeuvring Ship Motion in Shallow Water (3rd Report): Manoeuvrability of a Twin-Propeller Twin Rudder Ship. J. Kansai Soc. Nav. Archit. 1989, 211, 115–126. [Google Scholar]
- Sutulo, S.; Guedes Soares, C. On the Application of Empiric Methods for Prediction of Ship Manoeuvring Properties and Associated Uncertainties. Ocean Eng. 2019, 186, 106111. [Google Scholar] [CrossRef]
- Perera, L.P.; Carvalho, J.P.; Guedes Soares, C. Fuzzy Logic Based Decision Making System for Collision Avoidance of Ocean Navigation under Critical Collision Conditions. J. Mar. Sci. Technol. 2011, 16, 84–99. [Google Scholar] [CrossRef]
- Varela, J.M.; Guedes Soares, C. Interactive 3D Desktop Ship Simulator for Testing and Training Offloading Manoeuvres. Appl. Ocean Res. 2015, 51, 367–380. [Google Scholar] [CrossRef]
- Clarke, D. A History of Ship Manoeuvrability Theory and Practice. In Proceedings of the International Conference on Marine Simulation and Ship Manoeuvrability, Newcastle upon Tyne, UK, 8–11 September 2015; pp. 1–27. [Google Scholar]
- Sutulo, S.; Guedes Soares, C. An Algorithm for Optimized Design of Maneuvering Experiments. J. Sh. Res. 2002, 46, 214–227. [Google Scholar] [CrossRef]
- Hinostroza, M.A.; Xu, H.; Guedes Soares, C. Path-Planning and Path-Following Control System for Autonomous Surface Vessel. In Maritime Transportation and Harvesting of Sea Resources; Guedes Soares, C., Teixeira, A.P., Eds.; Taylor & Francis Group: London, UK, 2018; pp. 991–998. [Google Scholar]
- Inoue, S.; Murayama, K. Calculation of Turning Ship Derivatives in Shallow Water. West Japan Soc. Nav. Archit. 1969, 37, 73–85. [Google Scholar]
- Sutulo, S.; Guedes Soares, C. Development of a Multifactor Regression Model of Ship Maneuvering Forces Based on Optimized Captive-Model Tests. J. Sh. Res. 2006, 50, 311–333. [Google Scholar] [CrossRef]
- Delefortrie, G.; Eloot, K.; Lataire, E.; Van Hoydonck, W.; Vantorre, M. Captive Model Tests Based 6 DOF Shallow Water Manoeuvring Model. In Proceedings of the 4th MASHCON, Hamburg, Germany, 23–25 May 2016. [Google Scholar] [CrossRef]
- Kaidi, S.; Smaoui, H.; Sergent, P. Modeling the Maneuvering Behavior of Container Carriers in Shallow Water. J. Waterw. Port Coastal Ocean Eng. 2018, 144, 04018017. [Google Scholar] [CrossRef]
- Lataire, E.; Vantorre, M.; Delefortrie, G.; Candries, M. Mathematical Modelling of Forces Acting on Ships during Lightering Operations. Ocean Eng. 2012, 55, 101–115. [Google Scholar] [CrossRef]
- Xu, H.; Hinostroza, M.A.; Wang, Z.; Guedes Soares, C. Experimental Investigation of Shallow Water Effect on Vessel Steering Model Using System Identification Method. Ocean Eng. 2020, 199, 106940. [Google Scholar] [CrossRef]
- Abkowitz, M.A. Measurement of Hydrodynamic Characteristics from Ship Maneuvering Trials by System Identification. SNAME Trans. 1980, 88, 283–318. [Google Scholar]
- Luo, W.; Guedes Soares, C.; Zou, Z. Parameter Identification of Ship Maneuvering Model Based on Support Vector Machines and Particle Swarm Optimization. J. Offshore Mech. Arct. Eng. 2016, 138, 031101. [Google Scholar] [CrossRef]
- Xu, H.; Hinostroza, M.A.; Guedes Soares, C. Estimation of Hydrodynamic Coefficients of a Nonlinear Manoeuvring Mathematical Model With Free-Running Ship Model Tests. Int. J. Marit. Eng. 2018, 160, A-213–A-226. [Google Scholar] [CrossRef]
- Moreira, L.; Fossen, T.I.; Guedes Soares, C. Path Following Control System for a Tanker Ship Model. Ocean Eng. 2007, 34, 2074–2085. [Google Scholar] [CrossRef]
- Xu, H.; Guedes Soares, C. Waypoint-Following for a Marine Surface Ship Model Based on Vector Field Guidance Law. In Maritime Technology and Engineering 3; Guedes Soares, C., Santos, T.A., Eds.; Taylor & Francis Group: London, UK, 2016; Volume 1, pp. 409–418. [Google Scholar]
- Xu, H.; Guedes Soares, C. An Optimized Energy-Efficient Path Following Algorithm for Underactuated Marine Surface Ship Model. Int. J. Marit. Eng. 2018, 160, A-411–A-421. [Google Scholar] [CrossRef]
- Du, P.; Cheng, L.; Tang, Z.J.; Ouahsine, A.; Hu, H.B.; Hoarau, Y. Ship Maneuvering Prediction Based on Virtual Captive Model Test and System Dynamics Approaches. J. Hydrodyn. 2022, 34, 259–276. [Google Scholar] [CrossRef]
- Miyauchi, Y.; Maki, A.; Umeda, N.; Rachman, D.M.; Akimoto, Y. System Parameter Exploration of Ship Maneuvering Model for Automatic Docking/Berthing Using CMA-ES. J. Mar. Sci. Technol. 2022, 27, 1065–1083. [Google Scholar] [CrossRef]
- Sukas, O.F.; Kinaci, O.K.; Bal, S. System-Based Prediction of Maneuvering Performance of Twin-Propeller and Twin-Rudder Ship Using a Modular Mathematical Model. Appl. Ocean Res. 2019, 84, 145–162. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons, Ltd.: Chichester, UK, 2011. [Google Scholar] [CrossRef]
- Xu, H.; Hassani, V.; Guedes Soares, C. Comparing Generic and Vectorial Nonlinear Manoeuvring Models and Parameter Estimation Using Optimal Truncated Least Square Support Vector Machine. Appl. Ocean Res. 2020, 97, 102061. [Google Scholar] [CrossRef]
- Berge, S.P.; Fossen, T.I. On the Properties of the Nonlinear Ship Equations of Motion. Math. Comput. Model. Dyn. Syst. 2000, 6, 365–381. [Google Scholar] [CrossRef]
- Maimun, A.; Priyanto, A.; Muhammad, A.H.; Scully, C.C.; Awal, Z.I. Manoeuvring Prediction of Pusher Barge in Deep and Shallow Water. Ocean Eng. 2011, 38, 1291–1299. [Google Scholar] [CrossRef]
- Hassani, V.; Fathi, D.; Ross, A.; Sprenger, F.; Selvik, Ø.; Berg, T.E.T.E.; Fathi, D.; Sprenger, F.; Berg, T.E.T.E. Time Domain Simulation Model for Research Vessel Gunnerus. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St-John’s, NL, Canada, 31 May–5 June 2015; ASME: St-John’s, NL, Canada, 2015; Volume 7, p. V007T06A013. [Google Scholar] [CrossRef]
- Vantorre, M.; Eloot, K. Requirements for Standard Harmonic Captive Manoeuvring Tests. Control Eng. Pract. 1998, 6, 643–652. [Google Scholar] [CrossRef]
- Eloot, K.; Delefortrie, G.; Vantorre, M.; Quadvlieg, F. Validation of Ship Manoeuvring in Shallow Water through Free-Running Tests. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St-John’s, NL, Canada, 31 May–5 June 2015; ASME: St-John’s, NL, Canada, 2015; Volume 7, p. V007T06A017. [Google Scholar] [CrossRef]
- Sutulo, S.; Guedes Soares, C. An Algorithm for Offline Identification of Ship Manoeuvring Mathematical Models from Free-Running Tests. Ocean Eng. 2014, 79, 10–25. [Google Scholar] [CrossRef]
- Xu, H.; Hinostroza, M.A.; Guedes Soares, C. Modified Vector Field Path-Following Control System for an Underactuated Autonomous Surface Ship Model in the Presence of Static Obstacles. J. Mar. Sci. Eng. 2021, 9, 652. [Google Scholar] [CrossRef]
- Lu, S.; Cheng, X.; Liu, J.; Li, S.; Yasukawa, H. Maneuvering Modeling of a Twin-Propeller Twin-Rudder Inland Container Vessel Based on Integrated CFD and Empirical Methods. Appl. Ocean Res. 2022, 126, 103261. [Google Scholar] [CrossRef]
- Mucha, P.; Dettmann, T.; Ferrari, V.; el Moctar, O. Experimental Investigation of Free-Running Ship Manoeuvers under Extreme Shallow Water Conditions. Appl. Ocean Res. 2019, 83, 155–162. [Google Scholar] [CrossRef]
- Guedes Soares, C.; Sutulo, S.; Francisco, R.A.; Santos, F.M.; Moreira, L. Full-Scale Measurements of The Manoeuvring Capabilities of A Catamaran. In Proceedings of the International Conference on Hydrodynamics of High Speed Craft, RINA, London, UK, 24–25 November 1999; pp. 1–12. [Google Scholar] [CrossRef]
- Guedes Soares, C.; Francisco, R.A.; Moreira, L.; Laranjinha, M. Full-Scale Measurements of the Maneuvering Capabilities of Fast Patrol Vessels, Argos Class. Mar. Technol. 2004, 41, 7–16. [Google Scholar] [CrossRef]
- Xu, H.; Hinostroza, M.A.; Hassani, V.; Guedes Soares, C. Real-Time Parameter Estimation of a Nonlinear Vessel Steering Model Using a Support Vector Machine. J. Offshore Mech. Arct. Eng. 2019, 141, 061606. [Google Scholar] [CrossRef]
- Suzuki, R.; Tsukada, Y.; Ueno, M. Estimation of Full-Scale Ship Manoeuvrability in Adverse Weather Using Free-Running Model Test. Ocean Eng. 2020, 213, 107562. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, H.; Xia, L.; Zou, Z.; Guedes Soares, C. Kernel-Based Support Vector Regression for Nonparametric Modeling of Ship Maneuvering Motion. Ocean Eng. 2020, 216, 107994. [Google Scholar] [CrossRef]
- Zhu, M.; Hahn, A.; Wen, Y.-Q.; Bolles, A. Identification-Based Simplified Model of Large Container Ships Using Support Vector Machines and Artificial Bee Colony Algorithm. Appl. Ocean Res. 2017, 68, 249–261. [Google Scholar] [CrossRef]
- Luo, W.; Moreira, L.; Guedes Soares, C. Manoeuvring Simulation of Catamaran by Using Implicit Models Based on Support Vector Machines. Ocean Eng. 2014, 82, 150–159. [Google Scholar] [CrossRef]
- Åström, K.J.; Källström, C.G. Identification of Ship Steering Dynamics. Automatica 1976, 12, 9–22. [Google Scholar] [CrossRef]
- Wang, H.; Liu, J.; Zhi, J.; Fu, C. The Improvement of Quantum Genetic Algorithm and Its Application on Function Optimization. Math. Probl. Eng. 2013, 2013, 1–10. [Google Scholar] [CrossRef]
- Ding, F. Least Squares Parameter Estimation and Multi-Innovation Least Squares Methods for Linear Fitting Problems from Noisy Data. J. Comput. Appl. Math. 2023, 426, 115107. [Google Scholar] [CrossRef]
- Xu, L.; Ding, F.; Zhu, Q. Separable Synchronous Multi-Innovation Gradient-Based Iterative Signal Modeling from On-Line Measurements. IEEE Trans. Instrum. Meas. 2022, 71, 6501313. [Google Scholar] [CrossRef]
- Xu, L. Parameter Estimation for Nonlinear Functions Related to System Responses. Int. J. Control Autom. Syst. 2023, 21, 1780–1792. [Google Scholar] [CrossRef]
- Wang, N.; Sun, J.C.; Er, M.J.; Liu, Y.C. Hybrid Recursive Least Squares Algorithm for Online Sequential Identification Using Data Chunks. Neurocomputing 2016, 174, 651–660. [Google Scholar] [CrossRef]
- Qian, L.; Zheng, Y.; Li, L.; Ma, Y.; Zhou, C.; Zhang, D. A New Method of Inland Water Ship Trajectory Prediction Based on Long Short-Term Memory Network Optimized by Genetic Algorithm. Appl. Sci. 2022, 12, 4073. [Google Scholar] [CrossRef]
- Bonci, M.; Viviani, M.; Broglia, R.; Dubbioso, G. Method for Estimating Parameters of Practical Ship Manoeuvring Models Based on the Combination of RANSE Computations and System Identification. Appl. Ocean Res. 2015, 52, 274–294. [Google Scholar] [CrossRef]
- Xu, H.; Guedes Soares, C. Convergence Analysis of Hydrodynamic Coefficients Estimation Using Regularization Filter Functions on Free-Running Ship Model Tests with Noise. Ocean Eng. 2022, 250, 111012. [Google Scholar] [CrossRef]
- Wang, N.; Er, M.J.; Han, M. Large Tanker Motion Model Identification Using Generalized Ellipsoidal Basis Function-Based Fuzzy Neural Networks. IEEE Trans. Cybern. 2015, 45, 2732–2743. [Google Scholar] [CrossRef]
- Dong, Q.; Wang, N.; Song, J.; Hao, L.; Liu, S.; Han, B.; Qu, K. Math-Data Integrated Prediction Model for Ship Maneuvering Motion. Ocean Eng. 2023, 285, 115255. [Google Scholar] [CrossRef]
- Luo, W.; Li, X. Measures to Diminish the Parameter Drift in the Modeling of Ship Manoeuvring Using System Identification. Appl. Ocean Res. 2017, 67, 9–20. [Google Scholar] [CrossRef]
- Zhang, X.-G.; Zou, Z.-J. Estimation of the Hydrodynamic Coefficients from Captive Model Test Results by Using Support Vector Machines. Ocean Eng. 2013, 73, 25–31. [Google Scholar] [CrossRef]
- Wang, Z.; Zou, Z.; Guedes Soares, C. Identification of Ship Manoeuvring Motion Based on Nu-Support Vector Machine. Ocean Eng. 2019, 183, 270–281. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, S. Sparse Algorithm for Robust LSSVM in Primal Space. Neurocomputing 2018, 275, 2880–2891. [Google Scholar] [CrossRef]
- Ma, H.; Ding, F.; Wang, Y. A Novel Multi-Innovation Gradient Support Vector Machine Regression Method. ISA Trans. 2022, 130, 343–359. [Google Scholar] [CrossRef]
- Ma, H.; Ding, F.; Wang, Y. Multi-Innovation Newton Recursive Methods for Solving the Support Vector Machine Regression Problems. Int. J. Robust Nonlinear Control 2021, 31, 7239–7260. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Van Gestel, T.; De Brabanter, J.; De Moor, B.; Vandewalle, J. Least Squares Support Vector Machines; World Scientific: Singapore, 2002. [Google Scholar] [CrossRef]
- Xu, H.; Hassani, V.; Guedes Soares, C. Truncated Least Square Support Vector Machine for Parameter Estimation of a Nonlinear Manoeuvring Model Based on PMM Tests. Appl. Ocean Res. 2020, 97, 102076. [Google Scholar] [CrossRef]
- Xu, H.; Guedes Soares, C. Hydrodynamic Coefficient Estimation for Ship Manoeuvring in Shallow Water Using an Optimal Truncated LS-SVM. Ocean Eng. 2019, 191, 106488. [Google Scholar] [CrossRef]
- Xu, H.; Guedes Soares, C. Manoeuvring Modelling of a Containership in Shallow Water Based on Optimal Truncated Nonlinear Kernel-Based Least Square Support Vector Machine and Quantum-Inspired Evolutionary Algorithm. Ocean Eng. 2020, 195, 106676. [Google Scholar] [CrossRef]
- Hinostroza, M.; Xu, H.; Guedes Soares, C. Manoeuvring Test for a Self-Running Ship Model in Various Water Depth Conditions. In Sustainable Development and Innovations in Marine Technologies; Georgiev, P., Guedes Soares, C., Eds.; Taylor & Francis Group: Abingdon, UK, 2019; pp. 187–196. [Google Scholar]
- Sutulo, S.; Guedes Soares, C. Development of a Core Mathematical Model for Arbitrary Manoeuvres of a Shuttle Tanker. Appl. Ocean Res. 2015, 51, 293–308. [Google Scholar] [CrossRef]
- Inoue, S.; Hirano, M.; Kijima, K.; Takashina, J. A Practical Calculation Method of Ship Maneuvering Motion. Int. Shipbuild. Prog. 1981, 28, 207–222. [Google Scholar] [CrossRef]
- Inoue, S.; Hirano, M.; Kijima, K. Hydrodynamic Derivatives on Ship Manoeuvring. Int. Shipbuild. Prog. 1981, 28, 112–125. [Google Scholar] [CrossRef]
- SNAME. Nomenclature for Treating the Motion of a Submerged Body through a Fluid; Society of Naval Architects and Marine Engineers: New York, NY, USA, 1950. [Google Scholar]
- Sprenger, F.; Maron, A.; Delefortrie, G.; van Zwijnsvoorde, T.; Cura-Hochbaum, A.; Lengwinat, A.; Papanikolaou, A. Experimental Studies on Seakeeping and Maneuverability of Ships in Adverse Weather Conditions. J. Sh. Res. 2017, 61, 131–152. [Google Scholar] [CrossRef]
- Eloot, K.; Vantorre, M.; Delefortrie, G.; Lataire, E. Running Sinkage and Trim of the DTC Container Carrier in Harmonic Sway and Yaw Motion: Open Model Test Data for Validation Purposes. In Proceedings of the 4th International Conference on Ship Manoeuvring in Shallow and Confined Water (MASHCON): Ship Bottom Interaction, Hamburg, Germany, 23–25 May 2016; Uliczka, K., Böttner, C.-U., Kastens, M., Eloot, K., Delefortrie, G., Vantorre, M., Candries, M., Lataire, E., Eds.; Bundesanstalt für Wasserbau: Hamburg, Germany, 2016; pp. 251–261. [Google Scholar] [CrossRef]
- el Moctar, O.; Shigunov, V.; Zorn, T. Duisburg Test Case: Post-Panamax Container Ship for Benchmarking. Sh. Technol. Res. 2012, 59, 50–64. [Google Scholar] [CrossRef]
- Van Kerkhove, G.; Vantorre, M.; Delefortrie, G. Advanced Model Testing Techniques for Ship Behaviour in Shallow and Confined Water. In Proceedings of the AMT ’09: 1st International Conference on Advanced Model Measurement Technology for the EU Maritime Industry, Nantes, France, 1–2 September 2009; pp. 158–172. [Google Scholar]
- Papanikolaou, A.; Zaraphonitis, G.; Bitner-Gregersen, E.; Shigunov, V.; El Moctar, O.; Guedes Soares, C.; Reddy, D.N.; Sprenger, F. Energy Efficient Safe SHip Operation (SHOPERA). Transp. Res. Procedia 2016, 14, 820–829. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory. IEEE Trans. Neural Networks 1995, 8, 187. [Google Scholar] [CrossRef]
- Hansen, P.C. The Discrete Picard Condition for Discrete Ill-Posed Problems. BIT Numer. Math. 1990, 30, 658–672. [Google Scholar] [CrossRef]
- Hansen, P.C.; O’Leary, D.P. The Use of the L-Curve in the Regularization of Discrete Ill-Posed Problems. SIAM J. Sci. Comput. 1993, 14, 1487–1503. [Google Scholar] [CrossRef]
- Hwang, W. Application of System Identification to Ship Maneuvering. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1980. [Google Scholar]
- Taylor, K.E. Summarizing Multiple Aspects of Model Performance in a Single Diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]




| Coef. | Dimensional Factor | Coef. | Dimensional Factor | Coef. | Dimensional Factor |
|---|---|---|---|---|---|
| Description | |
|---|---|
| Length between pp (Lpp) | 3.984 m |
| Draught (T) | 0.163 m |
| Beam (B) | 0.572 m |
| Block coefficient (Cb) | 0.661 |
| Mass | 242.8 kg |
| centre of gravity in x-direction ) | −0.052 m |
| Moment of inertia along z-axis ) | 219 kg m2 |
| ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Training set size | 1200 | 1300 | 1500 | 1700 | 2000 | 2300 | 2900 |
| ID | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Training set size | 4000 | 5000 | 6000 | 7000 | 8000 | 9000 | 10,000 |
| ID | SURGE | SWAY | YAW | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R | E′ | STD | R | E′ | STD | R | STD | ||
| REF. | 1.000 | 0.000 | 0.704 | 1.000 | 0.000 | 5.829 | 1.000 | 0.000 | 7.422 |
| 1 | −0.783 | 2.232 | 1.785 | −0.114 | 6.734 | 6.168 | 0.990 | 1.027 | 7.352 |
| 2 | −0.772 | 2.133 | 1.785 | −0.069 | 6.598 | 6.168 | 0.992 | 0.914 | 7.352 |
| 3 | −0.668 | 1.919 | 1.785 | 0.254 | 5.984 | 6.168 | 0.992 | 0.943 | 7.352 |
| 4 | 0.102 | 1.776 | 1.785 | 0.548 | 5.316 | 6.168 | 0.992 | 0.956 | 7.352 |
| 5 | 0.654 | 1.648 | 1.785 | 0.693 | 4.778 | 6.168 | 0.992 | 0.944 | 7.352 |
| 6 | 0.685 | 1.619 | 1.785 | 0.860 | 3.802 | 6.168 | 0.992 | 0.962 | 7.352 |
| 7 | 0.768 | 1.412 | 1.785 | 0.909 | 3.032 | 6.168 | 0.992 | 0.961 | 7.352 |
| 8 | 0.767 | 1.413 | 1.785 | 0.938 | 2.472 | 6.168 | 0.992 | 0.958 | 7.352 |
| 9 | 0.779 | 1.322 | 1.785 | 0.938 | 2.472 | 6.168 | 0.992 | 0.950 | 7.352 |
| 10 | 0.779 | 1.304 | 1.785 | 0.949 | 2.017 | 6.168 | 0.992 | 0.956 | 7.352 |
| 11 | 0.779 | 1.309 | 1.785 | 0.947 | 2.083 | 6.168 | 0.992 | 0.962 | 7.352 |
| 12 | 0.778 | 1.312 | 1.785 | 0.947 | 2.091 | 6.168 | 0.992 | 0.954 | 7.352 |
| 13 | 0.778 | 1.312 | 1.785 | 0.961 | 1.719 | 6.168 | 0.992 | 0.964 | 7.352 |
| 14 | 0.778 | 1.314 | 1.785 | 0.960 | 1.730 | 6.168 | 0.992 | 0.960 | 7.352 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Guedes Soares, C. Data-Driven Parameter Estimation of Nonlinear Ship Manoeuvring Model in Shallow Water Using Truncated Least Squares Support Vector Machines. J. Mar. Sci. Eng. 2023, 11, 1865. https://doi.org/10.3390/jmse11101865
Xu H, Guedes Soares C. Data-Driven Parameter Estimation of Nonlinear Ship Manoeuvring Model in Shallow Water Using Truncated Least Squares Support Vector Machines. Journal of Marine Science and Engineering. 2023; 11(10):1865. https://doi.org/10.3390/jmse11101865
Chicago/Turabian StyleXu, Haitong, and C. Guedes Soares. 2023. "Data-Driven Parameter Estimation of Nonlinear Ship Manoeuvring Model in Shallow Water Using Truncated Least Squares Support Vector Machines" Journal of Marine Science and Engineering 11, no. 10: 1865. https://doi.org/10.3390/jmse11101865
APA StyleXu, H., & Guedes Soares, C. (2023). Data-Driven Parameter Estimation of Nonlinear Ship Manoeuvring Model in Shallow Water Using Truncated Least Squares Support Vector Machines. Journal of Marine Science and Engineering, 11(10), 1865. https://doi.org/10.3390/jmse11101865







