Molecular Dynamics Investigation of the Effect of Shear during Extrusion on the Permeation Behavior of CH₄ in High-Density Polyethylene

Abstract

Deep-water flexible composite pipes have been widely employed in the domain of deep-water oil and gas transportation, and high-density polyethylene (HDPE) is used to seal the inner sheath of internal oil and gas media containing H₂S and CH₄, due to its favorable barrier properties and mechanical properties. The morphological evolution of HDPE during the extrusion process exerts a direct impact on the material’s barrier properties. The grand canonical Monte Carlo (GCMC) approach and the molecular dynamics (MD) method were coupled in this study to examine the morphological evolution of HDPE under various shear rates as well as the penetration of methane (CH₄) in HDPE under various shear rates. The results indicate that with an increase in shear rate, the HDPE undergoes decoupling, leading to the formation of a densely arranged, rigidly oriented structure. Gas solubility and diffusion coefficients exhibit an initial increase followed by a subsequent reduction as the shear rate increases, which corresponds to the evolution of microscopic morphology. The current simulation can effectively forecast the microscopic morphology and material permeability coefficient and provide valuable insights for enhancing the barrier effectiveness of the inner sheath.

1. Introduction

The deep-water composite flexible pipeline, also known as the “blood vessel” of the deep-water oil and gas and mineral development system, is an essential transportation equipment in the process of developing deep-water oil and gas resources [1,2,3]. Composite flexible pipes provide several advantages over traditional carbon steel pipelines, such as fatigue resistance [4], high temperature and pressure resistance, and so on. They are extensively utilized in deep-water oil and gas exploration and mineral development.

The structure of a flexible deep-water pipeline is generally comprised of four key core components: metal interlocking carcass layers, metal armor layers, inner and outer sheath layers, and end fittings, as shown in Figure 1. As a critical component, the sheath layers are the fundamental layer to seal the oil and gas inside and isolates the seawater from the outside at high temperatures and pressures, and thermoplastic materials such as medium-density polyethylene (MDPE), HDPE, and polyvinylidene fluoride (PVDF) are frequently used in engineering for improving pipe sealing and corrosion resistance [5,6,7]. HDPE is widely used as a sheath layer for materials because of its high melt flow rate (MFR), wide broad molecular weight (M_W), and high degree of crystallinity, which, in turn, provide good processing characteristics, structural, strength and toughness [8,9,10,11]. By virtue of its chemical resistance and abrasion resistance, it is often used as a key inner sheath layer in composite flexible pipelines to resist oil and gas permeation [12,13]. Nevertheless, as the pressure and temperature rise in the depths of the ocean, the pipeline’s performance criteria are confronted with novel challenges. Research indicates that the potential failure of deep-sea pipelines might be attributed to the occurrence of gas leakage within the bushing under conditions of elevated temperature and pressure [13,14], so it is necessary to improve the service life of flexible pipelines by enhancing the barrier performance of the inner sheath layer. The barrier properties of the inner sheath are mainly affected by the material properties and the molding process [15], and the extrusion molding process is often used for large-diameter and long-distance sheath layers [16]. Therefore, gaining knowledge about the interplay between extrusion molding process factors and their impact on gas permeation behavior is advantageous for the further evaluation and enhancement of gas barrier properties.

The extrusion molding process involves various parameters, including screw speed, traction speed, cooling conditions, extrusion temperature, and other factors. The screw speed, being a vital component in the extrusion process, significantly influences the quality of polymer molding. The polymer melt is thermally plasticized in the extruder, and, on the one hand, the process of helical extrusion in a screw results in the generation of shear forces between the melt and the screw surface, as well as the inner wall of the barrel [17]. On the other hand, friction between the melt and the die wall causes the wall slip, which forms a molten film. Since the inner and outer melts move at different speeds, shearing action is generated Under these shear effects, the microstructure of polymer molecules changes, which leads to big changes in the flow state, viscoelasticity, crystallinity, and density of polymers [18]; the mechanisms by which these microscopic changes lead to macroscopic property changes are not adequately comprehended. Therefore, it is imperative to investigate the effects of screw speed and wall friction on material properties from a shear action perspective. Huang [19] employed a multi-scale computer simulation approach to investigate the coupling behavior between stress and morphology in polymer blends to directly estimate the composition–stress–morphology relationships observed in real extruders through atomic molecular dynamic simulations and conventional rheological simulations. Baig [20] employed non-equilibrium molecular dynamics simulations to investigate the effect of shear on the structure and entanglement network of a linear polymer melt and explained the non-linear variation of rheological properties with the applied shear rate from the perspective of molecular chain space conformation.

Research on the influence of barrier properties of thermoplastic polymeric materials is primarily centered on the field of permeation-selective polymer membranes. This study investigates the correlation between process parameters and barrier properties through the orthogonal experiments and molecular dynamics methods. Mcgonigle [21] investigated the relationship between permeability, diffusivity, solubility coefficients, and polymer chain arrangement for extruded amorphous and biaxially oriented polyester films and demonstrated that the permeability coefficient is related to the ability to form crystal structures. Mozaffari [22] investigated the permeability coefficients of CH₄, carbon dioxide, and propane in polystyrene films by combining molecular dynamics simulation methods with experiments, and demonstrated that the computed values were consistent with the empirical values. Zulhairun [23] investigated the effect of melt extrusion rate on the gas permeability of hollow fiber polysulfone (PSF) films and characterized the impact of process parameters on the barrier properties from the morphology and surface properties of the films through microscopic crystallographic observation and gas permeation experiments. Adewole [15] investigated the effects of temperature, pressure, and crystallization rate on natural gas’s permeability, solubility, and diffusion coefficient of HDPE and its nanocomposites.

For the problem of the relationship between extrusion process parameters and permeability performance still being unclear, and the high experimental cost, computational simulation provides a promising solution to such problems. Molecular simulation can predict various physicochemical and transport properties of molecules through their static structures and behaviors. This approach enables the investigation not only to investigate the microscopic composition and intermolecular interactions of materials at multiple scales and from different perspectives but also to realize macroscopic behaviors such as solution–diffusion of gases in polymers through molecular simulation [24,25,26]. Nevertheless, the current research primarily centers on investigating the effects of temperature and pressure parameters on the permeability of gases in polymers, and the investigation impact of shear on the barrier properties of flexible composite pipes remains incomplete. Consequently, it is imperative to conduct further investigations in this area.

In this paper, HDPE, a commonly employed material for the inner sheath of flexible marine pipes, was taken as the matrix, and CH₄ was considered a penetrant. The molecular dynamics simulation was employed to systematically investigate the permeation behavior of HDPE with CH₄ under various shear rates. This study investigates the impact of various shear rates on molecular micromorphology and investigates the effects and mechanisms of shear rates on gas solubility and diffusion coefficient. This research aims to offer theoretical insights for enhancing the extrusion molding process parameters of thermoplastic materials.

2. Numerical Theory

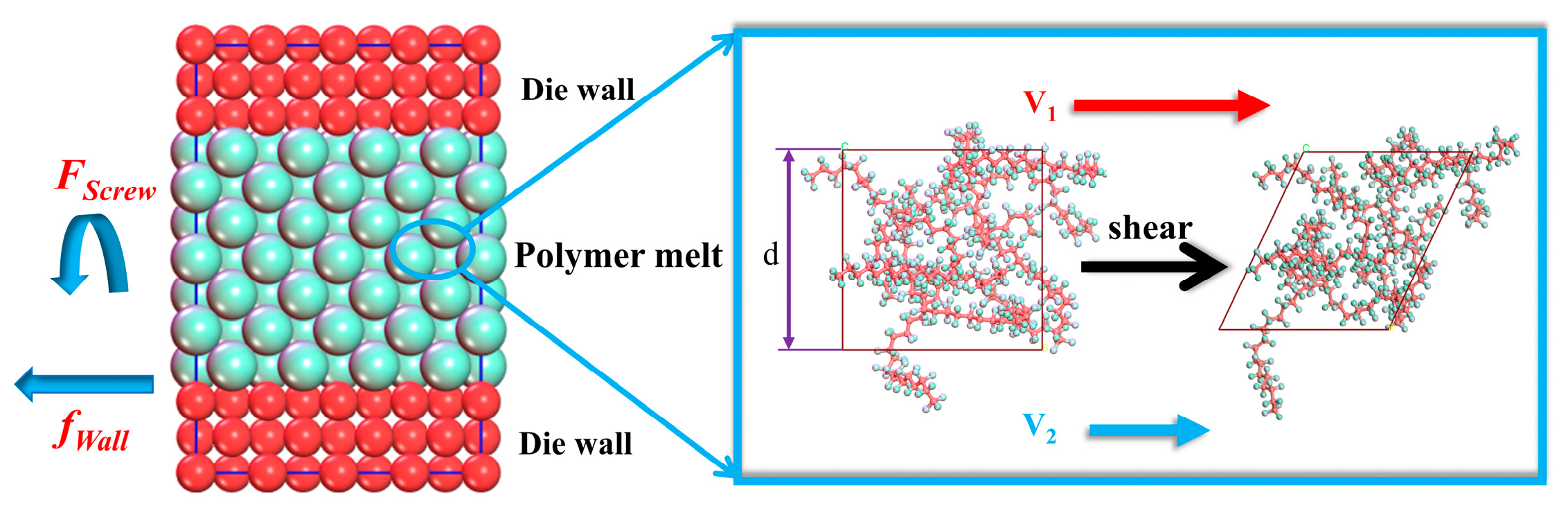
2.1. Shear Action

The numerical simulation of the flow of polymer melt under shear is similar to the experimental approach, wherein shear is induced in the fluid by positioning polymer molecules between two parallel plates. The top plate is moved in one direction while the bottom plate moves in the opposite direction, each with a predetermined average velocity. This motion generates a shear effect on the polymer melt confined between the plates and the shear rate magnitude is defined as the ratio of the difference in velocity between the two plates to the distance between them, as depicted in Figure 2. In molecular simulations, the shear-simulated molecule usually requires a Lees–Edwards boundary condition, and the shear unit needs to be periodic.

In the conventional screw extrusion process, the material and barrel screw rub each other and shear, resulting in the transportation of molten material into the die runner [27]. This process occurs continuously and consistently, ensuring the material takes on a specific shape as it moves towards the die [28]. The extrusion process carried out through an extruder is a non-isothermal non-stationary complex process. Additionally, the flow of polymer in the die runner during this process can be described as a non-isothermal steady-state flow [29]. Hence, the extrusion process in the extruder is simulated by applying a shear rate to the polymer melt, which occurs under non-isothermal and non-stationary shear conditions. Subsequently, the flow process within the die can be simulated through the utilization of isothermal steady-state relaxation [30]. At the molecular level, the thermodynamic state of the molecular chains is nearly equivalent to that of the surrounding molecular chains, thereby rendering the heat transfer effect negligible [31,32].

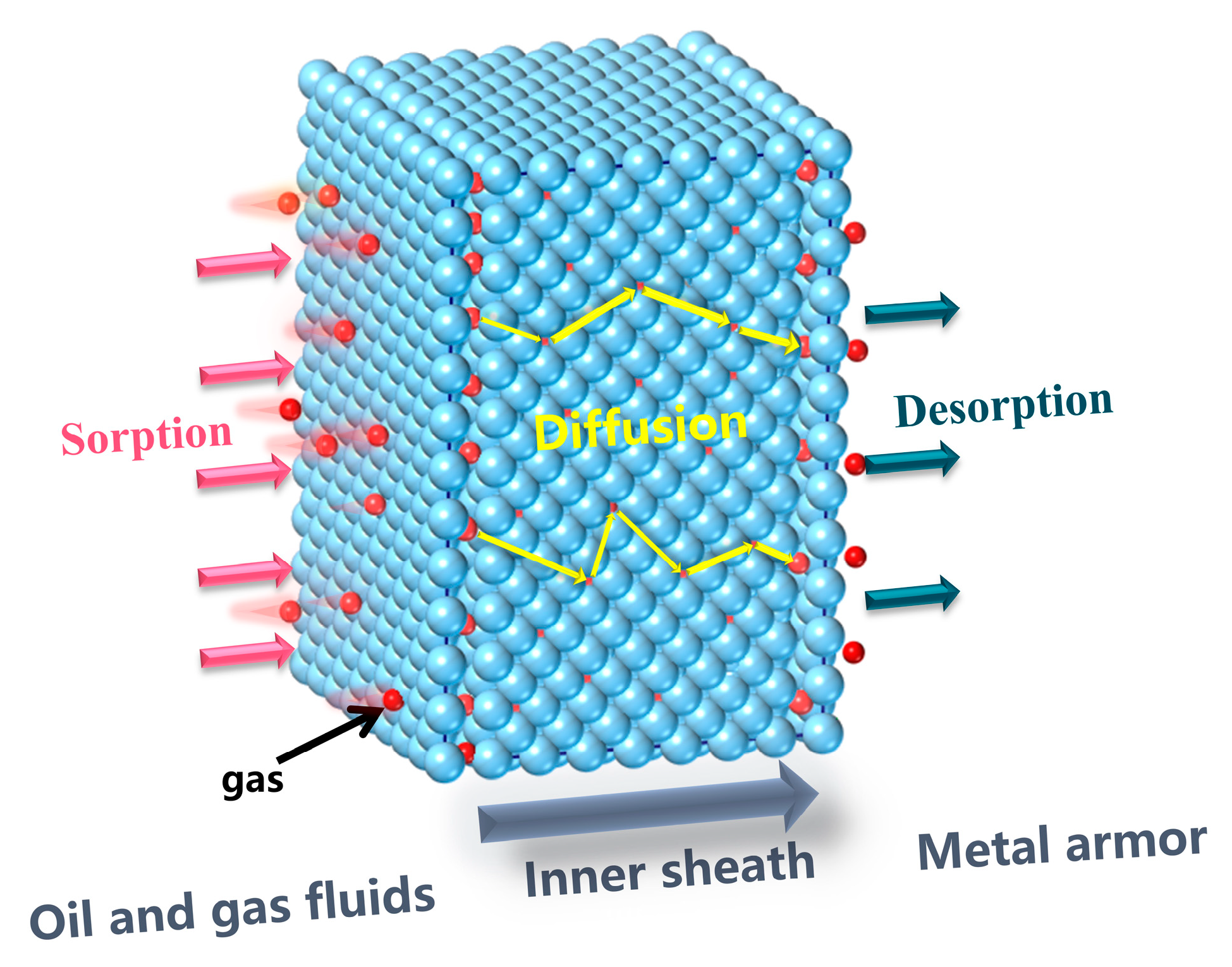
2.2. Gas Permeation

According to the physical–chemical theory of permeation, the permeation process of gas molecules in polymeric materials usually follows three processes, namely, sorption, diffusion, and desorption. In the initial stage, gas molecules are gradually adsorbed into the surface of the gas high-pressure side until equilibrium is reached. Subsequently, the gas molecules undergo diffusion, moving towards the interior of the material due to concentration gradients [22], as shown in Figure 3.

Consequently, to evaluate the ease of passage of permeable molecules through the polymer, the permeability coefficient is defined as:

$$P=D\times S$$

(1)

where the permeability coefficient P is given by the product of solubility coefficient S and diffusion coefficient D, reflects the thermodynamic and kinetic properties of the interaction between permeable molecules and polymers, respectively.

The solubility coefficient S describes the sorption capacity of the gas in the polymer at equilibrium, usually concerning the adsorption concentration C and pressure P_i of the gas in the polymer [33,34], as shown in Equation (2):

$$C=K_D{P}_i+\frac{C_H{P}_{i}b}{1+P_{i}b}$$

(2)

where K_D is the Henry constant, C_H is the Langmuir adsorption capacity, and b is the Langmuir constant. The solubility coefficient of gas molecules in the polymer is usually obtained by calculating the adsorption isotherm, obtaining the variation curve of the permeate molecule concentration C and pressure P_i by solving the slope limit corresponding to the curve when P_i is 0 [35], as shown in Equation (3):

$$S=\underset{\mathrm{p}\to 0}{\lim }\frac{C}{P}=K_D+C_H\mathrm{b}$$

(3)

The irregular thermal motion of molecules causes the diffusion of small molecules, and the Einstein diffusion equation relates the mean square displacement (MSD) of small molecules in Brownian motion to their diffusion coefficients [36], as shown in Equation (4):

$$D=\frac{1}{3}{\displaystyle {\int }_0^{\infty }\left\{\left[{\displaystyle {\sum }_i{V}_i\left(0\right)}\right]\left[{\displaystyle {\sum }_i{V}_i\left(t\right)}\right]\right\}}{d}_t$$

(4)

If the diffusion time is assumed to be infinite, then Equation (5) can be expressed as:

$$D_a=\frac{1}{6N_a}\underset{t\to \infty }{\lim }\frac{d}{d_t}\left({{\displaystyle {\sum }_{i=1}^N\left[r_i\left(t\right)-r_i\left(0\right)\right]}}^2\right)$$

(5)

where N_a is the number of particles of gas molecules, ${{\displaystyle {\sum }_{\mathrm{i}=1}^N\left[{\mathrm{r}}_{\mathrm{i}}\left(\mathrm{t}\right)-{\mathrm{r}}_{\mathrm{i}}\left(0\right)\right]}}^2$ is the mean squared displacement of gas molecules. The MSD value has been taken as the average value of the change in position of N penetrants in the system, and a is taken as the slope of the MSD curve obtained from molecular simulation. Therefore, Equation (5) can be simplified as Equation (6):

$$D=a/6$$

(6)

Molecular simulation has proven to be a dependable method for precisely simulating the sorption and diffusion processes of gas molecules. The diffusion coefficient D and solubility coefficient S of the material can be calculated by obtaining the adsorption isotherm and diffusion curve of the permeate through the grand canonical ensemble Monte Carlo (GCMC) and molecular dynamics (MD). The visualization of the gas permeation process and the calculation of the permeation coefficient can be achieved through the control of molecular structure parameters, pressure, and temperature.

3. Model and Simulation Methodology

3.1. Model Building and Optimization

In this paper, the visualization module was used to depict the molecular structures of CH₄ and polyethylene monomers, as well as to construct polyethylene molecular chains with a degree of polymerization of 200, using polyethylene as a repeating unit. A degree of polymerization of 200 not only satisfies the dimensions of the model better, but also ensures the flexibility of the polymer chains. On the other hand, the permeability coefficient of polymer materials is affected by the degree of polymerization, but the increase in the degree of polymerization has little effect on the permeability coefficient when the degree of polymerization is 200 and above. Doruker [37] also corroborated this by simulating and studying polyethylene with chain lengths of 50, 100, and 316 repeating units by molecular simulation, and found that the solubility and diffusion coefficients of the small molecules in it did not change significantly as the simulated system was increased.

Subsequently, the amorphous cell module was used to construct polymer cells containing 24 chains, followed by geometry optimization and annealing to eliminate unreasonable structures and chain segment effects in the system. The canonical ensemble (NVT) and isothermal–isobaric ensemble (NPT) were then utilized for a duration of 500 picoseconds (ps) each, in order to relax the system and achieve a stable equilibrium state. Since the density has a large influence on the permeability coefficient, it needs to be stabilized in the actual range, which is well-controlled in this paper, and the density is stabilized to 0.948 g/cm³ after relaxation, which is the same as the density range of HDPE used in actual production applications. This process resulted in the creation of HDPE cells that exhibited a density and structure consistent with the actual material, as depicted in Figure 4.

In this study, the compass II forcefield was employed, the electron potential was calculated by Ewald, and the statistical treatment of Ewald force was by the atom-based method. The initial velocities of particles during molecular dynamics calculation is generated randomly by Maxwell–Boltzmann distribution. Additionally, the thermostat parameter was Andersen, and the barostat was Berendsen. The calculated masses are set to Fine. The group-based method was used for the van der Waals interaction during non-bonding interactions, and the Ewald method was used for electrostatic interactions.

3.2. Simulation of HDPE Shear Process

To investigate the effect of shear on the microscopic morphology of the material, this component employs the above equilibrium conformation as the initial conformation. Shear fields are imposed on the cell at a range of shear rates, specifically 0.01 ps⁻¹, 0.025 ps⁻¹, 0.05 ps⁻¹, 0.075 ps⁻¹, and 0.1 ps⁻¹, for a duration of 100 ps at a temperature of 500 K. The shear direction involves motion within the XZ plane, specifically along the Z-direction to simulate the working conditions of HDPE inside the extruder. Subsequently, the canonical ensemble was employed at a temperature of 500 K for a duration of 500 ps to simulate the flow in the die. Subsequently, the isothermal–isobaric ensemble was utilized at a temperature of 300 K for a duration of 500 ps to simulate the cooling process of HDPE at ambient temperature. Ultimately, the simulated trajectory files and data were obtained to analyze the microscopic morphology and structural evolution of the polymer under shear action.

3.3. Simulation of Gas Sorption in HDPE

The GCMC method was employed to simulate the sorption process of CH₄ in HDPE under different shear rates, which is now widely used for sorption process simulation. The CGMC method aims to describe the equilibrium state of the polymer and gas at a given temperature (T) and pressure (P). By employing this method, the adsorption isotherm of the gas in the material can be obtained. This study employed the sorption module to simulate the sorption behavior of CH₄ in HDPE cells under various shear rates with fugacity ranging from 1 kPa to 10 MPa at a temperature of 298 K. The number of equilibrium steps selected for the simulation process is 1 × 10⁶, and the number of production steps is 1 × 10⁷. Gas adsorption isotherms were plotted using ten fugacity isotherm points, and solubility coefficients were calculated from the adsorption isotherms.

3.4. Simulation of Gas Diffusion in HDPE

The molecular dynamics (MD) method was employed to simulate the diffusion process of CH₄ in HDPE under different shear rates. CH₄ molecules were placed into the free volume of the cell at room temperature and pressure using the packing part component of the amorphous module. A 500 ps NVT calculation was performed to investigate the diffusive motion behavior of CH₄ in HDPE. The step size of the simulation is controlled within 1 fs, and the kinematic conformation information is obtained every 1000 steps. The output trajectory file was analyzed to obtain the gas molecule trajectories and MSD curves to determine the rate of gas diffusion.

4. Results and Discussion

4.1. The Influence Law of Shear Rate on Material Micro-Morphology

4.1.1. Results of Shear Action

As the shear rate increases, the molecular chains gradually unfold and develop a flow orientation, as depicted in Figure 5.

When the shear rate is low or the duration of shear is short, the molecular chains only undergo a slight inclination along the shear direction. Still, the level of deformation remains insufficient to surpass the interaction forces and entanglement constraints among the molecular chains, and the overall structure of the molecular chains still maintains the original irregularly entangled state. As the shear rate increases or the duration of shear action lengthens, it is observed that molecular chains gradually remove the entangled state and exhibit flow behavior. Consequently, relative displacement arises concerning the original polymer group, leading to the disruption of the initial entangled network. As a result, polymer chains can detach from the entangled potential barriers, causing the molecular chains to progressively unfold and align themselves. However, some molecular chain segments at the original moiety remain in the original entangled state. Although a certain degree of deformation has occurred, they have not yet reached a state of disentanglement.

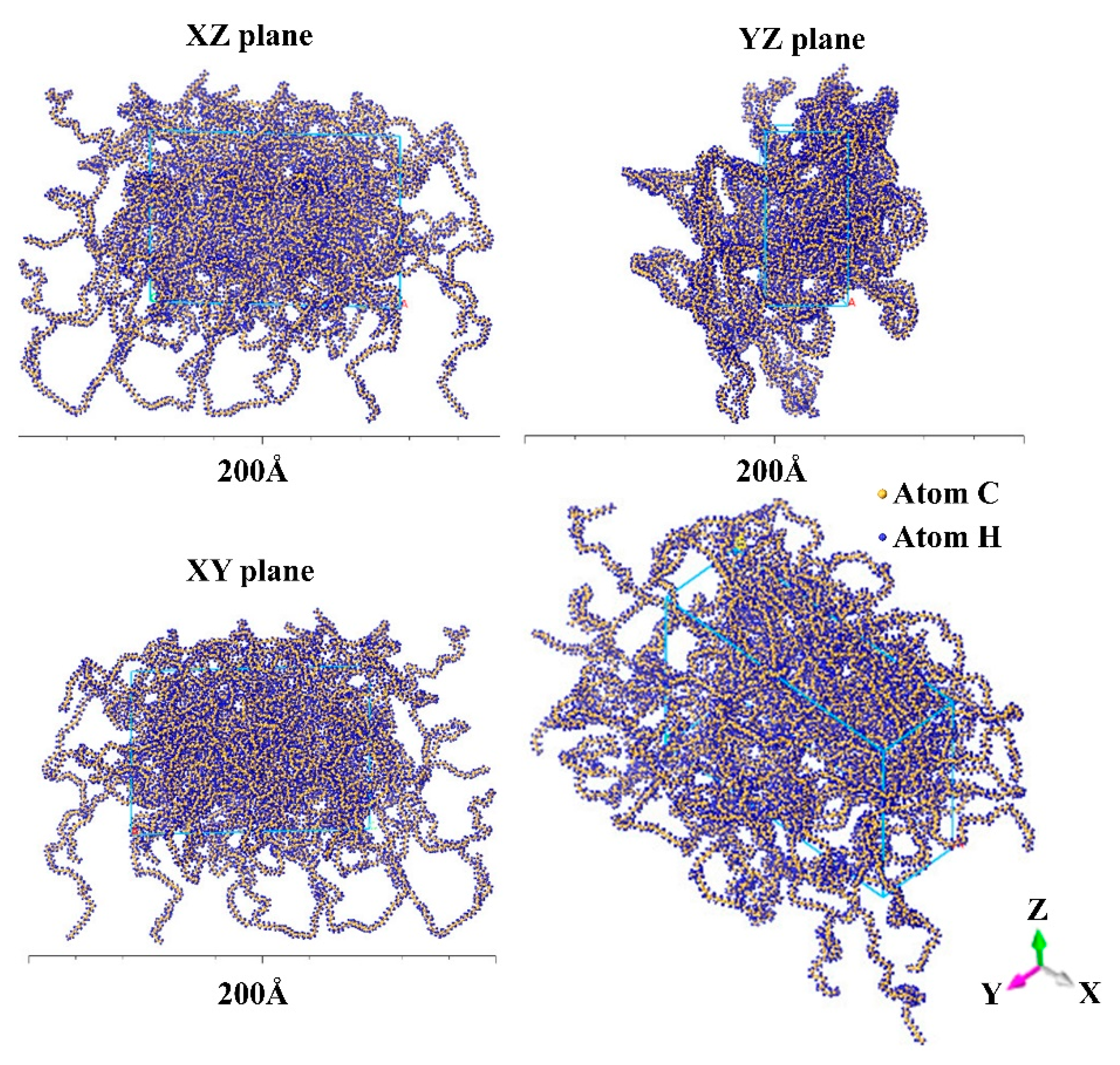
4.1.2. The Evolution of HDPE Micro-Morphology

In order to assess the effect of shear rate on the microscopic morphology of HDPE, this study analyzes the microscopic morphology of HDPE in terms of bond length, bond angle, and dihedral angle.

The radial distribution function (RDF) [38] quantifies the spatial distribution of particle B in relation to particle A by measuring the average density within spherical shells of varying radii centered around particle A. Therefore, the microstructure of the polymer can be analyzed by the image of the RDF, where the height of the peak reflects the strength of the interaction force; the position of the peak corresponds to the equilibrium coordination distance of the atomic pair. In this paper, the analysis of the radial distribution functions for C-C and C-H bonds is carried out, as depicted in Figure 6a,b. The first peak bond lengths are concentrated in the range of 1.53–1.55 Å and 1.09–1.11 Å, which is consistent with the C-C bond and C-H bond lengths in theory. This indicates that the bond is not affected by shear and the molecular structure is stable, regardless of whether it is due to the occurrence of disentanglement or the orientation of the bond along the direction of flow by the stress effect.

The bond angles describe the three-dimensional configuration of the chemical bonds connecting two atoms [39]. The C-C-C bond angle distribution in HDPE has been analyzed, as depicted in Figure 6c. It can be found that the bond angle distribution of HDPE at the shear rate ranging from 0 to 0.075 ps⁻¹ is closer, and the bond angle distribution is concentrated in the range of 111° to 116°. In contrast, at the shear rate of 0.1 ps⁻¹, it can be found that the peak distribution has an apparent rightward shift. The bond angle distribution is concentrated in the range of 113° to 118°, indicating that the molecular chain shows a noticeable stretching compared with the previous. However, the bond angles of the molecular chain remain stable, and the shear action is still insufficient to change the molecular chain’s basic chemical structure.

The dihedral angle reflects the relative arrangement of different planes in a molecule and serves as an essential parameter to describe the steric configuration and spatial orientation of a molecule [40]. The distribution of the dihedral angle of HDPE at different shear rates is depicted in Figure 6d. As the shear rate increases, the probability distribution of the dihedral angles at 0° and 360° increases significantly, corresponding to the “trans” conformation. In contrast, the probability distribution of dihedral angles associated with −120° and 120° decreases significantly, corresponding to the “gauche” conformation. This observation demonstrates that the molecular chain conformation changes drastically from a distorted, amorphous state with numerous gaps to a stable, tightly arranged crystalline structure.

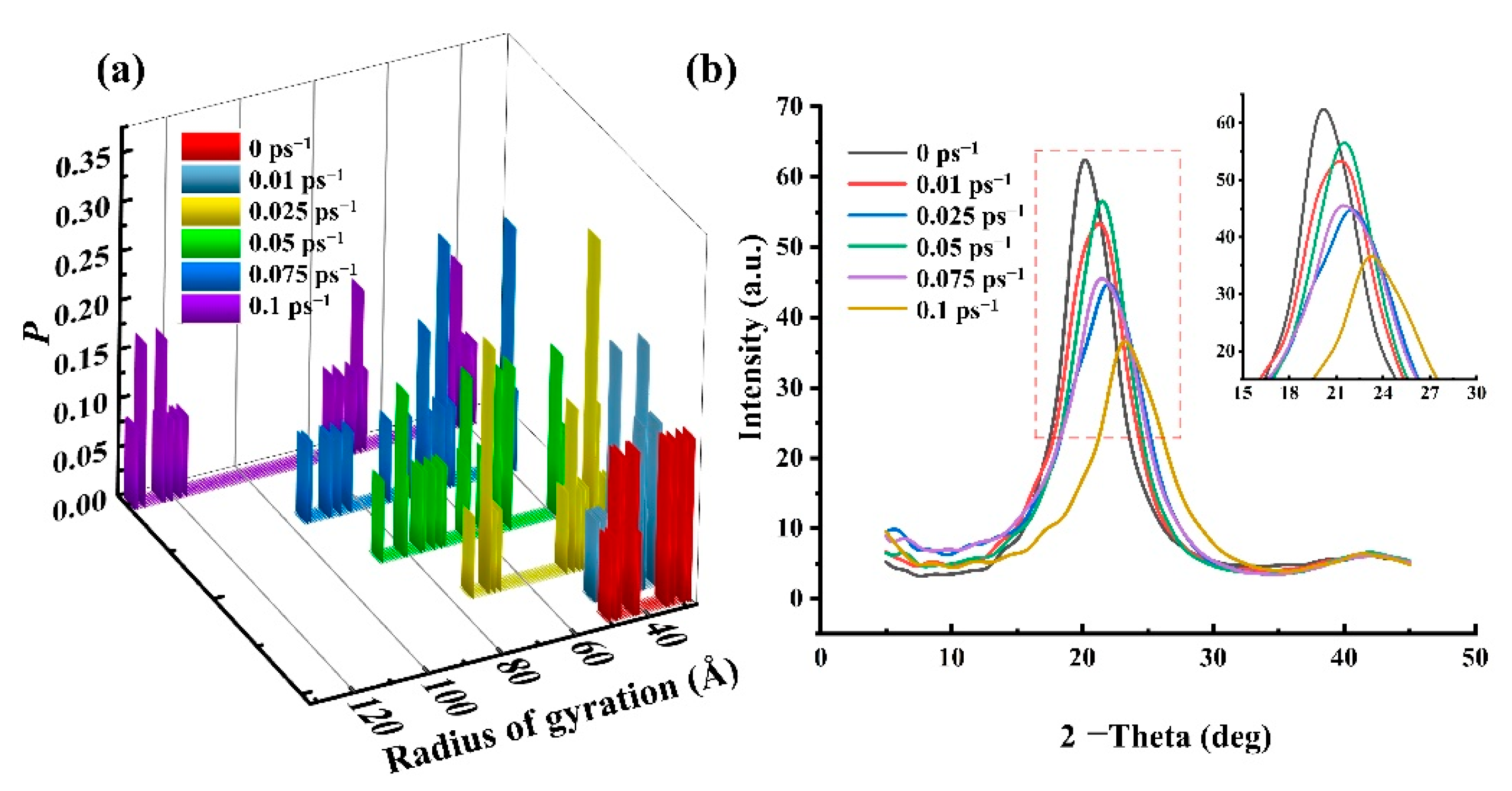
4.1.3. The Radius of Gyration of HDPE

The radius of gyration is defined as the root mean square of the distance from the center of mass of all the single chains of a molecular chain to the center of mass of the chain. A larger mean square radius of gyration indicates reduced flexibility of the molecular chain, while a smaller mean square radius suggests increased flexibility [41]. It can be seen from Figure 7a that at low shear rates, the molecular chains exhibit localized slipping and separation, resulting in the stretching of covalent bonds between monomers and opening of bond angles, and the polymer chains are partially stretched at this time. As the shear rate increases, the distribution of the radius of gyration of the molecular chains continues to expand, reaching a maximum range of 37.5–131.5 Å. The molecular chains are separated by stretching and gradually detach from the entangled lattice to form an oriented state along the shear direction due to the shear effect. The rigidity of the molecular chains gradually increases.

4.1.4. D-Spacing of HDPE

D-spacing reflects the nature of movement and interaction between two molecular chains. A decrease in chain spacing leads to an increase in intermolecular interaction strength and a higher degree of material compaction. It can be obtained by wide-angle X-ray diffraction (WAXD) [42]. The D-spacing is inversely proportional to the diffraction angle corresponding to the prominent diffraction peak. In this paper, the X-ray diffraction pattern of HDPE is obtained by the Forcite module to calculate the D-spacing of the HDPE. The calculation results are shown in Figure 7b, indicating that the diffraction angle related to the diffraction peak significantly increases upon the application of shear. As the shear rate becomes more extensive, the peak corresponding to the diffraction angle is no longer found to increase significantly, D-spacing is almost constant, and the density is stabilized in a particular range. However, the peak corresponding to the diffraction angle experiences a subsequent increase, representing a decrease in D-spacing. The interactions between molecules are strengthened, leading to an increase in the stiffness of the polymer chains. This observation further supports the notion that in regions of high shear, the arrangement and orientation of polymer molecular chains result in a more compact structure, thereby increasing the overall density.

4.2. Adsorption of CH₄ in HDPE under Different Shear Effects

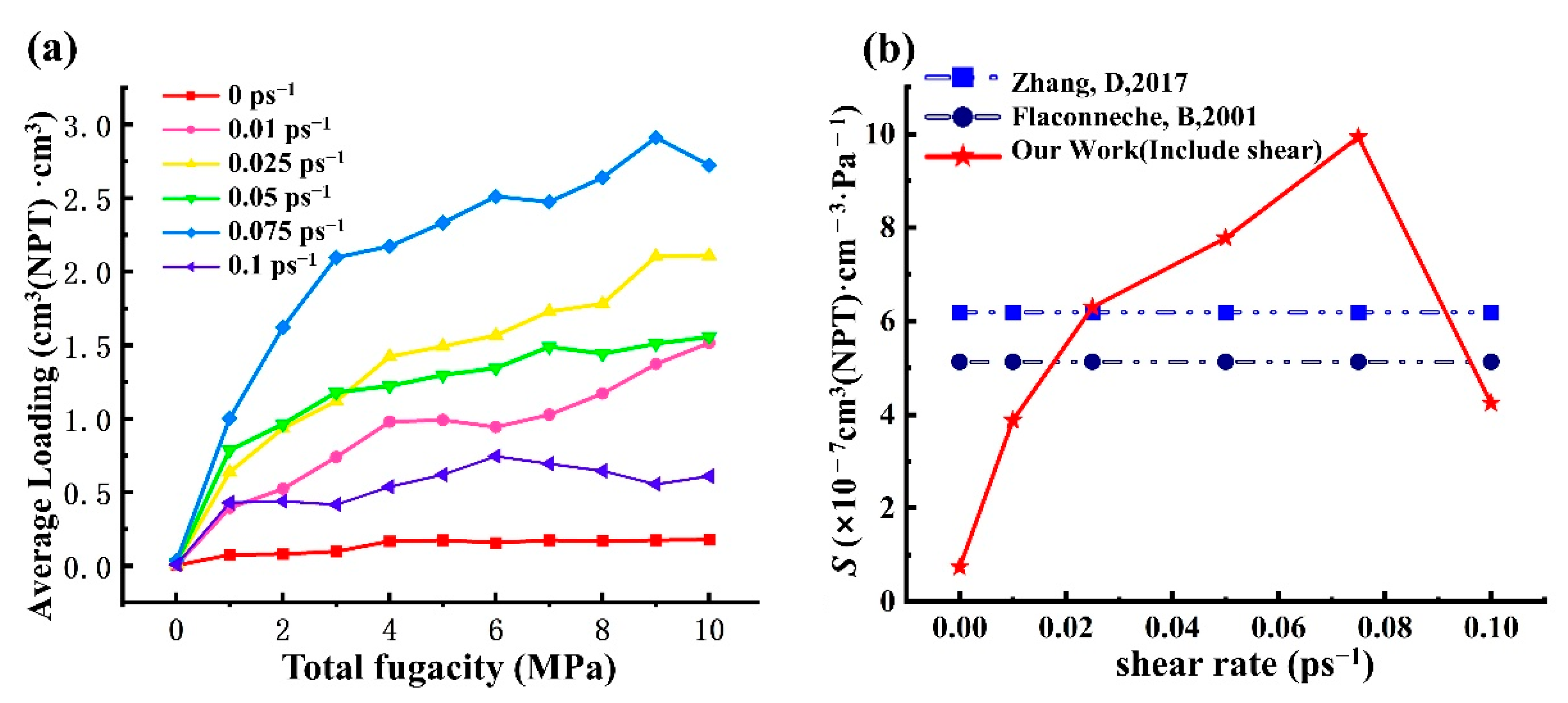
4.2.1. Gas Adsorption Isotherm and the Solubility Coefficient S

The adsorption isotherms of CH₄ in HDPE at a temperature of 303.15 K and a pressure range of 0–10 MPa are shown in Figure 8a. The results indicate that the sorption of CH₄ exhibits a positive correlation with increasing pressure. Furthermore, an increase in the shear rate within the range of 0 ps⁻¹ to 0.075 ps⁻¹ leads to an augmentation in sorption. However, at a shear rate of 0.1 ps⁻¹, a decrease in sorption is observed while maintaining the overall trend of the adsorption isotherm. To visualize the solubility coefficients more, we plotted the solubility coefficients versus shear rate curves and compared them with previous experimental studies [43,44], which obtained an empirical formula for calculating the permeability coefficient with respect to temperature and pressure from a large number of experimental studies which is widely recognized, as shown in Figure 8b. The solubility coefficients show an obvious trend that include an initial increase followed by a subsequent decrease as the shear rate increases, and the highest solubility coefficient is observed at the shear rate of 0.075 ps⁻¹.

4.2.2. The Isosteric Heat and Langmuir-Type Sites

The analysis of the causes of this phenomenon was conducted based on the concepts of isosteric heat and Langmuir-type sites. The isosteric heat is an essential criterion for the strength of sorption capacity. Typically, a higher isosteric heat corresponds to a stronger sorption capacity [45]. The isosteric heat of the material at different shear rates is shown in Figure 9. The overall isosteric heat value is less than 42 kJ/mol, indicating that this is primarily a physical sorption process [46]. The isosteric heat exhibits a positive correlation with the shear rate, suggesting that the sorption capacity strengthens as the shear rate increases, but this does not adequately explain the above variation process of the solubility coefficient well.

The quantity of Langmuir-type sites directly reflects the strength of the gas sorption capacity, as shown in Figure 10. The depicted portion in blue within the diagram represents the molecular chain of the polymer, while the red area indicates the sites where gas sorption occurs. The sorption behavior of CH₄ in HDPE exhibits selectivity rather than uniform distribution, and the quantity of sorption sites demonstrates a trend of initially increasing and subsequently decreasing with the shear rate. This implies that at lower shear rates, the chains demonstrate a phenomenon known as “opening-up” of the structure when subjected to shear [47]. This opening-up is commonly referred to as Langmuir-type sites, which can enhance the capacity of gas retention. Furthermore, as the shear rate increases, the structural openness intensifies, leading to a stronger sorption capacity. Subsequently, the molecular chains underwent untwisting under increased shear rates, resulting in the formation of densely oriented chain structures.

4.3. Diffusion of CH₄ in HDPE under Different Shear Effects

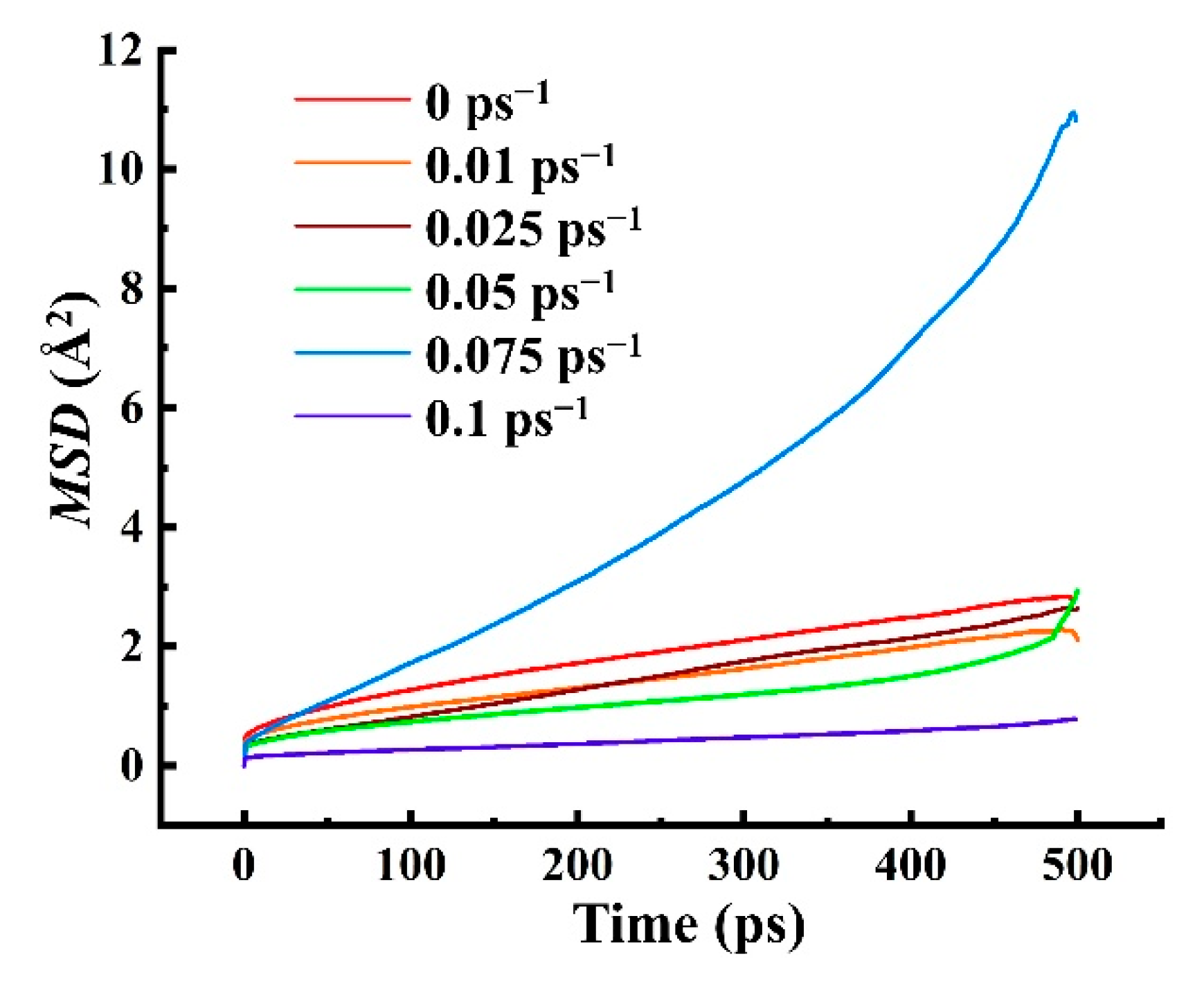
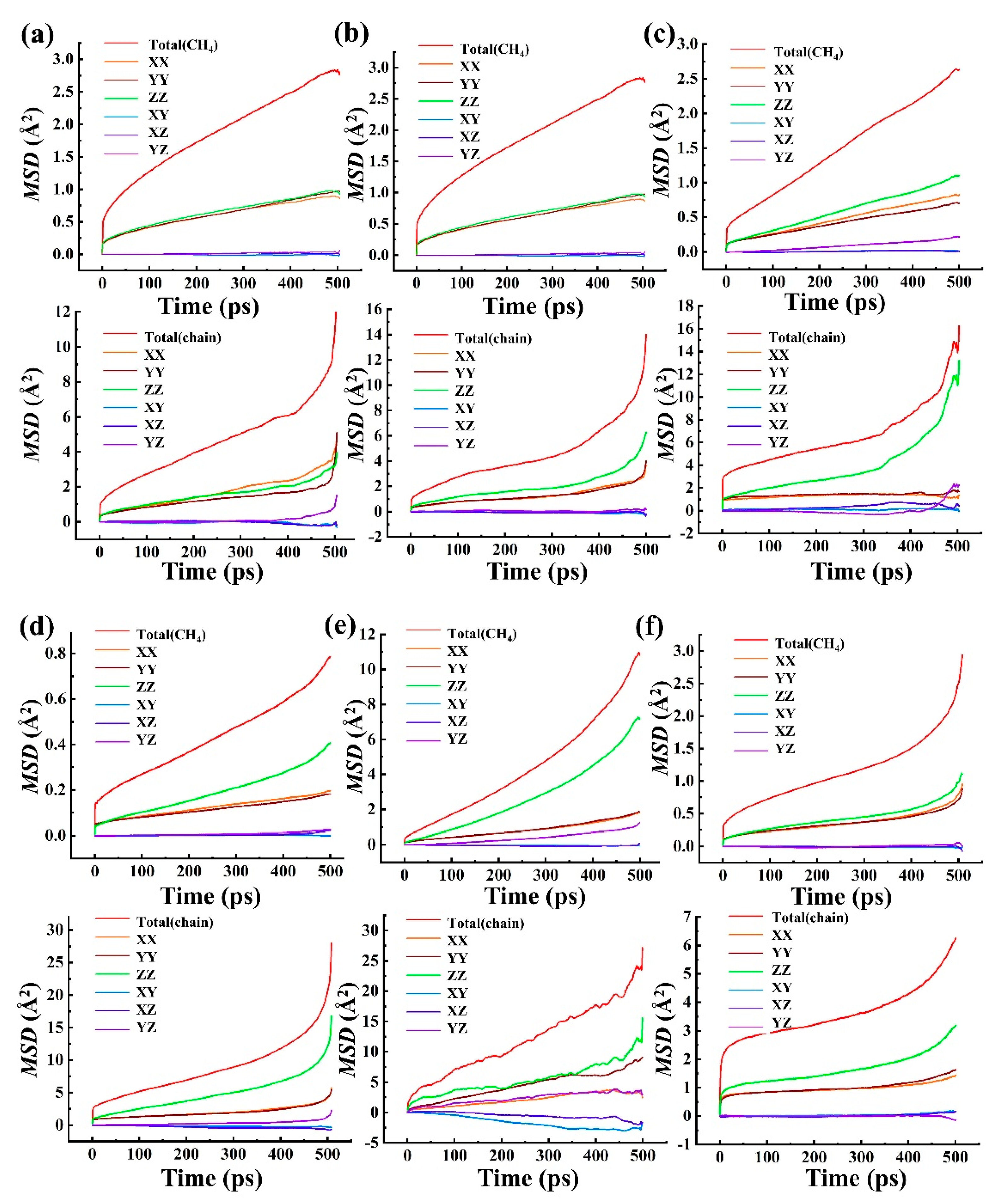
4.3.1. The Mean Square Displacement of Gas Diffusion and the Diffusion Coefficient D

The mean square displacement curve of the gas can reflect the diffusion of the gas. The diffusion curve of CH₄ in HDPE at a temperature of 303.15 K is shown in Figure 11a. At the end of the curve, noisy points appear due to statistical errors that need to be eliminated, and, consequently, the linear segment within the initial 450 ps is chosen to determine the diffusion rate. To visualize the gas diffusion rate more, the diffusion rate versus the shear rate curves was plotted and compared with previous experimental studies [43,44], as shown in Figure 11b. The diffusion rate shows an obvious trend that include an initial increase followed by a subsequent decrease as the shear rate increases, and the highest diffusion coefficient is observed at the shear rate of 0.075 ps⁻¹, consistent with the above trend.

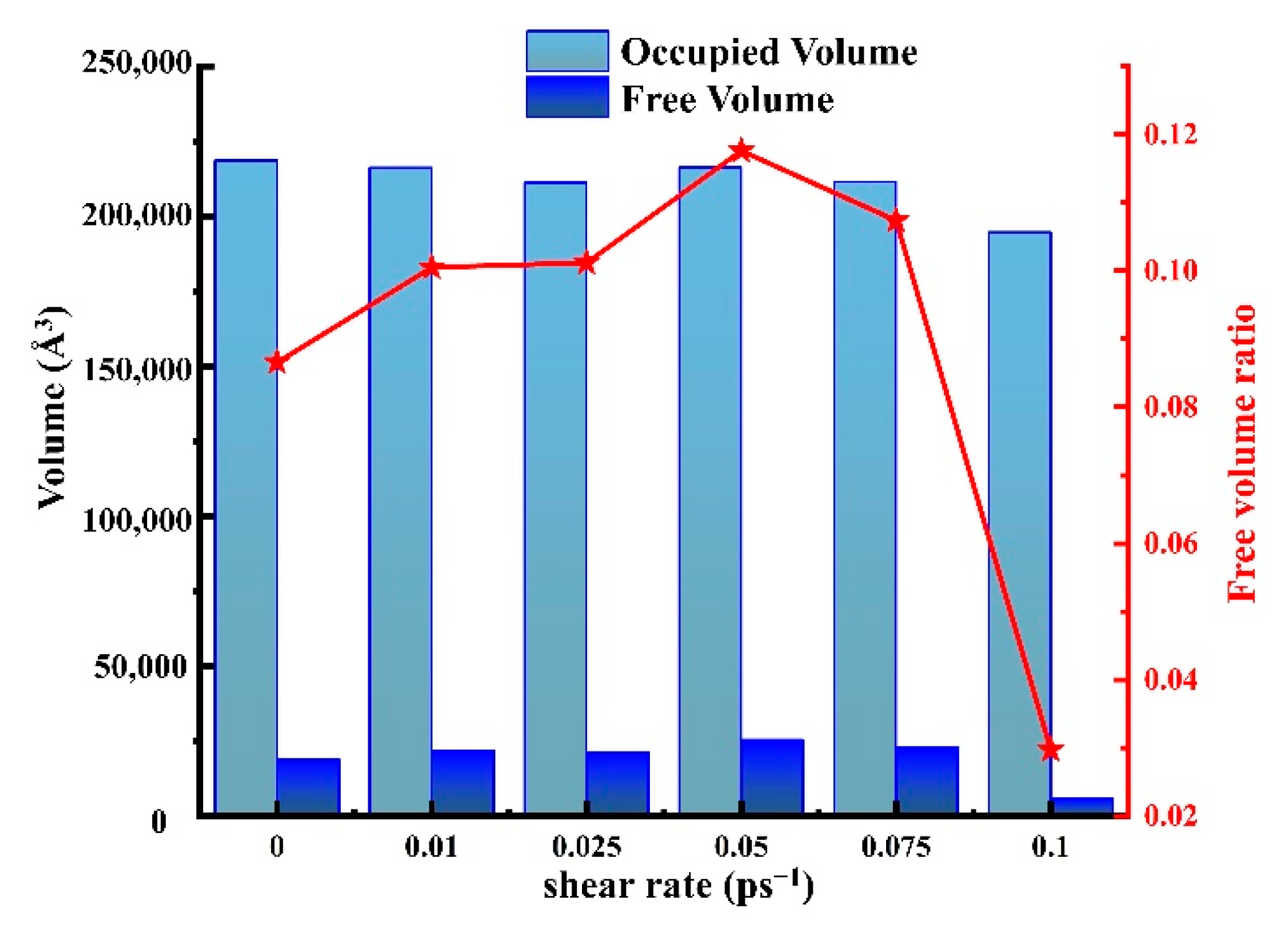
4.3.2. The Free Volume of HDPE and Motion of Polymer Chain Segments

The present situation is investigated by considering the free volume of HDPE and the change in the mobility of the polymer chain segments. Presently, the phenomenon of polymer diffusion is primarily associated with the concept of free volume within the materials [48,49,50]. Vrentas and Duda’s free volume theory [51,52] states that a polymer consists of a volume occupied by the polymer and a free volume not occupied by the polymer in the form of a “pore”. The free volume provides enough space for the movement of polymer chains and the diffusion of small molecules, and its size is directly related to the diffusion coefficient. This paper investigates the distribution of free volume inside the cell by utilizing the atom volume and surface module, as depicted in Figure 12. The red segment represents the free volume, while the blue segment corresponds to the volume occupied by the molecular chains. As the shear rate increases, the free volume inside the polymer cell, namely, the cavity, gradually increase and produce a gradual tendency to merge into clusters. When the shear rate reaches 0.1 ps⁻¹, the molecular chains undergo untwisting, resulting in a rapid decrease in the distribution of free volume. To facilitate a more understandable analysis, we computed the ratio between the free volume of the cell and the entire volume [53], as shown in Figure 13. The free volume ratio exhibits a pattern of initial increase followed by subsequent decrease as the shear rate increases. However, it is worth noting that the peak corresponding to the free volume ratio is observed at a value of 0.05 ps⁻¹, indicating that factors other than just the free volume contribute to the rate of diffusion.

The analysis focuses on the variation of the diffusion rate, concentrating on the motion of molecular chain segments [21]. The C atom within the polymer chain is defined as the marker atom, and its mean square displacement value is utilized to assess the distal motion of the chain segment. The results of molecular chain segment motion at different shear rates are shown in Figure 14. It can be observed that the motion of chain segments exhibits an increase in response to the applied shear rate when it is not untwisted. The maximum rate of motion for chain segments occurs at a shear rate of 0.075 ps⁻¹, while the motion rate of chain segments decreases significantly at 0.1 ps⁻¹, identical to the trend of the diffusion rate. It can be inferred that before the molecular chain is untwisted, the motion of the molecular chain segment is intensified in response to shear stress. This leads to a gradual opening-up of the molecular chain group internally, resulting in an increase in free volume. However, the overall molecular chain remains entangled, and the increase in chain segment motion is not readily observable. As the shear rate increases, the molecular chain undergoes untwisting, leading to a further enhancement of chain segment motion. Once completely untwisted, the molecular chain forms a dense and rigid structure, causing a weakening of chain segment motion and a reduction in molecular diffusion rate.

The chain segment motion and gas molecule diffusion motion direction at different shear rates were explored, as depicted in Figure 15. It can be observed that the molecular chain and gas diffusion motion exhibit similar trends. Specifically, the displacement sizes along the XX, YY, and ZZ directions are nearly identical, when there is no shear action. The displacement exhibits a gradual increase as the shear rate in the ZZ direction, corresponding to the direction of shear action. Conversely, the displacement gradually decreases along the other directions. In comparison to the molecular chain segment displacement observed at a shear rate of 0.075 ps⁻¹, a significant decrease in the values of chain segment displacement is observed in all directions when the shear rate is increased to 0.1 ps⁻¹. Hence, it can be inferred that the motion of chain segments plays a crucial part in determining the diffusion coefficient, with heightened chain segment motion leading to an augmentation in free volume. The free volume theory remains intact in explaining the static diffusion theory, while the dynamic diffusion theory of polymers is better understood through the concept of chain segment motion.

4.4. Permeability Coefficients

The permeation coefficient of the material can be determined by applying Equation (1) based on the solubility and diffusion coefficients calculated in this study. Nevertheless, there exists a variation in the distribution of shear rate in the radial direction of the runner when undergoing the extrusion molding process. The findings of the present investigation [4,54,55] demonstrate a gradual decrease in shear rate from the wall towards the center of the die. The surface of the polymer exhibits a higher degree of orientation in its structure, while the interior of the polymer displays an amorphous state. Combining the experimental and simulation results, it can be deduced that the surface morphology of polymer melts within the flow channel exhibits similarities with the shear rate from 0.08 ps⁻¹ to 0.1 ps⁻¹. In contrast, the internal microscopic structure of the molten material within the polymer exhibits similarities with the shear rate from 0.01 ps⁻¹ to 0.025 ps⁻¹. In this case, the polymer melt’s permeability coefficient is consistent with the actual situation.

5. Conclusions

The permeation behavior of transported oil and gas in the polymer sheath layer can lead to the failure of flexible composite pipes, and the shear action during the extrusion process of the polymer sheath layer directly affects the material’s barrier properties. This study employed molecular dynamics simulations to investigate the impact of shear on the morphological evolution of the sheath during extrusion molding as well as the penetration of CH₄ in HDPE at various shear rates. The results mentioned above can be summarized as follows:

(1)

The microstructural properties of HDPE exhibit differences across different shear rates. At lower shear rates, the chains exhibit an amorphous state. Still, when the shear rate increases, a gradual “opening-up” of structure occurs, in which the molecular chains remain entangled, with significant flexibility and consistent density. At a shear rate of 0.1 ps⁻¹, the polymer chains untwist and form a densified flow-oriented structure with increased rigidity, density, and decreased mobility;

(2)

To investigate the effect of shear rate on the solubility coefficients, the sorption characteristics of CH₄ in HDPE under different shear rates were conducted. The sorption of CH₄ under various shear rates is still a physical sorption process. The solubility coefficients exhibit a pattern of initially increasing and subsequently decreasing with increasing shear rate. Compared with the isosteric heat, the phenomenon can be more effectively explained by considering the Langmuir-type sites, which are influenced by the microstructure of the material;

(3)

The diffusion coefficient of CH₄ in HDPE was investigated under various shear rates. The solubility coefficients exhibit a pattern of initially increasing and subsequently decreasing with increasing shear rate as above. This analysis investigates the impact of cutting rate on the spread rate from the perspectives of free volume and chain movement. It is found that the free volume theory does not significantly influence the diffusion coefficient. However, the diffusion movement of gas molecules corresponds to the tendency of chain segments, indicating that the theory of chain movement provides a more comprehensive explanation for the process of gas dynamic diffusion compared to the free volume theory.

In this paper, we expected to combine the adsorption and diffusion coefficients of gases under different shear rates with the FEM simulations and experimentally obtained the shear rate distribution of the extrusion process to predict the microscopic morphological changes in materials and the material permeability coefficients. These predictions offer valuable insights for enhancing the barrier performance of the inner sheath layer during production.