Analysis of Water Hammer and Pipeline Vibration Characteristics of Submarine Local Hydraulic System
Abstract
:1. Introduction
2. Principle of Local Hydraulic System and Construction of AMESim Model
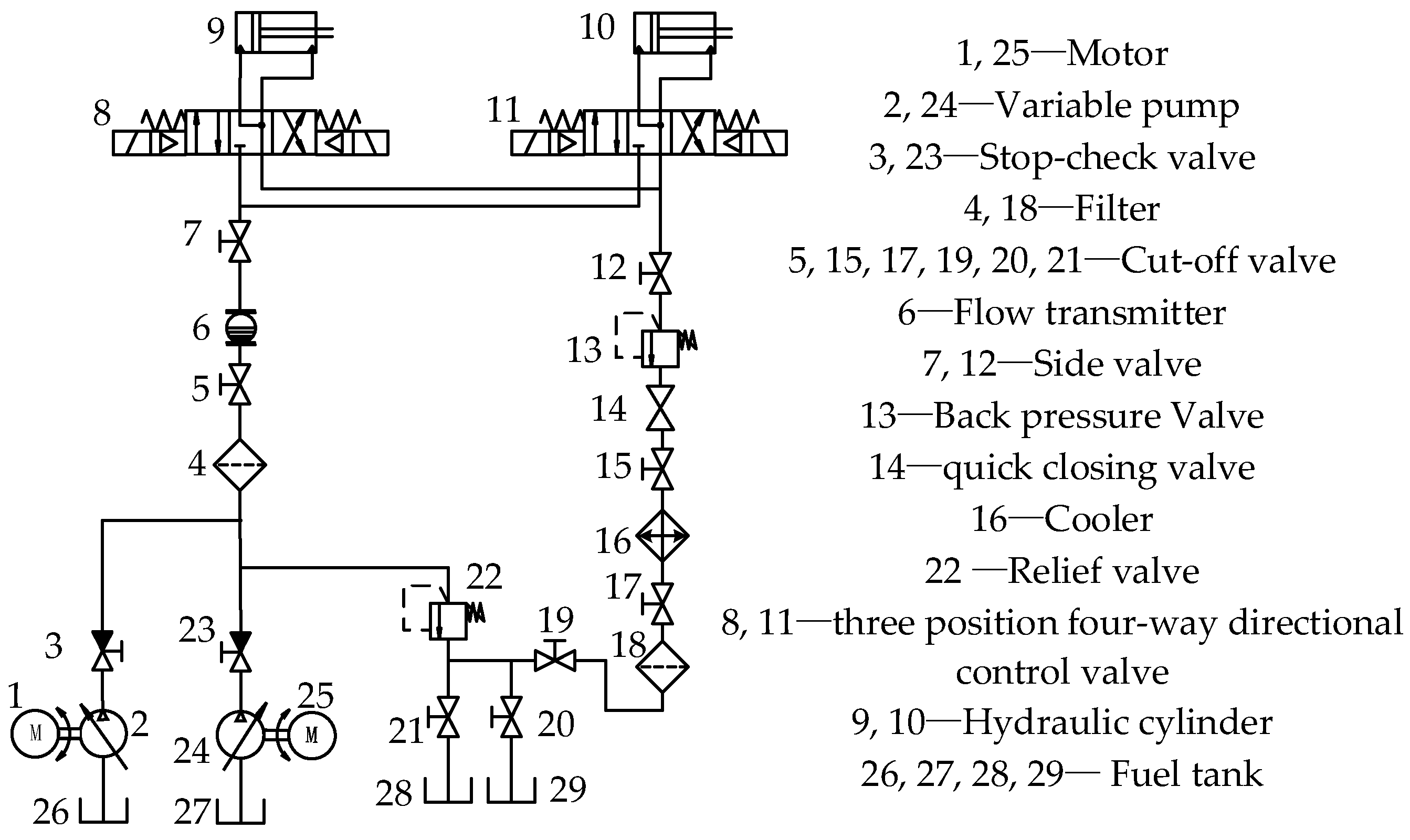
2.1. Principle of Local Hydraulic System
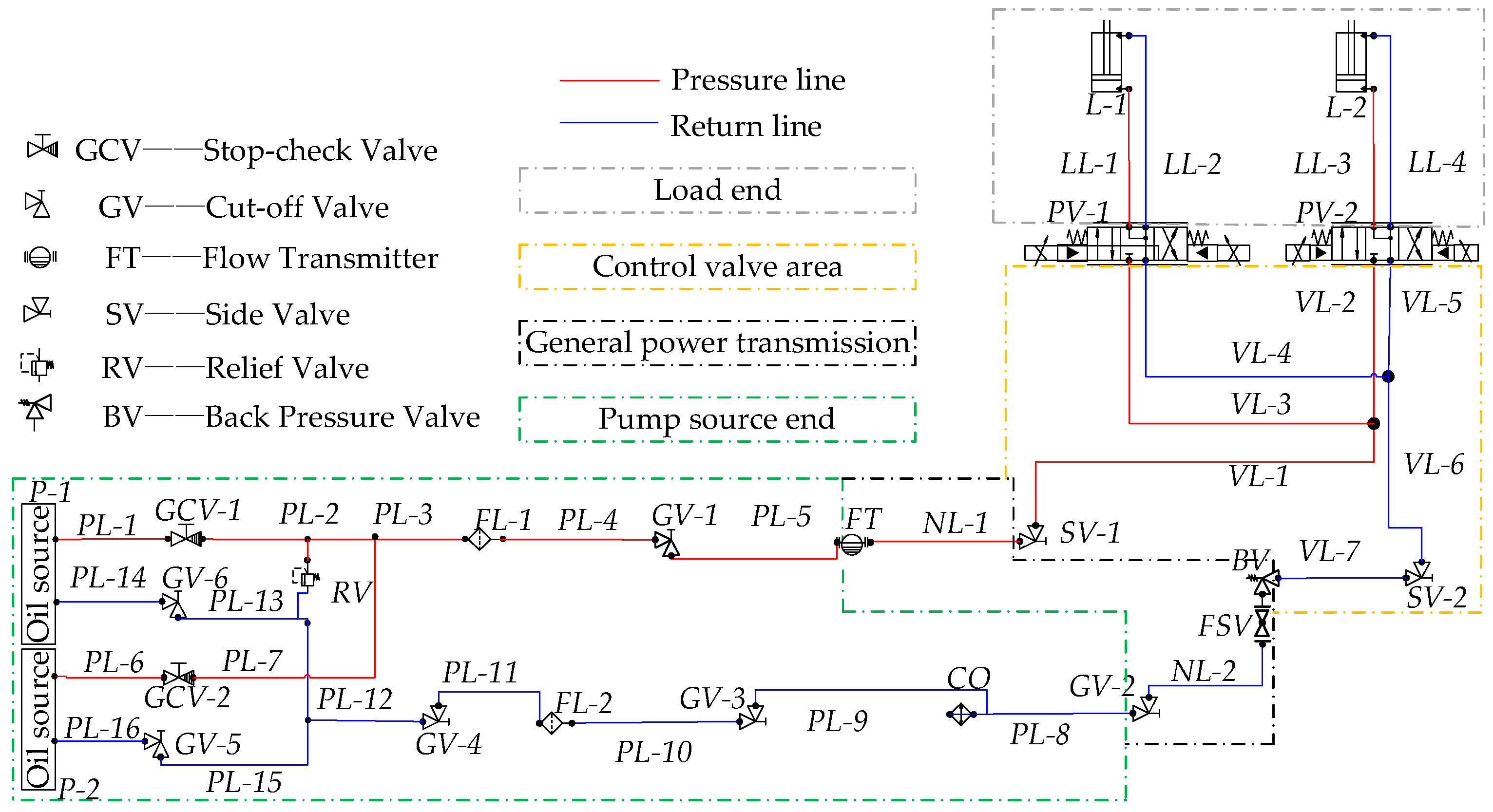
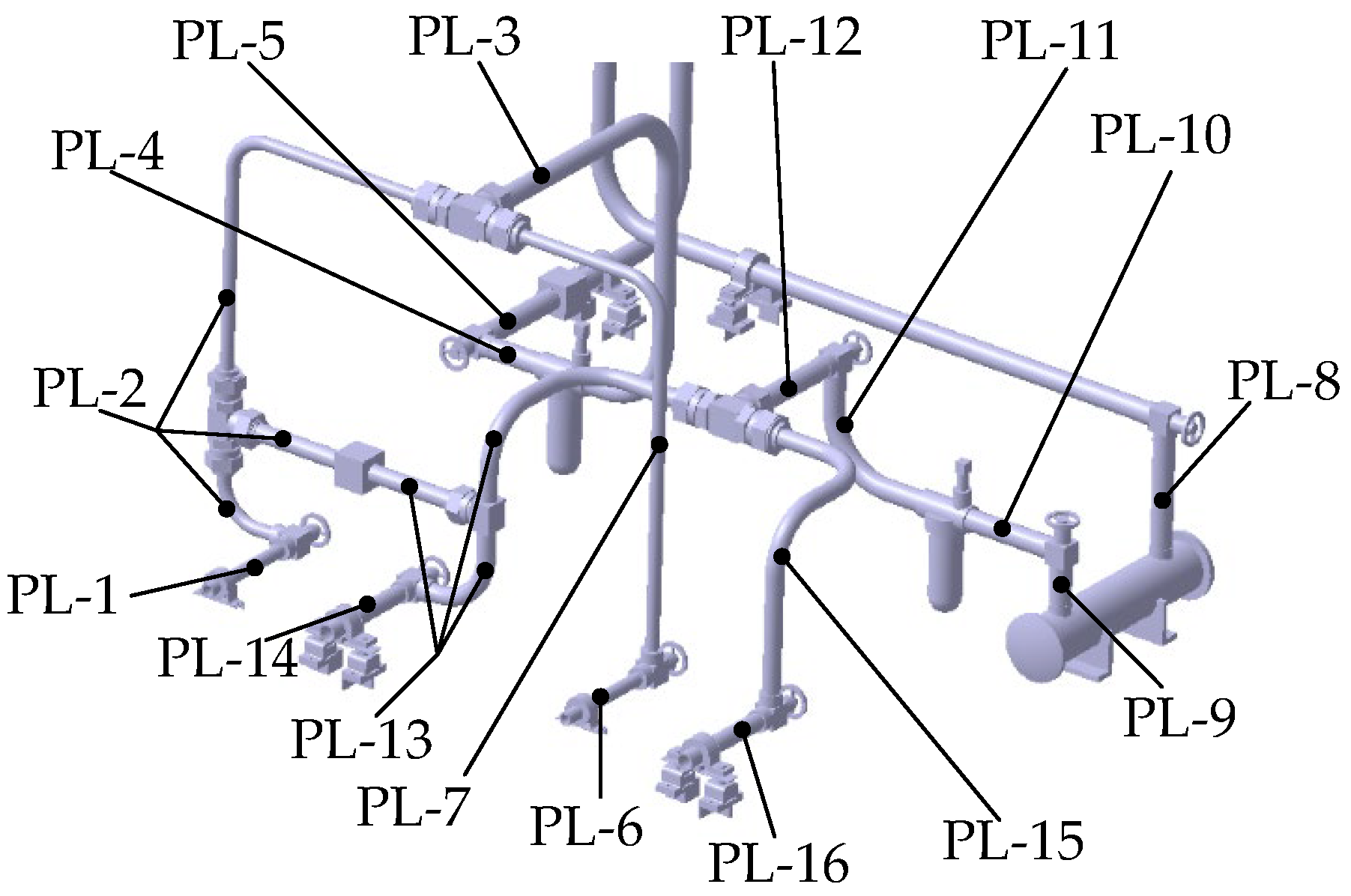
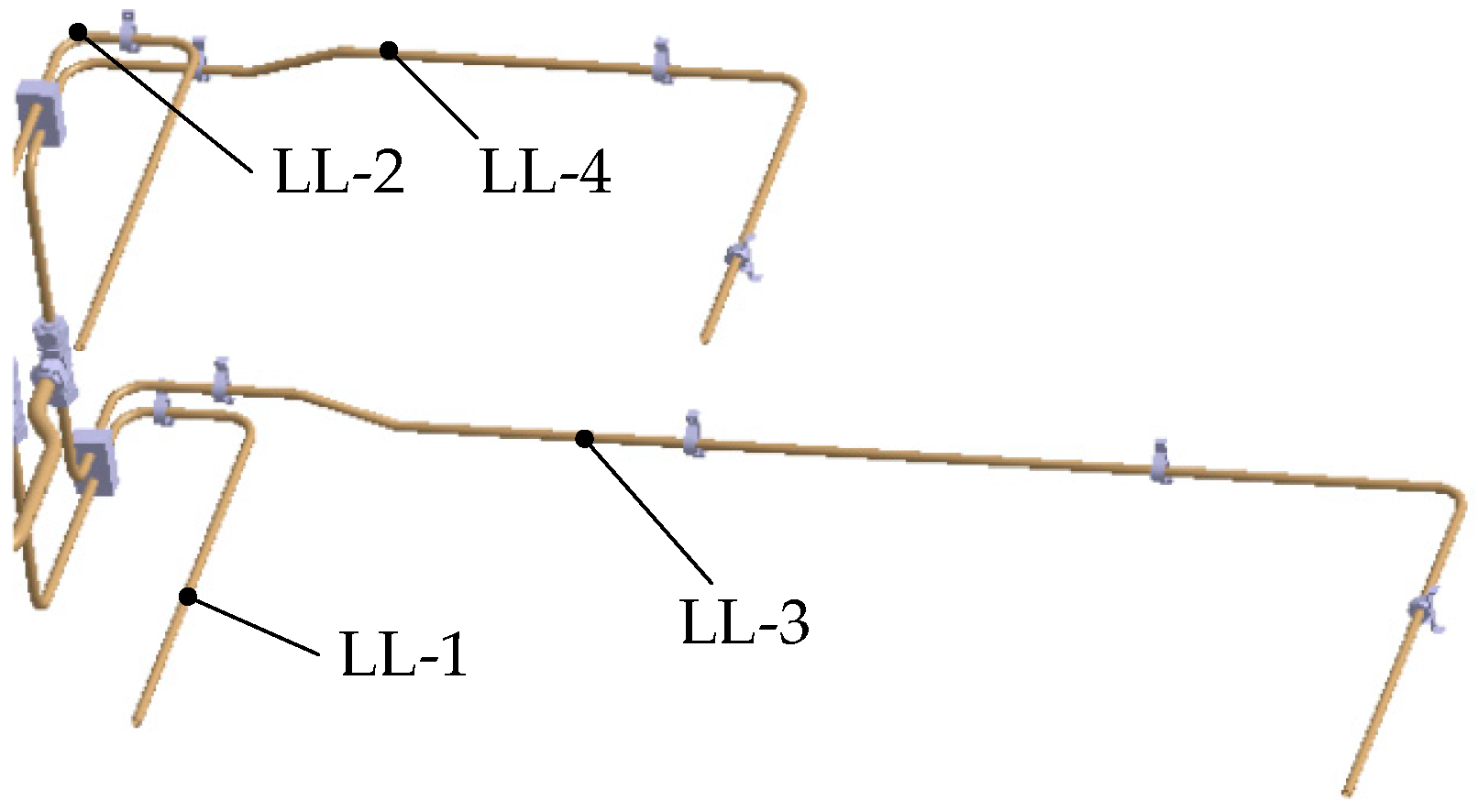
2.2. Topological Structure Division of Hydraulic Pipeline System
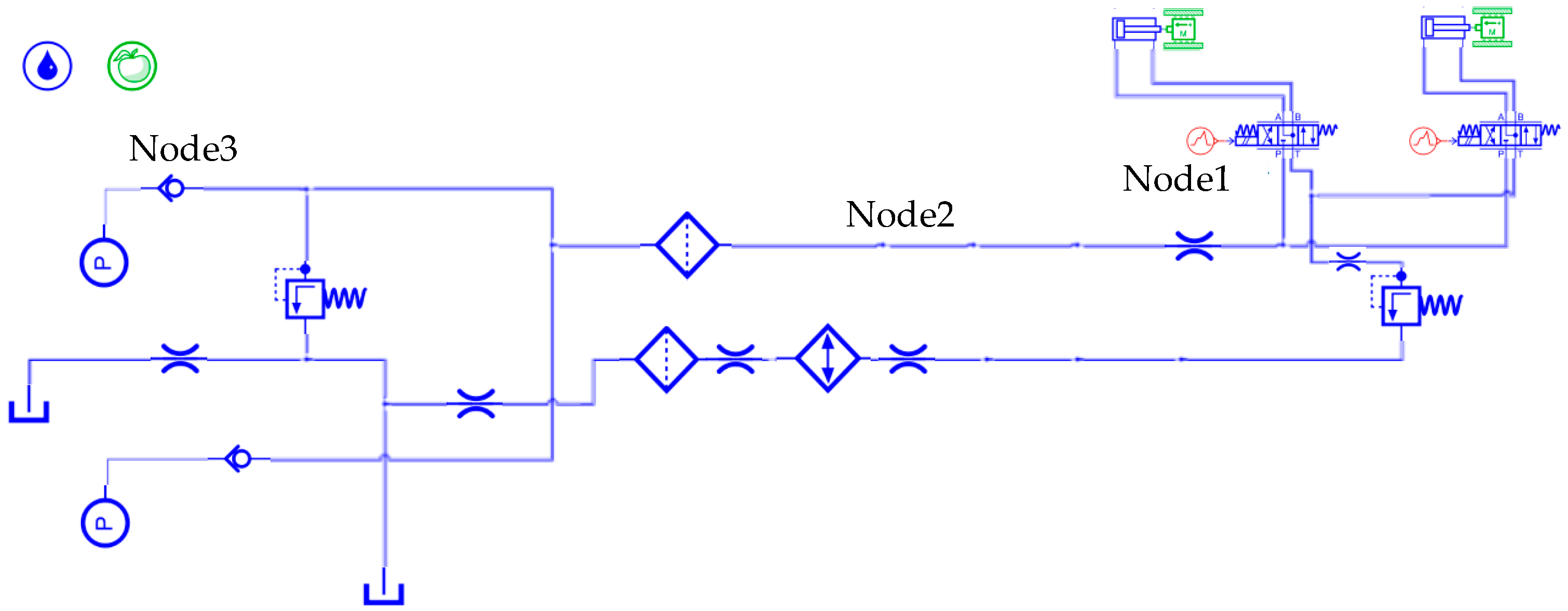
2.3. AMESim Modeling of Local Hydraulic System
3. Analysis of Water Hammer Transmission and Influence Law
3.1. Empirical Formula for Calculating Water Hammer Wave Pressure and Wave Velocity
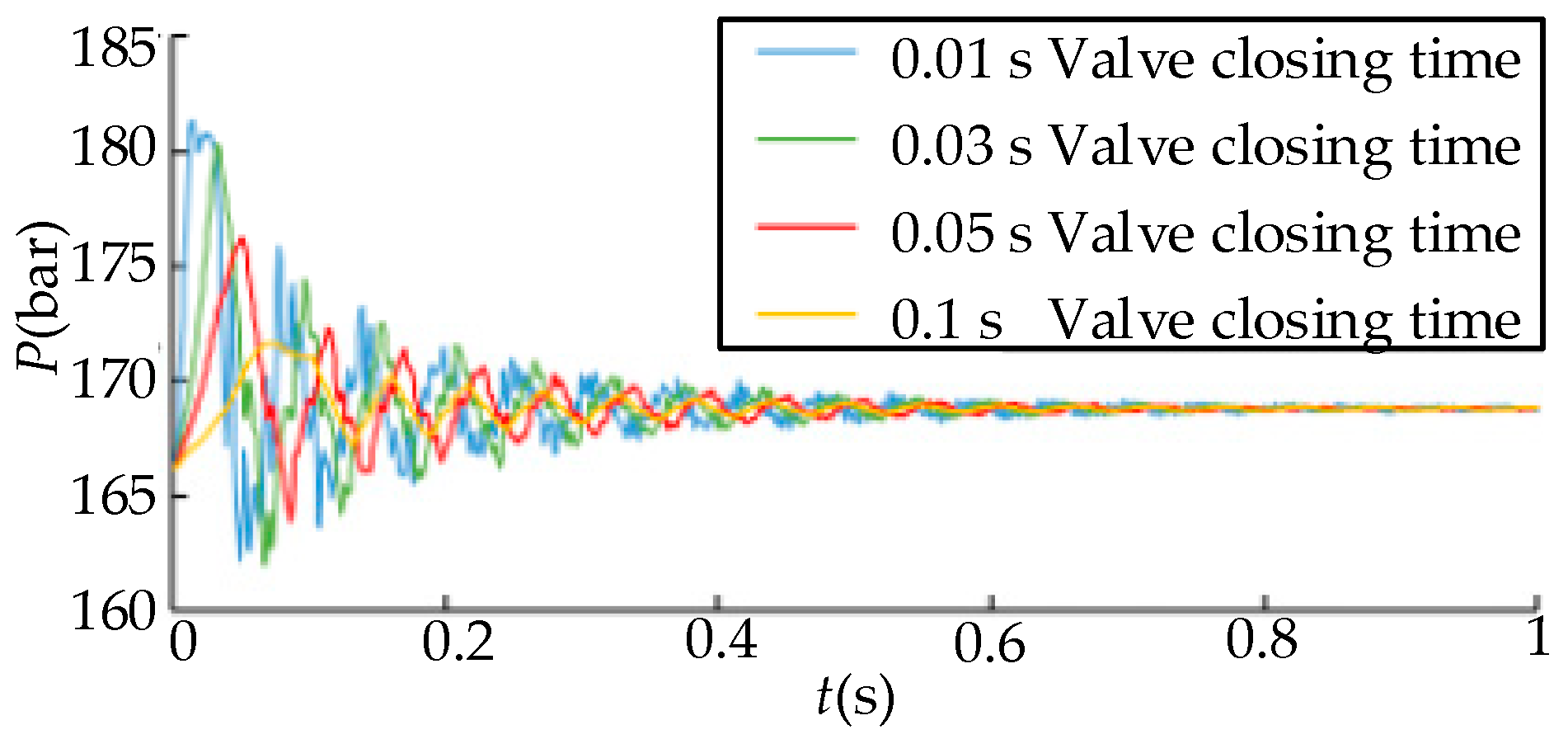
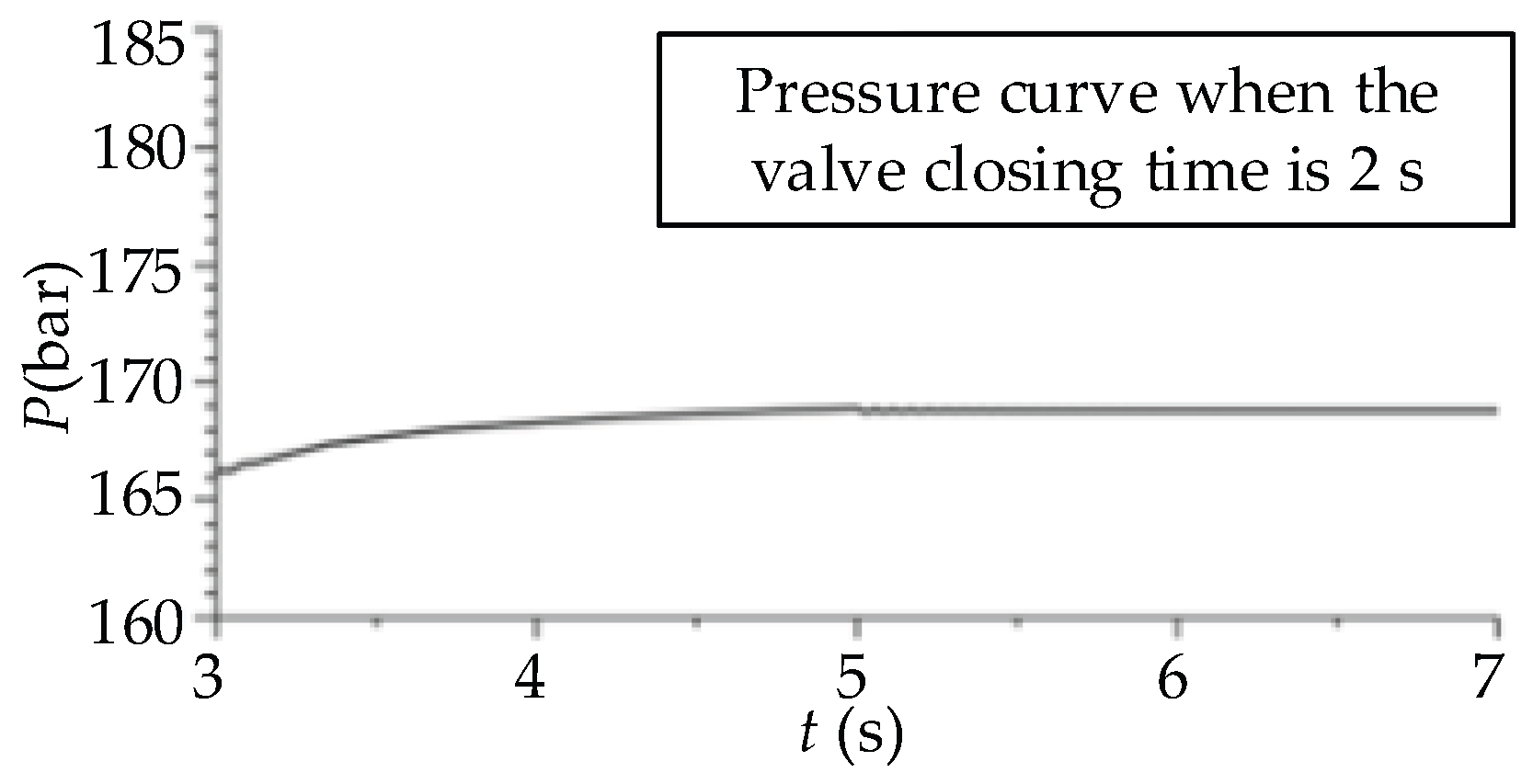
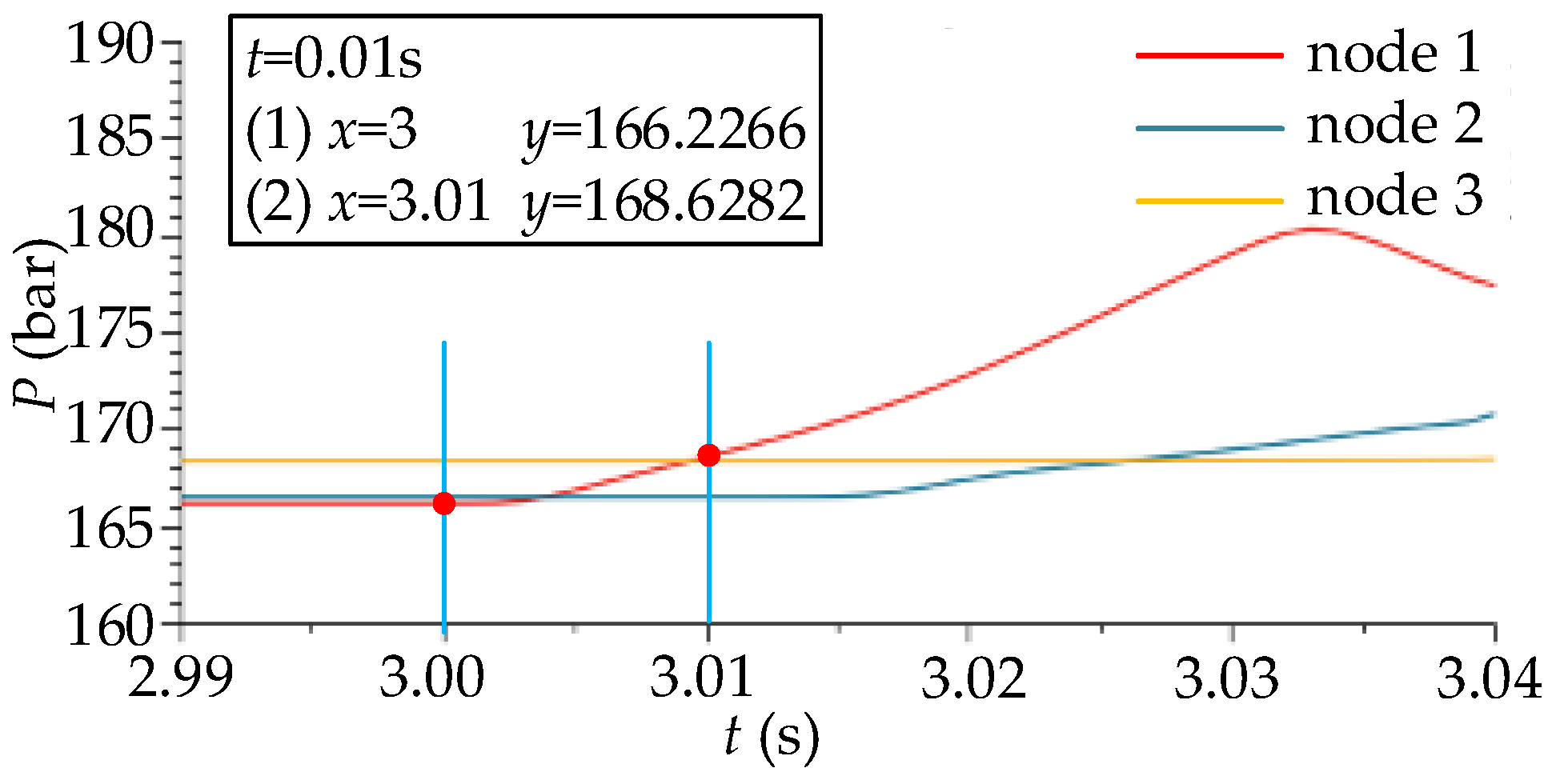
3.2. Analysis of the Influence of Valve Closing Time on Water Hammer
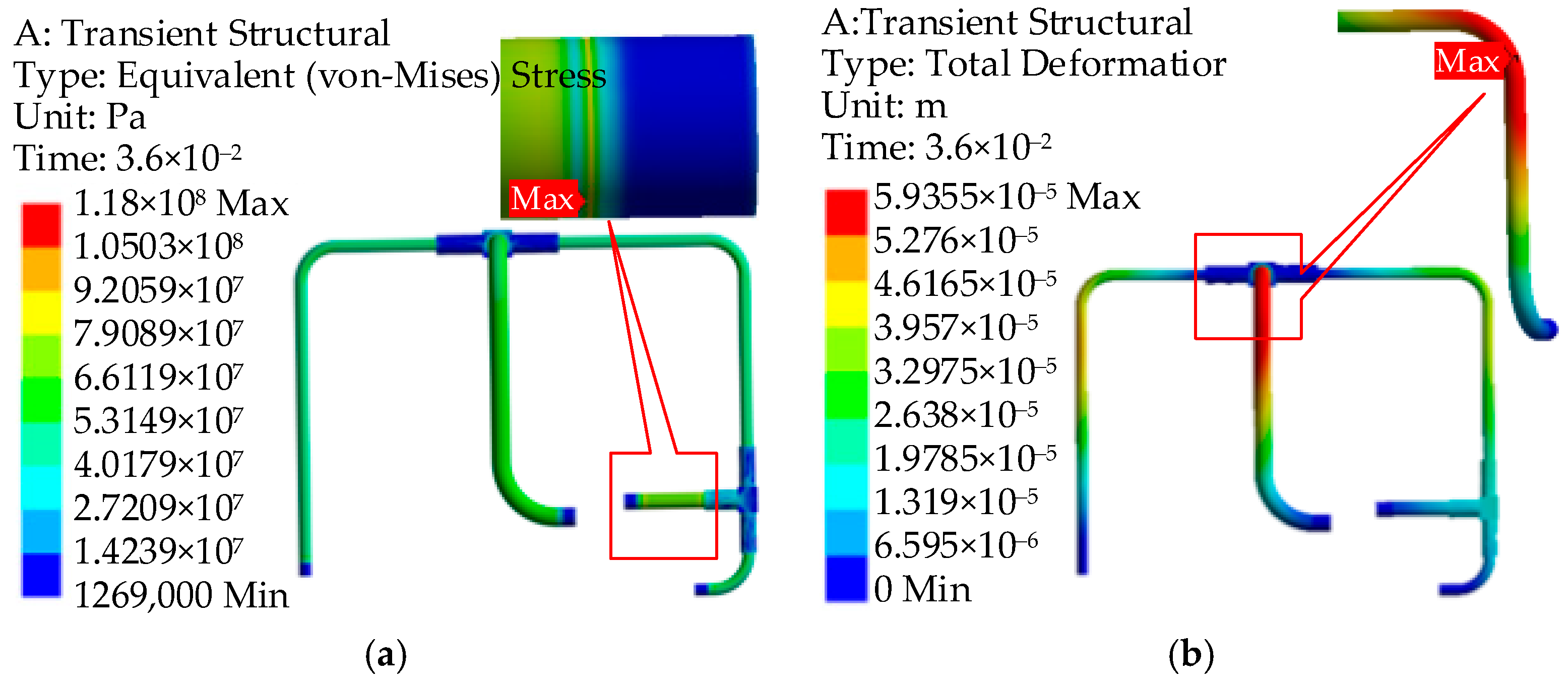
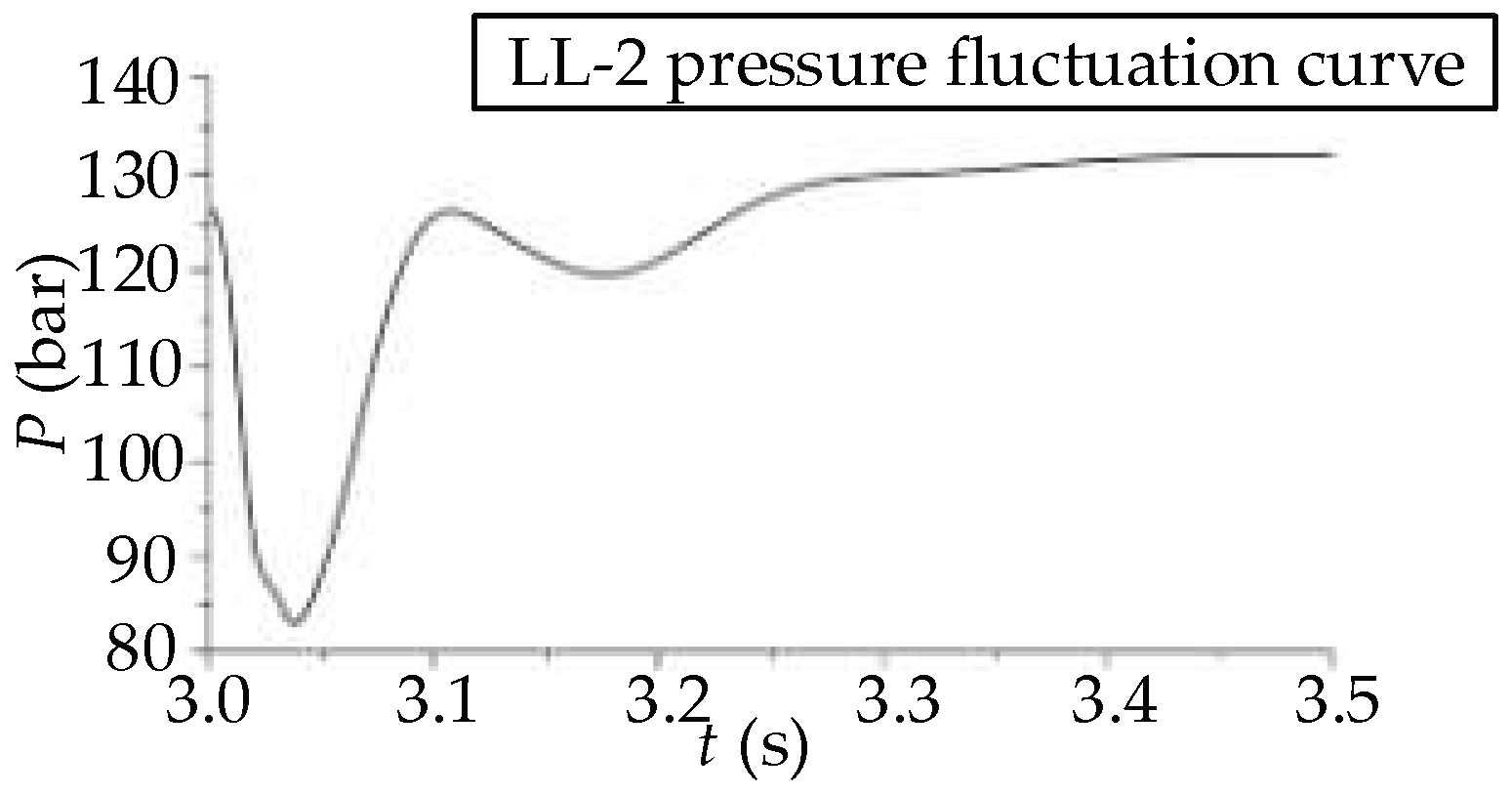
3.3. Analysis of the Transmission and Attenuation Characteristics of the Valve-Closing Water Hammer
4. Vibration Characteristics Analysis of the Submarine Hydraulic Pipeline System
4.1. Construction of FSI Vibration Model of the Submarine Hydraulic Pipeline System
4.1.1. Simplified Calculation of FSI
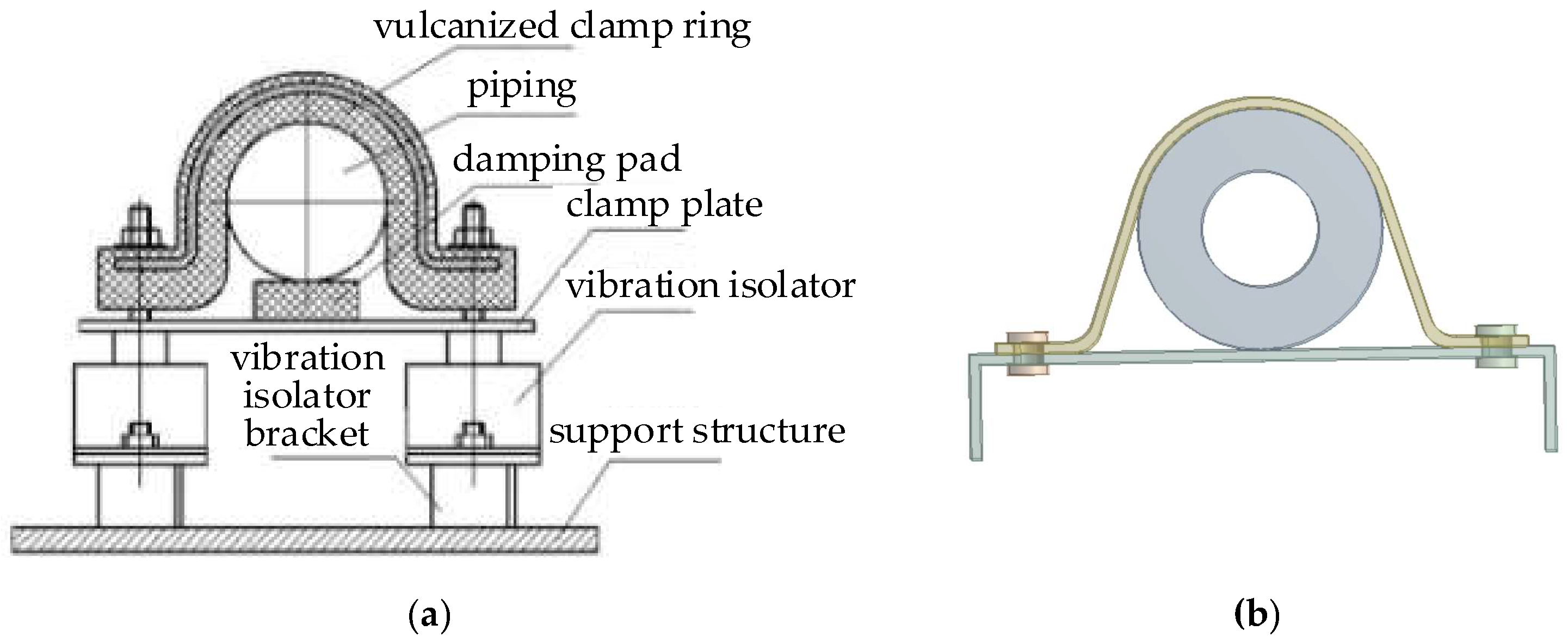
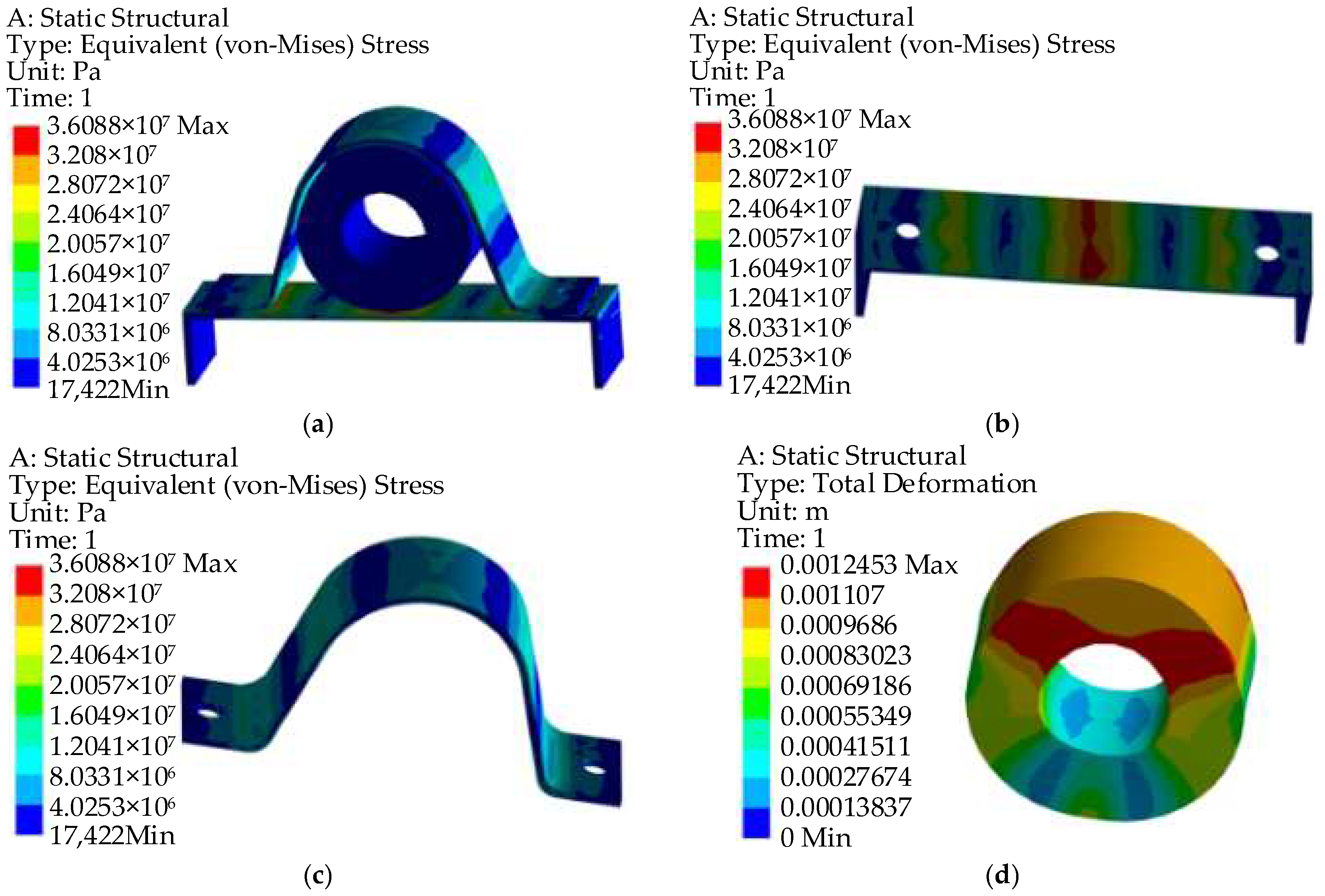
4.1.2. Establishment of a Clamp Dynamics Model for Submarine Hydraulic Pipelines
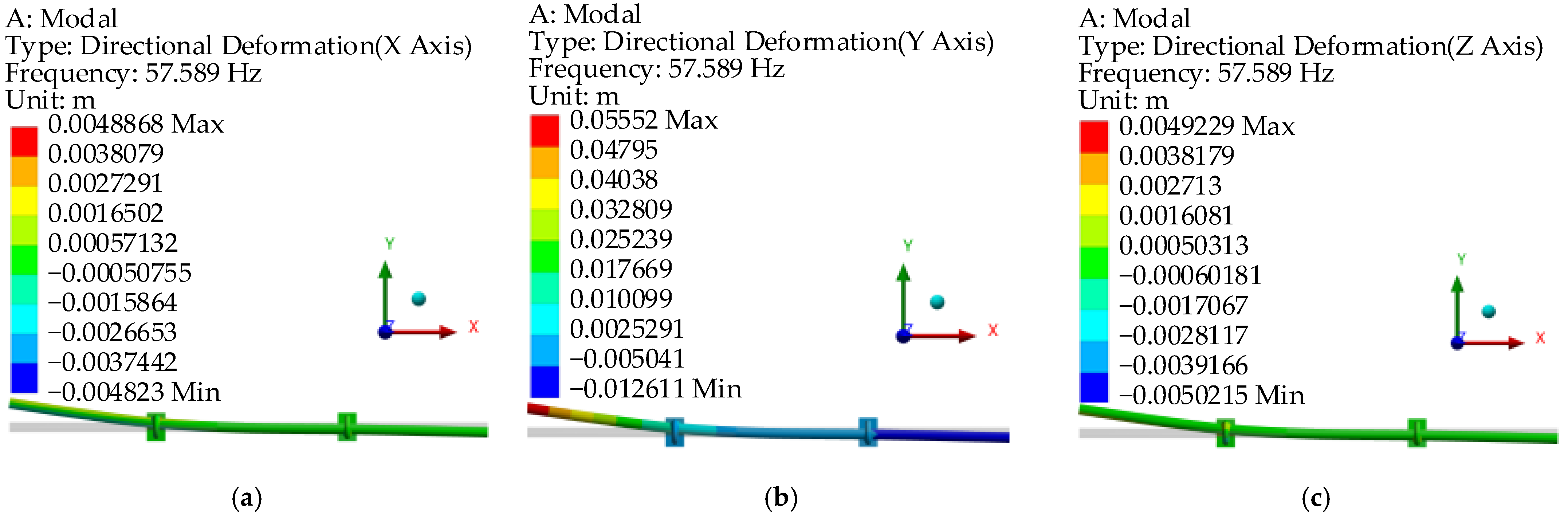
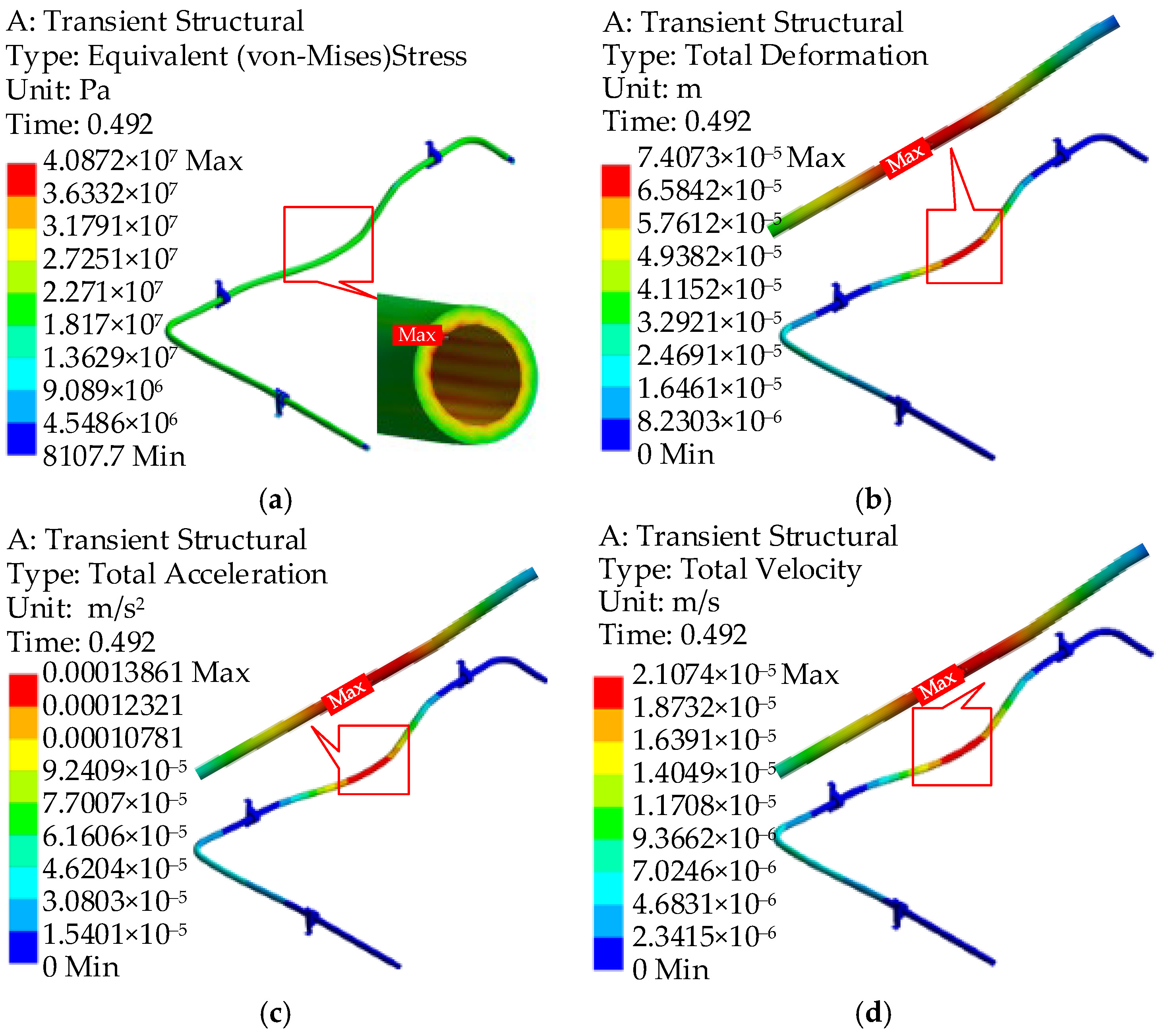
4.2. Modal Simulation Analysis of Pipelines in Different States
4.3. Analysis of Vibration Characteristics of Hydraulic Pipeline Systems
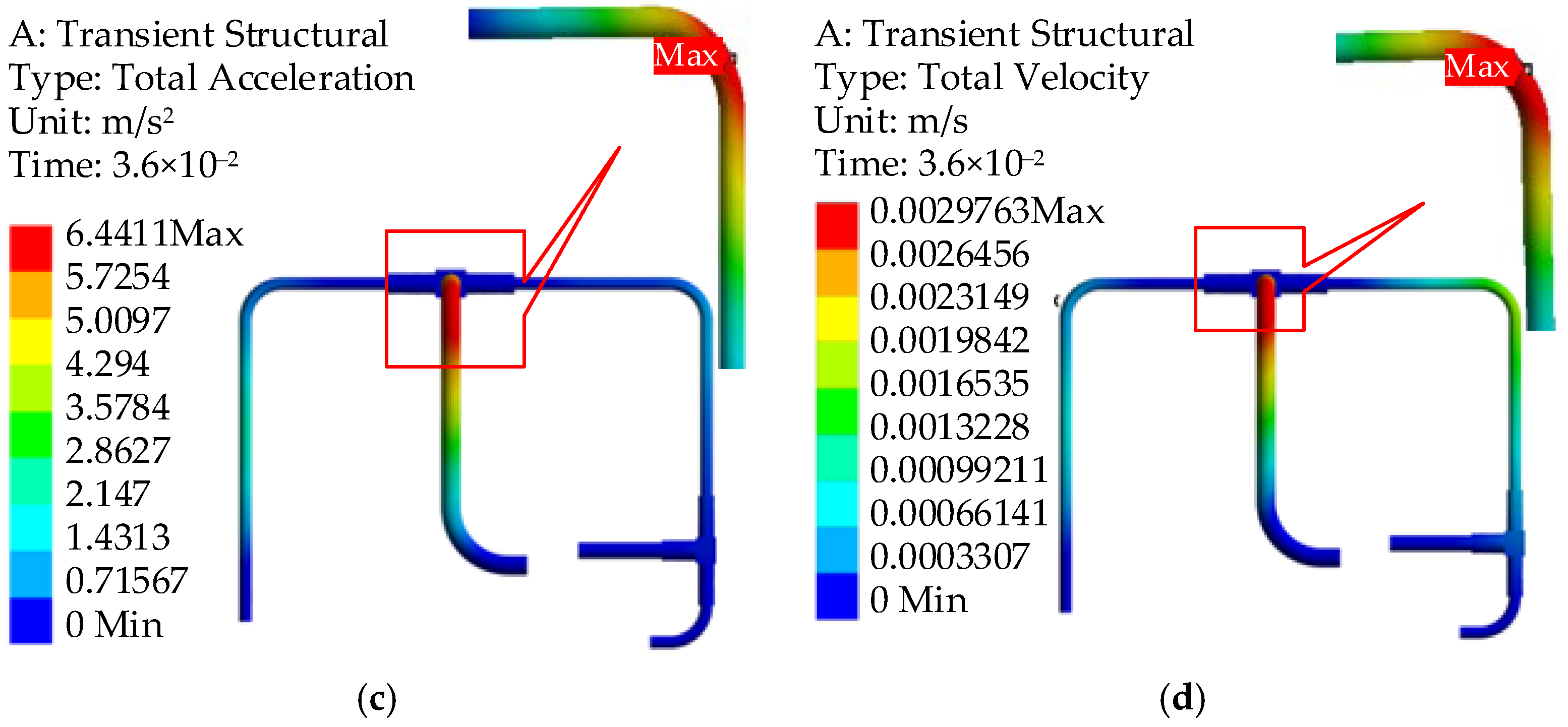
4.3.1. Analysis of the Vibration Characteristics of the Pipelines at the Pump Source End
4.3.2. Analysis of the Vibration Characteristics of the Pipelines at the Load End
5. Modal Experimental Study on Pipeline Units
5.1. Construction of Pipeline Modal Test Bench
5.2. Analysis of Modal Verification Test Results for Hydraulic Pipelines
6. Optimization Analysis of Passive Vibration Control for Pipelines
6.1. Parametric Modeling and Co-Simulation
6.2. Optimizing Variables and Objectives
6.3. Analysis of Optimization Results
7. Conclusions
- The shorter the commutation time of the directional valve, the more severe the water hammer fluctuation is. When the commutation time is large enough, the water hammer wave will not produce intense fluctuations but will increase steadily to a higher pressure.
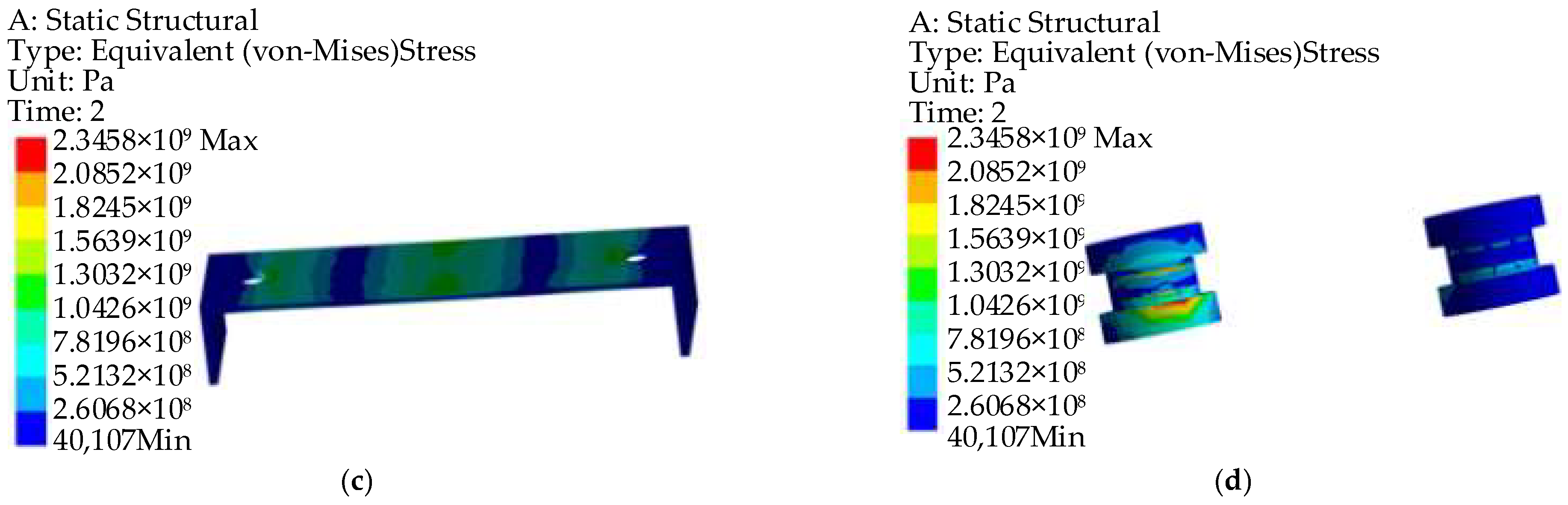
- The maximum vibration response of the pipeline under water hammer excitation mostly occurs at the position where the pipeline configuration changes, and the vibration stress has the same change trend as the fluid excitation. Under the water hammer excitation, the pipelines can meet the strength requirements.
- The modal finite element analysis and experimental verification of the pipeline are carried out. The results show that the error between the finite element calculation and the experimental results is within 5%. The structural stiffness (simulating bolt pre-tightening through interference fit) and mass (fluid density equivalent) related settings that have a significant influence on the modal are preliminary verified in this paper.
- The genetic algorithm is used to optimize the clamp layout. The difference between the predicted optimization results and the actual analysis results is within 5%, indicating that the optimization analysis method is feasible. Through optimization analysis, it is determined that the arrangement of the clamps should be close to the fixed support of the pipeline to avoid small areas of stress concentration.
- In this study, vibration analysis only considers the influence of the water hammer. In future work, the multi-source vibration modeling and analysis of the submarine hydraulic pipeline system should be constructed. Additionally, the multi-source vibration superposition mechanism and transmission law of the actuator, hydraulic valve, pipeline support, and hull should be studied in depth.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Experimental Apparatus and Measurement System

| Item | Manufacturer/Type | Performance |
|---|---|---|
| Hammer | YDL-2 | Charge sensitivity: 4.00 PC/N |
| Measuring range: 50 kN | ||
| Linearity: 0.83% | ||
| Natural frequency: 40 kHz | ||
| Resolution ratio: 0.025 N | ||
| Insulation resistance: >1012 Ω | ||
| Accelerometer | B&K BK4525-B-001 | Measuring range: ±700 m/s2 |
| Frequency range: 0–20 kHz | ||
| Sensitivity X-axis: 97.04 mV/g Y-axis: 97.21 mV/g Z-axis: 99.00 mV/g | ||
| PXIe chassis | National Instruments PXIe-1078 | 9 AC hybrid slots System slot bandwidth: 250 MB/s System bandwidth: 1 GB/s |
| PXIe controller | National Instruments PXIe-8820 | Dual-core processor (2.2 GHz) System slot bandwidth: 250 MB/s System bandwidth: 1 GB/s |
| Analog output card | National Instruments PXI-6723 | 32 analog output channels Conversion rate: 10 kHz Maximum sampling rate: 800 kS/s |
| Data acquisition card | National Instruments PXI-6221 | 16 AI channels 2 AO channels Maximum sampling rate: 250 kS/s |
| Vibration acquisition card | National Instruments PXIe-4497 | 24 resolution 24 channels Maximum sampling rate: 204.8 kS/s |
References
- Quan, L.X.; Kong, X.D.; Yu, B.; Bai, H.H. Research Status and Trends on Fluid-Structure Interaction Vibration Mechanism and Control of Hydraulic Pipeline. J. Mech. Eng. 2015, 51, 175–183. [Google Scholar] [CrossRef]
- Cai, Y.G. Pipeline Dynamics of Fluid Transmission; Zhejiang University Press: Hangzhou, China, 1990. [Google Scholar]
- Pal, S.; Hanmaiahgari, P.R.; Karney, B.W. An Overview of the Numerical Approaches to Water Hammer Modelling: The Ongoing Quest for Practical and Accurate Numerical Approaches. Water 2021, 13, 1597. [Google Scholar] [CrossRef]
- Zhang, D.S. Effect of Unsteady Friction and Valve Closing Law on Water Hammer. Master’s Thesis, Xi’an University of Technology, Xi’an, China, June 2021. [Google Scholar]
- Jiang, D.; Lu, Q.; Liu, Y.; Zhao, D. Study on Pressure Transients in Low Pressure Water-Hydraulic Pipelines. IEEE Access 2019, 7, 80561–80569. [Google Scholar] [CrossRef]
- Liu, Y. Research on Water Hammer Suppression Method Based on Valve Closing Rule in Hydraulic Pipeline. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, June 2021. [Google Scholar]
- Chen, Y.; Zhao, C.; Guo, Q.; Zhou, J.; Feng, Y.; Xu, K. Fluid-Structure Interaction in a Pipeline Embedded in Concrete During Water Hammer. Front. Energy Res. 2022, 10, 956209. [Google Scholar] [CrossRef]
- Afshar, M.H.; Rohani, M. Water hammer simulation by implicit method of characteristic. Int. J. Press. Vessel. Pip. 2008, 85, 851–859. [Google Scholar] [CrossRef]
- Mikota, G. Low Frequency Correction of a Multi-Degrees-of-Freedom Model for Hydraulic Pipeline Systems. IFAC-PapersOnLine 2015, 48, 435–440. [Google Scholar] [CrossRef]
- Mikota, G.; Manhartsgruber, B.; Kogler, H.; Hammerle, F. Modal Testing of Hydraulic Pipeline Systems. J. Sound Vib. 2017, 409, 256–273. [Google Scholar] [CrossRef]
- Sadat Hosseini, R.; Ahmadi, A.; Zanganeh, R. Fluid-Structure Interaction during Water Hammer in a Pipeline with Different Performance Mechanisms of Viscoelastic Supports. J. Sound Vib. 2020, 487, 115527. [Google Scholar] [CrossRef]
- Ulanov, A.M.; Bezborodov, S.A. Calculation Method of Pipeline Vibration with Damping Supports Made of the MR Material. Procedia Eng. 2016, 150, 101–106. [Google Scholar] [CrossRef]
- Bezborodov, S.A.; Ulanov, A.M. Calculation of Vibration of Pipeline Bundle with Damping Support Made of MR Material. Procedia Eng. 2017, 176, 169–174. [Google Scholar] [CrossRef]
- Chai, Q.D.; Zeng, J.; Ma, H.; Li, K.; Han, Q.K. Dynamic Modeling Approach for Nonlinear Vibration Analysis of the L–Type Pipeline System with Clamps. Chin. J. Aeronaut. 2020, 33, 3253–3265. [Google Scholar] [CrossRef]
- Chai, Q.D.; Fu, Q.; Ma, H.; Han, Q.K.; Zhang, D.Z. Modeling and Dynamic Characteristics Analysis for a Pipeline System with Single Double–Clamp. J. Vib. Shock. 2020, 39, 114–120. [Google Scholar]
- Chai, Q.D.; Piao, Y.H.; Ma, H.; Wu, W.X.; Sun, W. Calculation of Natural Characteristics and Experimental Methods of the Clamp-Pipe System. J. Aerosp. Power 2019, 34, 1029–1035. [Google Scholar]
- Gao, P.; Yu, T.; Zhang, Y.; Wang, J.; Zhai, J. Vibration Analysis and Control Technologies of Hydraulic Pipeline System in Aircraft: A Review. Chin. J. Aeronaut. 2021, 34, 83–114. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Y.X.; Li, S.M. Vibration Analysis and Optimization of Aircraft Engine Driven Pump Outlet Pipeline. Chin. Hydraul. Pneum. 2020, 9, 115–121. [Google Scholar]
- Liu, X.F.; Zhang, Y.L.; Zhang, D.C.; Yu, T.; Gao, P.X. Analysis and Test Verification of Stiffness and Damping Characteristics of Aviation Clamp with Cushion. J. Aerosp. Power 2022, 37, 274–282. [Google Scholar]
- Li, X.; Li, W.H.; Shi, J.; Li, Q.; Wang, S.P. Pipelines Vibration Analysis and Control Based on Clamps’ Locations Optimization of Multi-Pump System. Chin. J. Aeronaut. 2022, 35, 352–366. [Google Scholar] [CrossRef]
- Quan, L.X.; Zhang, Q.W.; Li, Z.C.; Sheng, S.W. Sensitivity Analysis and Optimization for Support Parameter of Aviation Hydraulic Pipeline. Chin. Hydraul. Pneum. 2017, 8, 95–99. [Google Scholar]
- Frahm, H. Device for Damping Vibrations of Bodies. Google Patents US989958A, 18 April 1911. [Google Scholar]
- Jiang, J.; Lou, J.; Deng, F. Control Measures about Vibration and Noise of Pipeline Onboard Marine Vessels. Vibroeng. Procedia 2015, 5, 377–382. [Google Scholar]
- Song, G.B.; Zhang, P.; Li, L.Y.; Singla, M.; Patil, D.; Li, H.N.; Mo, Y.L. Vibration control of a pipeline structure using pounding tuned mass damper. J. Eng. Mech. 2016, 142, 4016031. [Google Scholar] [CrossRef]
- Zhang, X.; Bian, S.; Wang, H.; Jia, X.; Wang, C. Effects of Valve Opening on Direct Water Hammer Pressure Characteristics in PMMA Pipelines. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 408. [Google Scholar] [CrossRef]
- Arefi, M.H.; Ghaeini-Hessaroeyeh, M.; Memarzadeh, R. Numerical Modeling of Water Hammer in Long Water Transmission Pipeline. Appl. Water Sci. 2021, 11, 140. [Google Scholar] [CrossRef]
- Ye, J.; Zeng, W.; Zhao, Z.; Yang, J.; Yang, J. Optimization of Pump Turbine Closing Operation to Minimize Water Hammer and Pulsating Pressures During Load Rejection. Energies 2020, 13, 1000. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, D.; Cheng, P.; Zang, Y. Research on Non-Contact Bolt Preload Monitoring Based on DIC. J. Phys. Conf. Ser. 2023, 1, 2528. [Google Scholar] [CrossRef]
- Pu, L.; Ji, M. Mechanical Design, 8th ed.; Higher Education Press: Beijing, China, 2006. [Google Scholar]
- Wang, B. Fluid-Structure Interaction Dynamic Analysis of the Typical Aircraft Hydraulic Pipeline. Master’s Thesis, Xi’an University of Technology, Xi’an, China, June 2013. [Google Scholar]
- Thomas, P.S. Analysis of Induced Vibrations in Fully-developed Turbulent Pipe Flow Using a Coupled LES and FEA Approach; Brigham Young University: Provo, UT, USA, 2009. [Google Scholar]






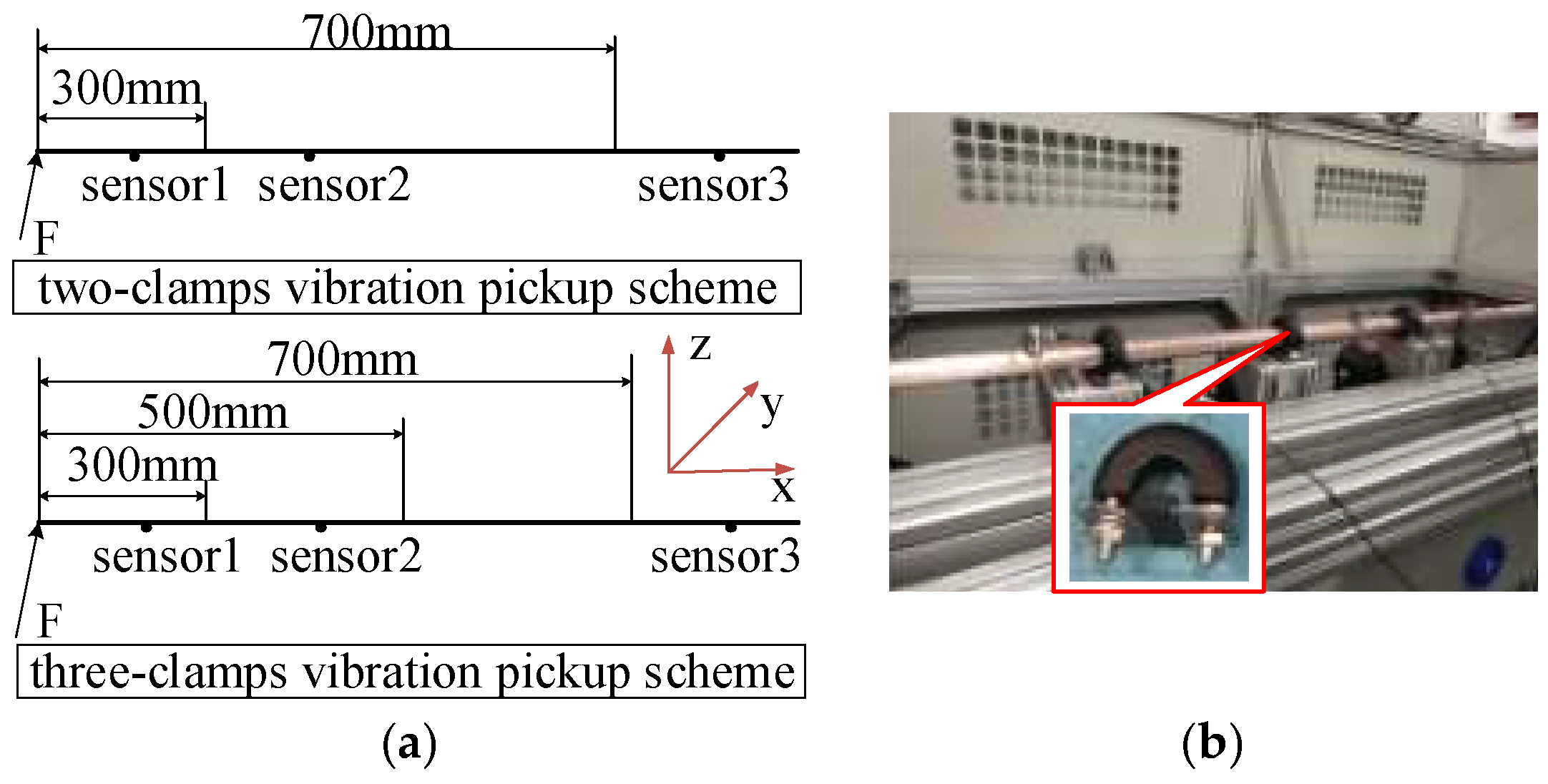

| Parameter Name | Value | Unit | Parameter Name | Value |
|---|---|---|---|---|
| rated pressure | 16 | MPa | rated speed r | 1400 r/min |
| installed power | ≤14 | kW | outlet flow q | 0–40 L/min |
| Phase | Time (s) | Purpose |
|---|---|---|
| 1 | 0–3 | system pressure reaches 16 MPa |
| 2 | 3–3.03 | directional valve switching, p port closed |
| 3 | 3.03–6.03 | p port keeps closed |
| Valve Closing Time (s) | Node 1 (bar) | Node 2 (bar) | Node 3 (bar) |
|---|---|---|---|
| 0.01 | 181.35 | 176.46 | 174.63 |
| 0.03 | 180.35 | 173.93 | 172.37 |
| 0.05 | 176.22 | 171.23 | 168.84 |
| 0.1 | 171.65 | 169.67 | 168.68 |
| No. | Outer Diameter × Wall Thickness (mm) | Material | State |
|---|---|---|---|
| right-angle elbow 1 | 38 × 3.5 | stainless steel | empty pipe |
| straight pipe 2 | 24 × 3 | white copper | liquid-filled |
| straight pipe 3 | 25 × 3.5 | stainless steel | liquid-filled |
| right-angle elbow 4 | 22 × 3 | white copper | liquid-filled |
| No. | Order | Frequency (Hz) | No. | Order | Frequency (Hz) |
|---|---|---|---|---|---|
| right-angle elbow 1 | 1 | 151.08 | straight pipe 2 | 1 | 98.13 |
| 2 | 529.70 | 2 | 268.91 | ||
| 3 | 577.34 | 3 | 522.69 | ||
| straight pipe 3 | 1 | 132.57 | right-angle elbow 4 | 1 | 72.92 |
| 2 | 363.17 | 2 | 244.23 | ||
| 3 | 705.45 | 3 | 262.57 |
| No. | Parameter | 1st-Order | 2nd-Order | 3rd-Order | No. | Parameter | 1st-Order | 2nd-Order | 3rd-Order |
|---|---|---|---|---|---|---|---|---|---|
| right-angle elbow 1 | test value (Hz) | 157.71 | 542.29 | 601.86 | straight pipe 2 | test value (Hz) | 97.14 | 264.57 | 514.19 |
| simulation value (Hz) | 151.08 | 529.7 | 577.34 | simulation value (Hz) | 98.13 | 268.91 | 522.69 | ||
| error | 4.20% | 2.32% | 4.07% | error | 1% | 1.6% | 1.7% | ||
| straight pipe 3 | test value (Hz) | 129.24 | 352.24 | 684.22 | right-angle elbow 4 | test value (Hz) | 70.69 | 243.83 | 265.49 |
| simulation value (Hz) | 132.57 | 363.17 | 705.45 | simulation value (Hz) | 72.92 | 244.23 | 262.57 | ||
| error | 2.6% | 3.1% | 3.1% | error | 3.2% | 0.16% | 1.1% |
| Parameter | 1st-Order Natural Frequency | Error | |
|---|---|---|---|
| Test Value (Hz) | Simulation Value (Hz) | ||
| two clamps | 57.86 | 57.59 | 0.47% |
| three clamps | 74.14 | 75.12 | 1.32% |
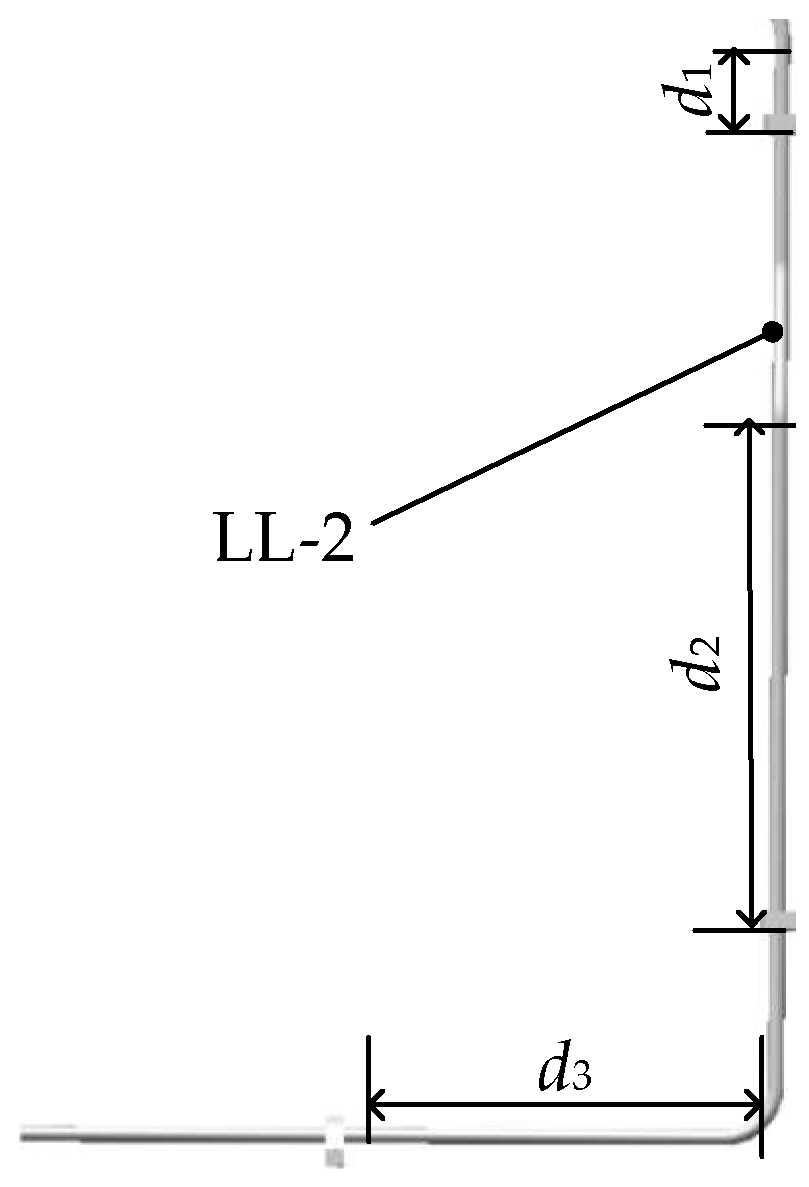
| Design Variable | d1 | d2 | d3 |
|---|---|---|---|
| Value range (mm) | 4.5~250 | 4.5~860 | 4.5~920 |
| Design Point | d1 (mm) | d2 (mm) | d3 (mm) | Maximum Stress (×107 Pa) |
|---|---|---|---|---|
| 1 | 127.25 | 432.25 | 462.25 | 4.6429 |
| 2 | 4.5 | 432.25 | 462.25 | 4.6933 |
| 3 | 250 | 432.25 | 462.25 | 4.6966 |
| 4 | 127.25 | 4.5 | 462.25 | 4.6352 |
| 5 | 127.25 | 860 | 462.25 | 4.7765 |
| 6 | 127.25 | 432.25 | 4.5 | 4.749 |
| 7 | 127.25 | 432.25 | 920 | 4.6245 |
| 8 | 27.45 | 84.475 | 90.084 | 4.7115 |
| 9 | 227.05 | 84.475 | 90.084 | 4.6216 |
| 10 | 27.45 | 780.03 | 90.084 | 4.8336 |
| 11 | 227.05 | 780.03 | 90.084 | 4.7835 |
| 12 | 27.45 | 84.475 | 834.42 | 4.6575 |
| 13 | 227.05 | 84.475 | 834.42 | 4.6179 |
| 14 | 27.45 | 780.03 | 834.42 | 4.7665 |
| 15 | 227.05 | 780.03 | 834.42 | 4.6778 |
| Candidate Point | d1 (mm) | d2 (mm) | d3 (mm) | Maximum Stress (×107 Pa) | Verification Stress (×107 Pa) | Error/% |
|---|---|---|---|---|---|---|
| 1 | 249.66 | 415 | 871.62 | 4.048 | 4.5059 | 10.16 |
| 2 | 249.85 | 409.87 | 864.98 | 4.182 | 4.5069 | 7.21 |
| 3 | 248.8 | 395.18 | 892.5 | 3.921 | 4.2078 | 6.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quan, L.; Gao, J.; Guo, C.; Fu, C. Analysis of Water Hammer and Pipeline Vibration Characteristics of Submarine Local Hydraulic System. J. Mar. Sci. Eng. 2023, 11, 1885. https://doi.org/10.3390/jmse11101885
Quan L, Gao J, Guo C, Fu C. Analysis of Water Hammer and Pipeline Vibration Characteristics of Submarine Local Hydraulic System. Journal of Marine Science and Engineering. 2023; 11(10):1885. https://doi.org/10.3390/jmse11101885
Chicago/Turabian StyleQuan, Lingxiao, Jing Gao, Changhong Guo, and Chen Fu. 2023. "Analysis of Water Hammer and Pipeline Vibration Characteristics of Submarine Local Hydraulic System" Journal of Marine Science and Engineering 11, no. 10: 1885. https://doi.org/10.3390/jmse11101885
APA StyleQuan, L., Gao, J., Guo, C., & Fu, C. (2023). Analysis of Water Hammer and Pipeline Vibration Characteristics of Submarine Local Hydraulic System. Journal of Marine Science and Engineering, 11(10), 1885. https://doi.org/10.3390/jmse11101885





