Experimental Investigation of Surface Waves Effect on a Ducted Twin Vertical Axis Tidal Turbine
Abstract
:1. Introduction
2. Materials and Methods
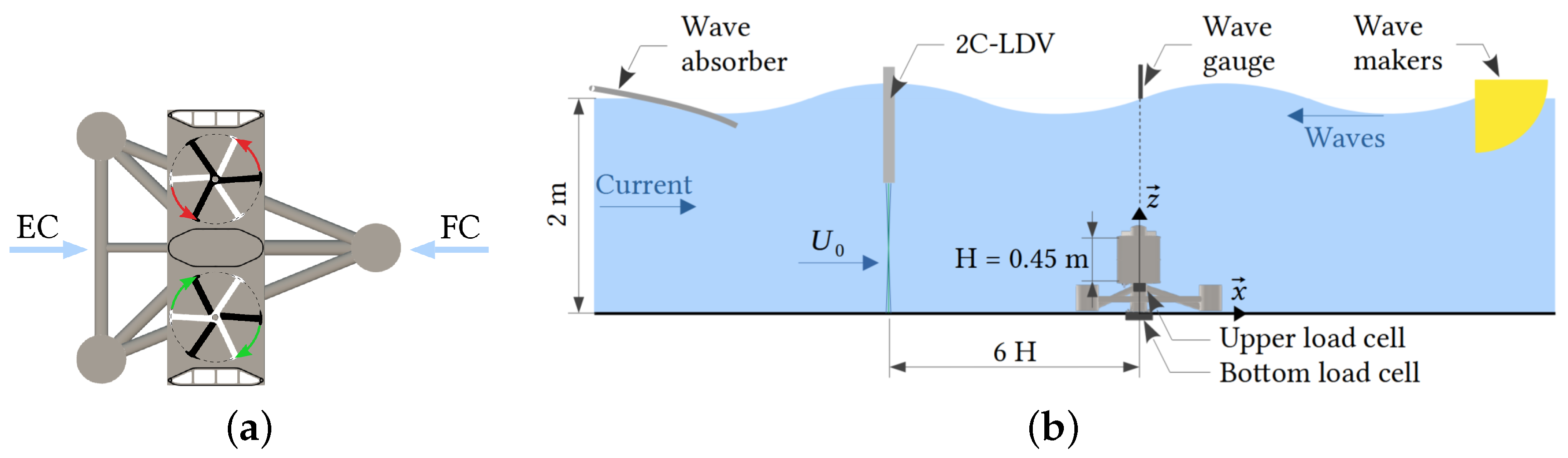
2.1. Turbine Model
2.2. Experimental Setup
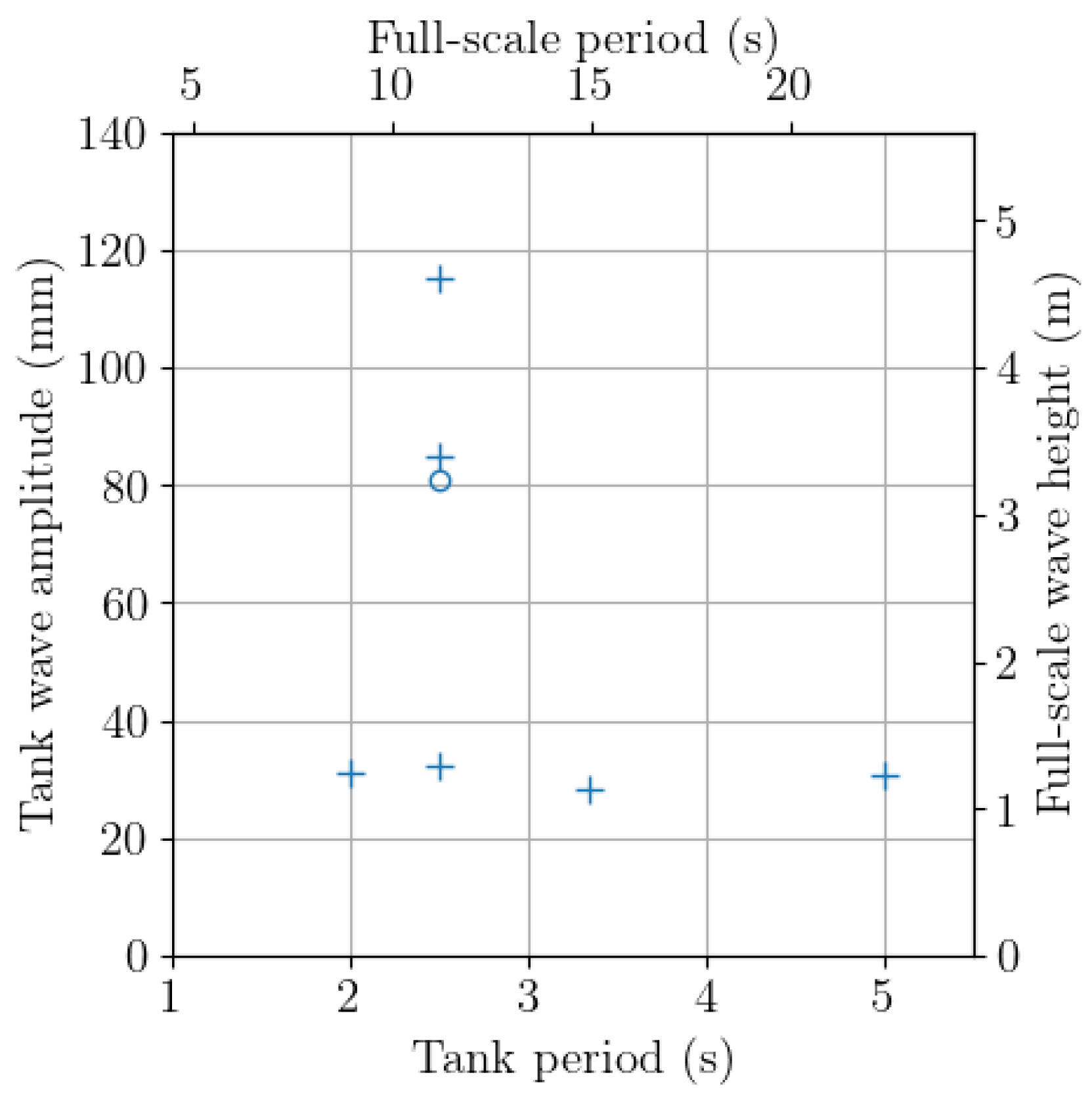
2.3. Flow Conditions
2.4. Data Processing
3. Effect of Surface Waves Opposing the Current on the 2-VATT Behaviour
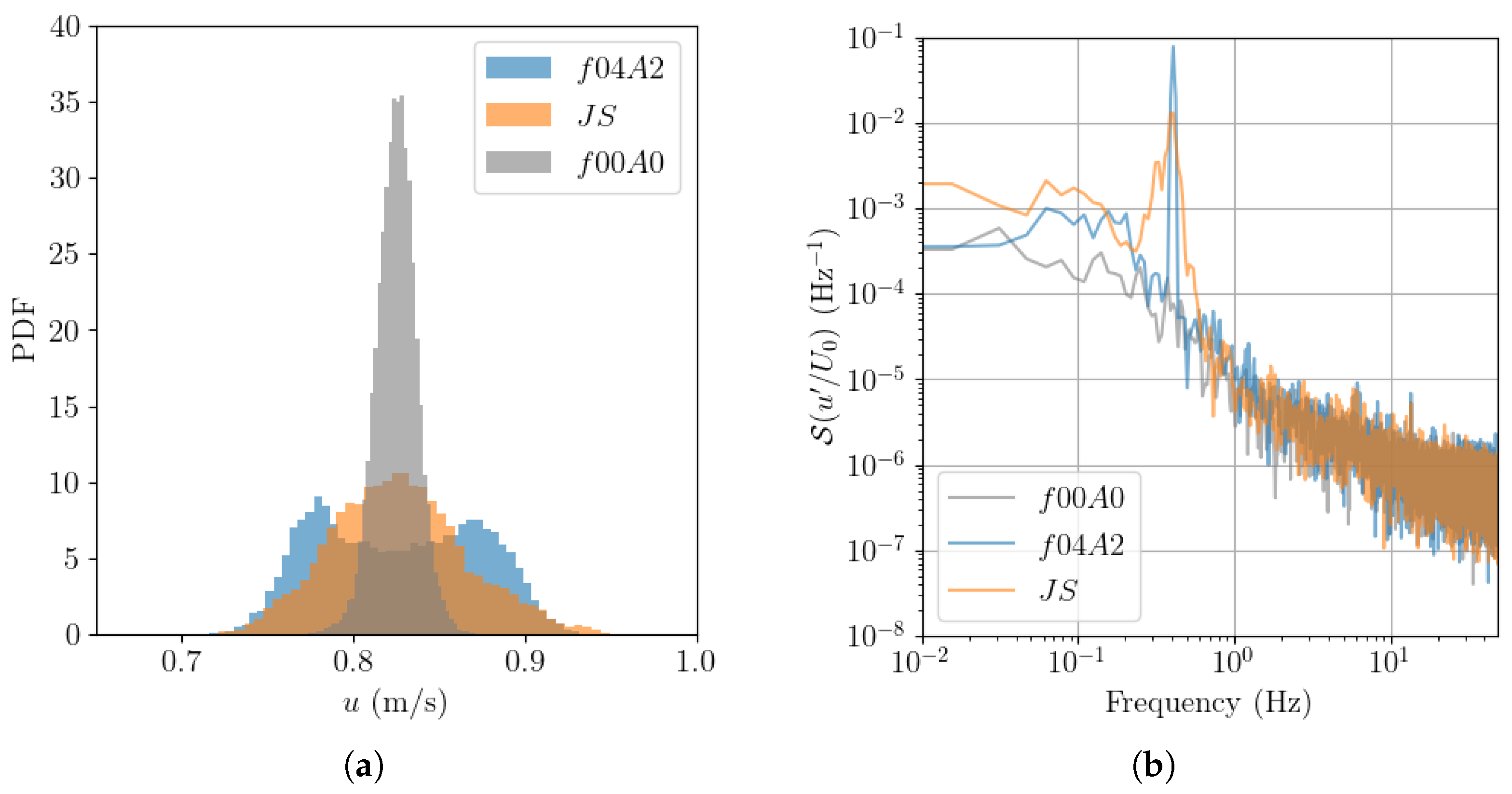
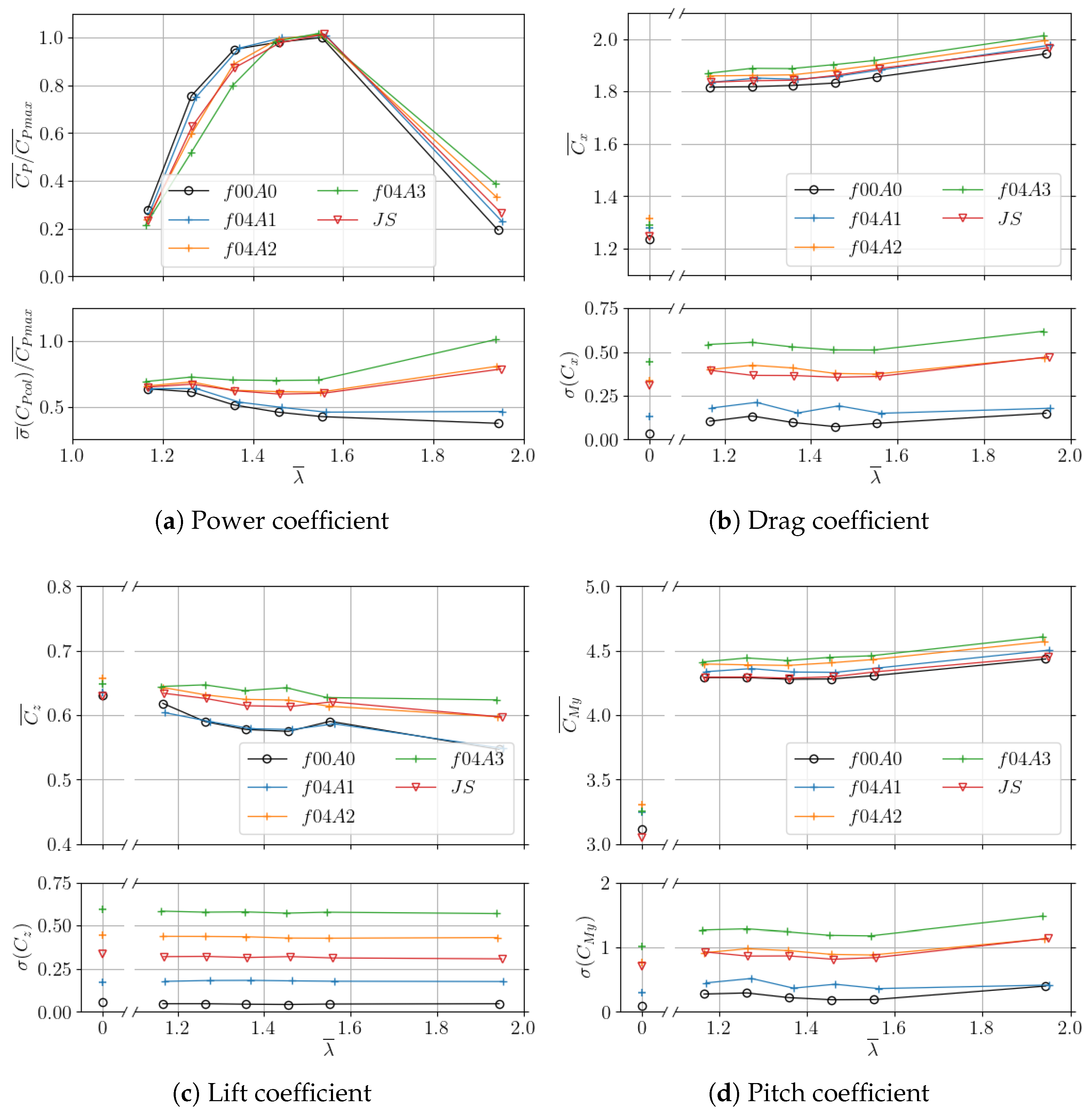
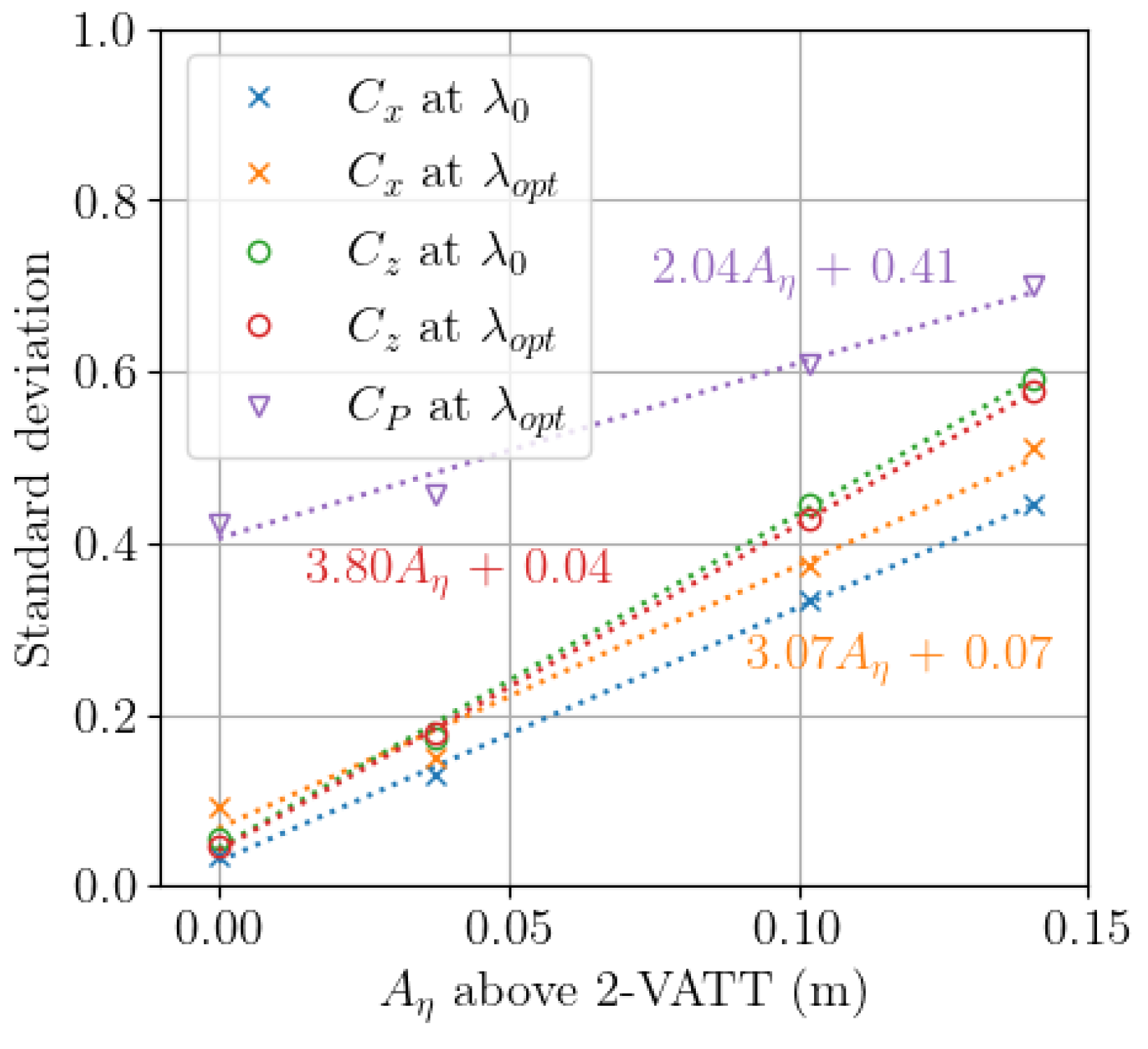
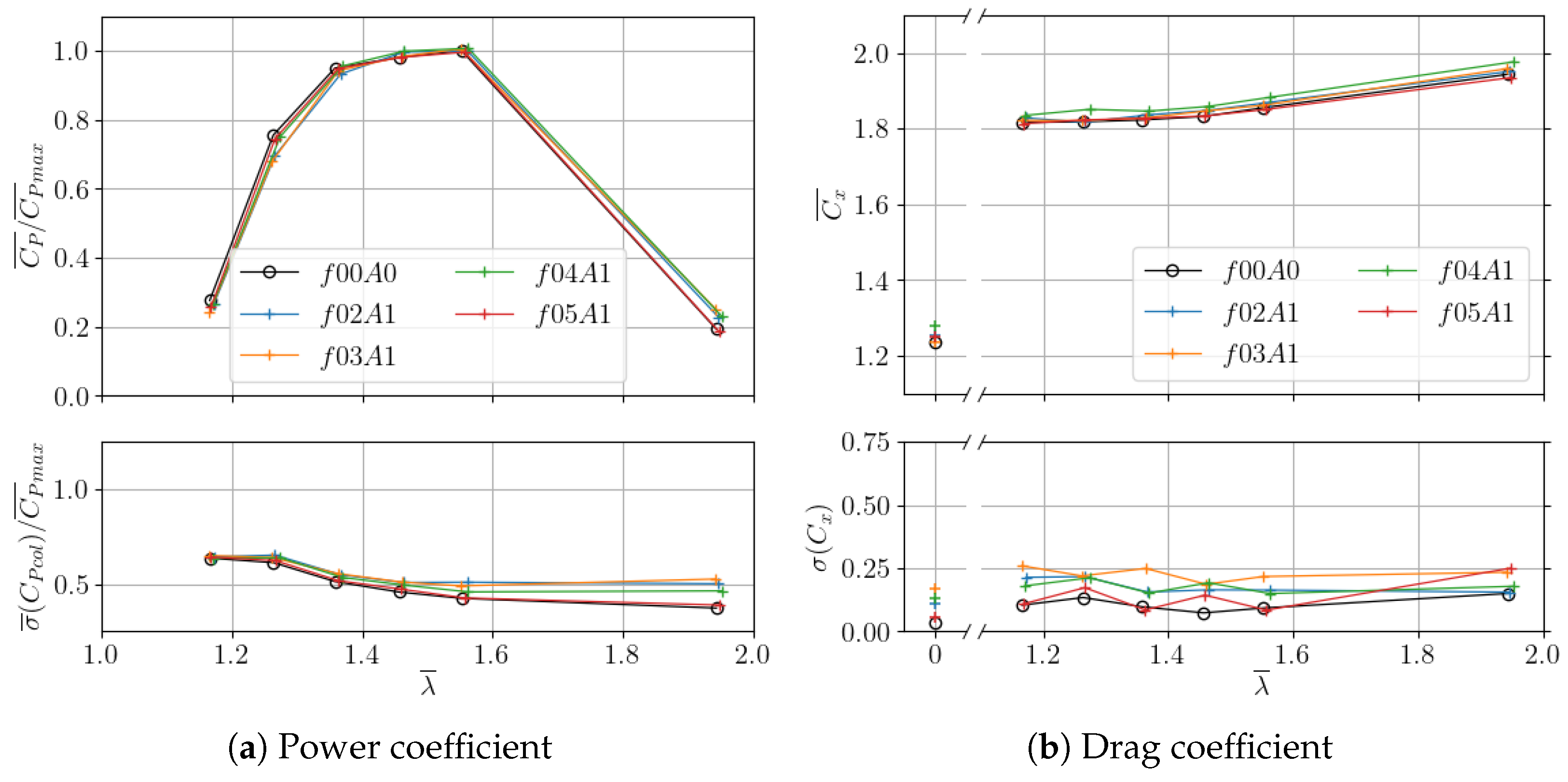
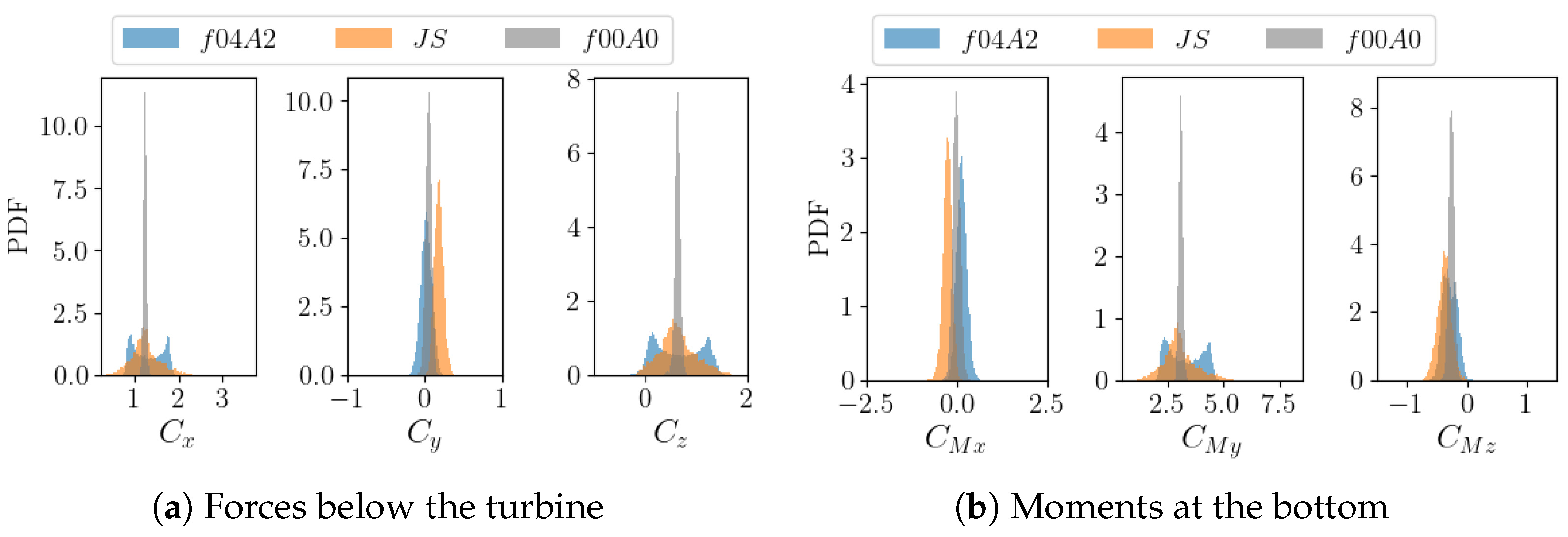
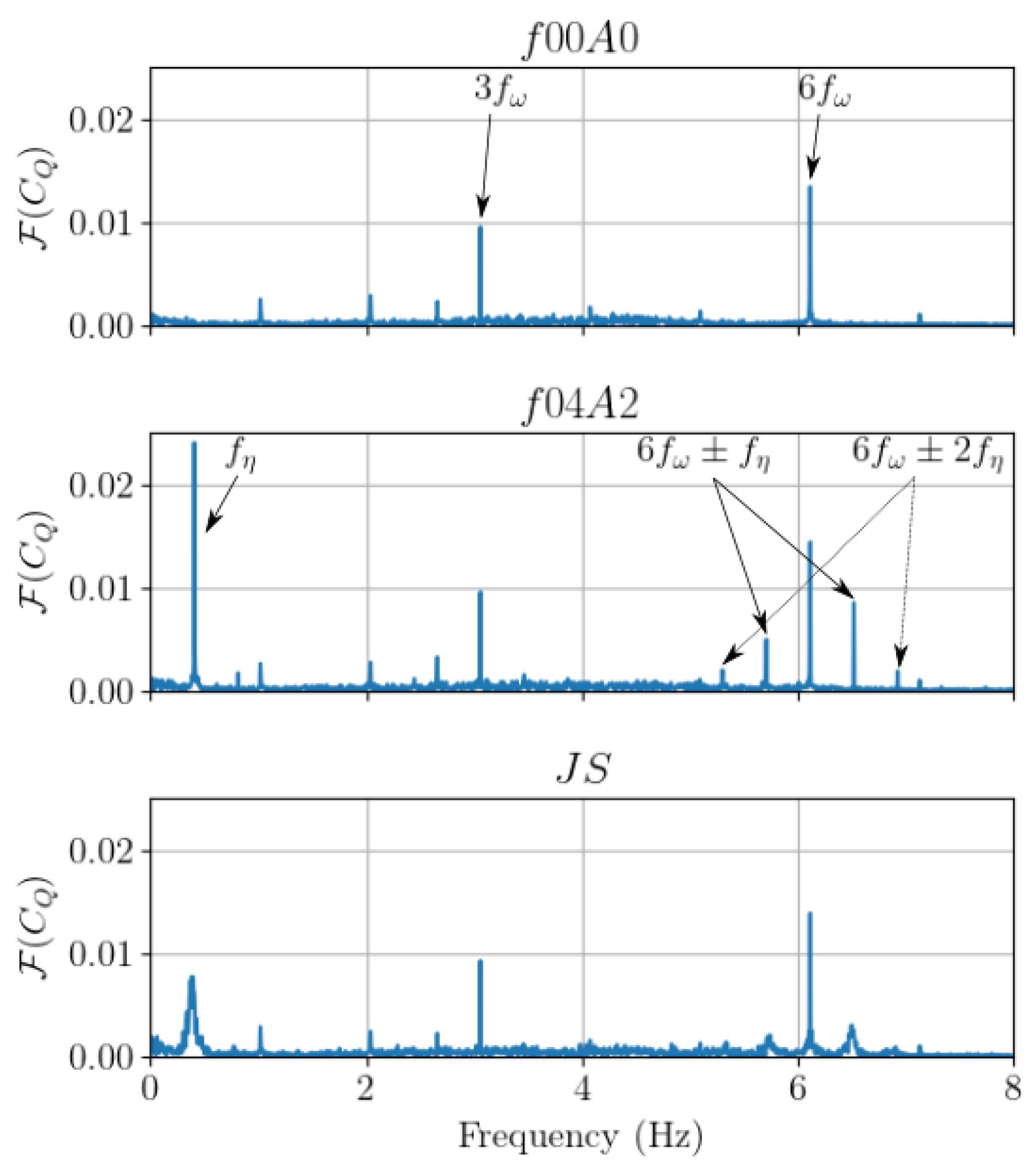
3.1. Wave Amplitude and Frequency Effect
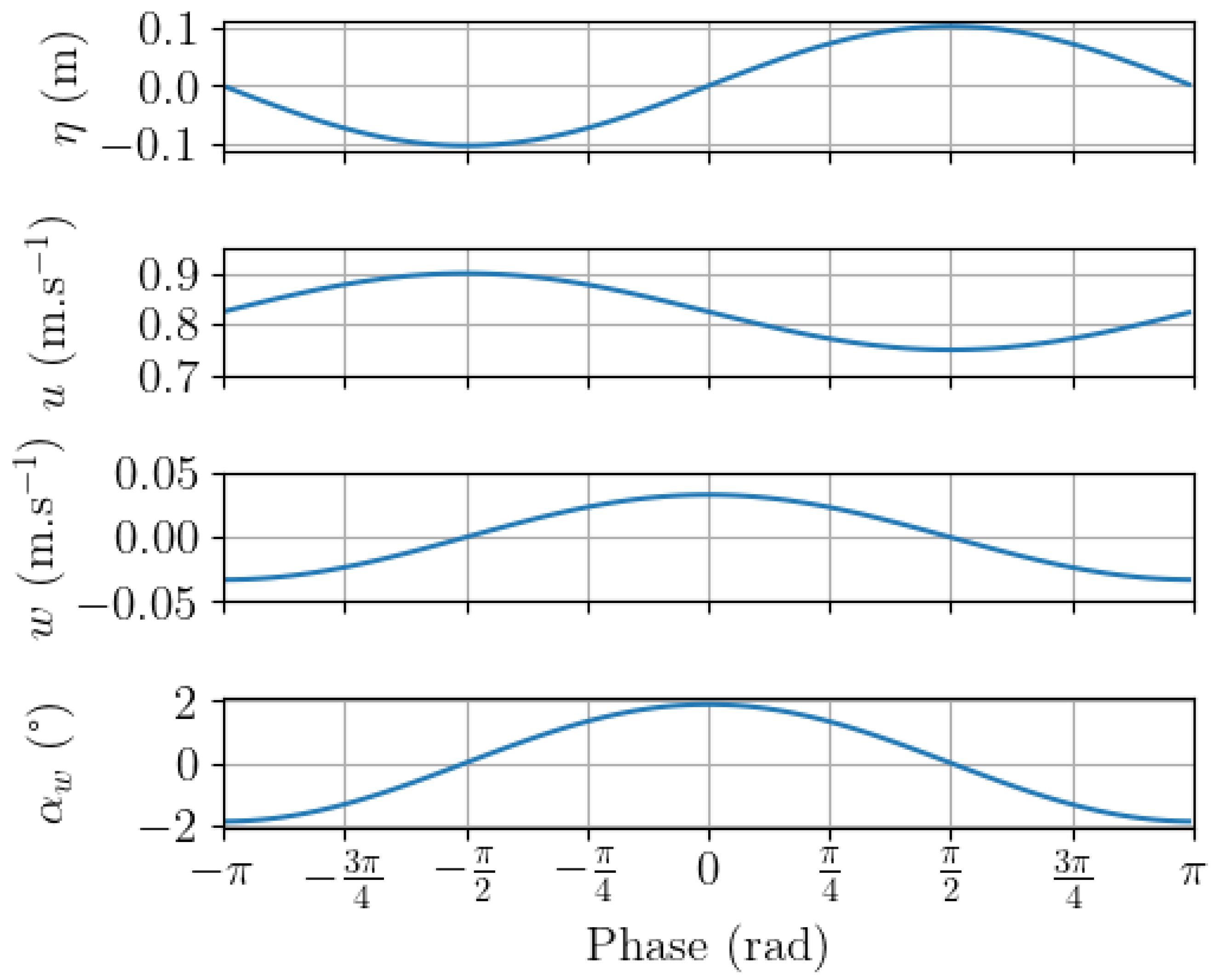
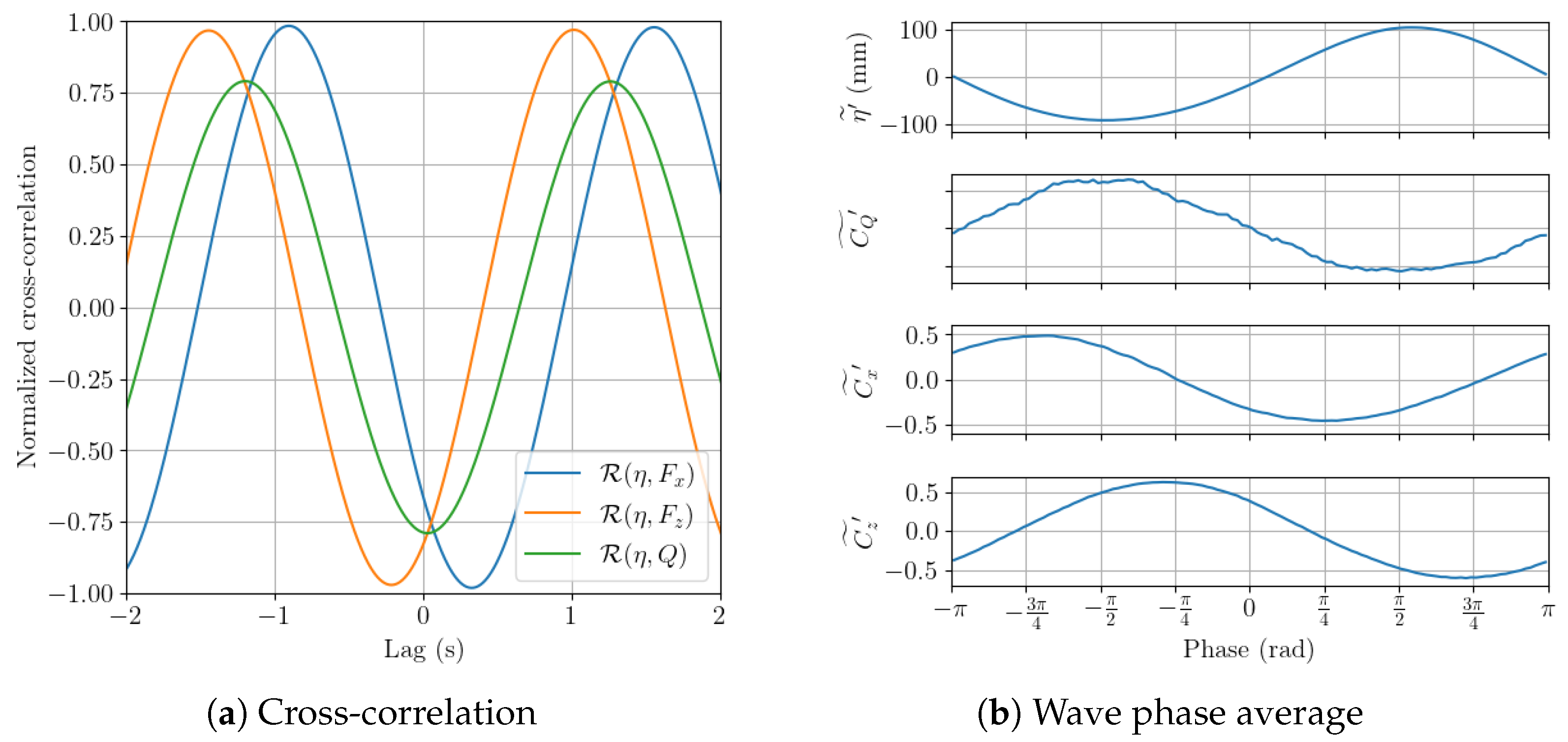
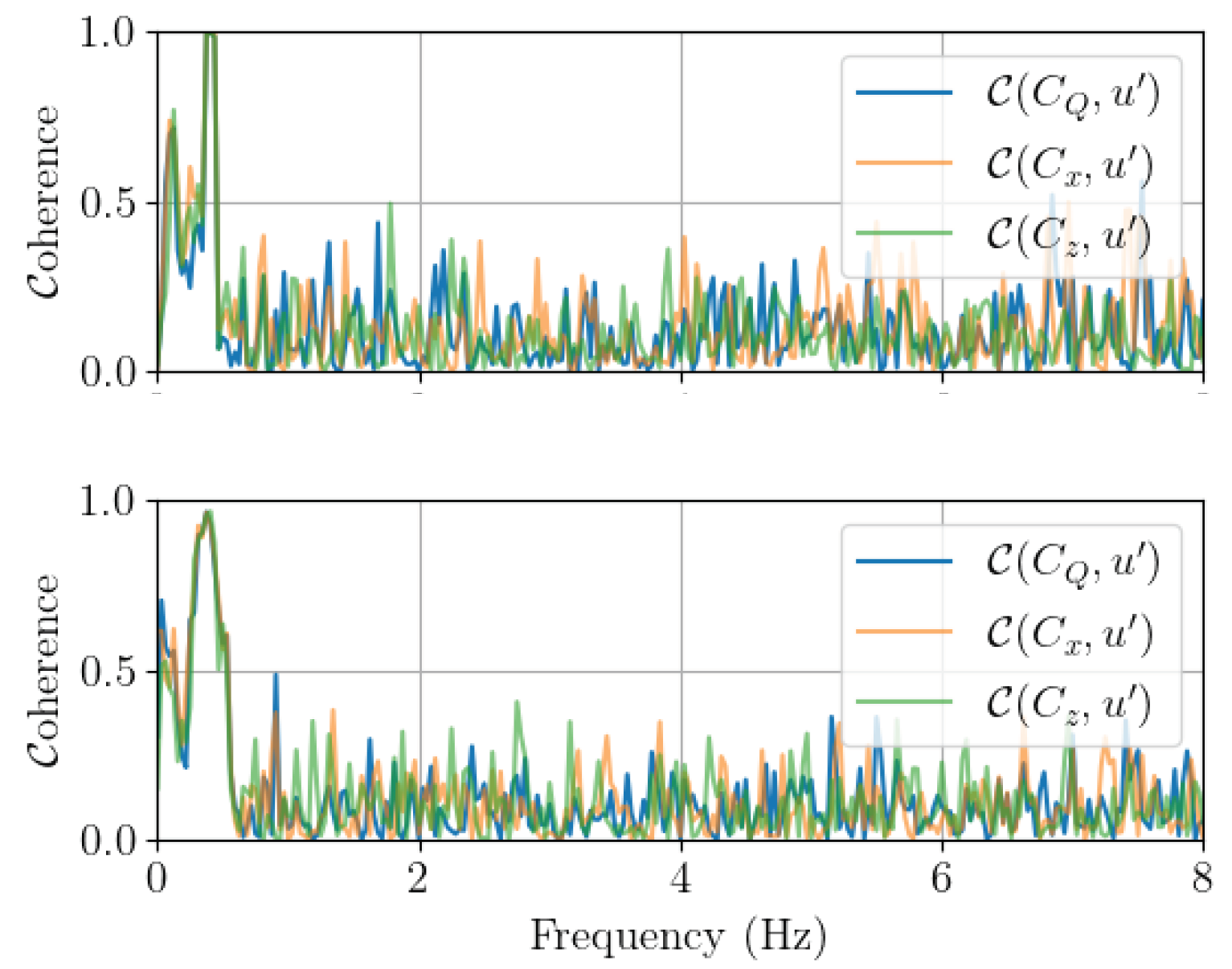
3.2. Wave–Current–Turbine Interaction
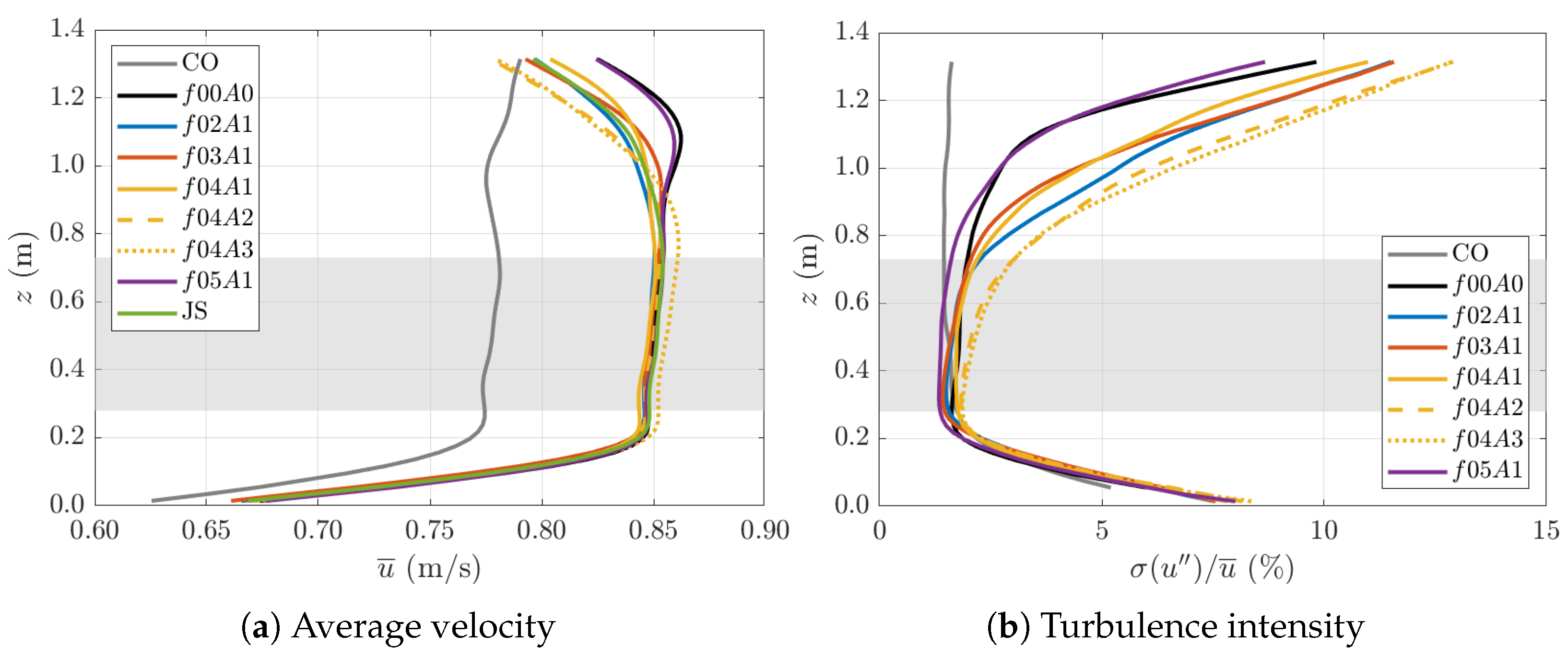
3.2.1. Parked Turbine
3.2.2. Operating Turbine
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA-OES. Tidal Current Energy: Developments Highlights; Technical Report; International Energy Agency: Paris, France, 2023. [Google Scholar]
- Sentchev, A.; Nguyen, T.D.; Furgerot, L.; Bailly du Bois, P. Underway velocity measurements in the Alderney Race: Towards a three-dimensional representation of tidal motions. Philos. Trans. R. Soc. A 2020, 378, 20190491. [Google Scholar] [CrossRef] [PubMed]
- Cossu, R.; Penesis, I.; Nader, J.R.; Marsh, P.; Perez, L.; Couzi, C.; Grinham, A.; Osman, P. Tidal energy site characterisation in a large tidal channel in Banks Strait, Tasmania, Australia. Renew. Energy 2021, 177, 859–870. [Google Scholar] [CrossRef]
- Mercier, P.; Guillou, S. The impact of the seabed morphology on turbulence generation in a strong tidal stream. Phys. Fluids 2021, 33, 055125. [Google Scholar] [CrossRef]
- Guillou, N.; Chapalain, G.; Neill, S.P. The influence of waves on the tidal kinetic energy resource at a tidal stream energy site. Appl. Energy 2016, 180, 402–415. [Google Scholar] [CrossRef]
- Bennis, A.C.; Furgerot, L.; Bailly Du Bois, P.; Poizot, E.; Méar, Y.; Dumas, F. A winter storm in Alderney Race: Impacts of 3D wave–current interactions on the hydrodynamic and tidal stream energy. Appl. Ocean Res. 2022, 120, 103009. [Google Scholar] [CrossRef]
- Perez, L.; Cossu, R.; Grinham, A.; Penesis, I. Tidal turbine performance and loads for various hub heights and wave conditions using high-frequency field measurements and Blade Element Momentum theory. Renew. Energy 2022, 200, 1548–1560. [Google Scholar] [CrossRef]
- Moreau, M.; Germain, G.; Maurice, G.; Richard, A. Sea states influence on the behaviour of a bottom mounted full-scale twin vertical axis tidal turbine. Ocean Eng. 2022, 265, 112582. [Google Scholar] [CrossRef]
- Gaurier, B.; Ordonez-Sanchez, S.; Facq, J.V.; Germain, G.; Johnstone, C.; Martinez, R.; Salvatore, F.; Santic, I.; Davey, T.; Old, C.; et al. MaRINET2 Tidal Energy Round Robin Tests—Performance Comparison of a Horizontal Axis Turbine Subjected to Combined Wave and Current Conditions. J. Mar. Sci. Eng. 2020, 8, 463. [Google Scholar] [CrossRef]
- Barltrop, N.; Varyani, K.S.; Grant, A.; Clelland, D.; Pham, X. Wave-current interactions in marine current turbines. Proc. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2006, 220, 195–203. [Google Scholar] [CrossRef]
- Gaurier, B.; Davies, P.; Deuff, A.; Germain, G. Flume tank characterization of marine current turbine blade behaviour under current and wave loading. Renew. Energy 2013, 59, 1–12. [Google Scholar] [CrossRef]
- Martinez, R.; Payne, G.S.; Bruce, T. The effects of oblique waves and currents on the loadings and performance of tidal turbines. Ocean Eng. 2018, 164, 55–64. [Google Scholar] [CrossRef]
- Ordonez-Sanchez, S.; Allmark, M.; Porter, K.; Ellis, R.; Lloyd, C.; Santic, I.; O’Doherty, T.; Johnstone, C. Analysis of a Horizontal-Axis Tidal Turbine Performance in the Presence of Regular and Irregular Waves Using Two Control Strategies. Energies 2019, 12, 367. [Google Scholar] [CrossRef]
- Martinez, R.; Ordonez-Sanchez, S.; Allmark, M.; Lloyd, C.; O’Doherty, T.; Germain, G.; Gaurier, B.; Johnstone, C. Analysis of the effects of control strategies and wave climates on the loading and performance of a laboratory scale horizontal axis tidal turbine. Ocean Eng. 2020, 212, 107713. [Google Scholar] [CrossRef]
- Morison, J.; Johnson, J.; Schaaf, S. The Force Exerted by Surface Waves on Piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Draycott, S.; Steynor, J.; Nambiar, A.; Sellar, B.; Venugopal, V. Rotational sampling of waves by tidal turbine blades. Renew. Energy 2020, 162, 2197–2209. [Google Scholar] [CrossRef]
- Ouro, P.; Dené, P.; Garcia-Novo, P.; Stallard, T.; Kyozuda, Y.; Stansby, P. Power density capacity of tidal stream turbine arrays with horizontal and vertical axis turbines. J. Ocean Eng. Mar. Energy 2022, 9, 203–208. [Google Scholar] [CrossRef]
- Bachant, P.; Wosnik, M. Experimental Investigation of Helical Cross-Flow Axis Hydrokinetic Turbines, Including Effects of Waves and Turbulence. In Proceedings of the ASME-JSME-KSME 2011 Joint Fluids Engineering Conference, Shizuoka, Japan, 24–29 January 2011; pp. 1895–1906. [Google Scholar] [CrossRef]
- Zhang, X.w.; Zhang, L.; Wang, F.; Zhao, D.Y.; Pang, C.Y. Research on the unsteady hydrodynamic characteristics of vertical axis tidal turbine. China Ocean Eng. 2014, 28, 95–103. [Google Scholar] [CrossRef]
- Lust, E.E.; Bailin, B.H.; Flack, K.A. Performance characteristics of a cross-flow hydrokinetic turbine in current only and current and wave conditions. Ocean Eng. 2021, 219, 108362. [Google Scholar] [CrossRef]
- Vergaerde, A.; De Troyer, T.; Muggiasca, S.; Bayati, I.; Belloli, M.; Kluczewska-Bordier, J.; Parneix, N.; Silvert, F.; Runacres, M.C. Experimental characterisation of the wake behind paired vertical-axis wind turbines. J. Wind. Eng. Ind. Aerodyn. 2020, 206, 104353. [Google Scholar] [CrossRef]
- Müller, S.; Muhawenimana, V.; Wilson, C.A.; Ouro, P. Experimental investigation of the wake characteristics behind twin vertical axis turbines. Energy Convers. Manag. 2021, 247, 114768. [Google Scholar] [CrossRef]
- Moreau, M.; Germain, G.; Maurice, G. Experimental performance and wake study of a ducted twin vertical axis turbine in ebb and flood tide currents at a 1/20th scale. Renew. Energy 2023, 214, 318–333. [Google Scholar] [CrossRef]
- Gaurier, B.; Germain, G.; Facq, J.V.; Bacchetti, T. Wave and Current Flume Tank of IFREMER at Boulogne-sur-mer. Description of the Facility and Its Equipment; Technical Report; IFREMER: Plouzané, France, 2018. [Google Scholar] [CrossRef]
- Brevik, I.; Bjørn, A. Flume experiment on waves and currents. I. Rippled bed. Coast. Eng. 1979, 3, 149–177. [Google Scholar] [CrossRef]
- Magnier, M. Étude Expérimentale des Courants de Marée et de la Houle sur la Dynamique Tourbillonnaire d’une Variation Bathymétrique et sur le Comportement d’une Hydrolienne. Ph.D. Thesis, Université de Lille, Lille, France, 2023. [Google Scholar]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Eake, K.; Euring, J.A.; Gicnapp, A.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the joint North Sea wave project (JONSWAP). Erganzungsheft zur Deutschen Hydrographischen Zeitschrift. 1973. A(8), Nr 12. Available online: https://pure.mpg.de/pubman/faces/ViewItemOverviewPage.jsp?itemId=item_3262854 (accessed on 1 January 2020).
- Bachant, P.; Wosnik, M. Effects of Reynolds Number on the Energy Conversion and Near-Wake Dynamics of a High Solidity Vertical-Axis Cross-Flow Turbine. Energies 2016, 9, 73. [Google Scholar] [CrossRef]
- Molin, B. Hydrodynamique des Structures Offshore; Editions Technip: Paris, France, 2002. [Google Scholar]
- Saouli, Y.; Magnier, M.; Germain, G.; Gaurier, B.; Druault, P. Experimental characterisation of the waves propagating against current effects on the wake of a wide bathymetric obstacle. In Proceedings of the 18ème Journées de l’Hydrodynamique, Poitiers, France, 22–24 November 2022; pp. 1–12. [Google Scholar]
- Xin, Z.; Li, X.; Li, Y. Coupled effects of wave and depth-dependent current interaction on loads on a bottom-fixed vertical slender cylinder. Coast. Eng. 2023, 183, 104304. [Google Scholar] [CrossRef]
- EDF; SEENEOH. Paimpol-Bréhat Tidal Turbine Test Site Documentation v1.2; Technical Report; EDF: London, UK, 2022. [Google Scholar]
- Moreau, M.; Bloch, N.; Maurice, G.; Germain, G. Experimental study of the upstream bathymetry effects on a ducted twin vertical axis tidal turbine. Renew. Energy 2023. under review. [Google Scholar] [CrossRef]


| Case | Wave Type | (Hz) | (s) | (mm) |
|---|---|---|---|---|
| No wave | − | − | − | |
| Regular | 0.2 | 5.0 | 30 | |
| Regular | 0.3 | 3.3 | 38 | |
| Regular | 0.4 | 2.5 | 37 | |
| Regular | 0.4 | 2.5 | 102 | |
| Regular | 0.4 | 2.5 | 141 | |
| Regular | 0.5 | 2.0 | 42 | |
| JONSWAP | 0.4 | 2.5 | 107 |
| (a). Ratio of Load Ranges | |||
|---|---|---|---|
| Case | |||
| 6.68 | 5.72 | 6.22 | |
| 9.58 | 5.87 | 8.81 | |
| (b). Ratio of Extreme Loads | |||
| Case | |||
| 1.41 | 1.87 | 1.38 | |
| 1.76 | 1.96 | 1.49 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreau, M.; Germain, G.; Maurice, G. Experimental Investigation of Surface Waves Effect on a Ducted Twin Vertical Axis Tidal Turbine. J. Mar. Sci. Eng. 2023, 11, 1895. https://doi.org/10.3390/jmse11101895
Moreau M, Germain G, Maurice G. Experimental Investigation of Surface Waves Effect on a Ducted Twin Vertical Axis Tidal Turbine. Journal of Marine Science and Engineering. 2023; 11(10):1895. https://doi.org/10.3390/jmse11101895
Chicago/Turabian StyleMoreau, Martin, Grégory Germain, and Guillaume Maurice. 2023. "Experimental Investigation of Surface Waves Effect on a Ducted Twin Vertical Axis Tidal Turbine" Journal of Marine Science and Engineering 11, no. 10: 1895. https://doi.org/10.3390/jmse11101895
APA StyleMoreau, M., Germain, G., & Maurice, G. (2023). Experimental Investigation of Surface Waves Effect on a Ducted Twin Vertical Axis Tidal Turbine. Journal of Marine Science and Engineering, 11(10), 1895. https://doi.org/10.3390/jmse11101895







