CFD Study of the Non-Linear Physical Phenomena of the TLP of a 15-MW-Class FOWT under Extreme Waves
Abstract
:1. Introduction
2. Numerical Set-Up
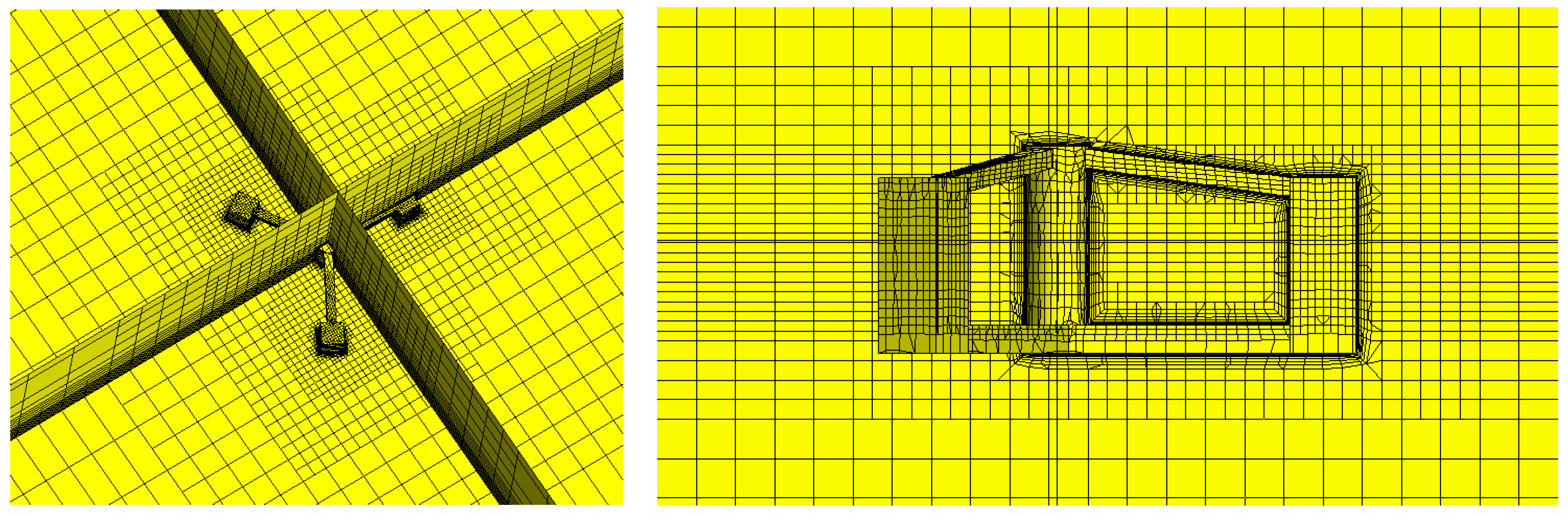
2.1. Model
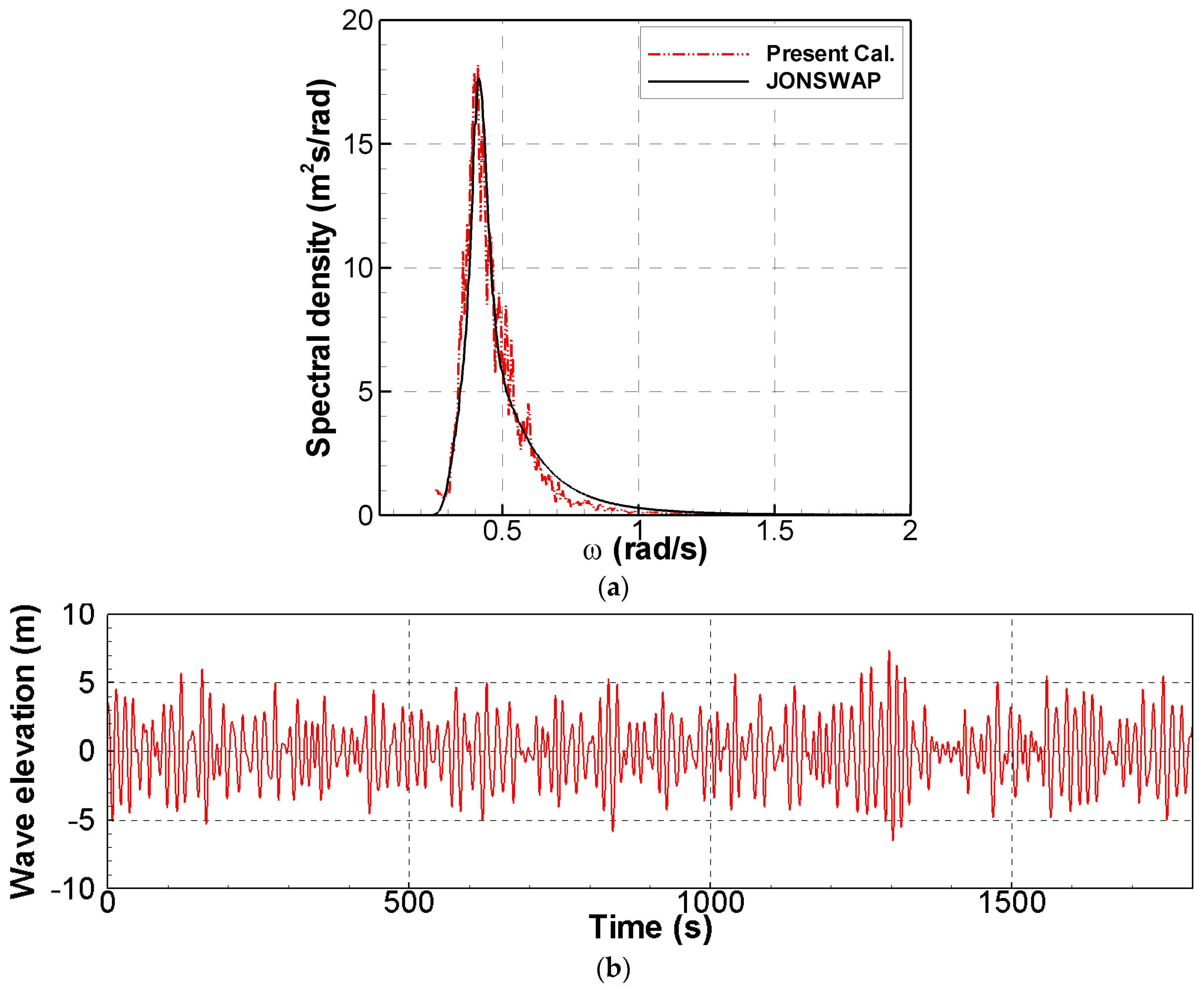
2.2. Environmental Conditions
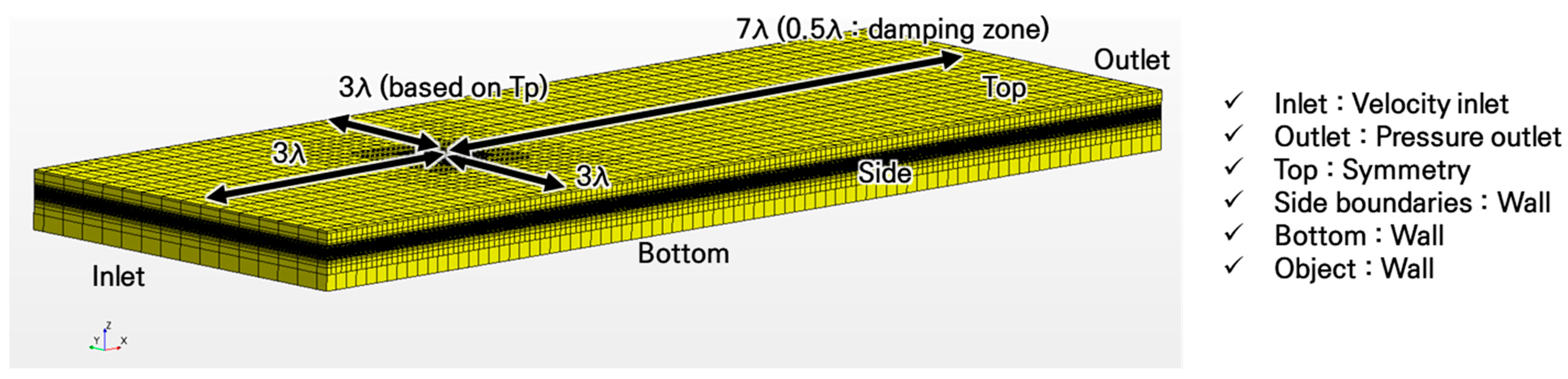
2.3. Numerical Method
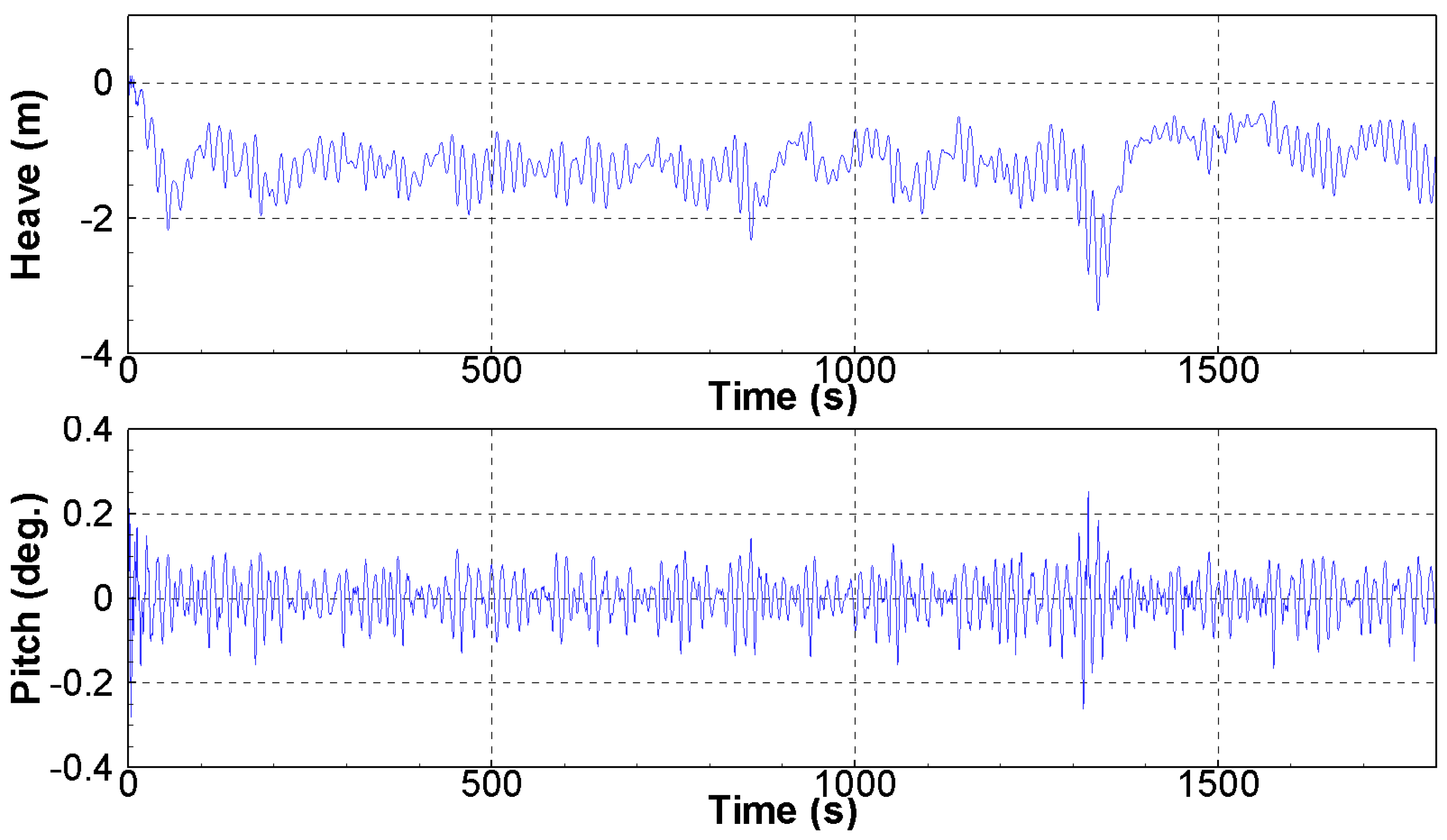
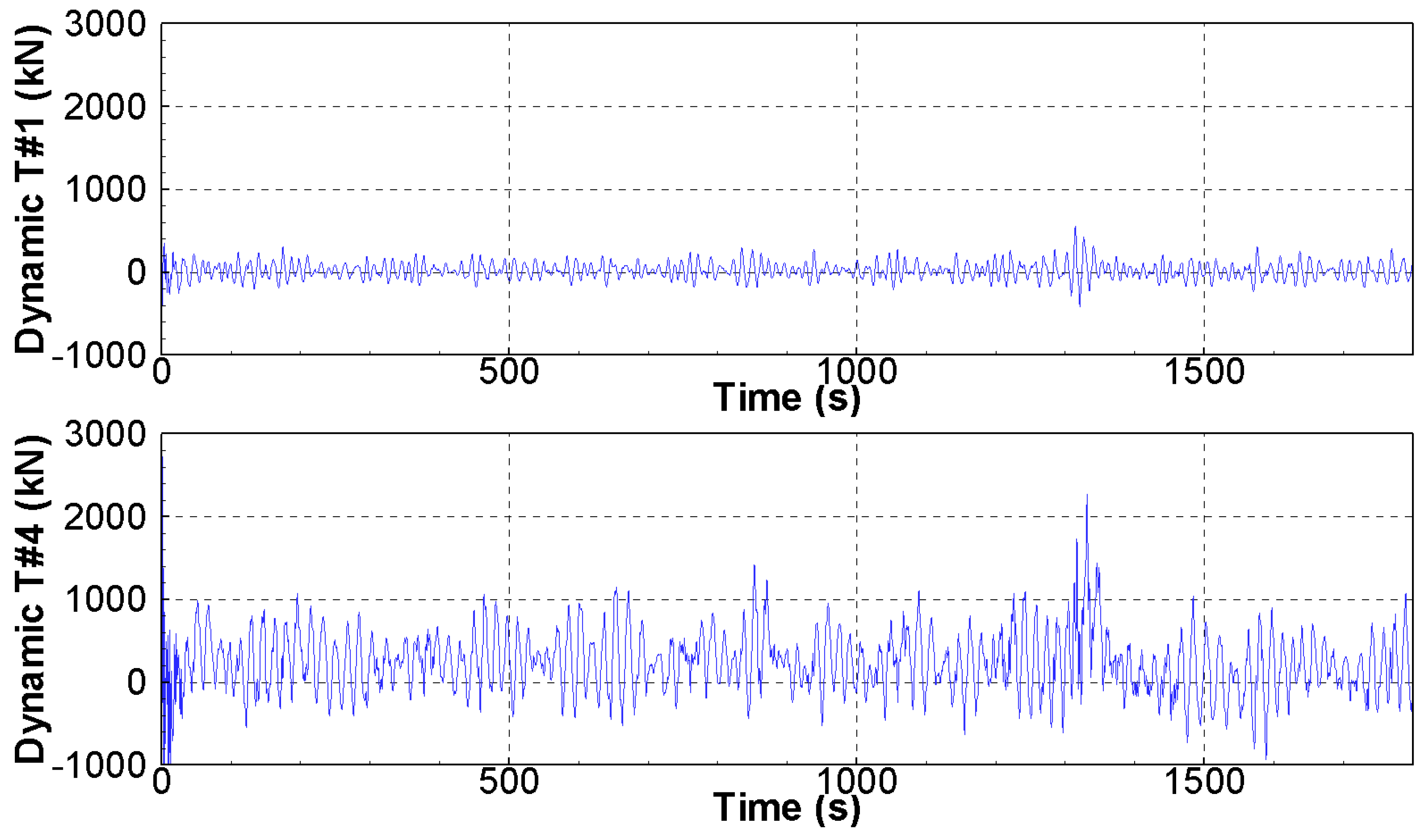
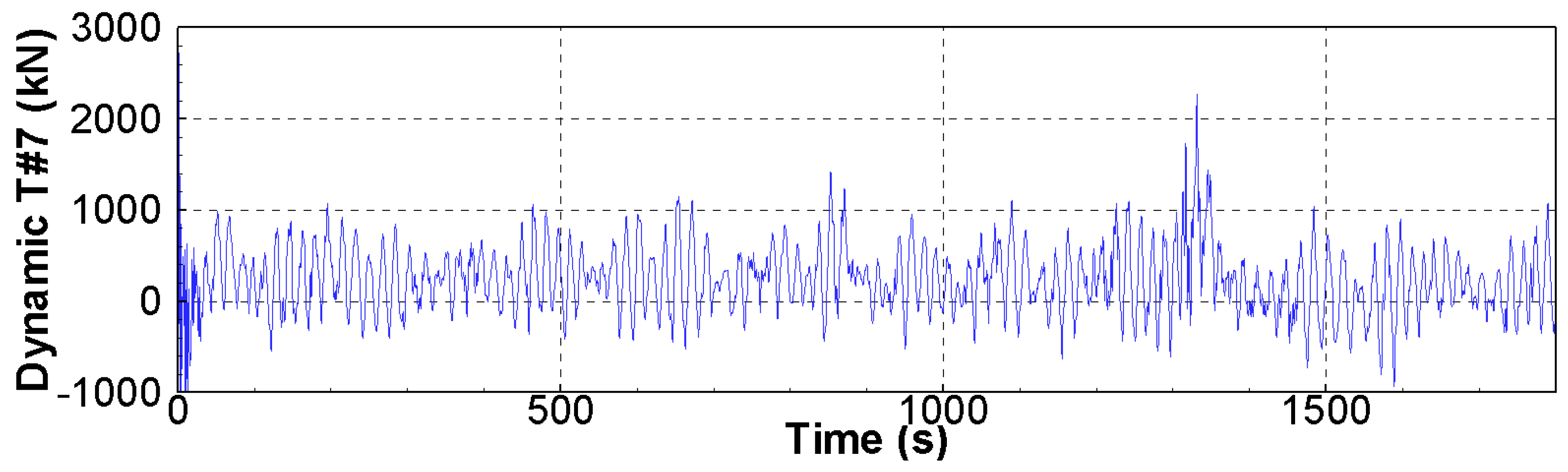
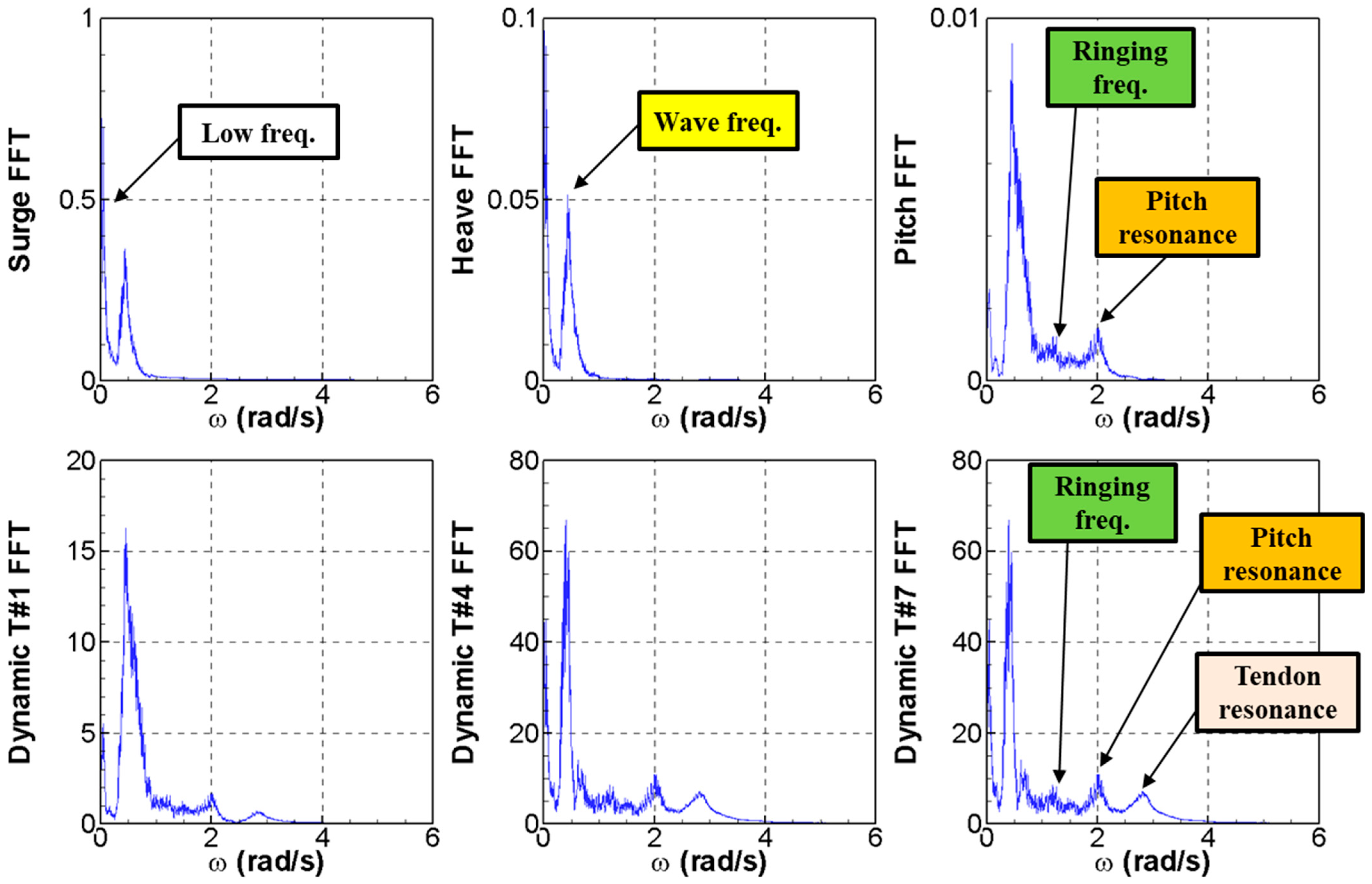
3. Results
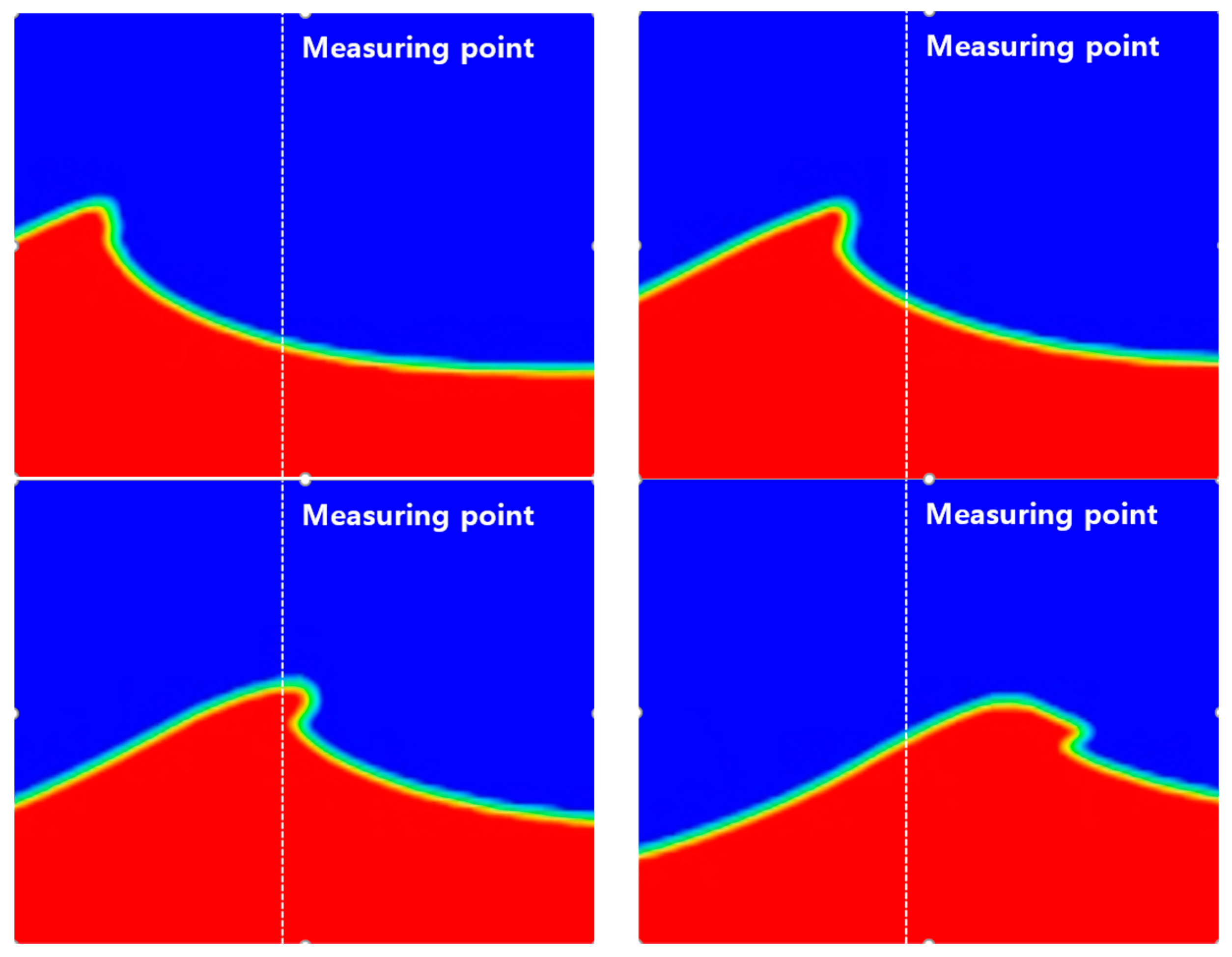
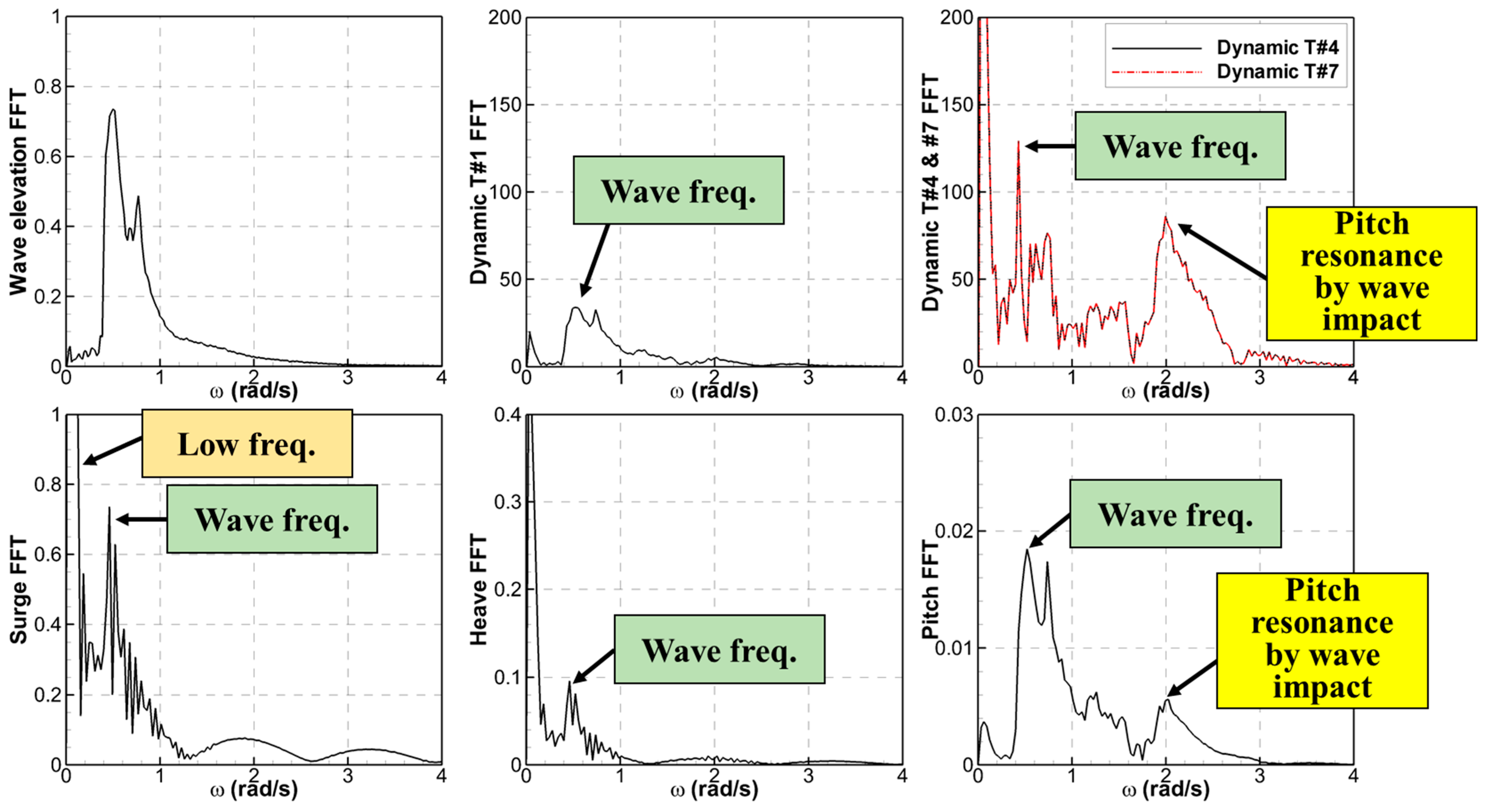
3.1. Springing and Ringing Phenomena
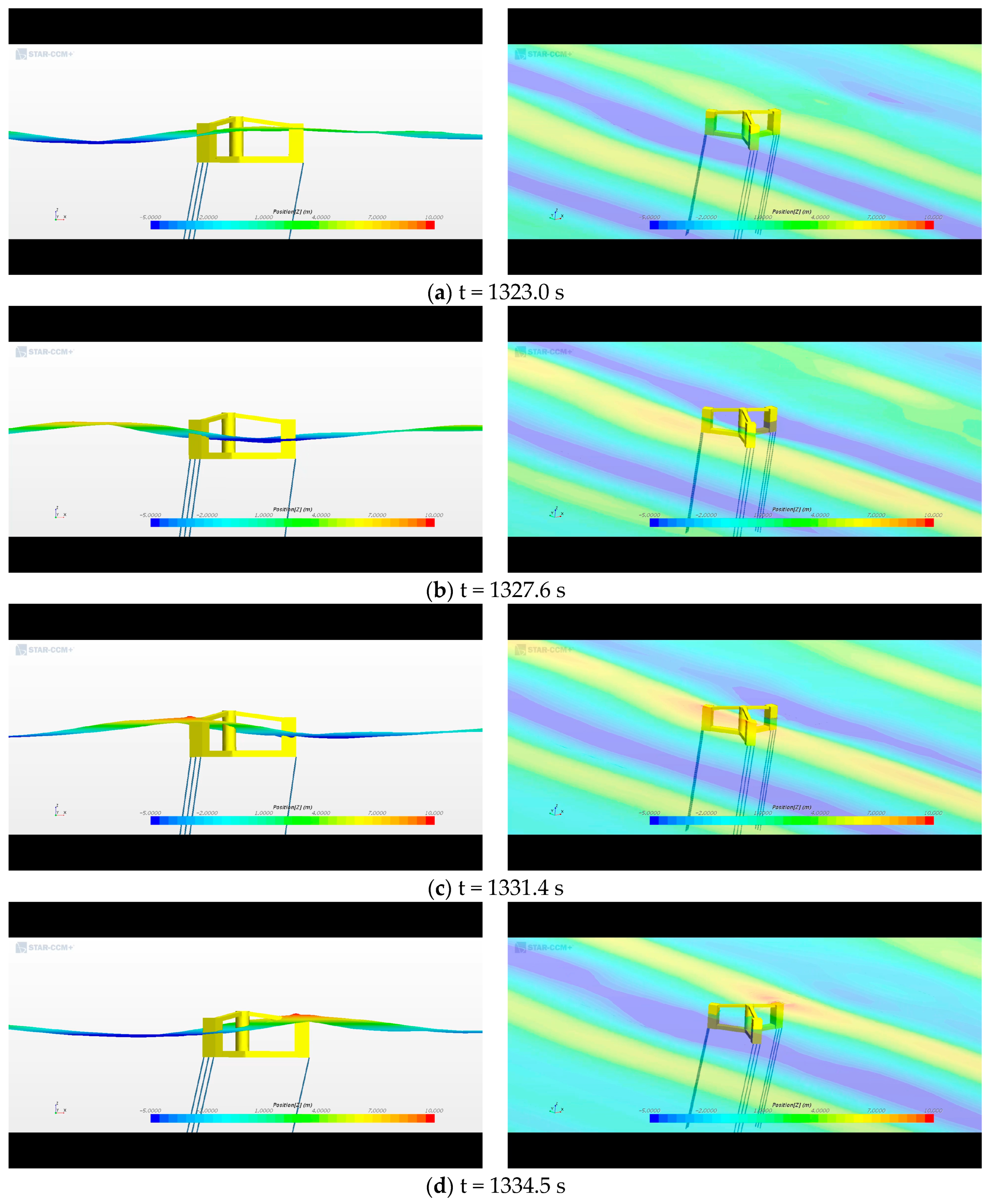
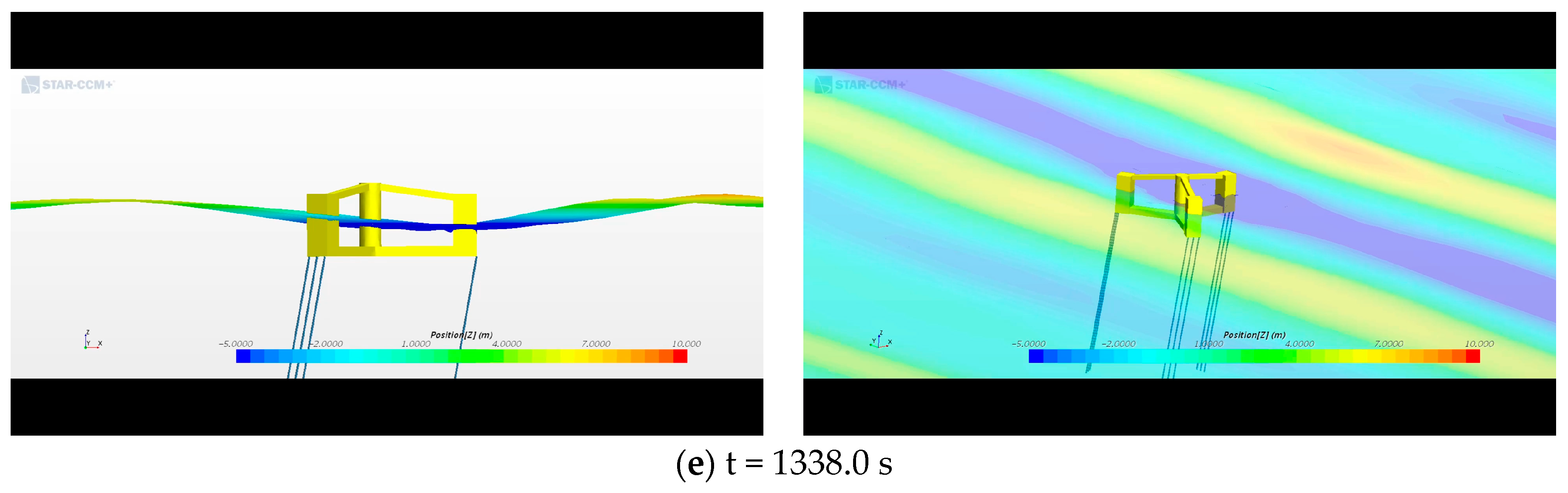
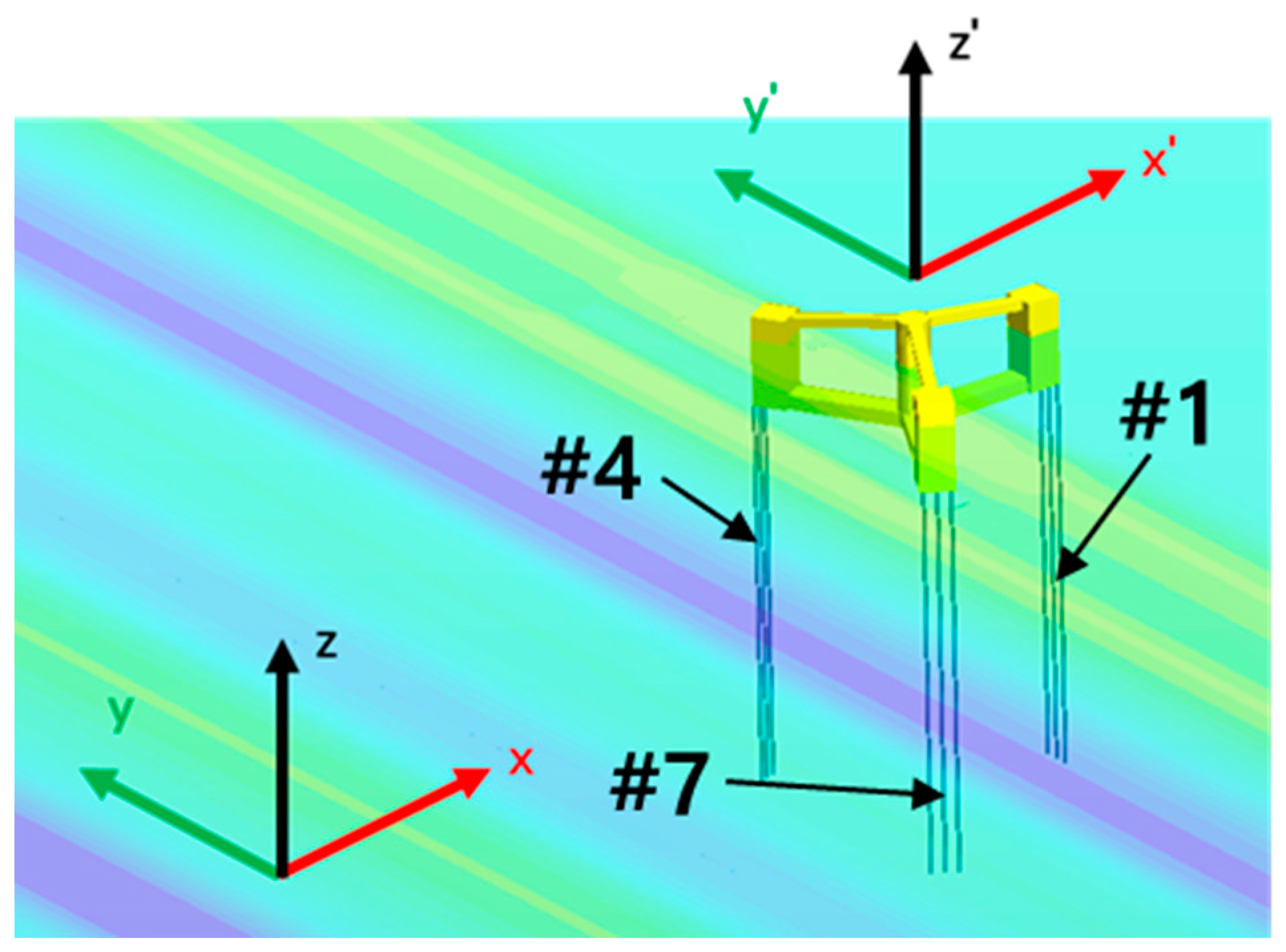
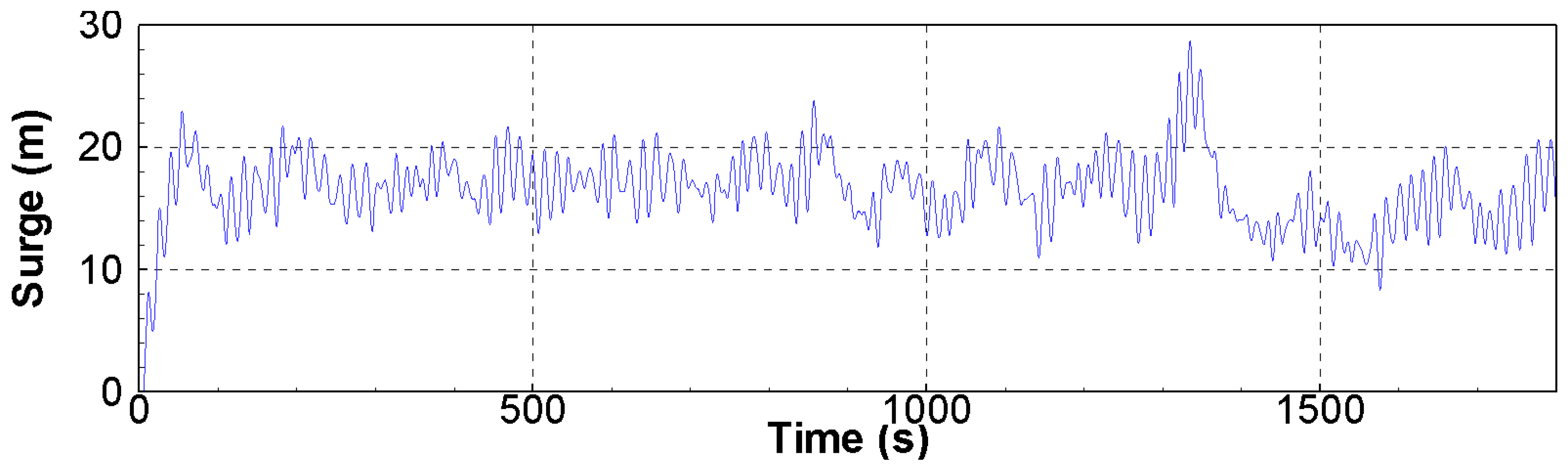
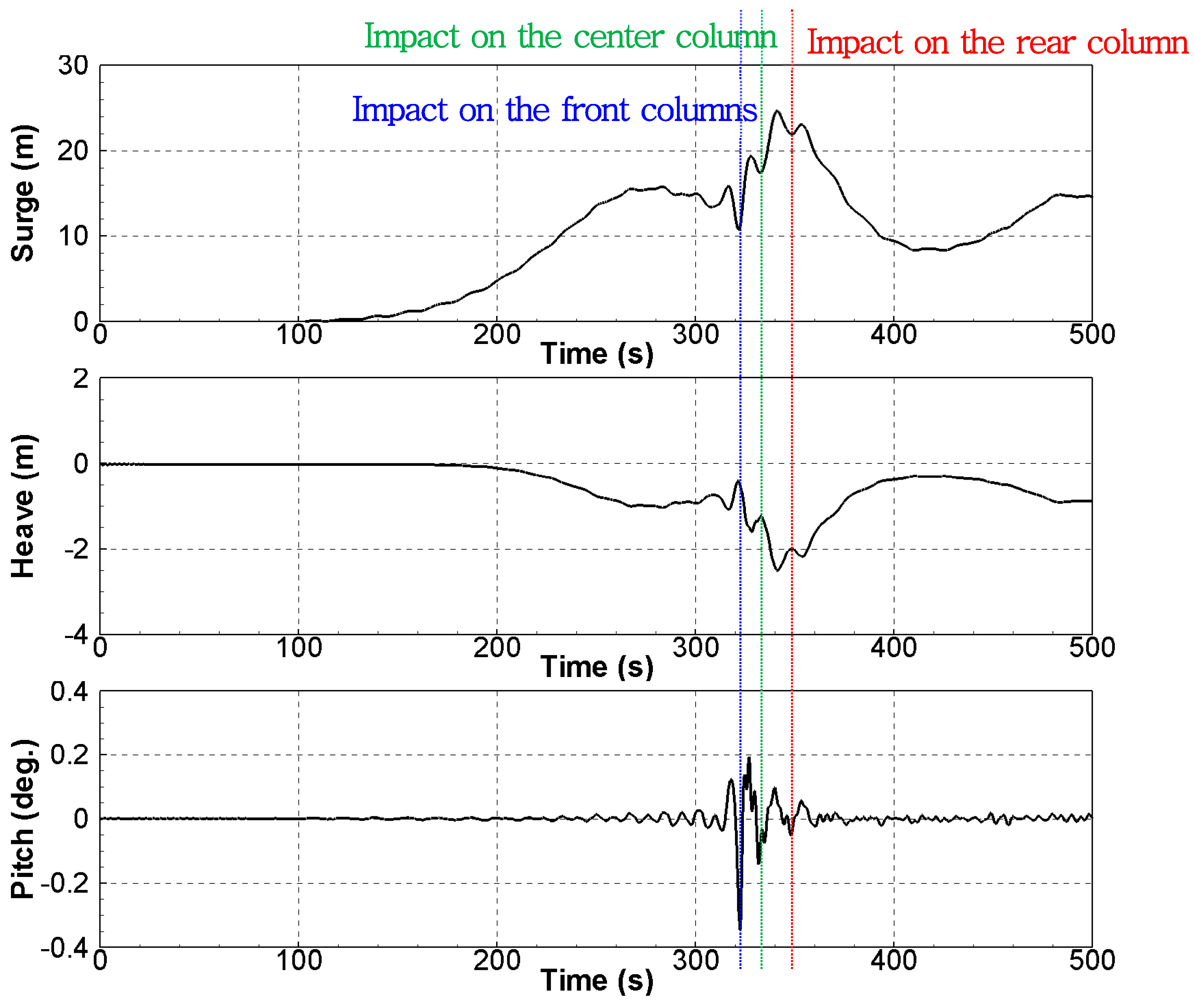
3.2. Whipping Phenomenon
4. Conclusions
- In terms of the low-frequency motion, the surge–heave coupled motion occurred because of the set-down caused by the surge motion. In addition, the effect of the heave–pitch coupled motion was minimal under this wave condition.
- In this study, the resonance frequency of the tendons occurred. The resonance frequency of a tendon should be considered when determining its stiffness during the design stage. However, the tendon resonance frequency has little effect on the TLP motion.
- In the irregular wave simulation, ringing and springing responses were observed. In the ringing and springing frequencies, the wave energy was very small in this study; therefore, it was clearly observed that the ringing and springing phenomena occurred owing to the impulse forces and the wave sum frequency, respectively.
- In this study, a whipping simulation was performed. Green water impacts occurred in the following order: front, center, and rear columns, and large surge offsets occurred after the green water impacts each column. It can be observed that the tensions from the wave and pitch resonance motion were large. After the green water hit the deck of the TLP, the pitch resonance motion occurred via the whipping phenomenon, and a large tendon tension could occur by the pitch resonance motion via the whipping phenomenon.
- In future work, the numerical simulation results of this study will be validated using model tests. In addition, in further numerical simulations, various wave and heading conditions will be considered to account for non-linear physical phenomena contributing to the TLP motions and changes in tension.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Butterfield, S.; Musial, W.; Jonkman, J.; Sclavounos, P. Engineering Challenges for Floating Offshore Wind Turbines; No. NREL/CP-500-38776; National Renewable Energy Lab (NREL): Golden, CO, USA, 2007. [Google Scholar]
- Mercier, J.A. Evolution of tension leg platform technology. In Proceedings of the 3rd International Conference on the Behavior of Offshore Structures, Cambridge, MA, USA, 9–12 February 1982. [Google Scholar]
- De Boom, W.C.; Pinkster, J.A.; Tan, P.S.G. Motion and tether force prediction for a deep water tension leg platform. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2–5 May 1983. [Google Scholar]
- Matsui, T.; Suzuki, T.; Sakoh, Y. Second-order diffraction forces on floating three-dimensional bodies in regular waves. Int. J. Offshore Polar Eng. 1992, 2, 175–185. [Google Scholar]
- Matsui, T.; Sakoh, T.; Nozu, T. Second-order sum-frequency oscillations of tension-leg platforms: Prediction and measurement. Appl. Ocean Res. 1993, 15, 107–118. [Google Scholar] [CrossRef]
- Chen, X.N.; Molin, B.; Petitjean, F. Numerical evaluation of the springing loads on tension leg platforms. Mar. Struct. 1995, 8, 501–524. [Google Scholar] [CrossRef]
- Kim, C.H.; Zhao, C.; Zou, J. Springing and ringing due to nonlinear waves on a coupled TLP. In Proceedings of the International Offshore and Polar Engineering Conference, Hague, The Netherlands, 11–16 June 1995. [Google Scholar]
- Zou, J.; Ormberg, H.; Standsberg, C.T. Prediction of TLP responses model tests vs. analysis. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 2004. [Google Scholar]
- Srinivasan, C.; Gaurav, G.; Serino, G.; Miranda, S. Ringing and springing response of triangular TLPs. Int. Shipbuild. Prog. 2011, 58, 141–163. [Google Scholar]
- Davies, K.B.; Leverette, S.J.; Spillane, M.W. Ringing response of TLP and GBS platforms. In Proceedings of the 7th International Conference on the Behavior of Offshore Structures, Cambridge, MA, USA, 12–15 July 1994. [Google Scholar]
- Faltinsen, O.M.; Newman, J.N.; Vinje, T. Nonlinear wave loads on a slender vertical cylinder. J. Fluid Mech. 1995, 289, 179–198. [Google Scholar] [CrossRef]
- Malenica, S.; Molin, B. Third-harmonic wave diffraction by a vertical cylinder. J. Fluid Mech. 1995, 302, 203–229. [Google Scholar] [CrossRef]
- Xue, M. Three-Dimensional Fully-Nonlinear Simulations of Waves and Wave Body Interactions. Ph.D. Thesis, Department of Ocean Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA, 1997. [Google Scholar]
- Liu, Y.; Xue, M.; Yue, D.K.P. Computation of fully nonlinear three-dimensional wave-wave and wave-body interactions. Part 2. Nonlinear waves and forces on a body. J. Fluid Mech. 2001, 438, 41–66. [Google Scholar] [CrossRef]
- Cho, Y.S.; Nam, B.W.; Hong, S.Y.; Kim, J.H.; Kim, H.J. Numerical study on wave-induced motion response of tension leg platform in waves. J. Ocean Eng. Technol. 2014, 28, 508–516. [Google Scholar] [CrossRef]
- Kim, T.Y. Study on the Nonlinear Motions of Floating Offshore Platforms Induced by Varying Bathymetry and High-Frequency Wave Loads. Ph.D. Thesis, Department of Industrial Engineering and Naval Architecture, Seoul National University, Seoul, Republic of Korea, 2015. [Google Scholar]
- Roald, L.; Jonkman, J.; Robertson, A.; Chokani, N. The effect of second-order hydrodynamics on floating offshore wind turbines. Energy Procedia 2013, 35, 253–264. [Google Scholar] [CrossRef]
- Han, Z.; Zhao, Y.; Su, J.; He, Y.; Xu, Y.; Wu, F.; Jiang, Z. On the hydrodynamic responses of a multi-column TLP floating offshore wind turbine model. Ocean Eng. 2022, 253, 111262. [Google Scholar] [CrossRef]
- Kim, T.; Madsen, F.J.; Bredmose, H.; Pegalajar-Jurado, A. Numerical analysis and comparison study of the 1:60 scaled DTU 10 MW TLP floating wind turbine. Renew. Energy 2023, 202, 210–221. [Google Scholar] [CrossRef]
- Nematbakhsh, A.; Bachynski, E.E.; Gao, Z.; Moan, T. Comparison of wave load effects on a TLP wind turbine by using computational fluid dynamics and potential flow theory approaches. Appl. Ocean Res. 2015, 53, 142–154. [Google Scholar] [CrossRef]
- Allen, C.; Viselli, A.; Dagher, H.; Goupee, A.; Gaertner, E.; Abbas, N.; Hall, M.; Barter, G. Definition of the UMaine VolturnUS-S Reference Platform Developed for the IEA Wind 15-Megawatt Offshore Reference Wind Turbine; No. NREL/TP-5000-76773; National Renewable Energy Lab (NREL): Golden, CO, USA, 2020. [Google Scholar]
- Hong, S.Y.; Ha, Y.J.; Nam, B.W.; Kim, K.H.; Hwang, S.C.; Kim, H.J.; Kim, J.; Huang, Z.J. CFD modeling practice for calculation of FPSO bow impact by focusing wave. In Proceedings of the 29th International Ocean and Polar Engineering Conference, Honolulu, HI, USA, 16–21 June 2019. [Google Scholar]
- TESK CFD JDP Report (TechnipFMC, ExxonMobil, Samsung Heavy Industries, Korea Research Institute of Ships and Ocean Engineering) ‘MODELING PRACTICE: SEMI VIM’.






| Parameter | Value | |
|---|---|---|
| Water Depth (m) | 137 | |
| Length Overall/Beam Overall (m) | 74.25/84.11 | |
| Radius between the Center and Outer Columns (m) | 42.5 | |
| Center Column Diameter (m) | 10 | |
| Center Colum Height (m) | 33 | |
| Outer Column Square Width (m) | 10.5 | |
| Outer Column Height (m) | 28 | |
| Freeboard_Center Column (m) | 15 | |
| Freeboard_Outer Column (m) | 10 | |
| Ponton Width/Depth (m) | 8/4.5 | |
| Deck Width/Depth (m) | 4/3 | |
| Draft (m) | 18 | |
| Displacement (ton) | 11,123 | |
| COG (m) | (0, 0, 41.3) | |
| Moment of Inertia (kg·m2) | (2.83 × 1010, 2.83 × 1010, 6.53 × 109) | |
| Number of Tendons | 9 (3 per each column) | |
| Total Pre-Tension (ton) | 3782 | |
| Tendon Axial Stiffness (kN) | 1,799,000 | |
| Tendon Modeling | Linear Spring | |
| Resonance Period(s) | Surge | 46.72 (0.134 rad/s) |
| Heave | 2.18 (2.882 rad/s) | |
| Pitch | 3.00 (2.094 rad/s) | |
| Parameter | Value |
|---|---|
| Spectrum | JONSWAP |
| Tp (s) | 15.1 |
| Hs (m) | 7.08 (60% of 11.8 m, 50-year return periods) |
| γ | 2.5 |
| Item | Value |
|---|---|
| Discretization Scheme | Finite Volume Method (FVM) |
| Pressure and Velocity Field | Semi-Implicit Method for Pressure-Linked Equations (SIMPLE) |
| Time Step | Adjustable Time Step (target CFL = 0.5) |
| Sub-iterations | 10 |
| Convection Schemes | Second-order Upwind |
| Temporal Schemes | Second-order Implicit |
| Turbulence Model | (Laminar Flow) |
| Mesh Motion | Deforming Mesh |
| Simulation Time | 30 min (1800 s) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ha, Y.-J.; Kim, K.-H.; Park, J.-Y. CFD Study of the Non-Linear Physical Phenomena of the TLP of a 15-MW-Class FOWT under Extreme Waves. J. Mar. Sci. Eng. 2023, 11, 1915. https://doi.org/10.3390/jmse11101915
Ha Y-J, Kim K-H, Park J-Y. CFD Study of the Non-Linear Physical Phenomena of the TLP of a 15-MW-Class FOWT under Extreme Waves. Journal of Marine Science and Engineering. 2023; 11(10):1915. https://doi.org/10.3390/jmse11101915
Chicago/Turabian StyleHa, Yoon-Jin, Kyong-Hwan Kim, and Ji-Yong Park. 2023. "CFD Study of the Non-Linear Physical Phenomena of the TLP of a 15-MW-Class FOWT under Extreme Waves" Journal of Marine Science and Engineering 11, no. 10: 1915. https://doi.org/10.3390/jmse11101915
APA StyleHa, Y.-J., Kim, K.-H., & Park, J.-Y. (2023). CFD Study of the Non-Linear Physical Phenomena of the TLP of a 15-MW-Class FOWT under Extreme Waves. Journal of Marine Science and Engineering, 11(10), 1915. https://doi.org/10.3390/jmse11101915







