Numerical Analysis on Effect of Structural Parameters on Flow Field and Internal Trajectory in Gas–Steam Ejection Systems
Abstract
:1. Introduction
2. Computational Model
2.1. Geometric Model
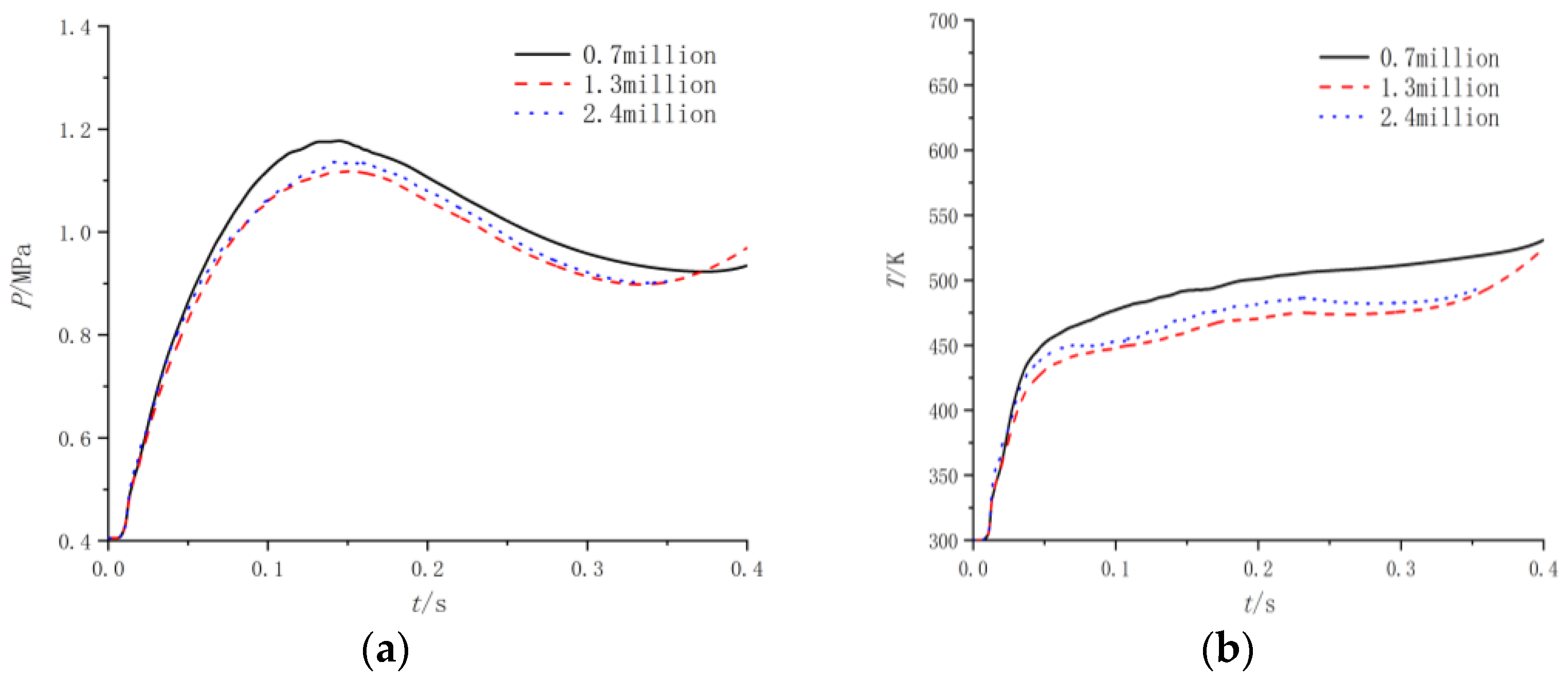
2.2. Computational Grids
3. Numerical Method
3.1. Governing Equations
3.2. Vaporization Model
3.3. Turbulence Model
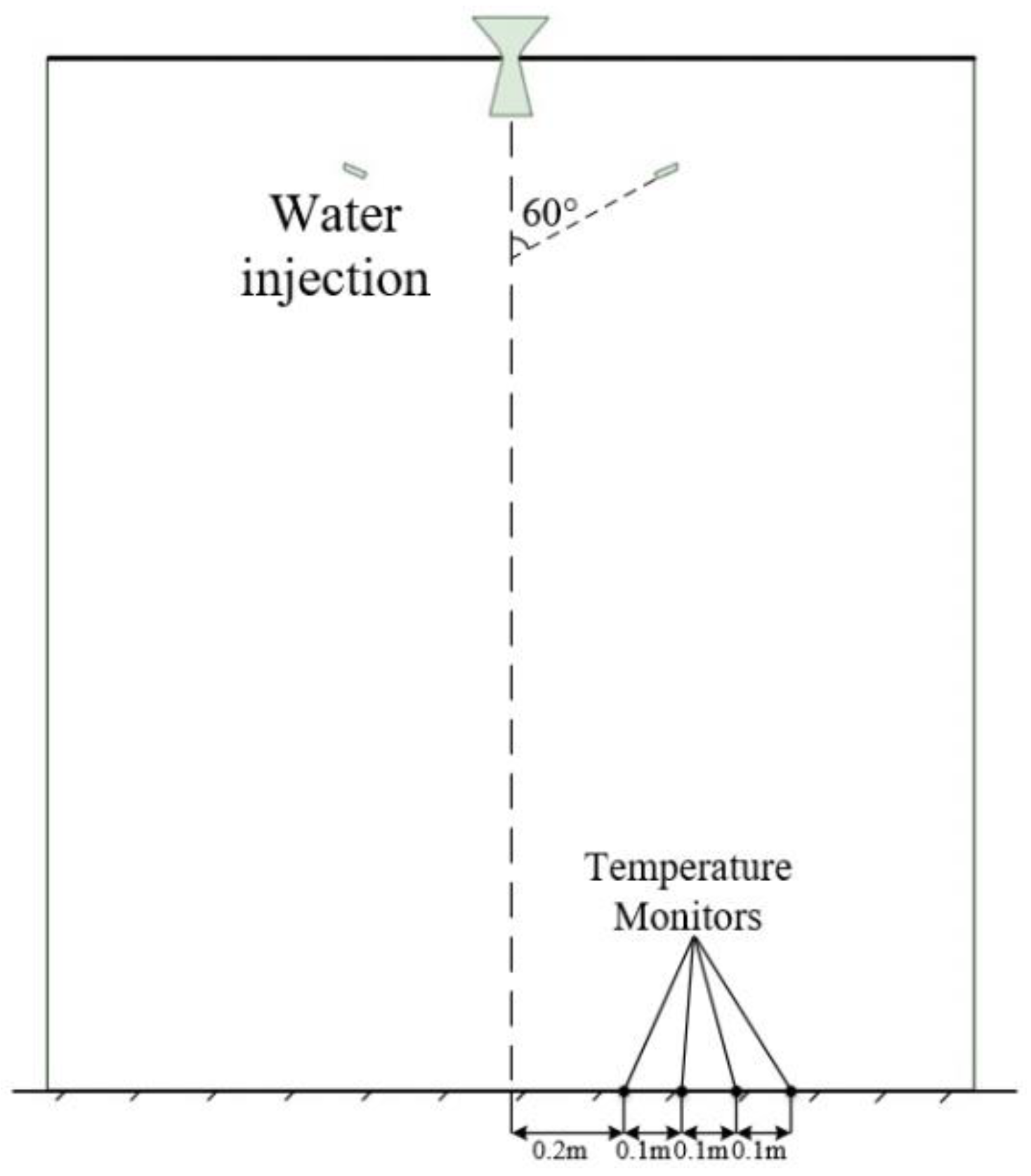
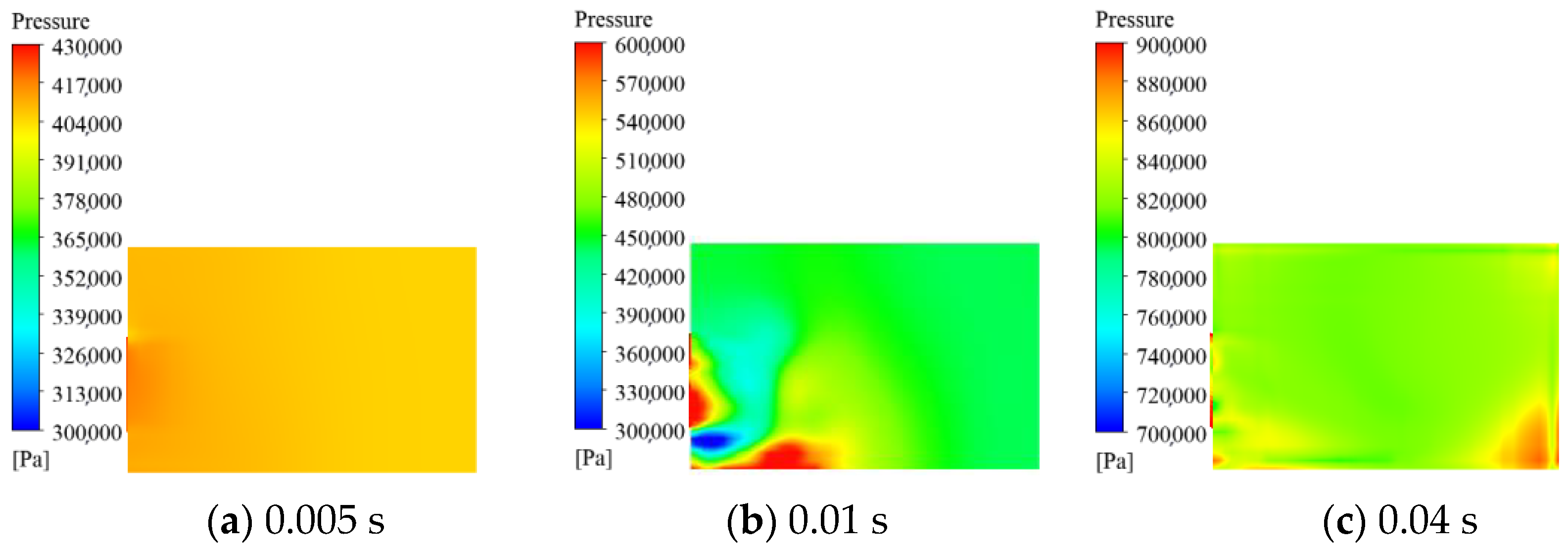
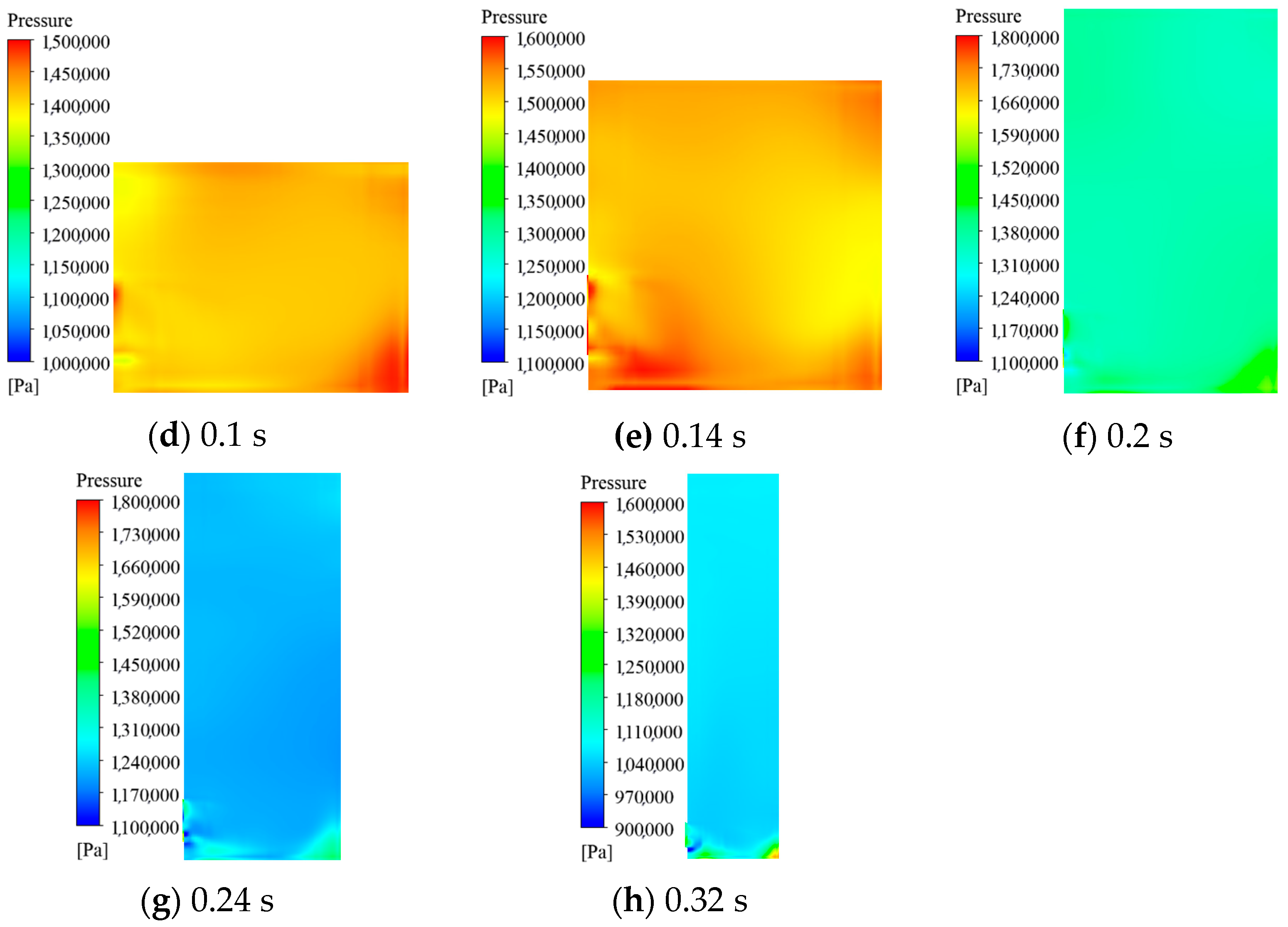
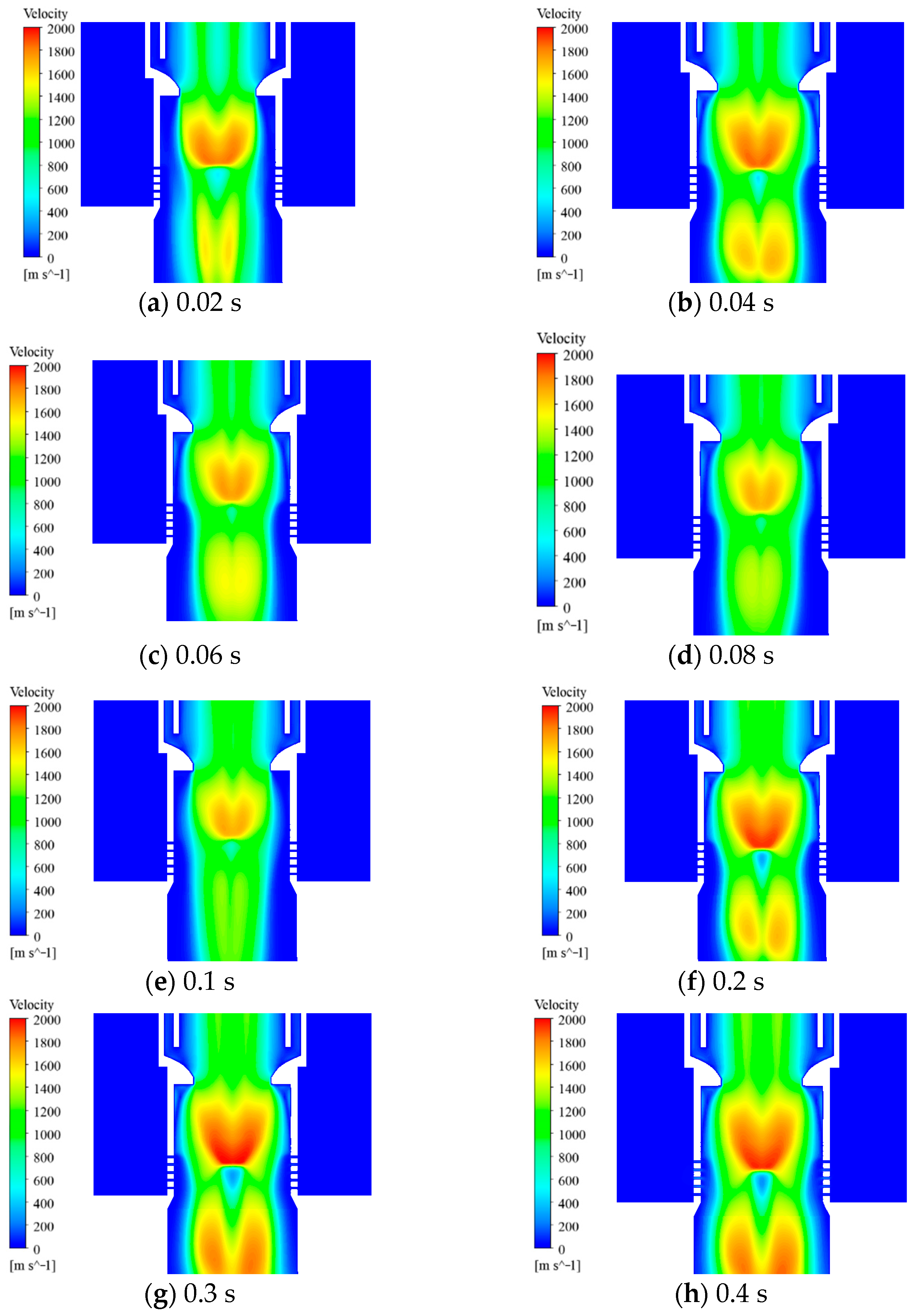
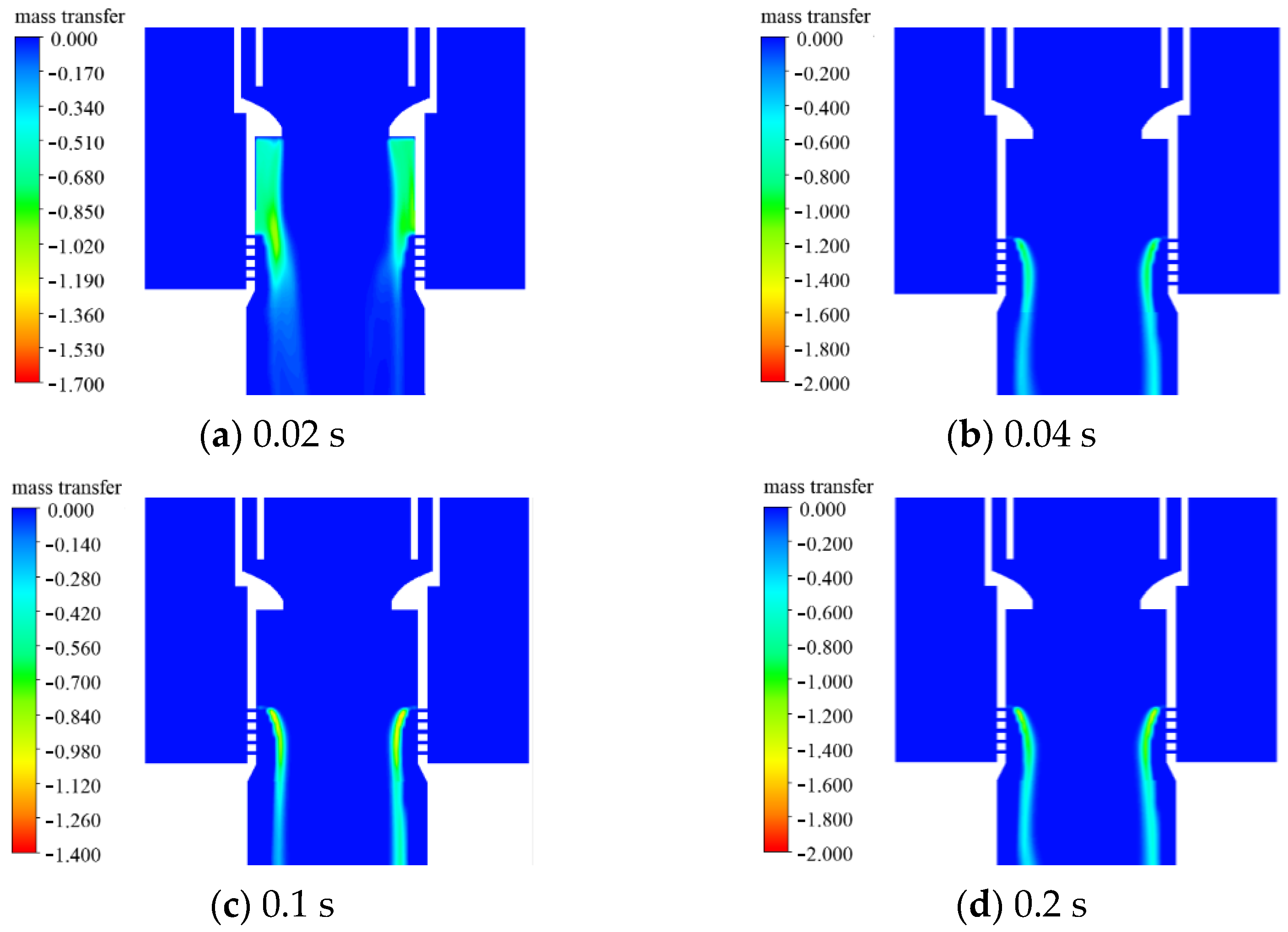
3.4. Model Validation
4. Computational Results
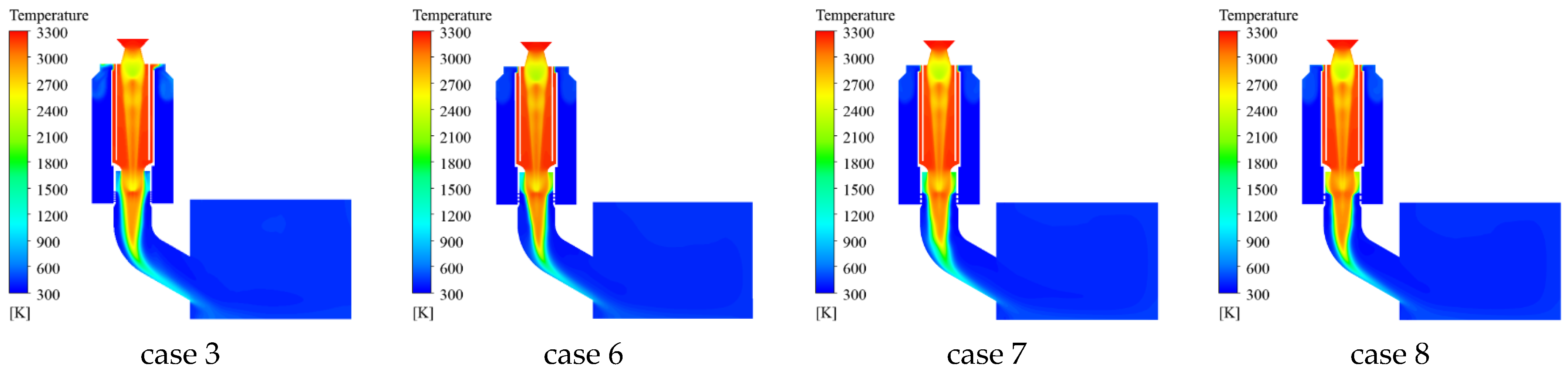
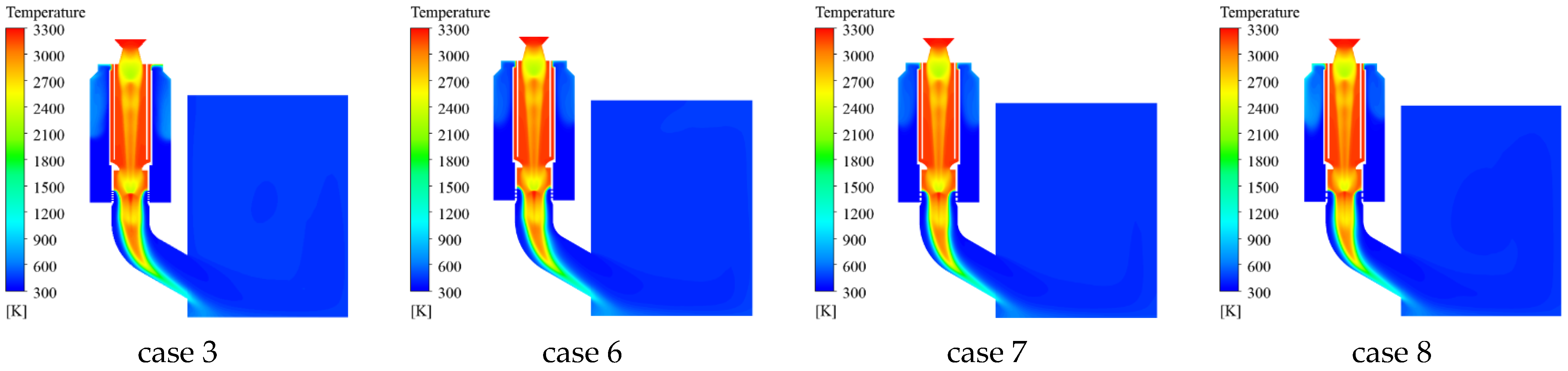
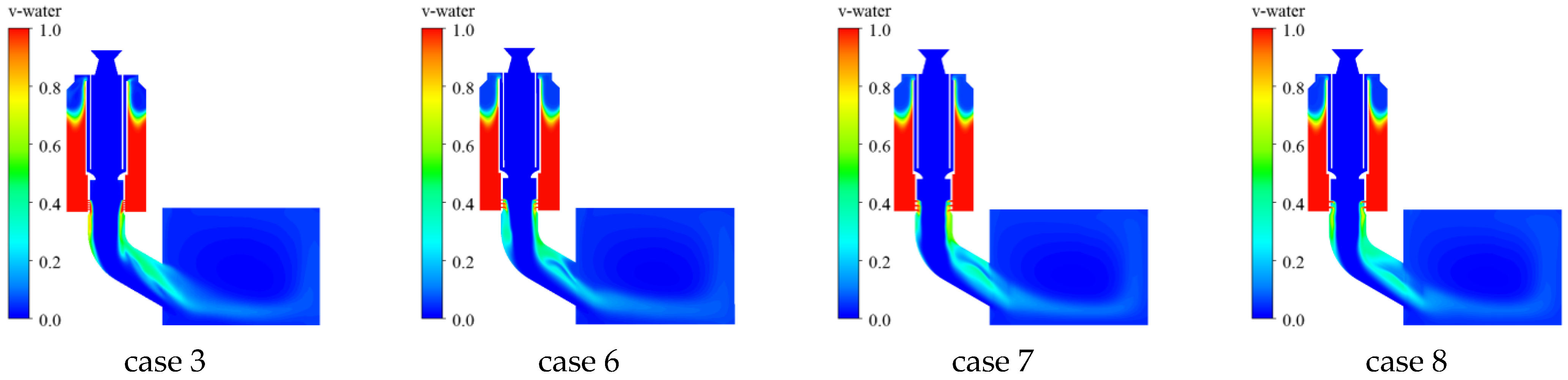
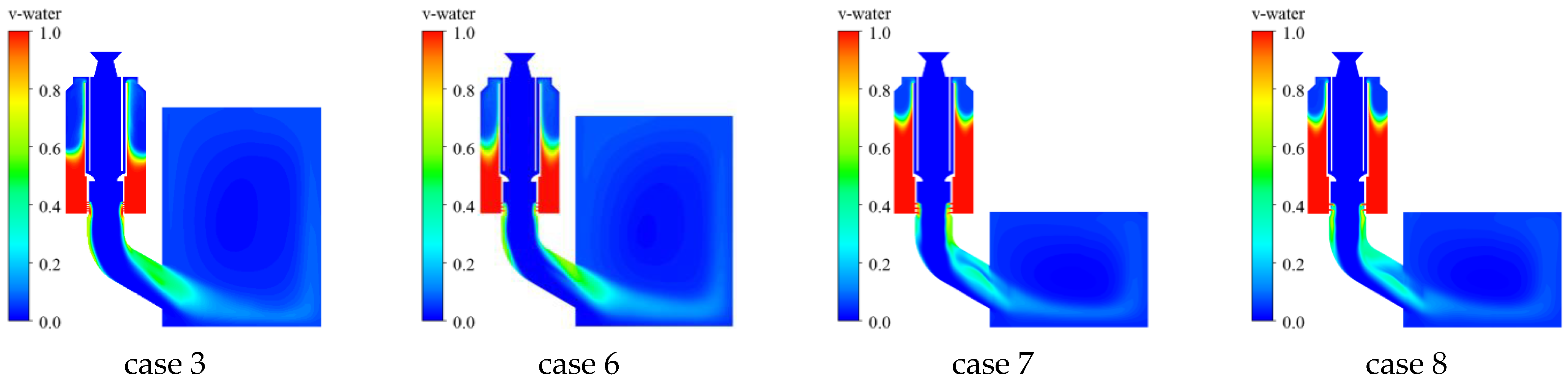
4.1. Influence of Spray Hole
- -
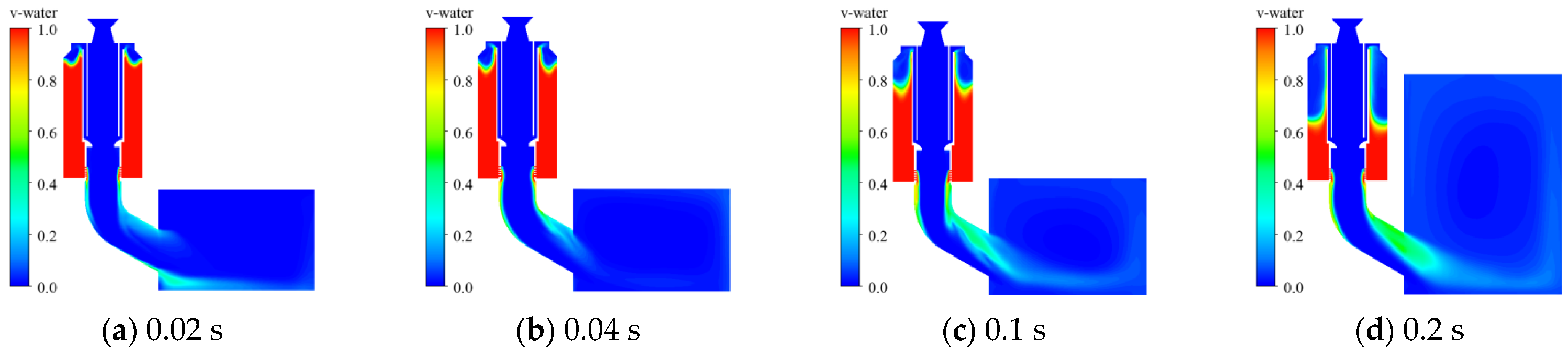
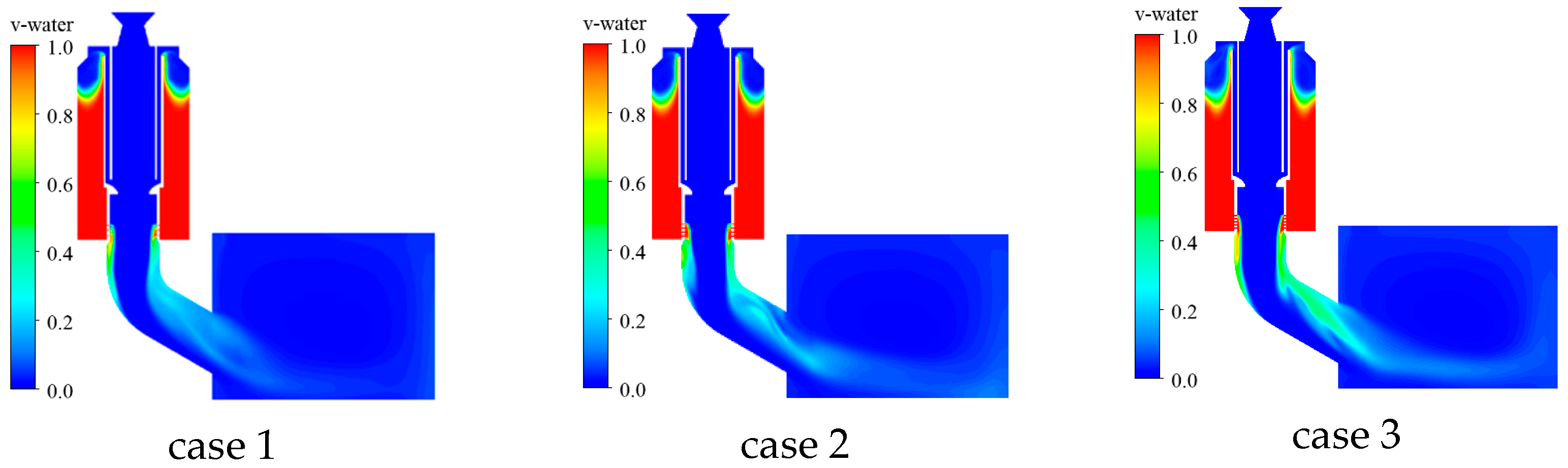
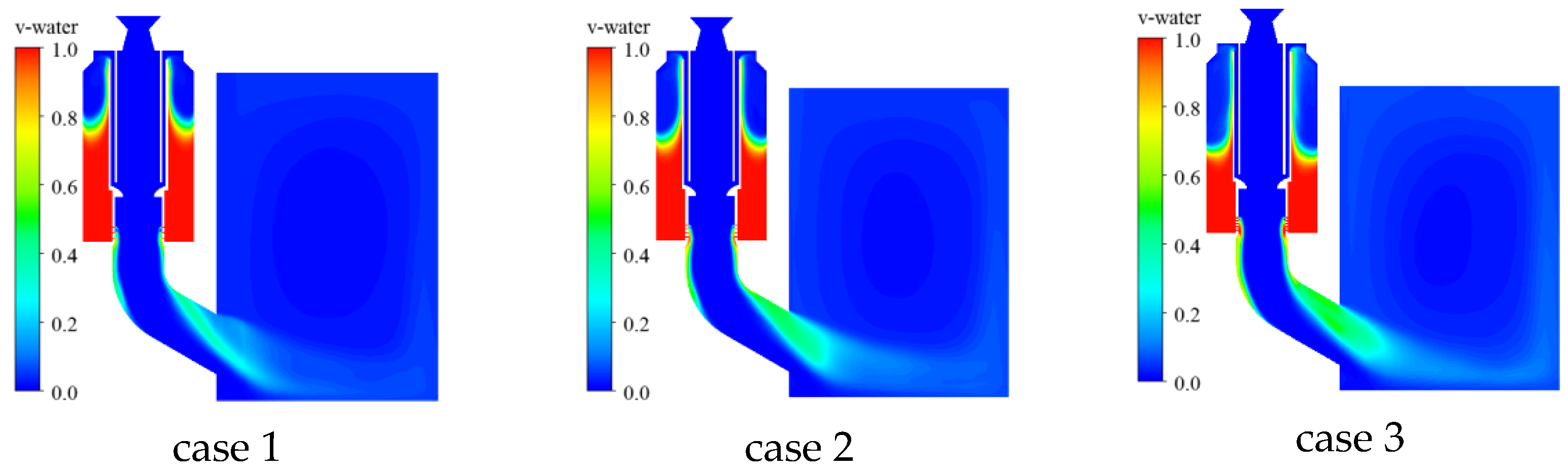
- The water volume fraction distributions under different spray hole diameters are shown in Figure 19 and Figure 20. For smaller spray holes, the water flow rate acts better on the wall surface of the elbow [41]. The larger the diameter of the water spray hole, the greater the water flow in the water spray hole, and the stronger the inhibition effect on the gas impact under the action of gravity; so, it is not easy to flow along the inner wall surface of the elbow.
- -
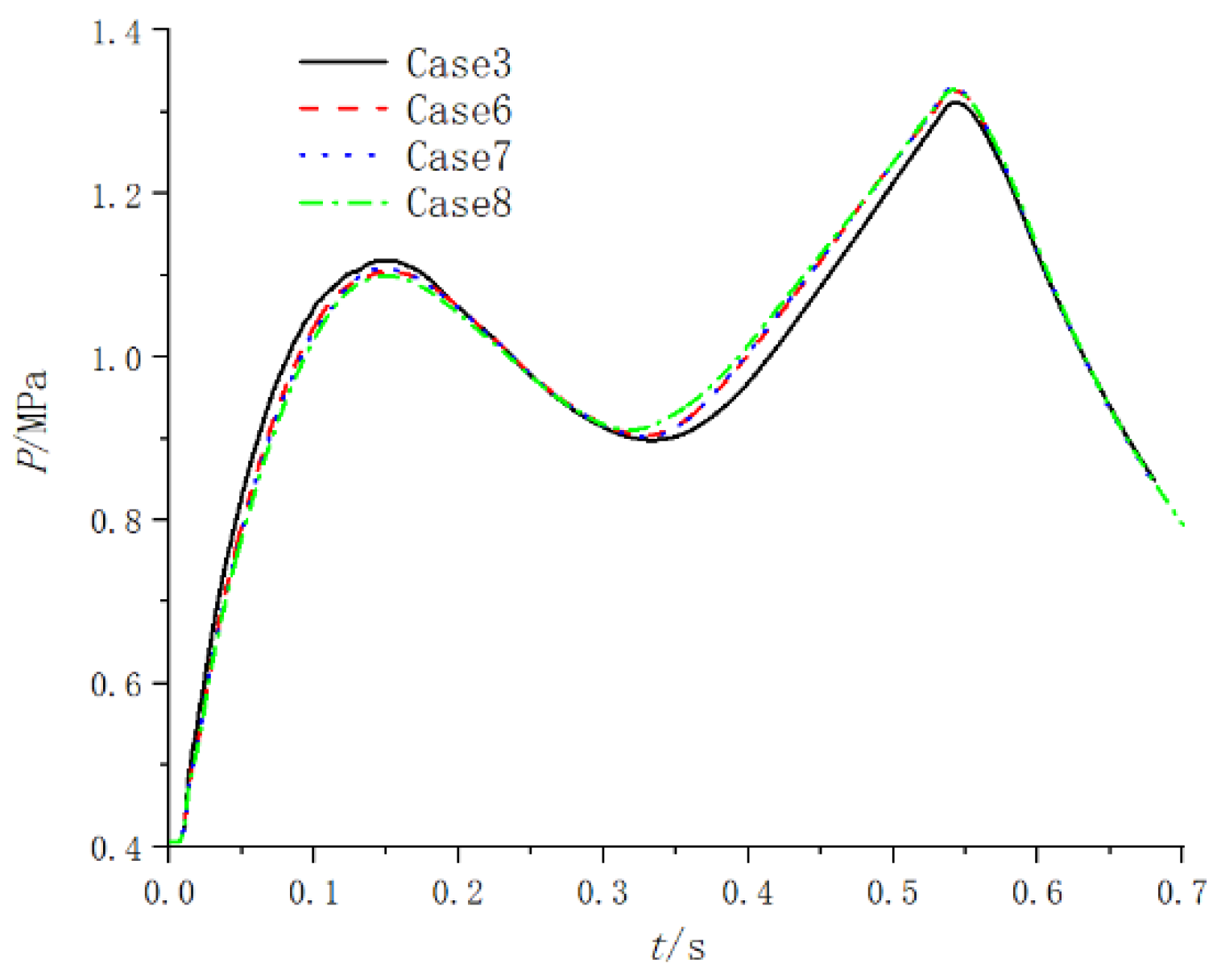
- The average pressure in the launcher under different spray hole diameters is shown in Figure 21; it can be seen that the average pressure difference is relatively small. In Figure 21, there are two peaks in the pressure change inside the emission tube. The first peak is due to the continuous flow of gas into the launcher, and the missile has not yet moved; so, the pressure inside the launcher will continue to increase. When the missile begins to move, the pressure begins to decrease. The second peak is caused by the peak pressure of the gas generator at the corresponding time. The maximum pressure does not exceed 1.329 MPa during the ejection process.
- -
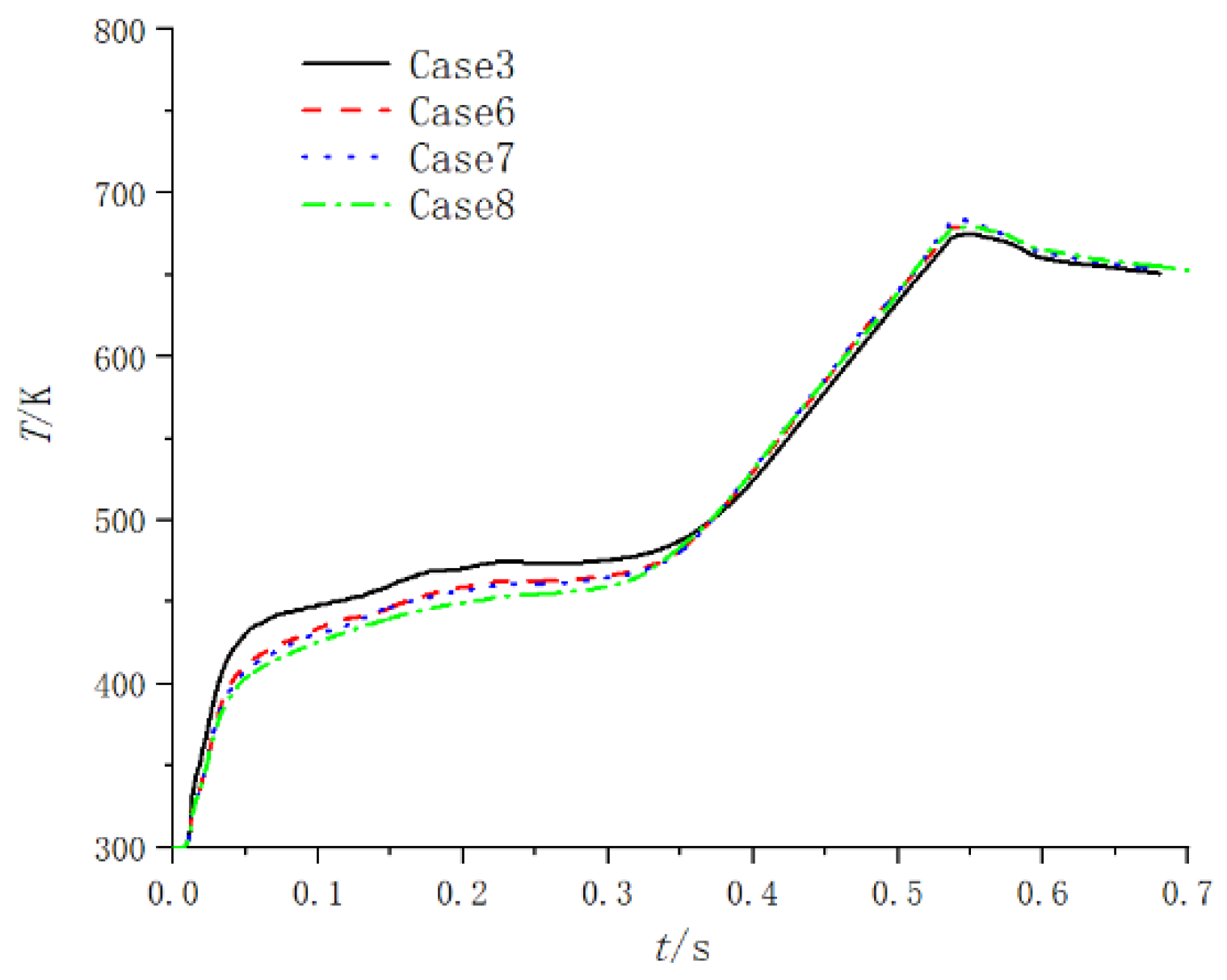
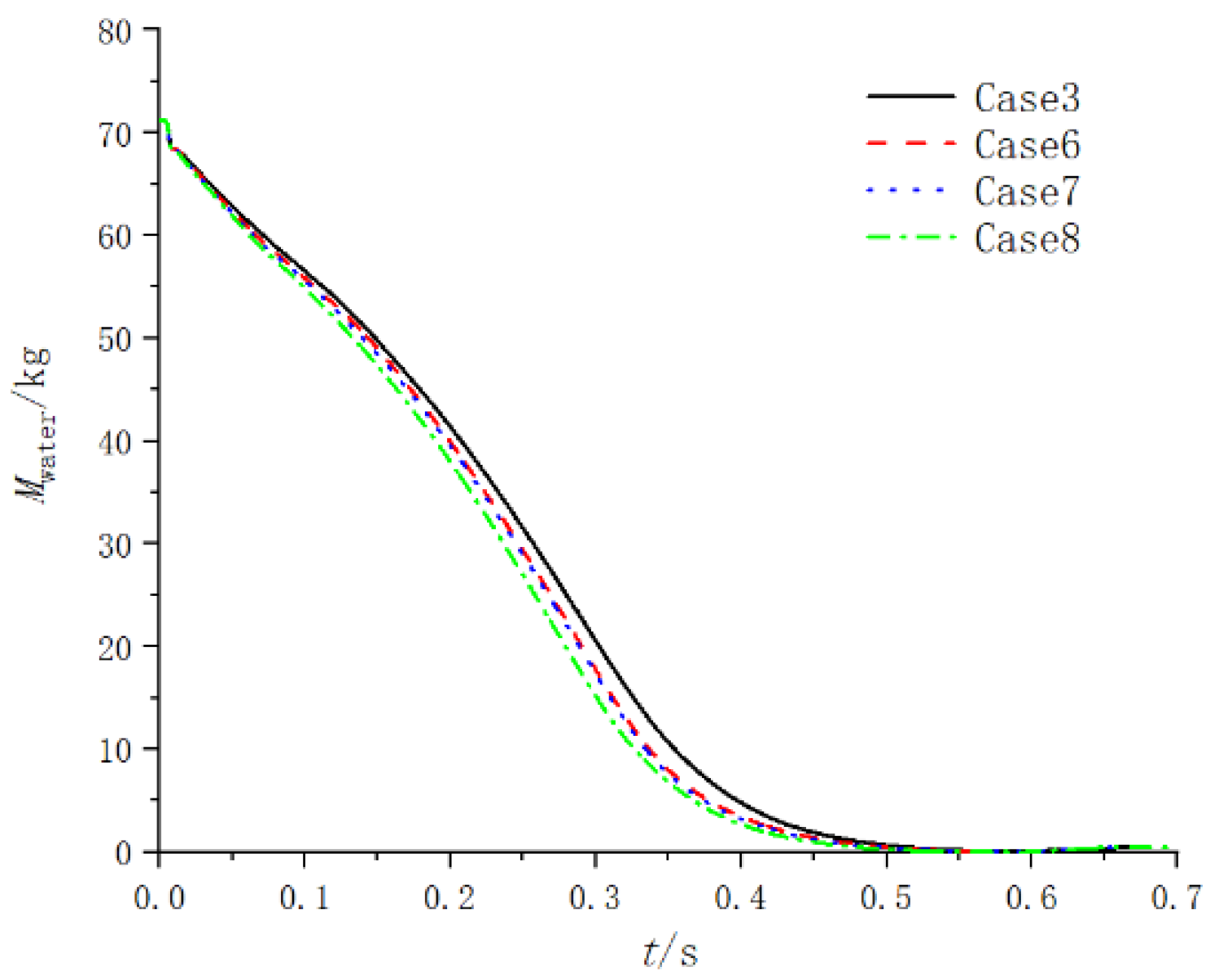
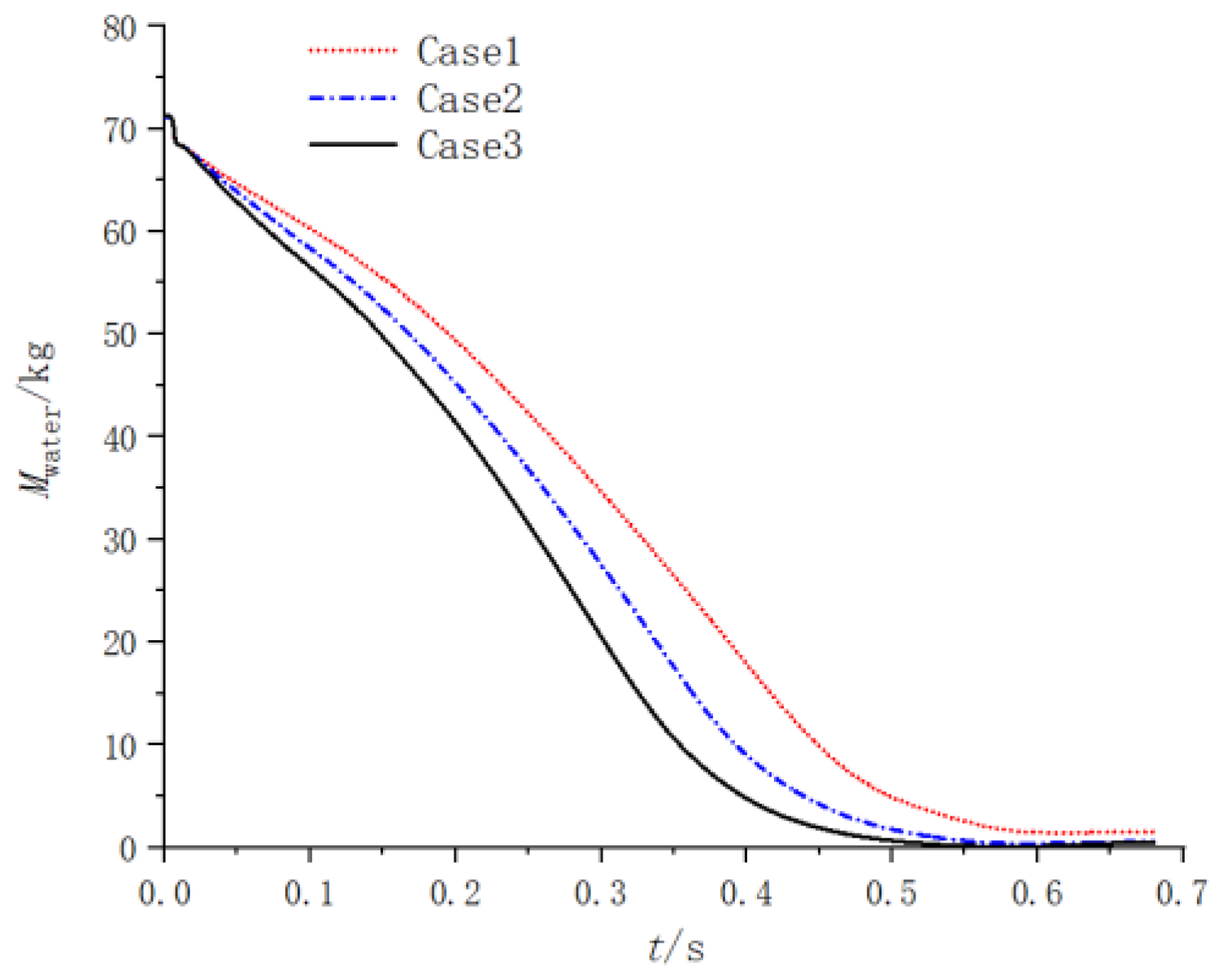
- The changes in the total water mass in the launcher under different spray hole diameters are shown in Figure 23. In the early stages of the launch process, the larger diameter of the spray hole corresponds to a faster decrease in water flow quality, resulting in a lower temperature.
- -
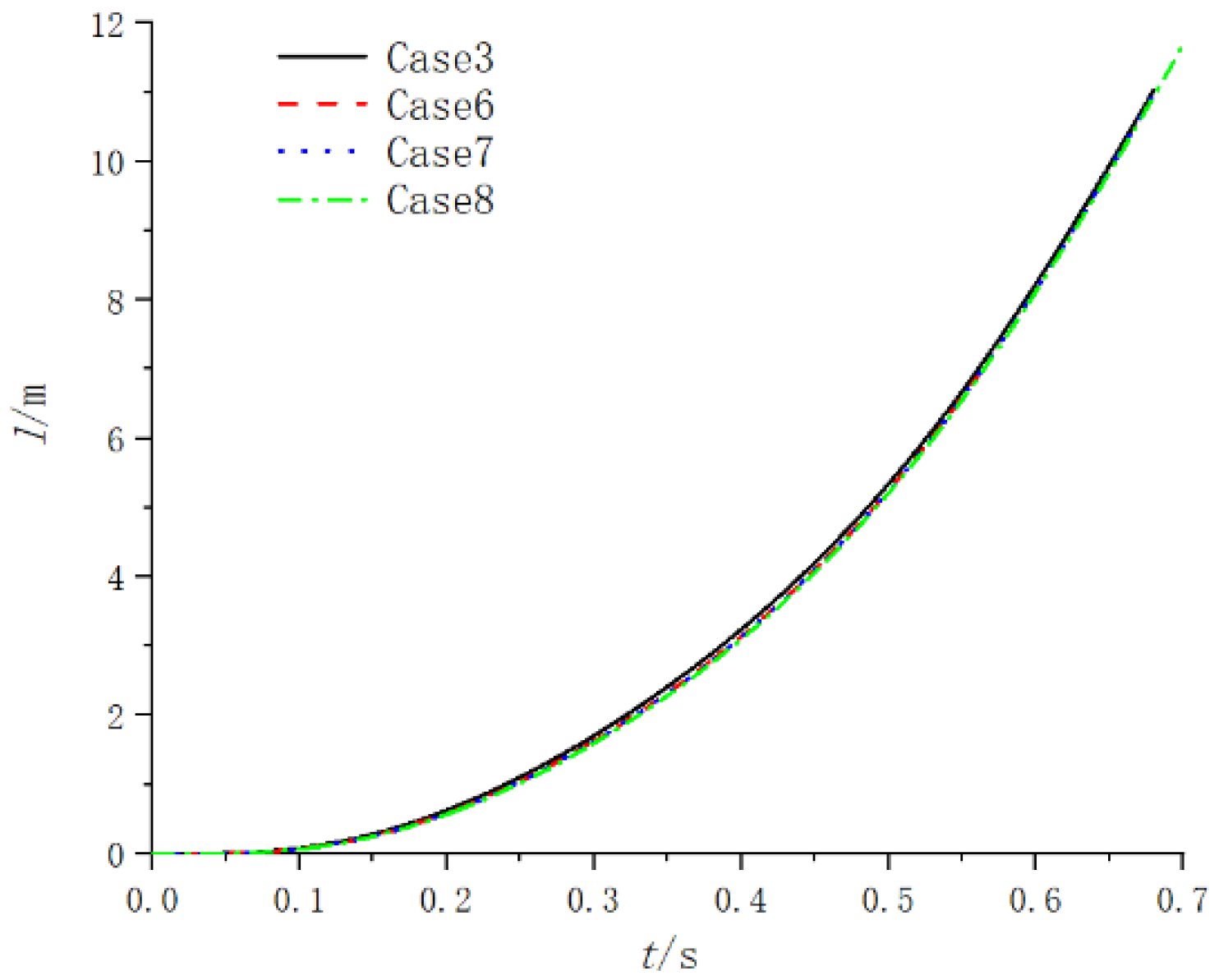
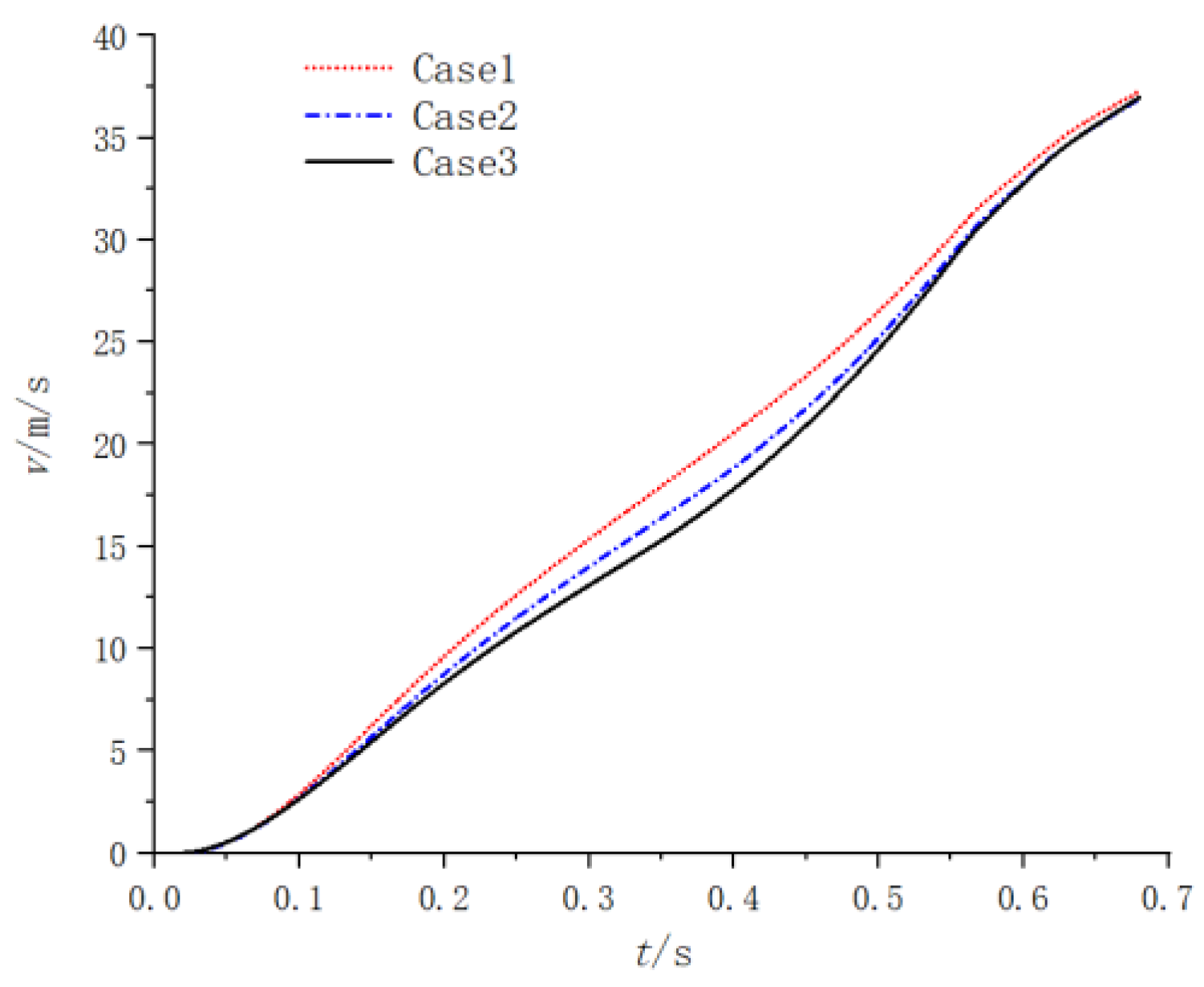
- The acceleration, velocity and displacement curves of the projectile motion under different spray hole diameters are shown in Figure 24, Figure 25 and Figure 26. The difference between the interior ballistic curves corresponding to the four cases is very small. When the total spray area is fixed, the diameter of the spray hole has little influence on the flow field and internal ballistics characteristics of the gas–steam ejection device.
- -
- Next, the diameter of the spray hole is maintained unchanged, and the impact of total spray area on the gas–steam ejection flow field and launch tube ballistic parameters is studied. The change in total spray area is adjusted by the number of spray holes.
- -
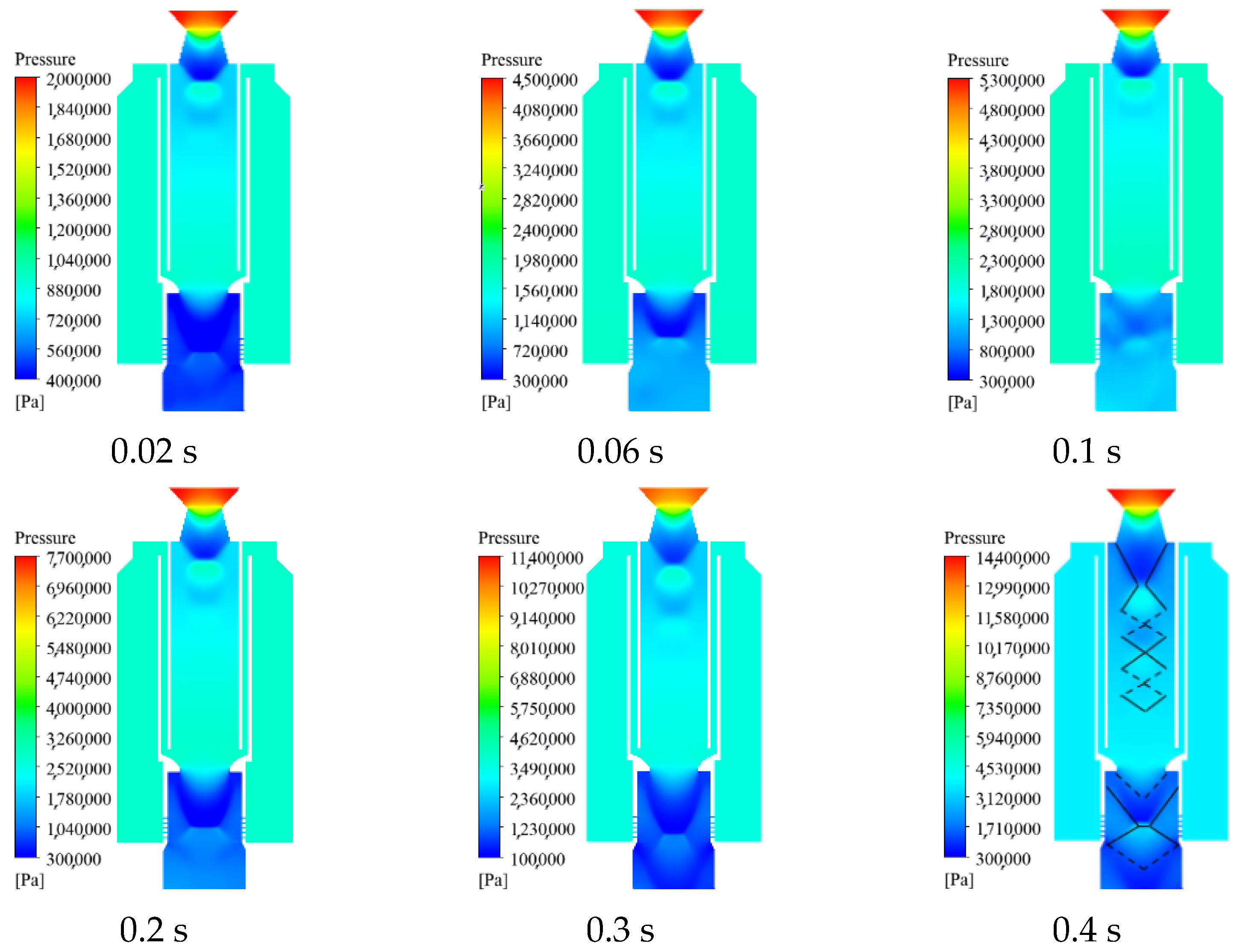
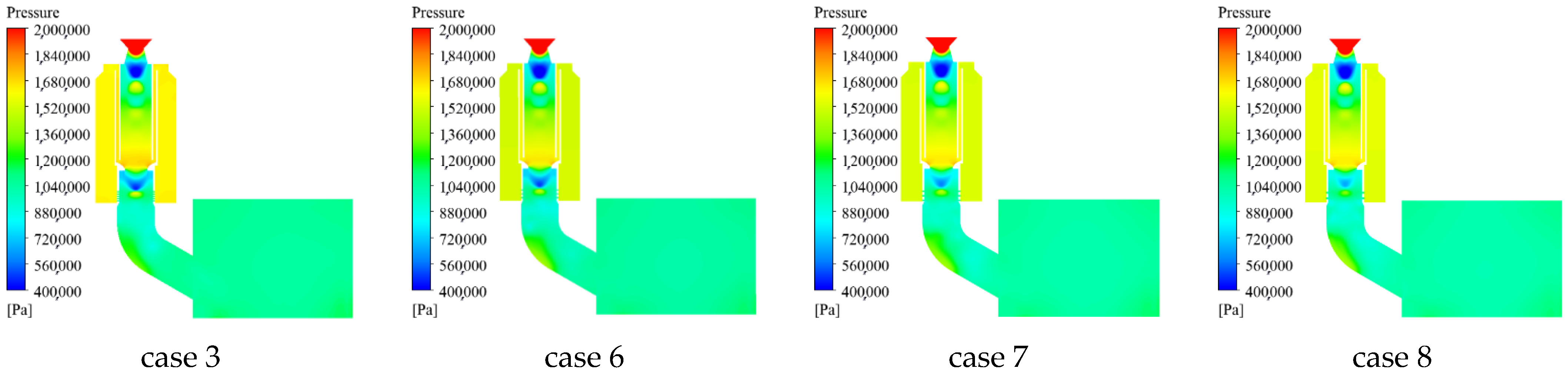
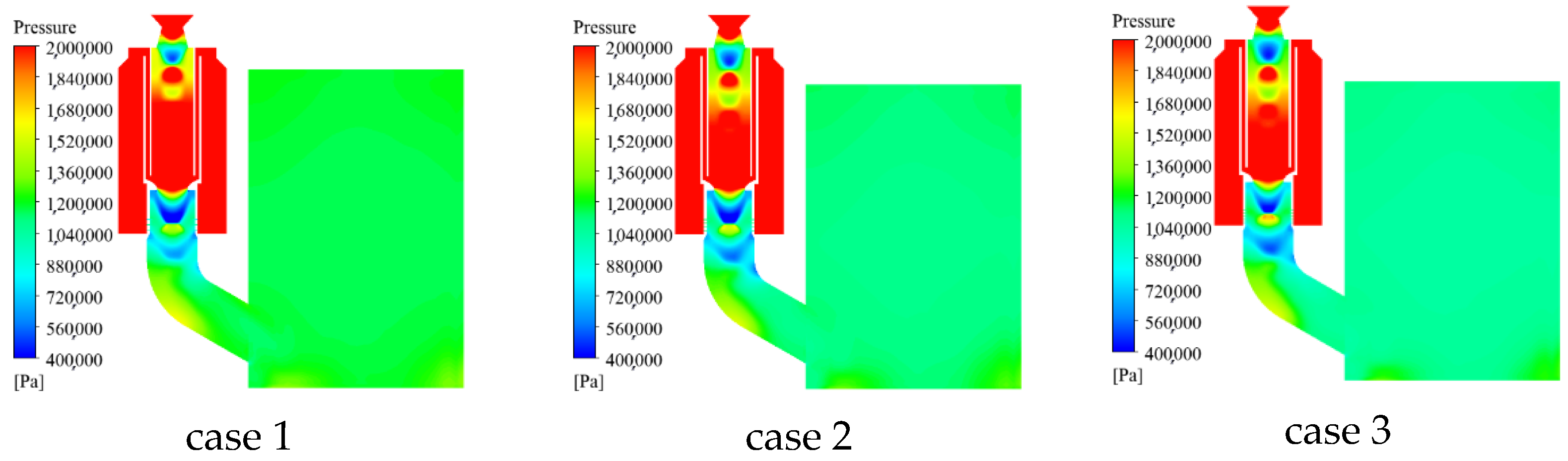
- The pressure distribution within the device at two different times under different total spray areas is shown in Figure 27 and Figure 28. It can be seen from Figure 27 and Figure 28 that the larger total area there is, the lower the pressure of the ejection device. Since the number of spray holes is related to the spray flow rate, the more spray holes there are, the greater the spray flow rate value, resulting in a decrease in the pressure value.
4.2. Influence of Throat
- -
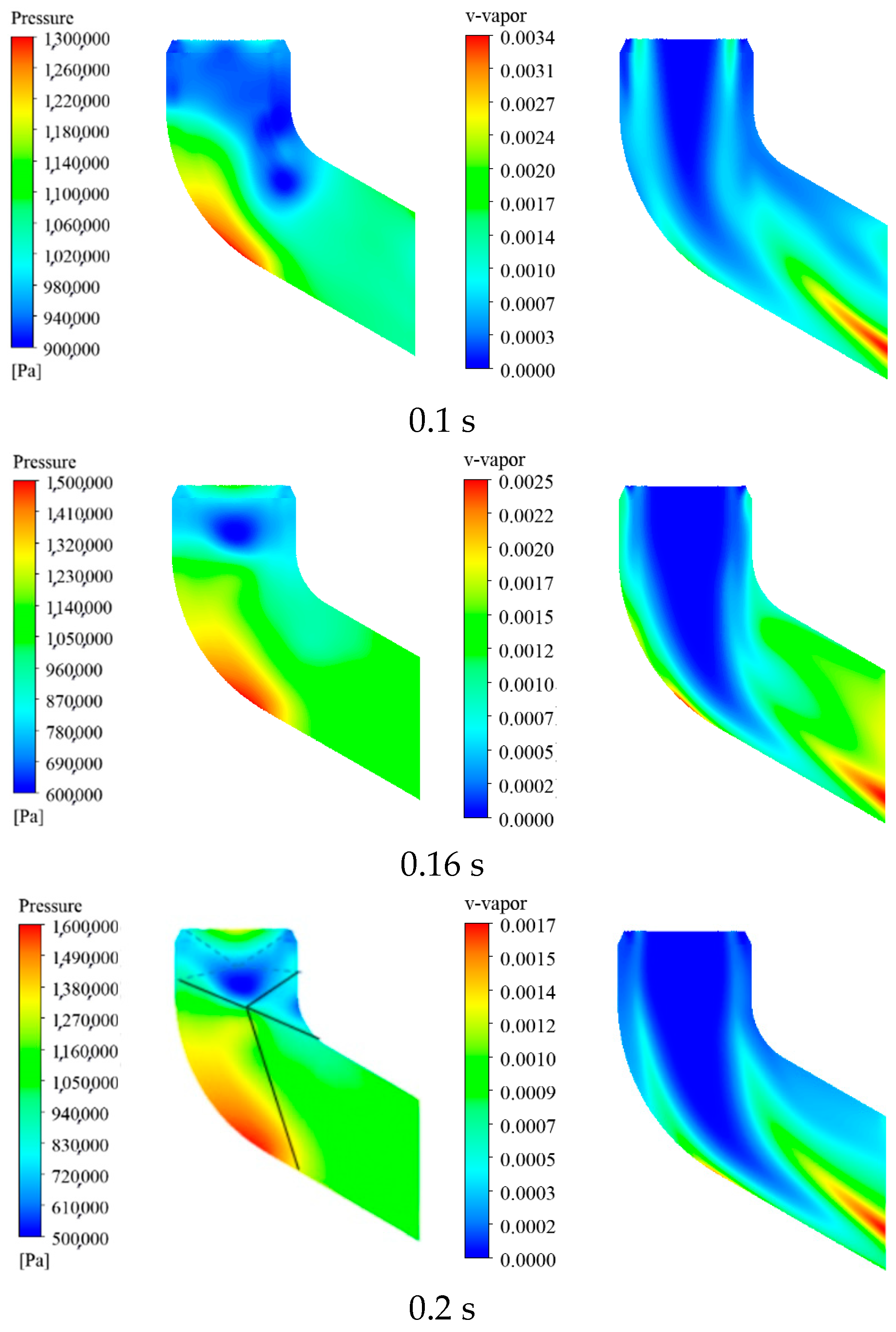
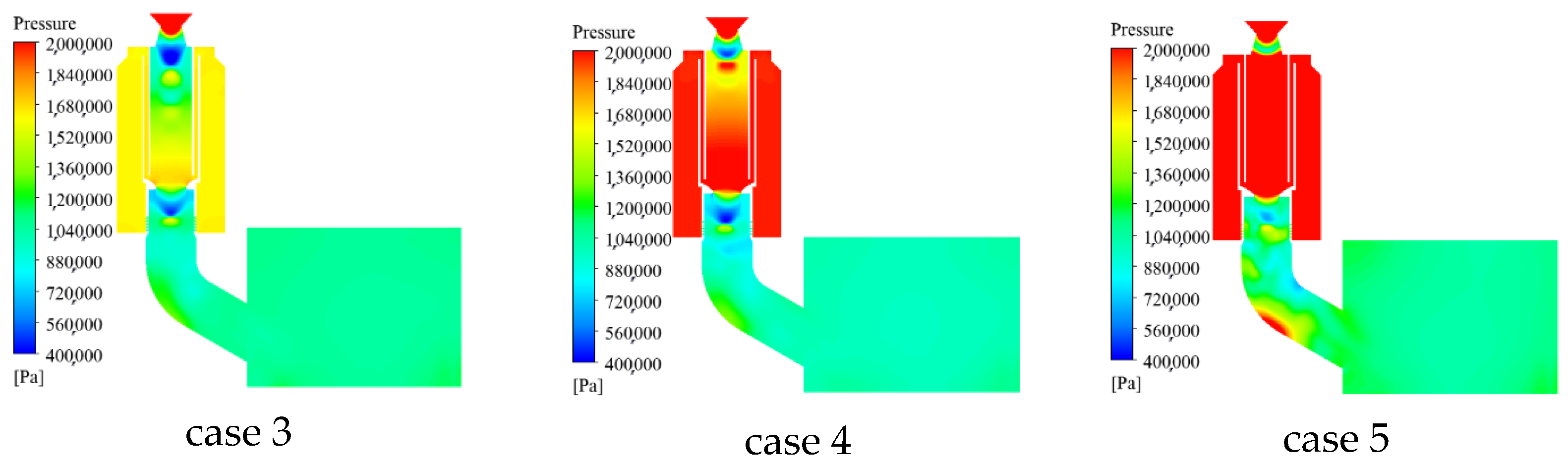
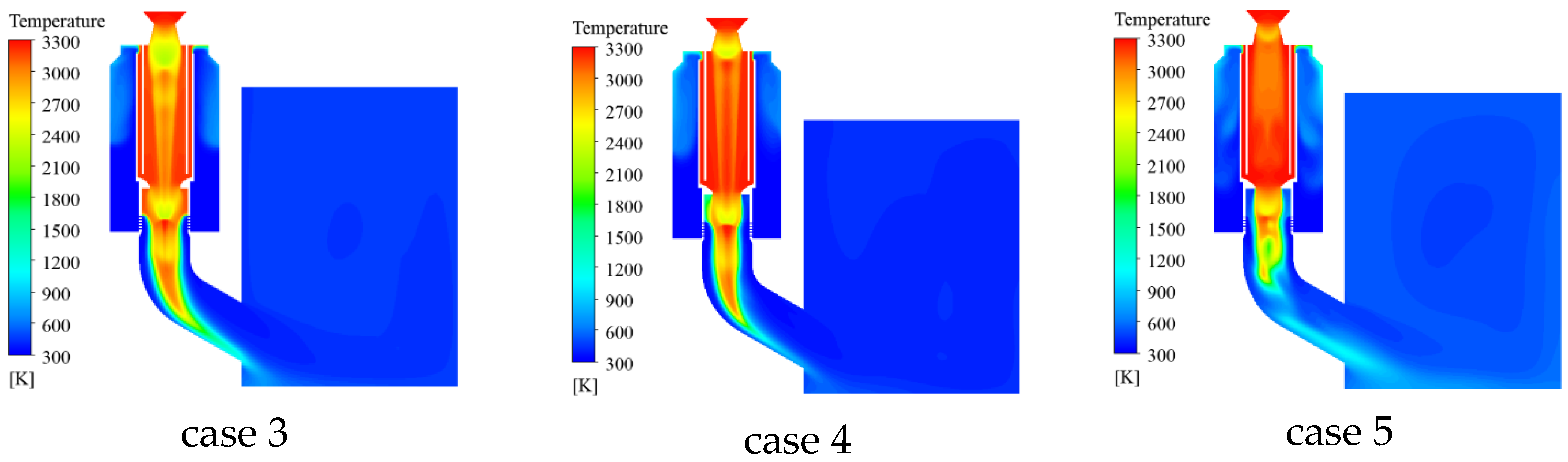
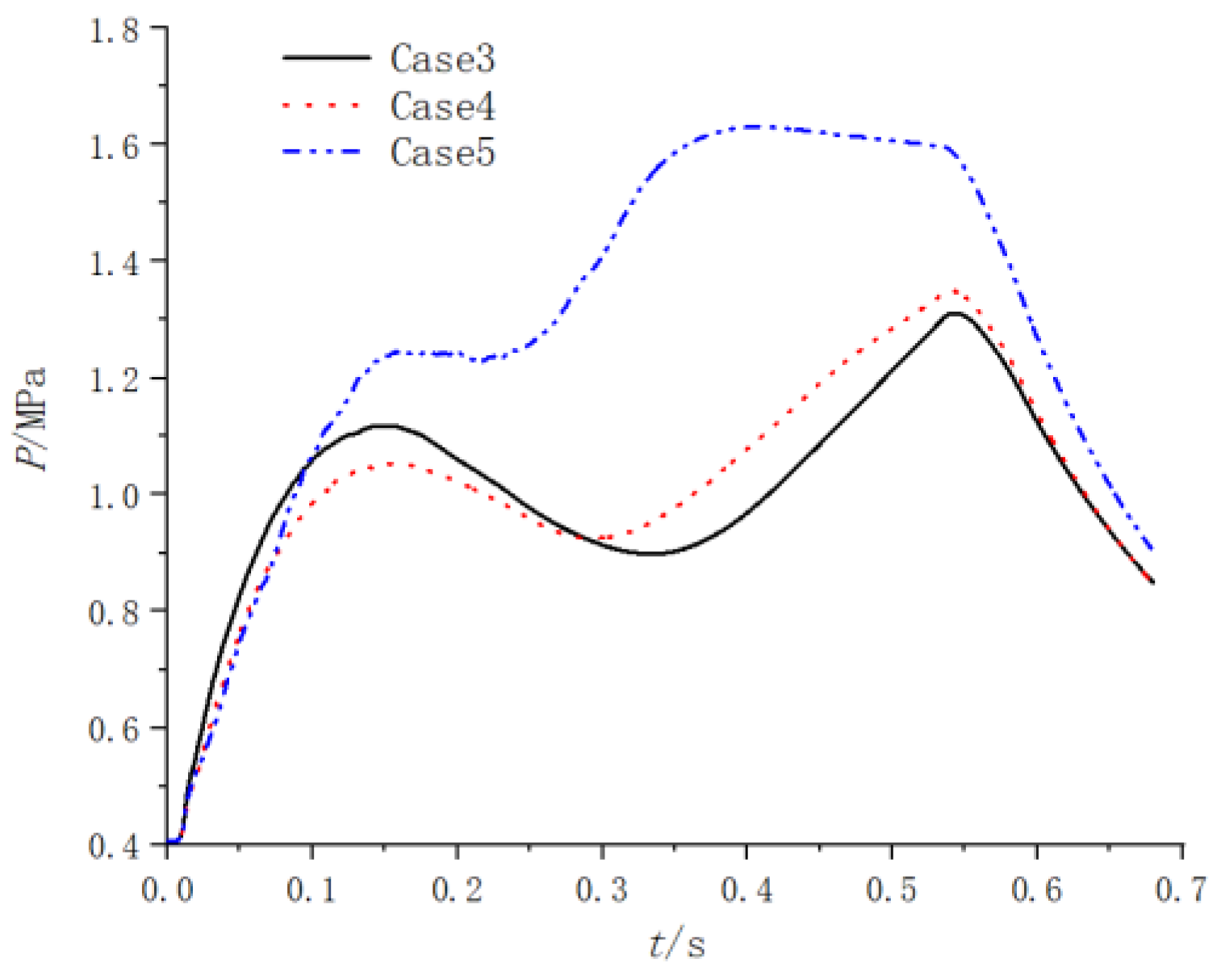
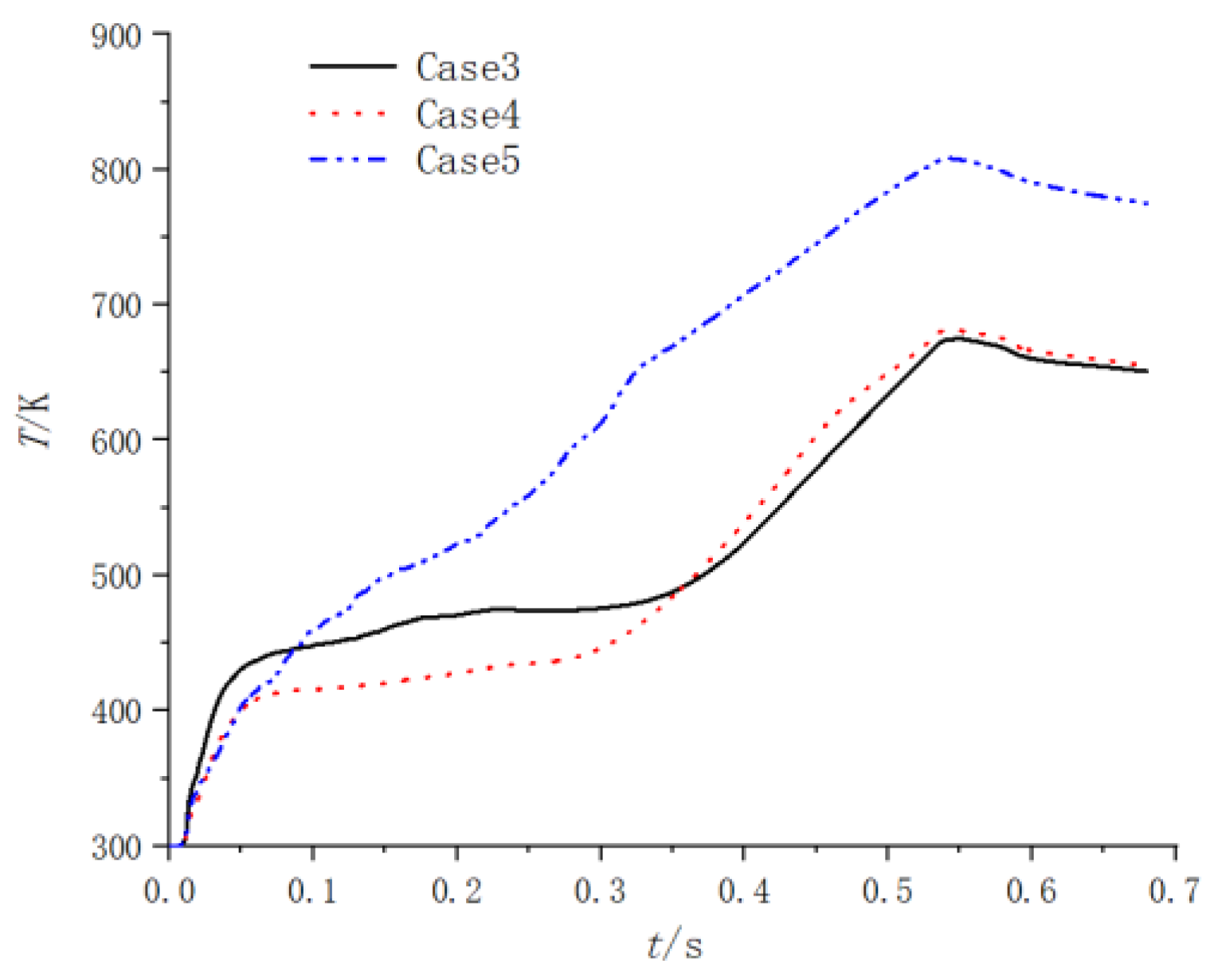
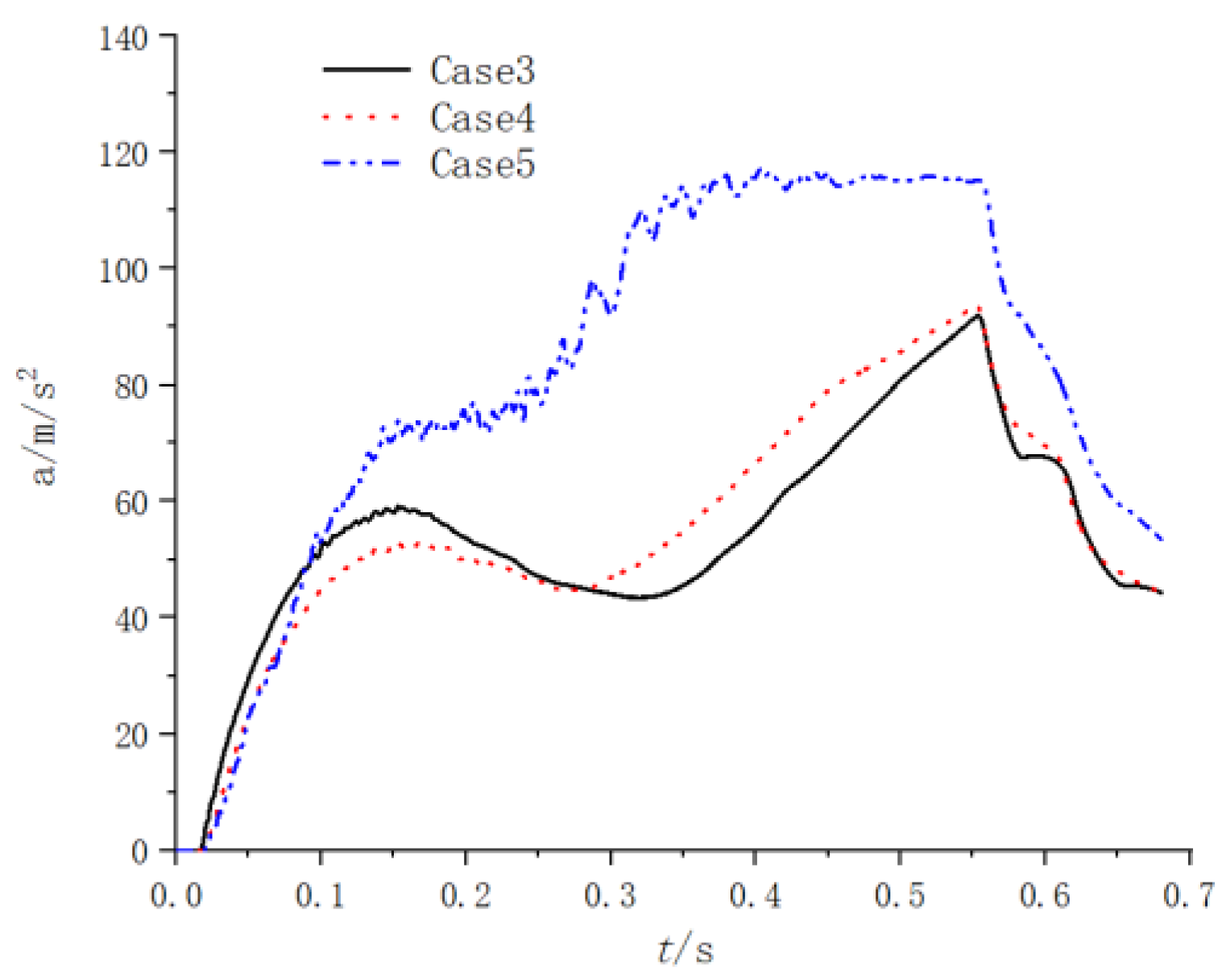
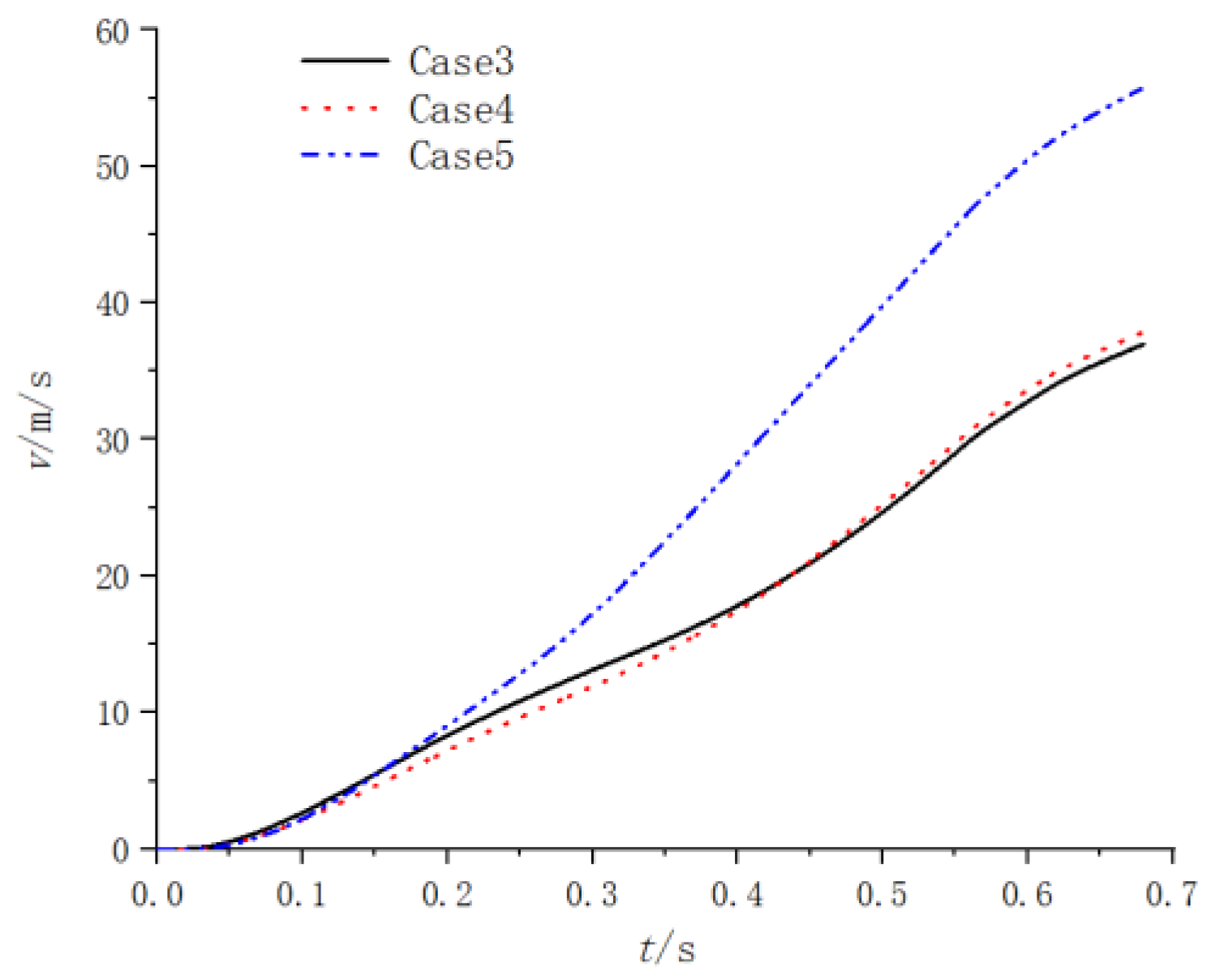
- The pressure distributions at two different times under three different throat diameters of the secondary nozzle are shown in Figure 39 and Figure 40. From Figure 39 and Figure 40, it can be seen that the pressure variation pattern within the entire device is basically consistent under three cases, and a significant water spray pressure difference is generated near the water spray hole. As the throat diameter decreases, the gas is limited when it reaches the secondary nozzle, and the pressure in the water chamber within the gas action area increases. Therefore, in case 5, where the throat diameter is the smallest, the spray pressure difference value inside and outside the spray hole is the largest.
- -
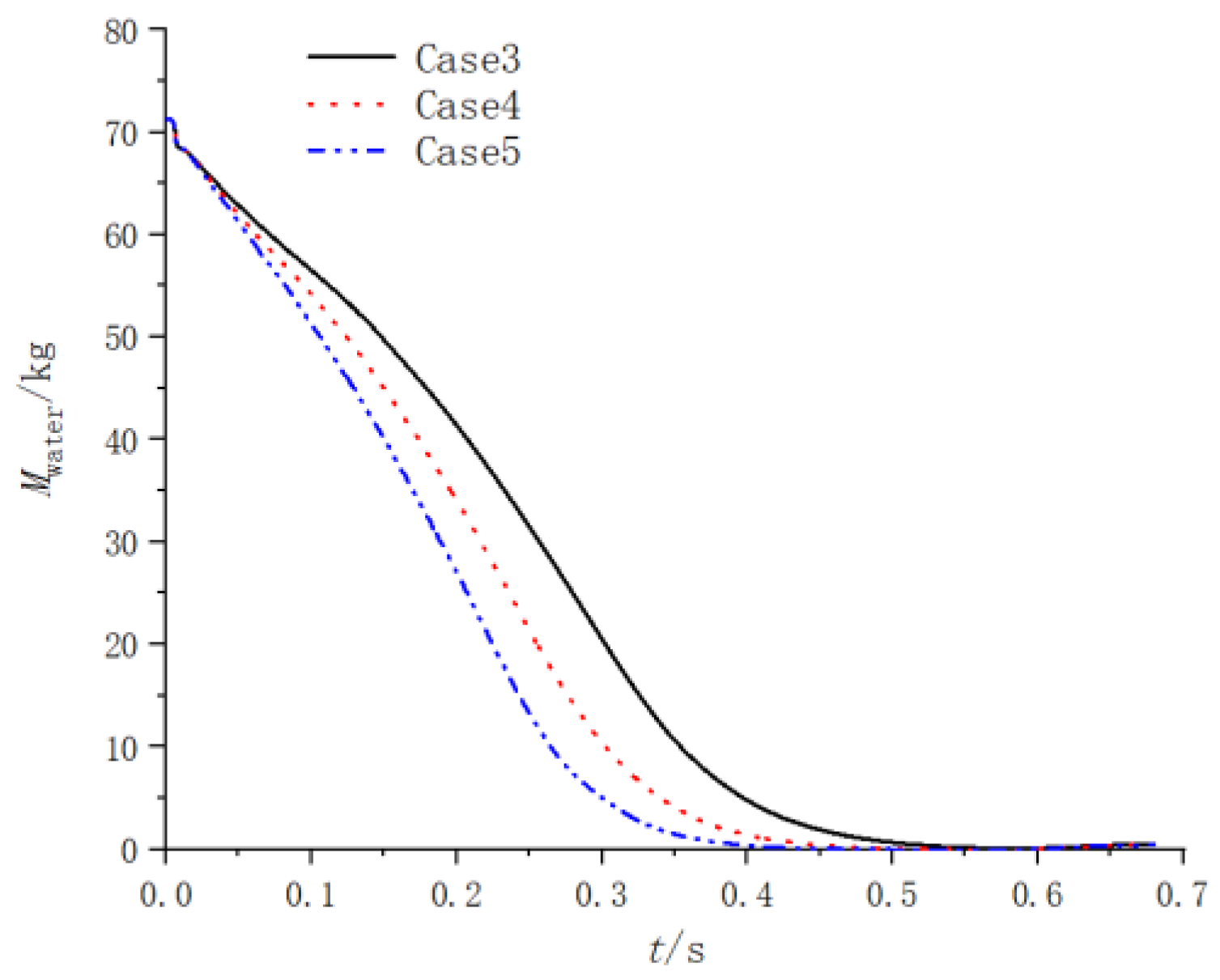
- The contours of water volume fraction of three different secondary nozzle throat diameters at two different time points are shown in Figure 43 and Figure 44. It can be seen from Figure 43 and Figure 44 that the increase in spray pressure directly leads to an increase in spray flow rate, and therefore the water consumption in the water chamber of case 5 is the fastest.
5. Conclusions
- (1)
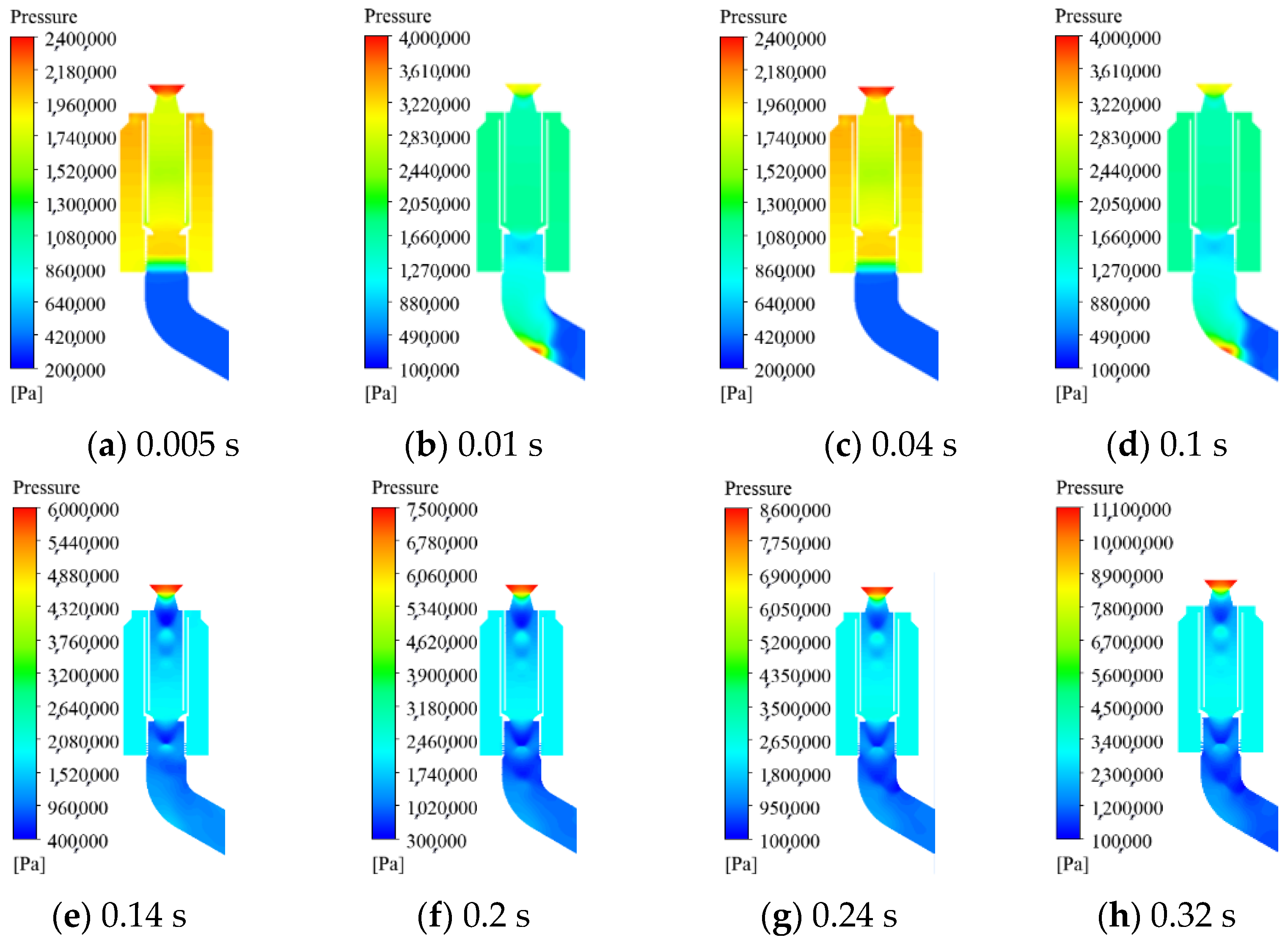
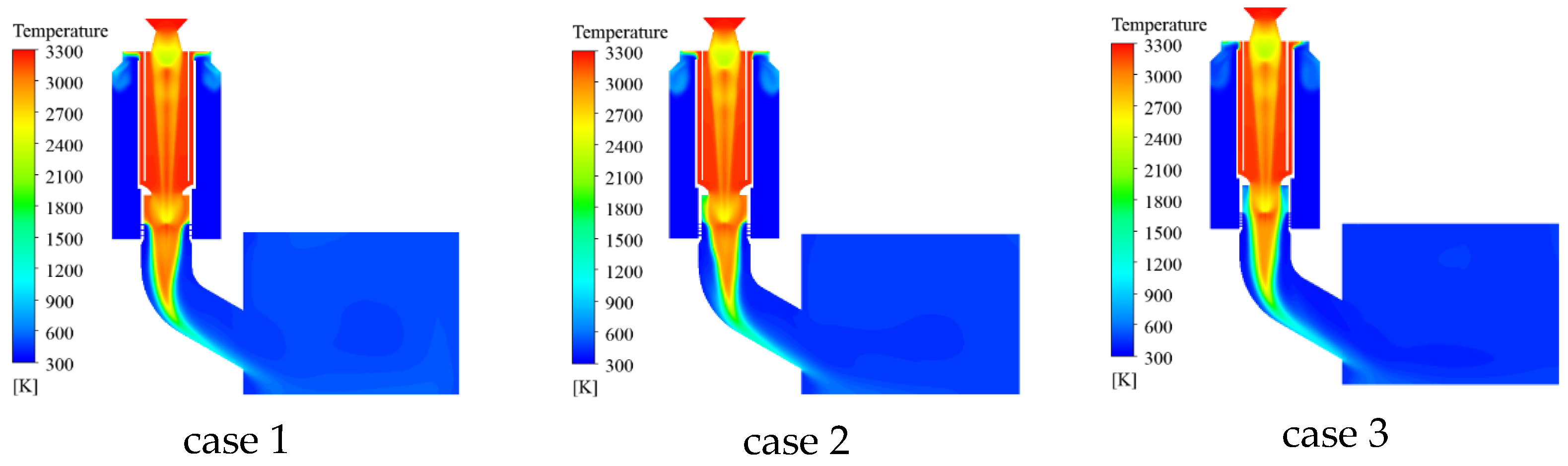
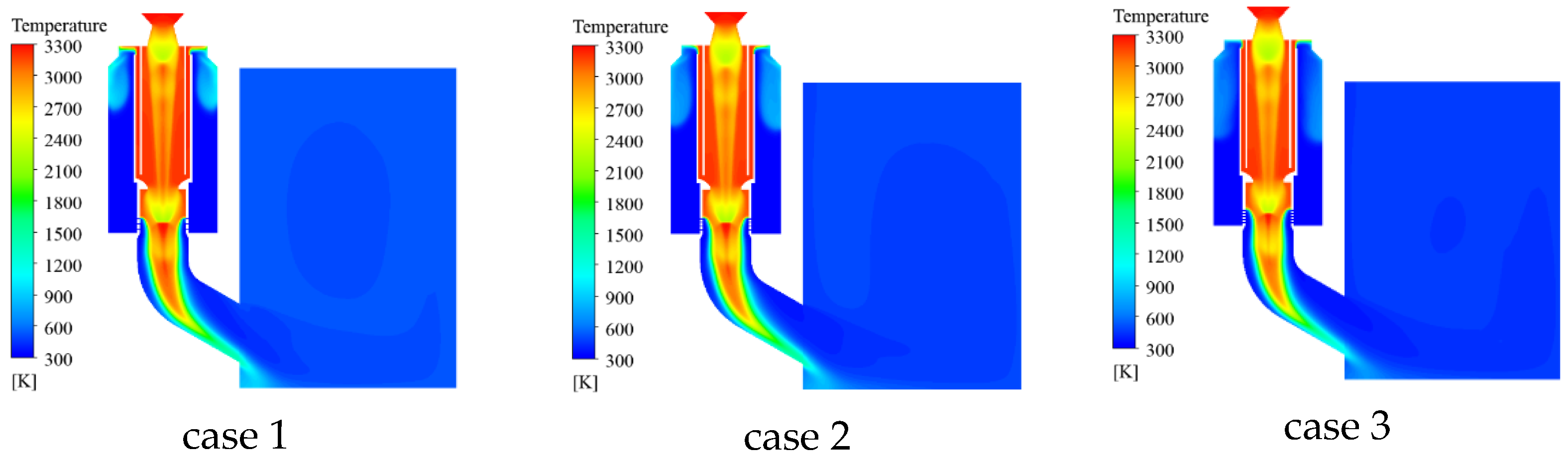
- During the operation of the gas–steam ejection device, an interaction between compression waves and expansion waves is noticed in the guide tube. The generation of steam has a compression effect on the gas. The water flowing out of the spray hole vaporizes when contacting the gas vapor. Due to the action of water flow, a slight compression is also noticed in the central area of the spray hole, leading to an increase in pressure. The gas jet near the spiracle is first compressed due to the increase in water flow, and then gradually expands outward. Although there are some changes in the spray holes and throats of the gas–steam ejection device, the heat entering the launcher is gradually reduced by the action of water flow. The average temperature inside the launcher is below 820 K. The total load acting on the missile body fluctuates.
- (2)
- With the total spray area fixed, the change in the diameter of the spray hole has little influence on the overall system performance; however, if the spray hole is too large, its load and temperature distribution become unstable. When the diameter of a single spray hole is fixed and the total spray area increases, the pressure and temperature of the gas–steam ejection devices decrease, and the water volume in the water chamber decreases faster. The pressure fluctuation of the ejection device is unstable, and the load of the projectile body is also more unstable. It is the total spray area of the spray holes, instead of the diameter or number of the spray holes, that has a major impact on the flow field and interior trajectory of the gas–steam ejection device.
- (3)
- When the number and size of the spray holes are held constant, the larger the size of the secondary nozzle throat, the smaller the spray pressure difference near the spray holes, the more stable the water vapor interface, and the slower the water consumption in the water chamber. For smaller throat diameters of the secondary nozzle, the pressure of the ejection device is high, the temperature rises sharply, and the acceleration change in the projectile body is unstable. The throat diameter of the secondary nozzles should be no less than 100 mm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sankaran, S.; Ignatius, J.K.; Ramkumar, R.; Satyanarayana, T.N.V.; Chakravarthy, S.R.; Panchapakesan, N.R. Suppression of high mach number rocket jet noise by water injection. J. Spacecr. Rocket. 2009, 46, 1164–1170. [Google Scholar] [CrossRef]
- Bruce, T.V.; Bachchan, N.; Peroomian, O. Multiphase Modeling of Water Injection on Flame Deflector. In Proceedings of the 21st AIAA Computational Fluid Dynamics Conference, San Diego, CA, USA, 24–27 June 2013; pp. 24–27. [Google Scholar]
- Song, J.; Song, X.H.; Cai, Q.; She, H.Q. Numerical analysis of wake field characteristics in rocket self-ejection low pressure chamber. J. Solid Rocket Technol. 2021, 44, 839–849. [Google Scholar]
- Zhang, S.K.; Yao, Y.; Meng, X.H. Simulation of the underwater environment missiles launched and the ballistic trajectory out of water. Tactical Missile Technol. 2015, 1, 102–107. [Google Scholar]
- Cheng, H.J.; Chen, L.; Zhao, Y.; Liu, Z. Smoothing effect influence of annular baffle structural parameter on the pressure impact of gas-ejection. J. Vib. Shock 2018, 37, 193–199, 258. [Google Scholar]
- Zhao, J.P.; Zhang, L.; She, H.Q.; Guo, J.B. Study on the influence of bypass clearance on gas ejection parameters. J. Aerosp. Power 2023, 38, 2407–2414. [Google Scholar]
- Li, R.F.; Le, G.G.; Ma, D.W. The influence of combustion product properties on gas-ejection interior ballistic and load characteristics. Acta Armamentarii 2016, 37, 245–252. [Google Scholar]
- Rui, S.Z.; Xing, Y.M.; Liang, C. Numerical simulation of gas-liquid two-phase flow in high temperature and high pressure supersonic cross flow. J. Aerosp. Power 2011, 26, 991–996. [Google Scholar]
- Zhang, R.J.; Bao, F.T. Comparison of internal ballistic properties between gas and steam launching systems in two different models of water injection. J. Solid Rocket Technol. 2005, 28, 5–9. [Google Scholar]
- Hu, X.L.; Le, G.G.; Ma, D.W. Numerical study of gas-steam ejection gas-liquid two-phase flow field under water. J. Aerosp. Power 2015, 30, 164–172. [Google Scholar]
- Xiao, H.B.; Zhao, S.P. Numerical simulation of the complex flow field in combustion gas-steam launching system. J. Solid Rocket Technol. 2009, 32, 392–395. [Google Scholar]
- Yuan, Z.F. Similitude method in the interior ballistics of ejectors. Acta Armamentarii 1987, 1, 8–18. [Google Scholar]
- Zhao, S.P.; Bao, F.T. Analysis of several coefficients of interior ballistic evaluation for gas and steam launching system. J. Solid Rocket Technol. 2003, 26, 7–10. [Google Scholar]
- Ni, H.C. Changeable depth launch and energy adjustable ejection power system. Shipborne Weapons 1998, 6, 16–25. [Google Scholar]
- Liu, B.W.; Jiang, Y. Influence of vaporization effect on gas-liquid two-phase flow field of ejection in combustion gas and vapor mode. J. Solid Rocket Technol. 2014, 2, 156–160. [Google Scholar]
- Hui, W.H.; Yang, Y.L.; Ma, Y.J. Multiphase vaporization calculation and influence analysis of gas-steam ejection water injection process. J. Proj. Rocket. Missiles Guid. 2021, 41, 113–116, 119. [Google Scholar]
- Yan, F.; Shi, S.Y.; Jiang, Y. Research on interior ballistic of gas-steam ejection. Ship Sci. Technol. 2017, 39, 118–122. [Google Scholar]
- Bai, J.H.; Hu, X.B. Impact of injection angle and initial particles diameter on interior flow characteristic of silo. J. Solid Rocket Technol. 2013, 36, 165–169. [Google Scholar]
- Shi, Q.S.; Qiang, X.W.; Wang, H.; He, D.N.; Shen, B.L. Research on the law of the water-spray pressure difference in the gas-steam ejection power system. Ship Sci. Technol. 2020, 42, 157–160, 169. [Google Scholar]
- Hu, X.L.; Li, R.F.; Xie, N.G.; Liu, Q.Y.; Ma, D.W. Study on vaporization mechanism of gas-steam ejection power equipment containing water chamber. J. Solid Rocket Technol. 2018, 41, 792–798. [Google Scholar]
- Belhadj Mohamed, A.; Orfi, J. Evaporation of water/ammonia binary liquid film by mixed convection inside isothermal vertical plates. Desalin. Water Treat. Sci. Eng. 2013, 51, 1966–1972. [Google Scholar] [CrossRef]
- Zhao, X.; Cheng, H.J.; Zhao, Y.; Gao, L. Influence of nozzle structure parameters on interior ballistic property of gas ejection. J. Proj. Rocket. Missiles Guid. 2020, 40, 83–88. [Google Scholar]
- Ishii, M. Thermo-Fluid Dynamic Theory of Two-Phase Flow. NASA Sti/Recon Tech. Rep. A 1975, 75, 29657. [Google Scholar]
- Zhao, S.P. Study of calculation model of launching interior trajectory. Ship Sci. Technol. 2007, 29, 130–133. [Google Scholar]
- Xu, X.W.; Li, H.; Bai, Y. Numerical Simulation of Missile Vertical Thermal Launch Based on Moving Grid Layering Method. Ship Electron. Eng. 2022, 42, 98–101. [Google Scholar]
- Guo, J.Y.; Hu, X.L.; Sun, C.B.; Zhang, X.F.; Ma, D.W. Chamber width influence on gas-ejection load. J. Ordnance Equip. Eng. 2016, 37, 42–44, 94. [Google Scholar]
- Zhao, X.; Cheng, H.J.; Zhao, Y. Comparative analysis of smooth pressure effect between different obstacles on gas ejection. Tactical Missile Technol. 2020, 2, 44–50. [Google Scholar]
- Cheng, H.J.; Zhao, X.; Zhao, Y.; Guo, L. Influence of structural parameters of diversion cone on smooth effect of gas ejection bottom pressure impact. J. Propuls. Technol. 2019, 40, 2444–2453. [Google Scholar]
- Wang, L.Q.; Hao, Z.R.; Wu, D.Z. Numerical simulation of initial flow field of underwater gas jet. J. Eng. Thermophys. 2009, 30, 1132–1135. [Google Scholar]
- Cai, Z.W.; Kang, H.F.; Zhao, M.M. Study on launch dynamics of shipborne missile system. Sh. Sci. Technol. 2021, 43, 10–12. [Google Scholar]
- Li, E.Y.; Le, G.G.; Ma, D.W.; Xie, B.X. Numerical study on factors of interior ballistic for low-temperature gas-ejection. J. Aerosp. Power 2017, 32, 1296–1306. [Google Scholar]
- Cheng, H.J.; Chen, L.; Lin, R. Gas ejection technology of ballistic missile. J. Proj. Rocket. Missiles Guid. 2017, 37, 109–112. [Google Scholar]
- Pan, X.; Jiang, Y.; Wang, B.M.; Ren, Y.B. Dynamics characteristics and influencing factors of multistage canister ejection of rockets. Acta Armamentarii 2022, 43, 1277–1287. [Google Scholar]
- Chen, Z.; Guo, X.; Yu, R.; Yu, J.; Wang, Z.H.; Wu, M.; Deng, K.Q.; Pang, A.M. Research on interior ballistic performance of piston-type horizontal ejection device. J. Solid Rocket Technol. 2022, 45, 316–321. [Google Scholar]
- Zhao, C.Y.; Jiang, Y.; Wang, H.Z. Dynamics Analysis of the Vehicle-mounted Missile System Launching on the Move Based on Multi-body Dynamics. J. Proj. Rockets Missiles Guid. 2020, 40, 91–93. [Google Scholar]
- Zhao, X.; Cheng, H.J.; Zhao, Y.; Gao, L. Influence of diversion cone on gas-ejection internal ballistic. J. Solid Rocket Technol. 2020, 43, 243–249. [Google Scholar]
- Wang, H.H.; Jiang, Y.; Yang, C.Z.; Niu, Y.S. Influence of module gas pressure difference on ejection of multistage piston cylinder ejection. J. Proj. Rocket. Missiles Guid. 2022, 42, 78–84. [Google Scholar]
- Koutsourakis, N.; Bartzis, J.G.; Markatos, N.C. Evaluation of reynolds stress, k-ε and RNG k-ε turbulence models in street canyon flows using various experimental datasets. Environ. Fluid Mech. 2012, 12, 379–403. [Google Scholar]
- Li, J.; Jiang, Y.; Yu, S.Z.; Zhou, F. Cooling effect of water injection on a high-temperature supersonic jet. Energies 2015, 8, 13194–13210. [Google Scholar] [CrossRef]
- Kandula, M.; Lonergan, M. Effective jet properties for the estimation of turbulent mixing noise reduction by water injection. In Proceedings of the 13th AIAA (American Institute of Aeronautics and Astronautics)/CEAS Aeroacoustics Conference (28th AIAA Aeroacoustics Conference), Rome, Italy, 21–23 May 2007; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2007. [Google Scholar]
- Berlemont, A.; Desjonqueres, P.; Gouesbet, G. Particlelagrangian simulation in turbulent flows. Int. J. Multiph. Flow 1990, 16, 19–34. [Google Scholar] [CrossRef]
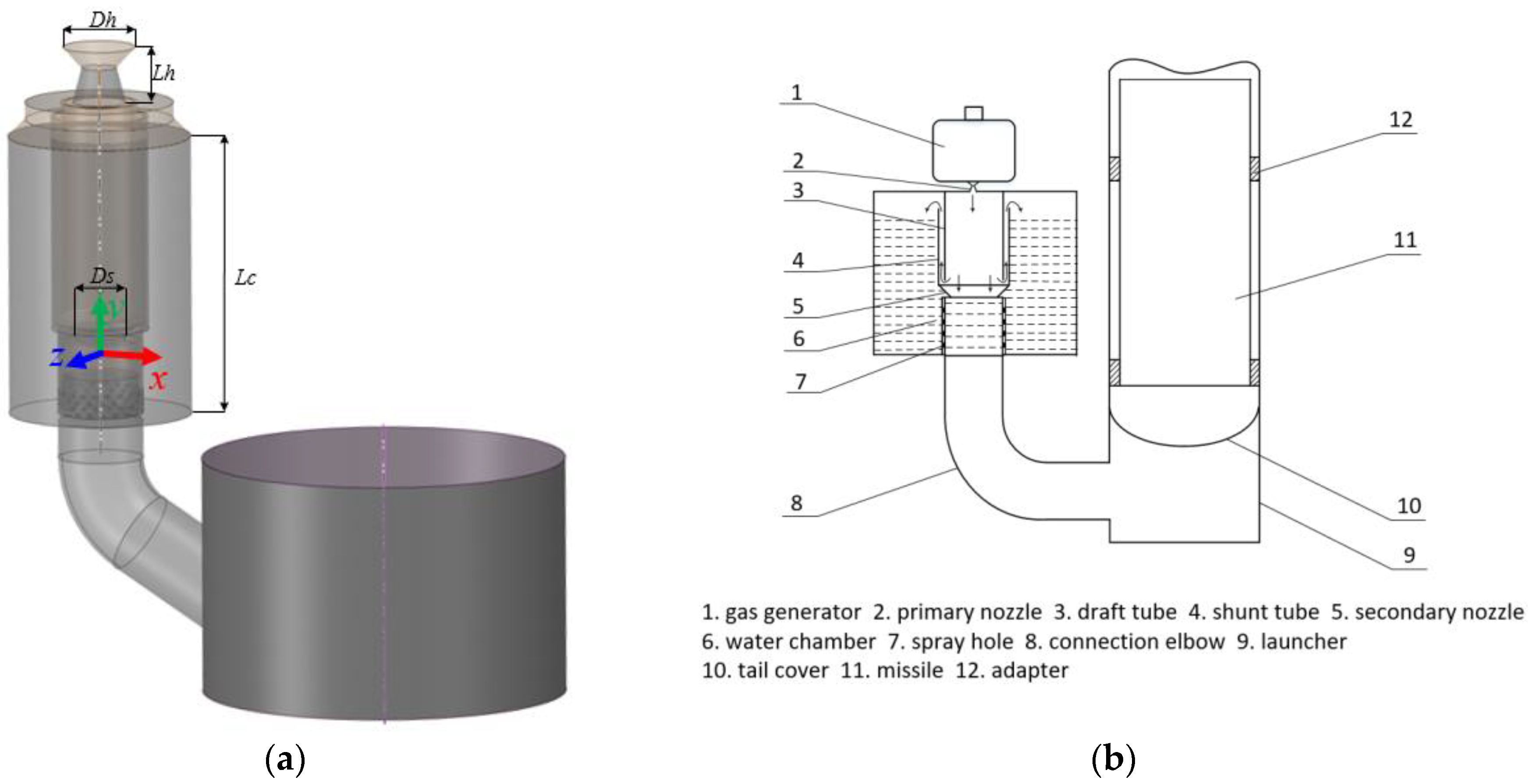


















| Geometric Dimension | Geometric Length |
|---|---|
| First stage nozzle inlet diameter | Dh |
| Length of first stage nozzle | Lh |
| Water chamber length | Lc |
| Second stage nozzle diameter | Ds |
| Monitoring Point | T1 | T2 | T3 | T4 |
|---|---|---|---|---|
| Experimental temperature (K) | 471.36 | 420.38 | 460.26 | 413.59 |
| Simulation temperature (K) | 456.61 | 405.73 | 445.32 | 407.24 |
| Error | 3.13% | 3.48% | 3.25% | 1.54% |
| Case | Spray Hole Diameter d/mm | Number of Rows of Spray Holes | Number of Roles per Row | Secondary Throat Diameter/mm |
|---|---|---|---|---|
| 1 | 4 | 6 | 50 | 120 |
| 2 | 4 | 8 | 50 | 120 |
| 3 | 4 | 10 | 50 | 120 |
| 4 | 4 | 10 | 50 | 110 |
| 5 | 4 | 10 | 50 | 100 |
| 6 | 6 | 7 | 32 | 120 |
| 7 | 8 | 5 | 25 | 120 |
| 8 | 10 | 4 | 20 | 120 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Li, R.; Chen, X.; Gou, J.; Li, B.; Le, G. Numerical Analysis on Effect of Structural Parameters on Flow Field and Internal Trajectory in Gas–Steam Ejection Systems. J. Mar. Sci. Eng. 2023, 11, 1937. https://doi.org/10.3390/jmse11101937
Liu B, Li R, Chen X, Gou J, Li B, Le G. Numerical Analysis on Effect of Structural Parameters on Flow Field and Internal Trajectory in Gas–Steam Ejection Systems. Journal of Marine Science and Engineering. 2023; 11(10):1937. https://doi.org/10.3390/jmse11101937
Chicago/Turabian StyleLiu, Bing, Renfeng Li, Xiaohan Chen, Jinlan Gou, Bangming Li, and Guigao Le. 2023. "Numerical Analysis on Effect of Structural Parameters on Flow Field and Internal Trajectory in Gas–Steam Ejection Systems" Journal of Marine Science and Engineering 11, no. 10: 1937. https://doi.org/10.3390/jmse11101937
APA StyleLiu, B., Li, R., Chen, X., Gou, J., Li, B., & Le, G. (2023). Numerical Analysis on Effect of Structural Parameters on Flow Field and Internal Trajectory in Gas–Steam Ejection Systems. Journal of Marine Science and Engineering, 11(10), 1937. https://doi.org/10.3390/jmse11101937







