Acoustic Field Radiation Prediction and Verification of Underwater Vehicles under a Free Surface
Abstract
:1. Introduction
2. Theoretical Foundations
2.1. Reynolds-Averaged Navier–Stokes Equations (RANS)
2.2. SST k-ω Turbulence Model
2.3. Lighthill Acoustic Analogy
2.4. Ffowcs Williams–Hawkings Acoustic Analogy
2.5. Volume of Fluid Method
3. Simulation and Verification of the Propeller
3.1. Geometric Model
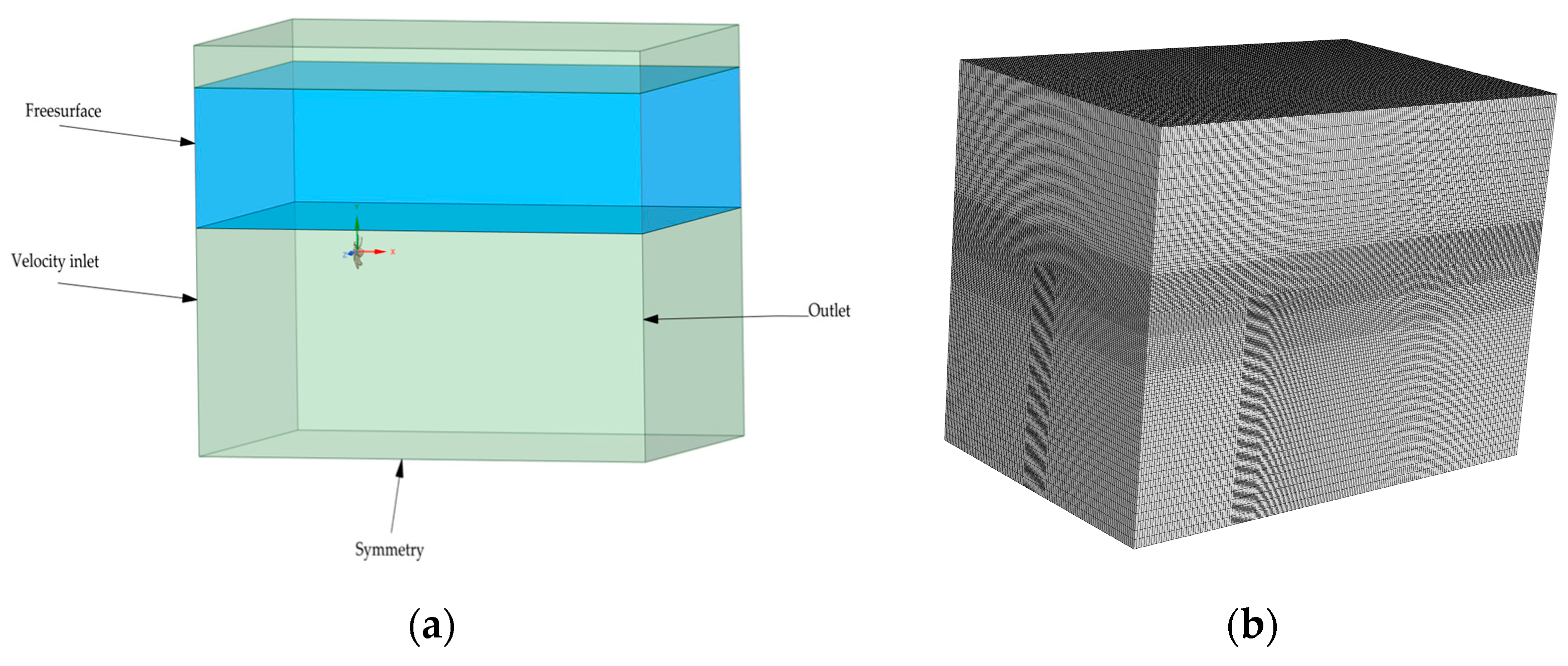
3.2. Setting Boundary Conditions for the Propeller Model
3.3. Propeller Performance Verification
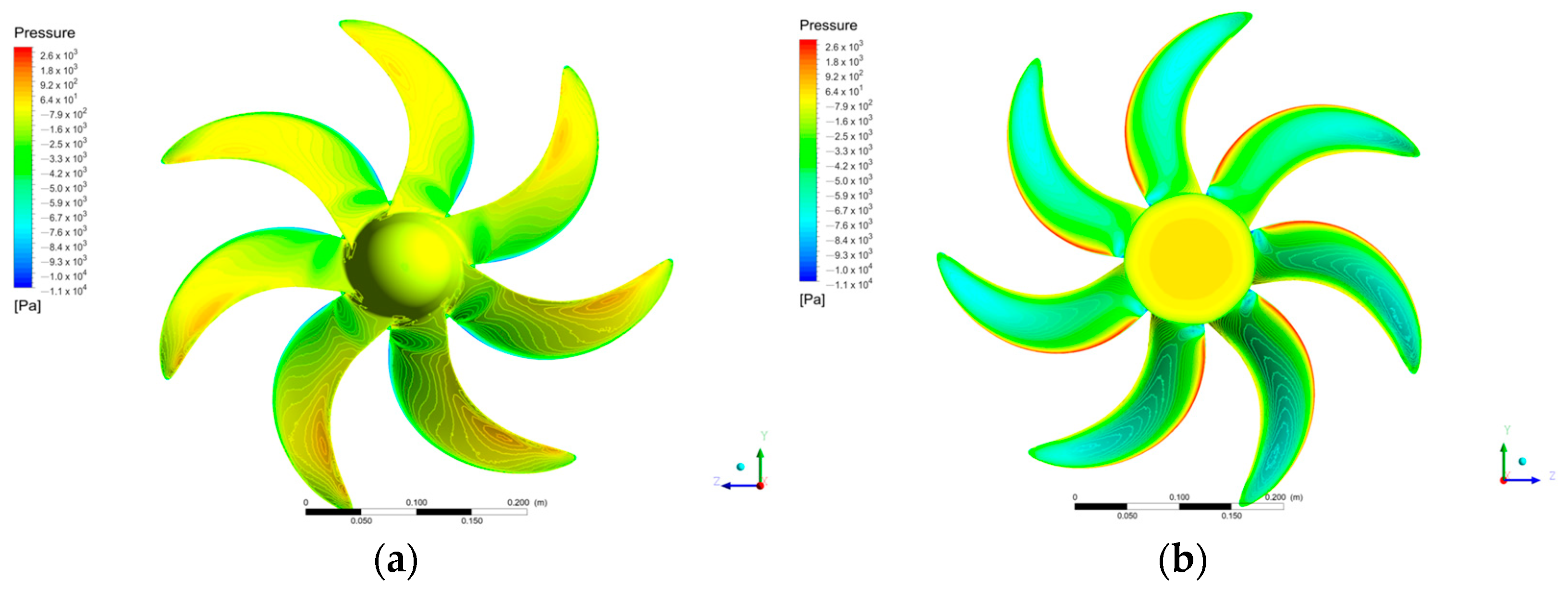
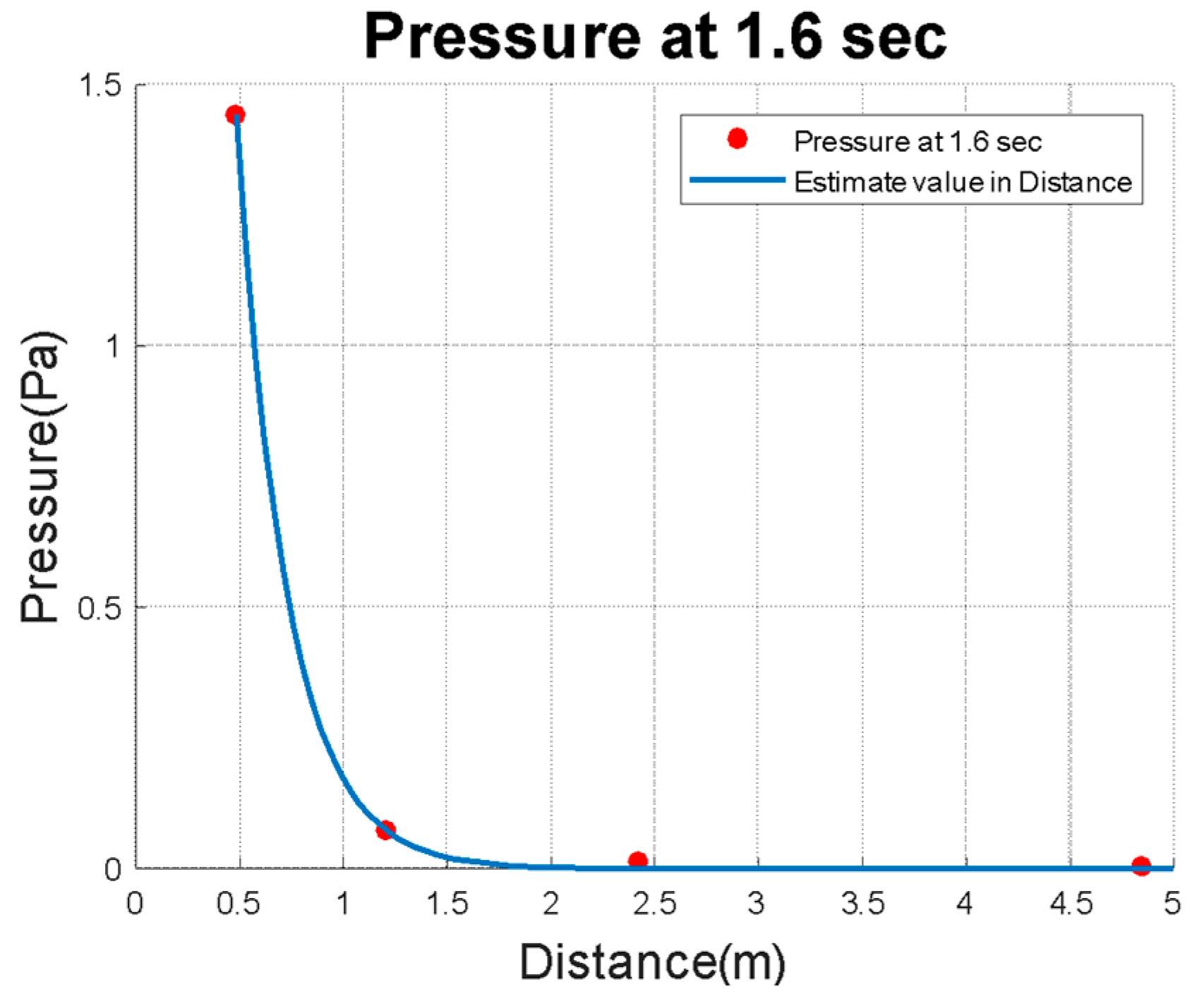
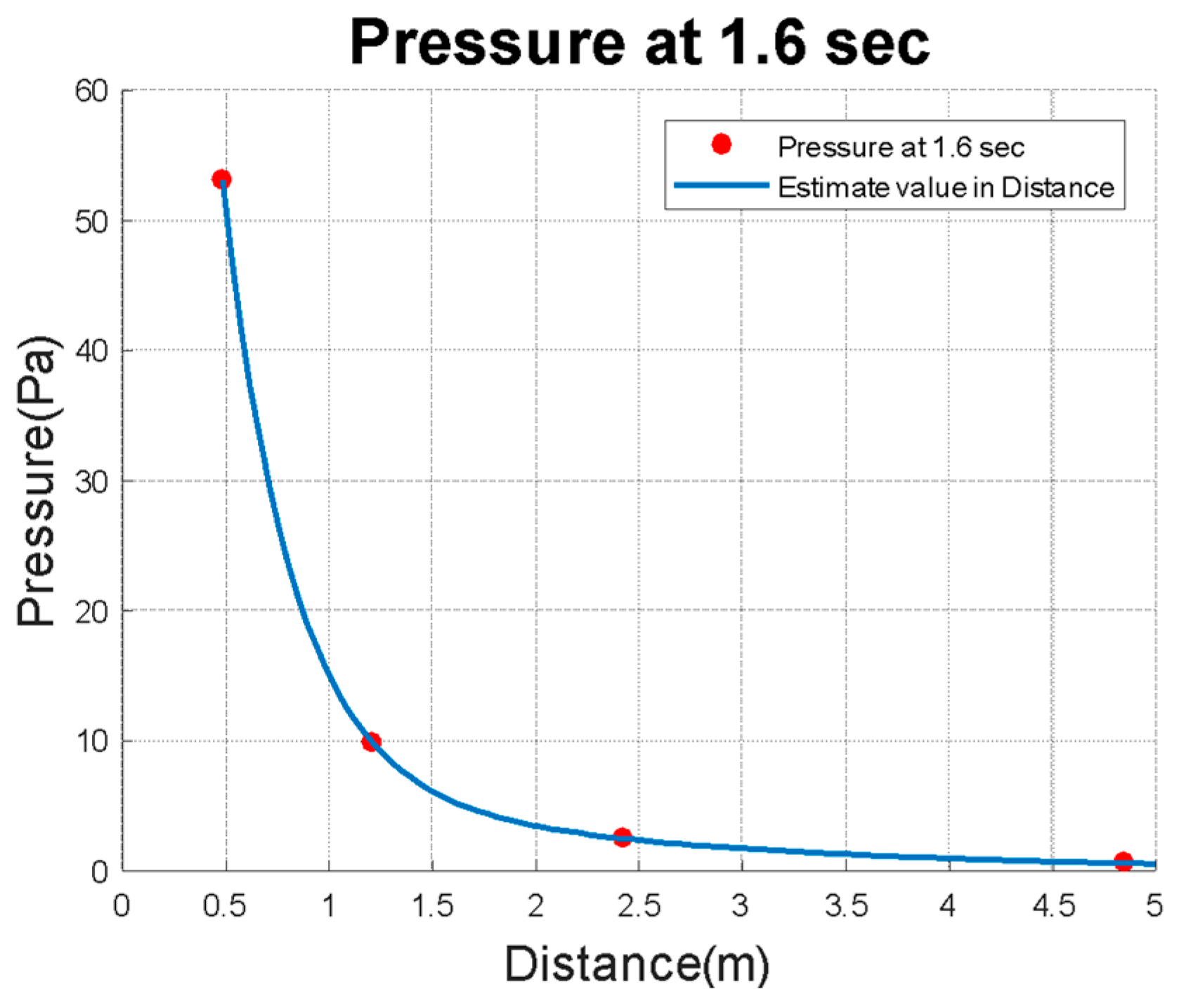
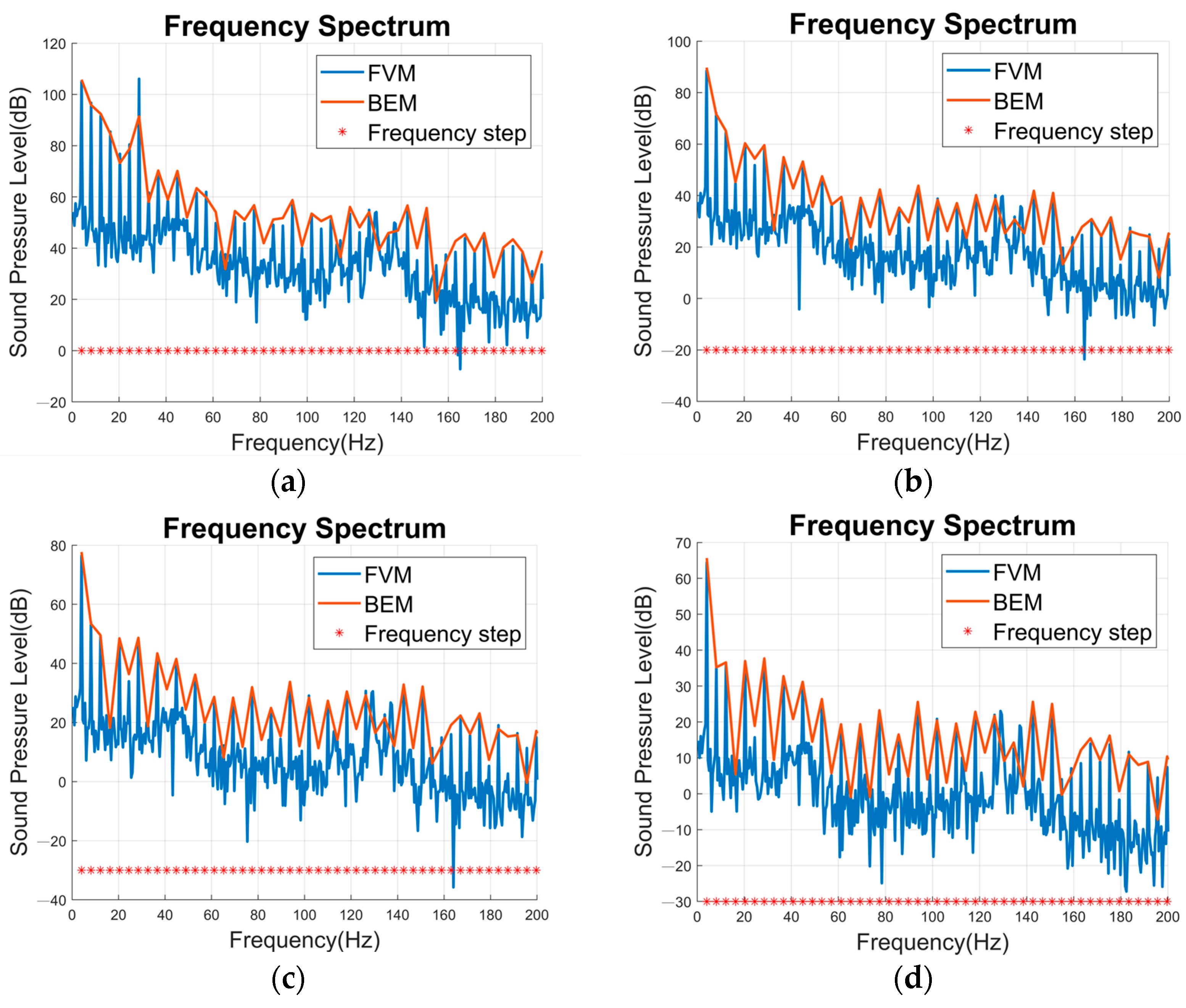
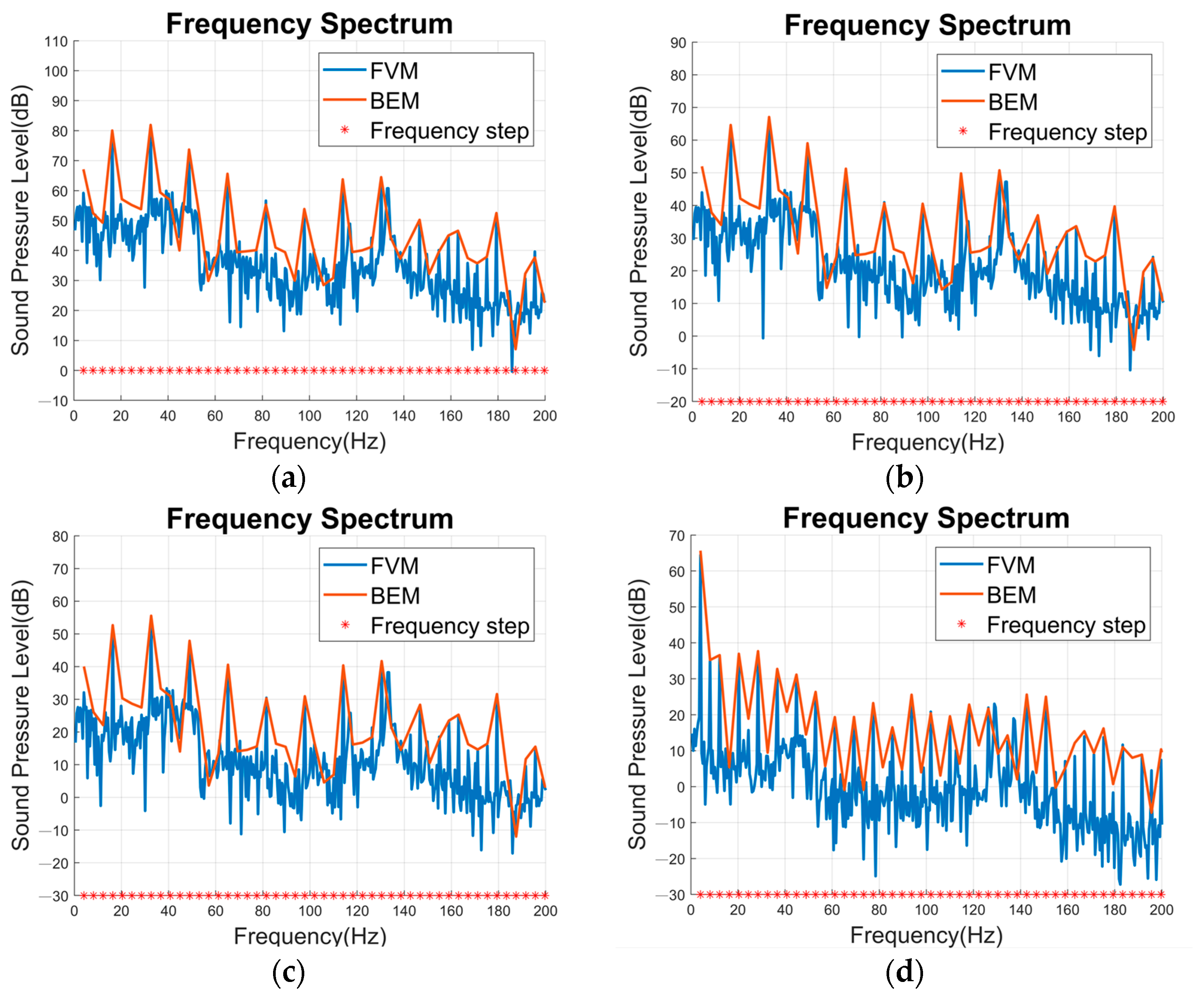
3.4. Calculation and Analysis of the Sound Field Radiation of the Propeller
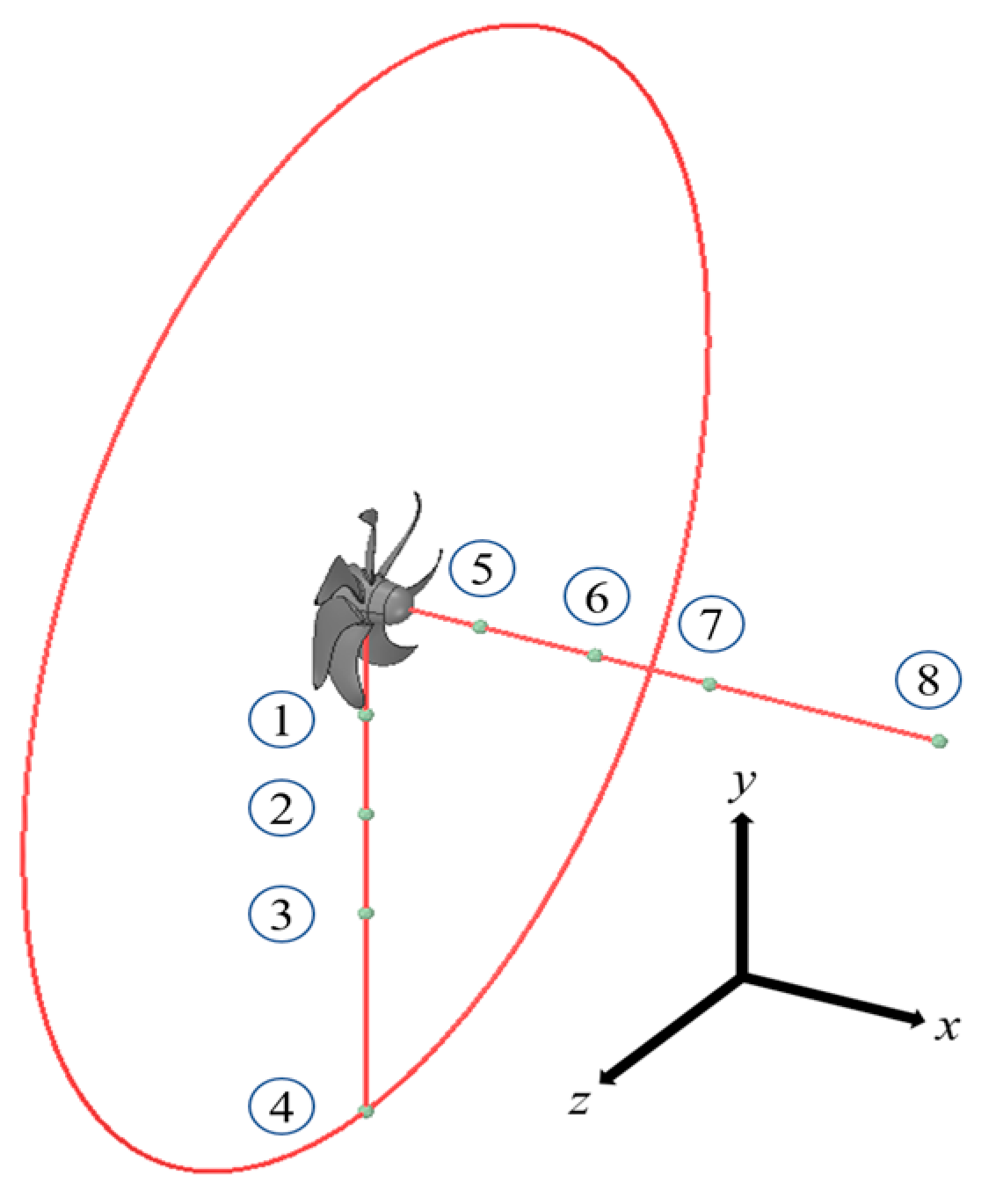
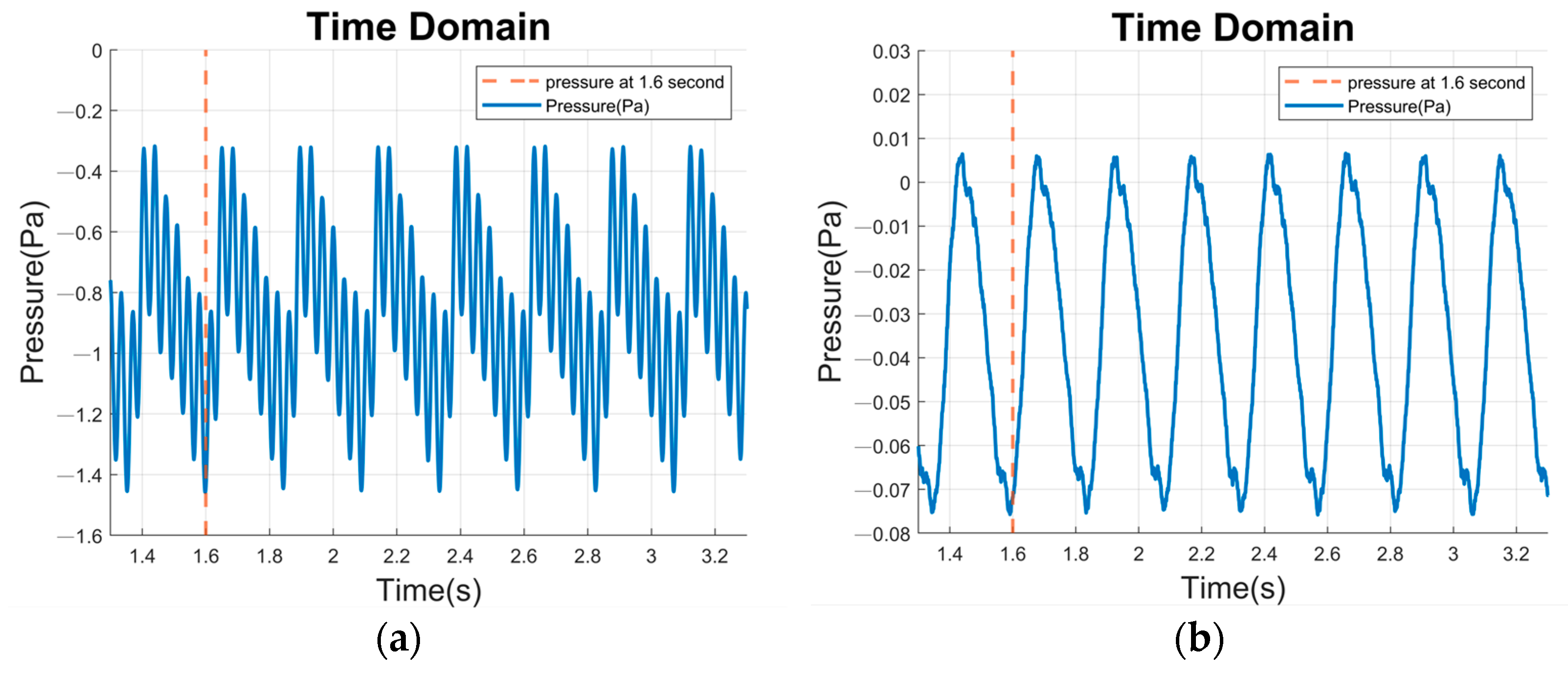
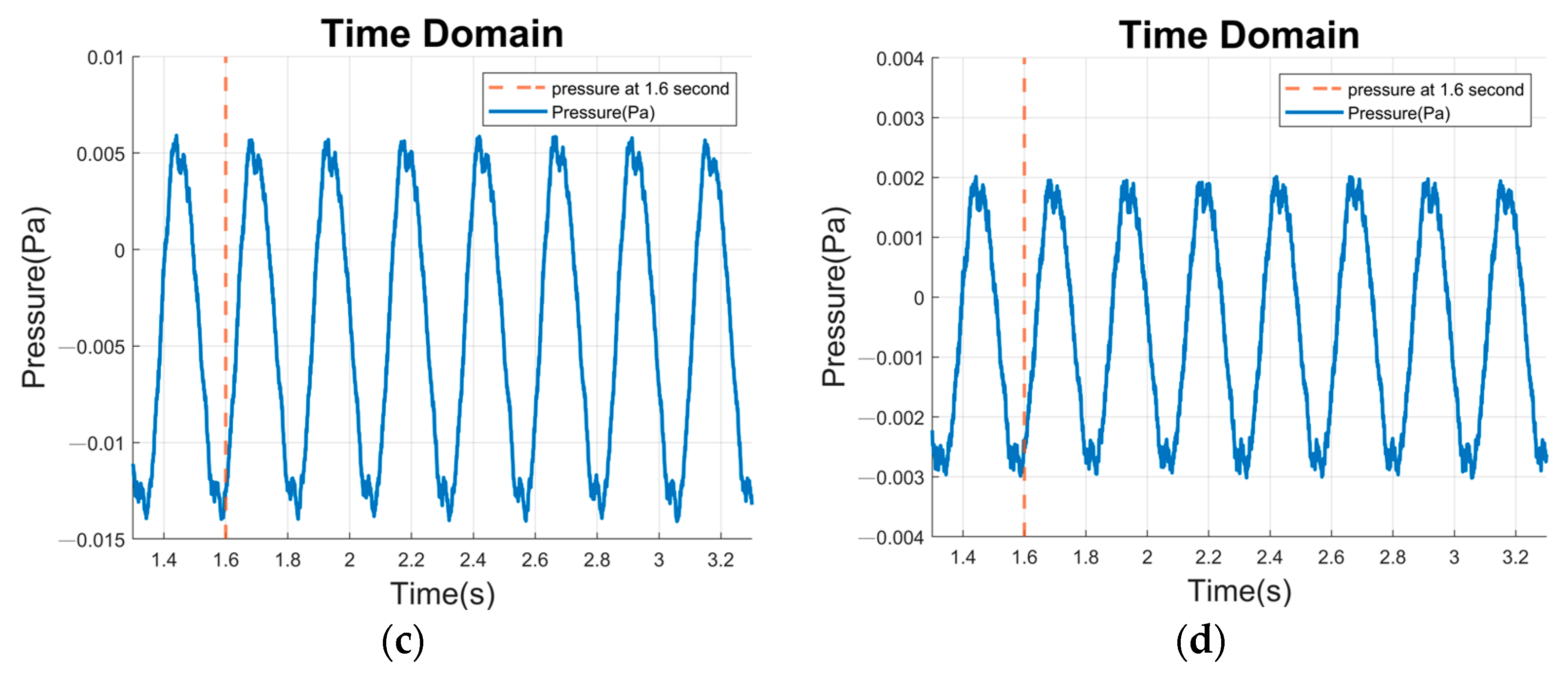
3.5. Sound Field Radiation Verification
4. Analysis of the Radiation Sound Field of Underwater Vehicles
4.1. Geometric Model Studied
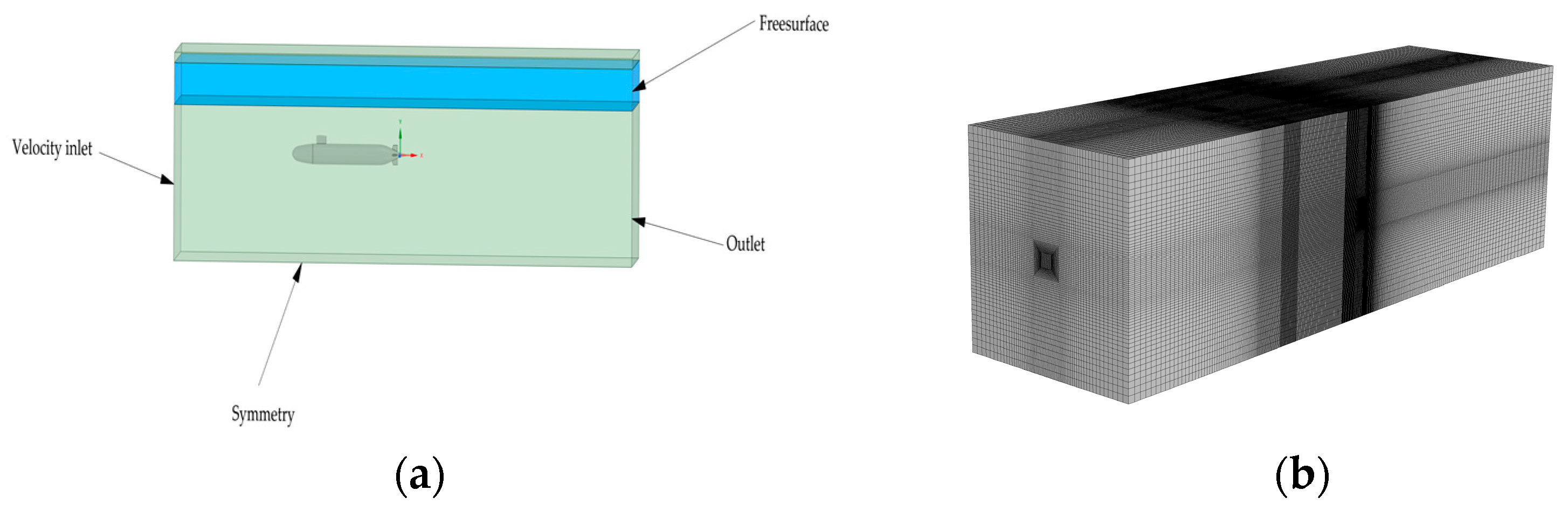
4.2. Boundary Condition Setting for the Underwater Vehicle
4.3. Analysis and Verification of Hull Resistance
4.4. Simulation Verification of Underwater Vehicle Self-Propulsion Test
4.5. Propeller Performance Analysis of the Free Surface Effect
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Song, K.W.; Guo, C.Y.; Wang, C.; Sun, C.; Li, P.; Wang, W. Numerical analysis of the effects of stern flaps on ship resistance and propulsion performance. Ocean Eng. 2019, 193, 106621. [Google Scholar] [CrossRef]
- Moura, N.D.; Seixas, J.; Ramos, R. Passive sonar signal detection and classification based on independent component analysis. In Sonar Systems; InTech: Makati, Philippines, 2011. [Google Scholar]
- Wittekind, D.; Schuster, M. Propeller cavitation noise and background noise in the sea. Ocean Eng. 2016, 120, 116–121. [Google Scholar] [CrossRef]
- Groves, N.C.; Huang, T.T.; Chang, M.S. Geometric Characteristics of DARPA (Defense Advanced Research Projects Agency) SUBOFF Models (DTRC Model Numbers 5470 and 5471); David W Taylor Naval Ship Research and Development Center: Carderock, MD, USA, 1989. [Google Scholar]
- Liu, H.L.; Huang, T.T. Summary of DARPA Suboff Experimental Program Data; Naval Surface Warfare Center, Carderock Division (NSWCCD): Carderock, MD, USA, 1998. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar]
- Chase, N. Simulations of the DARPA Suboff Submarine including Self-Propulsion with the E1619 Propeller. Master’s Thesis, University of Iowa, Iowa, IA, USA, 2012. [Google Scholar]
- Choi, J.H. Numerical Analysis on Underwater Propeller Noise with Hull-Appendage Effect. Master’s Thesis, Seoul National University, Seoul, Republic of Korea, 2019. [Google Scholar]
- Felice, F.D.; Felli, F.M.; Liefvendahl, M.; Svennberg, U. Numerical and experimental analysis of the wake behavior of a generic submarine propeller. In Proceedings of the First International Symposium on Marine Propulsors, Trondheim, Norway, 22–24 June 2009. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comp. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Califano, A.; Steen, S. Numerical simulations of a fully submerged propeller subject to ventilation. Ocean Eng. 2011, 38, 1582–1599. [Google Scholar] [CrossRef]
- Paik, K.J. Numerical study on the hydrodynamic characteristics of a propeller operating beneath a free surface. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 655–667. [Google Scholar] [CrossRef]
- Eom, M.J.; Jang, Y.H.; Paik, K.J. A study on the propeller open water performance due to immersion depth and regular wave. Ocean Eng. 2021, 219, 108265. [Google Scholar] [CrossRef]
- Eom, M.J.; Paik, K.J.; Jang, Y.H.; Ha, J.Y.; Park, D.W. A method for predicting propeller performance considering ship motion in regular waves. Ocean Eng. 2021, 232, 109135. [Google Scholar] [CrossRef]
- Cianferra, M.; Armenio, V. Scaling properties of the Ffowcs-Williams and Hawkings equation for complex acoustic source close to a free surface. J. Fluid Mech. 2021, 927, A2. [Google Scholar] [CrossRef]
- Hu, J.; Ning, X.S.; Zhao, W.; Li, F.G.; Ma, J.C.; Zhang, W.P.; Sun, S.L.; Zou, M.S.; Lin, C.G. Numerical simulation of the capitating noise of contra-rotating propellers based on detached eddy simulation and the Ffowcs Williams–Hawkings acoustics equation. Phys. Fluids 2021, 33, 116–121. [Google Scholar] [CrossRef]
- Noughabi, A.K.; Bayati, M.; Tadjfar, M. Investigation of cavitation phenomena on noise of underwater Propeller. In Proceedings of the ASME 2017 Fluids Engineering Division Summer Meeting, Waikoloa, HI, USA, 30 July–3 August 2017; pp. 1–8. [Google Scholar]
- TM-2007-214853; Farassat, F. Derivation of Formulations 1 and 1A of Farassat. NASA: Washington, DC, USA, 2007.
- Koushan, K.; Spence, S.J.; Hamstad, T. Experimental investigation of the effect of waves and ventilation on thruster loadings. In Proceedings of the 1st International Symposium on Marine Propulsors, Trondheim, Norway, 22–24 June 2009. [Google Scholar]
- Paik, B.G.; Lee, C.M.; Lee, S.J. Comparative measurements on the flow structure of a marine propeller wake between an open free surface and closed surface flows. J. Mar. Sci. Technol. 2005, 10, 123–130. [Google Scholar] [CrossRef]
- Kim, S.; Kinnas, S.A. Prediction of acoustic field induced by a tidal turbine under straight or oblique inflow via a BEM/FW-H approach. Ocean Syst. Eng. 2023, 13, 147–172. [Google Scholar]
- Yao, Q.; Zhang, Y.O.; Li, Y.F.; Zhang, T. Similarity analysis of the flow-induced noise of a benchmark submarine. Front. Phys. 2023, 11, 270. [Google Scholar]
- Kimmerl, J.; Moustafa, A.M. Visualization of underwater radiated noise in the near-and far-field of a propeller-hull configuration using CFD simulation results. J. Mar. Sci. Eng. 2023, 11, 834. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Cañada, CA, USA, 1998. [Google Scholar]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Menter, F.; Ferreira, J.C.; Esch, T.; Konno, B. The SST turbulence model with improved wall treatment for heat transfer predictions in gas turbines. In Proceedings of the International Gas Turbine Congress, Tokyo, Japan, 2–7 November 2003. [Google Scholar]
- Menter, F.R. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Lighthill, M.J. On sound generated aerodynamically I. General theory. Philos. Trans. Ser. A Math. Phys. Sci. 1952, 211, 564–587. [Google Scholar]
- Lighthill, M.J. On sound generated aerodynamically II. Turbulence as a source of sound. Philos. Trans. Ser. A Math. Phys. Sci. 1954, 212, 1–32. [Google Scholar]
- Williams, J.F.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Philos. Trans. Ser. A Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar]
- Desmet, W.; Sas, P.; Vandepitte, D. Numerical Acoustics Theoretical Manual; LMS International: Leuven, Belgium, 1998. [Google Scholar]
- Geng, F.; Kalkman, I.; Suiker, A.S.J.; Blocken, B. Sensitivity analysis of airfoil aerodynamics during pitching motion at a Reynolds number of 1.35 × 105. J. Wind Eng. Ind. Aerodyn. 2018, 183, 315–332. [Google Scholar]
- Guo, H.; Guo, C.Y.; Hu, J.; Lin, J.F.; Zhong, X.H. Influence of jet flow on the hydrodynamic and noise performance of propeller. Phys. Fluids 2021, 33, 065123. [Google Scholar]
- Chiu, S.J. Hull Shape Optimization Design and Hydrodynamics Analysis of an Underwater Vehicle. Master’s Thesis, National Taiwan Ocean University, Taiwan, China, 2018. [Google Scholar]
- Liu, L.W.; Chen, M.X.; Yu, J.W.; Zhang, Z.G. Full-scale simulation of self-propulsion for a free-running submarine. Phys. Fluids 2021, 33, 047103. [Google Scholar]
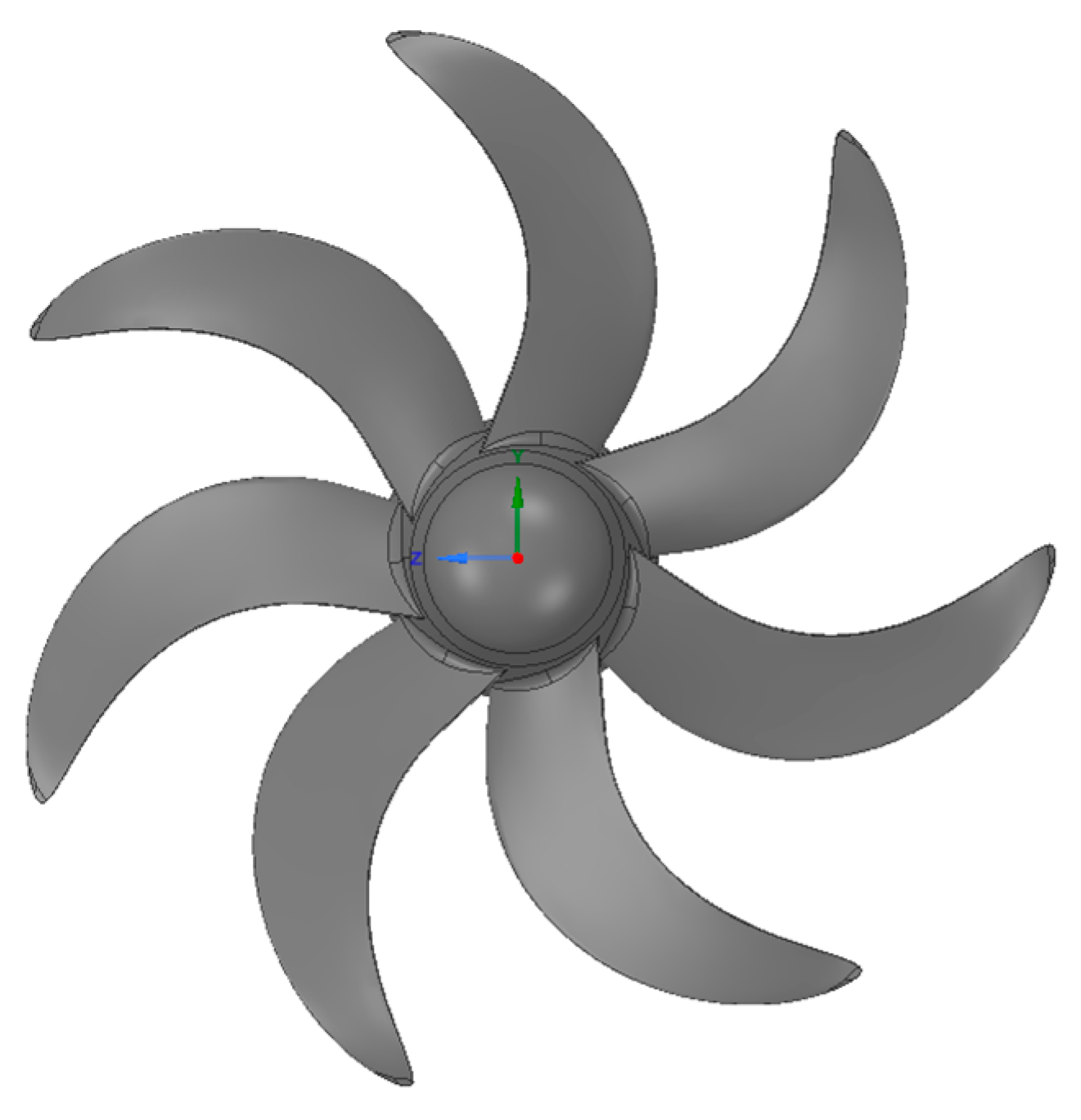
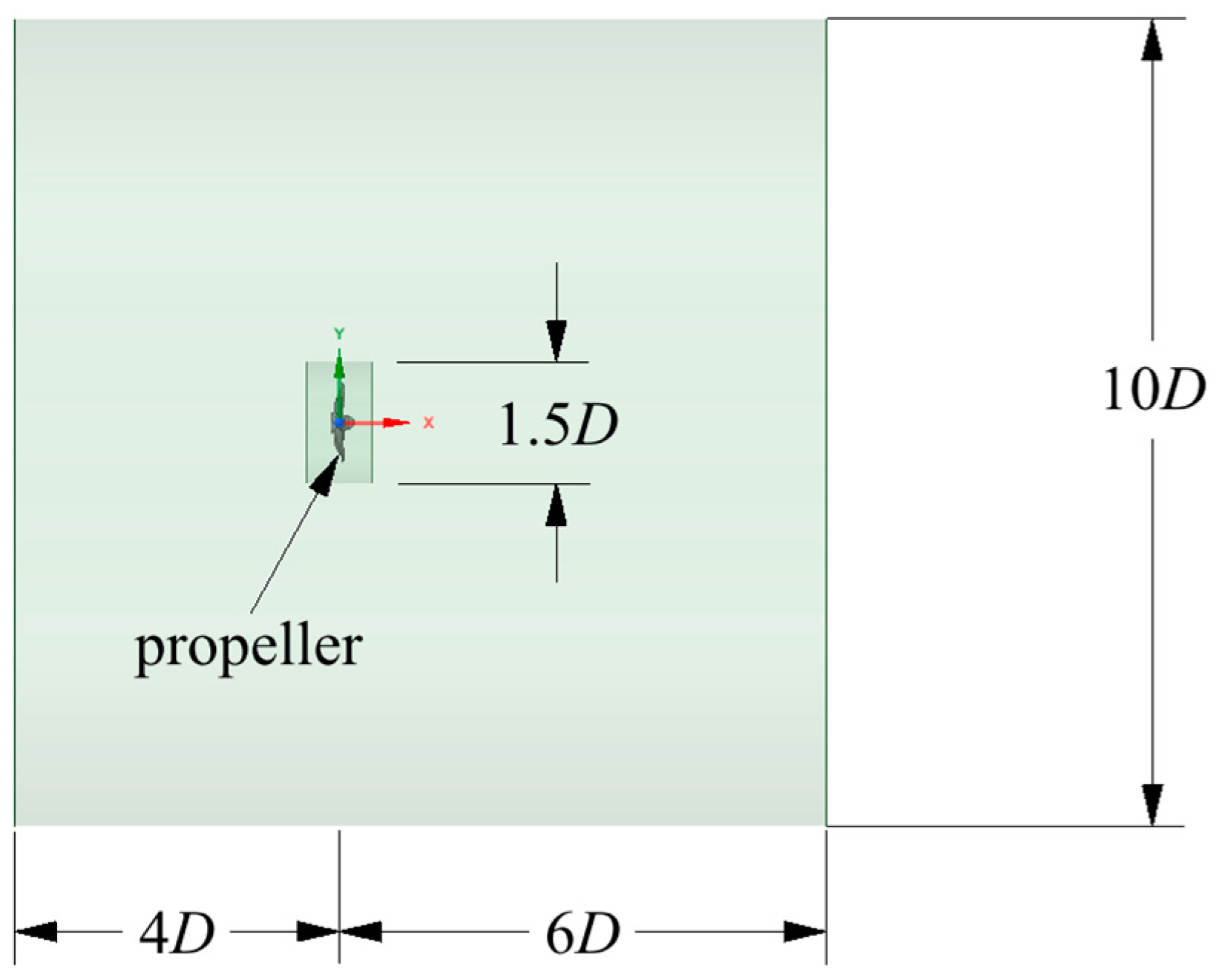
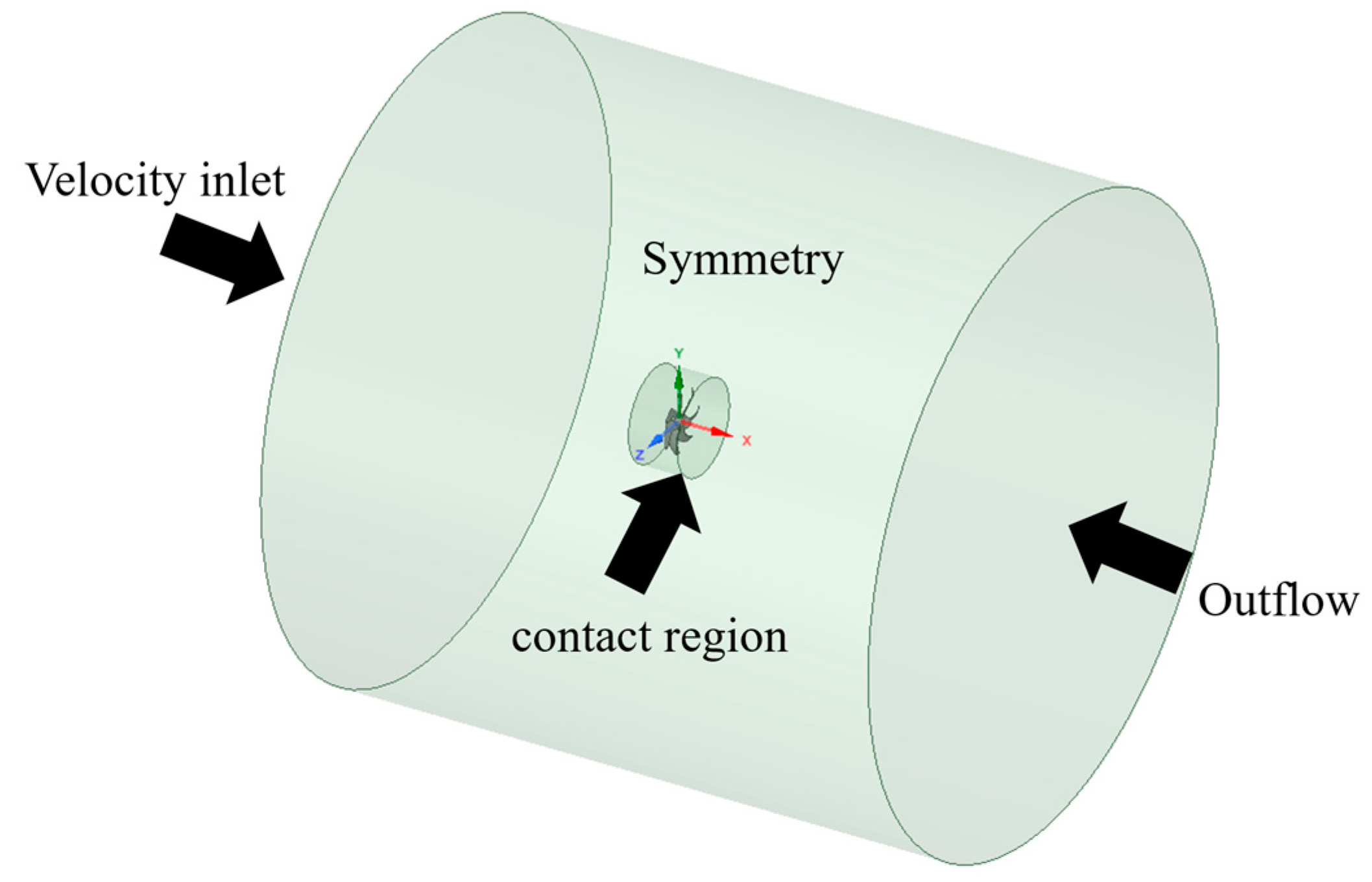

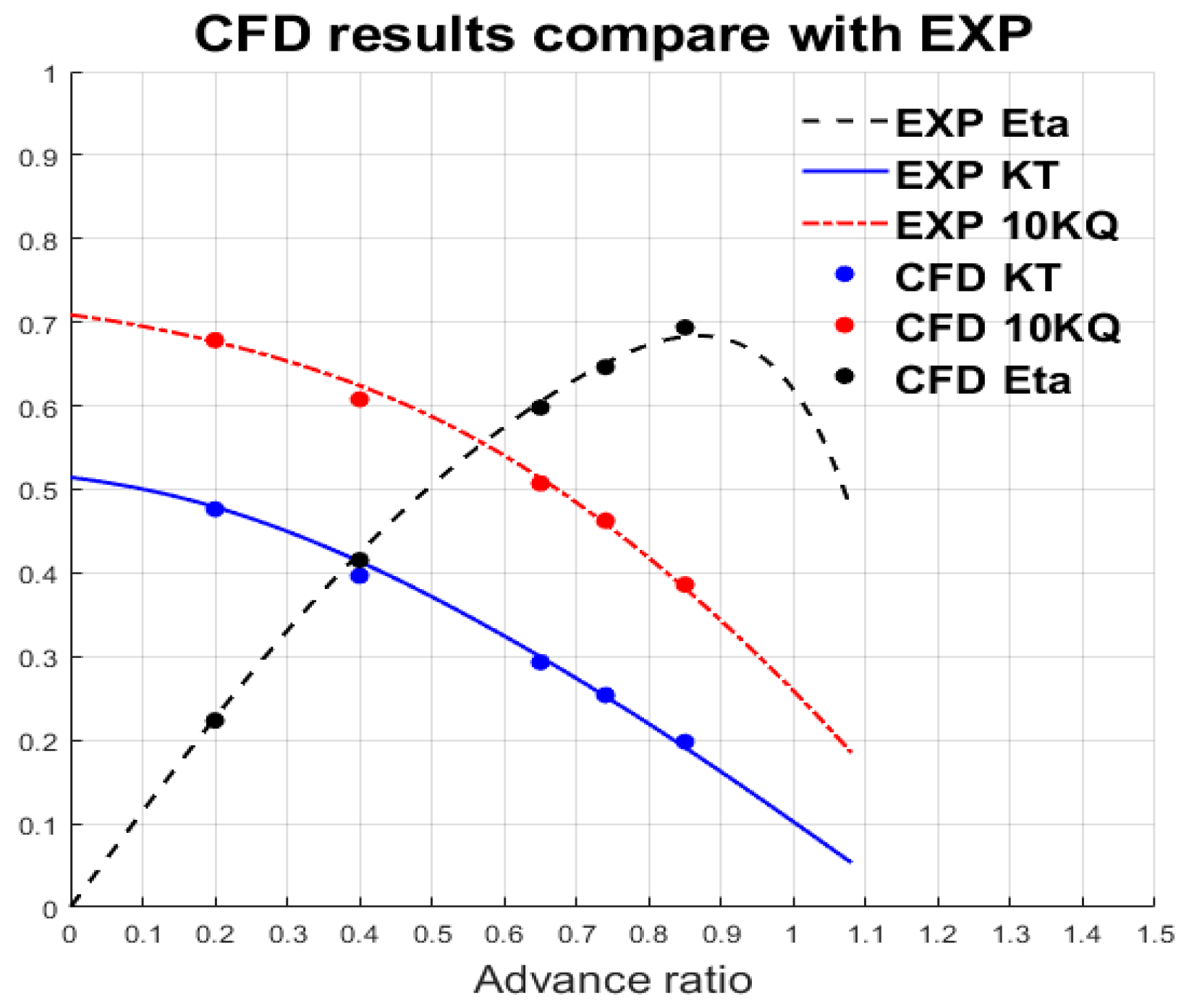

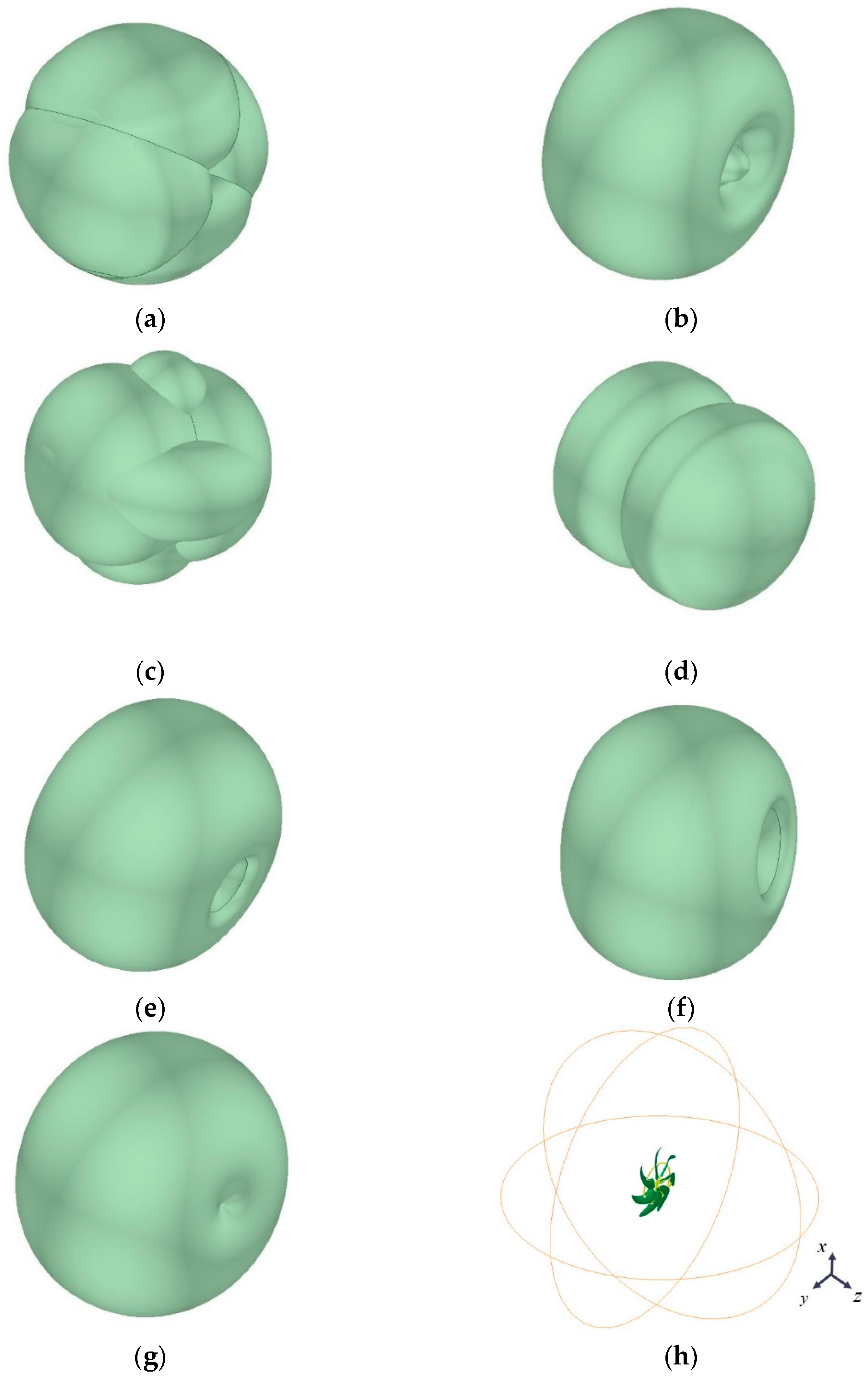

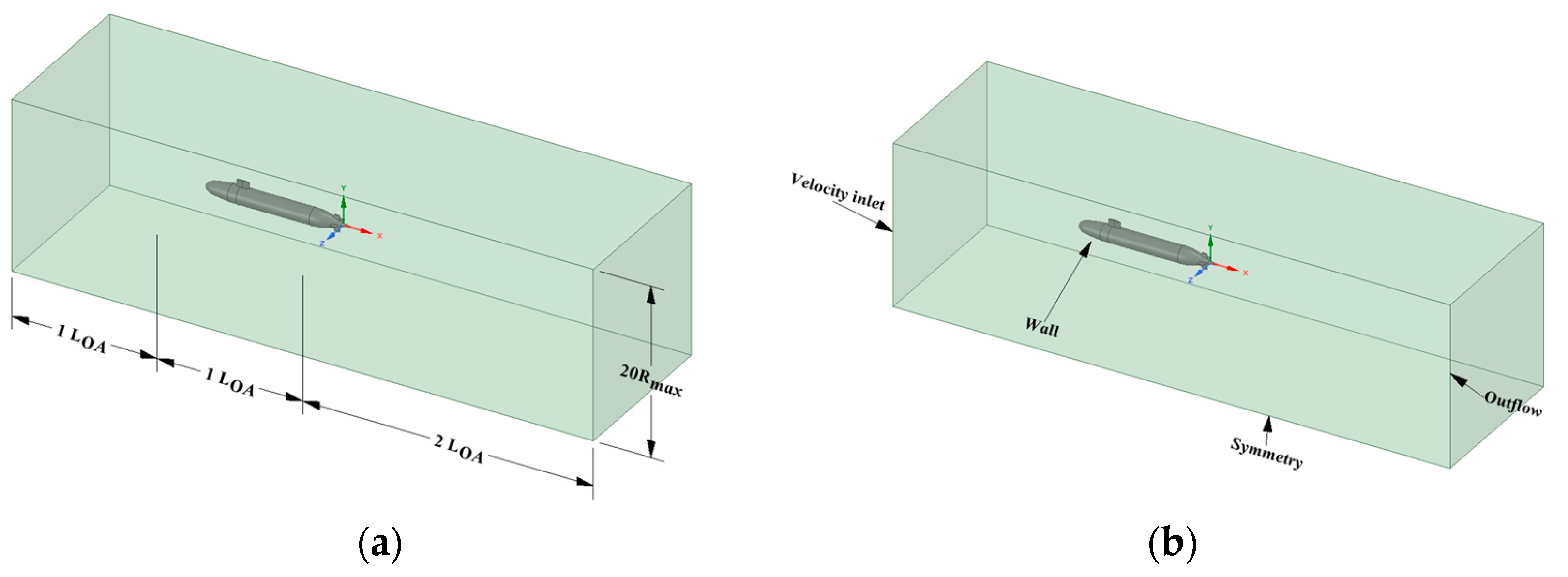

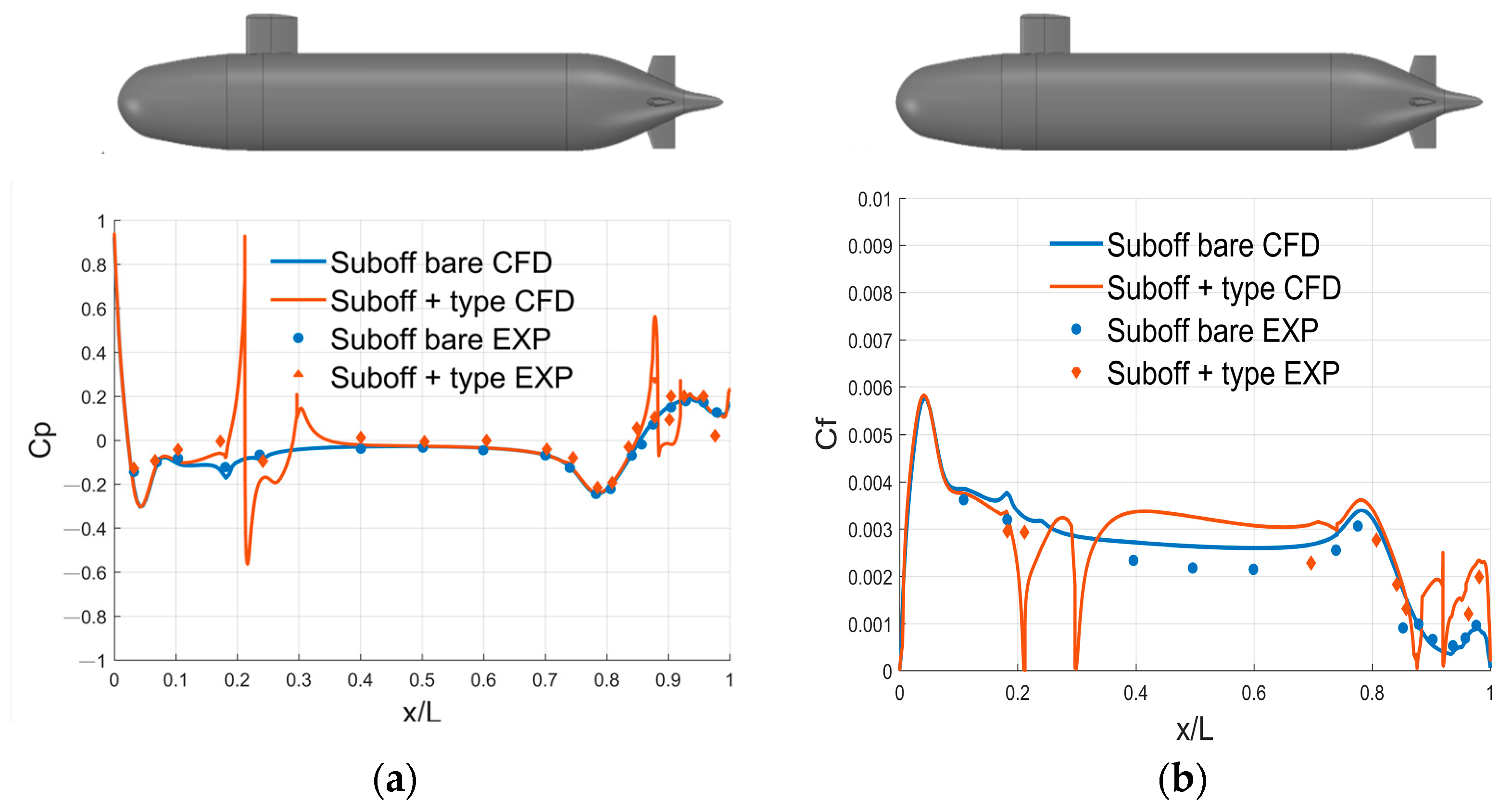
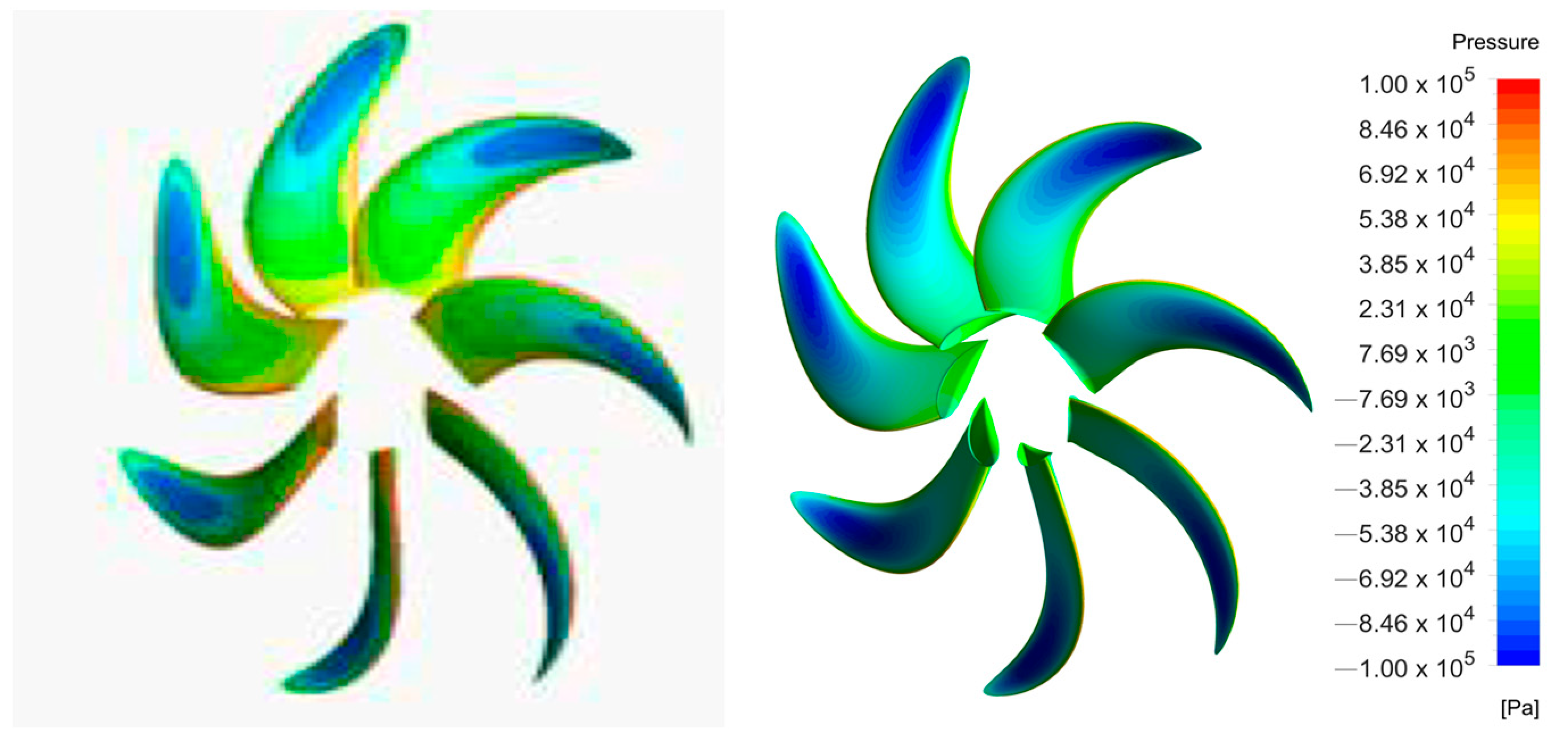
| Description | Symbol | Parameters |
|---|---|---|
| Number of blades | B | 7 |
| Propeller diameter (m) | D | 0.485 |
| Pitch ratio at 0.7R | P0.7/D | 1.15 |
| Hub ratio | Dh/D | 0.226 |
| Chord length at 0.75R (m) | C0.75 | 0.0068 |
| Expansion area ratio | Ag/A | 0.608 |
| INSEAN E1619 | EXP. | CFD | Diff. | |
|---|---|---|---|---|
| 0.85 J | KT | 0.196 | 0.1995 | 1.78% |
| 10KQ | 0.388 | 0.3875 | −0.12% | |
| 0.74 J | KT | 0.250 | 0.2539 | 1.56% |
| 10KQ | 0.450 | 0.4626 | 2.80% | |
| 0.65 J | KT | 0.302 | 0.2932 | −2.90% |
| 10KQ | 0.515 | 0.5072 | −1.52% | |
| 0.4 J | KT | 0.412 | 0.3966 | −3.70% |
| 10KQ | 0.621 | 0.6078 | −2.19% | |
| 0.2 J | KT | 0.481 | 0.4764 | −0.97% |
| 10KQ | 0.680 | 0.6785 | −0.17% | |
| FVM | BEM | Diff. | |
|---|---|---|---|
| 4.0752 Hz | |||
| Point 1 | 108 (dB) | 105.8 (dB) | 2.2 (dB) |
| Point 2 | 91.59 (dB) | 89.74 (dB) | 1.85 (dB) |
| Point 3 | 79.49 (dB) | 77.69 (dB) | 1.8 (dB) |
| Point 4 | 67.46 (dB) | 65.66 (dB) | 1.8 (dB) |
| 28.5264 Hz | |||
| Point 1 | 109.1 (dB) | 91.41 (dB) | 17.69 (dB) |
| Point 2 | 61.65 (dB) | 59.56 (dB) | 2.09 (dB) |
| Point 3 | 50.38 (dB) | 48.65 (dB) | 1.73 (dB) |
| Point 4 | 39.52 (dB) | 37.68 (dB) | 1.84 (dB) |
| FVM | BEM | Diff. | |
|---|---|---|---|
| 16.3008 Hz | |||
| Point 5 | 81.73 (dB) | 80.03 (dB) | 1.7 (dB) |
| Point 6 | 66.34 (dB) | 64.61 (dB) | 1.73 (dB) |
| Point 7 | 54.34 (dB) | 52.66 (dB) | 1.68 (dB) |
| Point 8 | 42.59 (dB) | 40.93 (dB) | 1.66 (dB) |
| 32.6016 Hz | |||
| Point 5 | 81.89 (dB) | 81.88 (dB) | 0.01 (dB) |
| Point 6 | 66.32 (dB) | 67.06 (dB) | 0.74 (dB) |
| Point 7 | 54.73 (dB) | 55.54 (dB) | 0.81 (dB) |
| Point 8 | 43.98 (dB) | 44.68 (dB) | 0.7 (dB) |
| Description | Symbol Flag | Parameters |
|---|---|---|
| Overall length | LOA | 4.356 m |
| Vertical mark spacing | LPP | 4.261 m |
| Maximum hull radius | Rmax | 0.254 m |
| Center of buoyancy | FB | 0.254 LOA |
| Drainage volume | Vdisp | 0.718 m3 |
| Wet cut-off area | SW | 6.338 m2 |
| (m/s) | [5] EXP. (N) | [34] LES (N) Diff. (%) | Present (N) Diff. (%) |
|---|---|---|---|
| 3.050 | 102.3 | 106.4 (3.963%) | 105.778 (3.40%) |
| 6.096 | 389.2 | 384.6 (−1.173%) | 384.566 (−1.19%) |
| 7.161 | 526.6 | 519.2 (−1.408%) | 519.682 (−1.31%) |
| 9.152 | 821.1 | 820.5 (−0.067%) | 822.645 (0.19%) |
| Self-Propulsion | |||
|---|---|---|---|
| [8] EXP. (N) | CFD (N) | Diff. (%) | |
| KT | 0.2618 | 0.2446 | −6.57% |
| 10KQ | 0.4603 | 0.4651 | 1.02% |
| BPF | [8] EXP SPL (dB) | CFD SPL (dB) Diff. (%) | BEM SPL (dB) Diff. (%) |
|---|---|---|---|
| 1st BPF 214.06 Hz | 116.8 | 111.98 (−4.13%) | 111.6 (−4.45%) |
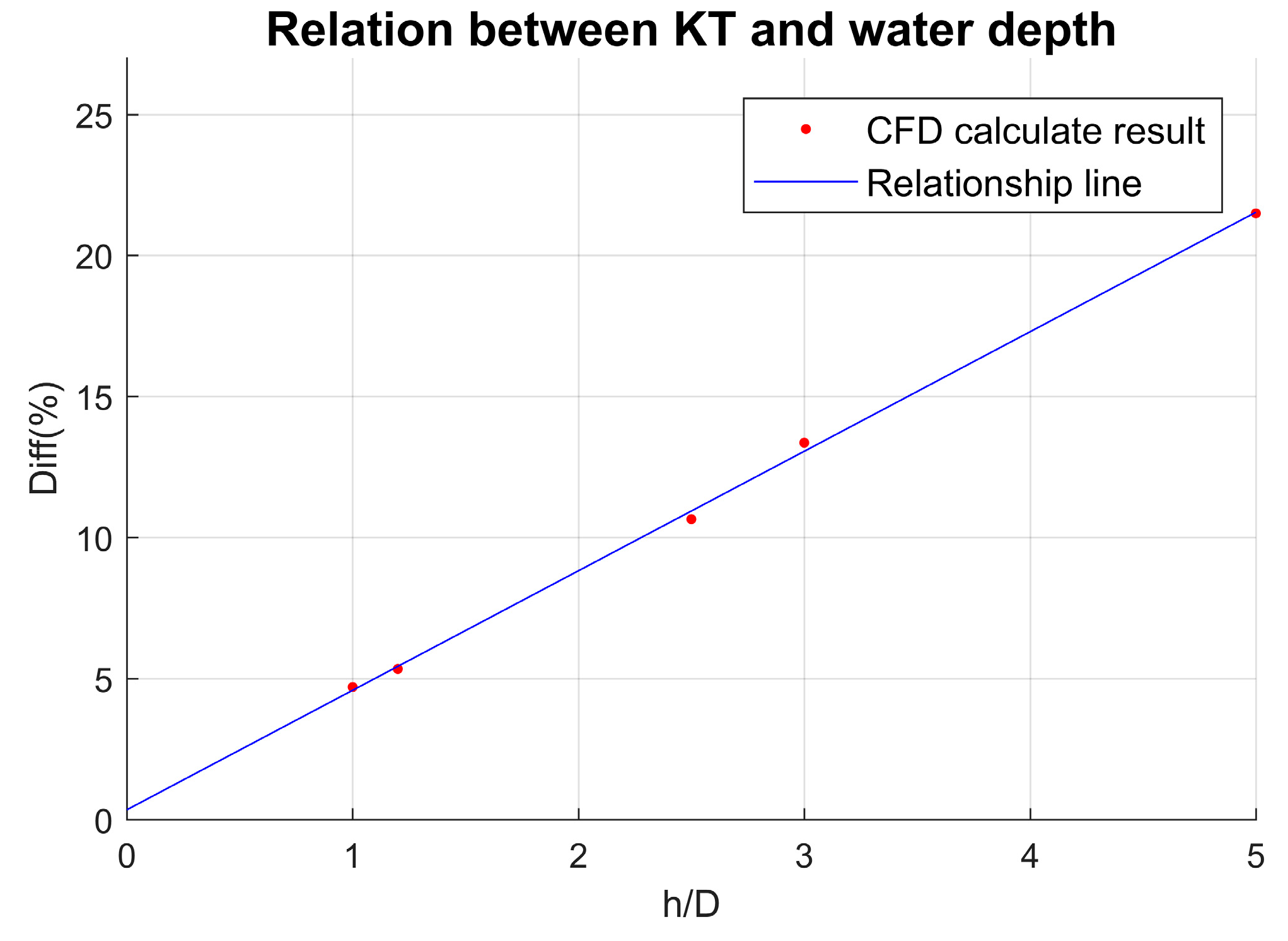
| h/D | h (m) | T (N) | KT EXP = 0.196 |
|---|---|---|---|
| 1 | 0.485 | 188.19 | 0.2052 4.7% |
| 1.2 | 0.582 | 189.34 | 0.2069 5.34% |
| 2.5 | 1.2125 | 198.88 | 0.2169 10.65% |
| 3 | 1.455 | 203.76 | 0.2222 13.36% |
| 5 | 2.425 | 218.37 | 0.2381 21.49% |
| h/Ds | h (m) | T (N) | KT EXP = 0.2618 |
|---|---|---|---|
| 5 | 1.31 | 1055.61 | 0.2400 −8.33% |
| 9 | 2.358 | 1075.49 | 0.2445 −6.61% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-W.; Pan, C.-C.; Lin, Y.-H.; Shih, C.-F.; Shen, J.-H.; Chang, C.-M. Acoustic Field Radiation Prediction and Verification of Underwater Vehicles under a Free Surface. J. Mar. Sci. Eng. 2023, 11, 1940. https://doi.org/10.3390/jmse11101940
Chen Y-W, Pan C-C, Lin Y-H, Shih C-F, Shen J-H, Chang C-M. Acoustic Field Radiation Prediction and Verification of Underwater Vehicles under a Free Surface. Journal of Marine Science and Engineering. 2023; 11(10):1940. https://doi.org/10.3390/jmse11101940
Chicago/Turabian StyleChen, Yung-Wei, Cheng-Cheng Pan, Yi-Hsien Lin, Chao-Feng Shih, Jian-Hong Shen, and Chun-Ming Chang. 2023. "Acoustic Field Radiation Prediction and Verification of Underwater Vehicles under a Free Surface" Journal of Marine Science and Engineering 11, no. 10: 1940. https://doi.org/10.3390/jmse11101940
APA StyleChen, Y.-W., Pan, C.-C., Lin, Y.-H., Shih, C.-F., Shen, J.-H., & Chang, C.-M. (2023). Acoustic Field Radiation Prediction and Verification of Underwater Vehicles under a Free Surface. Journal of Marine Science and Engineering, 11(10), 1940. https://doi.org/10.3390/jmse11101940






