1. Introduction
Autonomous underwater vehicles (AUVs) have the advantages of high safety, good maneuverability, and intelligence compared with other types of underwater platforms, and have been widely used in seabed surveys and underwater equipment maintenance, etc.
The dynamic model of an AUV is of high nonlinear, fast time-varying, and strong coupling [
1]. It is difficult to obtain the hydrodynamic coefficient of underwater vehicles accurately, and it is hard to ensure the accuracy of its mathematical model [
2]. Meanwhile, the underwater vehicle will be strongly disturbed by the sea currents and waves during its steering [
3]. Therefore, the control of underwater vehicles is faced with severe challenges.
To ensure the stability and control accuracy of AUV underwater motion, a variety of control algorithms are applied to the AUV system. For example, PID control and its improved algorithm [
4], fuzzy control method [
5], neural network method [
6], linear quadratic regulator (LQR)-based control method [
7], sliding mode control method [
8], adaptive control method [
9,
10], robust control method [
11], etc. The PID-improved method has good robustness and transient response, but it cannot deal with the disturbance of the external environment quickly and effectively [
4]. Although the AUV control method using LQR can achieve a balance between energy consumption and response characteristics in the process of steering [
7] and achieve the optimal control of the AUV, it needs to model the AUV dynamic accurately, and when the parameters of the AUV model are changed, the control effect will be greatly deviated [
12]. The sliding mode control has excellent robustness and can suppress the deviation caused by the model change. Still, it will produce jitters in the control system response, so it is often combined with other control methods to improve the control effect [
8]. In addition, the underactuated control of an AUV [
13] and underwater simultaneous localization and mapping [
14] are also the focuses of research.
On the other hand, with the increasing complexity of AUV steering tasks, the control performance requirements of AUVs are also increasing. Compared with the cross rudder, X-rudder, has higher maneuverability and roll control ability [
15], which is the development trend of the AUV rudder in the future. However, due to the special arrangement of the X-rudder, each rudder surface has the control ability of depth and course. Compared with the cross rudder and the control of the X-rudder has a decoupling problem, and it is difficult to control the horizontal plane dynamic independently when an AUV is controlled for changing depth. Therefore, it is very important to study an effective decoupling control of depth and course of AUVs with X-rudder.
However, most of the recent research on the AUV control algorithm is focused on the cross-tail rudder. Ma et al. proposed an AUV depth control method based on a model predictive control [
16], and the simulation results show that the method has good dynamic control performance. Hui et al. proposed an AUV depth controller based on
adaptive theory to solve the problem of hydrodynamic parameter perturbation and external disturbance during AUV steering [
17]. The simulation results show that the controller has a good dynamic response and can guarantee an anti-disturbance ability and robustness.
The strong robustness of adaptive control can effectively cope with the uncertain disturbance caused by AUV underwater movement. The model reference adaptive control (MRAC) [
18] can identify unknown parameters in the system and disturbance online [
19]. According to the identified parameters, the control law is adjusted to eliminate the disturbance of the external environment to the controlled object [
20,
21], so that the output of the closed-loop system of the controlled model can follow the output of the ideal reference model, and the anti-disturbance ability of the system is improved [
22]. In addition, Sedghi et al. proposed an adaptive robust control method for the AUV with saturated inputs and uncertainties [
23]. And Zong proposed a decentralized adaptive neuro-output feedback saturated control for AUVs [
24].
However, the traditional MRAC will have high-frequency oscillation control signals under the condition of high adaptive gain. To solve this problem, Cao et al. proposed
adaptive control theory in 2006 [
25]. Based on MRAC, the control method introduces a low-pass filter structure into the feedback loop to filter the high-frequency signals, so that the output of the
adaptive controller can be kept in the low-frequency range, and the coupling problem between the adaptive law of the controller and the robustness performance is solved, so that the closed-loop system can have good robustness while ensuring a dynamic performance [
26]. The asymptotic stability and controllability accuracy of the system are improved [
27]. The
adaptive controller based on output feedback ensures that the input/output signals of the system have a consistent performance boundary through piecewise constant adaptive law and low-pass filtering control signals. Moreover, the error between the closed-loop adaptive system and the ideal system is small enough by reducing the sampling step, and the controller performance is systematically improved.
According to the design idea of an AUV depth controller for a cross rudder, an adaptive control method of AUVs with X-rudder is proposed in this paper. In this method, model predictor, disturbance estimator, and adaptive control law are used to compensate for the coupling disturbance and un-modeled dynamics of depth and course plane, and a dual coupling controller of the depth and course channel is designed to make the X-rudder jointly control depth and course. The X-rudder angle allocation algorithm is designed to assign the stern rudder instructions to four rudder angles. Simulation and experiment results show that the algorithm is effective.
The main contribution of this article is that the L1AC algorithm is realized for AUV X-tudder control, and the model uncertainty of the rudder force is adaptively decoupled for horizontal steering and vertical steering. On the other hand, the L1AC algorithm is proposed on the basis of LQR state feedback, so that the control performance can be close to the LQR control for the nominal model, which can improve the control accuracy and reduce the overshoot for AUV with X-rudder.
2. Mathematical Model for AUV with X-Rudder
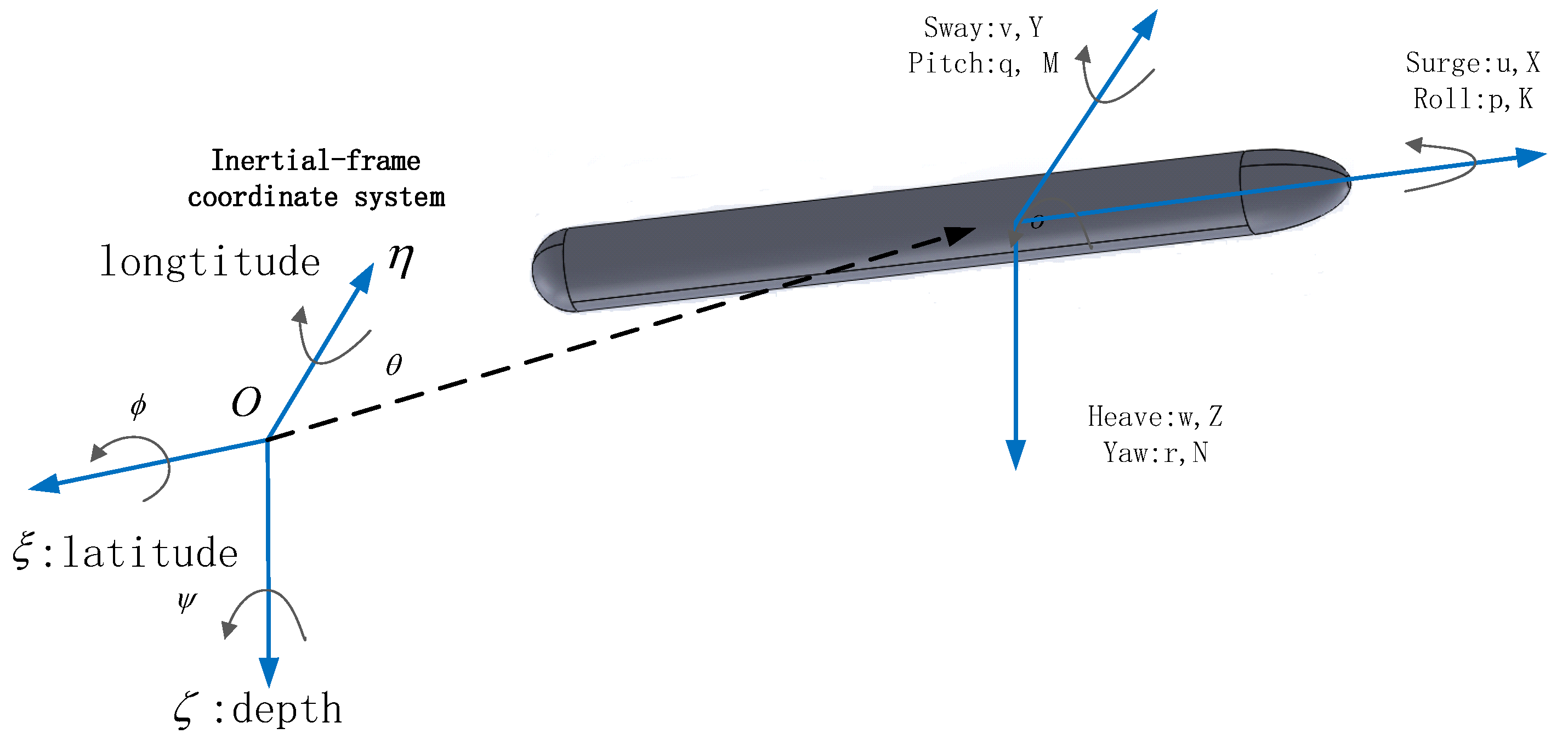
The dynamic characteristics of the autonomous underwater vehicle are usually described as a rigid body with six degrees of freedom, and its kinematics and dynamics equations are established according to Newton’s law. The earth reference system and the rigid body reference system are established, respectively, as shown in
Figure 1. The head direction, side direction, and down direction are the
and
axis, respectively.
The linear velocity of the AUV in the
direction is
, the angular velocity is
, the moment of inertia is
, and the forces and moment are
and
, respectively. The coordinates of the center of gravity on the
z-axis is
; other variables include roll
, pitch
, heading angle
, depth
, and mass
m. Then, the dynamic moment equations of the vehicle in the
direction can be described as
The layout of the stern X-rudder is shown in
Figure 2, consisting of four rudder surfaces arranged vertically to each other, namely
, and
.
The maneuvering effect of the stern X-rudder is usually mapped to the horizontal and vertical planes, i.e., the virtual rudder
, and the virtual stern rudder
.
The hydrodynamic forces and moments of AUV can be described as
where
, and
are the hydrodynamic coefficients, and
n is the propeller rotation speed.
Linearization of Dynamic Models
For the first, the optimal controller based on LQR is designed for the linear dynamic model, and the adaptive law is then designed for the control system with LQR state feedback. Therefore, it is necessary to linearize the above nonlinear model.
In the design of the AUV control algorithm, the control task is usually divided into horizontal steering and vertical steering. The former focuses on the AUV’s heading, while the latter focuses on the AUV’s depth. For the vertical plane motion of the AUV, the state is selected as
, and the state space equation form of the linear vertical dynamic model is
where
. Variable
and
represent the model uncertainty and the environmental disturbance on the vertical force and pitch moment.
Similarly, the state of horizontal motion is chosen as
, and the state space equation form of the linear horizontal dynamic model is
where
. Variable
and
represent the uncertainty of the model and the environmental disturbance on the horizontal force and yaw moment.
In the above linearization process, nonlinear parts and environmental disturbance are modeled as uncertainties. These modeling uncertainties are bounded by the manipulation characteristics of AUVs, so the following assumptions are made in this paper.
Assumption A1. The nonlinear uncertainty of vertical linear model (4) is bounded, there exists such that Assumption A2. The nonlinear uncertainty of horizontal linear model (5) is bounded, there exists such that The above constant , and describes the boundary of the model uncertainty and environmental disturbance, and the boundary of these uncertainties and disturbance will be used for the selection of the post-text adaptive controller parameters. Too large an uncertain limitation will limit the controller’s design to reduce the adaptive controller’s performance.
3. Control Algorithm
The structure of the L1AC algorithm for AUV vertical plane control proposed in the paper is shown in
Figure 3, and the horizontal plane controller is similar. First, the LQR-based state feedback controller is designed on the basis of the linear dynamic model; Secondly, the disturbance estimator and adaptive controller are designed based on the state feedback closed-loop system. Lastly, the control laws for the horizontal and vertical planes are synthesized. The course controller and depth controller are designed in the same way and are finally converted to the command angles of the X-rudder.
3.1. The Depth and Heading Contoller Based on LQR for AUV
When the AUV control algorithm is designed, the control of the vertical and the horizontal plane is usually designed independently. For the control of the depth plane, the simplified linear model form is
The form of state feedback controller is as follows:
And, for the control of course surface, the simplified linear model form is
The form of state feedback controller is as follows:
The above state feedback parameters , and are obtained using the LQR method and can be realized by using the matlab function. The feedback gain is calculated with and , where , and are the weight matrices for states and inputs, respectively.
For linear state space models, various state feedback control algorithms are proposed. For the control of an AUV, the linear quadratic regulator (LQR) is an excellent choice. The LQR algorithm constructs the quadratic performance cost function of the error state quantity and the control quantity, and achieves the desiblack control effect by adjusting the intensity of the penalty. Relatively speaking, the LQR method is more intuitive to adjust. The designer’s tolerance for the error of the state quantity or the penalty paid by the actuator determines the optimal control quantity of the final design.
Comparing (4) and (10), as well as (5) and (12), the LQR-based state feedback controller ignores the environmental disturbances. In the presence of model uncertainties and environmental disturbances, the control performance of the LQR algorithm is bound to degrade.
3.2. Control Performance Improved with L1 Adaptive Control Algorithm
For the nominal model, LQR can get an excellent adjustment effect. However, when there are modeling uncertainties and environmental disturbances in the system model, the optimal performance will be destroyed. Obviously, when there is an external disturbance in the systems (4) and (5), the controller (11) and (13) will inevitably have tracking errors. In addition, in the course of AUV navigation, the parameters of the dynamic model will change under the influence of environmental factors, which will cause the poles of the closed-loop system to shift, thus affecting the response time, overshoot, and other performance of the closed-loop system.
Various adaptive control and robust control methods have been proposed for the environmental disturbance and model uncertainty. The former estimates environmental disturbances online and compensates for them in the control law. The latter takes into consideration the uncertainty range of the dynamic model; the control law with good stability is designed to ensure that the system still has good control performance when the system parameters change. Both adaptive control and robust control methods no longer consider the optimal performance of the dynamic response process of the system but focus on the stability of the closed-loop system.
Different from model reference adaptive control (MRAC) and robust control algorithms, the L1AC algorithm can consider both dynamic tracking performance and the anti-disturbance ability of the system. The control algorithm consists of two control components. The first control component designs a stable control law for the nominal model, and the second control component compensates for the uncertainty and disturbance of the nominal model, so that the final performance of the system is similar to that of the nominal model.
Because of this characteristic, in this study, the first component is designed using the optimal control law (LQR), and the second control law realizes the disturbance compensation.
Taking AUV’s depth controller as an example, its adaptive control algorithm is given below. The form of the controller is as follows:
where
is the feedback control law and
is the adaptive control law. For the feedback control law, we adapt the LQR control algorithm discussed above to give the controller the optimal control performance for the nominal model.
To compare the performance of the control algorithms of LQR and L1AC, the state feedback parameters in L1AC are the same as those of LQR for the following simulations and experiments.
By substituting control law (14) into model (10), we get
and the related matrix has the following form:
To realize adaptive control under model uncertainty and environmental disturbance, it is necessary to estimate and predict the disturbance, and the form of the prediction equation is
where
is the estimated value of
. And
,
is the estimated value of
, and
is the estimated value of another un-modelled dynamic.
These estimated values are updated with the following discrete-time equation:
where
is the predict error,
is adaption rate,
i is the number of adaption steps, and
is the intermediate variable of the adaption. Most of the equations in this research are described in a continuous-time equation, but the adaptive law uses discrete-time form, and the discrete-time adaption law has a faster convergence rate [
27].
Finally, the adaptive control law is given as
where
,
.
In the same way, a heading controller for
can be designed with a similar structure of
Figure 3. The L1AC controller is designed based on the Equations (12) and (13). As the equation of the horizontal linear dynamic equation is of three dimensions, there are three disturbance estimation values.
3.3. Rudder Command Conversion
As the controller solves the virtual rudder instructions
, the rudder angle instructions need to be assigned to the four rudder angles of the X-rudder, and the pseudo-inverse method is used to solve the rudder angle instructions.
,
and
The rudder angle allocation algorithm is one of the important research areas of X-rudder control. The allocation algorithm converts the horizontal control command and the vertical control command into the command of four rudder angles, so many allocation schemes exist. However, due to the small size of the AUV, the control of the four rudder surfaces is inevitably interfered with the flow field. The flow field interference is transformed into the coupling disturbance of the horizontal plane and vertical plane, which is the problem that the adaptive control algorithm in this paper concentrates on. In addition, when a particular rudder surface fails, the regular operation and safety of the AUV can be guaranteed through a reasonable distribution mechanism. We will carry out relevant work in the follow-up work.
3.4. Stability Analysis
This section analyzes the stability of the proposed algorithm for the vertical dynamic controller. And a similar method can be used for the proof of the control for horizontal motion.
To prove the stability of the proposed control algorithm, it is necessary to introduce a reference system. This reference system does not exist in the implementation of the algorithm, but only serves as a reference of the limit performance of the control algorithm. The form of the reference system is as follows.
where
,
is the state variable of the reference system.
is the adaptive control law,
and
is the disturbance.
where
,
,
.
To ensure the stability of the algorithm, the parameters
,
of the adaptive law should meet so that there exists a bounded positive
such that
where
,
Lemma 1. For the close loop reference system (24), subject to the condition (25), then That means that the reference system (24) is itself stable, and the proving method can be found in reference [25]. Next, we analyze the performance of the prediction Equation (18). Lemma 2. For the prediction Equation (18), if the adaption rate is chosen to satisfy (20), and if there exists a time τ such that the truncation function is bounded, then the prediction error can be systematically reduced both in transient and steady states by reducing the adaption rate .
The prediction error is defined as , and the proving method can be found in reference [25]. For a small enough adaption rate , the prediction error is bounded, then we define the boundary as . Theorem 1. Given the close loop system via (10), (14)∼(19), subject to the condition in (25), and the reference system in (23), then Proof. (By contradiction) Assume the bounds do not hold. Since
,
, we analyze the relationship between prediction error and reference error.
The adaptive controller
let reference error
, and
the relationship between reference error and prediction error
if we choose
according to (25),
That means the error between the close-loop system and reference system can be reduced to be arbitrarily small, and the reference system is BIBO, so it follows that the close-loop system with control law is stable. □
4. Controller Design and Simulation Result
This part verifies and analyzes the performance of the proposed algorithm based on simulation. The simulation includes two scenarios. First, the depth is controlled at the set value, and the course maneuver is carried out. Second, keep the AUV’s course constant and change the AUV’s depth.
Due to the dynamic coupling between horizontal motion and vertical motion, as well as the coupling of the X-rudder control force, there exists a cross disturbance between the depth control and course control. In particular, each control surface of the X-rudder produces a turning and pitch moment, and the manipulation force is difficult to model accurately. These uncertainties make the coupling characteristics of horizontal and vertical motion obvious.
The design and analysis of the proposed control algorithm focus on the transient performance of the state adjustment process, including overshoot and adjustment time, while the steady-state performance focuses on the steady error and disturbance suppression ability.
4.1. Dynamic Parameters of AUV
The research object of this paper is a small AUV, as shown in
Figure 4. The length of the AUV is about 2200 mm and the mass is 68 kg. The relevant configuration parameters are shown in
Table 1. One main propeller and four side propellers are mounted for maneuvering. In this study, the depth and course control is realized with the X-rudder on the stern, and the steering force can be decouped by the reasonable distribution of the rudder angle. The AUV sensor includes IMU, DVL, and depth sensors, through Kalman filtering, to measure the depth, course, inclination, and associated linear velocity and angular velocity.
According to the model parameters in the table, the controller is designed when the AUV speed is about 3 kn. First, the LQR control parameters of the virtual rudder and stern rudder are designed using a nominal model. Secondly, for the adaptive law, is selected to design the disturbance estimator and adaptive controller. In the program implementation, we choose the update step size to be 0.1 s. The smaller update rate will help improve the system’s adaptive capability and control performance. However, the current test platform usually adopts an update rate of 0.1 s, and the sample rate can meet the control requirements by analyzing it.
The control algorithm proposed in
Section 3 is used to design the controller separately. The relevant control parameters are shown in
Table 2.
The depth and heading controllers are designed based on the above control parameters. In this paper, Equation (
18) for disturbance estimation is updated in the discrete-time form, and the discrete-time form has a faster convergence rate. The
here is the update rate of this equation. In addition, in simulations and experiments, the algorithm is implemented in a fixed computation step way, and the update step of the overall algorithm is
T = 0.1 s.
Based on the above model coefficients and controller parameters, the
and
Bode diagram are shown in
Figure 5, respectively.
According to Equation (
24),
, and
correspond to the transfer function of the
,
and control instructions
to the closed-loop output, respectively. It can be seen that the force and moment disturbance can be effectively suppressed, and the command depth tracking is guaranteed without error.
It can be seen from Equation (
24) and
Figure 5 that the disturbance with frequency between 0.01 and 0.1 rad/s can be suppressed very well, which indicates that the L1AC algorithm proposed can provide effective depth adaptive control ability for the currents and waves disturbance in this frequency band. When the disturbance of the currents and waves is beyond the range, the disturbance suppression ability of the control algorithm can be improved by designing the corresponding
and
, which comes down to the design of the low-pass filter
.
4.2. Simulation of Heading Control
In the first simulation, the AUV maintained a depth of 5 m and the course changed from 0 degrees to 60 degrees. The LQR algorithm and L1AC algorithm are used to test the mathematical model. The simulation results are shown in
Figure 6,
Figure 7,
Figure 8 and
Figure 9. In the simulation, a nonlinear dynamic model is adopted, and there is a certain coupling between the vertical and horizontal motions, but there is no disturbance from the external environment.
Due to the coupling force, both depth and trim are affected during AUV steering, resulting in control deviation. Because the L1AC algorithm estimates these disturbance forces online and compensates for them, its control deviation is obviously smaller than the LQR algorithm.
The status of the rudder angle during the simulation of the two control algorithms is shown in
Figure 7. It can be seen that the rudder angle in the L1AC algorithm has a small range of fluctuations in the steady state, which is due to the existence of a disturbance estimation, resulting in a small control component in the rudder angle.
The disturbance estimation results of
,
are shown in
Figure 8 and
Figure 9. It can be seen that the disturbance estimation is larger during maneuvering but smaller under a steady state. This is due to the greater influence of coupling forces during maneuvering.
4.3. Simulation of Depth Control
In the second simulation, the AUV’s course remains constant, and the speed is set at 3 kn. The control algorithm maneuvers the X-rudder so that the depth changes from 5 m to 6 m. The LQR and L1AC algorithms are used to simulate this process, respectively, and the results are shown in
Figure 10.
It can be seen that both algorithms can complete the deepening manipulation after 10 s. The manipulation response of the L1AC algorithm is slightly slower than that of the LQR algorithm due to the introduction of a low-pass filter in the former, which causes a delay.
Figure 11 shows the command rudder angle in this process. The output instruction of the L1AC algorithm is the low–pass filter output of the LQR algorithm.
In this simulation, we cannot see the advantage of the L1AC algorithm. This is because, in the vertical plane motion, the cross-coupling effect is very small. There is no need to compensate for the model uncertainty and cross-interference force so the LQR algorithm has better simulation results.
However, in the actual control experiment, the environmental disturbance force is inevitable, and this advantage of the LQR algorithm is almost non-existent. The following experimental tests will confirm this result.
5. Experiment
Finally, the AUV in
Figure 4 is used to verify the proposed algorithm. The LQR algorithm in Equations (11)–(13) and the L1AC algorithm in Equation (
14) are compared and validated, mainly including two scenarios, namely course change manipulation and depth change manipulation.
Firstly, at the velocity of 3 kn, the AUV depth is maintained at 2 m, and the steering course is changed from 0 degrees to 60 degrees. The test results are shown in
Figure 12 and
Figure 13, respectively. The LQR and L1AC algorithms are tested. It can be seen that the heading control accuracy of L1AC is high, whether it is the process of maintaining the heading angle or the state after heading steering. This is because, in the lake test, the environmental disturbance force is unavoidable. The adaptive algorithm proposed in this paper can effectively estimate these disturbances and compensate for them.
In addition, due to the modeling errors of high-frequency dynamic characteristics, the AUV’s heading and depth have fluctuated in a small range.
As shown in
Figure 3, the control of the L1AC algorithm proposed by us consists of two components,
, in which
is the output of the LQR algorithm and
is the output of the adaptive control law. The L1AC algorithm realizes the online calculation and compensation for the disturbance compared to the LQR algorithm. Because of the compensation of disturbance, the L1AC has a better depth and heading control accuracy than LQR, as shown in
Figure 12.
On the other hand, the adaptive components
estimates disturbance, including the wave disturbance and un-modeling dynamic, so there is more jitter within it. Because
has more jitter components, the final control component is shown to be more oscillatory in
Figure 13.
Furthermore, in the L1AC algorithm, there are more changes in the rudder angle, which makes the AUV speed decrease significantly, as shown in
Figure 14.
In the second experiment, the AUV’s course is maintained at 0 degrees, and the sailing depth is steered from 2 m to 3 m. During this process, the navigation, depth, and pitch angle all fluctuate at the equilibrium value, which is different from the simulation result. Similarly, the control accuracy of the L1AC algorithm is higher than that of the LQR algorithm, and it is accompanied by more rudder angle fluctuations and a reduced speed.
It is worth noting that the LQR algorithm has poor performance for course control as shown in
Figure 15, and there is a course deviation of about 10 degrees, which is mainly due to the influence of the disturbance force of the water flow. The L1AC algorithm overcomes this problem well.
The above two experiments show that the proposed adaptive method can better compensate for the environmental interference and model uncertainty, and ensure the control accuracy and response speed of course and depth. However, due to the introduction of low-pass filter C(s), the response of the proposed control algorithm is delayed by about 1∼2 s. For AUV control, the response delay is acceptable to implement adaptive control.
By comparing the control ability of the LQR and L1AC algorithm, we can see that the L1AC has better depth and course steering accuracy, but there is a certain response delay. The design of the L1AC control algorithm requires a compromise between control accuracy and response delay, which is due to the design of the low pass filter
. On the other hand, as shown in
Figure 5, the design of
needs to consider the spectrum of wave disturbance. The lower the spectrum of
, the more anti-disturbance, but the greater the response delay.
The fluctuation in rudder angle is more frequent in the L1AC control algorithm, as shown in
Figure 16 and
Figure 17, and the faster rudder speed can be used to improve the performance of the L1AC algorithm, which puts forward higher requirements for the control device.
In addition, we can also see that the performance of the L1AC algorithm is similar to LQR within the simulation results. The implementation of the adaptive algorithm proposed by the paper is close to that of the LQR with the nominal model, so it can guarantee optimal control ability, to a certain extent, which is the difference between the L1AC method and the MRAC method.
6. Conclusions
In this paper, a scheme based on an adaptive control algorithm is designed to solve the decoupling control problem between depth control and heading control. Firstly, based on the linear model, the LQR controller is designed for horizontal and vertical motion, respectively. Secondly, the disturbance estimator and adaptive controller are designed to compensate for the coupling interference, environment interference, and model uncertainty according to model uncertainty, coupling force, and disturbance force. Finally, the pseudo-inverse method is used to design the X-rudder command angle. The simulation and experiment results show that the proposed controller can effectively improve the depth and course control performance of AUVs with an X-rudder.
Based on the analysis, we can find that the performance of the L1AC algorithm is close to that of LQR with the nominal model, so it can guarantee the optimal control ability, to a certain extent, under currents and wave disturbance. However, the design of the L1AC control algorithm requires a compromise between control accuracy and response delay. Furthermore, the fluctuation in rudder angle is more frequent in the L1AC algorithm than in LQR, which puts forward higher requirements for the control device.
For future research, with the introduction of the X-rudder, another important goal is to ensure fault safety. The follow-up research will study the control algorithm under the condition of some rudder surface failures.