Flow Field Pattern and Hydrodynamic Characteristics of a Grid Device Made with Various Grid Bar Spacings at Different Inclination Angles
Abstract
:1. Introduction
2. Materials and Methods
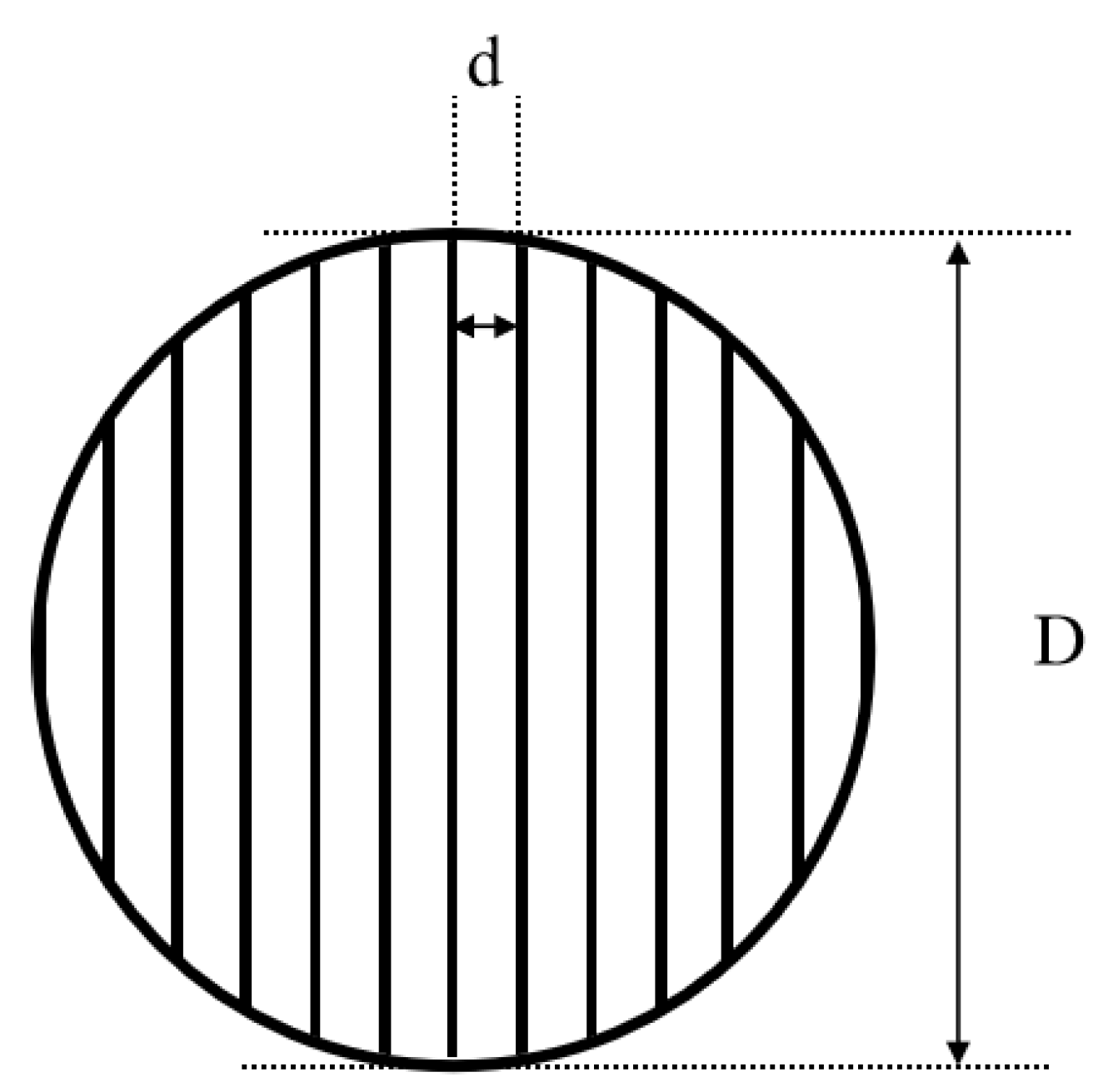
2.1. Circular Grid Design Structure
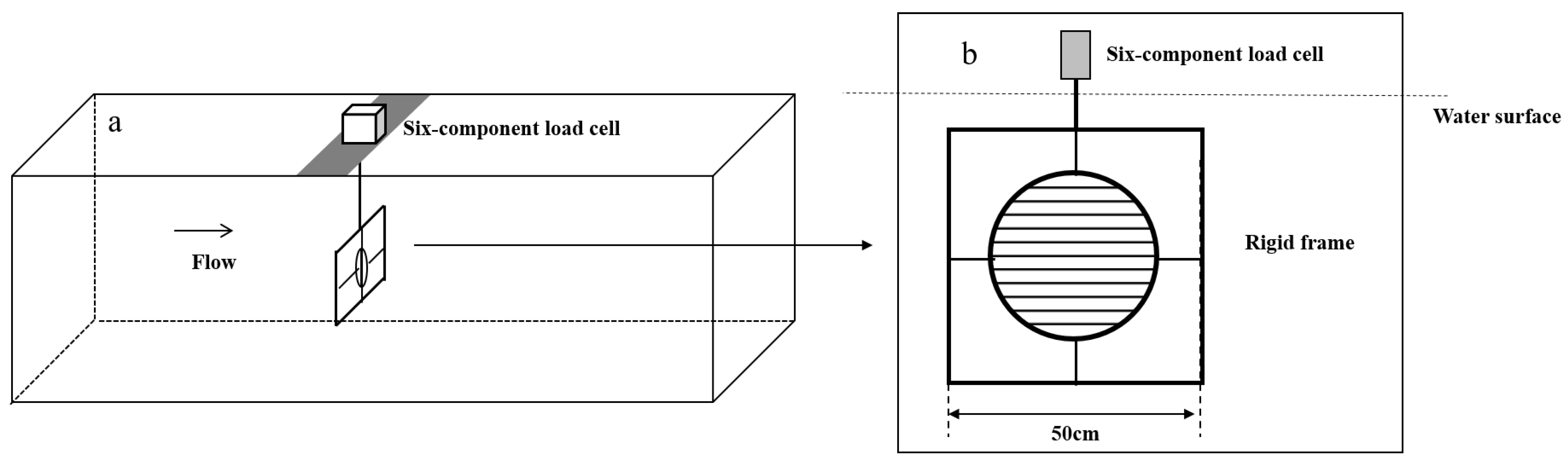
2.2. Physical Model Test Setup
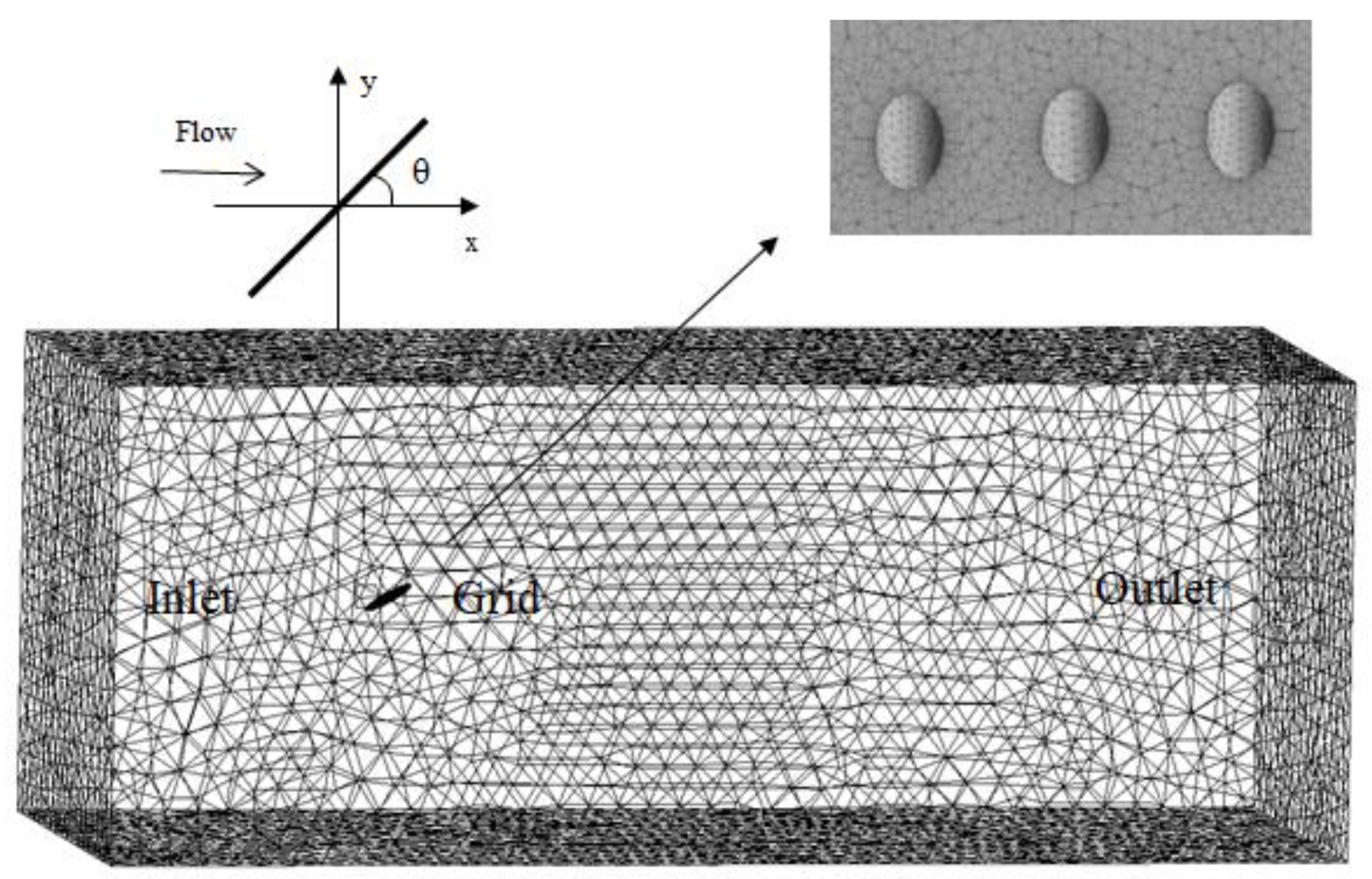
2.3. Numerical Fluid Flow Model
2.4. Data Post-Processing
3. Results
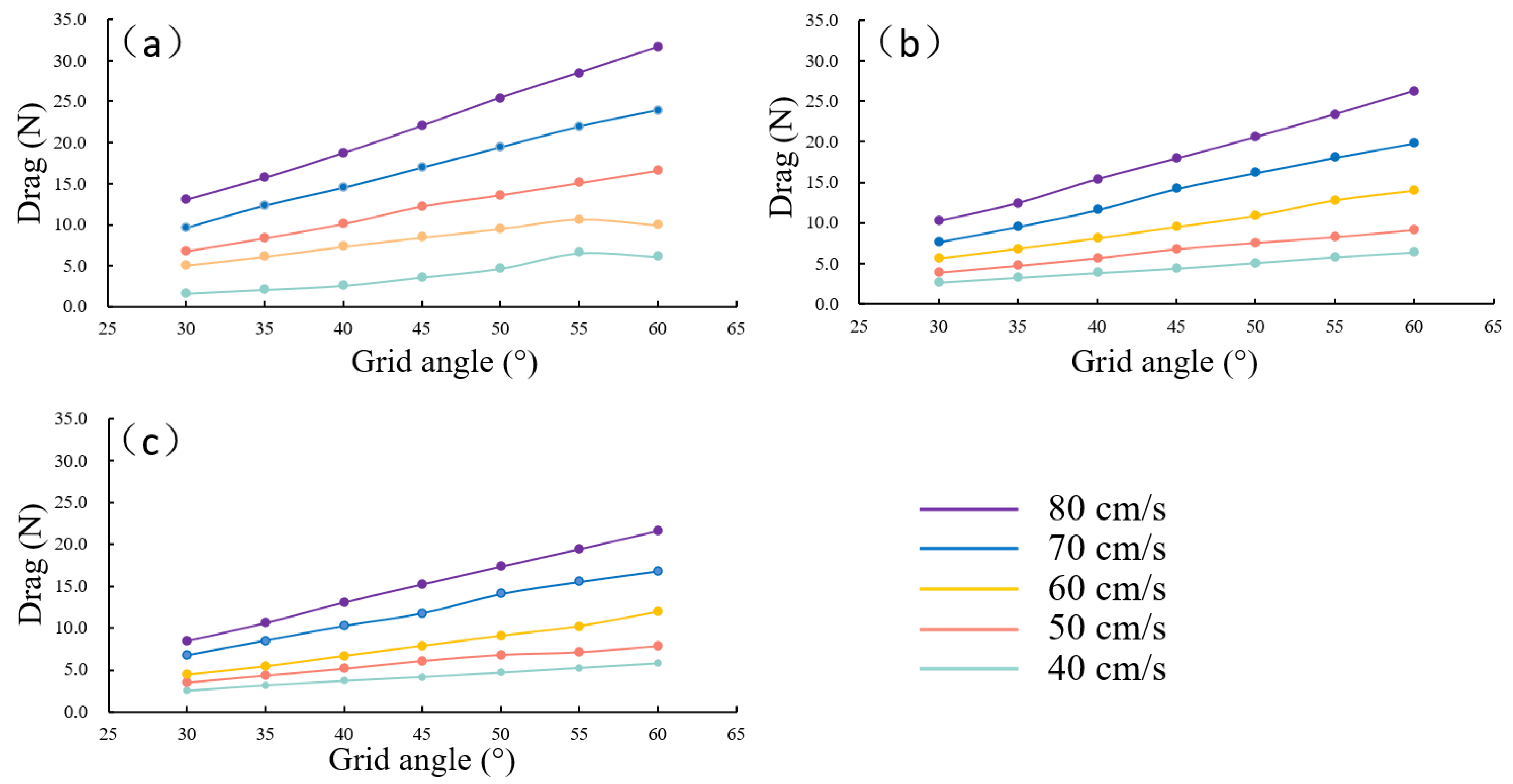
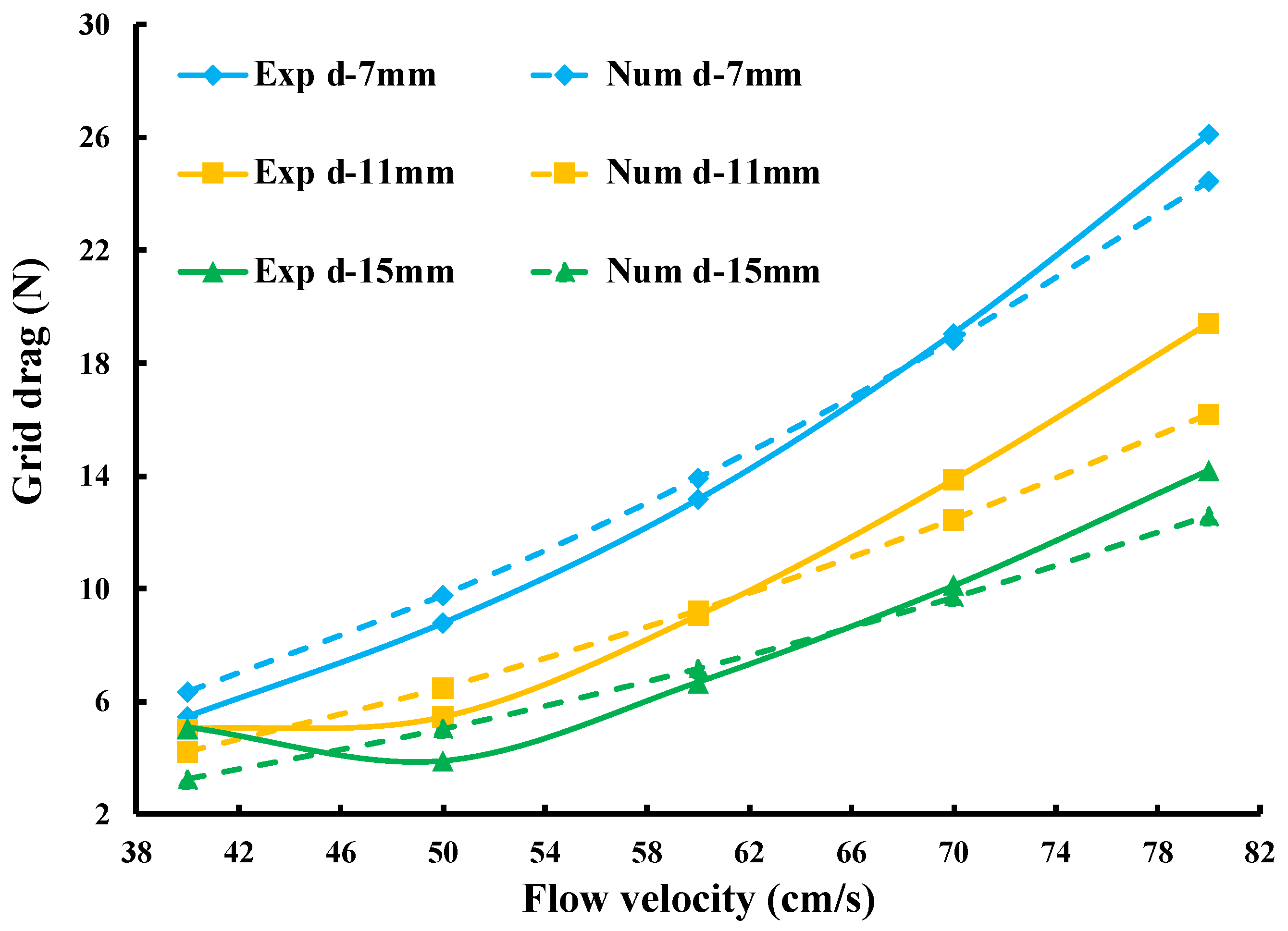
3.1. Influence of Grid Bar Spacing and Inclination Angle on Grid Drag
3.2. Comparison of Drag Forces between Numerical Simulation and Experimental Results
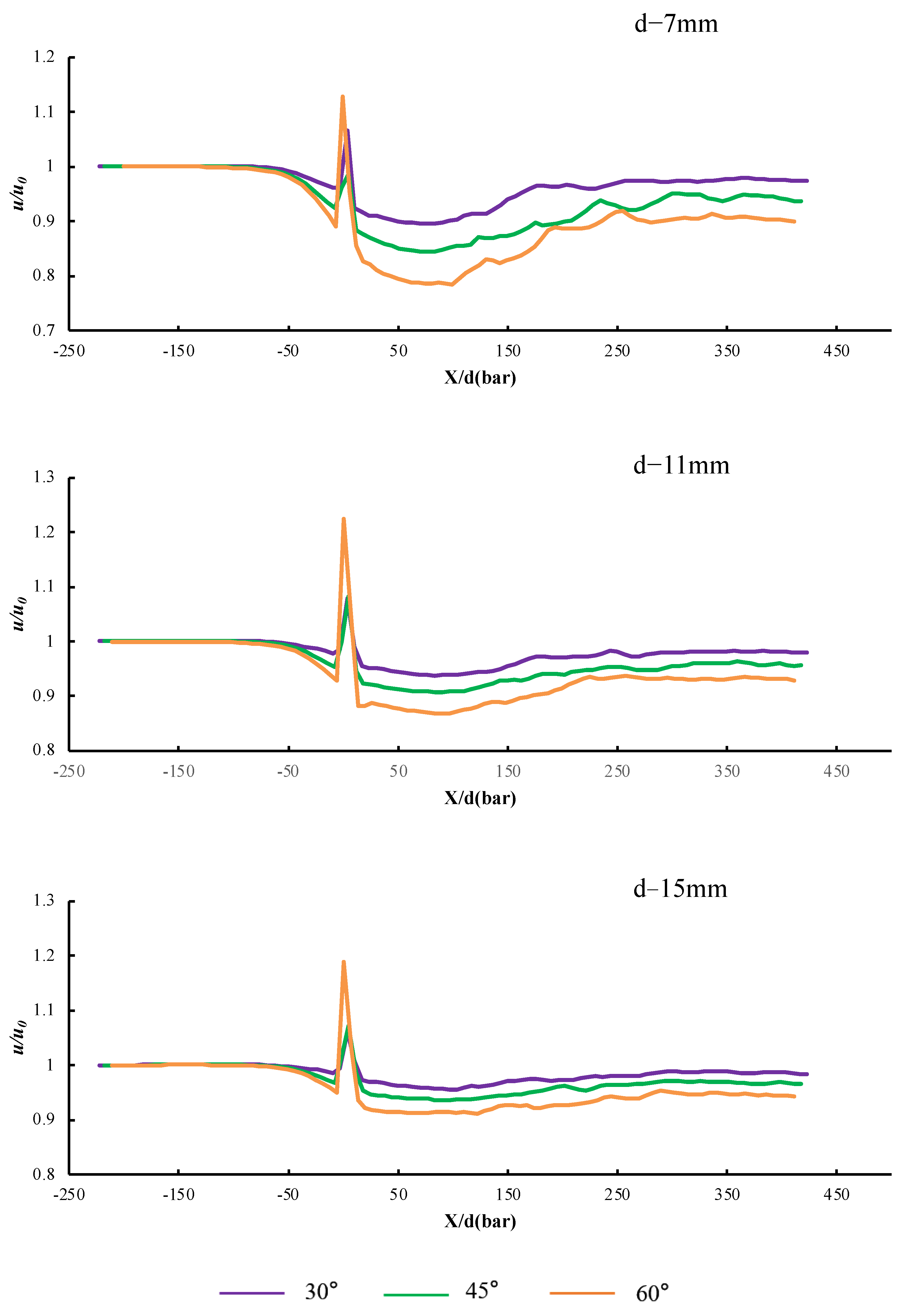
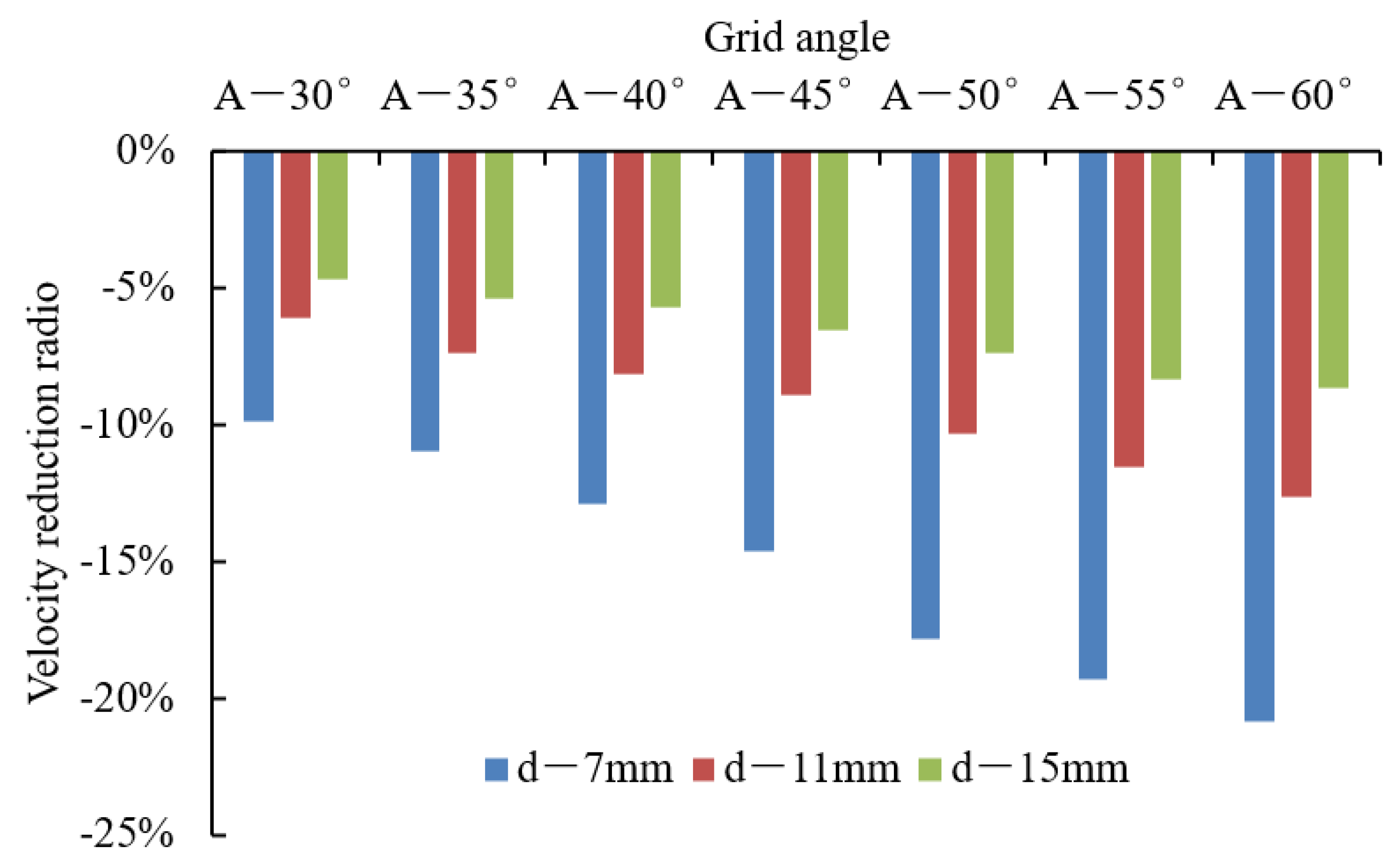
3.3. Velocity Fluctuations about the Grid Bar Centerline
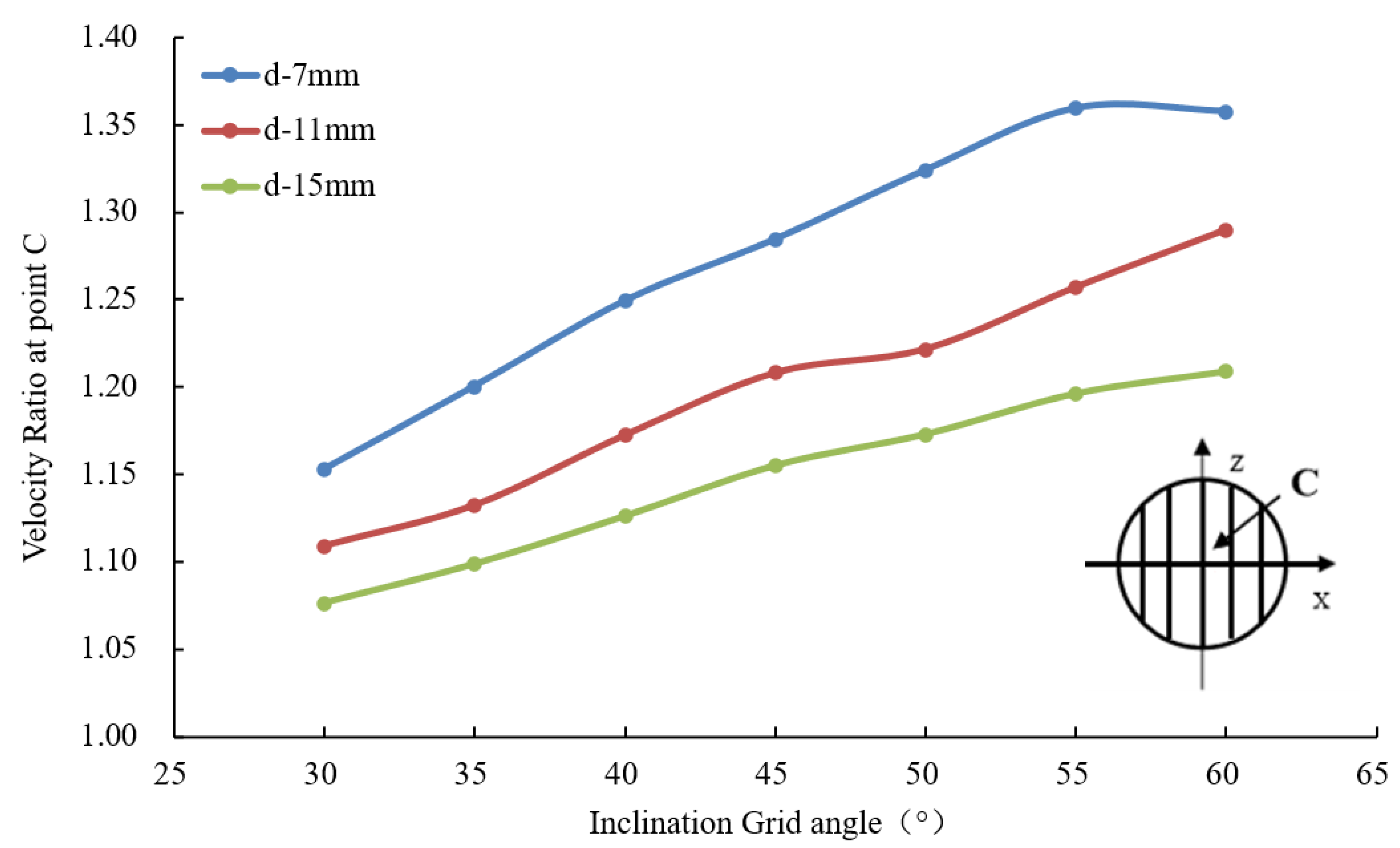
3.4. Velocity Field Curve along the Centerline of the Circular Grid
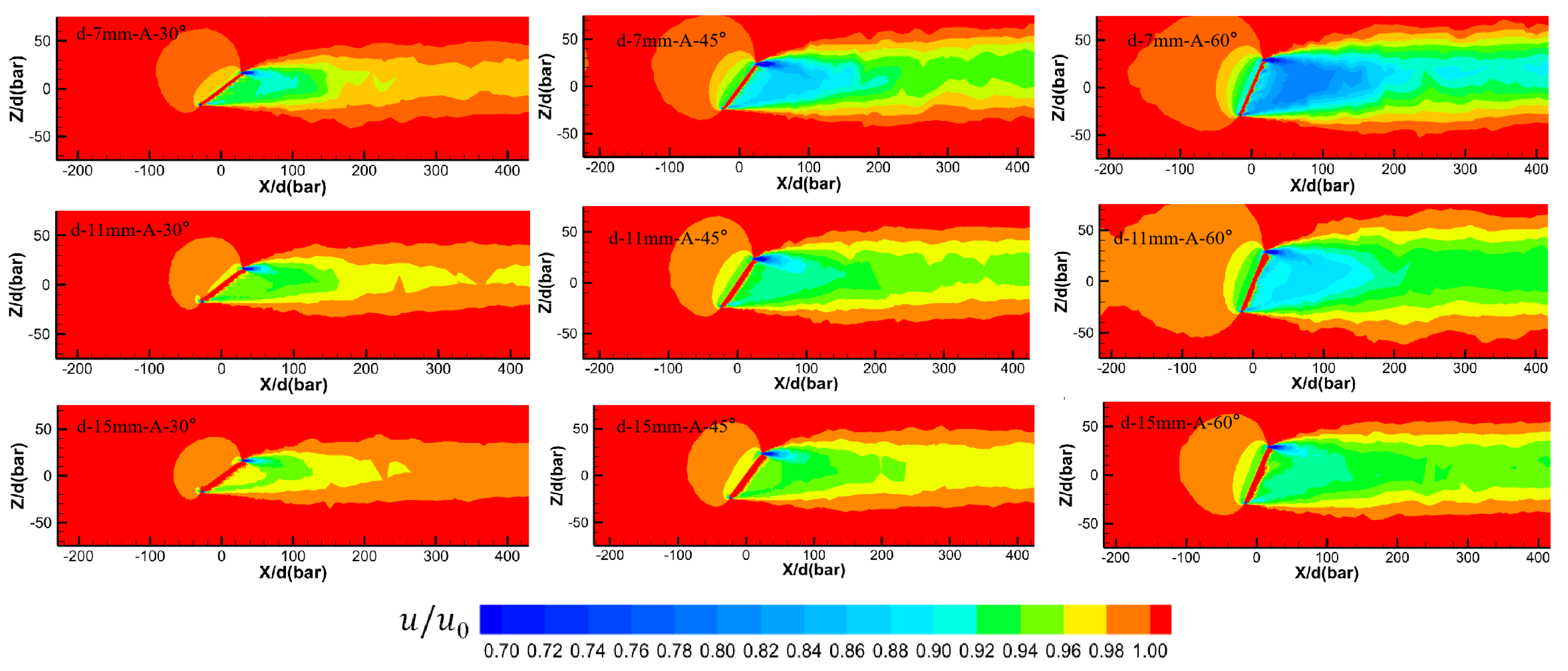
3.5. The Influence of Tilt Angle on the Flow Field Distribution around the Grid
4. Discussion
5. Conclusions
- (1)
- The drag forces of the circular increased with increasing inclination grid angle and decreased with increasing grid bar spacing. Therefore, circular grids with lower inclination grid angles and greater grid bar spacings could yield a lower drag and improve the selectivity of the trawl net;
- (2)
- The drag forces obtained from the numerical simulation were consistent with experimental results, indicating that this CFD method is suitable to simulate the flow field around the BRD;
- (3)
- The flow velocity reduction downstream to the circular flow in the wake region differed significantly depending on the grid bar spacing and grid inclination angle. However, the velocity ratio in the wake region of the circular flow increased with increasing bar spacing and decreasing inclination grid angle;
- (4)
- The results of this study can be used to improve and optimize the design of the combined codend–BRD system, which has a great impact on how the fish move, which, in turn, has an impact on gear selectivity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, X.X.; Huang, H.L.; Chen, X.Z. Research progress on by-catch reduction in the trawl fishery abroad. Mar. Fish. 2007, 8, 263–270. [Google Scholar] [CrossRef]
- Broadhurst, M.K.; Larsen, R.B.; Kennelly, S.J.; McShane, P. Use and success of composite square-mesh codends in reducing bycatch and in improving size-selectivity of prawns in Gulf St. Vincent, South Australia. Fish. Bull. 1999, 97, 434–448. Available online: https://spo.nmfs.noaa.gov/sites/default/files/03broadh.pdf (accessed on 1 June 2022).
- Broadhurst, M.K.; Millar, R.B.; Wooden, M.E.L.; Macbeth, W.G. Optimising codend configuration in a multispecies demersal trawl fishery. Fish. Manag. Ecol. 2006, 13, 81–92. [Google Scholar] [CrossRef]
- Grimaldo, E.; Brinkhof, J.; Herrmann, B.; Macbeth, W.G. Improved bycatch reduction in the mixed demersal trawl fishery for Norway pout (Trisopterus esmarkii). Estuar. Coast. Shelf Sci. 2023, 281, 108189. [Google Scholar] [CrossRef]
- Herrmann, B.; Sistiaga, M.; Larsen, R.B.; Nielsen, K.N.; Grimaldo, E. Understanding sorting grid and codend size selectivity of Greenland halibut (Reinhardtius hippoglossoides). Fish. Res. 2013, 146, 59–73. [Google Scholar] [CrossRef]
- Fan, W.; Sun, M.C. Experimental Studies on the Separation of Shrimp from Fish in Beam Trawling. Mar. Fish. 2000, 4, 106–109. [Google Scholar] [CrossRef]
- Wan, R.; Jia, M.X.; Guan, Q.L.; Huang, L.; Cheng, H.; Zhao, F.; He, P.; Hu, F. Hydrodynamic performance of a newly-designed Antarctic krill trawl using numerical simulation and physical modeling methods. Ocean Eng. 2019, 179, 173–179. [Google Scholar] [CrossRef]
- Eayrs, S. A Guide to Bycatch Reduction in Tropical Shrimp-Trawl Fisheries; Food and Agricultural Organization of the United Nations: Rome, Italy, 2007; pp. 10–25. ISBN 978-925-105-674-5. [Google Scholar]
- Grimaldo, E. The effects of grid angle on a modified Nordmore-grid in the Nordic Shrimp Fishery. Fish. Res. 2006, 77, 53–59. [Google Scholar] [CrossRef]
- Grimaldo, E.; Sistiaga, M.; Herrmann, B.; Cerbule, K.; Grimsmo, L.; Pettersen, H. Trawl Selectivity in the Barents Sea Demersal Fishery. In Fisheries and Aquaculture in the Modern World; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Grimaldo, E.; Larsen, R.B. The cosmos grid: A new design for reducing by-catch in the Nordic shrimp fishery. Fish. Res. 2005, 76, 187–197. [Google Scholar] [CrossRef]
- Feng, C.L.; Huang, H.L.; Chen, X.Z. Significance analysis on the main parameters of single boat mid-water trawl. Mar. Fish. 2007, 5, 8–12. [Google Scholar] [CrossRef]
- Feng, C.L.; Xu, G.D.; Huang, H.L.; Zhang, X.; Li, L.Z.; Zhang, Y.; Chen, X.Z. Efficiency analysis on the circular separator device for shrimp beam trawl. Mar. Fish. 2011, 33, 91–98. (In Chinese) [Google Scholar] [CrossRef]
- Veiga-Malta, T.; Breddermann, K.; Feekings, J.P.; Krag, L.; Paschen, M. Understanding the hydrodynamics of a size sorting grid in a crustacean fishery. Ocean Eng. 2020, 198, 106961. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, J.G.; Zhang, P.; Sun, M.C.; Qian, W.G. Separating performance for shrimps of sorting grid rigged in beam trawls. J. Shanghai Ocean Univ. 2008, 17, 726–733. (In Chinese) [Google Scholar]
- Riedel, R.; DeAlteris, J. Factors affecting hydrodynamic performance of the Nordmøre Grate System: A bycatch reduction device used in the Gulf of Maine shrimp fishery. Fish. Res. 1995, 24, 181–198. [Google Scholar] [CrossRef]
- Rangaraju, P.R.; Olek, J.; Diamond, S. An investigation into the influence of inter-aggregate spacing and the extent of the ITZ on properties of Portland cement concretes. Cem. Concr. Res. 2010, 40, 1601–1608. [Google Scholar] [CrossRef]
- Cha, B.-J.; Cho, S.-K.; Ahn, H.-C.; Kim, I.-O.; Craig, R. Development of a bycatch reduction device (BRD) for shrimp beam trawl using flexible materials. Iran. J. Fish. Sci. 2012, 11, 89–104. [Google Scholar] [CrossRef]
- Bi, C.W.; Zhao, Y.P.; Dong, G.H.; Xu, T.-J.; Gui, F.-K. Experimental investigation of the reduction in flow velocity downstream from a fishing net. Aquac. Eng. 2013, 57, 71–81. [Google Scholar] [CrossRef]
- Bi, C.W.; Zhao, Y.P.; Dong, G.H.; Xu, T.-J.; Gui, F.-K. Numerical simulation of the interaction between flow and flexible nets. J. Fluids Struct. 2014, 45, 180–201. [Google Scholar] [CrossRef]
- Tu, G.; Liu, H.; Ru, Z.; Shao, D.; Yang, W.; Sun, T.; Wang, H.; Gao, Y. Numerical analysis of the flows around fishing plane nets using the lattice Boltzmann method. Ocean Eng. 2020, 214, 107623. [Google Scholar] [CrossRef]
- Yao, H.; Cao, L.; Wu, D.; Gao, Y.; Qin, S.; Yu, F. PIV study on grid-generated turbulence in a free surface flow. Water 2021, 13, 909. [Google Scholar] [CrossRef]
- Nsangue, B.T.N.; Tang, H.; Xu, L.; Hu, F.; Dong, S.; Achille, N.P.; Zou, B. Comparison between physical model testing and numerical simulation using two-way fluid-structure interaction approach of new trawl design for coastal bottom trawl net. Ocean Eng. 2021, 233, 109112. [Google Scholar] [CrossRef]
- Wang, G.; Cui, Y.; Guan, C.; Gong, P.; Wan, R. Effects of Inclination Angles on the Hydrodynamics of Knotless Net Panels in Currents. J. Mar. Sci. Eng. 2023, 11, 1148. [Google Scholar] [CrossRef]
- Hu, F.; Oozeki, Y.; Tokai, T.; Matuda, K. Scale model of a new midwater trawl system for sampling pelagic larval and juvenile fish. Fish. Sci. 2001, 67, 254–259. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Araya-Schmidt, T.; Bayse, S.; Winger, P.; Frank, C.H. Smaller bar spacings in a Nordmøre grid reduces the bycatch of redfish (Sebastes spp.) in the offshore Northern shrimp (Pandalus borealis) fishery of eastern Canada. Aquac. Fish. 2023, 8, 661–671. [Google Scholar] [CrossRef]
- Winger, P.; Eayrs, S.; Glass, C. Fish Behavior Near Bottom Trawls; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; pp. 65–103. ISBN 978-081-381-536-7. [Google Scholar]
- Araya-Schmidt, T.; Bayse, S.M.; Winger, P.D.; Santos, M.R. Juvenile redfish (Sebastes spp.) behavior in response to Nordmøre grid systems in the offshore northern shrimp (Pandalus borealis) fishery of Eastern Canada. Front. Mar. Sci. 2022, 9, 920429. [Google Scholar] [CrossRef]
- Araya-Schmidt, T.; Legge, G.; Santos, M.; Frank, C.H. Flume Tank Testing of an Innovative Footgear Technology Using Simulated Seabeds. J. Ocean Technol. 2021, 16, 2. Available online: https://www.researchgate.net/publication/352374638 (accessed on 1 June 2021).
- Hickey, W.M.; Brothers, G.; Boulos, D.L. Bycatch reduction in the Northern shrimp fishery. Can. Tech. Rep. Fish. Aquat. Sci. 1993, 1964, 41. [Google Scholar] [CrossRef]
- Thierry, B.N.N.; Tang, H.; Xu, L.X.; You, X.; Hu, F.; Achile, N.P.; Kindong, R. Hydrodynamic performance of bottom trawls with different materials, mesh sizes, and twine thicknesses. Fish. Res. 2020, 221, 105403. [Google Scholar] [CrossRef]
- Isaksen, B.; Valdemarsen, J.W.; Larsen, R.B.; Karlsen, L. Reduction of fish by-catch in shrimp trawl using a rigid separator grid in the aft belly. Fish. Res. 1992, 13, 335–352. [Google Scholar] [CrossRef]
- Kim, H.Y. Analysis of the turbulent flow and tilt in the cod-end of a bottom trawl during fishing operations. Ocean Eng. 2013, 64, 100–108. [Google Scholar] [CrossRef]
- Thierry, N.N.B.; Tang, H.; Xu, L.; Hu, F.; You, X.; David, M.A.; Achille, N.P. Identifying the turbulent flow developing in-side and around the bottom trawl by Electromagnetic Current Velocity Meter approach in the flume tank. J. Hydrodyn. 2021, 33, 636–656. [Google Scholar] [CrossRef]


| Case | Total Elements | Fd(N) |
|---|---|---|
| Coarse | 1,997,907 | 5.78 |
| Medium | 3,782,339 | 6.23 |
| Fine | 7,104,885 | 7.63 |
| Finer | 8,851,000 | 7.75 |
| Experiment | - | 7.49 |
| (m/s) | |
|---|---|
| 0.5 | 1911.17 |
| 0.6 | 2293.4 |
| 0.7 | 2675.64 |
| 0.8 | 3057.87 |
| 0.9 | 3440.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Tang, H.; Thierry, N.N.B.; Yin, L.; Zhang, F.; Zhu, M.; Shan, C.; Xu, L.; Hu, F. Flow Field Pattern and Hydrodynamic Characteristics of a Grid Device Made with Various Grid Bar Spacings at Different Inclination Angles. J. Mar. Sci. Eng. 2023, 11, 1966. https://doi.org/10.3390/jmse11101966
Zhang C, Tang H, Thierry NNB, Yin L, Zhang F, Zhu M, Shan C, Xu L, Hu F. Flow Field Pattern and Hydrodynamic Characteristics of a Grid Device Made with Various Grid Bar Spacings at Different Inclination Angles. Journal of Marine Science and Engineering. 2023; 11(10):1966. https://doi.org/10.3390/jmse11101966
Chicago/Turabian StyleZhang, Can, Hao Tang, Nyatchouba Nsangue Bruno Thierry, Liqiang Yin, Feng Zhang, Meixi Zhu, Chenxu Shan, Liuxiong Xu, and Fuxiang Hu. 2023. "Flow Field Pattern and Hydrodynamic Characteristics of a Grid Device Made with Various Grid Bar Spacings at Different Inclination Angles" Journal of Marine Science and Engineering 11, no. 10: 1966. https://doi.org/10.3390/jmse11101966
APA StyleZhang, C., Tang, H., Thierry, N. N. B., Yin, L., Zhang, F., Zhu, M., Shan, C., Xu, L., & Hu, F. (2023). Flow Field Pattern and Hydrodynamic Characteristics of a Grid Device Made with Various Grid Bar Spacings at Different Inclination Angles. Journal of Marine Science and Engineering, 11(10), 1966. https://doi.org/10.3390/jmse11101966







