Empirical Fragility Assessment of Three-Waters and Railway Infrastructure Damaged by the 2015 Illapel Tsunami, Chile
Abstract
:1. Introduction
2. Materials and Methods
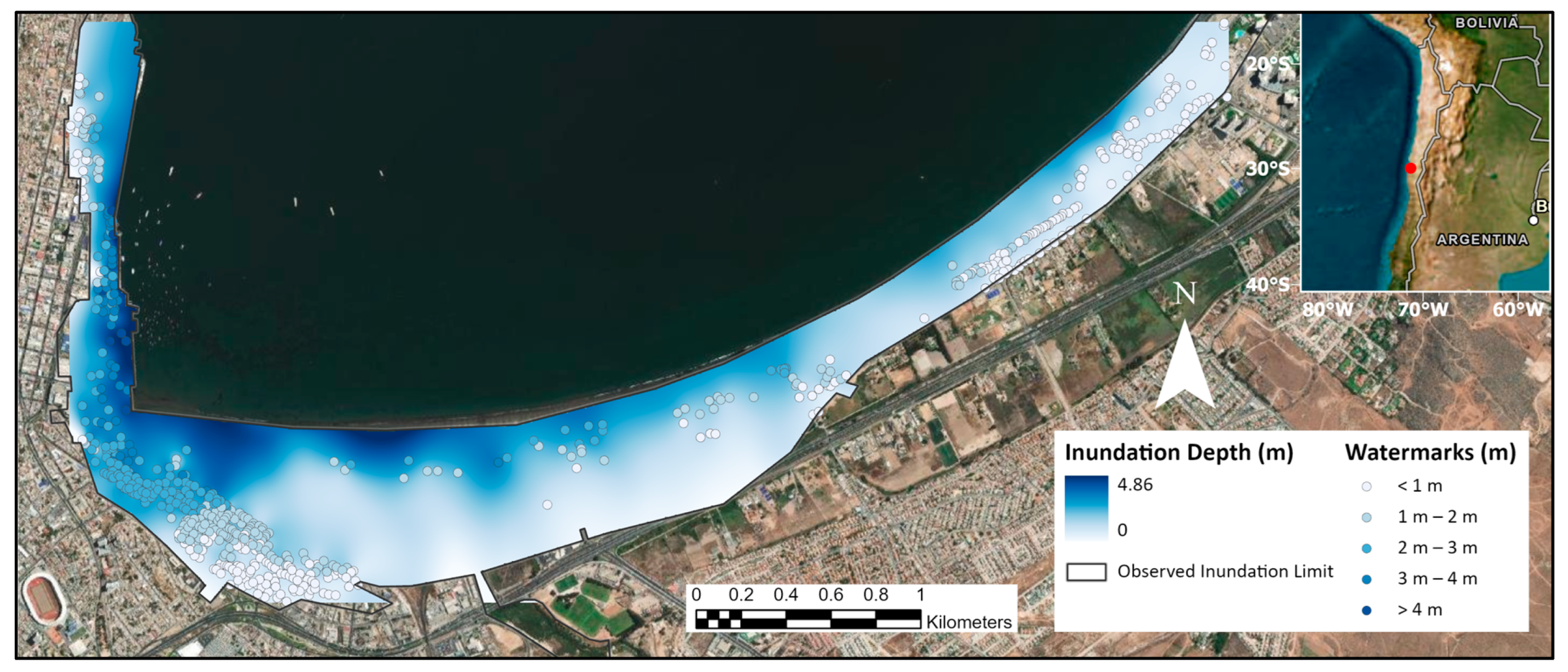
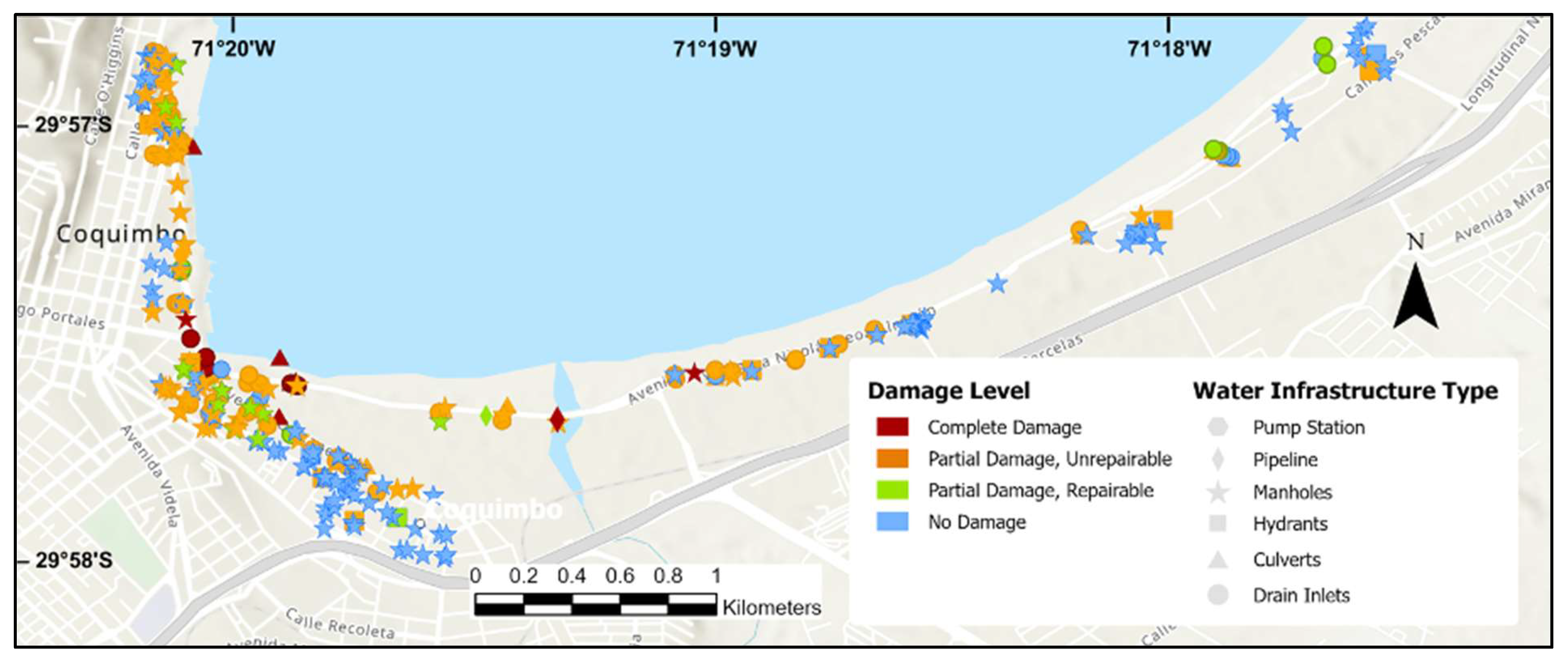
2.1. Survey Data
2.2. Developing Fragility Functions
3. Results and Discussion
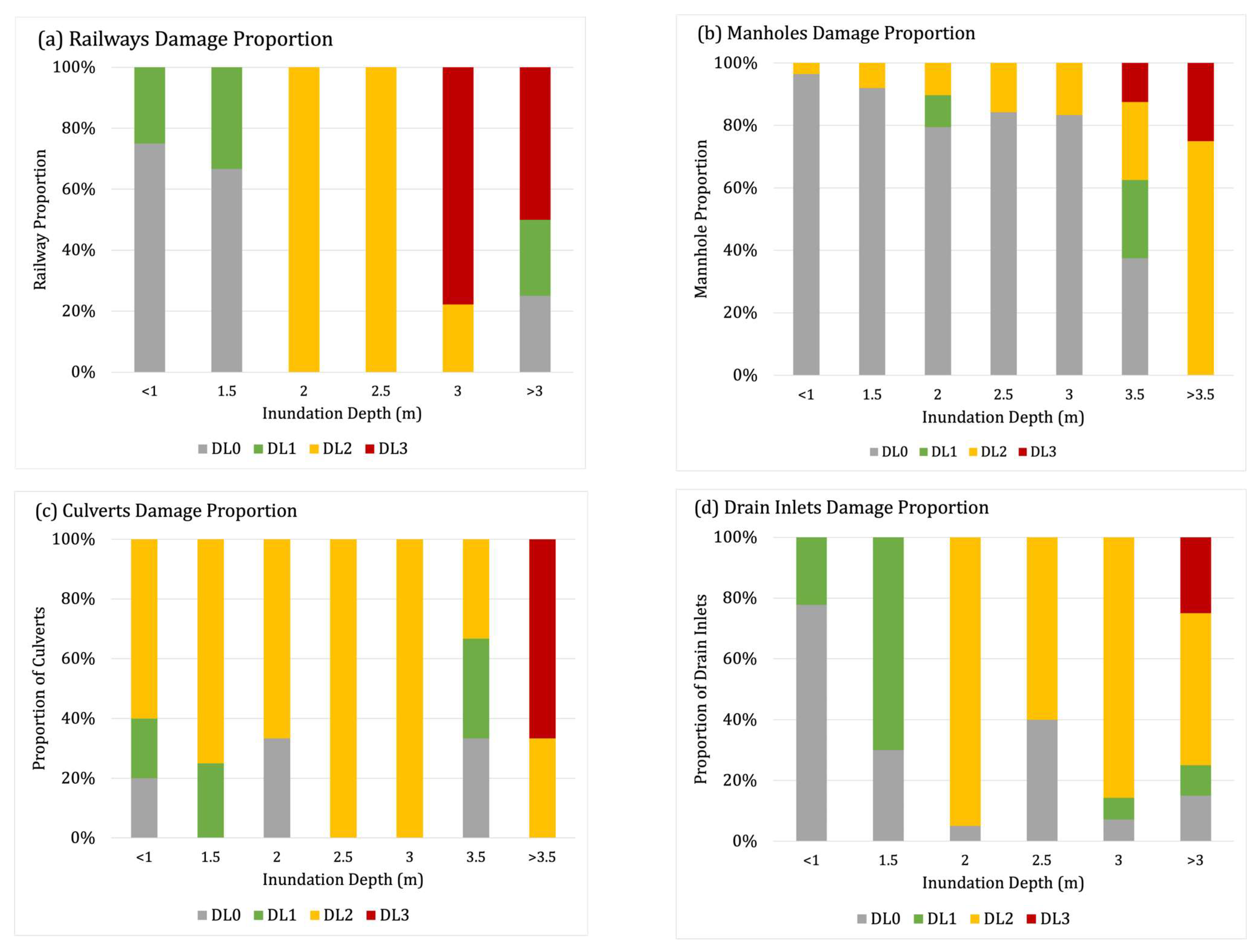
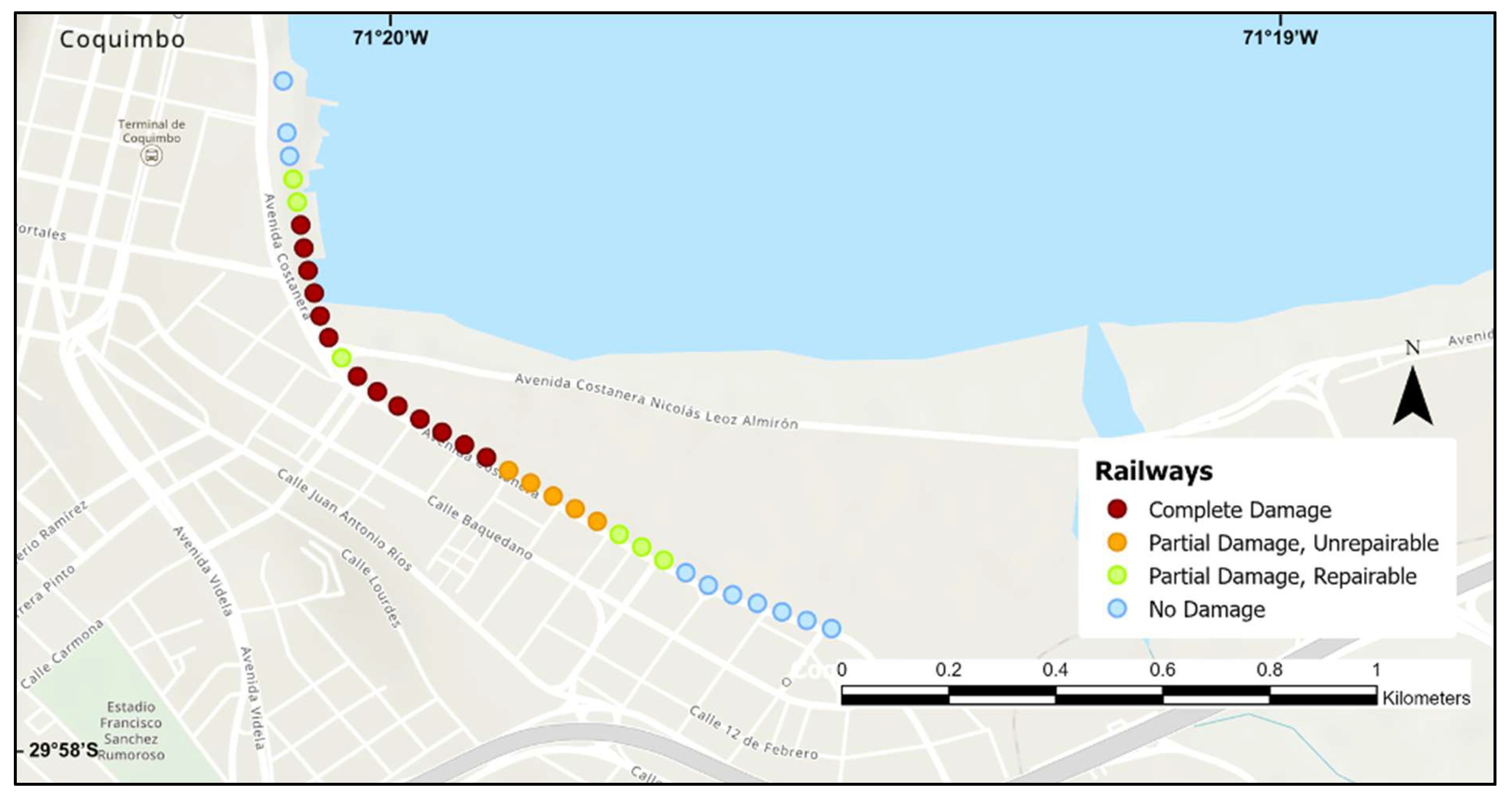
3.1. Network Component Damage Distribution
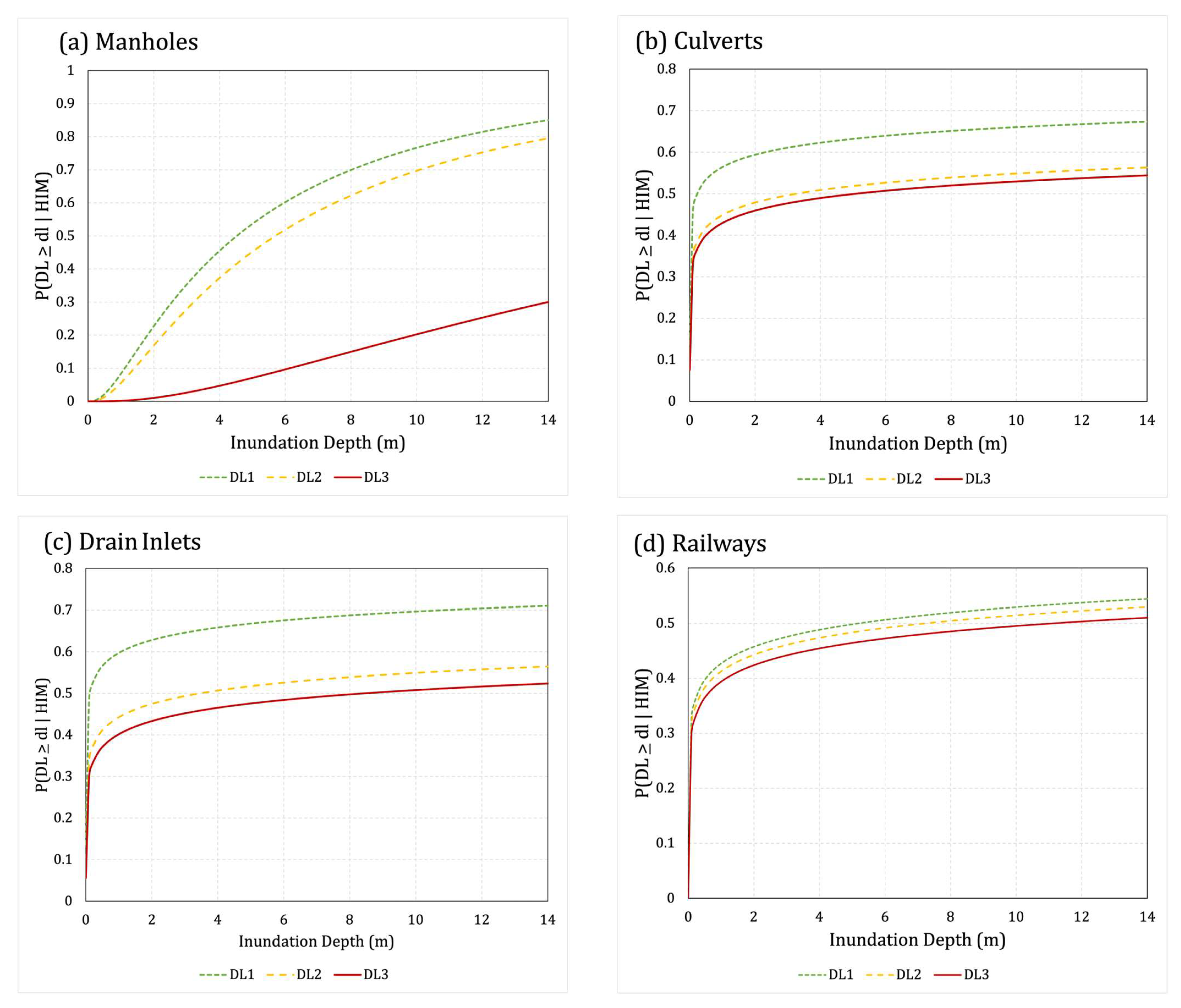
3.2. Three-Waters Infrastructure Fragility Curves
3.3. Railway Infrastructure Fragility Curves
3.4. Fragility Curve Comparison with Network Components
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Palliyaguru, R.; Amaratunga, D. Managing Disaster Risks through Quality Infrastructure and Vice Versa. Struct. Surv. 2008, 26, 426–434. [Google Scholar] [CrossRef]
- Williams, J.H.; Paulik, R.; Wilson, T.M.; Wotherspoon, L.; Rusdin, A.; Pratama, G.M. Tsunami Fragility Functions for Road and Utility Pole Assets Using Field Survey and Remotely Sensed Data from the 2018 Sulawesi Tsunami, Palu, Indonesia. Pure Appl. Geophys. 2020, 177, 3545–3562. [Google Scholar] [CrossRef]
- Jelínek, R.; Krausmann, E.; González, M.; Álvarez-Gómez, J.A.; Birkmann, J.; Welle, T. Approaches for Tsunami Risk Assessment and Application to the City of Cádiz, Spain. Nat. Hazards 2012, 60, 273–293. [Google Scholar] [CrossRef]
- Okumura, N.; Jonkman, S.N.; Esteban, M.; Hofland, B.; Shibayama, T. A Method for Tsunami Risk Assessment: A Case Study for Kamakura, Japan. Nat. Hazards 2017, 88, 1451–1472. [Google Scholar] [CrossRef]
- UNISDR (United Nations International Strategy for Disaster Reduction) Sendai Framework for Disaster Risk Reduction 2015–2030. Available online: http://www.wcdrr.org/uploads/Sendai_Framework_for_Disaster_Risk_Reduction_2015-2030.pdf (accessed on 9 March 2023).
- Koshimura, S.; Oie, T.; Yanagisawa, H.; Imamura, F. Developing Fragility Functions for Tsunami Damage Estimation Using Numerical Model and Post-Tsunami Data from Banda Aceh, Indonesia. Coast. Eng. J. 2009, 51, 243–273. [Google Scholar] [CrossRef]
- Lallemant, D.; Kiremidjian, A.; Burton, H. Statistical Procedures for Developing Earthquake Damage Fragility Curves. Earthq. Eng. Struct. Dyn. 2015, 44, 1373–1389. [Google Scholar] [CrossRef]
- Williams, J.H.; Wilson, T.M.; Horspool, N.; Lane, E.M.; Hughes, M.W.; Davies, T.; Le, L.; Scheele, F. Tsunami Impact Assessment: Development of Vulnerability Matrix for Critical Infrastructure and Application to Christchurch, New Zealand. Nat. Hazards 2019, 96, 1167–1211. [Google Scholar] [CrossRef]
- Williams, J.H.; Wilson, T.M.; Wotherspoon, L.; Paulik, R.; Lane, E.M.; Horspool, N.; Weir, A.; Hughes, M.W.; Schoenfeld, M.R.; Brannigan, D.; et al. Tsunami Damage and Post-Event Disruption Assessment of Road and Electricity Infrastructure: A Collaborative Multi-Agency Approach in Ōtautahi Christchurch, Aotearoa New Zealand. Int. J. Disaster Risk Reduct. 2022, 72, 102841. [Google Scholar] [CrossRef]
- González-Riancho, P.; Aliaga, B.; Hettiarachchi, S.; González, M.; Medina, R. A Contribution to the Selection of Tsunami Human Vulnerability Indicators: Conclusions from Tsunami Impacts in Sri Lanka and Thailand (2004), Samoa (2009), Chile (2010) and Japan (2011). Nat. Hazards Earth Syst. Sci. 2015, 15, 1493–1514. [Google Scholar] [CrossRef]
- Álvarez-Gómez, J.A.; Aniel-Quiroga, Í.; Gutiérrez-Gutiérrez, O.Q.; Larreynaga, J.; González, M.; Castro, M.; Gavidia, F.; Aguirre-Ayerbe, I.; González-Riancho, P.; Carreño, E. Tsunami Hazard Assessment in El Salvador, Central America, from Seismic Sources through Flooding Numerical Models. Nat. Hazards Earth Syst. Sci. 2013, 13, 2927–2939. [Google Scholar] [CrossRef]
- Aránguiz, R.; Urra, L.; Okuwaki, R.; Yagi, Y. Development and Application of a Tsunami Fragility Curve of the 2015 Tsunami in Coquimbo, Chile. Nat. Hazards Earth Syst. Sci. 2018, 18, 2143–2160. [Google Scholar] [CrossRef]
- Di Bacco, M.; Rotello, P.; Suppasri, A.; Scorzini, A.R. Leveraging Data Driven Approaches for Enhanced Tsunami Damage Modelling: Insights from the 2011 Great East Japan Event. Environ. Model. Softw. 2023, 160, 105604. [Google Scholar] [CrossRef]
- Virtriana, R.; Harto, A.B.; Atmaja, F.W.; Meilano, I.; Fauzan, K.N.; Anggraini, T.S.; Ihsan, K.T.N.; Mustika, F.C.; Suminar, W. Machine Learning Remote Sensing Using the Random Forest Classifier to Detect the Building Damage Caused by the Anak Krakatau Volcano Tsunami. Geomat. Nat. Hazards Risk 2023, 14, 28–51. [Google Scholar] [CrossRef]
- Izquierdo, T.; Fritis, E.; Abad, M. Analysis and Validation of the PTVA Tsunami Building Vulnerability Model Using the 2015 Chile Post-Tsunami Damage Data in Coquimbo and La Serena Cities. Nat. Hazards Earth Syst. Sci. 2018, 18, 1703–1716. [Google Scholar] [CrossRef]
- Tarbotton, C.; Dall’Osso, F.; Dominey-Howes, D.; Goff, J. The Use of Empirical Vulnerability Functions to Assess the Response of Buildings to Tsunami Impact: Comparative Review and Summary of Best Practice. Earth Sci. Rev. 2015, 142, 120–134. [Google Scholar] [CrossRef]
- Akiyama, M.; Frangopol, D.M.; Arai, M.; Koshimura, S. Reliability of Bridges under Tsunami Hazards: Emphasis on the 2011 Tohoku-Oki Earthquake. Earthq. Spectra 2013, 29, 295–314. [Google Scholar] [CrossRef]
- Suppasri, A.; Mas, E.; Charvet, I.; Gunasekera, R.; Imai, K.; Fukutani, Y.; Abe, Y.; Imamura, F. Building Damage Characteristics Based on Surveyed Data and Fragility Curves of the 2011 Great East Japan Tsunami. Nat. Hazards 2013, 66, 319–341. [Google Scholar] [CrossRef]
- Macabuag, J.; Rossetto, T.; Ioannou, I.; Eames, I. Investigation of the Effect of Debris-Induced Damage for Constructing Tsunami Fragility Curves for Buildings. Geosciences 2018, 8, 117. [Google Scholar] [CrossRef]
- Williams, J.H.; Wilson, T.M.; Horspool, N.; Paulik, R.; Wotherspoon, L.; Lane, E.M.; Hughes, M.W. Assessing Transportation Vulnerability to Tsunamis: Utilising Post-Event Field Data from the 2011 Tōhoku Tsunami, Japan, and the 2015 Illapel Tsunami, Chile. Nat. Hazards Earth Syst. Sci. 2020, 20, 451–470. [Google Scholar] [CrossRef]
- USGS M 8.3–48 Km W of Illapel, Chile (2015). Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us20003k7a/technical (accessed on 9 March 2023).
- Aránguiz, R.; González, G.; González, J.; Catalán, P.A.; Cienfuegos, R.; Yagi, Y.; Okuwaki, R.; Urra, L.; Contreras, K.; Del Rio, I.; et al. The 16 September 2015 Chile Tsunami from the Post-Tsunami Survey and Numerical Modeling Perspectives. Pure Appl. Geophys. 2016, 173, 333–348. [Google Scholar] [CrossRef]
- Paulik, R.; Williams, J.H.; Horspool, N.; Catalan, P.A.; Mowll, R.; Cortés, P.; Woods, R. The 16 September 2015 Illapel Earthquake and Tsunami: Post-Event Tsunami Inundation, Building and Infrastructure Damage Survey in Coquimbo, Chile. Pure Appl. Geophys. 2021, 178, 4837–4851. [Google Scholar] [CrossRef]
- Tomita, T.; Arikawa, T.; Takagawa, T.; Honda, K.; Chida, Y.; Sase, K.; Olivares, R.A.O. Results of Post-Field Survey on the Mw 8.3 Illapel Earthquake Tsunami in 2015. Coast. Eng. J. 2016, 58, 1650003-1-1650003–1650017. [Google Scholar] [CrossRef]
- Williams, J.; Paulik, R.; Aránguiz, R.; Wild, A. Infrastructure Network Component Vulnerability to Damage from the 2015 Illapel Tsunami, Coquimbo, Chile. Res. Sq. 2022; preprint. [Google Scholar] [CrossRef]
- Baldi, P.; Brunak, S.; Chauvin, Y.; Andersen, C.A.F.; Nielsen, H. Assessing the Accuracy of Prediction Algorithms for Classification: An Overview. Bioinformatics 2000, 16, 412–424. [Google Scholar] [CrossRef] [PubMed]
- Charvet, I.; Suppasri, A.; Kimura, H.; Sugawara, D.; Imamura, F. A Multivariate Generalized Linear Tsunami Fragility Model for Kesennuma City Based on Maximum Flow Depths, Velocities and Debris Impact, with Evaluation of Predictive Accuracy. Nat. Hazards 2015, 79, 2073–2099. [Google Scholar] [CrossRef]
- Eguchi, R.T.; Eguchi, M.T.; Bouabid, J.; Koshimura, S.; Graf, W.P. HAZUS Tsunami Benchmarking, Validation and Calibration; 2013. National Weather Service (NWS). Available online: https://nws.weather.gov/nthmp/2013mesmms/abstracts/TsunamiHAZUSreport.pdf (accessed on 13 July 2023).
- Graf, W.P.; Lee, Y.; Eguchi, R.T. New Lifelines Damage and Loss Function For Tsunami. In Proceedings of the 10th National Conference in Earthquake Engineering, Earthquake Engineering Research Institute, Anchorage, AK, USA, 21–25 July 2014; Available online: https://datacenterhub.org/resources/11732/download/10NCEE-000350.pdf (accessed on 13 June 2023).
- Marchand, M.; Buurman, J.; Pribadi, A.; Kurniawan, A. Damage and Casualties Modelling as Part of a Vulnerability Assessment for Tsunami Hazards: A Case Study from Aceh, Indonesia. J. Flood Risk Manag. 2009, 2, 120–131. [Google Scholar] [CrossRef]
- Duc, B.M.; Rodi, W. Numerical Simulation of Contraction Scour in an Open Laboratory Channel. J. Hydraul. Eng. 2008, 134, 367–377. [Google Scholar] [CrossRef]
- Sullivan, P.P.; McWilliams, J.C.; Moeng, C.-H. Simulation of Turbulent Flow over Idealized Water Waves. J. Fluid Mech. 2000, 404, 47–85. [Google Scholar] [CrossRef]
- Muhammad, N.; Ullah, N. Simulation of Flow on the Hydroelectric Power Dam Spillway via OpenFOAM. Eur. Phys. J. Plus 2021, 136, 1191. [Google Scholar] [CrossRef]
- Horspool, N.A.; Fraser, S. An Analysis of Tsunami Impacts to Lifelines. GNS Science 2016. Available online: https://www.eqc.govt.nz/assets/Publications-Resources/1605-Analysis-of-tsuami-impacts-to-lifelines.pdf (accessed on 3 October 2023).
- Reese, S.; Bradley, B.A.; Bind, J.; Smart, G.; Power, W.; Sturman, J. Empirical Building Fragilities from Observed Damage in the 2009 South Pacific Tsunami. Earth Sci. Rev. 2011, 107, 156–173. [Google Scholar] [CrossRef]
- Fritz, H.M.; Petroff, C.M.; Catalán, P.A.; Cienfuegos, R.; Winckler, P.; Kalligeris, N.; Weiss, R.; Barrientos, S.E.; Meneses, G.; Valderas-Bermejo, C.; et al. Field Survey of the 27 February 2010 Chile Tsunami. Pure Appl. Geophys. 2011, 168, 1989–2010. [Google Scholar] [CrossRef]
- Rossetto, T.; D’Ayala, D.; Ioannou, I.; Meslem, A. Evaluation of Existing Fragility Curves; Pitilakis, K., Crowley, H., Kaynia, A.M., Eds.; Springer: Dordrecht, The Netherlands, 2014; Volume 27, ISBN 978-94-007-7871-9. [Google Scholar]
- De Risi, R.; Goda, K.; Yasuda, T.; Mori, N. Is Flow Velocity Important in Tsunami Empirical Fragility Modeling? Earth Sci. Rev. 2017, 166, 64–82. [Google Scholar] [CrossRef]
| Component Type | DL0 | DL1 | DL2 | DL3 |
|---|---|---|---|---|
| No Damage | Partial Damage, Repairable | Partial Damage, Unrepairable | Complete Damage | |
| Railway | - | Minor scour of ballast, tracks in place | Scour to ballast, tracks pushed off ballast | Complete washout of ballast and tracks |
| Culvert | - | Minor scour around the culvert, may be blocked | Culvert heavily scoured out but in place, scour or aggradation may render culvert useless | Culvert completely scoured out, washed away |
| Manhole | - | Minor scour around manhole/foundation, minor damage to cover | Moderate–major damage to manhole surface or cover, shaft in place | Manhole shaft scoured out, washed away |
| Drain Inlet | - | Minor damage to grate, no damage to subsurface, temporary blockage or capacity reduction | Grate damaged, drain blocked, scour around drain, requires sediment removal or replacement | Drain inlet completely scoured out, washed away |
| Infrastructure Type | Flow Depth | Damage Level | |||||
|---|---|---|---|---|---|---|---|
| <1 m | m | >2 m | DL0 | DL1 | DL2 | DL3 | |
| Manholes | 56 | 64 | 69 | 147 | 12 | 28 | 2 |
| Culverts | 3 | 5 | 18 | 5 | 1 | 14 | 6 |
| Drain Inlets | 9 | 29 | 41 | 10 | 8 | 57 | 4 |
| Hydrants | 6 | 4 | 4 | 4 | 1 | 9 | 0 |
| Pipes | - | 2 | - | - | 1 | - | 1 |
| Pump Stations | - | 1 | - | - | - | 1 | - |
| Railways | 50 m | 550 m | 1100 m | 500 m | 300 m | 250 m | 650 m |
| Fragility Curve | Damage Level | μ | σ | Accuracy |
|---|---|---|---|---|
| Manholes | DL1 | 1.51 | 1.09 | 83% |
| DL2 | 1.74 | 1.09 | ||
| DL3 | 3.21 | 1.09 | ||
| Culverts | DL1 | −1.48 | 9.16 | 12% |
| DL2 | 1.18 | 9.16 | ||
| DL3 | 1.63 | 9.16 | ||
| Drain Inlets | DL1 | −2.12 | 8.58 | 19% |
| DL2 | 1.23 | 8.58 | ||
| DL3 | 2.13 | 8.58 | ||
| Railways | DL1 | 1.65 | 8.94 | 29% |
| DL2 | 1.98 | 8.94 | ||
| DL3 | 2.41 | 8.94 |
| Infrastructure Type | DL3 Probability at 2 m Inundation Depth | Source |
|---|---|---|
| Manholes | 0.01 | Present study |
| Culverts | 0.46 | |
| Drain Inlets | 0.43 | |
| Railways | 0.42 | |
| Mixed Roads | 0.07 | Williams et al. [2] |
| Asphalt Roads | 0.09 | |
| Concrete Roads | 0.04 | |
| Mixed-Attribute Utility Poles | 0.13 | |
| Mixed Roads | ≈0.05 | Williams et al. [20] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodwell, J.; Williams, J.H.; Paulik, R. Empirical Fragility Assessment of Three-Waters and Railway Infrastructure Damaged by the 2015 Illapel Tsunami, Chile. J. Mar. Sci. Eng. 2023, 11, 1991. https://doi.org/10.3390/jmse11101991
Rodwell J, Williams JH, Paulik R. Empirical Fragility Assessment of Three-Waters and Railway Infrastructure Damaged by the 2015 Illapel Tsunami, Chile. Journal of Marine Science and Engineering. 2023; 11(10):1991. https://doi.org/10.3390/jmse11101991
Chicago/Turabian StyleRodwell, Jessica, James H. Williams, and Ryan Paulik. 2023. "Empirical Fragility Assessment of Three-Waters and Railway Infrastructure Damaged by the 2015 Illapel Tsunami, Chile" Journal of Marine Science and Engineering 11, no. 10: 1991. https://doi.org/10.3390/jmse11101991
APA StyleRodwell, J., Williams, J. H., & Paulik, R. (2023). Empirical Fragility Assessment of Three-Waters and Railway Infrastructure Damaged by the 2015 Illapel Tsunami, Chile. Journal of Marine Science and Engineering, 11(10), 1991. https://doi.org/10.3390/jmse11101991






