Experimental Parameters Influencing the Cavitation Noise of an Oscillating NACA0015 Hydrofoil
Abstract
:1. Introduction
2. Materials and Methods
2.1. Nomenclature and Symbols
| AoA | angle of attack [°] |
| c | chord length [m] |
| reduced frequency of oscillation = | |
| absolute frequency of oscillation [Hz] | |
| limiting frequency of the FIR filter pass band [Hz] | |
| limiting frequency of the FIR filter stop band [Hz] | |
| sound pressure, time dependent [Pa] | |
| ambient pressure in cavitation tunnel [Pa] | |
| vapor pressure of water [Pa] | |
| r | distance sound source—receiver [m] |
| U | flow velocity [m/s] |
| cavitation volume, time dependent [m] | |
| FIR filter attenuation in the pass band [dB] | |
| FIR filter attenuation in the stop band [dB] | |
| frequency resolution in sound pressure level spectra [Hz] | |
| water density [kg/m] | |
| cavitation number = | |
| 𝆇 | saw-tooth shaped course of AoA with a fast increase |
| ∧ | equilateral course of AoA |
| ⩘ | saw-tooth shaped course of AoA with a fast decrease |
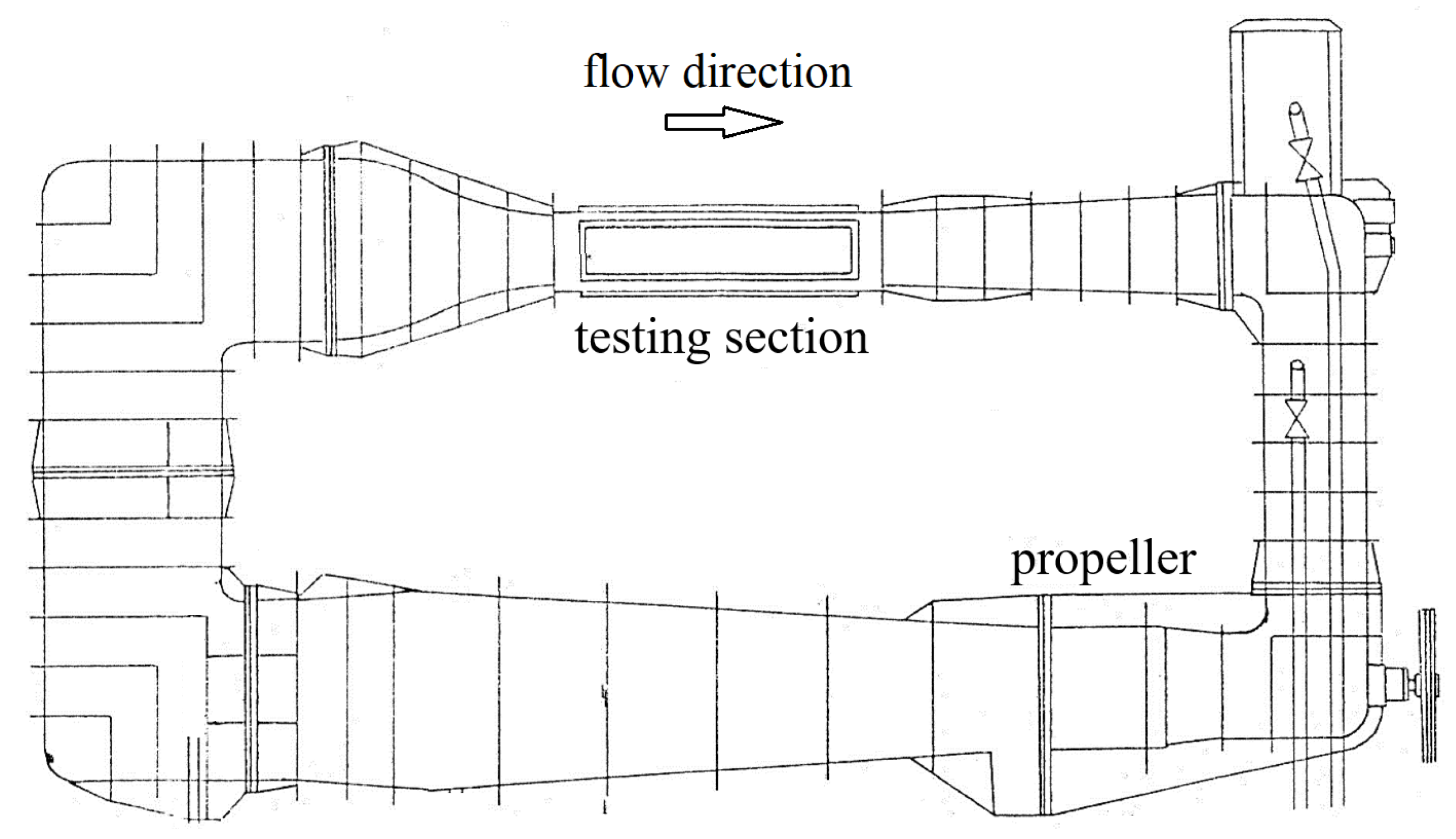
2.2. Experimental Setup
2.3. Post-Processing of Measurement Data
3. Results
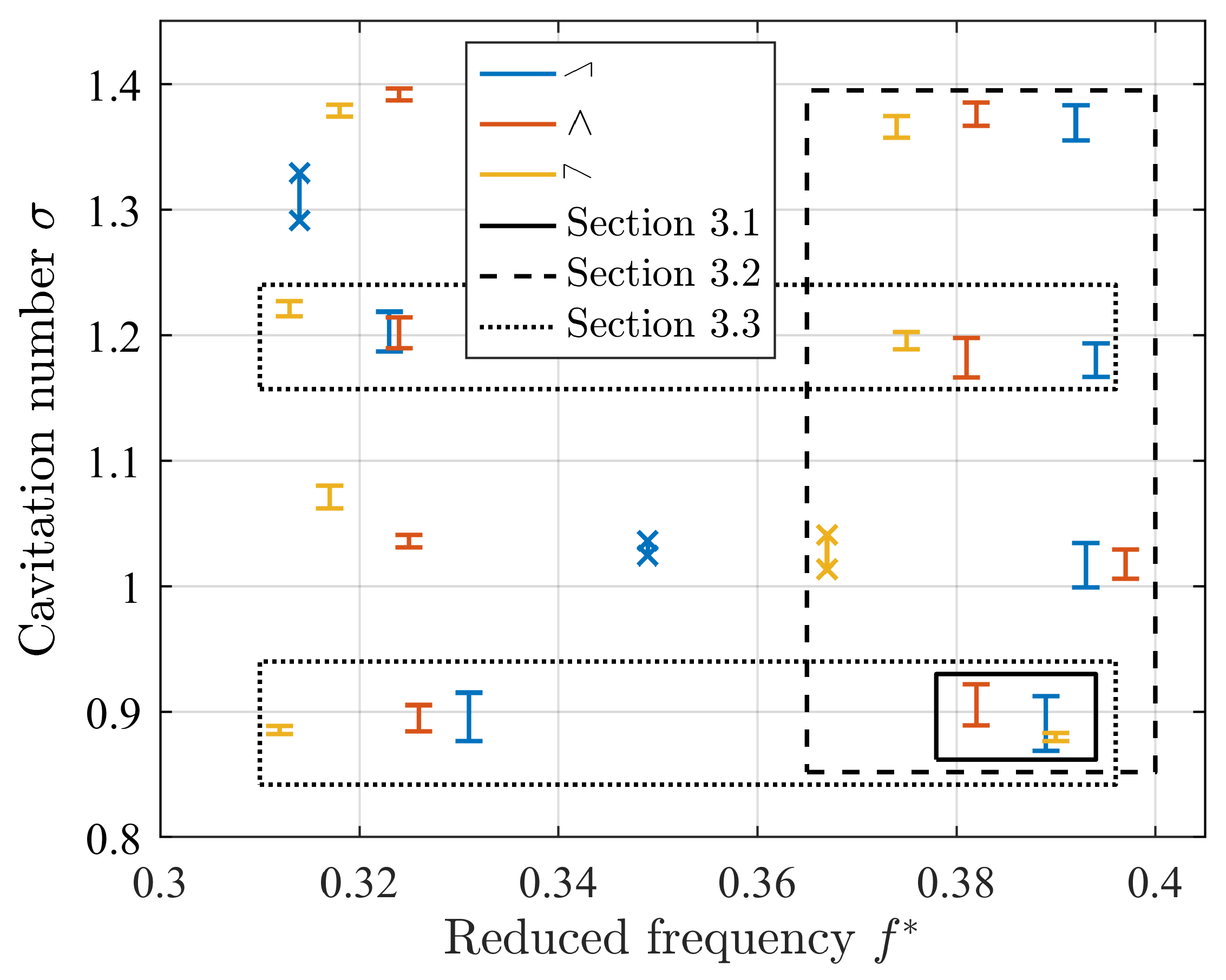
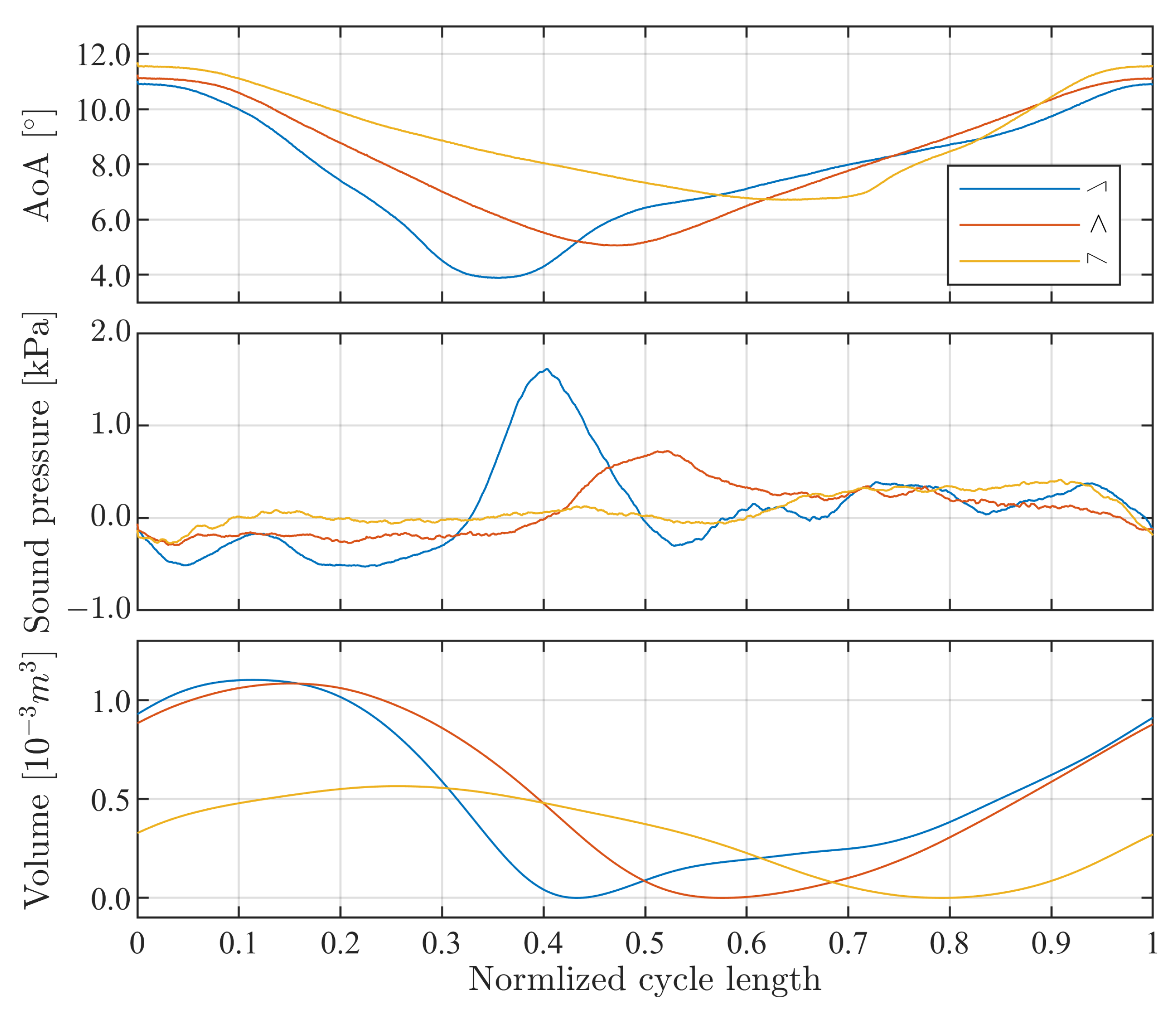
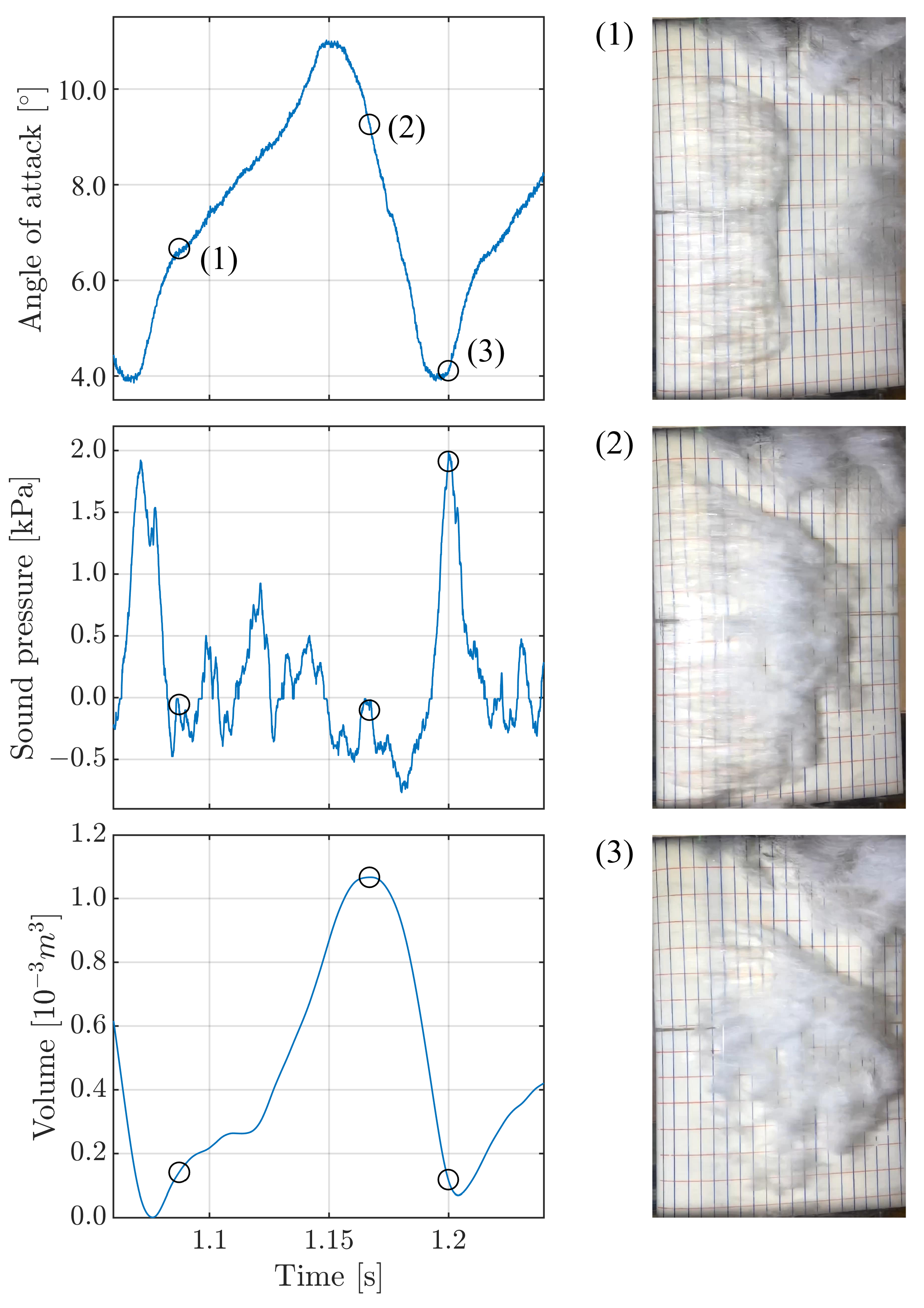
3.1. Influence of the Course of the Angle of Attack
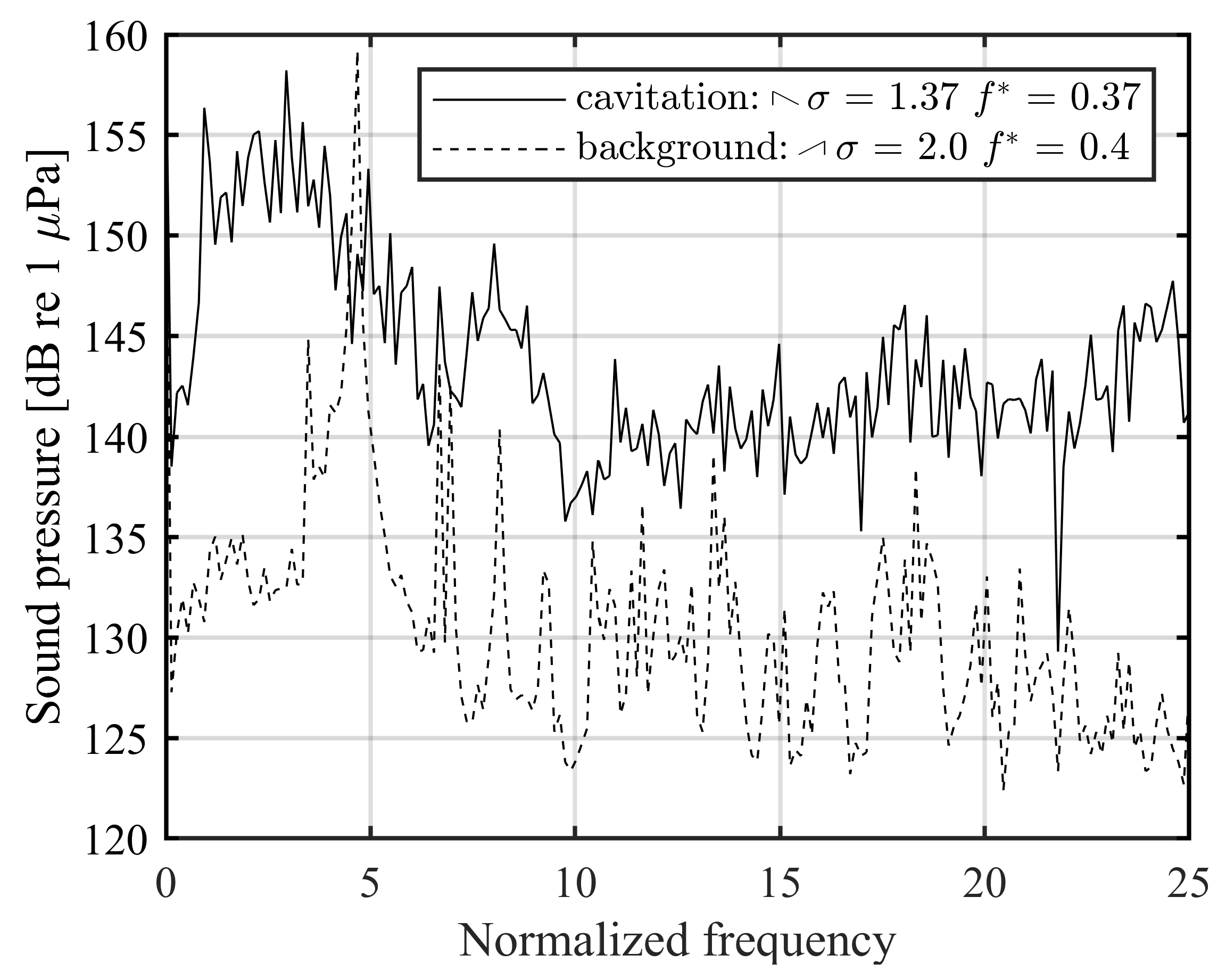
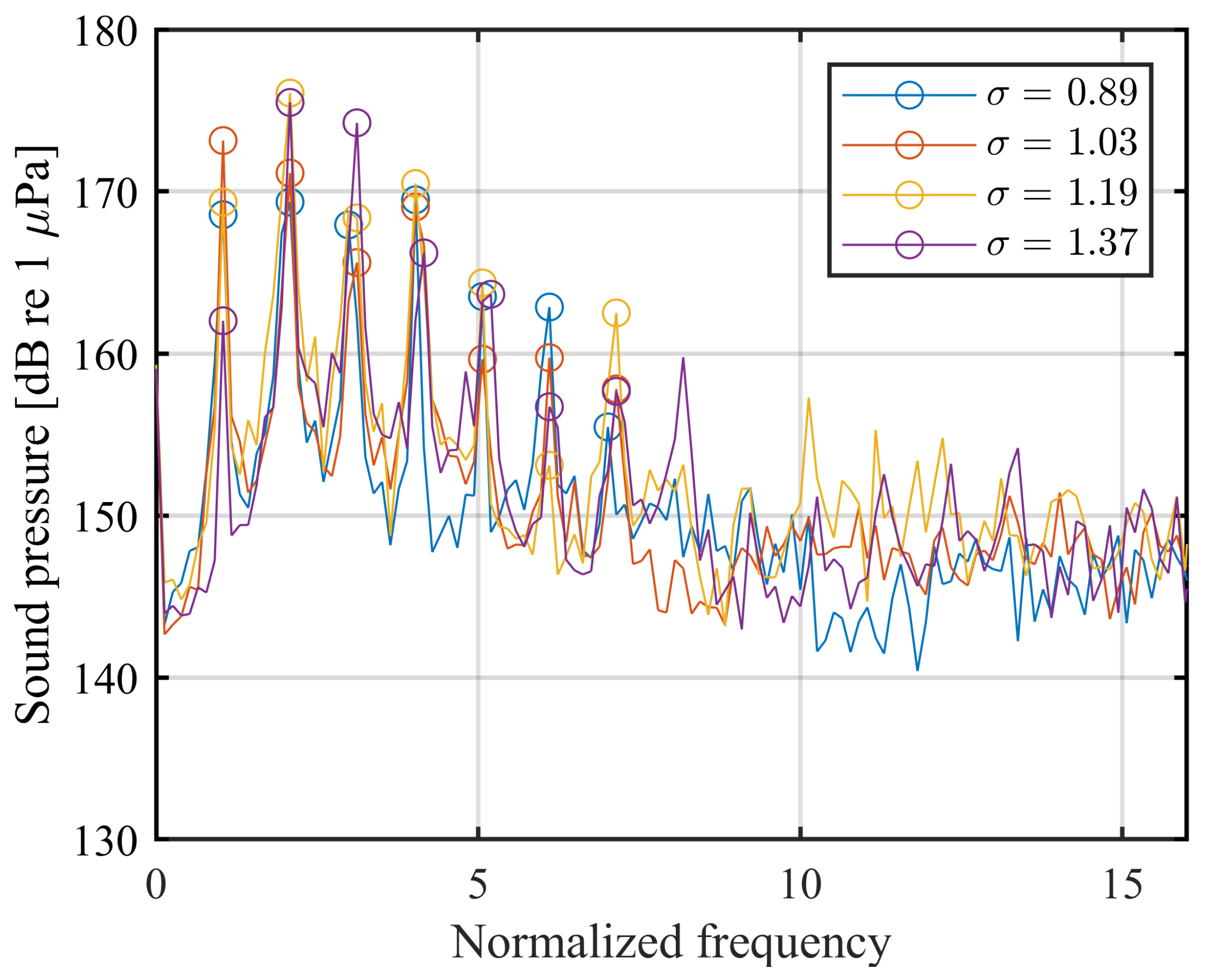
3.2. Influence of the Cavitation Number
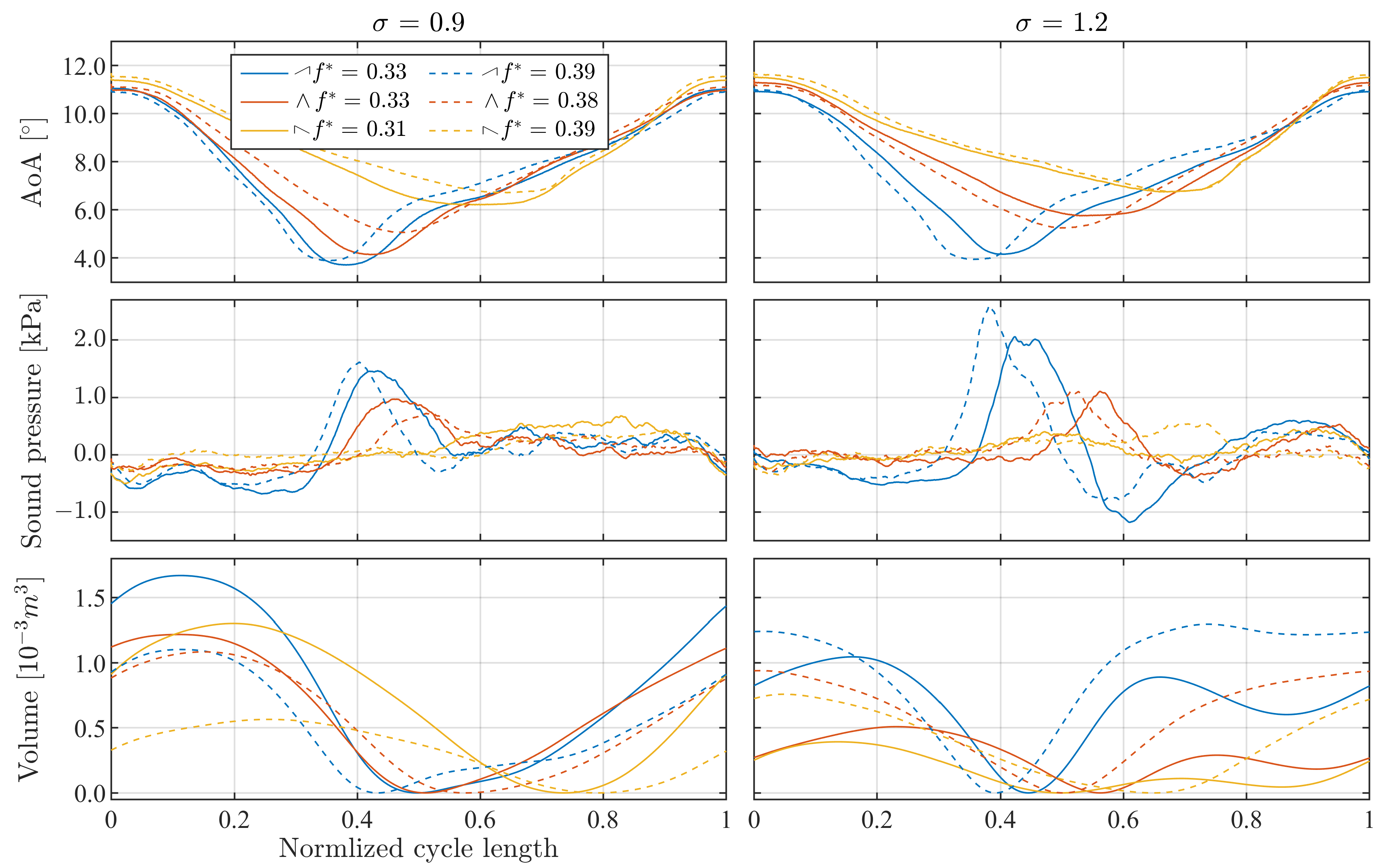
3.3. Influence of the Reduced Oscillation Frequency
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AoA | angle of attack |
| FIR | finite response filter |
| LED | light-emitting diode |
| NACA | foil type, first introduced by the National Advisory Committee for Aeronautics |
| PID | propulsion-improving device |
References
- Hildebrand, J.A. Anthropogenic and natural sources of ambient noise in the ocean. Mar. Ecol. Prog. Ser. 2009, 395, 5–20. [Google Scholar] [CrossRef]
- Andrew, R.K.; Howe, B.M.; Mercier, J.A.; Dzieciuch, M.A. Ocean ambient sound: Comparing the 1960s with the 1990s for a receiver off the California coast. Acoust. Res. Lett. Online 2002, 3, 65–70. [Google Scholar] [CrossRef]
- Committee on Potential Impacts of Ambient Noise in the Ocean on Marine Mammals. Ocean Noise and Marine Mammals; National Academies Press: Washington, DC, USA, 2003. [Google Scholar]
- Merchant, N.D.; Witt, M.J.; Blondel, P.; Godley, B.J.; Smith, G.H. Assessing sound exposure from shipping in coastal waters using a single hydrophone and Automatic Identification System (AIS) data. Mar. Pollut. Bull. 2012, 64, 1320–1329. [Google Scholar] [CrossRef] [PubMed]
- Veirs, S.; Veirs, V.; Wood, J.D.; Johnson, M. Ship noise extends to frequencies used for echolocation by endangered killer whales. PeerJ 2016, 4, e1657. [Google Scholar] [CrossRef] [PubMed]
- The Specialist Committee on Cavitation Induced Pressure Fluctuation. Final Report and Recommendations to the 22nd ITTC. In Proceedings of the 22nd International Towing Tank Conference, Shanghai, China, 5–11 September 1999. [Google Scholar]
- Schuster, M.; Daniel, J.M.; Wittekind, D.K.; Föhring, L.S. Future requirements for ships to limit underwater noise in the oceans. In Proceedings of the 116th Congress of the German Society for Maritime Technology; Schiffbautechnische Gesellschaft e.V.: Hamburg, Germany, 2022; Volume 1. [Google Scholar]
- Odabaşi, Y.A.; Fitzsimmons, P.A. Alternative methods for wake quality assessment. Int. Shipbuild. Prog. 1978, 25, 34–42. [Google Scholar] [CrossRef]
- Huse, E. Effect of Afterbody Forms and Afterbody Fins on the Wake Distribution of Single Screw Ships; Publication No. r31-74; Norwegian Ship Model Experiment Tank: Trondheim, Norway, 1972. [Google Scholar]
- Fahrbach, M. Bewertung der Güte von Nachstromfeldern. Diploma Thesis, Technische Universität Hamburg-Harburg, Hamburg, Germany, 2004. Available online: https://docplayer.org/42565978-Bewertung-der-guete-von-nachstromfeldern.html (accessed on 17 September 2023).
- Bugalski, T.; Szantyr, J.A. Numerical Analysis of the Unsteady Propeller Performance in the Ship Wake Modified By Different Wake Improvement Devices. Pol. Marit. Res. 2014, 21, 32–39. [Google Scholar] [CrossRef]
- Ji, B.; Luo, X.; Wu, Y. Unsteady cavitation characteristics and alleviation of pressure fluctuations around marine propellers with different skew angles. J. Mech. Sci. Technol. 2014, 28, 1339–1348. [Google Scholar] [CrossRef]
- Maquil, T. Underwater Radiated Noise of Ship Propellers. Oral presentation during the HSVA-Webinar, Hamburger Schiffbauversuchsanstalt, Hamburg, Germany, 1 June 2023.
- Cavitation Committee. Session on Propulsion: Cavitation. In Proceedings of the 15th International Towing Tank Conference, The Hague, The Netherlands, 3–10 September 1978; Volume 2, pp. 145–163. [Google Scholar]
- Franc, J.P.; Michel, J.M. Unsteady attached cavitation on an oscillating hydrofoil. J. Fluid Mech. 1988, 193, 171–189. [Google Scholar] [CrossRef]
- McKenney, E.A.; Brennen, C.E. On the dynamics and acoustics of cloud cavitation on an oscillating hydrofoil. In Proceedings of the ASME Symposium on Cavitation and Gas-Liquid Flows in Fluid Machinery and Devices, Lake Tahoe, NV, USA, 19–23 June 1994; American Society of Mechanical Engineers: New York, NY, USA, 1994; pp. 195–202. [Google Scholar]
- Reisman, G.; McKenney, E.A.; Brennen, C.E. Cloud cavitation on an oscillating hydrofoil. In Proceedings of the Twentieth Symposium on Naval Hydrodynamics, Santa Barbara, CA, USA, 21–26 August 1994. [Google Scholar]
- Pereira, F.A.; Di Felice, F.; Salvatore, F. Propeller Cavitation in Non-Uniform Flow and Correlation with the Near Pressure Field. J. Mar. Sci. Eng. 2016, 4, 70. [Google Scholar] [CrossRef]
- Hart, D.P.; Brennen, C.E.; Acosta, A.J. Observations of Cavitation on a Three-Dimensional Oscillating Hydrofoil. In Proceedings of the 25th Cavitation and Multiphase Flow Forum, Toronto, ON, Canada, 4–7 June 1990; Volume 98, pp. 49–52. [Google Scholar]
- Hashimoto, A.; Watanabe, S.; Asahara, T.; Sato, K.; Tsujimoto, Y. Unsteady Characteristics of Cavitation on an Oscillating Hydrofoil. 1st Report. Experimental Observation of Cavity Behavior. Trans. Jpn. Soc. Mech. Eng. Ser. B 2001, 67, 391–397. [Google Scholar] [CrossRef]
- Kato, K.; Dan, H.; Matsudaira, Y. Lock-in Phenomenon of Pitching Hydrofoil with Cavitation Breakdown. JSME Int. J. Ser. B 2006, 49, 797–805. [Google Scholar] [CrossRef]
- Zhang, M.; Huang, B.; Wu, Q.; Zhang, M.; Wang, G. The interaction between the transient cavitating flow and hydrodynamic performance around a pitching hydrofoil. Renew. Energy 2020, 161, 1276–1291. [Google Scholar] [CrossRef]
- Kravtsova, A.; Markovich, D.M.; Pervunin, K.S.; Timoshevskiy, M.V.; Hanjalić, K. High-speed visualization and PIV measurements of cavitating flows around a semi-circular leading-edge flat plate and NACA0015 hydrofoil. Int. J. Multiph. Flow 2014, 60, 119–134. [Google Scholar] [CrossRef]
- Wu, J.; Ganesh, H.; Ceccio, S.L. Multimodal partial cavity shedding on a two-dimensional hydrofoil and its relation to the presence of bubbly shocks. Exp. Fluids 2019, 60, 66. [Google Scholar] [CrossRef]
- Föhring, L.S.; Juhl, P.M.; Wittekind, D.K. Cavitation volume behaviour derived from full-scale pressure fluctuations. Ships Offshore Struct. 2023, 18, 541–549. [Google Scholar] [CrossRef]
- Huse, E. Pressure Fluctuations on the Hull Induced by Cavitating Propellers; Publication No. 111; Norwegian Ship Model Experiment Tank: Trondheim, Norway, 1972. [Google Scholar]
- Pereira, F.A.; Avellan, F.; Dupont, P. Prediction of Cavitation Erosion: An Energy Approach. J. Fluids Eng. 1998, 120, 719–727. [Google Scholar] [CrossRef]
- Brandt, A. Noise and Vibration Analysis: Signal Analysis and Experimental Procedures; Wiley: Chichester, UK, 2011. [Google Scholar]
- Marine Environment Protection Committee. Ship Underwater Radiated Noise Technical Report and Matrix; Annex to 74th Session; International Maritime Organisation: London, UK, 2019. [Google Scholar]




| Parameter | Values for Experimental Matrix | |||
|---|---|---|---|---|
| cavitation number | 0.89 | 1.04 | 1.20 | 1.36 |
| reduced oscillation frequency | 0.32 | 0.39 | ||
| position of maximum AoA within cycle | 0.3 ( 𝆇 ) | 0.5 (∧) | 0.7 (⩘) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Föhring, L.S.; Juhl, P.M.; Wittekind, D. Experimental Parameters Influencing the Cavitation Noise of an Oscillating NACA0015 Hydrofoil. J. Mar. Sci. Eng. 2023, 11, 2023. https://doi.org/10.3390/jmse11102023
Föhring LS, Juhl PM, Wittekind D. Experimental Parameters Influencing the Cavitation Noise of an Oscillating NACA0015 Hydrofoil. Journal of Marine Science and Engineering. 2023; 11(10):2023. https://doi.org/10.3390/jmse11102023
Chicago/Turabian StyleFöhring, Leonie S., Peter Møller Juhl, and Dietrich Wittekind. 2023. "Experimental Parameters Influencing the Cavitation Noise of an Oscillating NACA0015 Hydrofoil" Journal of Marine Science and Engineering 11, no. 10: 2023. https://doi.org/10.3390/jmse11102023
APA StyleFöhring, L. S., Juhl, P. M., & Wittekind, D. (2023). Experimental Parameters Influencing the Cavitation Noise of an Oscillating NACA0015 Hydrofoil. Journal of Marine Science and Engineering, 11(10), 2023. https://doi.org/10.3390/jmse11102023





