Vibrational Responses of an Ultra-Large Cold-Water Pipe for Ocean Thermal Energy Conversion: A Numerical Approach

Abstract

The transportation of seawater on a grand scale via an ultra-large cold-water pipe situated within the context of ocean thermal energy conversion (OTEC) floating installations inherently presents challenges associated with instability and potential malfunction in the face of demanding operational circumstances. This study endeavors to augment the stability and security of cold-water pipe (CWP) operations by scrutinizing their vibrational attributes across diverse boundary configurations. Initially, we invoke Euler–Bernoulli beam theory to forge the analytical framework and proffer a semi-analytical resolution by utilizing the generalized integral transform technique (GITT). Subsequently, we authenticate the convergence and precision of our proposed approach through comparative analysis with extant theories. Our findings underscore the conspicuous influence of boundary conditions on the convergence of transverse displacement. The influence of internal flow on the transverse displacement and the natural frequency manifests substantial variability under different boundary conditions. Significantly, an escalation in the internal flow velocity triggers a concomitant reduction in the natural frequency, ultimately culminating in instability once the critical velocity threshold is reached. Additionally, the reliance of the transverse displacement and the natural frequency on the clump weight at the bottom is markedly pronounced. Our discoveries propose that pipe stability can be ameliorated by adjusting the clump weight at the bottom. Furthermore, the novel insights obtained through our proposed approach can significantly aid in the early-stage design and analysis of CWP.

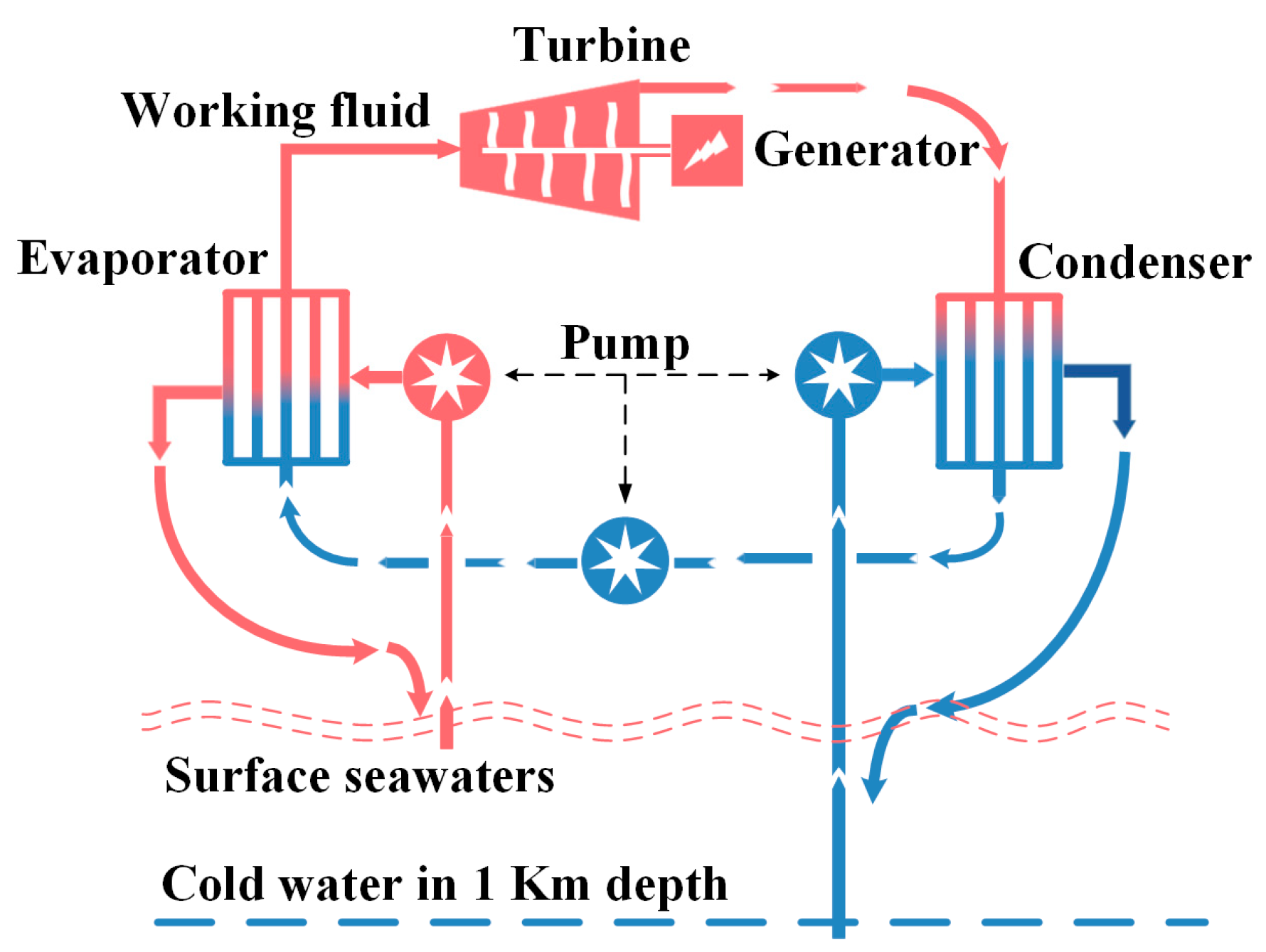
1. Introduction

Ocean thermal energy conversion (OTEC) is a method that utilizes the temperature difference between deep seawater and surface water to propel a thermodynamic engine cycle, ultimately producing useful work, typically in the form of electricity [1], as shown in Figure 1. OTEC stands out among ocean energy sources due to its substantial resource potential, surpassing that of other ocean energy forms. Additionally, OTEC technology can provide abundant cold water for air conditioning and refrigeration as well as desalinated fresh water for various applications [2]. The significance of OTEC lies in its potential to serve as a renewable base-load energy source for tropical islands, thereby reducing their reliance on imported fossil fuels, particularly oil [3].

A cold-water pipe (CWP) serves as a vital and intricate element inside floating ocean thermal energy conversion (OTEC) facilities, with its primary function being the transportation of deep seawater to the platform [4]. For large-scale commercial OTEC facilities, capable of producing 100 MW-net electricity, a CWP exhibits extraordinary dimensions, with lengths ranging from 800 to 1200 m and diameters reaching up to 12 m [5,6]. The flow rate of seawater transported through the pipe can reach approximately 10² m³/s [7]. Such a substantial internal flow rate raises concerns about potential instability, which could lead to CWP failure. Floating OTEC plants are commonly located in tropical regions to harness the significant temperature gradient between deep and surface seawater. However, these regions are also susceptible to severe weather conditions, including typhoons and tsunamis. Consequently, the design of an ultra-large cold-water pipe must account for its ability to operate reliably under the influence of extreme wind, wave, and OTEC platform motion. Construction of a CWP accounts for 15% to 20% of the total capital cost, according to cost assessment studies for OTEC development [8]. Therefore, maximizing the design and performance of CWPs in OTEC projects is of economic importance.

Research has focused on applicable mechanical issues in the cold-water pipe (CWP) system ever since ocean thermal energy conversion (OTEC) was first proposed. McGuinness and Scotti [9] reported a substantial CWP development program sponsored by the United States Department of Energy (DoE), encompassing design, analysis, and at-sea testing. A comprehensive time-domain analysis [10] and coupled CWP and platform responses were constructed to forecast the OTEC hull-CWP interaction during the program. To validate the accuracy of their procedures, Lockheed Missiles and Space Company (LMSC) constructed a 1:110 scale spar-type platform model to predict the seakeeping behavior of complete OTEC plants, including the platform and CWP [11]. The comparison between model test data and procedure prediction data revealed that the procedure could accurately predict OTEC platform motion but exhibited limitations in predicting CWP vibration. Kwon et al. [12] performed oscillation experiments on an OTEC riser under current and found that high current velocities caused vortex-induced vibration (VIV) and considerable cross-flow strains. Cao et al. [13] conducted model tests to explore the global responses of a CWP generated by low bending modes and their curvatures, which the analytical model after calibration effectively anticipated. Halkyard et al. [14] reviewed prior work on an OTEC CWP and discussed the present state of numerical modeling and the results of recent model testing. He et al. [15] examined the contribution of bottom tension and top tension to the vibration problem of a CWP using robust adaptive boundary controllers. Adiputra and Utsunomiya [16] investigated the influence of internal flow on a CWP’s stability, aiming to design commercial-scale OTEC systems. Subsequently, they utilized a numerical and analytical approach to analyze self-induced vibration in the CWP and predicted the critical velocity.

Bayrami et al. [17] used a probabilistic method to study the probabilistic response reactions of a fluid-conveying pipe. The critical fluid velocity can be forecast by mixing the Monte Carlo simulation and the Galerkin approach. Using generalized integral transform, Gu et al. [18] examined the effects of fluid velocity, temperature, and axial tension on fluid-conveying pipe dynamics. Li et al. [19] examined the influence of different internal flow velocities and soil stiffness on subsea free-spanning pipelines and found that greater internal flow velocities cause the pipe system to reach the lock-in state, while higher soil stiffness causes the system’s natural frequency to rise. Heydari Nosrat Abadi and Zamani Nouri [20] discussed the effects of fluid velocity, nanoparticle volume fraction, geometrical parameters, and temperature difference on the critical fluid velocity of pipelines. Soon et al. [21] utilized the finite element and Green’s function methods to investigate the dynamic behavior of a pipe mounted on the Winkler foundation and found that compared with the finite element method, Green’s function method is more accurate for higher fluid velocities.

Although previous studies have made significant contributions to predicting the vibrational responses of cold-water pipes through analytical, experimental, and numerical approaches, several challenges persist, motivating the current study. Firstly, the predictive performance of analytical and experimental methods is inherently limited by factors such as program precision, testing procedures, and environmental conditions. Even though computer-aided analysis studies combined with lab and at-sea tests have made predictions more accurate on coupled vessel-CWP systems, it is still hard to predict the dynamic reaction of a CWP with great accuracy. In essence, these methods excel in accurately predicting the motion of the OTEC platform but fall short in providing precise predictions for CWP dynamics. Secondly, previous numerical methods have estimated the critical velocity under conditions where loads are relatively small in number, either in the time domain or frequency domain. However, as the complexity of loads and categories increases, the convergence and accuracy of these numerical methods need improvement. Additionally, the assumption of ideal boundary conditions made in previous numerical predictions renders them impractical for real-world applications.

To address the challenges outlined earlier, this paper proposes the utilization of the generalized integral transform technique (GITT) to predict the vibrational responses of an ultra-large cold-water pipe while considering various load scenarios and variable boundary conditions. The GITT, originally developed for applications in heat and fluid flow [22,23,24], has been successfully extended to the analysis of dynamic behavior in diverse engineering systems, including axially moving beams [25], axially moving Timoshenko beams [26], damaged Euler–Bernoulli beams [27], axially moving orthotropic plates [28], bending of rectangular orthotropic plates [29,30,31], and pipes conveying a two-phase flow [32]. One of the primary advantages of employing the GITT is its ability to automatically and straightforwardly control calculation errors. Additionally, it demonstrates a very marginal escalation in total computing workload as the number of independent variables grows, making it a promising approach for addressing the complexities associated with ultra-large CWPs. Zarastvand [33] reported the sound insulation characteristics of plate structures, highlighting different theories including classical, shear deformation, and three-dimensional theories. Ghafouri [34] proposed an analytical strategy to investigate the exact effect of using three-dimensional (3D)-RACS in order to determine the sound transmission loss (STL) coefficient of a sandwich panel.

The current study primarily aims to provide analytical methods for analyzing the vibration characteristics of a cold-water pipe with different boundary conditions. We consider six combinations of boundary conditions, namely, simply supported-simply supported (S-S), clamped-clamped (C-C), clamped with clump weight (C-W), clamped-free (C-F), simply supported with clump weight (S-W), and simply supported-free (S-F). Notably, the cases of simply supported with clump weight (S-W) and clamped with clump weight (C-W) have not been previously explored in the literature. In contrast to previous research that mostly relied on finite integral transforms using trigonometric functions to analyze the dynamic characteristics of the pipe, this study adopts integral transforms utilizing beam eigenfunctions to examine the vibration of a CWP with different boundary conditions. Nevertheless, we faced numerical difficulties when dealing with beam functions expressed in their conventional hyperbolic function representations, notably for eigenfunctions above the 12th order [35]. To address this, Gartner et al. [36] and Gonçalves et al. [37] established a comprehensive expression for beam eigenfunctions in exponential form, which has proven to be applicable across different elastic boundary conditions. Additionally, eigenfunctions and eigenvalues for Euler–Bernoulli beams with one end restrained or simply supported and the other end with clump weight have not been presented in the literature in specific forms. In the present work, we introduce these eigenfunctions for Euler–Bernoulli beams with one end clamped or simply supported and the other end with clump weight in hyperbolic function forms for the first time as well as corresponding equations to calculate the eigenvalues.

In this work, the vibrational responses of a CWP are analyzed with the GITT under different boundary conditions. Convergence and accuracy of the present solutions are demonstrated by comparison with the results of the Galerkin method and the Fourier series expansion technique. The effects of internal flow, current, clump weight, and different boundary conditions are investigated. The present model can be used especially in designing naval, oil, and gas transportation, wind turbine, and civil structures subjected to variable constraint boundary conditions. The governing equations of transverse displacement are developed in Section 2. A numerical method of equations of motion is obtained by a generalized integral transform solution in Section 3. Verification of problems and calculation of numerical results using the GITT are addressed in Section 4. The conclusions of this paper are summarized in Section 5.

2. Theoretical Formulas

A cold-water pipe is subjected to internal flow, current, collision, and top-tension, as shown in Figure 2. Based on the following assumptions, an equation of motion was given by Monette and Pettigrew [38]. The main parameters of a CWP are presented in Table 1.

(1)

The dynamic behavior of the pipe is considered to be in a two-dimensional plane.

(2)

Given that as the ratio of the pipe length to the diameter is sufficiently large, the cold-water conduit system can be examined using the Euler–Bernoulli theory.

(3)

The internal flow is homogeneous and unidirectional.

(4)

The frictional force between the pipe and fluid is neglected.

(5)

The pipe’s cross-sectional area remains unchanged.

(6)

The effect of platform motion on the pipe is in the axial direction.

(7)

The weight of the pipe is uniformly distributed.

Figure 2. Schematic vibration of a cold-water pipe conveying liquid flow under marine environmental conditions.

Figure 2. Schematic vibration of a cold-water pipe conveying liquid flow under marine environmental conditions.

Table 1. The main parameters of the CWP.

Nomenclature	Description
EI	Bending stiffness (N/m2)
L	Pipe length (m)
ma	Added mass (kg/m)
mf	Mass of the internal flow per unit length (kg/m)
mr	Mass of the pipe per unit length (kg/m)
T(z)	Axial equivalent tension (N)
U	Velocity of the internal flow (m/s)
w(z,t)	Transverse displacement of the pipe (m)
Ai	Internal cross-sectional area (m2)
A0	External cross-sectional area (m2)
${\rho }_r$	Density of the pipe (kg/m3)
${\rho }_f$	Density of the seawater (kg/m3)
u	External flow velocity (m/s)
t	Time of vibration (s)
Ca	Added mass coefficient
Cd	Adapted drag coefficient
$\Omega$	Circular frequency (rad/s)
$\sigma$	Structural damping coefficient
g	Gravitational acceleration (m/s2)
Twc	Weight of the clump (N)
Td	Dry weight (N)

Table 1. The main parameters of the CWP.

Nomenclature	Description
EI	Bending stiffness (N/m2)
L	Pipe length (m)
ma	Added mass (kg/m)
mf	Mass of the internal flow per unit length (kg/m)
mr	Mass of the pipe per unit length (kg/m)
T(z)	Axial equivalent tension (N)
U	Velocity of the internal flow (m/s)
w(z,t)	Transverse displacement of the pipe (m)
Ai	Internal cross-sectional area (m2)
A0	External cross-sectional area (m2)
${\rho }_r$	Density of the pipe (kg/m3)
${\rho }_f$	Density of the seawater (kg/m3)
u	External flow velocity (m/s)
t	Time of vibration (s)
Ca	Added mass coefficient
Cd	Adapted drag coefficient
$\Omega$	Circular frequency (rad/s)
$\sigma$	Structural damping coefficient
g	Gravitational acceleration (m/s2)
Twc	Weight of the clump (N)
Td	Dry weight (N)

Therefore, the governing control equation of the pipe can be written as follows:

$$EI(1+(\frac{\sigma }{\Omega })\frac{\partial }{\partial t})\frac{{\partial }^{4}w}{\partial z^4}+(T(z)+m_f{U}^2)\frac{{\partial }^{2}w}{\partial z^2}+\frac{T_{top}}{L}\frac{\partial w}{\partial z}-2m_{f}U\frac{{\partial }^{2}w}{\partial z\partial t}+(m_r+m_f)\frac{{\partial }^{2}w}{\partial t^2}=f(z,t)$$

(1)

where the first, second, third, fourth, fifth, sixth, seventh, and last terms represent the flexural force, structural damping, axial equivalent tension, centrifugal force, top force, Coriolis force, inertia force, and external excitation, respectively [39].

The $w(z,t)$ denotes the transverse displacement, and the total top force is presented as: $T_{top}=T_{bt}+T_{wc}$. When the parametric vibration is not considered, axial equivalent tension can be represented by

$$T(z)=-T_{wc}-T_{bt}(1-\frac{z}{L})+A_0{P}_0(z)-A_i{P}_i(z)$$

(2)

where $T_{bt}=({\rho }_r-{\rho }_f)A_{r}gL$ and $T_{wc}=T_d={\rho }_r{A}_{r}gL$ represent the wet weight of the pipe and the weight of the clump, respectively. $A_r=A_0-A_i$, $A_r$ represents the cross-sectional area of the pipe. The water pressure inside and outside of the pipe is represented by $P_0(z)$, which can be further expressed by

$$\left\{\begin{array}{l}{P}_0(z)={\rho }_{f}gz+\Delta p\\ P_i(z)={\rho }_{f}gz\end{array}\right.$$

(3)

where $\Delta p$ denotes the pressure difference between the pipe’s interior and exterior at the same depth. The $\Delta p$ values vary from $0.5{\rho }_f{U}^2$ to ${\rho }_f{U}^2$, which depends on the geometry of the inlet [39]. In this study, $\Delta p={\rho }_f{U}^2$ is considered. The external excitation load on the pipe, i.e., $f(z,t)$, is caused by the surrounding water. Based on the Morison equation [40], when ignoring the vortex-induced vibration, this force can be expressed by

$$f(z,t)=f_i+f_d$$

(4)

where $f_i$ represents the inertia force

$$f_i={\rho }_f{A}_0(C_a+1)\frac{\partial u}{\partial t}-{\rho }_f{A}_0{C}_a\frac{{\partial }^{2}w}{\partial t^2}$$

(5)

and $f_d$ denotes the drag force

$$f_d=\frac{1}{2}{\rho }_f{D}_0{C}_d(u-\frac{\partial w}{\partial t})$$

(6)

Incorporating Equations (1)–(6), the pipe’s equation of motion is then expressed as follows:

$$\begin{array}{l}EI(1+(\frac{\sigma }{\Omega })\frac{\partial }{\partial t})\frac{{\partial }^{4}w}{\partial z^4}+(-T_{wc}-T_{bt}(1-\frac{z}{L})+A_0{P}_0(z)-A_i{P}_i(z)+m_f{U}^2)\frac{{\partial }^{2}w}{\partial z^2}+\frac{T_{top}}{L}\frac{\partial w}{\partial z}\\ -2m_{f}U\frac{{\partial }^{2}w}{\partial z\partial t}+m_e\frac{{\partial }^{2}w}{\partial t^2}+\frac{1}{2}{\rho }_f{D}_0{C}_d\frac{\partial w}{\partial t}=m_f(C_a+1)\frac{\partial u}{\partial t}+\frac{1}{2}{\rho }_f{D}_0{C}_{d}u\end{array}$$

(7)

where $m_e$ denotes the equivalent mass, i.e., $m_e=m_a+m_f+m_r$, $m_r={\rho }_r{A}_r$, $m_f={\rho }_f{A}_i$, $m_a=C_a{\rho }_f{A}_0$.

For the governing equations, the following dimensionless variables and parameters are employed:

$$\left\{\begin{array}{l}y=\frac{w}{L},x=\frac{z}{L},\tau =\frac{t}{L^2}\sqrt{\frac{EI}{m_e}},\eta =\frac{\sigma }{\Omega L^2}\sqrt{\frac{EI}{m_e}}\\ \upsilon =UL\sqrt{\frac{m_r}{EI}},\mu =uL\sqrt{\frac{m_r}{EI}},\varsigma =\frac{{\rho }_f{D}_0{C}_d{L}^2}{2\sqrt{EI{m}_e}}\\ {\theta }_{bt}=T_{bt}\frac{L^2}{EI},{\theta }_P=\Delta P\frac{A_i}{T_{bt}},{\theta }_{wc}=T_{wc}\frac{L^2}{EI}\\ {\theta }_{top}=T_{top}\frac{L^2}{EI},\xi =L\sqrt{\frac{m_f{T}_{top}}{EI{m}_e}},\zeta =m_f(C_a+1)\frac{\partial u}{\partial t}\frac{L^3}{EI}\end{array}\right.$$

(8)

Therefore, the dimensionless governing equation can be expressed by

$$\begin{array}{l}(1+\eta (\frac{\partial }{\partial \tau }))\frac{{\partial }^{4}y}{\partial x^4}+({\theta }_{top}{\upsilon }^2+{\theta }_{bt}x+{\theta }_P-{\theta }_{wc}-{\theta }_{bt})\frac{{\partial }^{2}y}{\partial x^2}+{\theta }_{top}\frac{\partial y}{\partial x}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-2\xi \upsilon \frac{{\partial }^{2}y}{\partial x\partial \tau }+\varsigma \frac{\partial y}{\partial \tau }+\frac{{\partial }^{2}y}{\partial {\tau }^2}=\zeta +\mu \varsigma \end{array}$$

(9)

The initial condition is defined as follows:

$$y(x,0)=0,\frac{\partial y(x,0)}{\partial x}={\upsilon }_0\sin (\pi x)$$

(10)

The following dimensionless boundary conditions are considered, as shown in Figure 3:

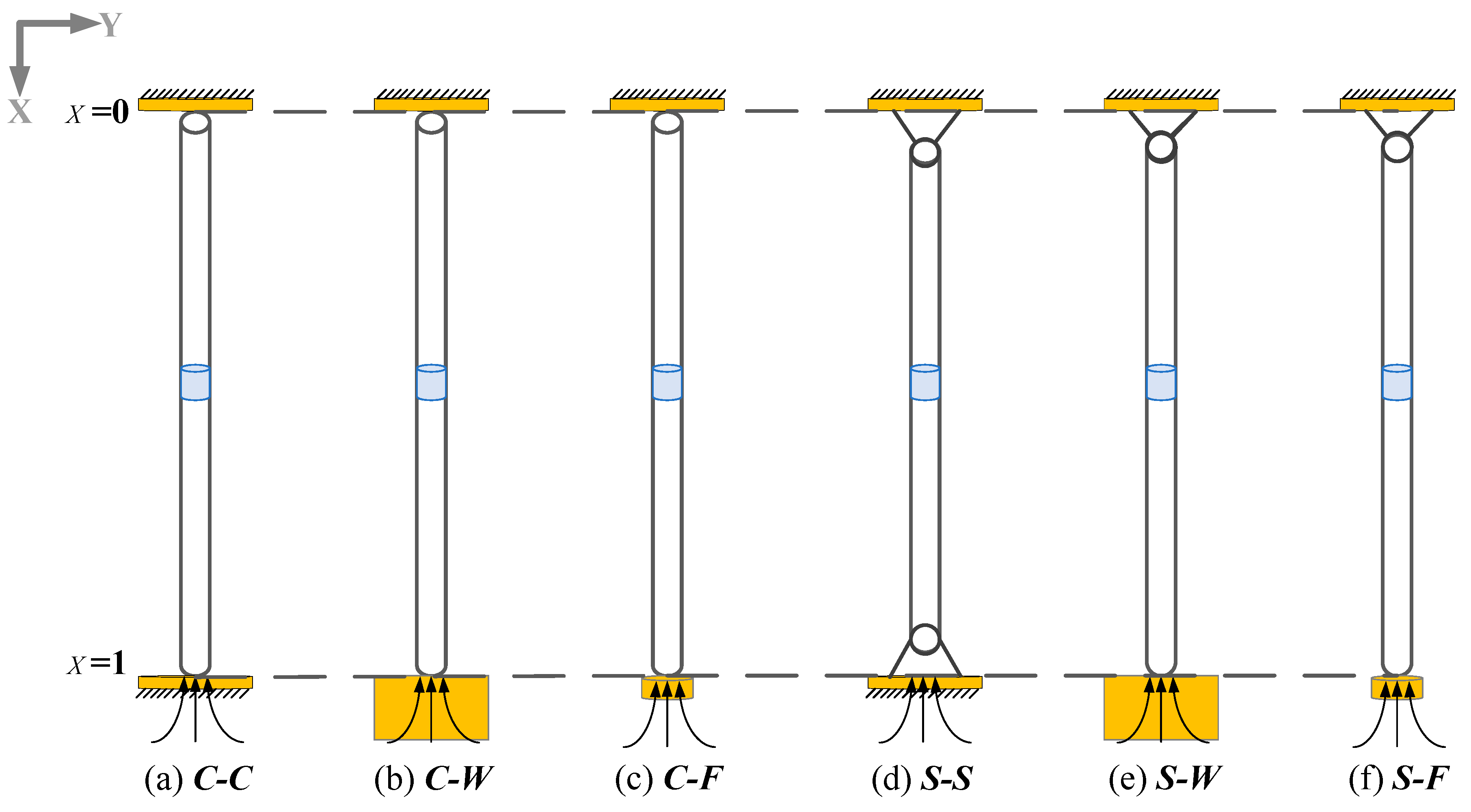
(a)

clamped-clamped boundary conditions (C-C)

$$y(0,\tau )=\frac{\partial y}{\partial x}\left|\begin{array}{c}\\ x=0\end{array}\right.= \mathrm{y}(1,\tau )=\frac{\partial y}{\partial x}\left|\begin{array}{c}\\ x=1\end{array}\right.=0$$

(11)

(b)

clamped-clump weight boundary conditions (C-W)

$$y(0,\tau )=\frac{\partial y}{\partial x}\left|\begin{array}{c}\\ x=0\end{array}\right.=\frac{{\partial }^{2}y}{\partial x^2}\left|\begin{array}{c}\\ x=1\end{array}\right.=0; \frac{{\partial }^{3}y}{\partial x^3}\left|\begin{array}{c}\\ x=1\end{array}\right.=K_{c}y(1,\tau )$$

(12)

where $K_c$ is defined as $T_{wc}{L}^2/EI.$

(c)

clamped-free boundary conditions (C-F)

$$y(0,\tau )=\frac{\partial y}{\partial x}\left|\begin{array}{c}\\ x=0\end{array}\right.=\frac{{\partial }^{2}y}{\partial x^2}\left|\begin{array}{c}\\ x=1\end{array}\right.=\frac{{\partial }^{3}y}{\partial x^3}\left|\begin{array}{c}\\ x=1\end{array}\right.=0$$

(13)

(d)

simply supported-simply supported boundary conditions (S-S)

$$y(0,\tau )=\frac{{\partial }^{2}y}{\partial x^2}\left|\begin{array}{c}\\ x=0\end{array}\right.=y(1,\tau )=\frac{{\partial }^{2}y}{\partial x^2}\left|\begin{array}{c}\\ x=1\end{array}\right.=0$$

(14)

(e)

simply supported-clump weight boundary conditions (S-W)

$$y(0,\tau )=\frac{{\partial }^{2}y}{\partial x^2}\left|\begin{array}{c}\\ x=0\end{array}\right.=\frac{{\partial }^{2}y}{\partial x^2}\left|\begin{array}{c}\\ x=1\end{array}\right.=0;\hspace{1em}\frac{{\partial }^{3}y}{\partial x^3}\left|\begin{array}{c}\\ x=1\end{array}\right.=K_{c}y(1,\tau )$$

(15)

(f)

simply supported-free boundary conditions (S-F)

$$y(0,\tau )=\frac{{\partial }^{2}y}{\partial x^2}\left|\begin{array}{c}\\ x=0\end{array}\right.=\frac{{\partial }^{2}y}{\partial x^2}\left|\begin{array}{c}\\ x=1\end{array}\right.=\frac{{\partial }^{3}y}{\partial x^3}\left|\begin{array}{c}\\ x=1\end{array}\right.=0$$

(16)

Figure 3. Schematic of the CWP systems with six different boundary conditions.

Figure 3. Schematic of the CWP systems with six different boundary conditions.

3. Proposed Vibration Model Using GITT Method

3.1. Eigenfunctions and Eigenvalues

The following definitions apply to integral transform pairs for the governing Equation (9):

$${\overline{y}}_i(\tau )={\displaystyle {\int }_0^1{y}_i(x)}y(x,\tau )dx,\hspace{1em}\mathrm{transform}, i=1,2,3,\dots ,$$

(17)

$$y(x,\tau )={\displaystyle \sum _{i=1}^{\infty }{y}_i(x){\overline{y}}_i(\tau )},\hspace{1em}\mathrm{inverse}. i=1,2,3,\dots ,$$

(18)

where $y_i(x)$ equals $y_{1i}(x)$, $y_{2i}(x)$, $y_{3i}(x)$, $y_{4i}(x)$, $y_{5i}(x)$, and $y_{6i}(x)$ for the C-C, C-W, C-F, S-S, S-W, and S-F boundary conditions, respectively. The normalized eigenfunctions $y_{1i}(x)$, $y_{2i}(x)$, $y_{3i}(x)$, $y_{4i}(x)$, $y_{5i}(x)$, and $y_{6i}(x)$ satisfy the following orthonormal property:

$${\displaystyle {\int }_0^1{y}_{ki}(x)}{y}_{kj}(x)dx={\delta }_{ij}{N}_i, k=1,2,3,4,5,6, i,j=1,2,3,\dots ,$$

(19)

where ${\delta }_{ij}$ is the Kronecker delta functions and $N_i$ is the normalization integral and is written as

$$N_i={\displaystyle {\int }_0^1{y}_i{}^2(x)}dx$$

(20)

For the transverse displacement, the following eigenvalue problems of Euler–Bernoulli beams in the coordinate “x” with different boundary conditions are employed:

$$\frac{d^4{y}_{ki}(x)}{d{x}^4}={\lambda }_{ki}{}^4{y}_{ki}(x), 0<x<1, i=1,2,3,\dots \mathrm{and} k=1,2,3,4,5,6$$

(21)

(a)

C-C

$$y_{1i}(x)={(-1)}^i\cos ({\lambda }_{1i}x)-\sin ({\lambda }_{1i}x)\cot {(\frac{{\lambda }_{1i}}{2})}^{{(-1)}^i}-\frac{{(-1)}^i{e}^{-{\lambda }_{1i}x}}{1-{(-1)}^i{e}^{-{\lambda }_{1i}}}+\frac{e^{-{\lambda }_{1i}(1-x)}}{1-{(-1)}^i{e}^{-{\lambda }_{1i}}}$$

(22)

where the value of ${\lambda }_{1i}$ satisfies

$${(-1)}^i\tan (\frac{{\lambda }_{1i}}{2})=\frac{1-e^{-{\lambda }_{1i}}}{1+e^{-{\lambda }_{1i}}}, \mathrm{and} i=1,2,3,\dots$$

(23)

(b)

C-W

$$y_{2i}(x)=\sin ({\lambda }_{2i}x)-\sinh ({\lambda }_{2i}x)+\frac{\sin ({\lambda }_{2i})+\sinh ({\lambda }_{2i})}{\cos ({\lambda }_{2i})+\cosh ({\lambda }_{2i})}[\cosh ({\lambda }_{2i}x)+\cos ({\lambda }_{2i}x)]$$

(24)

where the value of ${\lambda }_{2i}$ satisfies

$${\lambda }_{2i}{}^3\frac{2+\cos {\lambda }_{2i}(e^{{\lambda }_{2i}}+e^{-{\lambda }_{2i}})}{(e^{{\lambda }_{2i}}-e^{-{\lambda }_{2i}})\cos {\lambda }_{2i}-\sin {\lambda }_{2i}(e^{{\lambda }_{2i}}+e^{-{\lambda }_{2i}})}=K_c, \mathrm{and} i=1,2,3,\dots$$

(25)

(c)

C-F

$$y_{3i}(x)=\cos ({\lambda }_{3i}x)-\frac{1+{(-1)}^i{e}^{-{\lambda }_{3i}}}{1-{(-1)}^i{e}^{-{\lambda }_{3i}}}\sin ({\lambda }_{3i}x)-\frac{e^{-{\lambda }_{3i}x}}{1-{(-1)}^i{e}^{-{\lambda }_{3i}}}+\frac{{(-1)}^i{e}^{-{\lambda }_{3i}(1-x)}}{1-{(-1)}^i{e}^{-{\lambda }_{3i}}}$$

(26)

where the value of ${\lambda }_{3i}$ satisfies

$$\cos {\lambda }_{3i}=\frac{-2e^{-{\lambda }_{3i}}}{1+e^{-2{\lambda }_{3i}}} \mathrm{and} i=1,2,3,\dots$$

(27)

(d)

S-S

$$y_{4i}(x)=\sin ({\lambda }_{4i}x)$$

(28)

where the value of ${\lambda }_{4i}$ satisfies

$${\lambda }_{4i}=i\pi ; \mathrm{and} i=1,2,3,\dots$$

(29)

(e)

S-W

$$y_{5i}(x)=\sin ({\lambda }_{5i}x)+\frac{\sin ({\lambda }_{5i})}{\sinh ({\lambda }_{5i})}\sinh ({\lambda }_{5i}x)$$

(30)

where the value of ${\lambda }_{5i}$ satisfies

$${\lambda }_{5i}{}^3\frac{\sin ({\lambda }_{5i})(e^{2{\lambda }_{5i}}+1)-(e^{2{\lambda }_{5i}}-1)\cos ({\lambda }_{5i})}{2\sin ({\lambda }_{5i})(e^{2{\lambda }_{5i}}-1)}=K_c, i=1,2,3,\dots$$

(31)

(f)

S-F

$$y_{6i}(x)=\sqrt{2}[\sin ({\lambda }_{6i}x)-\frac{e^{-{\lambda }_{6i}}\sin ({\lambda }_{6i})}{1-e^{-2{\lambda }_{6i}}}{e}^{-{\lambda }_{6i}x}+\frac{e^{-{\lambda }_{6i}(1-x)}\sin ({\lambda }_{6i})}{1-e^{-2{\lambda }_{6i}}}]$$

(32)

where the value of ${\lambda }_{6i}$ satisfies

$${\lambda }_{61}=0, \tan {\lambda }_{6i}=\frac{(1-e^{-2{\lambda }_{6i}})}{(1+e^{-2{\lambda }_{6i}})}, \mathrm{and} i=2,3,4,\dots$$

(33)

3.2. Transformed Governing Equation

The following system of algebraic equations results from transforming the governing Equation (9) in the “x” direction by ${\displaystyle {\int }_0^1{\tilde{y}}_i(x)dx}$, which also incorporates the inverse Formulas (17) and (18).

$$\begin{array}{l}\frac{d^2{\overline{y}}_i(\tau )}{d{\tau }^2}-2\xi \upsilon {\displaystyle \sum _{j=1}^{\infty }{A}_{ij}}\frac{d{\overline{y}}_j(\tau )}{d\tau }+(\varsigma +\eta {\lambda }_i{}^4)\frac{d{\overline{y}}_i(\tau )}{d\tau }+{\lambda }_i{}^4{\overline{y}}_i(\tau )+{\theta }_{top}{\displaystyle \sum _{j=1}^{\infty }{A}_{ij}}{\overline{y}}_j(\tau )\\ ({\theta }_{top}{\upsilon }^2+{\theta }_P-{\theta }_{wc}){\displaystyle \sum _{j=1}^{\infty }{B}_{ij}}{\overline{y}}_j(\tau )+{\theta }_{BT}{\displaystyle \sum _{j=1}^{\infty }{C}_{ij}}{\overline{y}}_j(\tau )=D_{ij}\end{array}$$

(34)

where the following equations are used to find the coefficients:

$$\left\{\begin{array}{l}{A}_{ij}={\displaystyle {\int }_0^1{\tilde{y}}_i(x)}\frac{d{\tilde{y}}_j(x)}{dx}dx\\ B_{ij}={\displaystyle {\int }_0^1{\tilde{y}}_i(x)}\frac{d^2{\tilde{y}}_j(x)}{d{x}^2}dx\\ C_{ij}={\displaystyle {\int }_0^1{\tilde{y}}_i(x)}(x-1)\frac{d^2{\tilde{y}}_j(x)}{d{x}^2}dx\\ D_{ij}={\displaystyle {\int }_0^1{\tilde{y}}_i(x)(\mu \zeta +\epsilon )dx}\end{array}\right.$$

(35)

The numerical solution of ${\overline{y}}_i(\tau )$ can be calculated according to the integral transformed ordinary differential Equation (34) and the initial condition Equation (10). Subsequently, the semi-analytic solution $y(x,\tau )$ can be obtained according to the transformation rule of Equation (18) and based on the ND-Solve routine of Mathematica Wolfram, where it is necessary to determine the number of truncation terms in the inversion process of NW.

3.3. Variation in the Fundamental Frequency

To derive the fundamental circular frequency of the pipe system, the truncated Equations (34) and (35) can be written in matrix form as follows:

$$\mathbf{M}\ddot{\mathbf{y}}(\mathbf{t})\mathbf{+}\mathbf{C}\dot{\mathbf{y}}\mathbf{(}\mathbf{t})\mathbf{+}\mathbf{K}\mathbf{y}(\mathbf{t})\mathbf{=}\mathbf{F}(\mathbf{t})$$

(36)

The basic circular frequency may be calculated using typical eigenvalue techniques for a complex general matrix in the generalized eigenvalue problem of Equation (36).

4. Results and Discussion

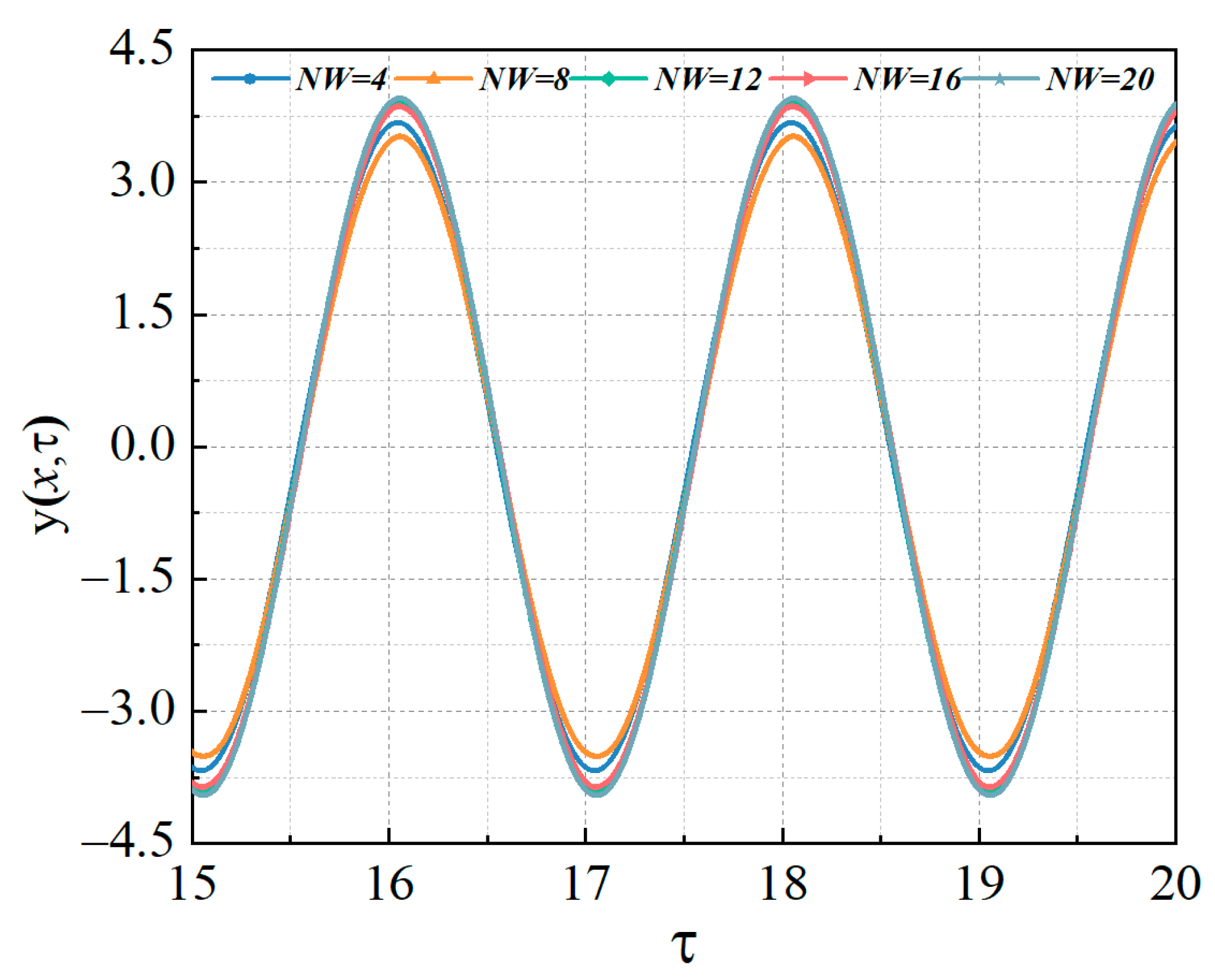
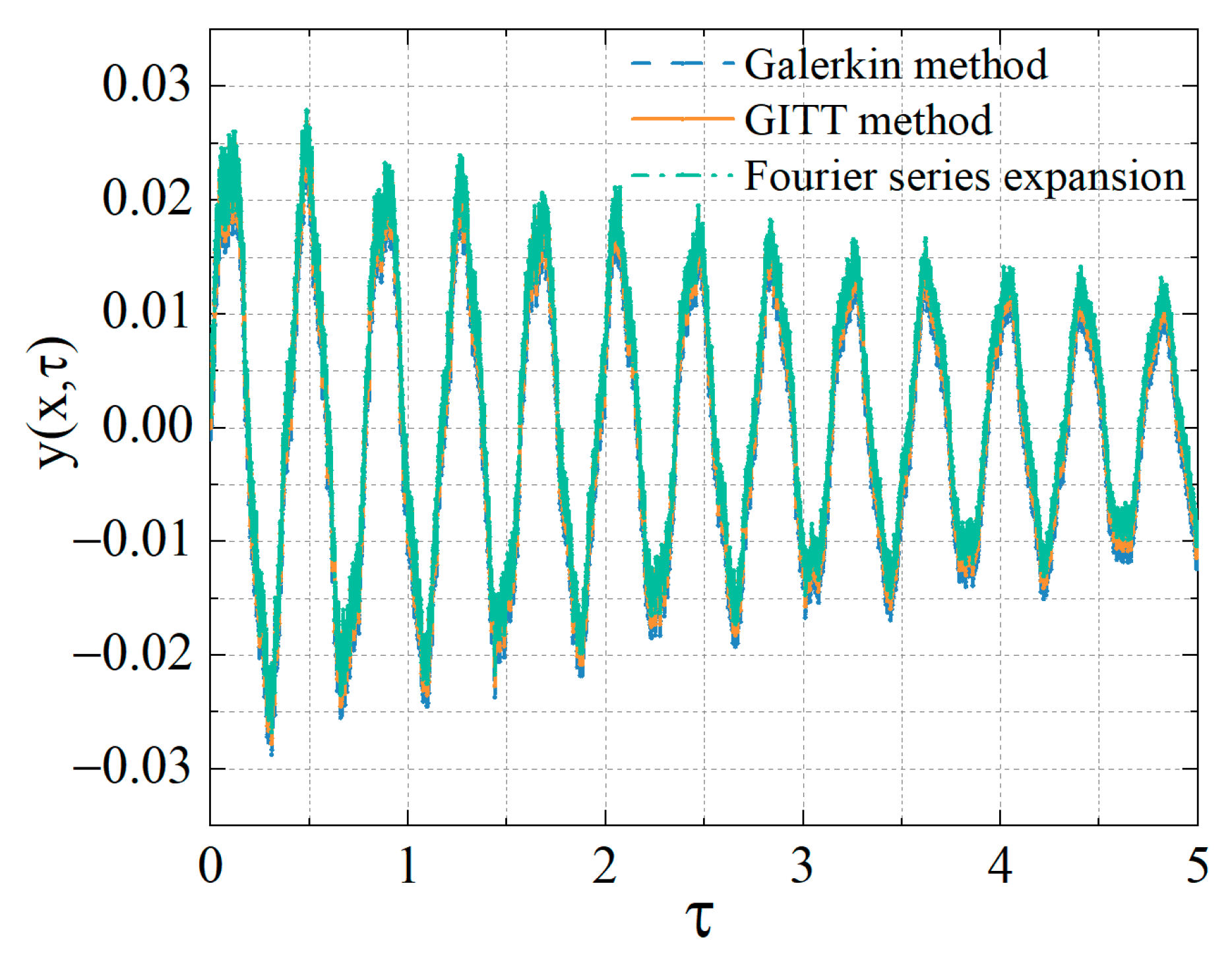
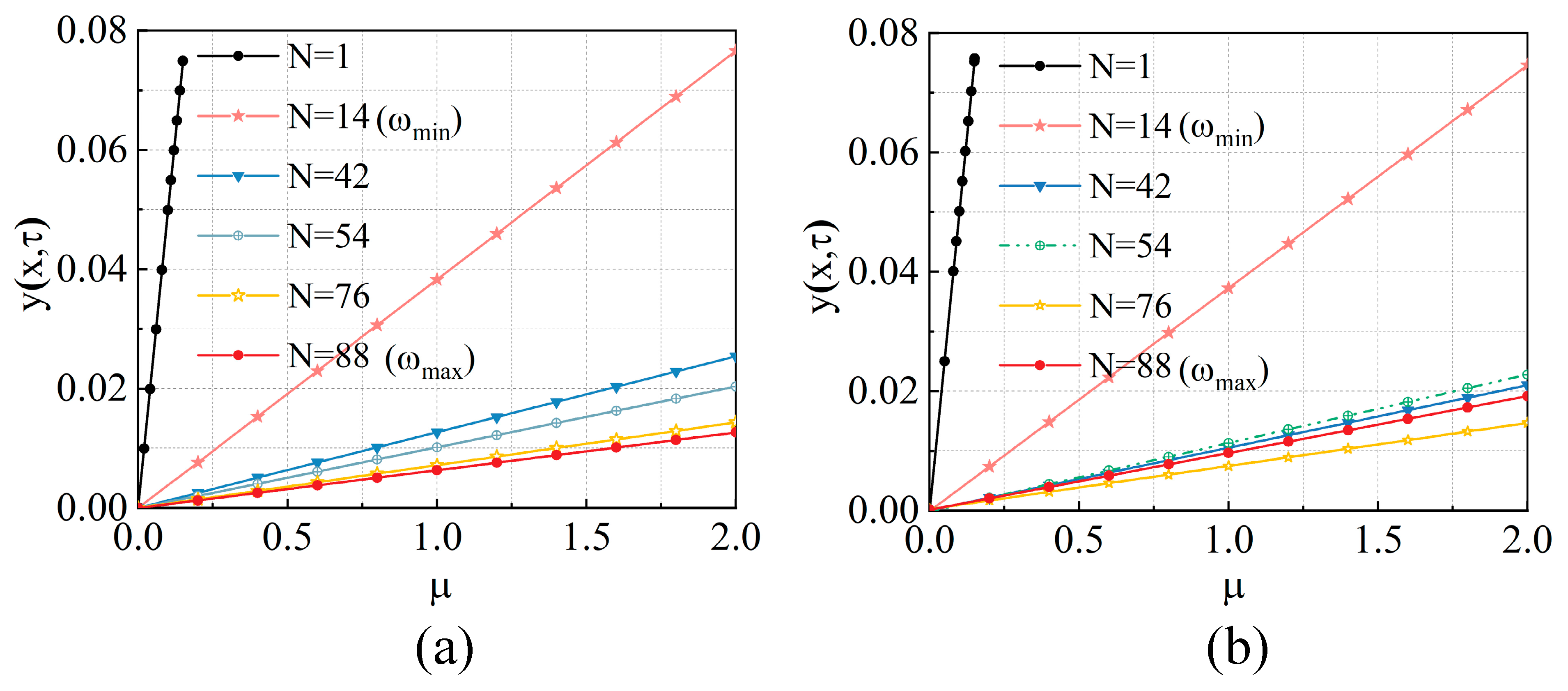
4.1. Convergence and Accuracy

The convergence of the GITT was proved with S-S boundary conditions. Considering the values for the internal flow velocity of 6.0 and the external flow velocity of 1.0, the parameters of the numerical model as shown in

Table 2. Parameters of the numerical model.

Property	Value
Length (m)	1000
Density of the pipe (kg/m3)	1206
Density of the seawater (kg/m3)	1025
Inner diameter (m)	1.5
Outer diameter (m)	1.6
Section area (m2)	0.243
Dry weight (N/m)	$2.88\times {10}^3$
Wet weight (N/m)	$4.32\times {10}^2$
Young’s modulus (Pa)	$1.38\times {10}^{10}$
Circular frequency (rad/s)	110
Hysteretic damping loss factor	0.016
Additional mass coefficient	1.0

. The transverse displacement at the midpoint of the pipe is presented in Figure 4 for truncation orders of NW = 4, 8, 12, 16, and 20. As shown, the midpoint vibration pattern of the pipe was found to be consistent, and the GITT instantly converged once the truncation order was greater than 12. All results were obtained with a truncation order of NW = 16 in the following analyses. The figure demonstrates that the GITT converges rapidly and accurately as NW increases. The figure also indicates that the truncation order of NW = 16 is sufficient to obtain a reliable solution for the problem. The figure illustrates the effectiveness and efficiency of the GITT for solving the vibration problem of OTEC CWPs.

To demonstrate the accuracy of the GITT, a cold-water pipe was studied under S-S boundary conditions with internal and external flow. Comparisons were made between the results obtained using the GITT and the Galerkin and Fourier series expansion techniques. Figure 5 shows the time histories of the dimensionless lateral displacement of the pipe at the center ($x$ = 0.5). The results obtained by the GITT and those obtained by the Galerkin method and the Fourier series expansion technique are in excellent agreement with each other.

4.2. Parametric Study

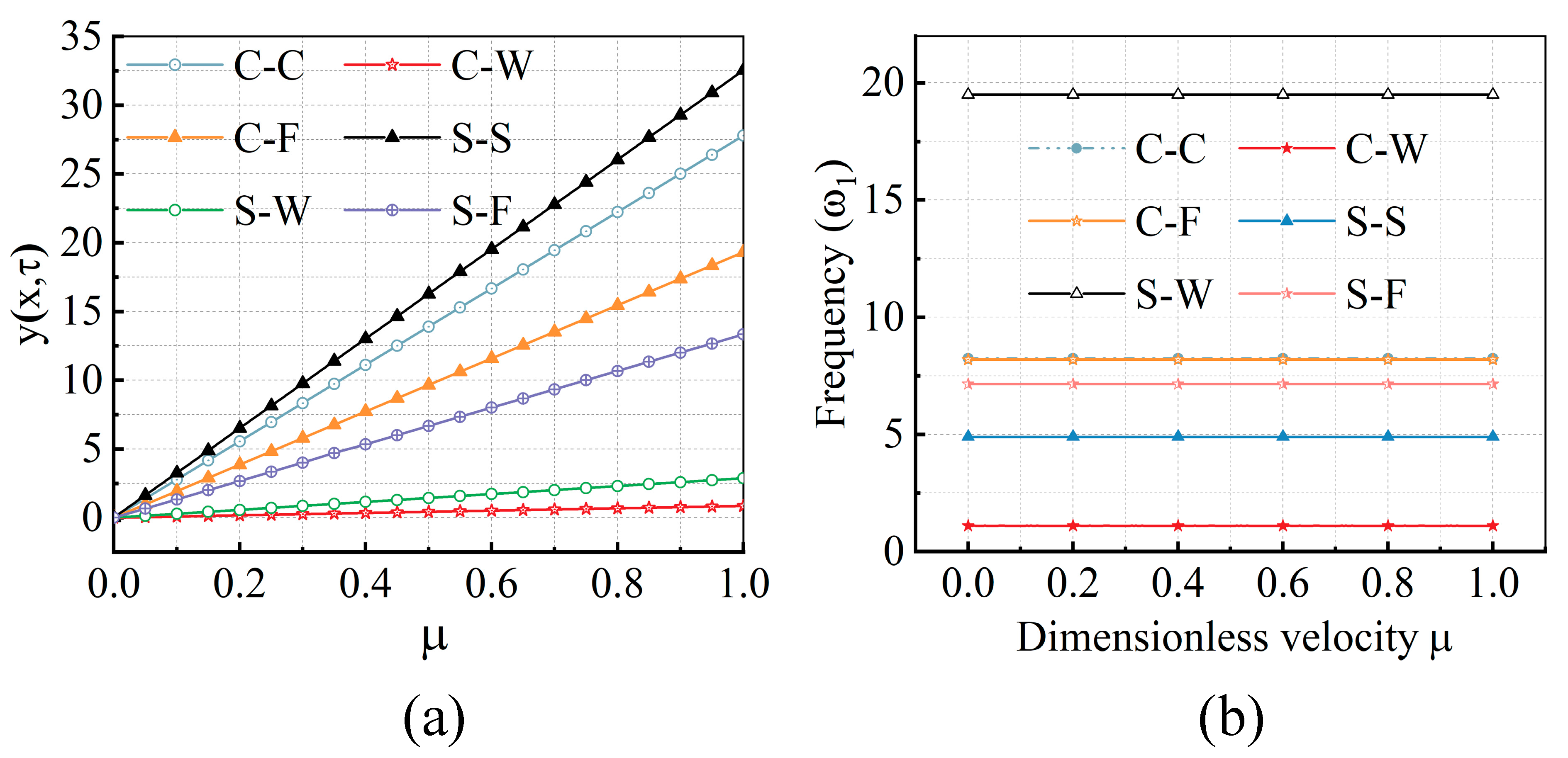
4.2.1. Effects of the Boundary Condition

To illustrate the effect of the boundary condition on the dimensionless transverse displacement at the midpoint of the pipe, the OTEC CWP subjected to internal and external flow under the C-C, C-W, C-F, S-S, S-W, and S-F boundary conditions was investigated.

The time histories of the pipe at the point ($x$ = 0.25, 0.5, 0.75) under different boundary conditions were given in Figure 6, where $y{(x,\tau )}_{\max }$ represents the peak transverse displacement in each second. It was noted that the dimensionless internal flow velocity was equal to 0.02 and the dimensionless external flow velocity was equal to 0. The peak displacement of the terminal boundary condition C-F was the largest of all the boundary conditions [41], and the pipe with the terminal boundary condition C-W had the smallest. It can also be observed in Figure 6 that the transverse displacement of the pipe with the boundary conditions C-C, C-W, S-S, and S-W was stably convergent, while it was divergent with the boundary conditions C-F and S-F.

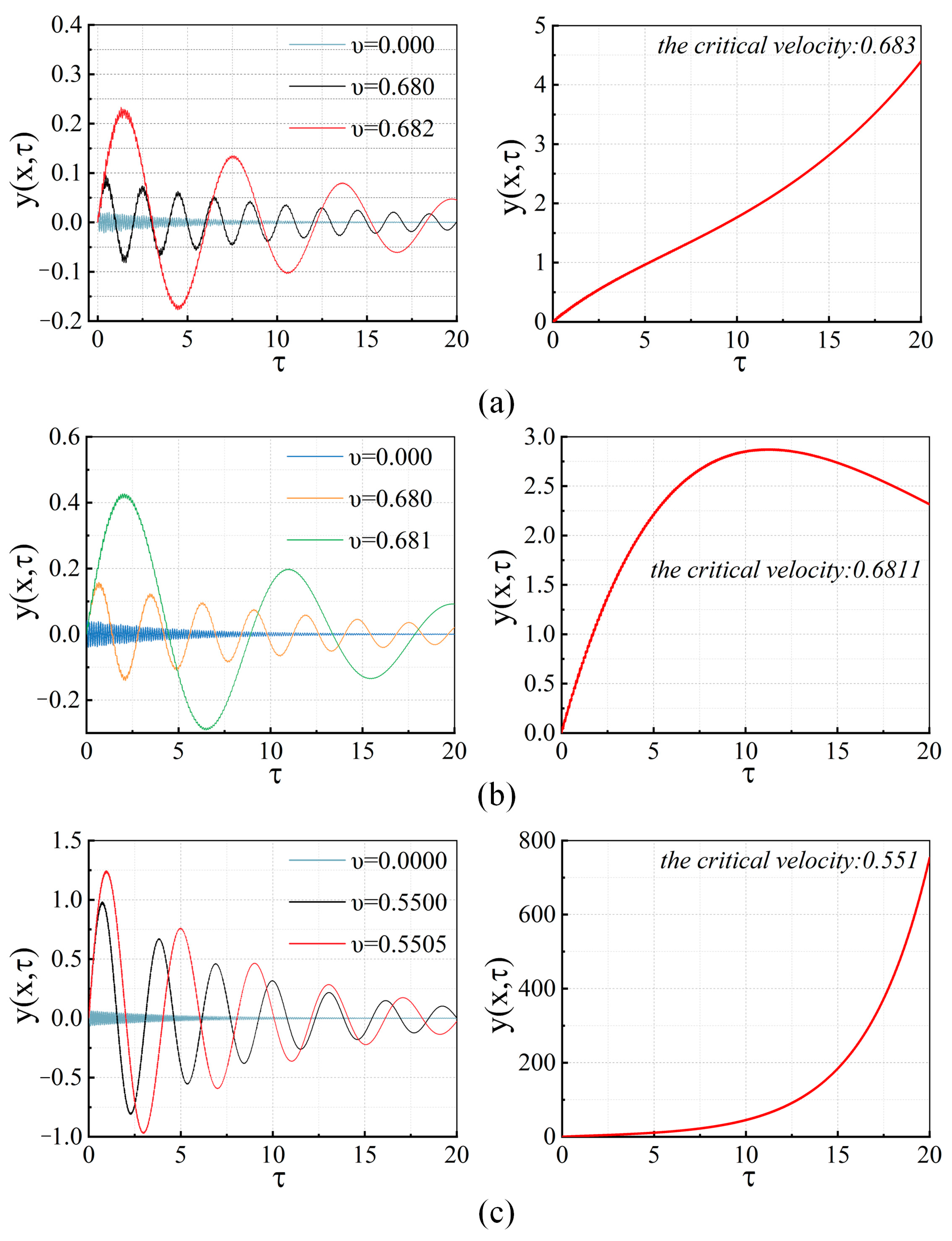
4.2.2. Effects of Internal Flow

To show the effect of the internal flow on the dimensionless transverse displacement and the first-mode natural frequency of the pipe, the dynamic behavior of the cold-water pipe under different boundary conditions was investigated. Considering the values of the dimensionless internal flow velocity from 0 to 1, followed by the dimensionless external flow velocity ($\mu =0$) and the clump weight $T_{wc}=T_d$, the dimensionless transverse displacement and the first-mode frequency of the pipe are presented in Figure 7 and Figure 8. It was noted that the normalization integral N_i equals 1 for the C-C, C-W, and C-F boundary conditions and 0.5 for the S-S, S-W, and S-F boundary conditions.

Figure 7 shows that the variation in the dimensionless transverse displacement with time $\tau$ obtained from the simulation with various dimensionless velocities under C-C, C-F, and S-S boundary conditions. In Figure 7, at a relatively small velocity, the dimensionless transverse displacement was about the same for all types of boundary conditions, but the gap widens dramatically as the dimensionless velocity increases. The dimensionless critical velocity ${\upsilon }_c$ occurs when the first-mode natural frequency reaches the zero point. The simulation continues until the dimensionless velocity reaches the dimensionless critical velocity ${\upsilon }_c$. The dimensionless critical velocity of the pipe was 0.6830, 0.6811, and 0.5510, which corresponds to the C-C, C-F, and S-S boundary conditions, respectively.

From Figure 7, the first-mode natural frequency of the pipe versus the dimensionless internal flow velocity can be plotted as shown in Figure 8. As indicated, the first-mode natural frequency of the pipe may be sensitive to the internal flow velocity. As shown in Figure 8a, the first-mode natural frequency slowly decreases and approaches zero as the dimensionless internal flow velocity increases. In this case, it was equivalent to reducing the stiffness of the pipe. The greater the dimensionless internal flow velocity, the faster the first-mode natural frequency decreases. The critical frequency of the pipe was 8.246, 8.160, and 9.246, corresponding to the C-C, C-F, and S-S boundary conditions, respectively (see

Table 3. The first-mode natural frequency and the dimensionless critical velocity under different boundary conditions.

Boundary Condition	Frequency (Hz)	Critical Velocity (${\mathit{\upsilon }}_{\mathit{c}}$)
C-C	8.246	0.6830
C-W	58.785	-
C-F	8.160	0.6811
S-S	9.246	0.5510
S-W	27.336	-
S-F	7.146	-

). As shown in Figure 8b, the results of the GITT and the solution provided by Xu [42] have good agreement. The relative error of the first-mode natural frequency was less than 4.5%. Therefore, the applied GITT can provide reliable results under a modest internal flow velocity. The first-mode natural frequency and dimensionless internal flow velocity were fitted via MATLAB software (2021b) to obtain the functional relationship with the C-C, C-F, and S-S boundary conditions, as shown in Equation (37).

$$\begin{array}{l}{\omega }_1(\upsilon )=-0.06605\cdot e^{6.726\cdot \upsilon }+8.485\cdot e^{-0.3306\cdot \upsilon } \mathrm{with} \mathrm{C}-\mathrm{C}, \mathrm{C}-\mathrm{F};\\ {\omega }_2(\upsilon )=-0.01479\cdot e^{11.02\cdot \upsilon }+9.34\cdot e^{-0.614\cdot \upsilon } \mathrm{with} \mathrm{S}-\mathrm{S}.\end{array}$$

(37)

Figure 9 shows the vibration of the dimensionless transverse displacement and the first-mode natural frequency with respect to the dimensionless internal flow velocity obtained from the simulation, with a different point of the pipe under the C-W, S-W, and S-F boundary conditions. In Figure 9a, the dimensionless transverse displacement does not seem to be affected by the increase in the internal flow at a relatively small velocity but increases remarkably when the dimensionless internal flow velocity is more significant than 0.6 under the C-W boundary condition. In Figure 9b,c, as the dimensionless internal flow velocity increases, the development tendency of the dimensionless transverse displacement was about the same for the S-W and S-F boundary conditions but was more sensitive to the internal flow velocity under the S-F boundary condition. On the other hand, Figure 9d shows that the first-mode natural frequency does not seem to be affected by the increase in the internal flow velocity for all types of boundary conditions and was 58.785, 27.336, and 7.146, corresponding to the C-W, S-W, and S-F boundary conditions, respectively.

4.2.3. Effects of External Flow

To analyze the effect of the external flow on the dimensionless transverse displacement and the first-mode frequency of the pipe, the dynamic behavior of the cold-water pipe under different boundary conditions was investigated. Considering the values of the dimensionless external flow velocity from 0 to 1, followed by the dimensionless internal flow velocity ($\upsilon =0$) and the clump weight $T_{wc}=T_d$, the dimensionless transverse displacement and the first-mode frequency at the midpoint of the pipe can be plotted as shown in Figure 10.

In Figure 10a, as for the increase in the external flow velocity, the dimensionless transverse displacement was about linear for all types of boundary conditions, but the gap enlarged remarkably under different boundary conditions. The external flow had the most significant influence on the dimensionless transverse displacement of the pipe under the S-S boundary condition but a minor influence under the C-W boundary condition. Figure 10b shows that the first-mode natural frequency does not seem to be affected by the increase in the external flow velocity. The first-mode frequency was about the same for the C-C and C-F boundary conditions.

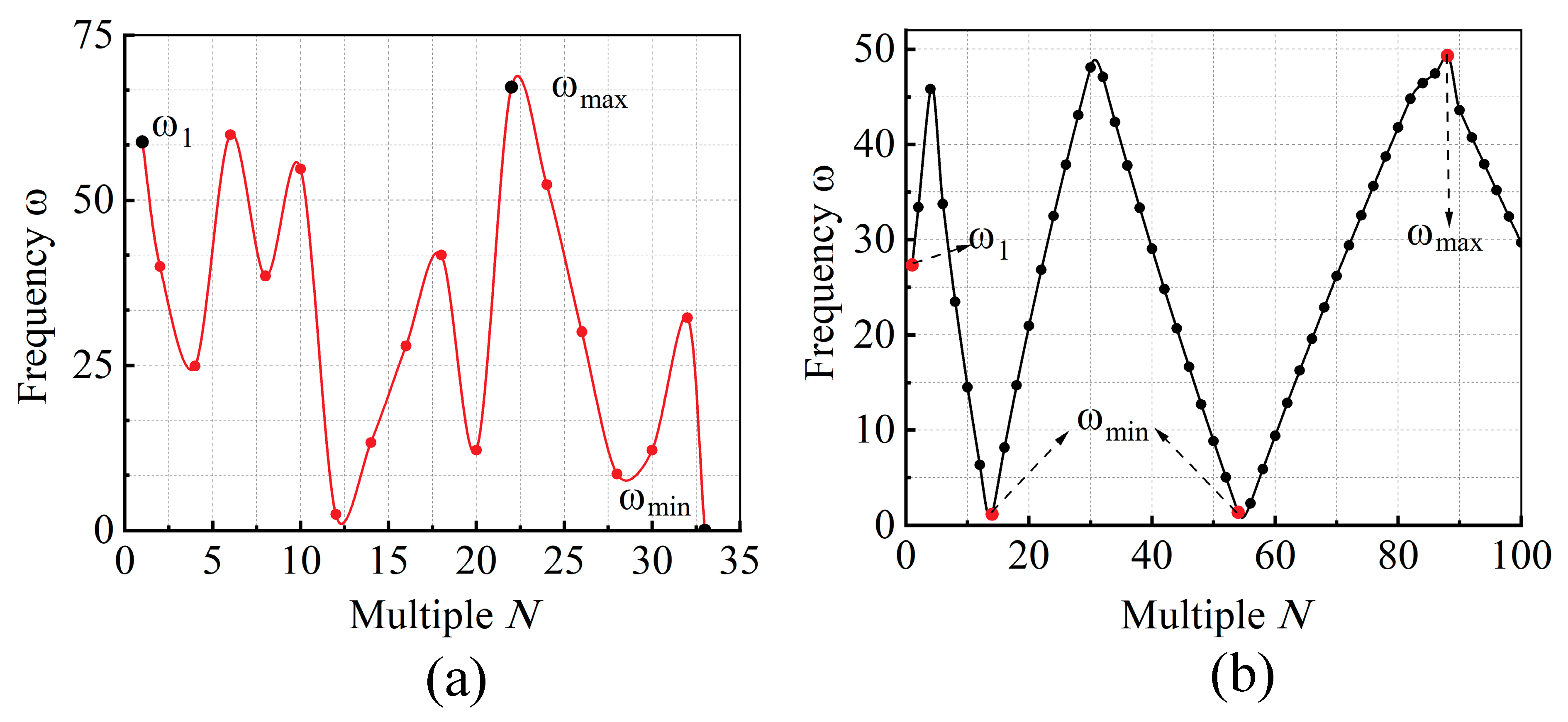
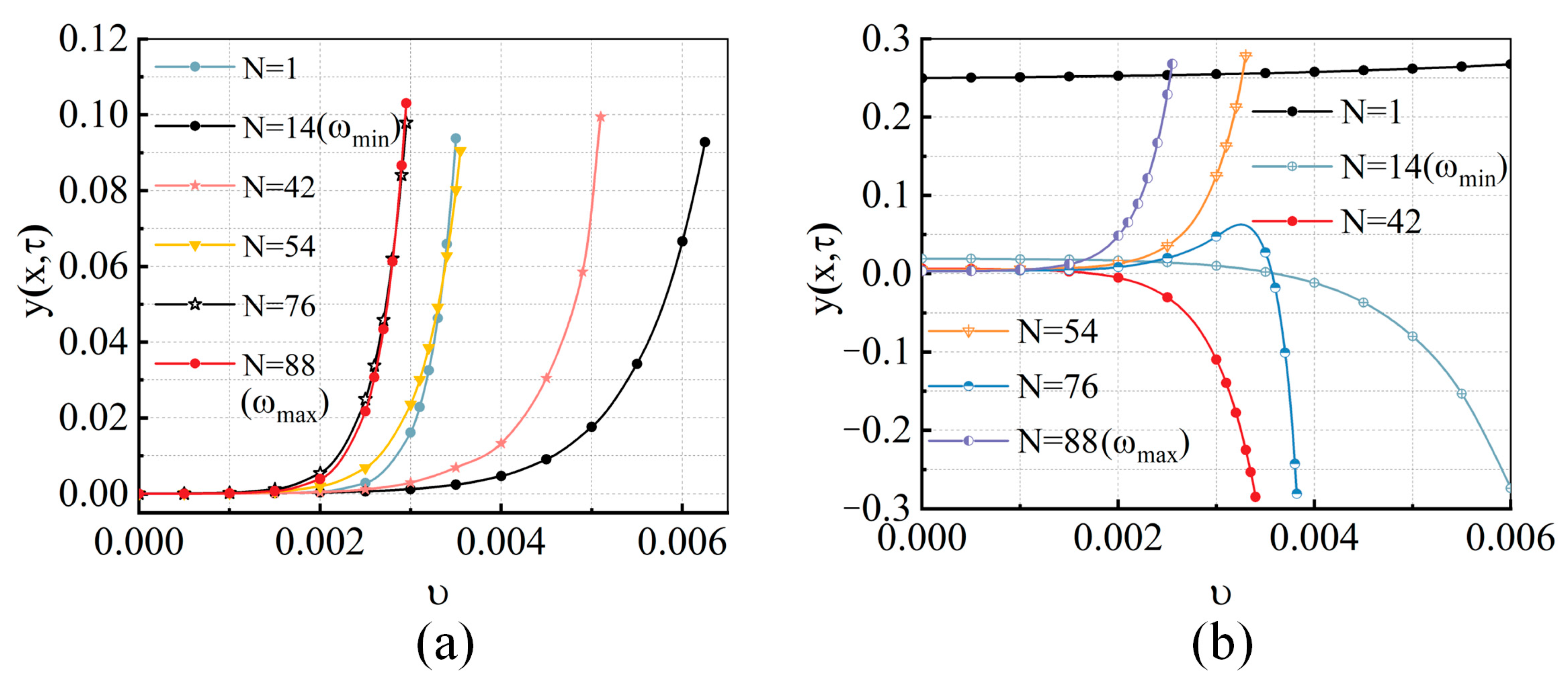
4.2.4. Effects of the Clump Weight

To figure out the effect of the clump weight on the dimensionless transverse displacement and first-mode frequency of the pipe, the dynamic behavior of the cold-water pipe under different boundary conditions was investigated. In all previous results, we set the weight of the clump as one time the pipe’s dry weight. When the weight of the clump was set as N times, the end constraints at the bottom can be changed from weak to strong. To this end, the clump weight was defined as follows:

$$T_{wc}{}^{\prime }=N{T}_d=N{\rho }_r{A}_{r}gL$$

(38)

where N denotes the multiples.

This section discusses the results of the analytical simulations in particular. The simulation was done for a pipe under the C-W and S-W boundary conditions. By imposing the different clump weights at the bottom, the first-mode natural frequency for the two types of boundary conditions of pipe can be assessed. Figure 11a shows that the effect of the clump weight on the first-mode natural frequency was not small. For the multiples of the clump weight, N was set from 1 to 33, which led to the first-mode natural frequency decreasing first and then increasing, and so forth. It is worth noting that the first-mode natural frequency reached its maximum value at N = 22 and became zero at N = 33. Figure 11b shows that the first-mode natural frequency had about the same development trends for the C-W and S-W boundary conditions, but it reached its maximum value at N = 88 and minimum value at N = 14 or 53. It can be concluded that the different clump weights at the bottom of the pipe can effectively affect the first-mode natural frequency and further the stability of the pipe.

To investigate the effect of the internal flow velocity on the dimensionless transverse displacement at the midpoint of the pipe with different clump weights under the C-W boundary condition, Figure 12 was produced. Figure 12a,b were for the external flow velocity $\mu =0$ and $\mu =0.5$, respectively. In Figure 12a, the dimensionless transverse displacement was much influenced by the clump weight. It can be concluded that with the increase in the clump weight, the same dimensionless internal flow velocity corresponded to a more significant dimensionless transverse displacement. Figure 12b shows that pipe vibration appears in second-order mode shapes due to the combined action of internal and external flow. It was observed that as the clump weight increased, the dimensionless internal flow velocity required for the mode shape of the vibration to turn into the second mode was smaller. Figure 12a,b together show that the external flow seems to affect the mode shape of the vibration, and the dependence of the critical internal flow velocity on the clump weight was very sensitive for 12 < N < 33.

To figure out the effect of the external flow velocity on the dimensionless transverse displacement, a pipe with different clump weights under the C-W boundary condition was investigated. In Figure 13a, at the dimensionless internal flow velocity $\upsilon =0$, the dimensionless transverse displacement changed linearly with the external flow velocity. The influence of external flow had a greater effect on the small value of the clump weight compared with the higher ones. Figure 13b depicts the comparison results for the lateral displacement of the pipe with different clump weights subjected to external flow and internal fluid ($\upsilon =0.001$). The results indicate that the clump weights had a huge effect on the lateral displacement and mode shape of the vibration. The amplitude of the dimensionless transverse displacement increased and the mode shape of vibration became the second mode as one region of the clump weight increased. The results in Figure 12 and Figure 13 show that by setting the weight of the clump as an appropriate value, the transverse displacement and the natural frequency can be changed to improve the stability of the pipe under the C-W boundary condition.

The different clump weights were considered to investigate the effect of the dimensionless internal velocity on the dimensionless transverse displacement under the S-W boundary condition. In Figure 14a, the amplitude of the dimensionless transverse displacement decreased with one region (1 < N < 14) of the clump weight increasing at the same internal flow rate, which indicated that as the clump weight increased, the natural frequency decreased, resulting in an increase in the stability of the pipe. However, the continuing increase in the weight of the clump decreased the stability of the pipe, which can cause serious oscillation phenomena at a very small velocity. As shown in Figure 14b, the effect of the external flow was added. At a relatively small velocity, the clump weight can effectively decrease the motion amplitude and change the mode shape of the vibration at the region of 1 < N < 14. After that, the increasing clump weight and internal flow trigger instability and lead to the failure of the pipe.

Figure 15 depicts the comparison results for the variation in the dimensionless transverse displacement with different clump weights under the S-W boundary condition, where $\upsilon$ was taken as 0 and 0.001, respectively. It was shown that the effect of the clump weight on the transverse displacement under the S-W boundary condition was significant and that these effects were about the same for the C-W boundary condition. At a relatively large value, the clump weight was able to decrease the lateral displacement of the pipe. Figure 15a,b together show that the effect of internal flow on the lateral displacement was very small compared with external flow under the S-W boundary condition but was not small under the C-W boundary condition (see Figure 13). On the other hand, the mode shape of the vibration did not change as the clump weight increased.

5. Conclusions

This paper investigated the vibrational characteristics of an ultra-large cold-water pipe (CWP) for ocean thermal energy conversion (OTEC) under different boundary conditions. The generalized integral transform technique (GITT) was utilized to solve the governing vibration equation, and the semi-analytic solutions were expressed by eigenfunctions and eigenvalues in the form of a combination of numerically stable exponential and trigonometric function forms. The convergence and accuracy of the GITT was demonstrated in comparison to the Galerkin method and the Fourier series expansion technique. The CWP’s vibrational characteristics were analyzed using the GITT for different boundary conditions, internal and external flow velocities, and clump weights. The following conclusions were obtained:

(1)

The eigenfunctions and eigenvalues were calculated for the C-W and S-W boundary conditions using the GITT for the first time.

(2)

The boundary conditions had a significant effect on the convergence of the transverse displacement, in that different boundary conditions changed the eigenfunctions and eigenvalues of the displacement function.

(3)

The first-mode natural frequency of the pipe decreased as the internal flow velocity increased under the C-C, C-F, and S-S boundary conditions but remained constant under the C-W, S-W, and S-F boundary conditions. The first-mode natural frequency is important as it likely to be associated with the critical velocity during the operation of a CWP.

(4)

The increase in the transverse displacement with an increasing external flow velocity showed a proportional relationship, and peak displacement of the pipe under the C-W boundary condition was smaller compared with the other boundary conditions.

(5)

By setting the weight of the clump at the bottom, the transverse displacement and the first-mode natural frequency of the pipe were adjusted, and the effect was better with the S-W boundary condition. The results of this research can be an important reference for improving the stability and safety of an ultra-large CWP by adjusting the clump weight.

Numerous new results obtained by the proposed approach can assist in the development and analysis of early-stage CWP design.