Morphological Response of a Highly Engineered Estuary to Altering Channel Depth and Restoring Wetlands
Abstract
:1. Introduction
2. Methods
2.1. Modeling Rationale
2.1.1. Time and Spatial Scale
2.1.2. Schematized Domain
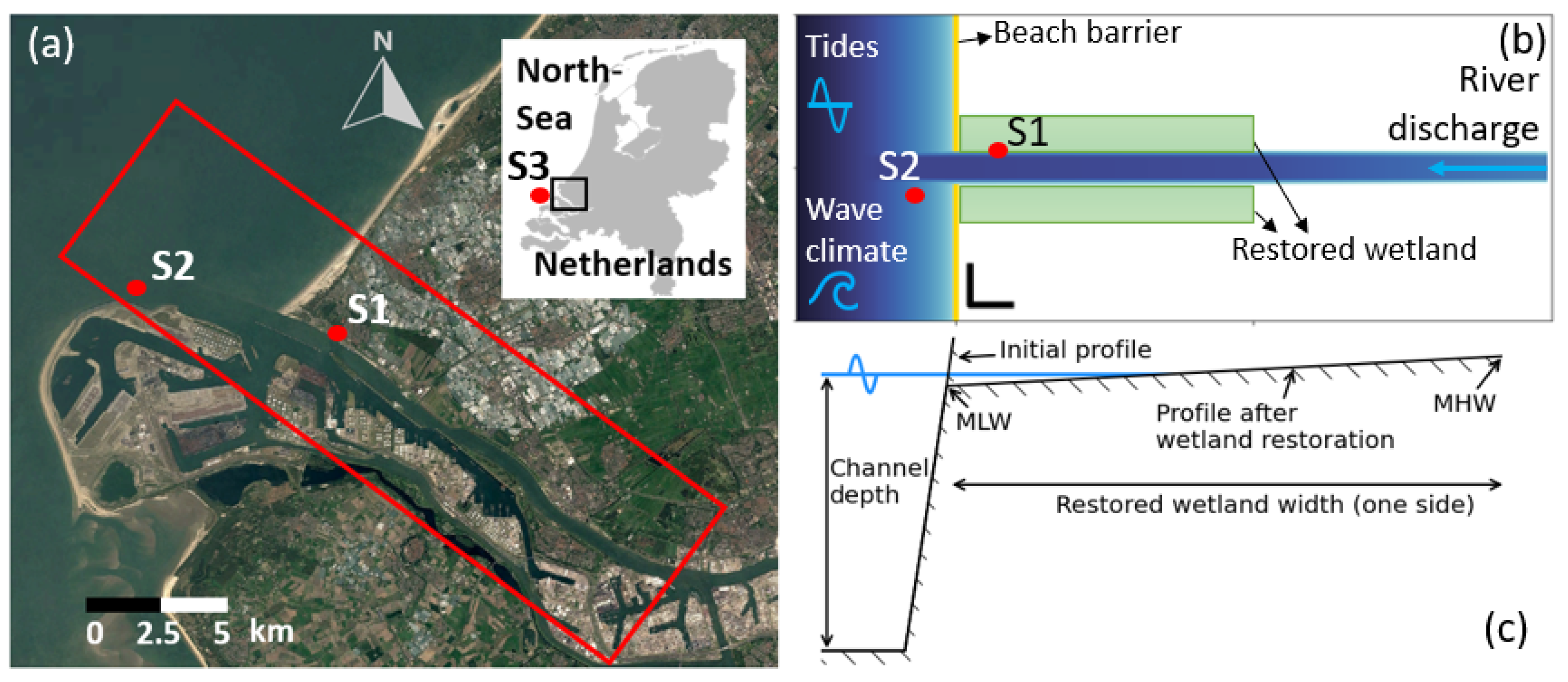
2.1.3. Study Area
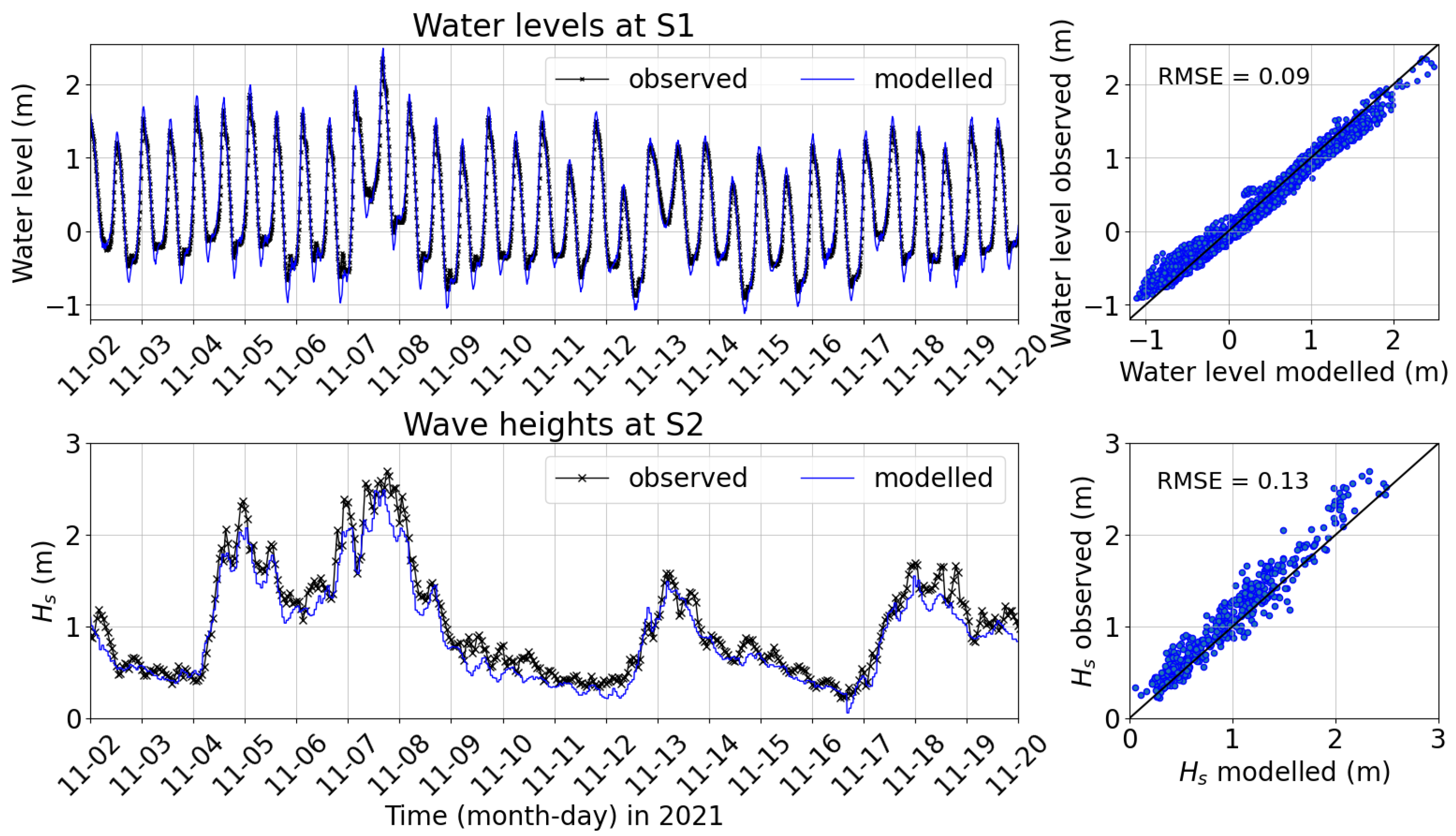
2.2. Model Setup
2.2.1. Model Description
2.2.2. Schematized Bathymetry
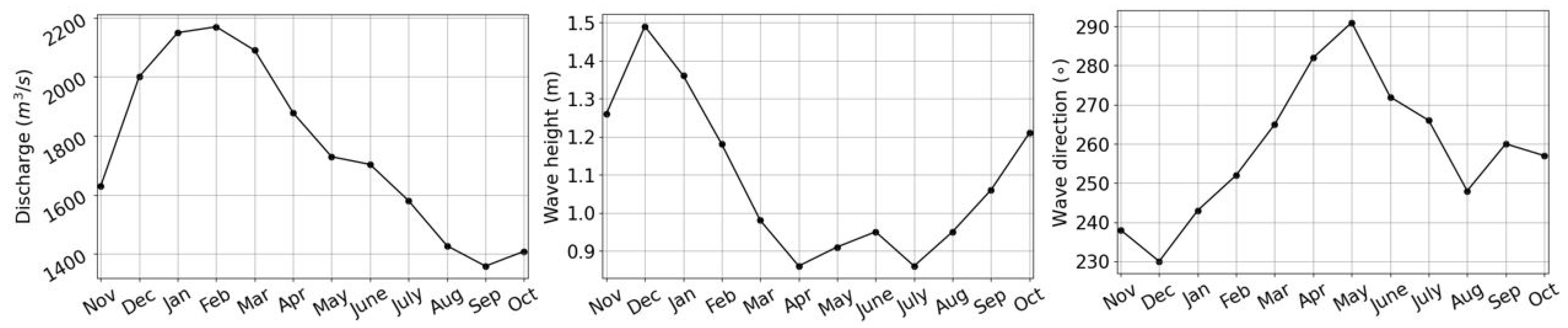
2.2.3. Model Forcing
2.2.4. Morphological Settings
2.2.5. Vegetation
2.3. Large-Scale Interventions
2.4. Model Output Analysis
3. Results
3.1. Reference Scenario
3.1.1. Hydrodynamics
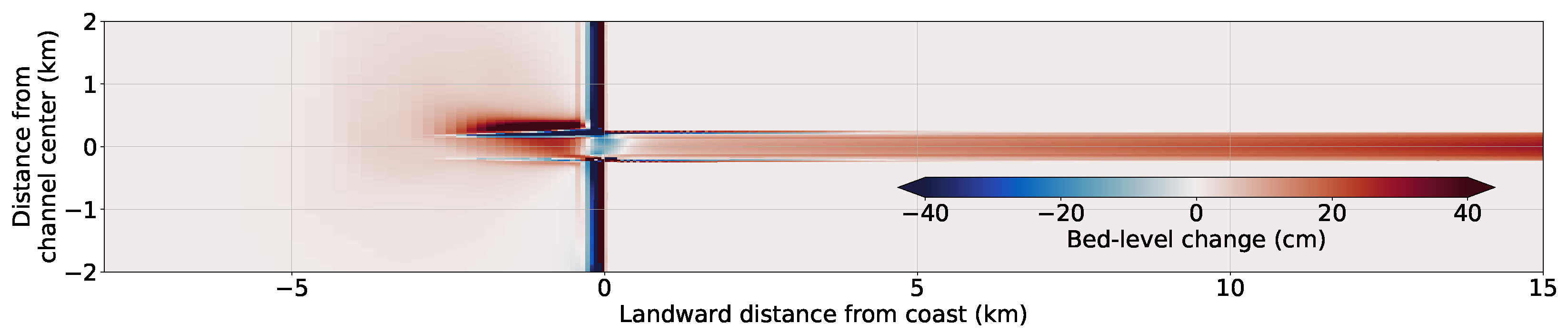
3.1.2. Morphological Patterns
3.2. Changing Channel Depth
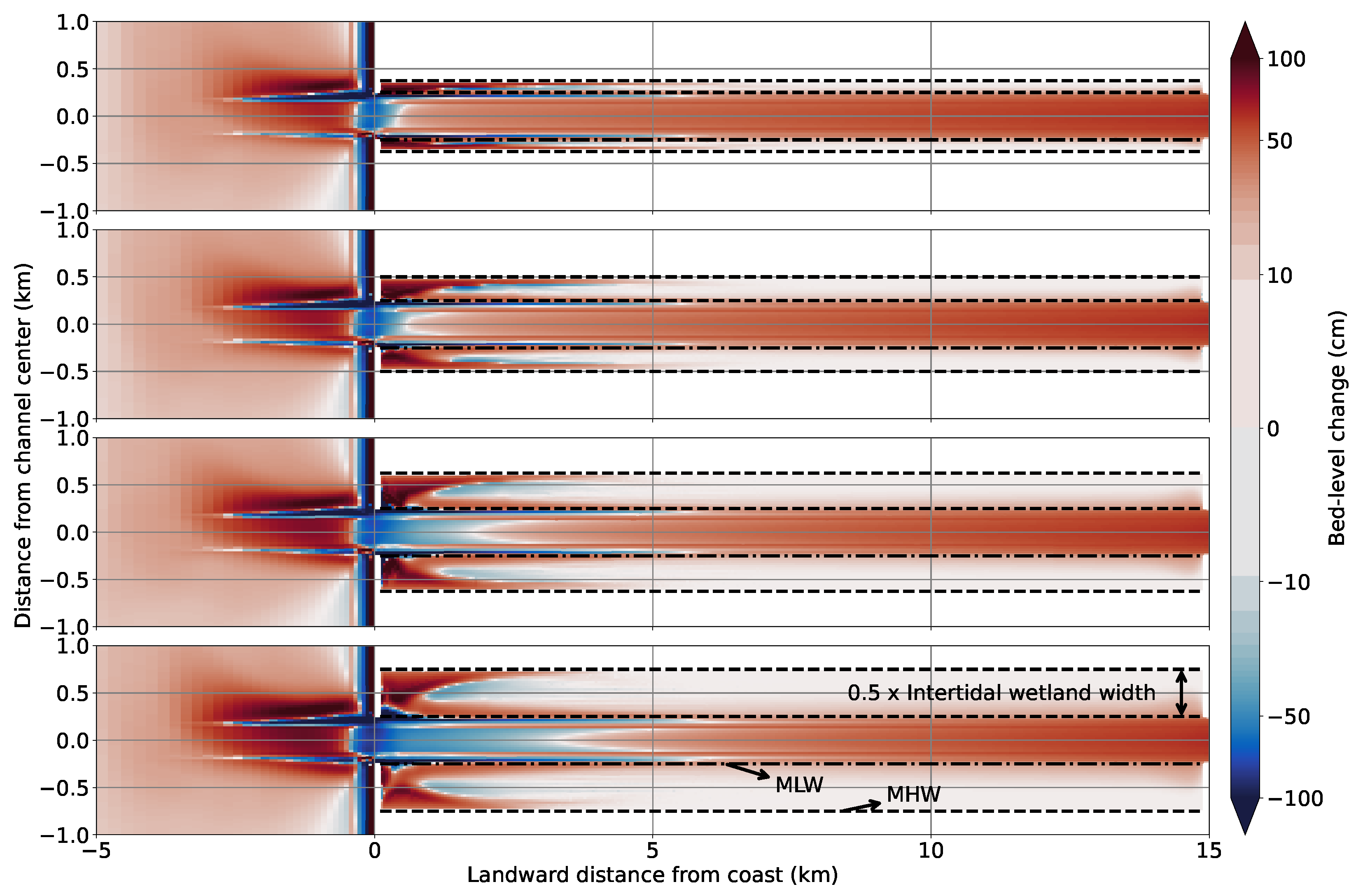
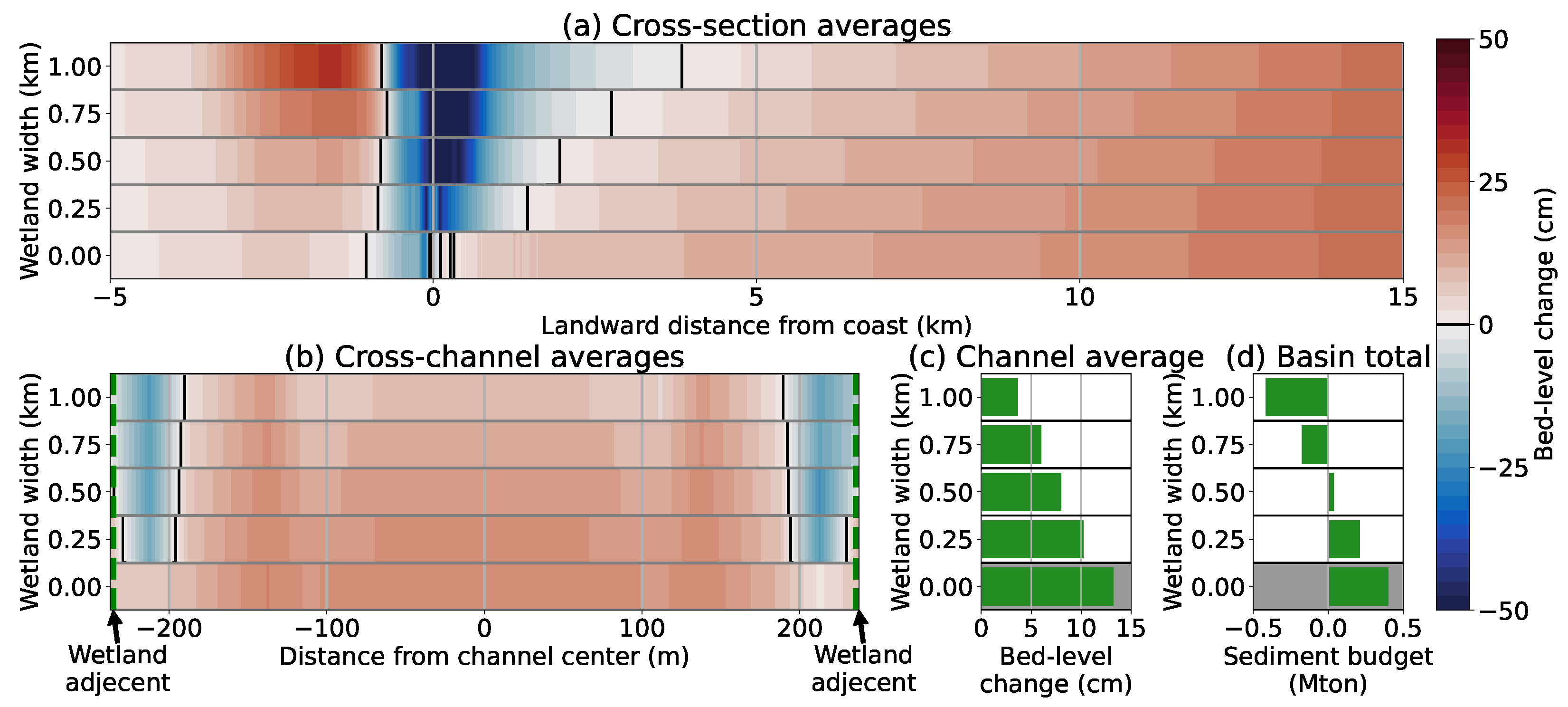
3.3. Changing Wetland Width and Location
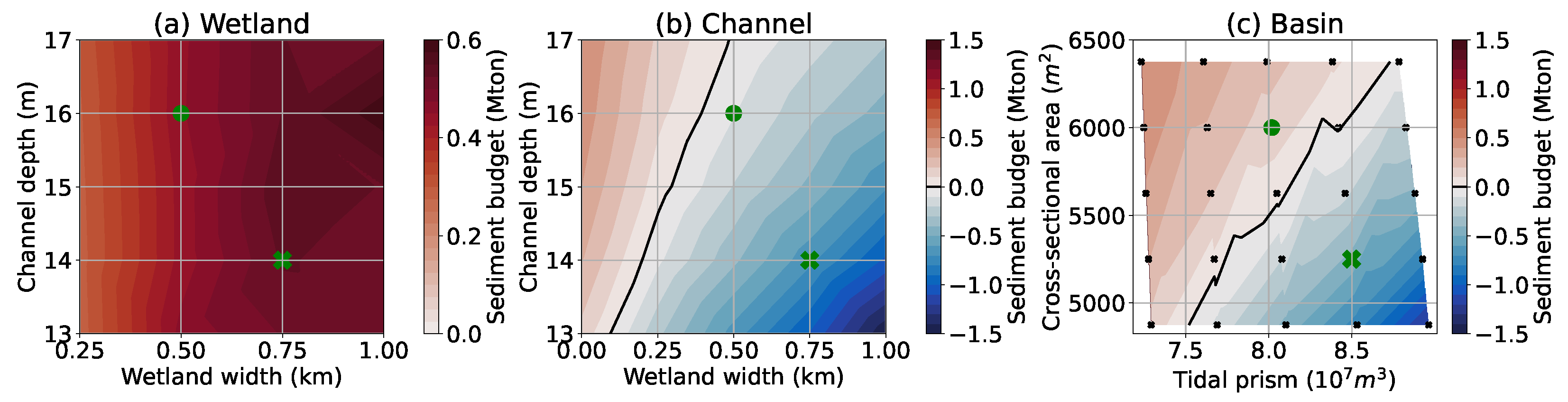
3.4. Channel Depth versus Wetland Width
4. Discussion
4.1. Model Input Conditions
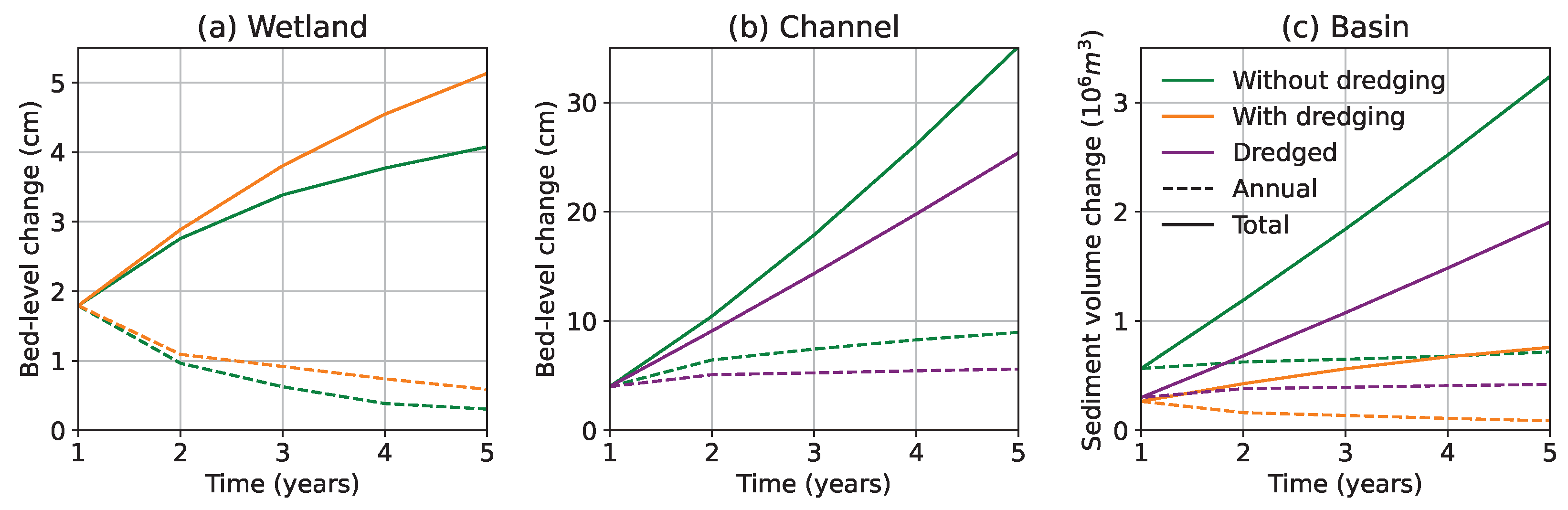
4.2. Model Timescale
4.3. Steering Estuarine Morphology Using Large-Scale Interventions
4.4. Tidal Prism Cross-Sectional Area Relationship
4.5. Implications for Estuarine Management
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1
Appendix A.2
Appendix A.3
Appendix A.3.1. Cohesive Sediments
Appendix A.3.2. Non-Cohesive Sediments
References
- Giosan, L.; Syvitski, J.; Constantinescu, S.; Day, J. Climate change: Protect the world’s deltas. Nature 2014, 516, 31–33. [Google Scholar] [CrossRef] [PubMed]
- Cox, J.; Lingbeek, J.; Weisscher, S.; Kleinhans, M. Effects of sea-level rise on dredging and dredged estuary morphology. J. Geophys. Res. Earth Surf. 2022, 127, 1–20. [Google Scholar] [CrossRef]
- Eslami, S.; Hoekstra, P.; Nguyen Trung, N.; Ahmed Kantoush, S.; Van Binh, D.; Duc Dung, D.; Tran Quang, T.; van der Vegt, M. Tidal amplification and salt intrusion in the Mekong Delta driven by anthropogenic sediment starvation. Sci. Rep. 2019, 9, 18746. [Google Scholar] [CrossRef] [PubMed]
- Leuven, J.R.F.W.; Pierik, H.J.; van der Vegt, M.; Bouma, T.J.; Kleinhans, M.G. Sea-level-rise-induced threats depend on the size of tide-influenced estuaries worldwide. Nat. Clim. Chang. 2019, 9, 986–992. [Google Scholar] [CrossRef]
- Costanza, R.; d’Arge, R.; de Groot, R.; Farber, S.; Grasso, M.; Hannon, B.; Limburg, K.; Naeem, S.; O’Neill, R.V.; Paruelo, J.; et al. The value of the world’s ecosystem services and natural capital. Nature 1997, 387, 253–260. [Google Scholar] [CrossRef]
- Du, J.L.; Yang, S.L.; Feng, H. Recent human impacts on the morphological evolution of the Yangtze River delta foreland: A review and new perspectives. Estuar. Coast. Shelf Sci. 2016, 181, 160–169. [Google Scholar] [CrossRef]
- Van Dijk, W.M.; Cox, J.R.; Leuven, J.R.; Cleveringa, J.; Taal, M.; Hiatt, M.R.; Sonke, W.; Verbeek, K.; Speckmann, B.; Kleinhans, M.G. The vulnerability of tidal flats and multi-channel estuaries to dredging and disposal. Anthr. Coasts 2021, 4, 36–60. [Google Scholar] [CrossRef]
- Syvitski, J.P.; Kettner, A.J.; Overeem, I.; Hutton, E.W.; Hannon, M.T.; Brakenridge, G.R.; Day, J.; Vörösmarty, C.; Saito, Y.; Giosan, L.; et al. Sinking deltas due to human activities. Nat. Geosci. 2009, 2, 681–686. [Google Scholar] [CrossRef]
- Schmitt, R.; Rubin, Z.; Kondolf, G. Losing ground-scenarios of land loss as consequence of shifting sediment budgets in the Mekong Delta. Geomorphology 2017, 294, 58–69. [Google Scholar] [CrossRef]
- de Jonge, V.N.; Schückel, U. Exploring effects of dredging and organic waste on the functioning and the quantitative biomass structure of the Ems estuary food web by applying Input Method balancing in Ecological Network Analysis. Ocean Coast. Manag. 2019, 174, 38–55. [Google Scholar] [CrossRef]
- Sanches Fernandes, L.F.; Sampaio Pinto, A.A.; Salgado Terencio, D.P.; Leal Pacheco, F.A.; Vitor Cortes, R.M. Combination of ecological engineering procedures applied to morphological stabilization of estuarine banks after dredging. Water 2020, 12, 391. [Google Scholar] [CrossRef]
- Cox, J.; Leuven, J.; Pierik, H.; van Egmond, M.; Kleinhans, M. Sediment deficit and morphological change of the Rhine–Meuse river mouth attributed to multi-millennial anthropogenic impacts. Cont. Shelf Res. 2022, 244, 104766. [Google Scholar] [CrossRef]
- Wang, Y.H.; Tang, L.Q.; Wang, C.H.; Liu, C.J.; Dong, Z.D. Combined effects of channel dredging, land reclamation and long-range jetties upon the long-term evolution of channel-shoal system in Qinzhou bay, SW China. Ocean Eng. 2014, 91, 340–349. [Google Scholar] [CrossRef]
- Pye, K.; Blott, S.J. The geomorphology of UK estuaries: The role of geological controls, antecedent conditions and human activities. Estuar. Coast. Shelf Sci. 2014, 150, 196–214. [Google Scholar] [CrossRef]
- Dunn, F.E.; Darby, S.E.; Nicholls, R.J.; Cohen, S.; Zarfl, C.; Fekete, B.M. Projections of declining fluvial sediment delivery to major deltas worldwide in response to climate change and anthropogenic stress. Environ. Res. Lett. 2019, 14, 084034. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y.; Thompson, C.; Wang, X.; Cai, T.; Chang, Y. Differential sediment trapping abilities of mangrove and saltmarsh vegetation in a subtropical estuary. Geomorphology 2018, 318, 270–282. [Google Scholar] [CrossRef]
- Kirwan, M.L.; Guntenspergen, G.R.; D’Alpaos, A.; Morris, J.T.; Mudd, S.M.; Temmerman, S. Limits on the adaptability of coastal marshes to rising sea level. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Temmerman, S.; Meire, P.; Bouma, T.J.; Herman, P.M.; Ysebaert, T.; De Vriend, H.J. Ecosystem-based coastal defence in the face of global change. Nature 2013, 504, 79–83. [Google Scholar] [CrossRef]
- Hu, Z.; Borsje, B.W.; van Belzen, J.; Willemsen, P.W.; Wang, H.; Peng, Y.; Yuan, L.; De Dominicis, M.; Wolf, J.; Temmerman, S.; et al. Mechanistic modeling of marsh seedling establishment provides a positive outlook for coastal wetland restoration under global climate change. Geophys. Res. Lett. 2021, 48, e2021GL095596. [Google Scholar] [CrossRef]
- Nesshöver, C.; Assmuth, T.; Irvine, K.N.; Rusch, G.M.; Waylen, K.A.; Delbaere, B.; Haase, D.; Jones-Walters, L.; Keune, H.; Kovacs, E.; et al. The science, policy and practice of nature-based solutions: An interdisciplinary perspective. Sci. Total Environ. 2017, 579, 1215–1227. [Google Scholar] [CrossRef]
- Ganju, N.K. Marshes are the new beaches: Integrating sediment transport into restoration planning. Estuaries Coasts 2019, 42, 917–926. [Google Scholar] [CrossRef]
- Wiberg, P.L.; Fagherazzi, S.; Kirwan, M.L. Improving predictions of salt marsh evolution through better integration of data and models. Annu. Rev. Mar. Sci. 2020, 12, 389–413. [Google Scholar] [CrossRef] [PubMed]
- Dam, G.; van der Wegen, M.; Labeur, R.J.; Roelvink, D. Modeling centuries of estuarine morphodynamics in the Western Scheldt estuary. Geophys. Res. Lett. 2016, 43, 3839–3847. [Google Scholar] [CrossRef]
- Luan, H.L.; Ding, P.X.; Wang, Z.B.; Ge, J.Z. Process-based morphodynamic modeling of the Yangtze Estuary at a decadal timescale: Controls on estuarine evolution and future trends. Geomorphology 2017, 290, 347–364. [Google Scholar] [CrossRef]
- Elmilady, H.; Van der Wegen, M.; Roelvink, D.; Jaffe, B. Intertidal area disappears under sea level rise: 250 years of morphodynamic modeling in San Pablo Bay, California. J. Geophys. Res. Earth Surf. 2019, 124, 38–59. [Google Scholar] [CrossRef]
- Nahon, A.; Bertin, X.; Fortunato, A.B.; Oliveira, A. Process-based 2DH morphodynamic modeling of tidal inlets: A comparison with empirical classifications and theories. Mar. Geol. 2012, 291, 1–11. [Google Scholar] [CrossRef]
- Duong, T.M.; Ranasinghe, R.; Walstra, D.; Roelvink, D. Assessing climate change impacts on the stability of small tidal inlet systems: Why and how? Earth-Sci. Rev. 2016, 154, 369–380. [Google Scholar] [CrossRef]
- Duong, T.M.; Ranasinghe, R.; Luijendijk, A.; Walstra, D.; Roelvink, D. Assessing climate change impacts on the stability of small tidal inlets: Part 1-Data poor environments. Mar. Geol. 2017, 390, 331–346. [Google Scholar] [CrossRef]
- Duong, T.M.; Ranasinghe, R.; Thatcher, M.; Mahanama, S.; Wang, Z.B.; Dissanayake, P.K.; Hemer, M.; Luijendijk, A.; Bamunawala, J.; Roelvink, D.; et al. Assessing climate change impacts on the stability of small tidal inlets: Part 2-Data rich environments. Mar. Geol. 2018, 395, 65–81. [Google Scholar] [CrossRef]
- van der Wegen, M.; Dastgheib, A.; Roelvink, J. Morphodynamic modeling of tidal channel evolution in comparison to empirical PA relationship. Coast. Eng. 2010, 57, 827–837. [Google Scholar] [CrossRef]
- Rijkswaterstaat. Kenmerkende Waarden Getijgebied 2011.0; Report; RWS: Utrecht, The Netherlands, 2013.
- Grasmeijer, B.; Huisman, B.; Luijendijk, A.; Schrijvershof, R.; van der Werf, J.; Zijl, F.; de Looff, H.; de Vries, W. Modelling of annual sand transports at the Dutch lower shoreface. Ocean Coast. Manag. 2022, 217, 105984. [Google Scholar] [CrossRef]
- Reinson, G.E. Transgressive barrier island and estuarine systems. In Facies Models Response to Sea Level Change; Geological Association of Canada: St. John’s, NL, Canada, 1992; pp. 179–194. [Google Scholar]
- Hijma, M.P.; Cohen, K.M.; Hoffmann, G.; Van der Spek, A.J.; Stouthamer, E. From river valley to estuary: The evolution of the Rhine mouth in the early to middle Holocene (western Netherlands, Rhine-Meuse delta). Neth. J. Geosci. 2009, 88, 13–53. [Google Scholar] [CrossRef]
- Paalvast, P.; van der Velde, G. Long term anthropogenic changes and ecosystem service consequences in the northern part of the complex Rhine-Meuse estuarine system. Ocean Coast. Manag. 2014, 92, 50–64. [Google Scholar] [CrossRef]
- Pierik, H.J.; Stouthamer, E.; Schuring, T.; Cohen, K.M. Human-caused avulsion in the Rhine-Meuse delta before historic embankment (The Netherlands). Geology 2018, 46, 935–938. [Google Scholar] [CrossRef]
- Gouw, M.J.; Hijma, M.P. From apex to shoreline: Fluvio-deltaic architecture for the Holocene Rhine–Meuse delta, the Netherlands. Earth Surf. Dyn. 2022, 10, 43–64. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Baptist, M.; Babovic, V.; Rodríguez Uthurburu, J.; Keijzer, M.; Uittenbogaard, R.; Mynett, A.; Verwey, A. On inducing equations for vegetation resistance. J. Hydraul. Res. 2007, 45, 435–450. [Google Scholar] [CrossRef]
- Partheniades, E.J. Erosion and deposition of cohesive soils. J. Hydraul. Div. 1965, 91, 105–139. [Google Scholar] [CrossRef]
- Van Rijn, L. Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas; Aqua Publications: Blokzijl, The Netherlands, 1993; Volume 1006. [Google Scholar]
- Deltares. D-Flow user manual. In Delft3D FM Suite; Deltares: Delft, The Netherlands, 2021. [Google Scholar]
- Deltares. D-WAVE user manual. In Delft3D FM Suite; Deltares: Delft, The Netherlands, 2021. [Google Scholar]
- Deltares. D-Morphology user manual. In Delft3D FM Suite; Deltares: Delft, The Netherlands, 2021. [Google Scholar]
- Dean, R.G. Equilibrium beach profiles: Characteristics and applications. J. Coast. Res. 1991, 7, 53–84. [Google Scholar]
- Van der Spek, A.; Van der Werf, J.; Grasmeijer, B.; Schrijvershof, R.; Vermaas, T. The lower shoreface of the Dutch coast—An overview. Ocean Coast. Manag. 2022, 230, 106367. [Google Scholar] [CrossRef]
- Kreischer. EN: Deepening Nieuwe Waterweg, Report on Fieldwork and Labresearch; Report (dutch); Gemeentewerken Rotterdam: Rotterdam, The Netherlands, 2014. [Google Scholar]
- Temmerman, S.; Bouma, T.J.; Govers, G.; Wang, Z.B.; De Vries, M.B.; Herman, P.M.J. Impact of vegetation on flow routing and sedimentation patterns: Three-dimensional modeling for a tidal marsh. J. Geophys. Res. Earth Surf. 2005, 110. [Google Scholar] [CrossRef]
- Sloff, K.; van der, R.S.; Huismans, Y.; Fuhrhop, H. Morphological Model of the RhineMeuse Delta; Report; Deltares: Delft, The Netherlands, 2012. [Google Scholar]
- RWS. National Water Authority; Live Database; RWS: Utrecht, The Netherlands, 2022.
- Klijn, F.; Hegnauer, M.; Beersma, J.; Sperna Weiland, F. Wat Betekenen de Nieuwe Klimaatscenario’s Voor de Rivierafvoeren van Rijn en Maas? Samenvatting van Onderzoek Met GRADE Naar Implicaties van Nieuwe klimaatprojecties voor Rivierafvoeren; Deltares & KNMI: Delft, The Netherlands, 2015. [Google Scholar]
- Snippen, E.; Fioole, A.; Geelen, H.; Kamsteeg, A.; Spijk, A.; Visser, T. Sediment in (be)weging. In Sedimentbalans Rijn-Maasmonding Periode 1990–2000; Report, RWS-RIZA, Afdeling WRE; RWS: Utrecht, The Netherlands, 2005. [Google Scholar]
- Balke, T.; Stock, M.; Jensen, K.; Bouma, T.J.; Kleyer, M. A global analysis of the seaward salt marsh extent: The importance of tidal range. Water Resour. Res. 2016, 52, 3775–3786. [Google Scholar] [CrossRef]
- Willemsen, P.; Smits, B.; Borsje, B.; Herman, P.; Dijkstra, J.; Bouma, T.; Hulscher, S. Modelling decadal salt marsh development: Variability of the salt marsh edge under influence of waves and sediment availability. Water Resour. Res. 2022, 58, e2020WR028962. [Google Scholar] [CrossRef]
- Suzuki, T.; Arikawa, T. Numerical analysis of bulk drag coefficient in dense vegetation by immersed boundary method. In Proceedings of the 32nd International Conference on Coastal Engineering, ICCE 2010, Shanghai, China, 30 June–5 July 2010. [Google Scholar]
- Vuik, V.; Jonkman, S.N.; Borsje, B.W.; Suzuki, T. Nature-based flood protection: The efficiency of vegetated foreshores for reducing wave loads on coastal dikes. Coast. Eng. 2016, 116, 42–56. [Google Scholar] [CrossRef]
- Jarrett, J.T. Tidal Prism-Inlet Area Relationships; US Department of Defense, Department of the Army, Corps of Engineers: Washington, DC, USA, 1976; Volume 3.
- Stive, M.J.; Rakhorst, R. Review of empirical relationships between inlet cross-section and tidal prism. J. Water Resour. Environ. Eng. 2008, 23, 89–95. [Google Scholar]
- Williams, J.J.; Esteves, L.S. Guidance on Setup, Calibration, and Validation of Hydrodynamic, Wave, and Sediment Models for Shelf Seas and Estuaries. Adv. Civ. Eng. 2017, 2017, 5251902. [Google Scholar] [CrossRef]
- Port of Rotterdam. HydroMeteoBundel nr. 4 1; report; Port of Rotterdam: Rotterdam, The Netherlands, 2012. [Google Scholar]
- Cox, J.R.; Huismans, Y.; Knaake, S.; Leuven, J.; Vellinga, N.; van der Vegt, M.; Hoitink, A.; Kleinhans, M. Anthropogenic Effects on the Contemporary Sediment Budget of the Lower Rhine-Meuse Delta Channel Network. Earth’s Future 2021, 9, e2020EF001869. [Google Scholar] [CrossRef]
- Dam, G.; Van der Wegen, M.; Taal, M.; Van der Spek, A. Contrasting behaviour of sand and mud in a long-term sediment budget of the Western Scheldt estuary. Sedimentology 2022, 69, 2267–2283. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, L.; Tao, J.; Gong, Z.; Guo, L.; van der Wegen, M.; Townend, I.; Zhang, C. The role of salinity in fluvio-deltaic morphodynamics: A long-term modelling study. Earth Surf. Process. Landforms 2020, 45, 590–604. [Google Scholar] [CrossRef]
- Tarpley, D.R.N.; Harris, C.K.; Friedrichs, C.T.; Sherwood, C.R. Tidal Variation in Cohesive Sediment Distribution and Sensitivity to Flocculation and Bed Consolidation in An Idealized, Partially Mixed Estuary. J. Mar. Sci. Eng. 2019, 7, 334. [Google Scholar] [CrossRef]
- Temmerman, S.; Bouma, T.J.; Van de Koppel, J.; Van der Wal, D.D.; De Vries, M.B.; Herman, P.M.J. Vegetation causes channel erosion in a tidal landscape. Geology 2007, 35, 631–634. [Google Scholar] [CrossRef]
- Van Maren, D.; van Kessel, T.; Cronin, K.; Sittoni, L. The impact of channel deepening and dredging on estuarine sediment concentration. Cont. Shelf Res. 2015, 95, 1–14. [Google Scholar] [CrossRef]
- Luan, H.L.; Ding, P.X.; Wang, Z.B.; Ge, J.Z.; Yang, S.L. Decadal morphological evolution of the Yangtze Estuary in response to river input changes and estuarine engineering projects. Geomorphology 2016, 265, 12–23. [Google Scholar] [CrossRef]
- Dijkstra, Y.M.; Schuttelaars, H.M.; Schramkowski, G.P.; Brouwer, R.L. Modeling the transition to high sediment concentrations as a response to channel deepening in the Ems River Estuary. J. Geophys. Res. Ocean. 2019, 124, 1578–1594. [Google Scholar] [CrossRef]
- Cox, R.; Wadsworth, R.; Thomson, A. Long-term changes in salt marsh extent affected by channel deepening in a modified estuary. Cont. Shelf Res. 2003, 23, 1833–1846. [Google Scholar] [CrossRef]
- Khojasteh, D.; Glamore, W.; Heimhuber, V.; Felder, S. Sea level rise impacts on estuarine dynamics: A review. Sci. Total Environ. 2021, 780, 146470. [Google Scholar] [CrossRef] [PubMed]
- Siemes, R.W.A.; Borsje, B.W.; Daggenvoorde, R.J.; Hulscher, S.J.M.H. Artificial Structures Steer Morphological Development of Salt Marshes: A Model Study. J. Mar. Sci. Eng. 2020, 8, 326. [Google Scholar] [CrossRef]
- Galappatti, R. A depth integrated model for suspended transport. In Communications on Hydraulics 1983-07; Delft University of Technology: Delft, The Netherlands, 1983. [Google Scholar]



| Symbol | Variable | Unit | Value | Reference |
|---|---|---|---|---|
| Hydrodynamic parameters | ||||
| Manning friction coefficient | s | 0.023 | [42] | |
| JONSWAP friction coefficient | s | 0.038 | [42] | |
| Morphological parameters | ||||
| Specific density | kg | 2650 | [42] | |
| Dry bed density sand | kg | 1600 | [42] | |
| Dry bed density mud | kg | 500 | [42] | |
| Median grain size sand | m | 200 | [47] | |
| Settling velocity mud | mm | 0.25 | [42] | |
| Critical stress for erosion of mud | N/ | 0.5 | [42] | |
| Vegetation parameters | ||||
| Vegetation drag coefficient | 0.7 | [42] | ||
| Uniform vegetation stem diameter | mm | 4.3 | [48] | |
| Uniform vegetation height | m | 0.5 | [48] | |
| K | Max. stem density | Stems | 1200 | [48] |
| Scenarios | |||||
|---|---|---|---|---|---|
| 1. Channel depth (; m) | 13 | 14 | 15 | 16 | 17 |
| 2. Total intertidal wetland width (; km) | 0 | 0.25 | 0.5 | 0.75 | 1.0 |
| 3. Lateral wetland location * (km–km) | 0–15 | 0–5 | 5–10 | 10–15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siemes, R.W.A.; Duong, T.M.; Willemsen, P.W.J.M.; Borsje, B.W.; Hulscher, S.J.M.H. Morphological Response of a Highly Engineered Estuary to Altering Channel Depth and Restoring Wetlands. J. Mar. Sci. Eng. 2023, 11, 2150. https://doi.org/10.3390/jmse11112150
Siemes RWA, Duong TM, Willemsen PWJM, Borsje BW, Hulscher SJMH. Morphological Response of a Highly Engineered Estuary to Altering Channel Depth and Restoring Wetlands. Journal of Marine Science and Engineering. 2023; 11(11):2150. https://doi.org/10.3390/jmse11112150
Chicago/Turabian StyleSiemes, Rutger W. A., Trang Minh Duong, Pim W. J. M. Willemsen, Bas W. Borsje, and Suzanne J. M. H. Hulscher. 2023. "Morphological Response of a Highly Engineered Estuary to Altering Channel Depth and Restoring Wetlands" Journal of Marine Science and Engineering 11, no. 11: 2150. https://doi.org/10.3390/jmse11112150
APA StyleSiemes, R. W. A., Duong, T. M., Willemsen, P. W. J. M., Borsje, B. W., & Hulscher, S. J. M. H. (2023). Morphological Response of a Highly Engineered Estuary to Altering Channel Depth and Restoring Wetlands. Journal of Marine Science and Engineering, 11(11), 2150. https://doi.org/10.3390/jmse11112150








