Deep-Neural-Network-Based Receiver Design for Downlink Non-Orthogonal Multiple-Access Underwater Acoustic Communication
Abstract
:1. Introduction
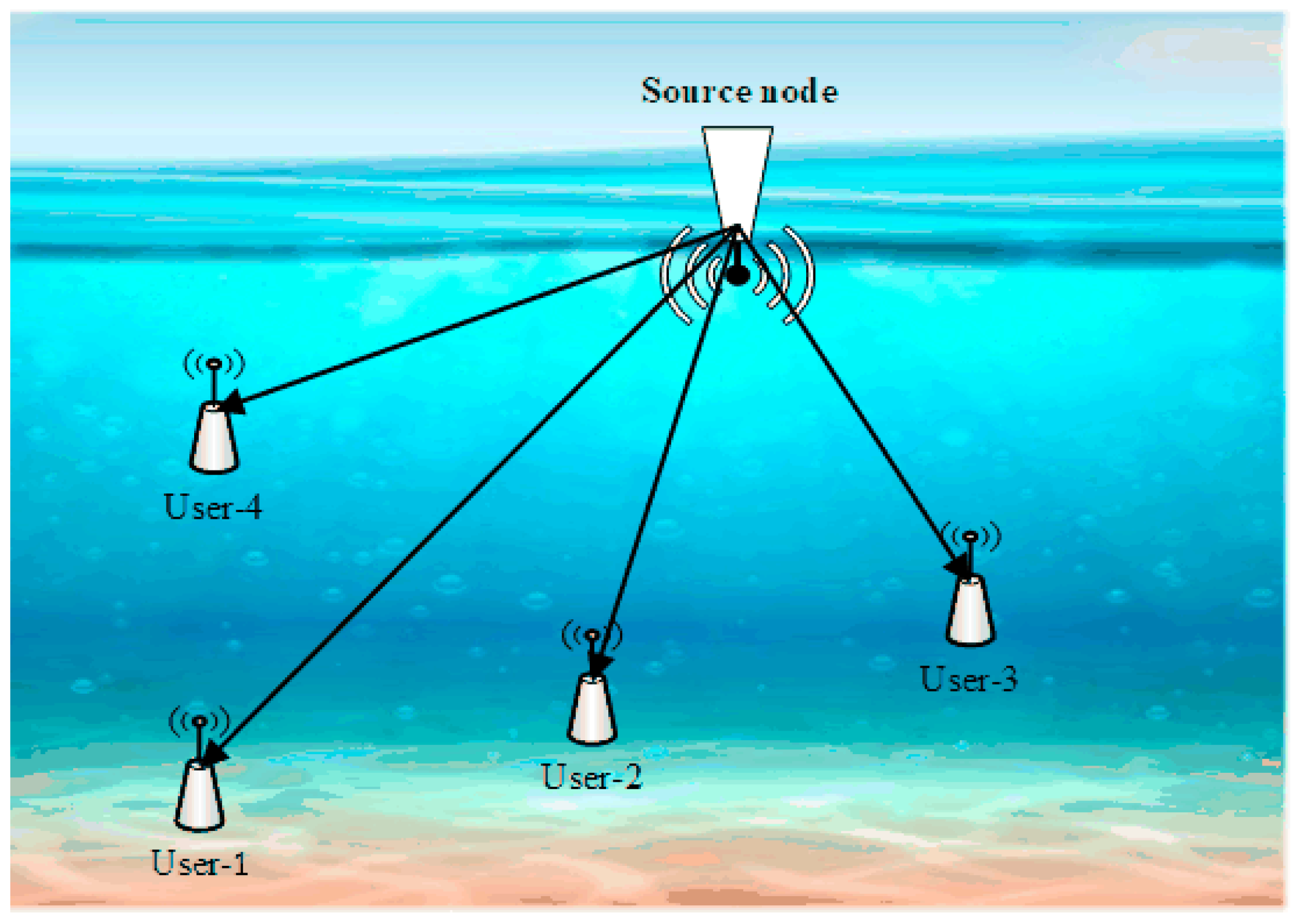
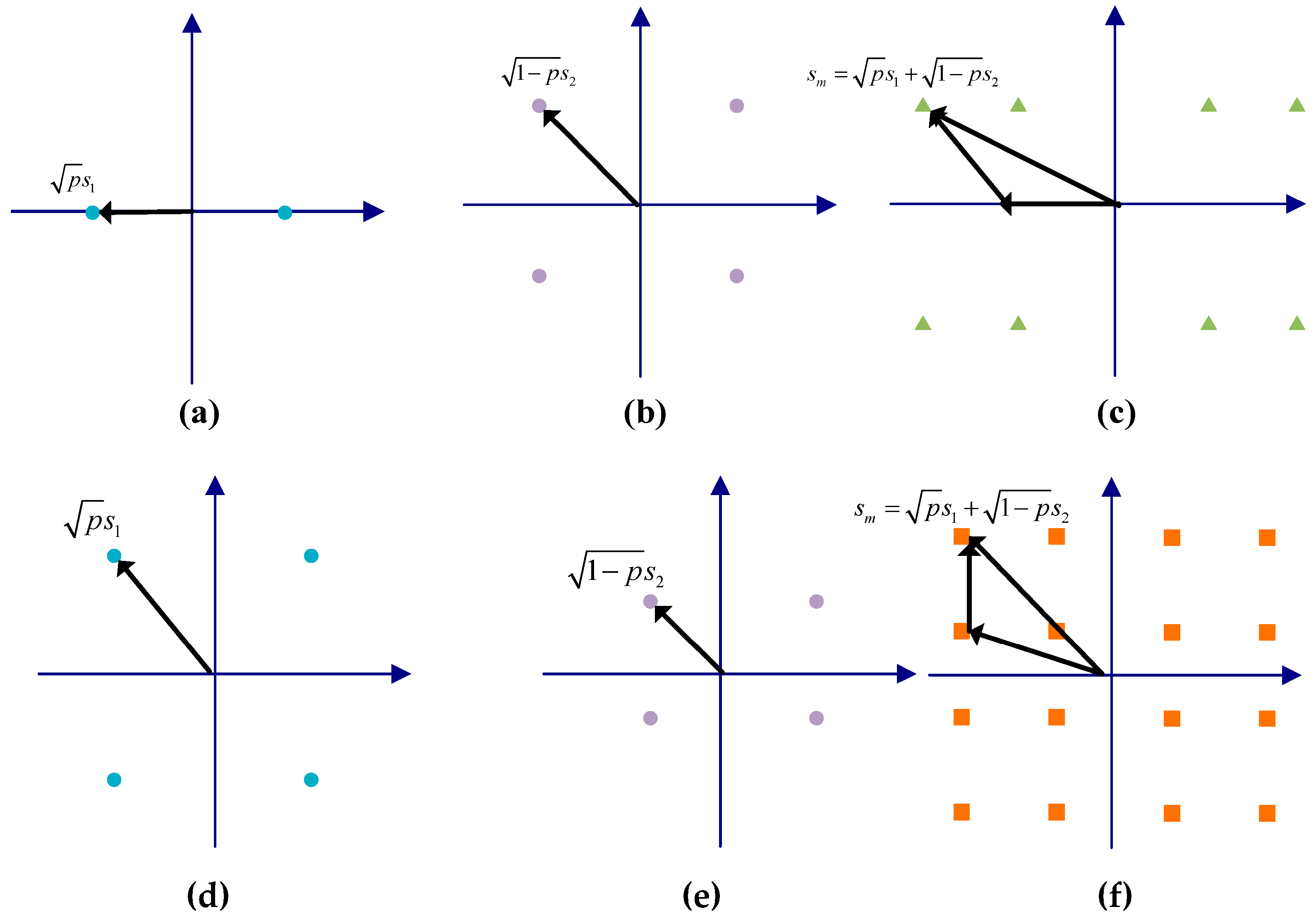
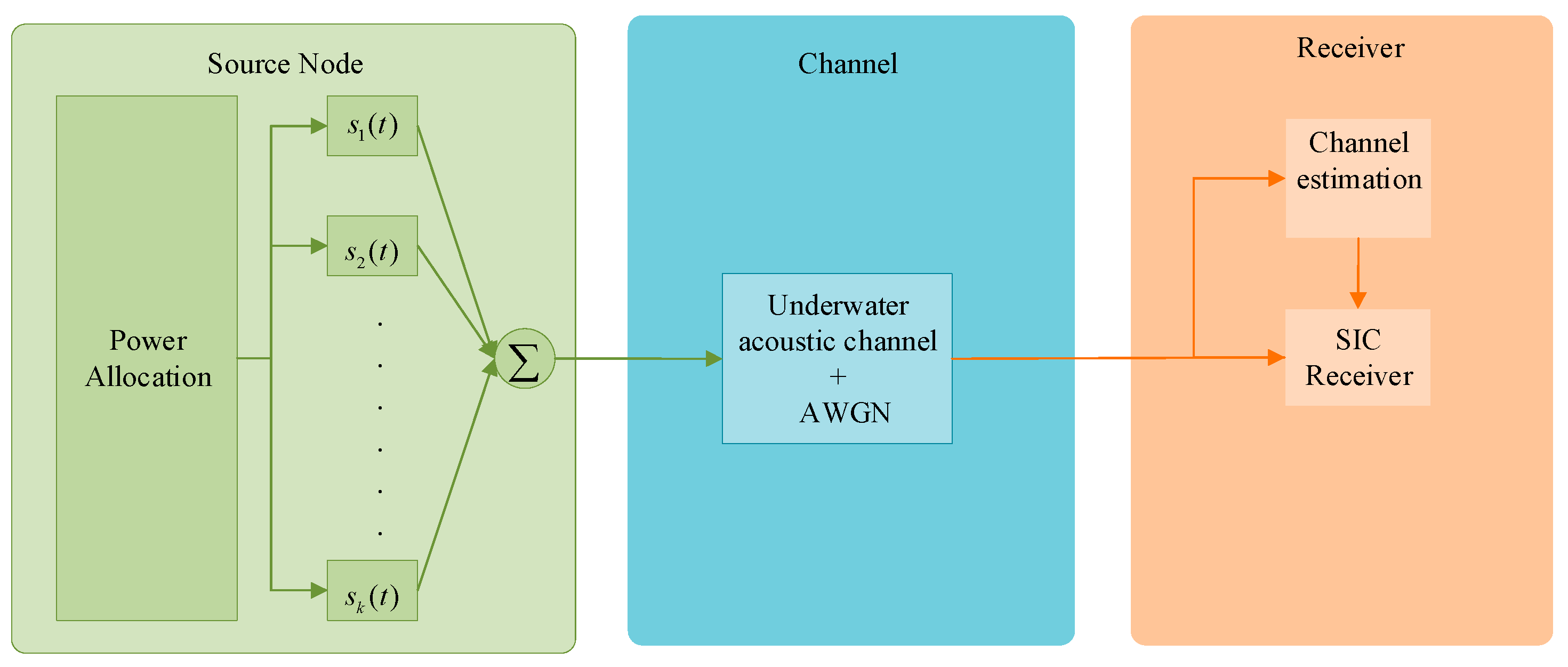
2. Downlink NOMA Underwater Acoustic Communication
3. Deep Neural Network
1D Convolution Neural Network
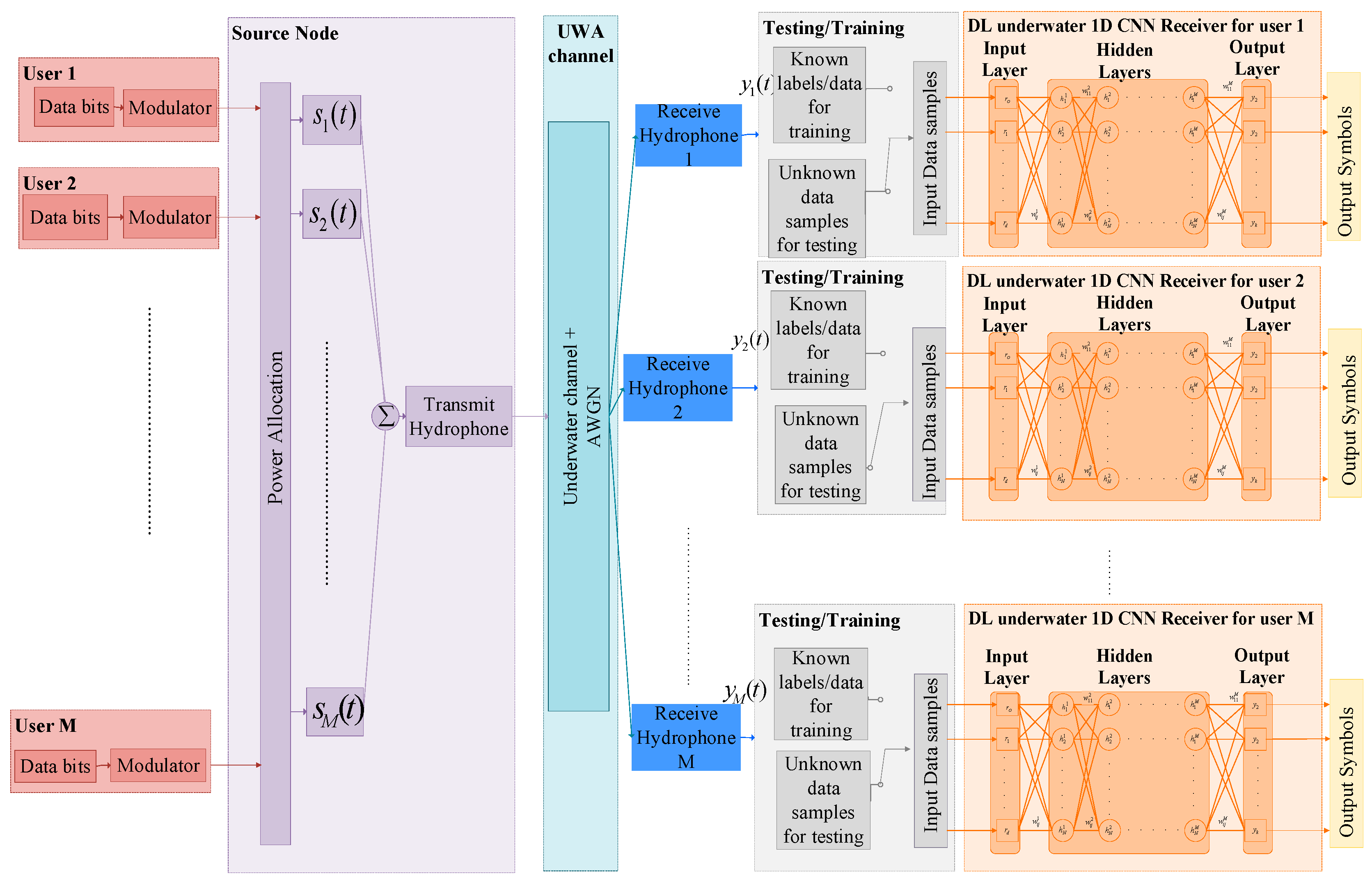
4. Downlink Underwater Acoustic Communication Using a Deep Neural Network Receiver
5. Underwater Acoustic Communication Dataset Generation for DL DNN Receiver
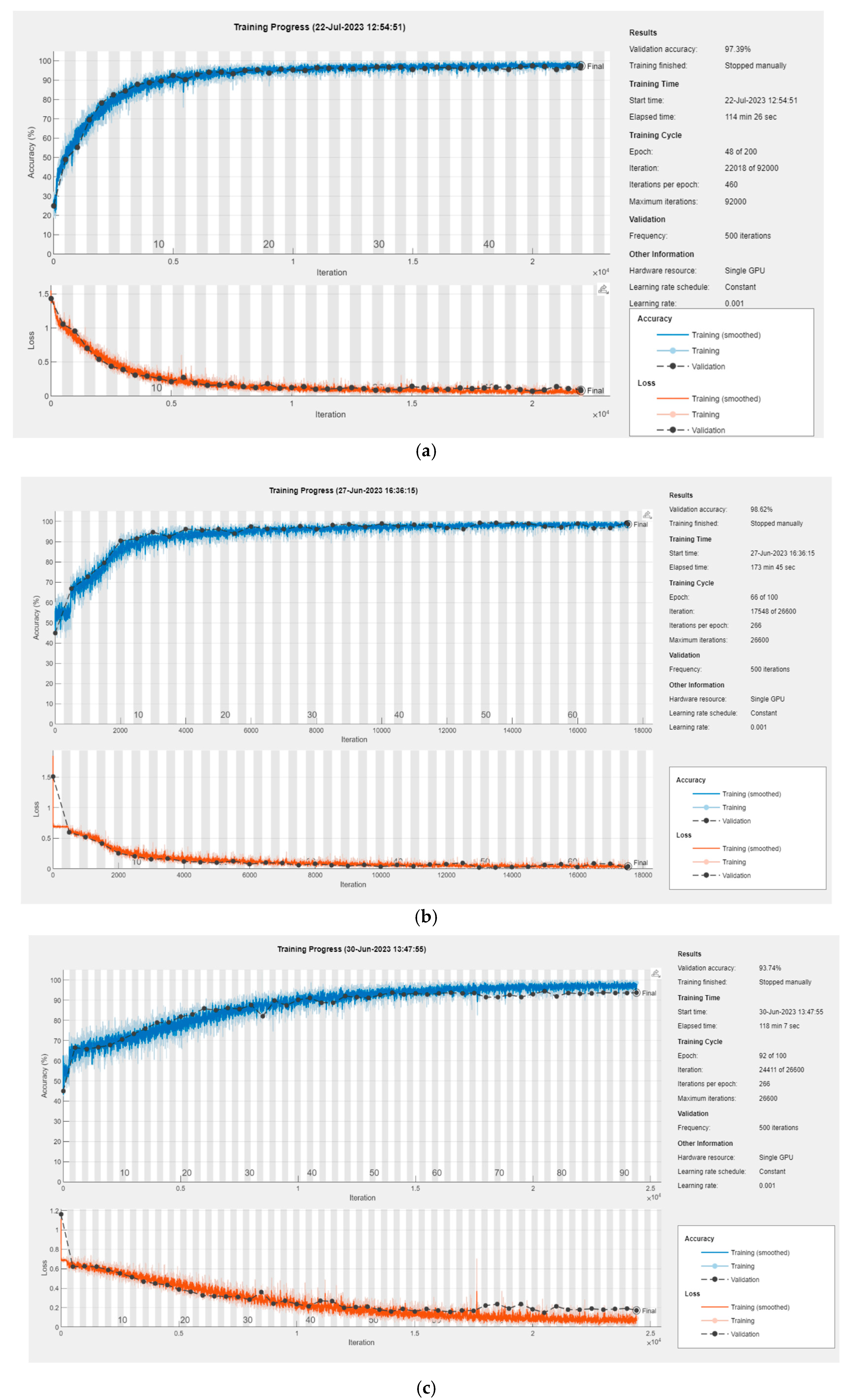
6. Training and Analysis of DNN Receiver
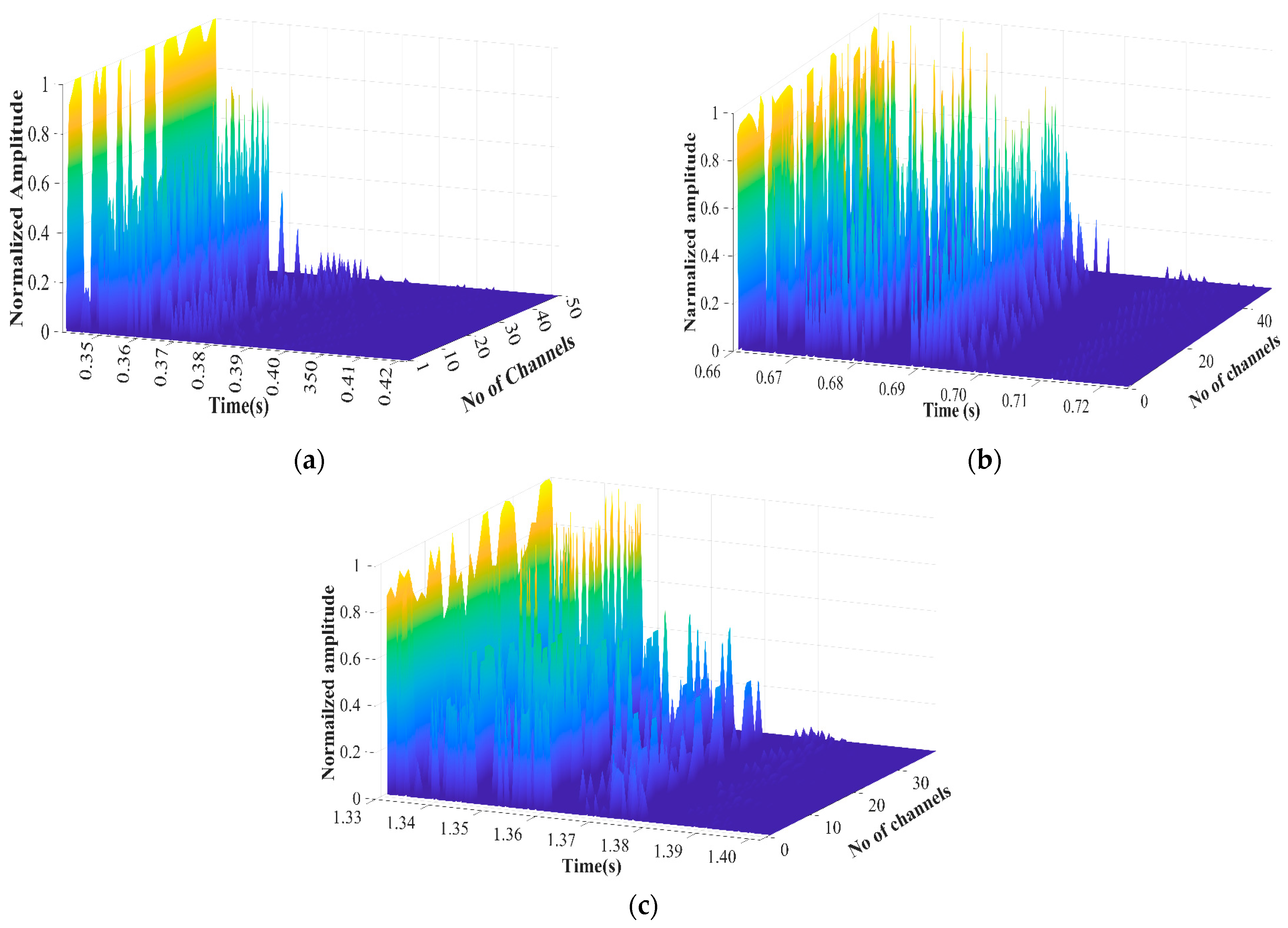
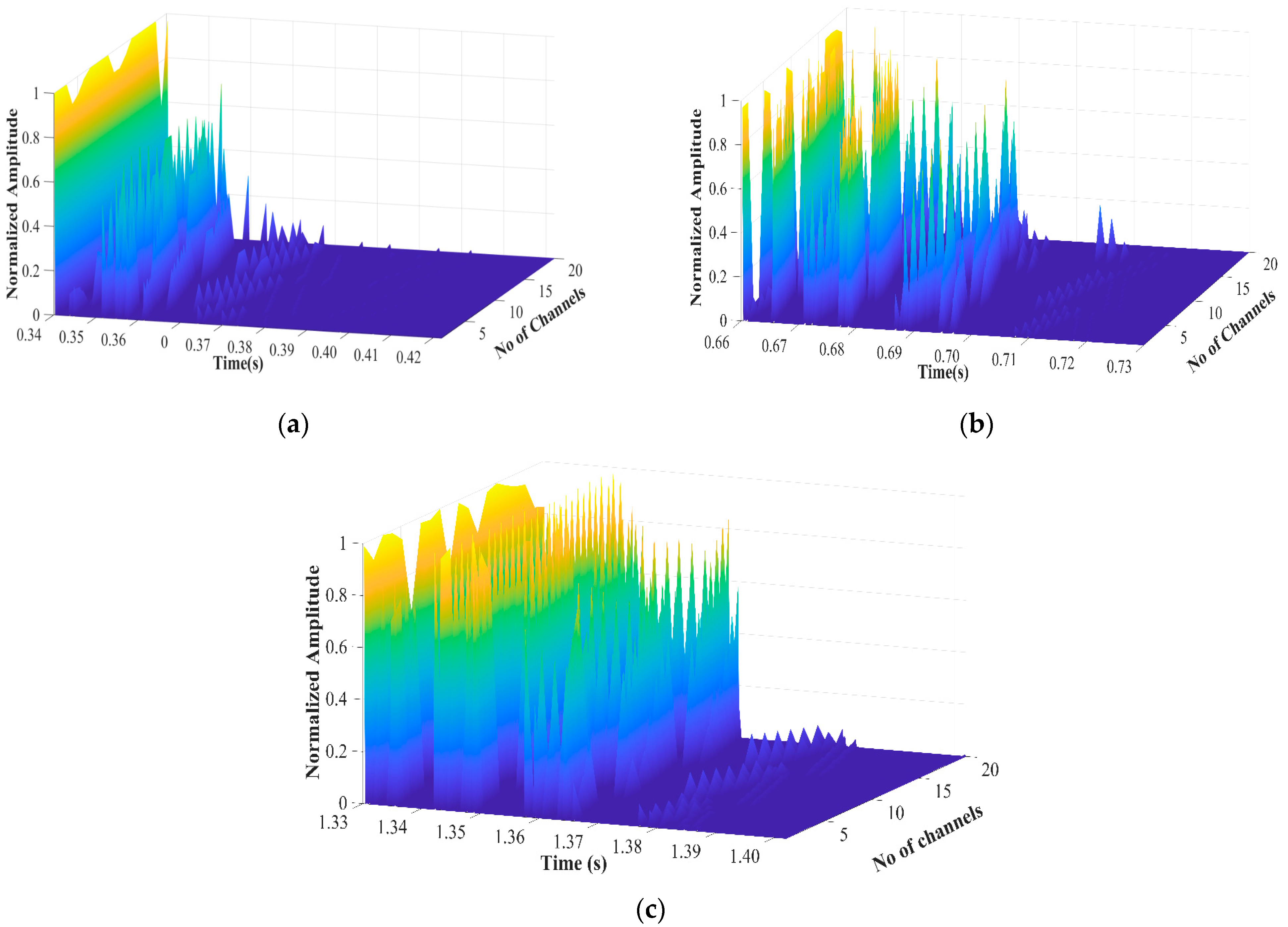
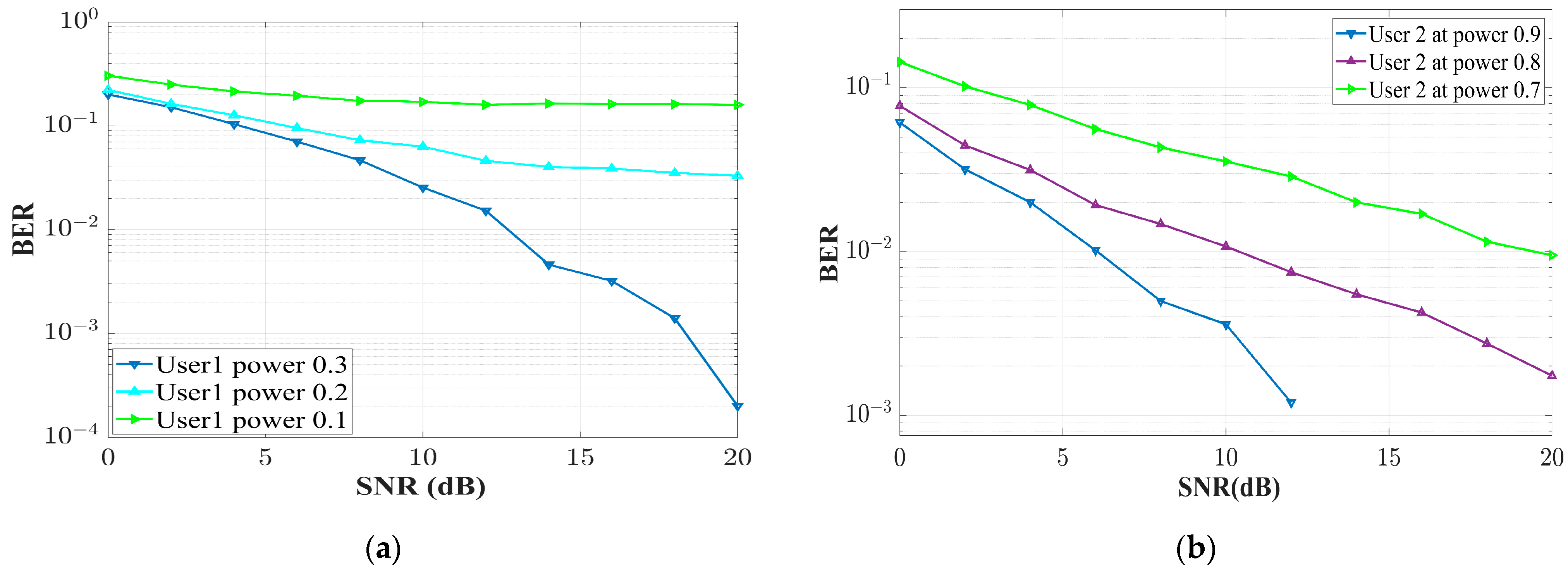
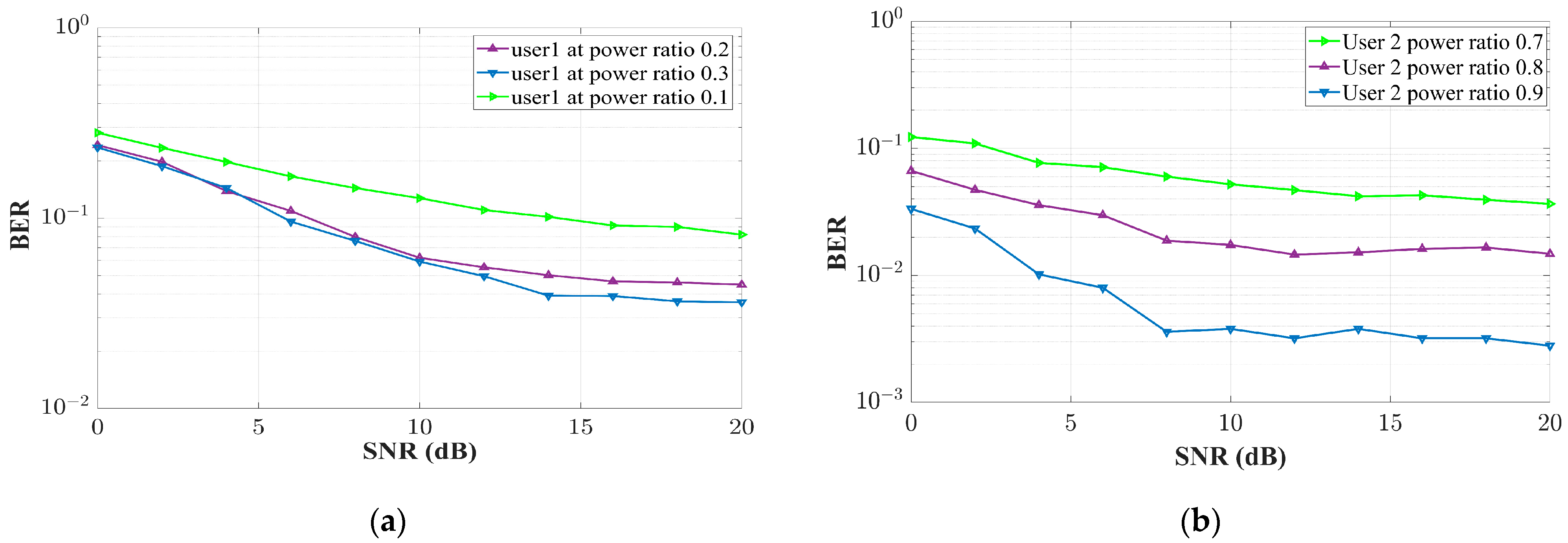
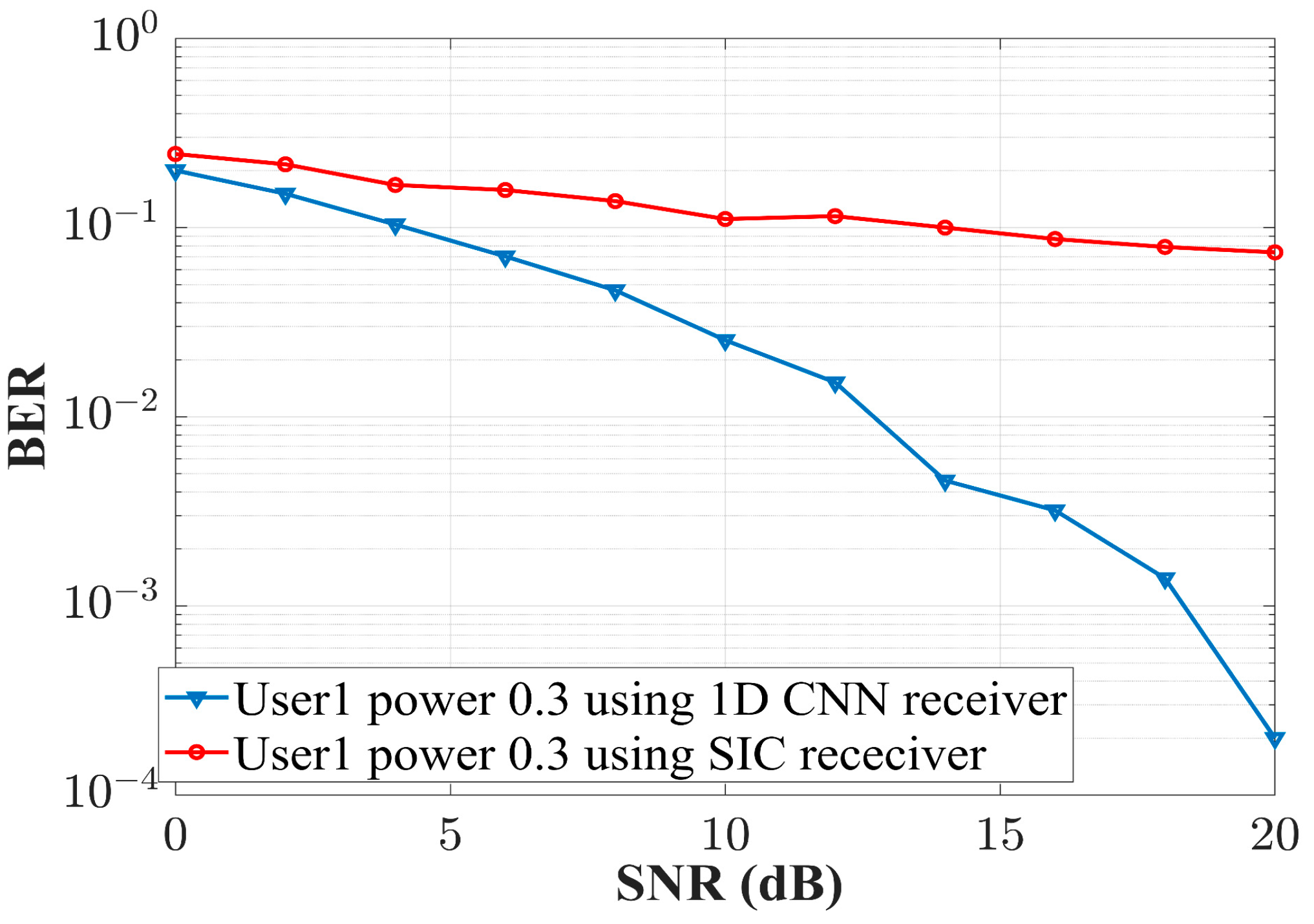
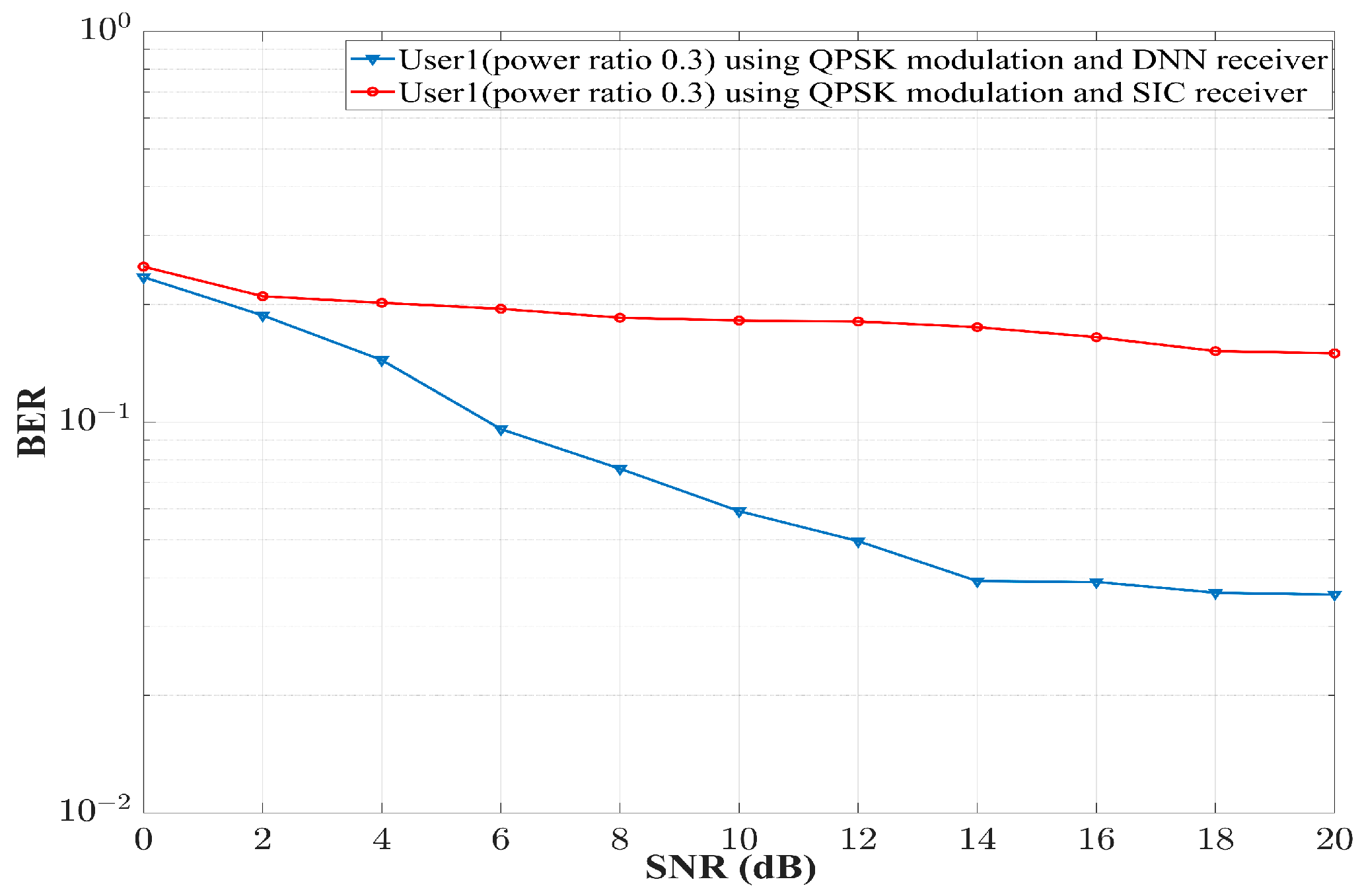
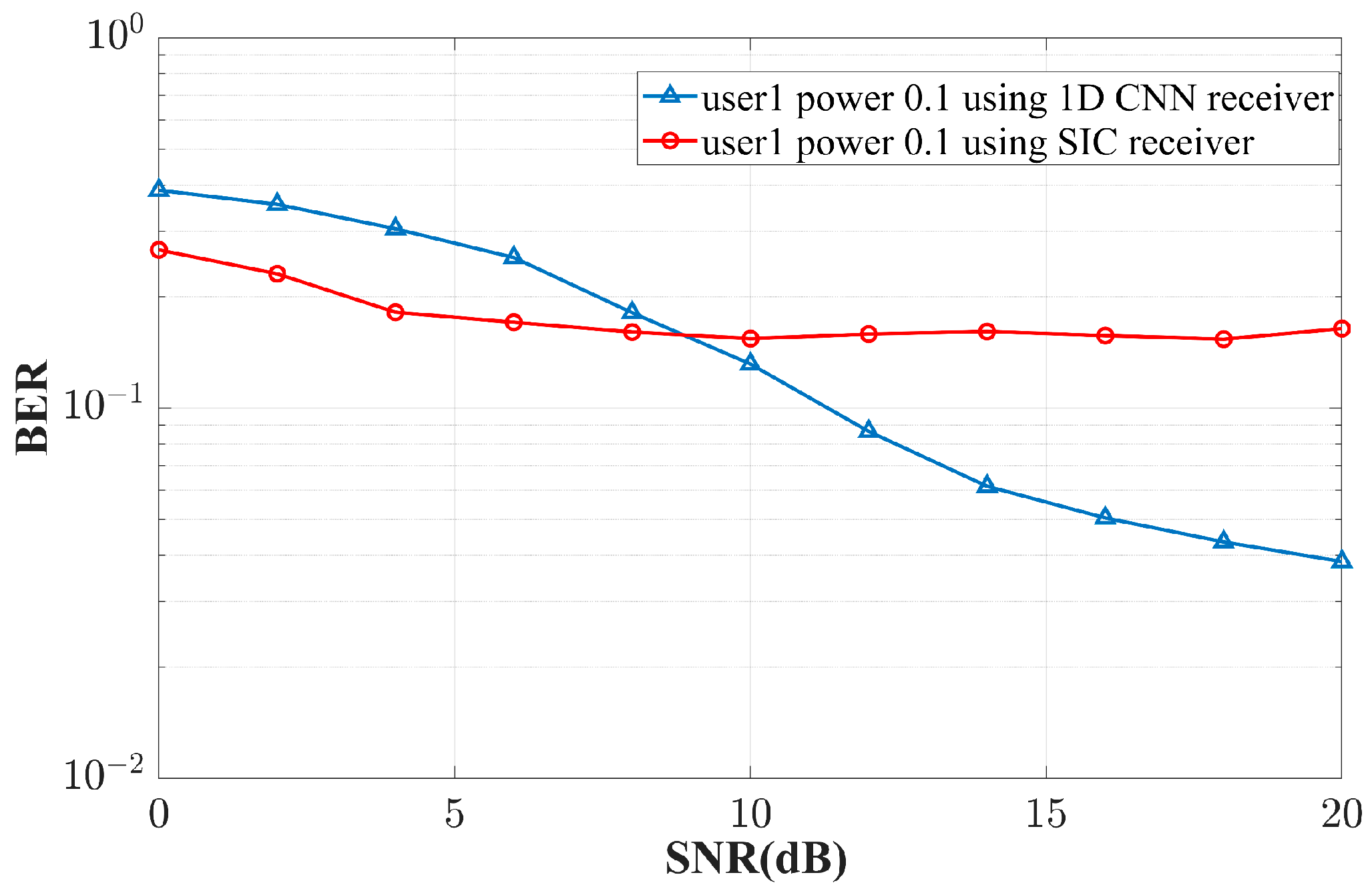
7. Simulation Results and Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Campagnaro, F.; Steinmetz, F.; Renner, B.-C. Survey on low-cost underwater sensor networks: From niche applications to everyday use. J. Mar. Sci. Eng. 2023, 11, 125. [Google Scholar] [CrossRef]
- Li, S.; Qu, W.; Liu, C.; Qiu, T.; Zhao, Z. Survey on high reliability wireless communication for underwater sensor networks. J. Netw. Comput. Appl. 2019, 148, 102446. [Google Scholar] [CrossRef]
- Stojanovic, M.; Preisig, J. Underwater acoustic communication channels: Propagation models and statistical characterization. IEEE Commun. Mag. 2009, 47, 84–89. [Google Scholar] [CrossRef]
- Ranjha, A.; Javed, M.A.; Srivastava, G.; Lin, J.C.-W. Intercell Interference Coordination for UAV enabled URLLC with perfect/imperfect CSI using cognitive radio. IEEE Open J. Commun. Soc. 2022, 4, 197–208. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, X. Broadband cancellation method in an adaptive co-site interference cancellation system. Int. J. Electron. 2022, 109, 854–874. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, S.; Li, M.; Zhao, N.; Wu, M. A new adaptive co-site broadband interference cancellation method with auxiliary channel. Digit. Commun. Netw. 2022, in press. [Google Scholar] [CrossRef]
- Li, A.; Masouros, C.; Swindlehurst, A.L.; Yu, W. 1-bit massive MIMO transmission: Embracing interference with symbol-level precoding. IEEE Commun. Mag. 2021, 59, 121–127. [Google Scholar] [CrossRef]
- Li, A.; Masouros, C.; Vucetic, B.; Li, Y.; Swindlehurst, A.L. Interference exploitation precoding for multi-level modulations: Closed-form solutions. IEEE Trans. Commun. 2020, 69, 291–308. [Google Scholar] [CrossRef]
- Ranjha, A.; Javed, M.A.; Srivastava, G.; Asif, M. Quasi-Optimization of Resource Allocation and Positioning for Solar-Powered UAVs. IEEE Trans. Netw. Sci. Eng. 2023, 10, 4071–4081. [Google Scholar] [CrossRef]
- Asif, M.; Ihsan, A.; Khan, W.U.; Ranjha, A.; Zhang, S.; Wu, S.X. Energy-efficient beamforming and resource optimization for AmBSC-assisted cooperative NOMA IoT networks. IEEE Internet Things J. 2023, 10, 12434–12448. [Google Scholar] [CrossRef]
- Morozs, N.; Mitchell, P.; Zakharov, Y.V. TDA-MAC: TDMA without clock synchronization in underwater acoustic networks. IEEE Access 2017, 6, 1091–1108. [Google Scholar] [CrossRef]
- Cho, A.-R.; Yun, C.; Lim, Y.-K.; Choi, Y. Asymmetric propagation delay-aware TDMA MAC protocol for mobile underwater acoustic sensor networks. Appl. Sci. 2018, 8, 962. [Google Scholar] [CrossRef]
- Yin, J.; Du, P.; Yang, G.; Zhou, H. Space-division multiple access for CDMA multiuser underwater acoustic communications. J. Syst. Eng. Electron. 2015, 26, 1184–1190. [Google Scholar] [CrossRef]
- Rahmati, M.; Petroccia, R.; Pompili, D. In-network collaboration for CDMA-based reliable underwater acoustic communications. IEEE J. Ocean. Eng. 2019, 44, 881–894. [Google Scholar] [CrossRef]
- Stojanovic, M.; Freitag, L. Multichannel detection for wideband underwater acoustic CDMA communications. IEEE J. Ocean. Eng. 2006, 31, 685–695. [Google Scholar] [CrossRef]
- Yang, T. Spatially multiplexed CDMA multiuser underwater acoustic communications. IEEE J. Ocean. Eng. 2015, 41, 217–231. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, S.; Catipovic, J.; Willett, P. Asynchronous multiuser reception for OFDM in underwater acoustic communications. IEEE Trans. Wirel. Commun. 2013, 12, 1050–1061. [Google Scholar] [CrossRef]
- Ma, L.; Zhou, S.; Qiao, G.; Liu, S.; Zhou, F. Superposition coding for downlink underwater acoustic OFDM. IEEE J. Ocean. Eng. 2016, 42, 175–187. [Google Scholar] [CrossRef]
- Qiao, G.; Xing, S.; Zhou, F. A Multi-User Detection Scheme Based on Polar Code Construction in Downlink Underwater Acoustic OFDM Communication System. IEEE Access 2019, 7, 65973–65981. [Google Scholar] [CrossRef]
- Bernard, C.; Bouvet, P.-J.; Pottier, A.; Forjonel, P. Multiuser chirp spread spectrum transmission in an underwater acoustic channel applied to an AUV fleet. Sensors 2020, 20, 1527. [Google Scholar] [CrossRef]
- Zuberi, H.H.; Liu, S.; Sohail, M.Z.; Pan, C. Multi-user underwater acoustic communication using binary phase-coded hyperbolic frequency-modulated signals. IET Commun. 2022, 16, 1415–1427. [Google Scholar] [CrossRef]
- Yuan, F.; Wei, Q.; Cheng, E. Multiuser chirp modulation for underwater acoustic channel based on VTRM. Int. J. Nav. Archit. Ocean. Eng. 2017, 9, 256–265. [Google Scholar] [CrossRef]
- Liu, S.; Zuberi, H.H.; Lou, Y.; Farooq, M.B.; Shaikh, S.; Raza, W. M-ary nonlinear sine chirp spread spectrum for underwater acoustic communication based on virtual time-reversal mirror method. EURASIP J. Wirel. Commun. Netw. 2021, 2021, 112. [Google Scholar] [CrossRef]
- Yang, G.; Zhou, F.; Lou, Y.; Qiao, G.; Ahmed, N.; He, Y. Double-differential coded M-ary direct sequence spread spectrum for mobile underwater acoustic communication system. Appl. Acoust. 2021, 183, 108303. [Google Scholar] [CrossRef]
- Murad, M.; Tasadduq, I.A.; Otero, P. Coded-GFDM for reliable communication in underwater acoustic channels. Sensors 2022, 22, 2639. [Google Scholar] [CrossRef] [PubMed]
- Song, Y. Underwater acoustic sensor networks with cost efficiency for internet of underwater things. IEEE Trans. Ind. Electron. 2020, 68, 1707–1716. [Google Scholar] [CrossRef]
- Hussein, H.S.; Alanazi, T.M.; Shamim, M.Z.; Habeeb, M.S.; Usman, M.; Farrag, M. Fully quadrature subcarrier-index shift keying for efficient underwater acoustic communications. IEEE Access 2021, 9, 46975–46984. [Google Scholar] [CrossRef]
- Zuberi, H.H.; Liu, S.; Bilal, M.; Khan, R. Quadrature phase shift keying Sine chirp spread Spectrum under-water acoustic communication based on VTRM. In Proceedings of the 2022 19th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 16–20 August 2022; pp. 884–888. [Google Scholar]
- Cheon, J.; Cho, H.-S. Power allocation scheme for non-orthogonal multiple access in underwater acoustic communications. Sensors 2017, 17, 2465. [Google Scholar] [CrossRef]
- Goutham, V.; Harigovindan, V. NOMA based cooperative relaying strategy for underwater acoustic sensor networks under imperfect SIC and imperfect CSI: A comprehensive analysis. IEEE Access 2021, 9, 32857–32872. [Google Scholar] [CrossRef]
- Cho, S.E.; Song, H.C.; Hodgkiss, W.S. Successive interference cancellation for underwater acoustic communications. IEEE J. Ocean. Eng. 2011, 36, 490–501. [Google Scholar] [CrossRef]
- Yin, J.-w.; Zhu, G.-j.; Han, X.; Ge, W.; Li, L.; Tian, Y.-n. Iterative channel estimation-based soft successive interference cancellation for multiuser underwater acoustic communications. J. Acoust. Soc. Am. 2021, 150, 133–144. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Chang, Q.; Li, X. A deep learning approach for MIMO-NOMA downlink signal detection. Sensors 2019, 19, 2526. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.H.; Sejan, M.A.S.; Yoo, S.-G.; Kim, M.-A.; You, Y.-H.; Song, H.-K. Multi-User Joint Detection Using Bi-Directional Deep Neural Network Framework in NOMA-OFDM System. Sensors 2022, 22, 6994. [Google Scholar] [CrossRef] [PubMed]
- Shlezinger, N.; Fu, R.; Eldar, Y.C. DeepSIC: Deep soft interference cancellation for multiuser MIMO detection. IEEE Trans. Wirel. Commun. 2020, 20, 1349–1362. [Google Scholar] [CrossRef]
- Van Luong, T.; Shlezinger, N.; Xu, C.; Hoang, T.M.; Eldar, Y.C.; Hanzo, L. Deep learning based successive interference cancellation for the non-orthogonal downlink. IEEE Trans. Veh. Technol. 2022, 71, 11876–11888. [Google Scholar] [CrossRef]
- Qian, L.; Zheng, Y.; Li, L.; Ma, Y.; Zhou, C.; Zhang, D. A new method of inland water ship trajectory prediction based on long short-term memory network optimized by genetic algorithm. Appl. Sci. 2022, 12, 4073. [Google Scholar] [CrossRef]
- Yin, L.; Wang, L.; Li, T.; Lu, S.; Tian, J.; Yin, Z.; Li, X.; Zheng, W. U-Net-LSTM: Time Series-Enhanced Lake Boundary Prediction Model. Land 2023, 12, 1859. [Google Scholar] [CrossRef]
- Cao, B.; Zhao, J.; Lv, Z.; Gu, Y.; Yang, P.; Halgamuge, S.K. Multiobjective evolution of fuzzy rough neural network via distributed parallelism for stock prediction. IEEE Trans. Fuzzy Syst. 2020, 28, 939–952. [Google Scholar] [CrossRef]
- Shi, J.; Niu, W.; Li, Z.; Shen, C.; Zhang, J.; Yu, S.; Chi, N. Optimal adaptive waveform design utilizing an end-to-end learning-based pre-equalization neural network in an UVLC system. J. Light. Technol. 2022, 41, 1626–1636. [Google Scholar] [CrossRef]
- Yao, Y.; Zhao, J.; Li, Z.; Cheng, X.; Wu, L. Jamming and Eavesdropping Defense Scheme Based on Deep Reinforcement Learning in Autonomous Vehicle Networks. IEEE Trans. Inf. Forensics Secur. 2023, 18, 1211–1224. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, S.; Wang, B.; Liu, Y.; Bai, W.; Shen, X. Deep Learning-Based Signal Detection for Underwater Acoustic OTFS Communication. J. Mar. Sci. Eng. 2022, 10, 1920. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Y.; Gerstoft, P.; Zhou, F.; Qiao, G.; Yin, J. Deep transfer learning-based variable Doppler underwater acoustic communications. J. Acoust. Soc. Am. 2023, 154, 232–244. [Google Scholar] [CrossRef] [PubMed]
- Raza, W.; Ma, X.; Song, H.; Ali, A.; Zubairi, H.; Acharya, K. Long Short-Term Memory Neural Network assisted Peak to Average Power Ratio Reduction for Underwater Acoustic Orthogonal Frequency Division Multiplexing Communication. KSII Trans. Internet Inf. Syst. 2023, 17, 239–260. [Google Scholar] [CrossRef]
- Ma, X.; Raza, W.; Wu, Z.; Bilal, M.; Zhou, Z.; Ali, A. A nonlinear distortion removal based on deep neural network for underwater acoustic ofdm communication with the mitigation of peak to average power ratio. Appl. Sci. 2020, 10, 4986. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Zakharov, Y.V.; Li, J.; Li, Y.; Lin, C.; Li, X. Deep learning based single carrier communications over time-varying underwater acoustic channel. IEEE Access 2019, 7, 38420–38430. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, F.; Qiao, G.; Zhao, Y.; Yang, G.; Liu, X.; Lu, Y. Deep Learning-Based Cyclic Shift Keying Spread Spectrum Underwater Acoustic Communication. J. Mar. Sci. Eng. 2021, 9, 1252. [Google Scholar] [CrossRef]
- Qiao, G.; Liu, Y.; Zhou, F.; Zhao, Y.; Mazhar, S.; Yang, G. Deep learning-based M-ary spread spectrum communication system in shallow water acoustic channel. Appl. Acoust. 2022, 192, 108742. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Wang, H.; Wang, J.; Yang, F.; Meriaudeau, F. Deep learning aided OFDM receiver for underwater acoustic communications. Appl. Acoust. 2022, 187, 108515. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, B.; Zhang, Y.; Li, J.; Wu, C. Convolutional neural network based filter bank multicarrier system for underwater acoustic communications. Appl. Acoust. 2021, 177, 107920. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Zakharov, Y.; Li, X.; Li, J. Deep learning based underwater acoustic OFDM communications. Appl. Acoust. 2019, 154, 53–58. [Google Scholar] [CrossRef]
- Zhang, J.; Cao, Y.; Han, G.; Fu, X. Deep neural network-based underwater OFDM receiver. IET Commun. 2019, 13, 1998–2002. [Google Scholar] [CrossRef]
- Roodschild, M.; Gotay Sardiñas, J.; Will, A. A new approach for the vanishing gradient problem on sigmoid activation. Prog. Artif. Intell. 2020, 9, 351–360. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]

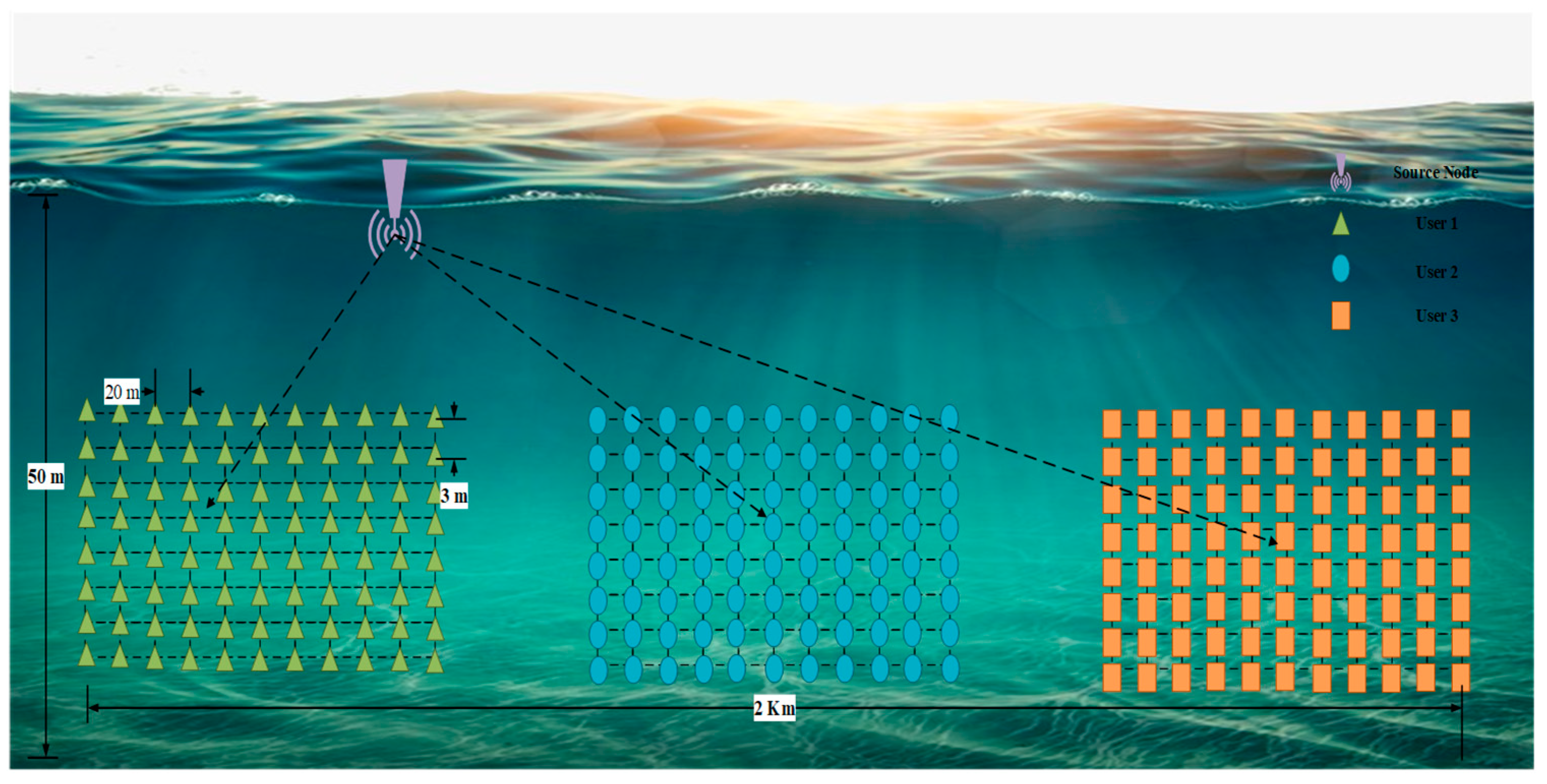


| Parameters | Values |
|---|---|
| Source station depth | 5 m |
| No. of users | 3 |
| Depth of users | [20:2:50] m |
| Distance of user 1 | [485 m, 515 m] |
| Distance of user 2 | [985 m, 1015 m] |
| Distance of user 3 | [1985 m, 2015 m] |
| Transducer beam angle (°) | [−20, 20] |
| Total depth | 50 m |
| 1D CNN Factors | User 1 | User 2 | User 3 |
|---|---|---|---|
| Sequence I/P layer(s) | 1 | 1 | 1 |
| Total no. of convolution layer(s) | 4 | 4 | 4 |
| Filter size of convolution layer(s) | [250, 120, 60, 30] | [250, 120, 60, 30] | [250, 120, 60, 30] |
| Number of filters in convolution layer(s) | [150, 100, 30, 20] | [150, 100, 30, 20] | [150, 100, 30, 20] |
| 1D max-pooling layer(s) | 4 | 4 | 4 |
| Number of flatten layer(s) | 1 | 1 | 1 |
| Total number of global max-pooling layer(s) | 1 | 1 | 1 |
| Number of neurons in fully connected layer | 120 | 120 | 120 |
| Total batch size | 200 | 200 | 200 |
| Hidden layer(s) activation function | ReLU | ReLU | ReLU |
| Type of optimizer | Adam | Adam | Adam |
| Output layer(s) activation function | Softmax | Softmax | Softmax |
| Learning rate | 10−3 | 10−3 | 10−3 |
| Total number of training channels | 50 | 50 | 50 |
| BPSK training dataset (two-user case) | 50,000 | 50,000 | NA |
| BPSK training dataset (three-user case) | 50,000 | 50,000 | 50,000 |
| QPSK training dataset (two-user case) | 125,000 | 125,000 | NA |
| Communication Parameters | Values |
|---|---|
| Carrier frequency | 12 kHz |
| Sampling frequency | 100 kHz |
| Modulation order(s) | [QPSK BPSK] |
| Duration of symbol | 10 ms |
| Power allocation coefficient (two-user case) | [0.7, 0.3] |
| Power allocation coefficient (three-user case) | [0.6, 0.3, 0.1] |
| Total number of symbols for testing | 50,000 |
| Total number of testing channels | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuberi, H.H.; Liu, S.; Bilal, M.; Alharbi, A.; Jaffar, A.; Mohsan, S.A.H.; Miyajan, A.; Khan, M.A. Deep-Neural-Network-Based Receiver Design for Downlink Non-Orthogonal Multiple-Access Underwater Acoustic Communication. J. Mar. Sci. Eng. 2023, 11, 2184. https://doi.org/10.3390/jmse11112184
Zuberi HH, Liu S, Bilal M, Alharbi A, Jaffar A, Mohsan SAH, Miyajan A, Khan MA. Deep-Neural-Network-Based Receiver Design for Downlink Non-Orthogonal Multiple-Access Underwater Acoustic Communication. Journal of Marine Science and Engineering. 2023; 11(11):2184. https://doi.org/10.3390/jmse11112184
Chicago/Turabian StyleZuberi, Habib Hussain, Songzuo Liu, Muhammad Bilal, Ayman Alharbi, Amar Jaffar, Syed Agha Hussnain Mohsan, Abdulaziz Miyajan, and Mohsin Abrar Khan. 2023. "Deep-Neural-Network-Based Receiver Design for Downlink Non-Orthogonal Multiple-Access Underwater Acoustic Communication" Journal of Marine Science and Engineering 11, no. 11: 2184. https://doi.org/10.3390/jmse11112184
APA StyleZuberi, H. H., Liu, S., Bilal, M., Alharbi, A., Jaffar, A., Mohsan, S. A. H., Miyajan, A., & Khan, M. A. (2023). Deep-Neural-Network-Based Receiver Design for Downlink Non-Orthogonal Multiple-Access Underwater Acoustic Communication. Journal of Marine Science and Engineering, 11(11), 2184. https://doi.org/10.3390/jmse11112184









