Predefined-Time and Prescribed-Performance Control Methods Combined with Second-Order Terminal Sliding Mode Control for an Unmanned Planing Hull System with Input Delay and Unknown Disturbance
Abstract
:1. Introduction
- (1)
- Porpoising disturbance due to the pitching moment of UPH systems was assumed to enhance sensitivity to variations in the unmatched uncertainties of UPH systems.
- (2)
- A second-order TSMC system was designed to accommodate the control input delay in a hydraulic rudder actuator system.
- (3)
- A second-order TSMC system with predefined-time control was designed to achieve improved settling-time convergence and robustness to unmatched disturbances when compared with a conventional TSMC system. Furthermore, it aimed to achieve a faster and more stable heading-angle response by the UPH than conventional TSMC for a perturbed environment.
- (4)
- Predefined-time and prescribed-performance control methods were used simultaneously for the first time to maximize the rejection performance and obtain stable tracking performance for an unmatched pitching-moment disturbance without adopting a complex disturbance observer. Consequently, the tracking performance of the heading-angle axis was largely improved by utilizing the proposed hybrid disturbance rejector.
- (5)
- The proposed second-order TSMC system with a hybrid disturbance rejector facilitated by predefined-time and prescribed-performance control exhibited a simpler controller structure than the conventional robust control systems equipped with a complex disturbance observer to estimate the disturbance.
- (6)
- To the best of our knowledge, predefined-time and prescribed-performance control methods have not been applied simultaneously in the field of USV control to improve disturbance rejection performance. In fact, this concept is not demonstrated in other control systems.
2. Modeling the UPH
2.1. Dynamics of UPH
2.2. The Modeling of the Drag Force and Pitching Moment of the UPH
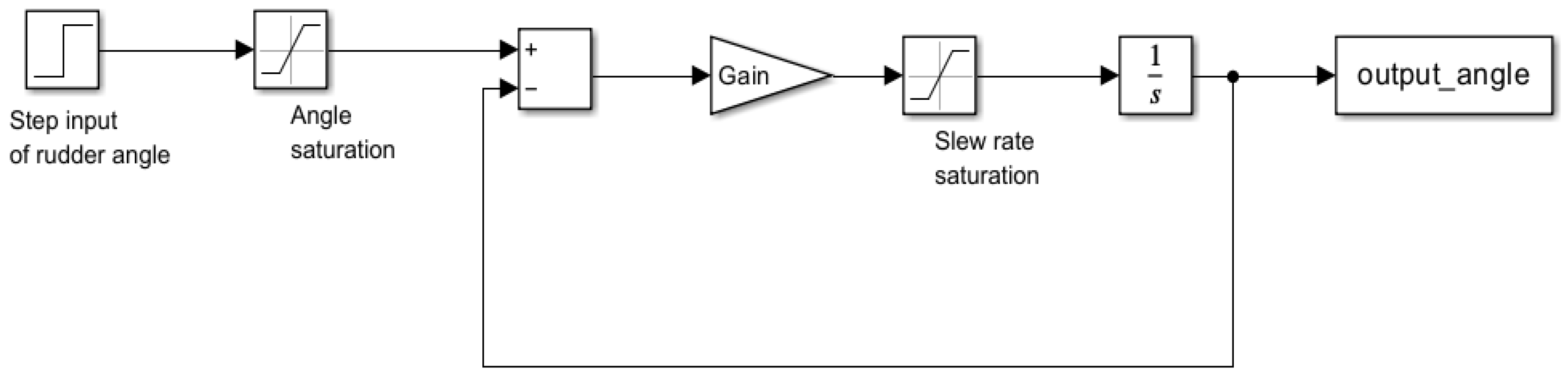
2.3. Modeling the Rudder Hydraulic Actuator
3. Controller Design of the UPH
3.1. Fundamentals Regarding Predefined-Time Stability and Prescribed-Performance Function
3.2. Predefined-Time TSMC Controller Design for Surge Velocity
3.3. Predefined-Time Second-Order TSMC System Design for Heading Angle
3.4. Predefined-Time and Prescribed-Performance Second-Order TSMC System Design for Suppressing the Disturbance of the Heading Angle
4. Simulation Results and Discussion
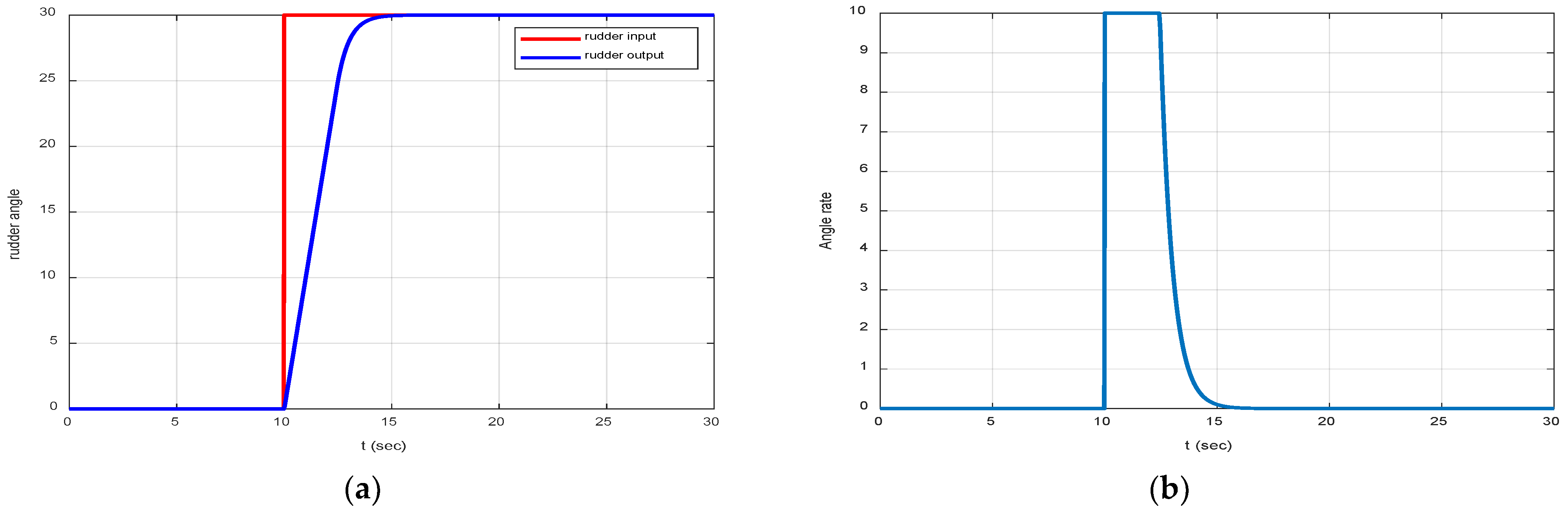
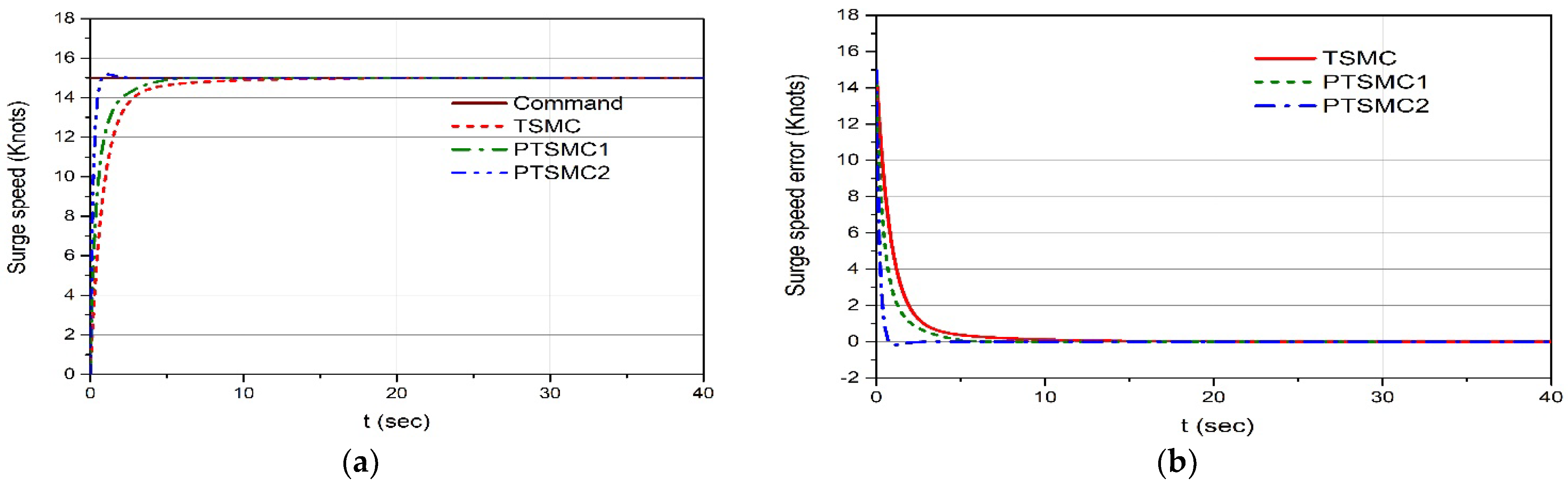
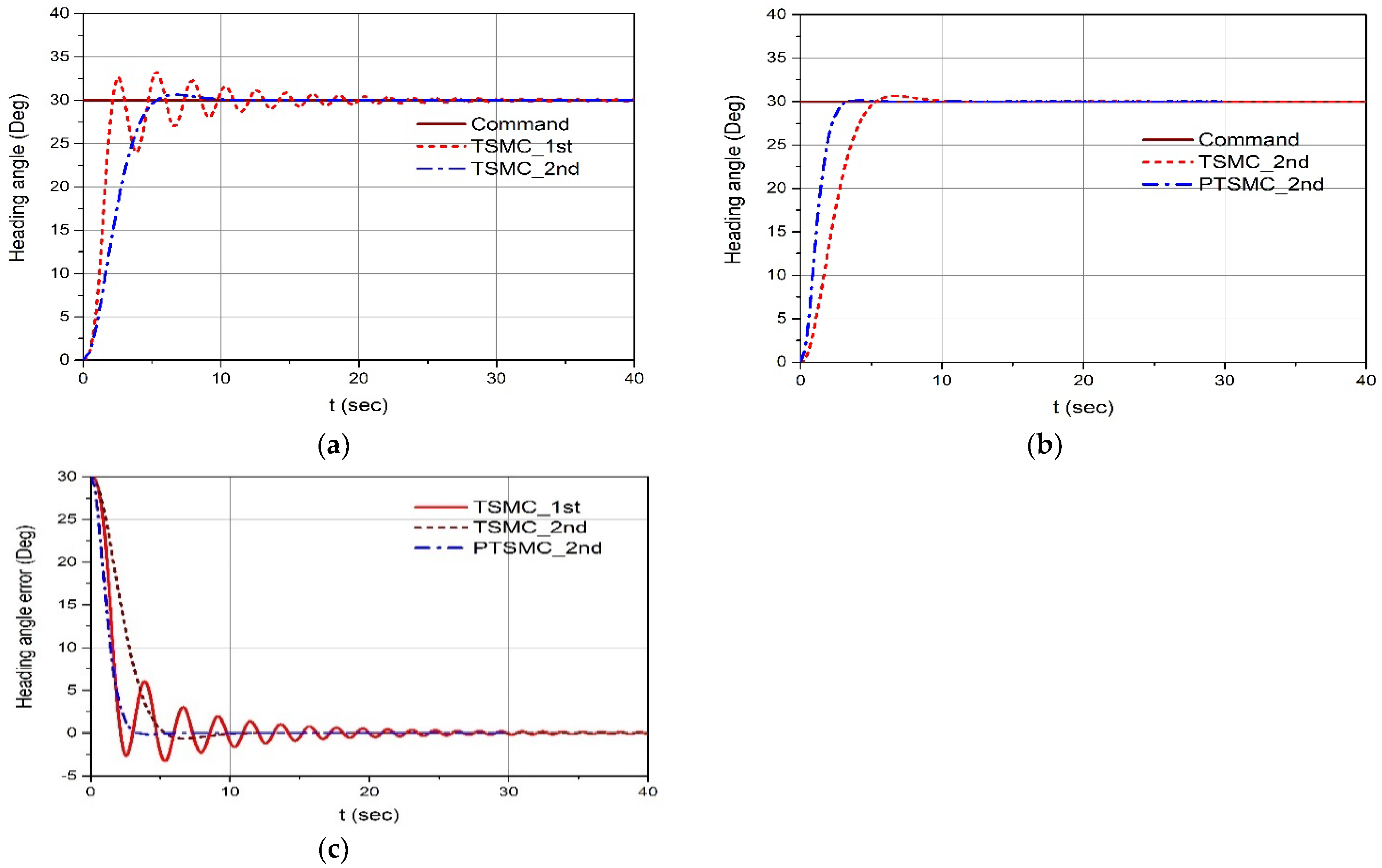
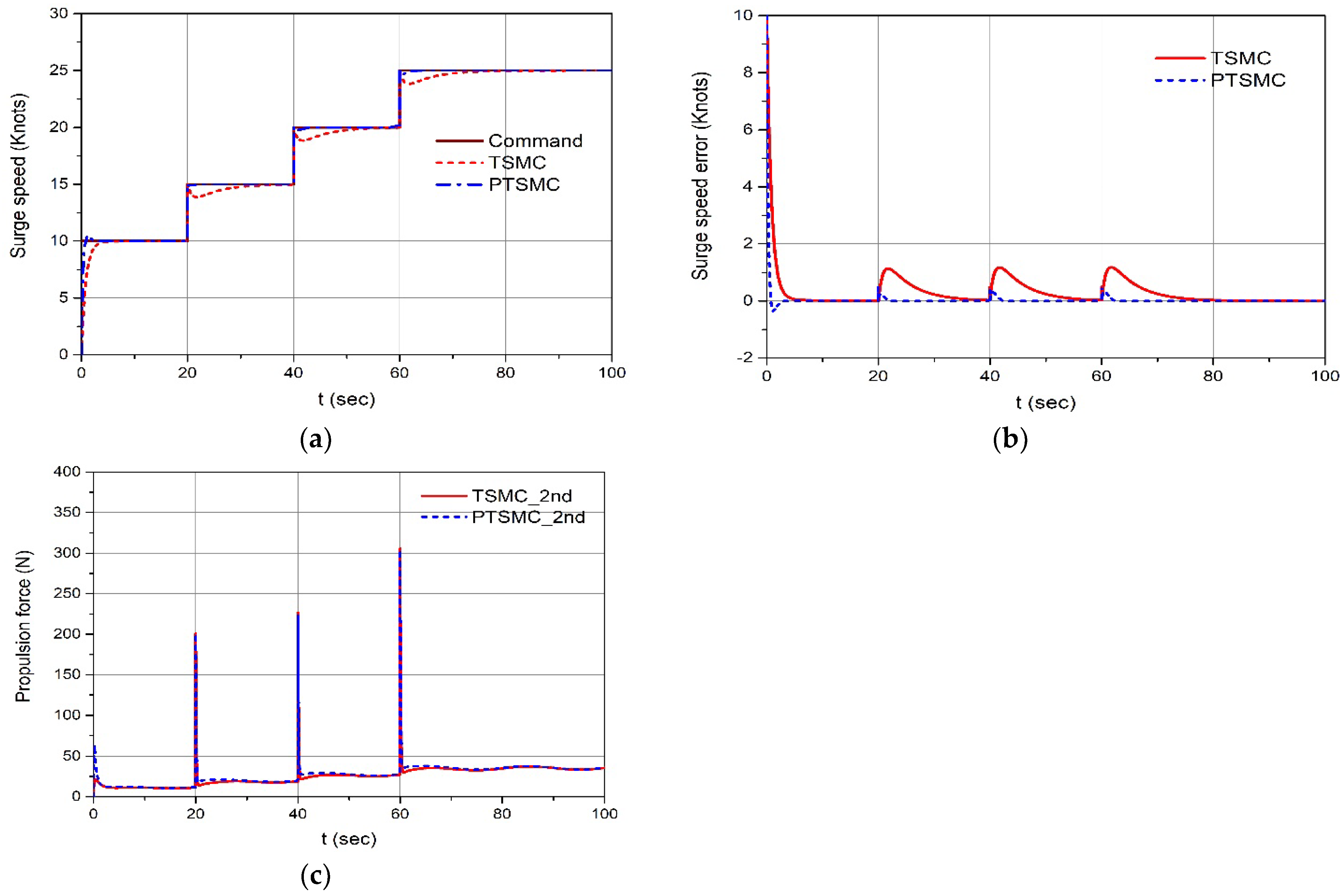
4.1. Simulation Results for the Step Command of Surge Velocity and Heading Angle
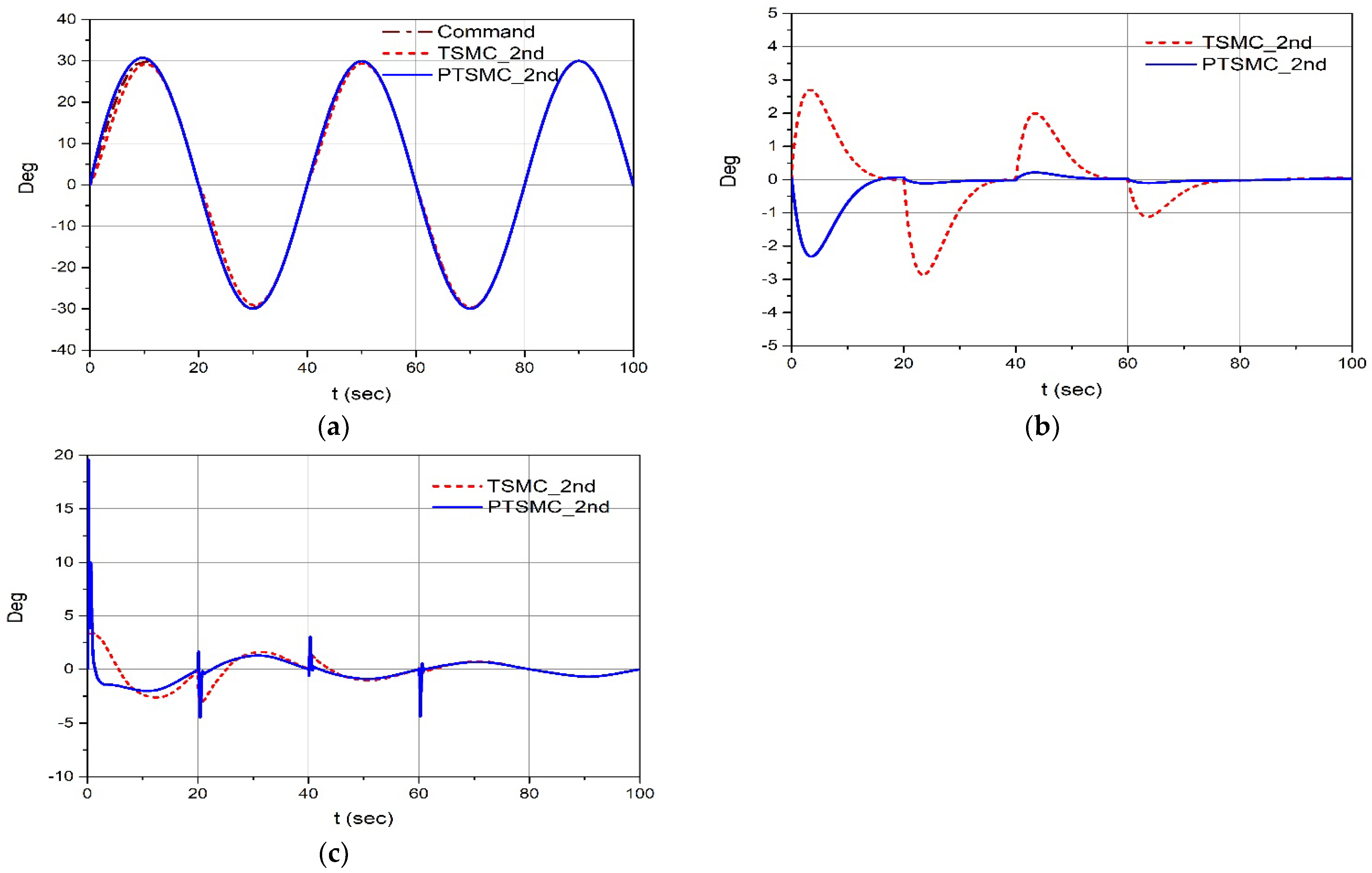
4.2. Simulation Results for the Multi-Step Command of Surge Velocity and Sine Wave Heading Angle
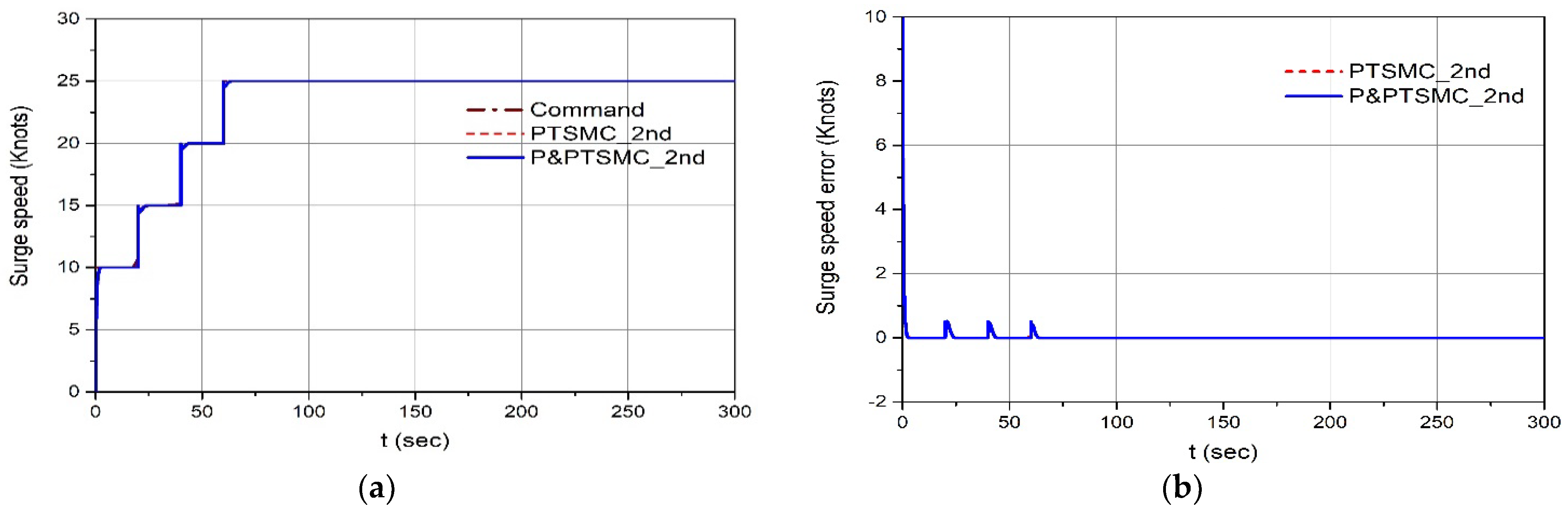
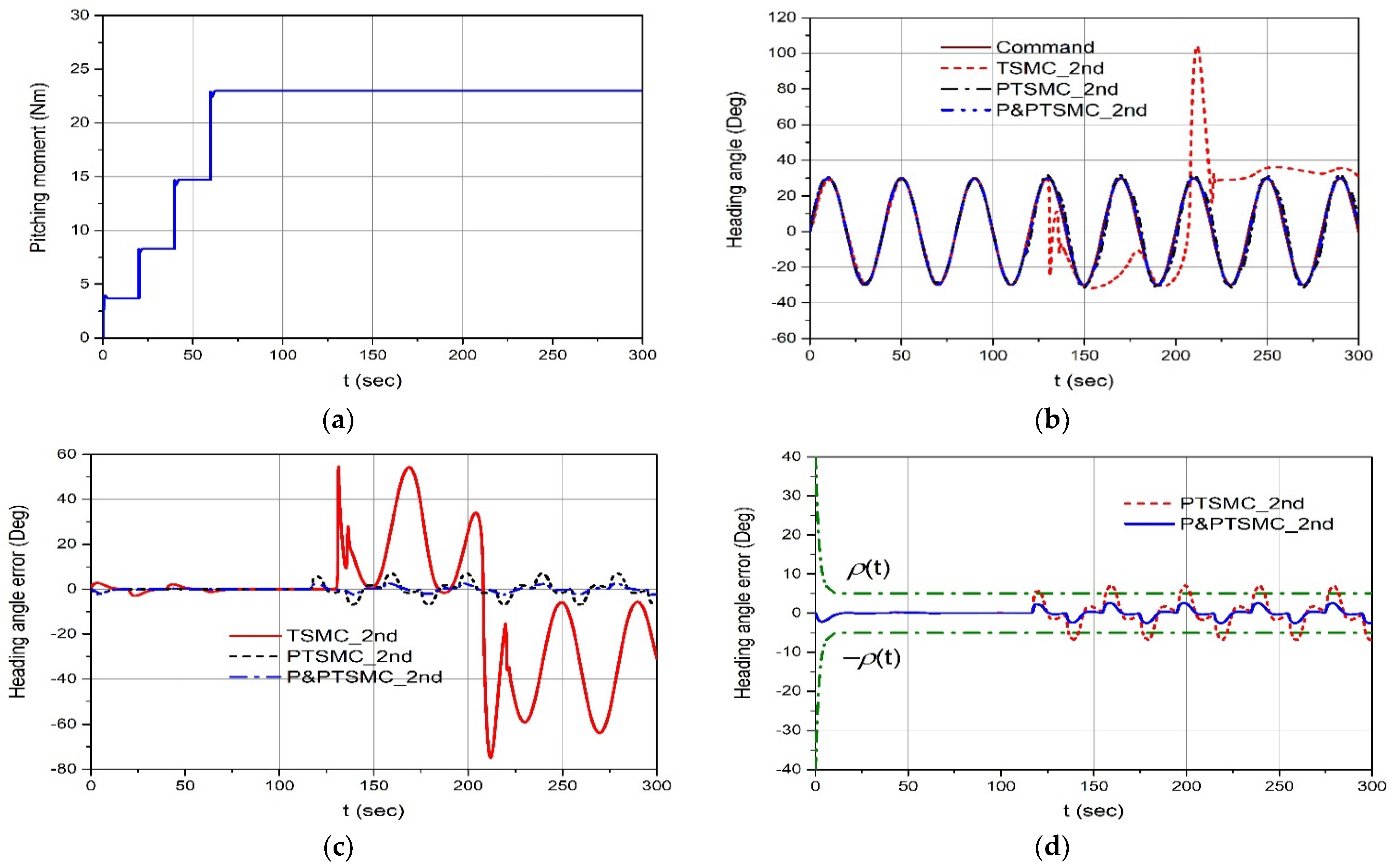
4.3. Simulation Results for the Multi-Step Command of Surge Velocity and Sine Wave Heading Angle for Pitching-Moment Disturbance
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Savitsky, D. Hydrodynamic design of planning hulls. Mar. Technol. SNAME News 1964, 1, 71–95. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding mode control design principles and applications to electric devices. IEEE Trans. Ind. Electron. 1993, 40, 23–36. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Z.; Zhang, J.; Zhou, D.; Dong, J. Adaptive sliding mode path following control system of the underactuated USV under the influence of ocean currents. J. Syst. Eng. Electron. 2018, 29, 1271–1283. [Google Scholar]
- Qiu, B.; Wang, G.; Fan, Y.; Mu, D.; Sun, X. Adaptive sliding mode trajectory control for unmanned surface vehicle with modeling uncertainties and input saturation. Appl. Sci. 2019, 9, 1240. [Google Scholar] [CrossRef]
- Kim, H.W.; Lee, J. Robust sliding mode control for a USV water-jet system. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 851–857. [Google Scholar] [CrossRef]
- Liu, W.; Ye, H.; Yang, X. Model-free adaptive sliding mode control method for unmanned surface vehicle course control. J. Mar. Sci. Eng. 2023, 11, 1904. [Google Scholar] [CrossRef]
- Khan, M.F.; Islam, R.U.; Iqbal, J. Control strategies for robotic manipulator. In Proceedings of the 2012 International Conference of Robotics and Artificial Intelligence, Rawalpindi, Pakistan, 22–23 October 2012. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shrinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Zhao, D.; Li, S.; Gao, F. A new terminal sliding mode control for robotic manipulator. Int. J. Control 2009, 82, 1804–1813. [Google Scholar] [CrossRef]
- Ahmad, S.; Uppal, A.A.; Azam, M.R.; Iqbal, J. Chattering free sliding mode control and state dependent Kalman filter design for underground gasification energy conversion process. Electronics 2023, 12, 876. [Google Scholar] [CrossRef]
- Wan, L.; Su, Y.; Shi, B. Global fast terminal sliding mode control based on radial basis function neural network for course keeping of unmanned surface vehicle. Int. J. Adv. Robot. Syst. 2019, 24, 1729881419829961. [Google Scholar] [CrossRef]
- Fan, Y.; Liu, B.; Wang, G.; Mu, D. Adaptive fast non-singular terminal sliding mode path following control for an underactuated unmanned surface vehicle with uncertainties and unknown disturbances. Sensors 2021, 21, 7454. [Google Scholar] [CrossRef]
- Alejando, F.G.; Herman, C. Adaptive integral terminal sliding mode control for an unmanned surface vehicle against external disturbances. IFAC-PapersOnLine 2021, 54, 202–207. [Google Scholar]
- Xu, D.; Liu, Z.; Song, J.; Zhou, X. Finite time trajectory tracking with full-state feedback of underactuated unmanned surface vessel based on nonsingular fast terminal sliding mode. J. Mar. Sci. Eng. 2022, 10, 1845. [Google Scholar] [CrossRef]
- Wang, D.; Kong, M.; Zhang, G.; Liang, X. Adaptive second-order fast terminal sliding-mode formation control for unmanned surface vehicles. J. Mar. Sci. Eng. 2022, 10, 1782. [Google Scholar] [CrossRef]
- Gong, X.W.; Yi, D.; Tezdogan, T.; Incecik, A. Adaptive neural network and extended state observer-based non-singular terminal sliding mode tracking control for an underactuated USV with unknown uncertainties. Appl. Ocean Res. 2023, 135, 103560. [Google Scholar]
- Ghadimi, P.; Loni, A.; Nowruzi, H.; Dashtimanesh, A.; Tavakoli, S. Parametric study of the effects of trim tabs on running trim and resistance of planning hulls. Adv. Shipp. Ocean Eng. 2014, 3, 1–12. [Google Scholar]
- Mansoori, M.; Fernades, A.C.; Ghassemi, H. Interceptor design of optimum trim control and minimum resistance of plaining boats. Appl. Ocean Res. 2017, 69, 100–115. [Google Scholar] [CrossRef]
- Sakaki, A.; Ghassemi, H.; Keyvani, S. Evaluation of the hydraulic performance of plaining boat with trim tab and interceptor and its optimization using generic algorithm. J. Mar. Sci. Appl. 2018, 18, 131–141. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Y.; Zhang, Y.; Nie, Y.; Tang, J.; Zhu, S. Disturbance-observer-based sliding mode control design for nonlinear unmanned surface vessel with uncertainties. IEEE Access 2019, 2019, 148522–148530. [Google Scholar] [CrossRef]
- Xu, D.; Liu, Z.; Zhou, X.; Yang, L.; Huang, L. Trajectory tracking of underactuated unmanned surface vessels: Nonsingular terminal sliding mode control with nonlinear disturbance observer. Appl. Sci. 2022, 12, 3004. [Google Scholar] [CrossRef]
- Yao, Q. Fixed-time trajectory tracking control for unmanned surface vessels in the presence of model uncertainties and external disturbances. Int. J. Control 2022, 95, 1133–1143. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, S.; Yan, Y. Fixed-time extended observer-based trajectory tracking and point stabilization control for marine surface vessels with uncertainties and disturbances. Ocean Eng. 2019, 186, 106109. [Google Scholar] [CrossRef]
- Li, M.; Guo, C.; Yu, H. Filtered extended state observer based line-of-sight guidance for path following of unmanned surface vehicles with unknown dynamics and disturbances. IEEE Access 2019, 7, 178401–178412. [Google Scholar] [CrossRef]
- Wang, N.; Zhu, Z.; Qin, H.; Deng, Z.; Sun, Y. Finite-time extended state observer-based exact tracking control of an unmanned surface vehicle. Int. J. Robust Nonlinear Control 2021, 312, 1704–1719. [Google Scholar] [CrossRef]
- Fan, Y.; Qiu, B.; Liu, L.; Yang, Y. Global fixed-time trajectory tracking control of underactuated USV based on fixed-time extended state observer. ISA Trans. 2023, 132, 267–277. [Google Scholar] [CrossRef]
- Sanchez-Torres, J.D.; Sanchez, E.; Loukianov, A.G. Predefined-time stability of dynamical systems with sliding modes. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 5842–5846. [Google Scholar]
- Jimenez-Rodriguez, E.; Sanchez-Torres, J.D.; Loukianov, A.G. On optimal predefined-time stabilization. Int. J. Robust Nonlinear Control 2017, 27, 3620–3642. [Google Scholar] [CrossRef]
- Sanchez-Torres, J.D.; Gomez-Gutierrez, D.; Lopez, E.; Loukianov, A.G. A class of predefined-time stable dynamical systems. IMA J. Math. Control Inf. 2018, 35, 1–29. [Google Scholar] [CrossRef]
- Ye, D.; Zou, A.M.; Sun, Z. Predefined-time predefined-bounded attitude tracking control for rigid spacecraft. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 464–472. [Google Scholar] [CrossRef]
- Wang, F.; Miao, Y.; Li, C.; Hwang, I. Attitude control of rigid spacecraft with predefined-time stability. J. Frankl. Inst. 2020, 357, 4212–4221. [Google Scholar] [CrossRef]
- Xie, S.; Chen, Q. Adaptive nonsingular predefined-time control for attitude stabilization of rigid spacecrafts. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 189–193. [Google Scholar] [CrossRef]
- Sanchez-Torres, J.D.; Defoort, M.; Munoz-Vazquez, M. Predefined-time stabilization of a class of nonholonomic systems. Int. J. Control 2020, 93, 2941–2948. [Google Scholar] [CrossRef]
- Pan, J.; Xiao, T.; Yan, H. Task-space multiple-biparite consensus for networked heterogenous Euler-Lagrange systems via hierarchical predefined-time control algorithm. Nonlinear Dyn. 2023, 111, 17095–17108. [Google Scholar] [CrossRef]
- Li, K.; Hua, C.; You, X.; Ahn, K. Output feedback predefined-time bipartite consensus control for high-order nonlinear multiagent systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 3069–3078. [Google Scholar] [CrossRef]
- Mao, B.; Wu, X.; Lu, J.; Chen, G. Predefined-time bounded consensus of multiagent systems with unknown nonlinearity via distributed adaptive fuzzy control. IEEE Trans. Cybern. 2022, 53, 2622–2635. [Google Scholar] [CrossRef] [PubMed]
- Liang, C.D.; Ge, M.F.; Liu, Z.W.; Ling, G.; Liu, F. Predefined-time formation tracking control of networked marine surface vehicles. Control Eng. Pract. 2021, 107, 104682. [Google Scholar] [CrossRef]
- Jiang, T.; Yan, Y.; Yu, S.H. Adaptive sliding mode control for unmanned surface vehicles with predefined-time tracking performances. J. Mar. Sci. Eng. 2023, 11, 1244. [Google Scholar] [CrossRef]
- Benchlioulis, C.P.; Rovithakis, G.A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance. IEEE Trans. Autom. Control 2008, 53, 2090–2099. [Google Scholar] [CrossRef]
- Li, Y.; Shao, X.; Tong, S. Adaptive fuzzy prescribed performance control of nontriangular structure nonlinear systems. IEEE Trans. Fuzzy Syst. 2020, 28, 2416–2426. [Google Scholar] [CrossRef]
- Li, K.; Li, Y. Fuzzy adaptive optimization prescribed performance control for nonlinear vehicle platoon. IEEE Trans. Fuzzy Syst. 2023. [Google Scholar] [CrossRef]
- Han, S.I. Fuzzy supertwisting dynamic surface control for MIMO strict-feedback nonlinear dynamic systems with supertwisting nonlinear disturbance observer and a new partial tracking error constraint. IEEE Trans. Fuzzy Syst. 2019, 27, 2101–2114. [Google Scholar] [CrossRef]
- Li, S.; Ma, T.; Luo, X.; Yang, Z. Adaptive fuzzy output regulation for unmanned surface vehicles with prescribed performance. Int. J. Control Autom. Syst. 2020, 18, 405–414. [Google Scholar] [CrossRef]
- Jiang, K.; Mao, L.; Su, Y.; Zheng, Y. Trajectory tracking control for underactuated USV with prescribed performance and input saturation. Symmetry 2021, 13, 2208. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, Q.; Dong, S.; Yu, H. Prescribed performance dynamic surface control for trajectory-tracking of unmanned surface vessel with input saturation. Appl. Ocean Res. 2021, 113, 102736. [Google Scholar] [CrossRef]
- Li, J.; Xiang, X.; Dong, D.; Yang, S. Saturated-command-deviation based finite-time adaptive control for dynamic positioning of USV with prescribed performance. Ocean Eng. 2022, 266, 112941. [Google Scholar] [CrossRef]
- Qu, Y.; Zhao, W.; Yu, Z.; Xiao, B. Distributed prescribed performance containment control for unmanned surface vehicles based on disturbance observer. ISA Trans. 2022, 125, 699–706. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.simerics.com/simulation-gallery/planing-hull (accessed on 27 October 2023).
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of homogenous systems. In Proceedings of the 1997 American Control Conference, Albuquerque, NM, USA, 6 June 1997; pp. 1073–1078. [Google Scholar]

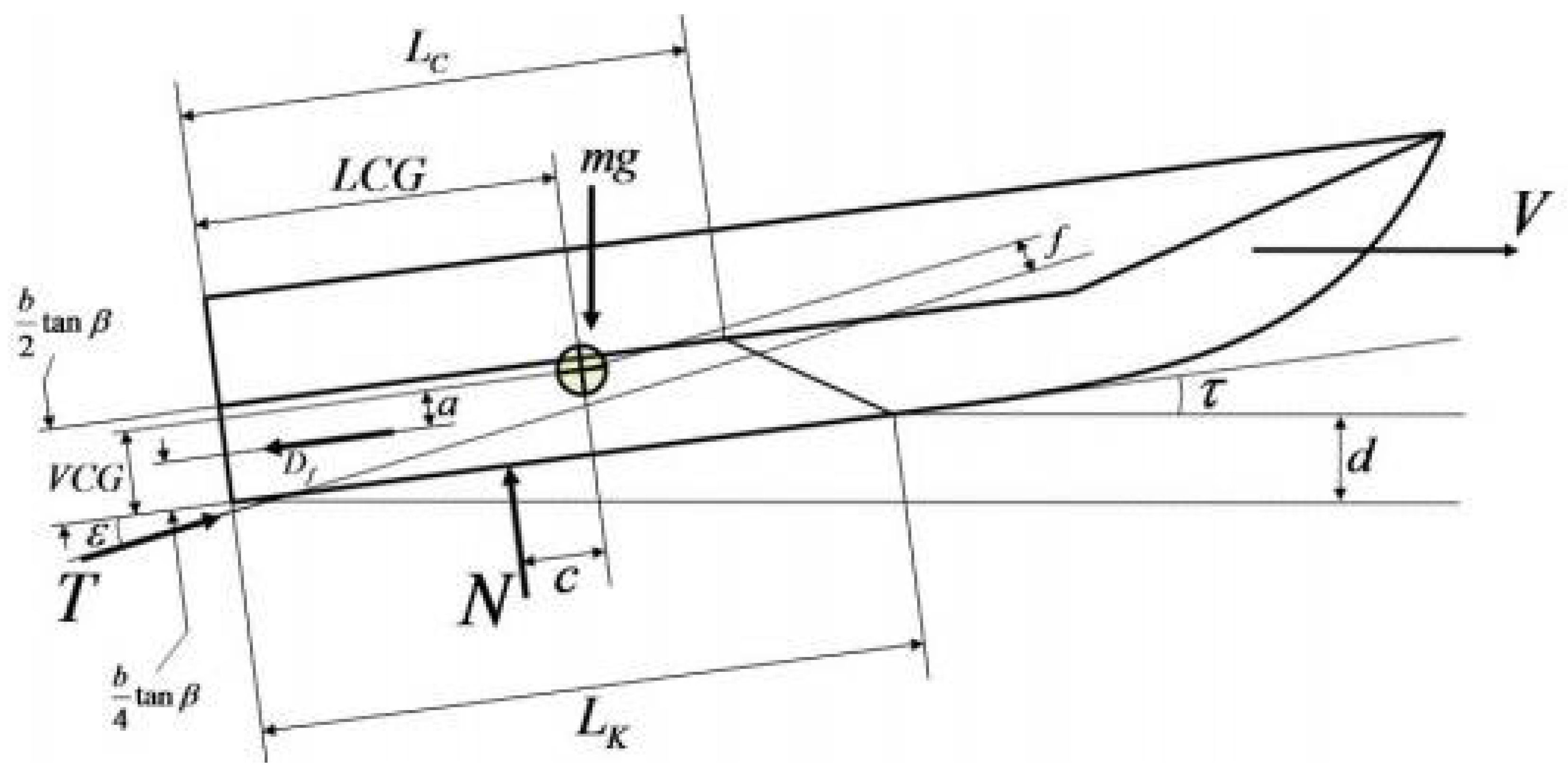

| Nomenclature | Force and Moment | Linear and Rotary Velocity | Position and Euler Angle |
|---|---|---|---|
| Surge | X | u | x |
| Sway | Y | v | y |
| Heave | Z | w | z |
| Roll | K | p | |
| Pitch | M | q | |
| Yaw | N | r |
| Symbol | Semantics |
|---|---|
| LCG | the longitudinal distance from the transom to the center of gravity |
| VCG | the perpendicular distance for the bottom from keel to the center of gravity |
| the vertical drag force and the propulsion force of the propeller | |
| the viscous friction drag of the body | |
| the distance between T, N, and the center of gravity, respectively | |
| the draft of the keel in the transom, the trim angle of keel, and the chine width | |
| , | The distance between and the center of gravity, and the speed of the boat |
| the angle between the propulsion force and trim line | |
| , | the inclination angle of the planing side and the weight of the body |
| the flooded length of the chine and the flooded length of keel |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| LCG, VCG | |||
| Parameter (Surge) | Value | Parameter (Heading) | Value |
|---|---|---|---|
| System | PSMC_2nd | P&PTSMC_2nd |
|---|---|---|
| ITAE (sec-deg) | 4557 (100%) | 3574 (78%) |
| Maximum absolute error (deg) | 7.02 (100%) | 2.58 (37%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, S. Predefined-Time and Prescribed-Performance Control Methods Combined with Second-Order Terminal Sliding Mode Control for an Unmanned Planing Hull System with Input Delay and Unknown Disturbance. J. Mar. Sci. Eng. 2023, 11, 2191. https://doi.org/10.3390/jmse11112191
Han S. Predefined-Time and Prescribed-Performance Control Methods Combined with Second-Order Terminal Sliding Mode Control for an Unmanned Planing Hull System with Input Delay and Unknown Disturbance. Journal of Marine Science and Engineering. 2023; 11(11):2191. https://doi.org/10.3390/jmse11112191
Chicago/Turabian StyleHan, Seongik. 2023. "Predefined-Time and Prescribed-Performance Control Methods Combined with Second-Order Terminal Sliding Mode Control for an Unmanned Planing Hull System with Input Delay and Unknown Disturbance" Journal of Marine Science and Engineering 11, no. 11: 2191. https://doi.org/10.3390/jmse11112191
APA StyleHan, S. (2023). Predefined-Time and Prescribed-Performance Control Methods Combined with Second-Order Terminal Sliding Mode Control for an Unmanned Planing Hull System with Input Delay and Unknown Disturbance. Journal of Marine Science and Engineering, 11(11), 2191. https://doi.org/10.3390/jmse11112191






