Ship Behavior Pattern Analysis Based on Graph Theory: A Case Study in Tianjin Port
Abstract
:1. Introduction
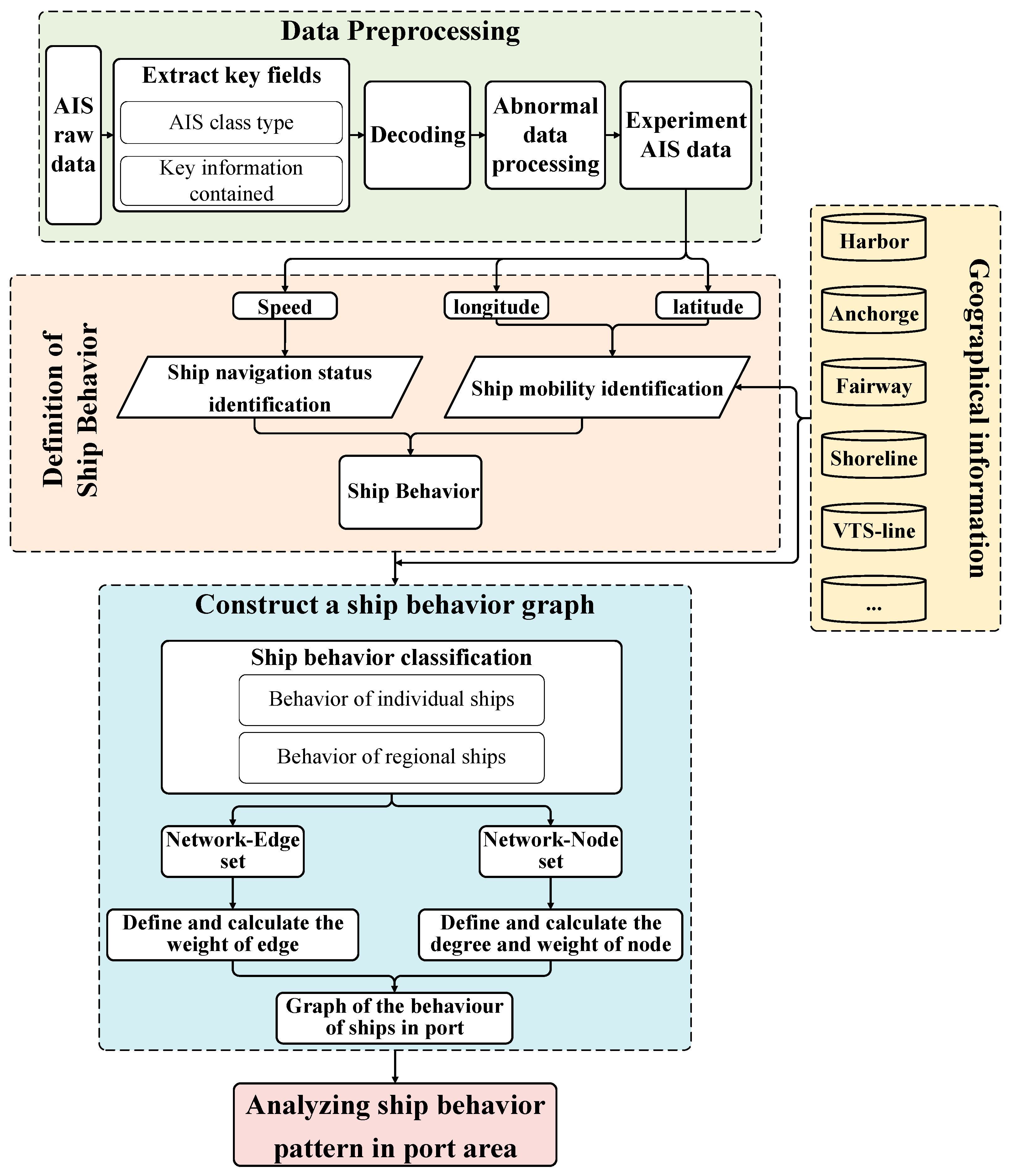
2. Methodology
2.1. AIS Data Preprocessing
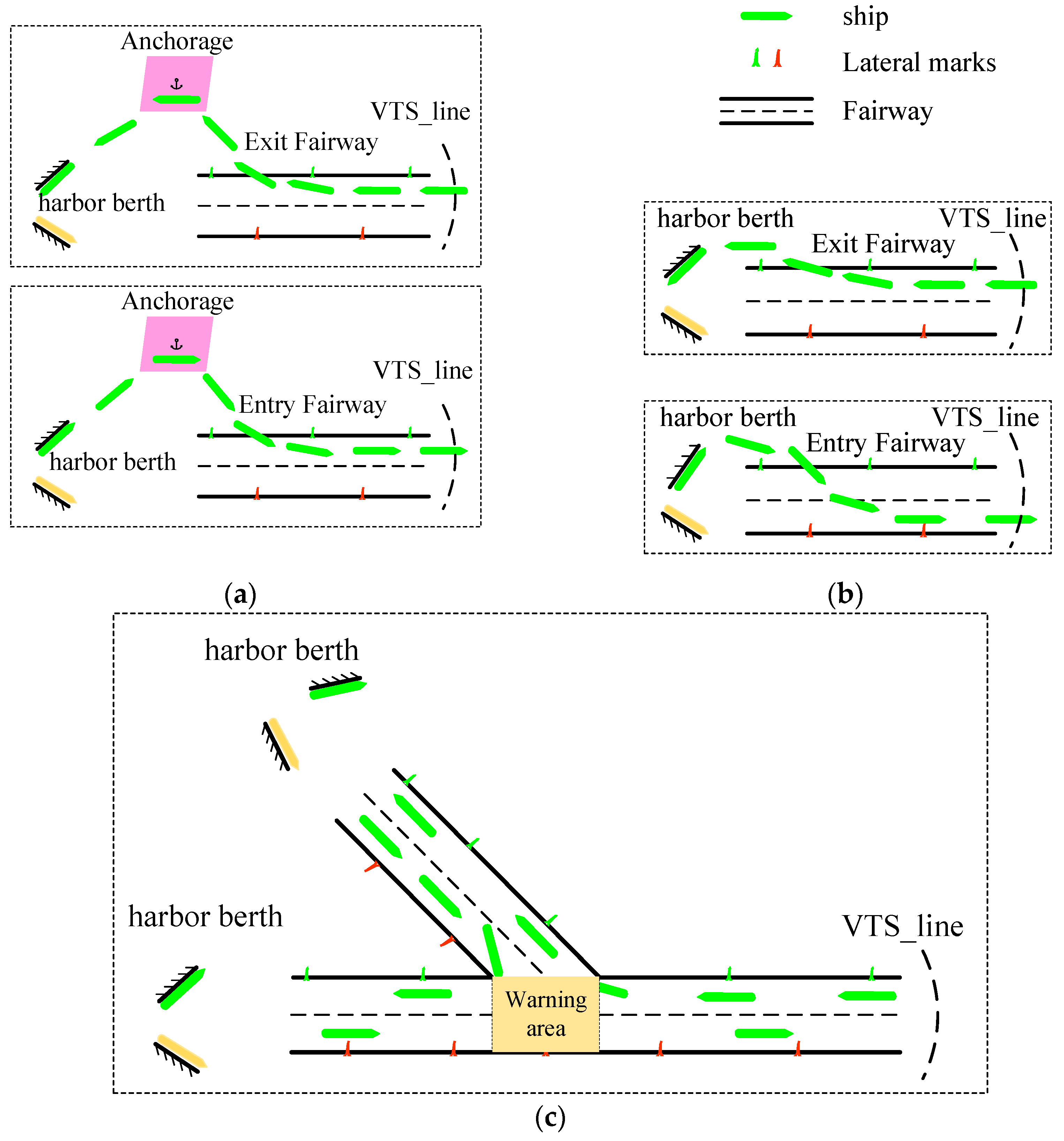
2.2. Port Geographical Information Representation
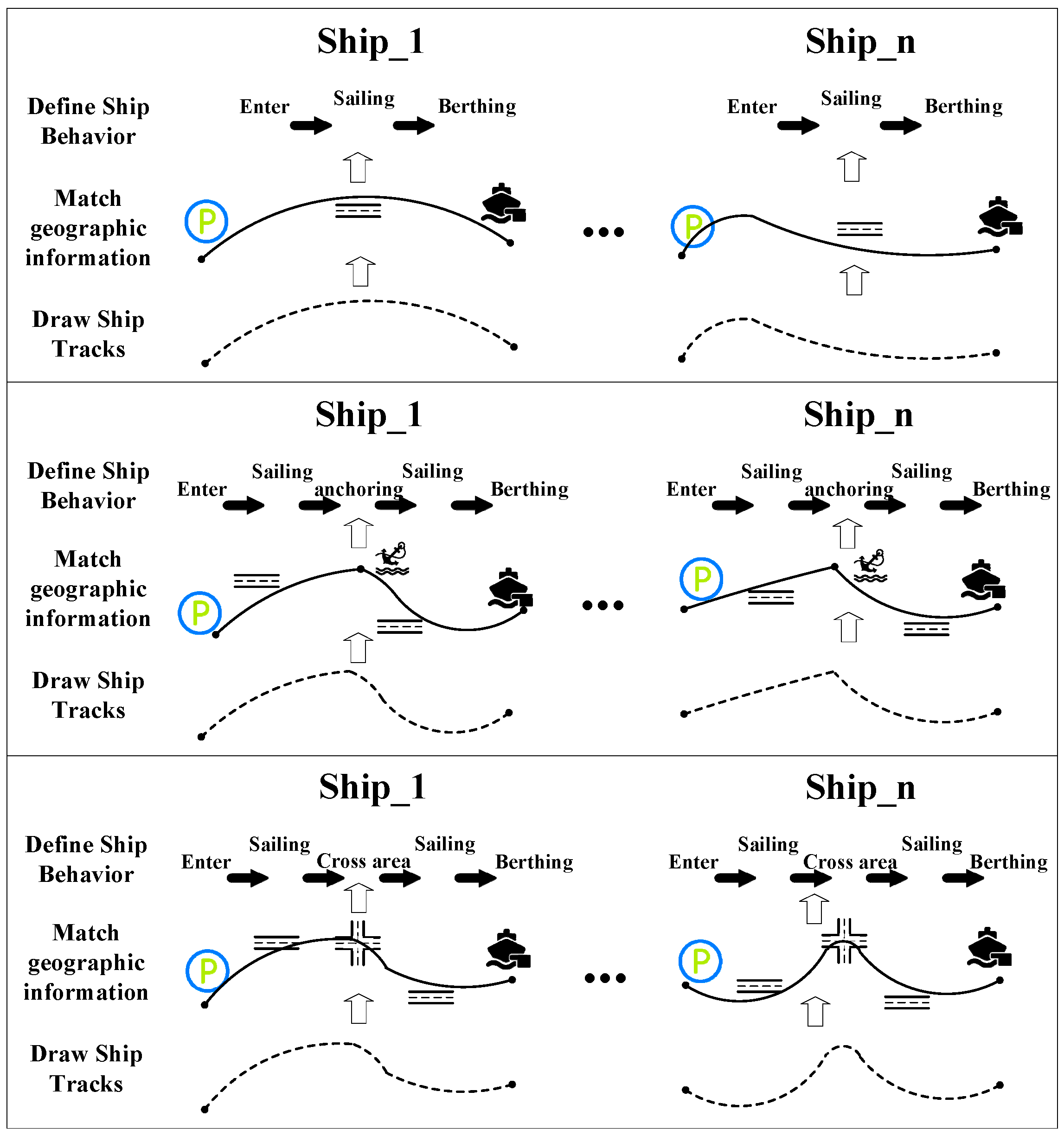
2.3. Identification of Ship Behavior
2.4. Ship Behavior Graph Construction
2.5. Network Structure Characteristics
3. Results
3.1. Research Area and Experimental Data
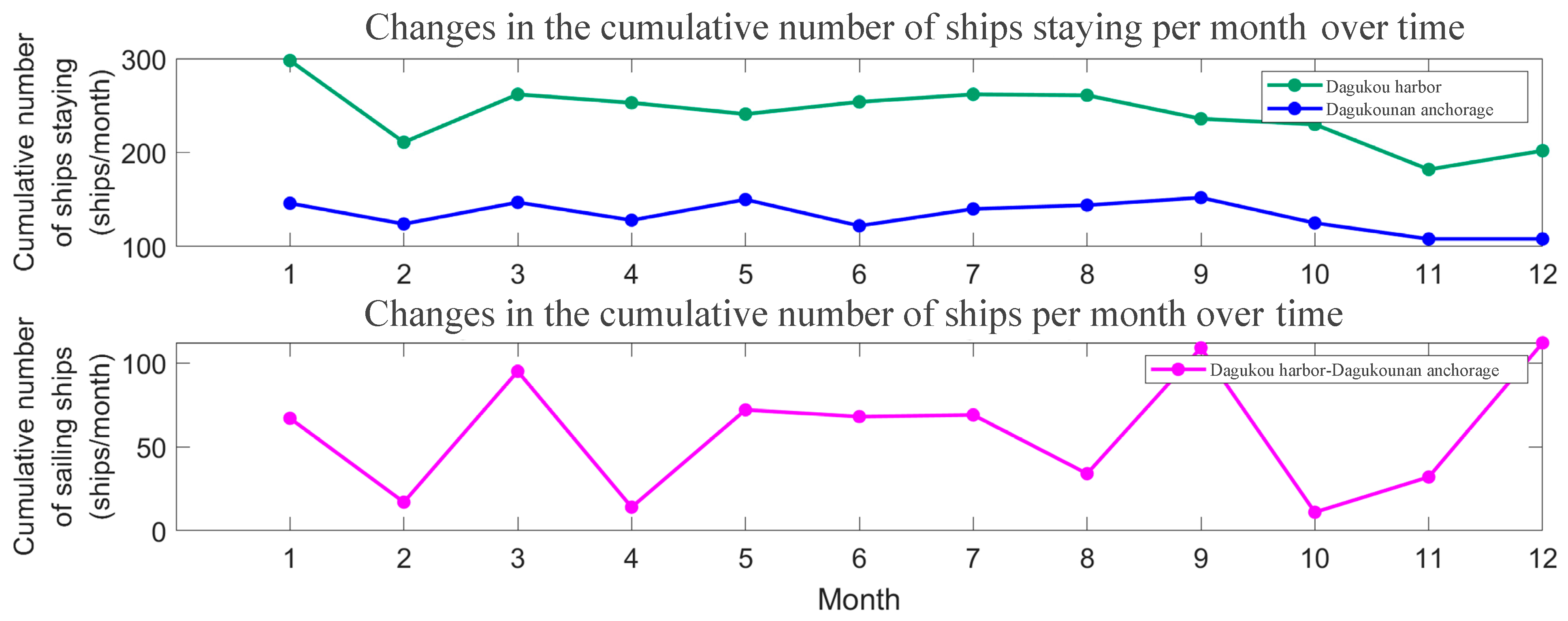
3.2. Behavior Patterns in Tianjin Port
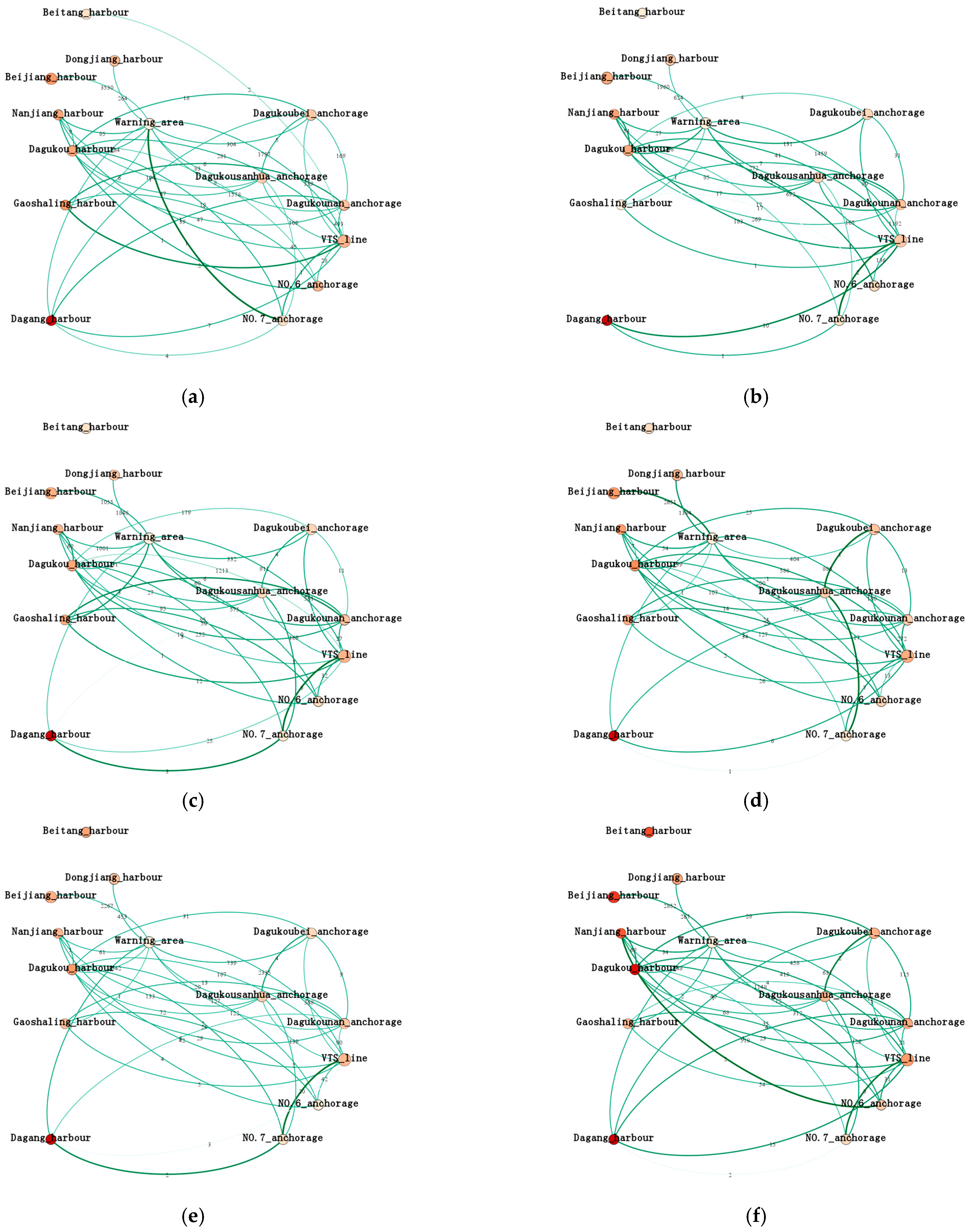
3.3. Network Structure Analysis
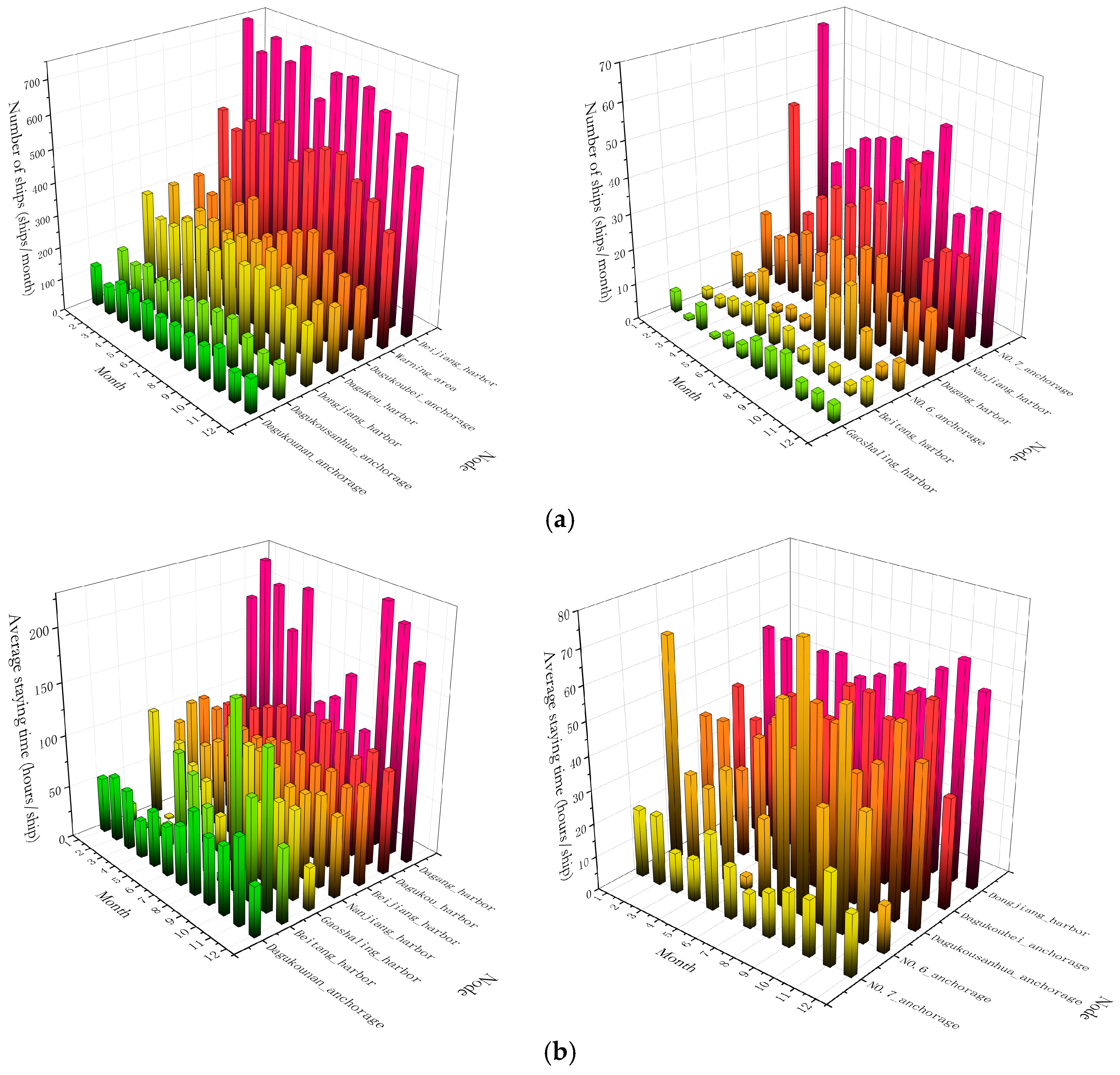
3.3.1. Node Weight Characteristics
3.3.2. Edge Weights Analysis
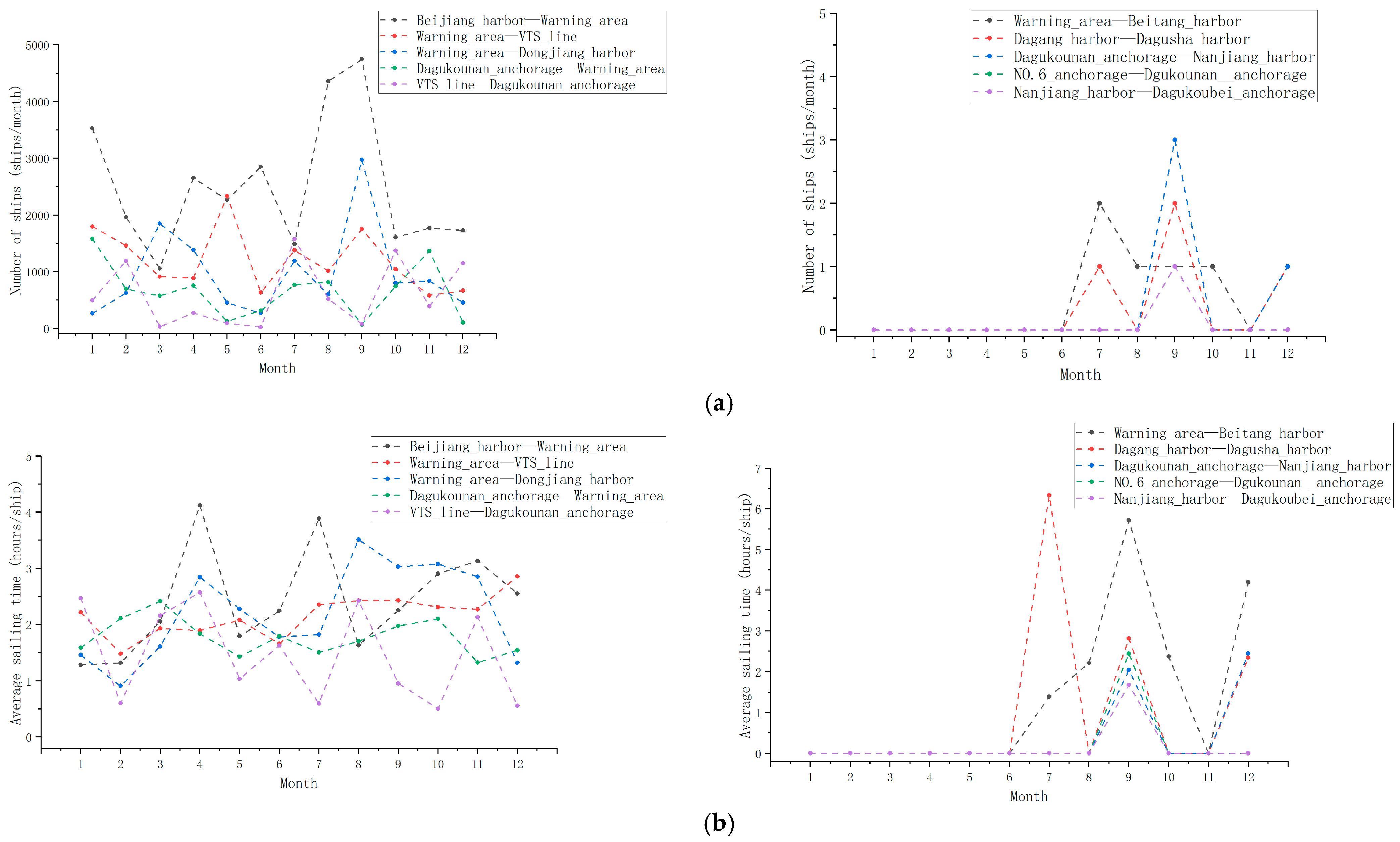
3.3.3. Frequent Patterns Analysis
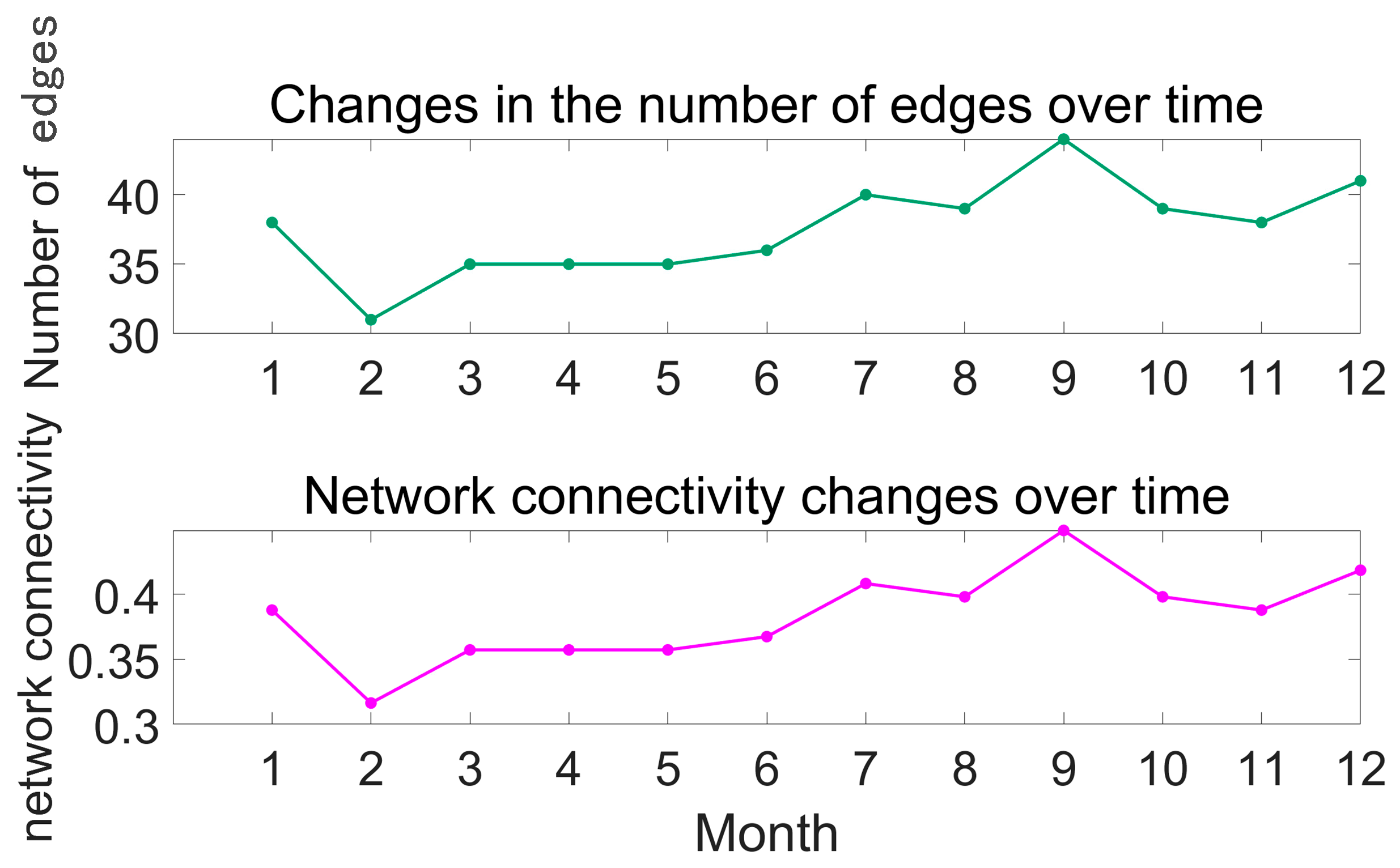
3.3.4. Network Connectivity Analysis
4. Discussion
- Unified management policy: Considering the correlation between the ship behavior patterns, it can be seen that the simple dispatching strategy targeting a certain port area or a certain channel is often ineffective. A unified management policy considering the similarities, differences, and correlations between the traffic in different port areas is needed. For instance, a sudden increase in the number of ships in an anchorage is not only related to the sudden increase in arriving ships but also connected to the lack of berths providing services for the increasing number of ships in this harbor.
- Flexible scheduling strategy: Flexible scheduling corresponding to changeable behavior patterns could improve the efficiency and safety of the port. The abnormal behavior of ships usually changes the network structure and weights of nodes and edges. The correlations between the nodes and edges imply that it will affect the ship behavior pattern in other functional areas. The flexible scheduling strategy aids in taking suitable measures in time to deal with emergencies.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oumimoun, B.; Nahiri, L.; Idmouida, H.; Addaim, A.; Guennoun, Z.; Minaoui, K. Software Defined AIS Receiver Implementation Based on RTL-SDR and GNU Radio. In Proceedings of the 2022 IEEE Asia Pacific Conference on Wireless and Mobile (APWiMob), Bandung, Indonesia, 9–10 December 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Billah, M.M.; Zhang, J.; Zhang, T. A Method for Vessel’s Trajectory Prediction Based on Encoder Decoder Architecture. J. Mar. Sci. Eng. 2022, 10, 1529. [Google Scholar] [CrossRef]
- Tritsarolis, A.; Kontoulis, Y.; Theodoridis, Y. The Piraeus AIS dataset for large-scale maritime data analytics. Data Brief 2022, 40, 107782. [Google Scholar] [CrossRef] [PubMed]
- Evmides, N.; Odysseos, L.; Michaelides, M.P.; Herodotou, H. An Intelligent Framework for Vessel Traffic Monitoring using AIS Data. In Proceedings of the 2022 23rd IEEE International Conference on Mobile Data Management (MDM), Paphos, Cyprus, 6–9 June 2022; pp. 413–418. [Google Scholar] [CrossRef]
- Iphar, C.; Le Berre, I.; Napoli, A.; Foulquier, É. Port call extraction and characterisation from maritime navigational data: An application to the Lesser Antilles. In Proceedings of the AGILE 2023 Conference, Orlando, FL, USA, 24–28 June 2023. [Google Scholar]
- Song, R.; Wen, Y.; Tao, W.; Zhang, Q.; Papadimitriou, E.; van Gelder, P. Semantic Modeling of Ship Behavior in Cognitive Space. J. Mar. Sci. Eng. 2022, 10, 1347. [Google Scholar] [CrossRef]
- Wen, Y.; Zhang, Y.; Huang, L.; Zhou, C.; Xiao, C.; Zhang, F.; Sui, Z. Semantic modelling of ship behavior in harbor based on ontology and dynamic bayesian network. ISPRS Int. J. Geo-Inf. 2019, 8, 107. [Google Scholar] [CrossRef]
- Zhou, Y.; Daamen, W.; Vellinga, T.; Hoogendoorn, S. Review of maritime traffic models from vessel behavior modeling perspective. Transp. Res. Part C Emerg. Technol. 2019, 105, 323–345. [Google Scholar] [CrossRef]
- Rong, H.; Teixeira, A.P.; Soares, C.G. Ship collision avoidance behaviour recognition and analysis based on AIS data. Ocean Eng. 2022, 245, 110479. [Google Scholar] [CrossRef]
- Chen, X.; Qi, L.; Yang, Y.; Luo, Q.; Postolache, O.; Tang, J.; Wu, H. Video-based detection infrastructure enhancement for automated ship recognition and behavior analysis. J. Adv. Transp. 2020, 2020, 7194342. [Google Scholar] [CrossRef]
- Wu, Y.; Chu, X.; Deng, L.; Lei, J.; He, W.; Królczyk, G.; Li, Z. A new multi-sensor fusion approach for integrated ship motion perception in inland waterways. Measurement 2022, 200, 111630. [Google Scholar] [CrossRef]
- Zhou, Y.; Daamen, W.; Vellinga, T.; Hoogendoorn, S.P. Ship classification based on ship behavior clustering from AIS data. Ocean Eng. 2019, 175, 176–187. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Liu, R.W.; Liu, Y.; Yuan, Z. Data-driven methods for detection of abnormal ship behavior: Progress and trends. Ocean Eng. 2023, 271, 113673. [Google Scholar] [CrossRef]
- Murray, B.; Perera, L.P. Ship behavior prediction via trajectory extraction-based clustering for maritime situation awareness. J. Ocean Eng. Sci. 2022, 7, 1–13. [Google Scholar] [CrossRef]
- Murray, B.; Perera, L.P. An AIS-based deep learning framework for regional ship behavior prediction. Reliab. Eng. Syst. Saf. 2021, 215, 107819. [Google Scholar] [CrossRef]
- Roy, U.; Wu, X. Ais-data based vessel traffic’s characteristics and travel behaviour analysis: A case study at houston ship channel. J. Ocean Technol. 2019, 14, 59–74. [Google Scholar]
- Mandalis, P.; Chondrodima, E.; Kontoulis, Y.; Pelekis, N.; Theodoridis, Y. Machine learning models for vessel traffic flow forecasting: An experimental comparison. In Proceedings of the 2022 23rd IEEE International Conference on Mobile Data Management (MDM), Paphos, Cyprus, 6–9 June 2022; pp. 431–436. [Google Scholar] [CrossRef]
- Li, H.; Gan, L.; Zheng, Y.; Wen, Y. Complexity of Waterway Networks in Port Waters. Navig. China 2015, 38, 94–98+130. [Google Scholar] [CrossRef]
- Guan, X.; Li, Z.; Ding, C.; Duan, W.; Li, X. Robustness analysis of complex network of container ports in the world under cascading failure. Navig. China 2021, 44, 84–89. [Google Scholar] [CrossRef]
- West, D.B. Introduction to Graph Theory; Prentice Hall: Upper Saddle River, NJ, USA, 2001; Volume 2. [Google Scholar]
- Sheriff, F. ELMOPP: An application of graph theory and machine learning to traffic light coordination. Appl. Comput. Inform. 2021. [Google Scholar] [CrossRef]
- Lu, H.; Wang, S. A study on multi-ASC scheduling method of automated container terminals based on graph theory. Comput. Ind. Eng. 2019, 129, 404–416. [Google Scholar] [CrossRef]
- Yu, W.; Wang, T. Ship channel route optimization based on graph theory. Chin. J. Ship Res. 2008, 01, 18–22. [Google Scholar]
- Tang, H.; Wei, L.; Yin, Y.; Qi, Y. Ship route planning based on probabilistic digraph model. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2020, 48, 105–109. [Google Scholar] [CrossRef]
- Yu, H.; Meng, Q.; Fang, Z.; Liu, J.; Xu, L. A review of ship collision risk assessment, hotspot detection and path planning for maritime traffic control in restricted waters. J. Navig. 2023, 75, 1–27. [Google Scholar] [CrossRef]
- Dirzka, C.; Acciaro, M. Global shipping network dynamics during the COVID-19 pandemic’s initial phases. J. Transp. Geogr. 2022, 99, 103265. [Google Scholar] [CrossRef] [PubMed]
- Kanrak, M.; Nguyen, H.O. Structure, characteristics and connectivity analysis of the Asian-Australasian cruise shipping network. Marit. Policy Manag. 2022, 49, 882–896. [Google Scholar] [CrossRef]
- Fritsch, F.N.; Carlson, R.E. Monotone piecewise cubic interpolation. SIAM J. Numer. Anal. 1980, 17, 238–246. [Google Scholar] [CrossRef]
- Sui, Z.; Wen, Y.; Huang, Y.; Zhou, C.; Du, L.; Piera, M.A. Node importance evaluation in marine traffic situation complex network for intelligent maritime supervision. Ocean Eng. 2022, 247, 110742. [Google Scholar] [CrossRef]
- He, S.; Zhu, J.; Zeng, Q.; Guo, X.; Yin, J.; Wei, T. Topology searching algorithm for multi-port hybrid circuit breakers based on graph theory. Front. Energy Res. 2023, 11, 1171815. [Google Scholar] [CrossRef]
- Yan, Z.; Cheng, L.; He, R.; Yang, H. Extracting ship stopping information from AIS data. Ocean Eng. 2022, 250, 111004. [Google Scholar] [CrossRef]
- Woolley-Meza, O.; Thiemann, C.; Grady, D.; Lee, J.J.; Seebens, H.; Blasius, B.; Brockmann, D. Complexity in human transportation networks: A comparative analysis of worldwide air transportation and global cargo-ship movements. Eur. Phys. J. B 2011, 84, 589–600. [Google Scholar] [CrossRef]

| Area | Ship Behavior |
|---|---|
| Anchorage | Moving in anchorage |
| Anchorage | |
| Fairway/Channel | Navigation |
| Anchoring | |
| Berth | Moving in berth |
| Berthing | |
| Other areas | Sailing in other areas |
| Anchoring in other areas |
| Time | Number of Nodes | Number of Edges | Average Node Degree | Network Connectivity |
|---|---|---|---|---|
| January 2021 | 14 | 38 | 5.429 | 0.387755 |
| February 2021 | 14 | 31 | 4.429 | 0.316327 |
| March 2021 | 14 | 35 | 5 | 0.357143 |
| April 2021 | 14 | 35 | 5 | 0.357143 |
| May 2021 | 14 | 35 | 5 | 0.357143 |
| June 2021 | 14 | 36 | 5.143 | 0.367347 |
| July 2021 | 14 | 40 | 5.714 | 0.408163 |
| August 2021 | 14 | 39 | 5.571 | 0.397959 |
| September 2021 | 14 | 44 | 6.286 | 0.44898 |
| October 2021 | 14 | 39 | 5.571 | 0.397959 |
| November 2021 | 14 | 38 | 5.429 | 0.387755 |
| December 2021 | 14 | 41 | 5.857 | 0.418367 |
| Period of Daytime | Speed (kn) | Period of Nighttime | Speed (kn) |
|---|---|---|---|
| 06:00–07:00 | 10.05 | 18:00–19:00 | 6.47 |
| 07:00–08:00 | 6.385 | 19:00–20:00 | 7.34 |
| 08:00–09:00 | 9.64 | 20:00–21:00 | 7.45 |
| 09:00–10:00 | 10.37 | 21:00–22:00 | 7.92 |
| 10:00–11:00 | 6.63 | 22:00–23:00 | 7.08 |
| 11:00–12:00 | 3.03 | 23:00–00:00 | 3.79 |
| 12:00–13:00 | 4.84 | 00:00–01:00 | 7.35 |
| 13:00–14:00 | 3.85 | 01:00–02:00 | 9.86 |
| 14:00–15:00 | 9.62 | 02:00–03:00 | 5.33 |
| 15:00–16:00 | 5.69 | 03:00–04:00 | 4.72 |
| 16:00–17:00 | 6.32 | 04:00–05:00 | 9.88 |
| 17:00–18:00 | 11.22 | 05:00–06:00 | 11.57 |
| Average sailing speed | 7.303 | Average sailing speed | 7.396 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Bai, X.; Liu, J. Ship Behavior Pattern Analysis Based on Graph Theory: A Case Study in Tianjin Port. J. Mar. Sci. Eng. 2023, 11, 2227. https://doi.org/10.3390/jmse11122227
Yu H, Bai X, Liu J. Ship Behavior Pattern Analysis Based on Graph Theory: A Case Study in Tianjin Port. Journal of Marine Science and Engineering. 2023; 11(12):2227. https://doi.org/10.3390/jmse11122227
Chicago/Turabian StyleYu, Hongchu, Xinyu Bai, and Jingxian Liu. 2023. "Ship Behavior Pattern Analysis Based on Graph Theory: A Case Study in Tianjin Port" Journal of Marine Science and Engineering 11, no. 12: 2227. https://doi.org/10.3390/jmse11122227
APA StyleYu, H., Bai, X., & Liu, J. (2023). Ship Behavior Pattern Analysis Based on Graph Theory: A Case Study in Tianjin Port. Journal of Marine Science and Engineering, 11(12), 2227. https://doi.org/10.3390/jmse11122227








